The Role of Adsorption Phenomena in ac Conductivity Measurements of Dielectric Nanoparticle Suspensions
Abstract
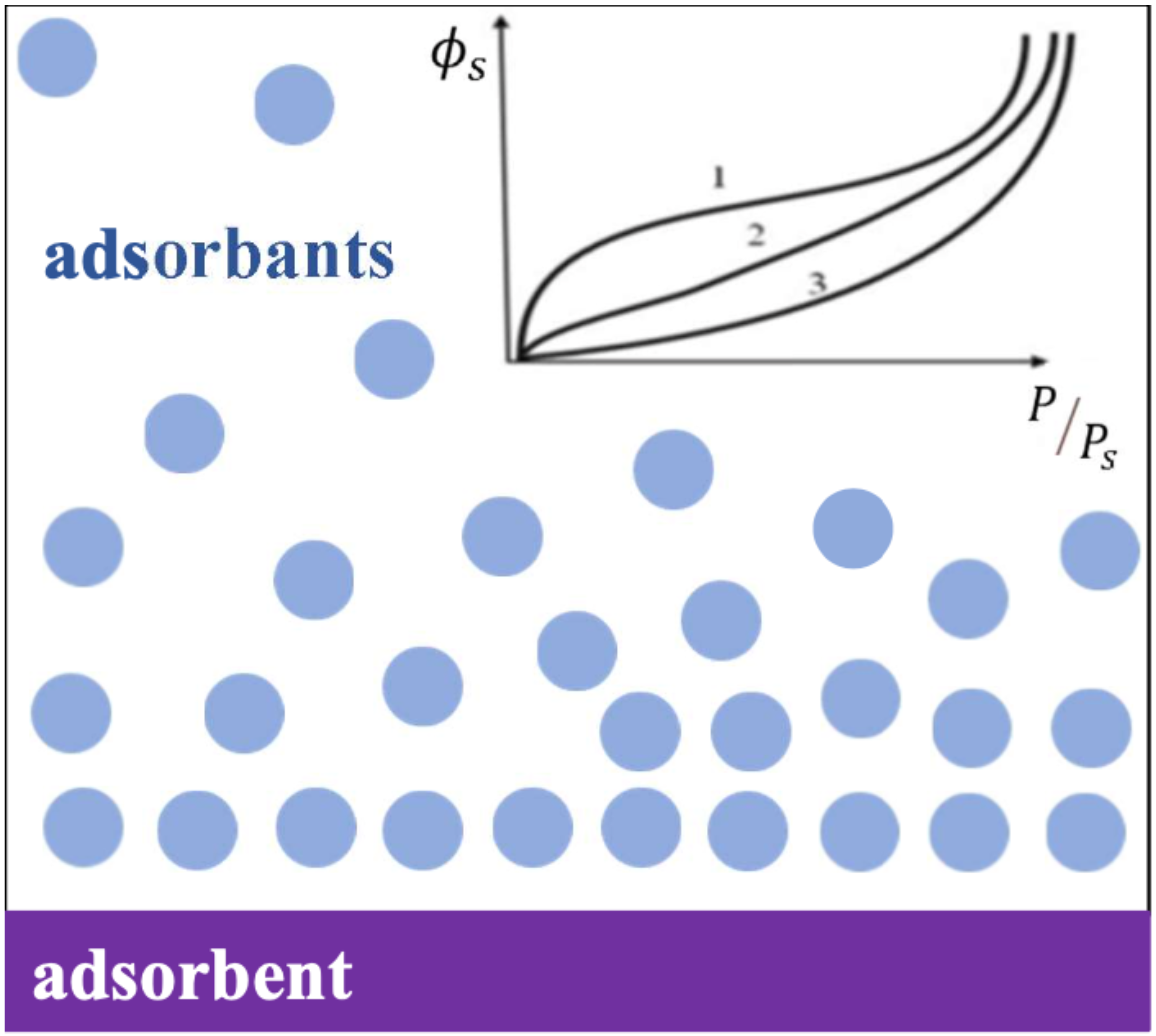
1. Introduction
2. Electrolytic Capacitance of the Boundary “Metal–Solvent”
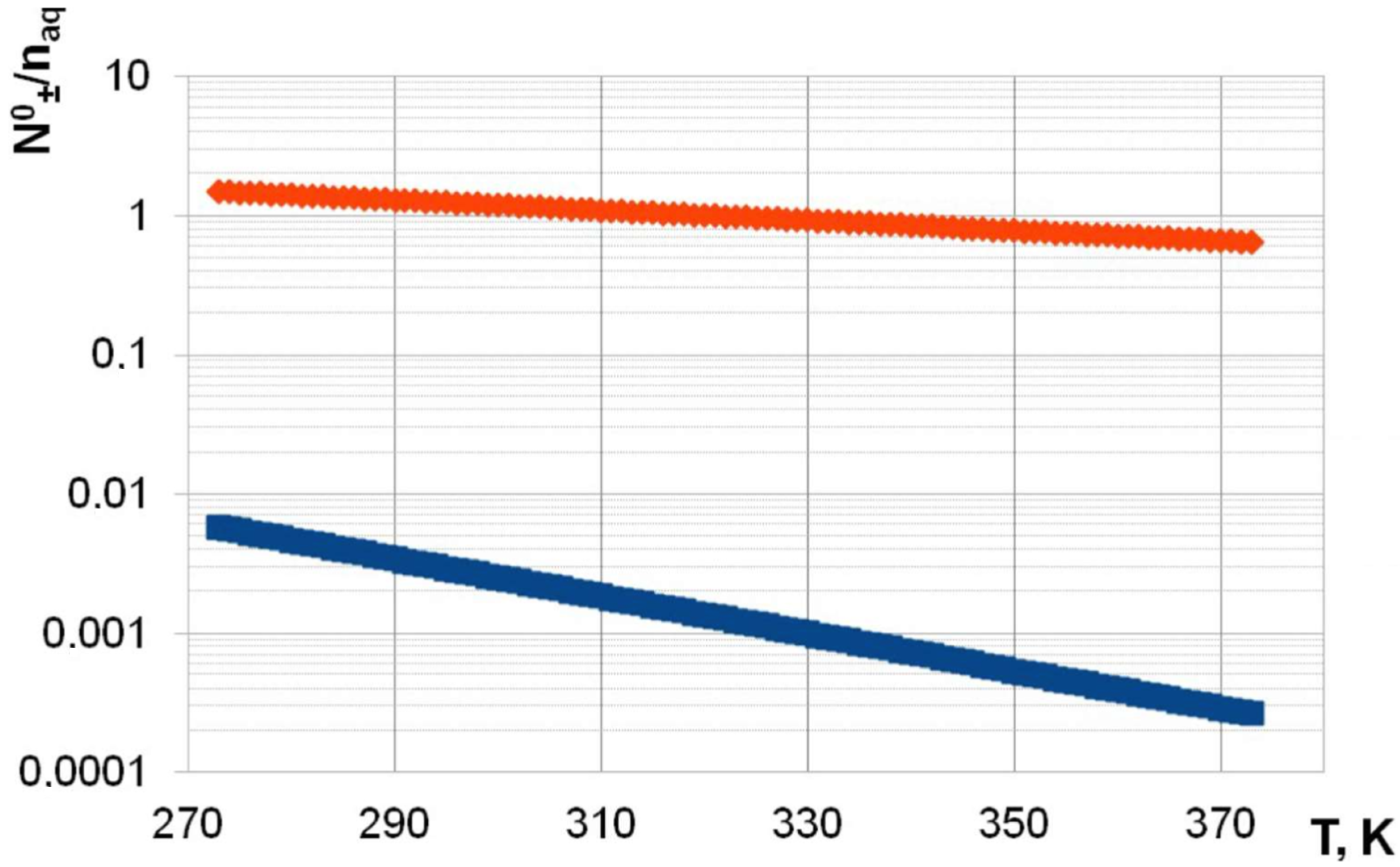
2.1. Peculiarities of Screening in the Bulk of Dilute Electrolyte
2.2. Role of the Image Forces in the Formation of a n Adsorption Layer at the “Metal–Pure Water” Interface
3. Impedance Measurements and Discrepancy of Their Results with Maxwell’s Theory
3.1. Impedance Measurements and Their Subtleties
- On the left-hand-side of Equation (24), Maxwell’s formula (1) for conductivity is used. The latter accounts for the current which occurs as the response to the electric field applied but ignores the diffusion contribution related to chemical potential gradient [25] (similar to the thermoelectric contribution, but proportional to instead of ). It is not present in Definition (1) and, as a consequence, it is not required in Equation (24).
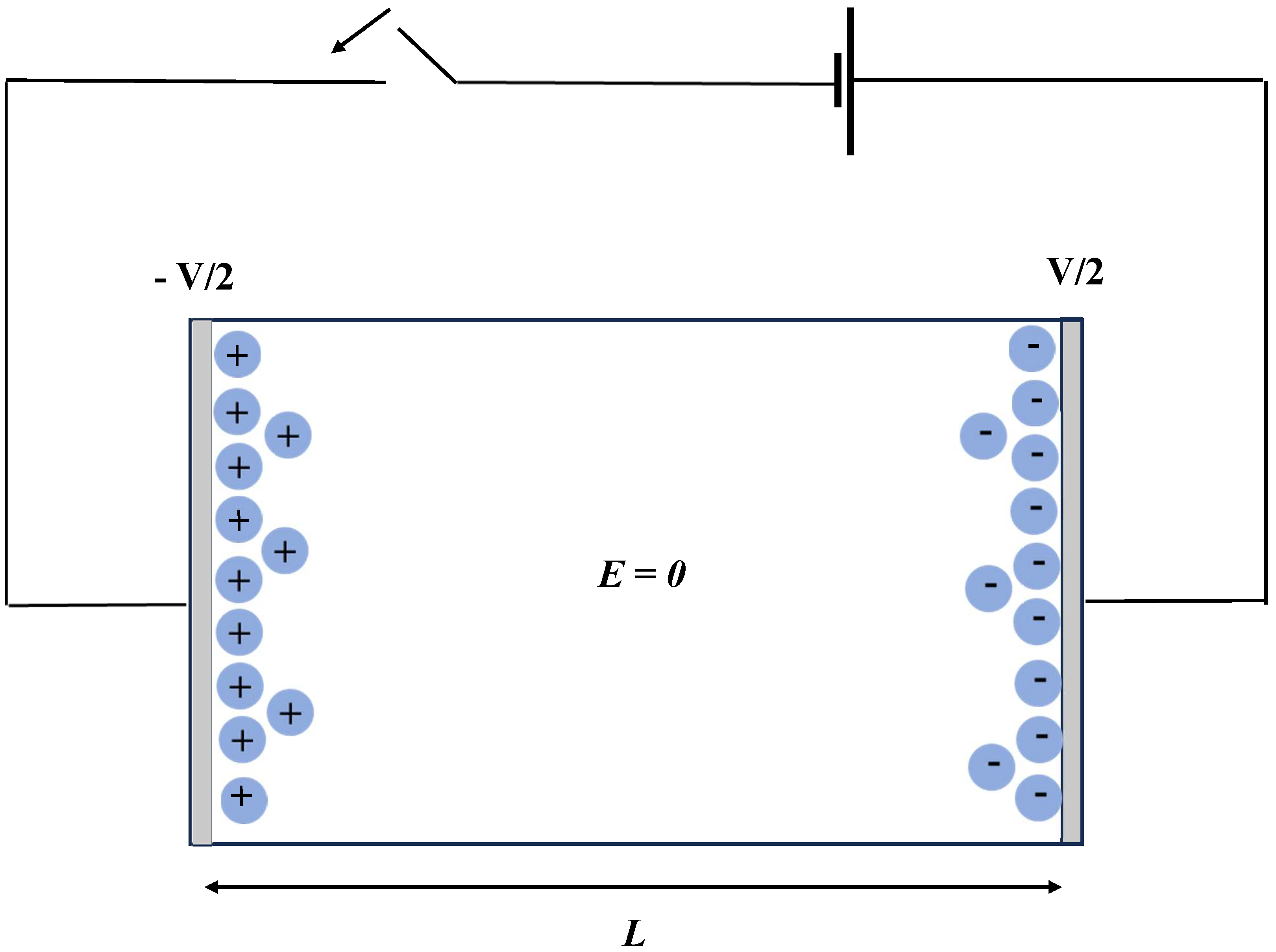
- The second term of Equation (24) also needs a comment. Different realizations of impedance circuits (Winston bridges, etc., see [9,24]) may contain a number of capacitances performing different functions in the measurement circuit. It is usually assumed that the main contribution to the capacitance, which appears in Equation (24), comes from the electrolyte-filled cell capacitance (schematically represented in Figure 4). In radio engineering, the value of such electrolytic capacitor is determined by the Debye length for the solvent (see, e.g., [24]).
- We note that capacitance is also affected by the nature of ion motion in the measuring cell volume. Therefore, the properties of the accumulation layers leading to the main dependence of the cuvette capacitance on the inclusion concentration also depend on the abovementioned current generated by the gradient of ionic chemical potentials (see, for example, [24,26]). Nevertheless, in the following discussion, in the wake of other authors, we accept the value of capacitance in its static limit using Equation (24) in the regime.
3.2. The Origin of Discrepancies
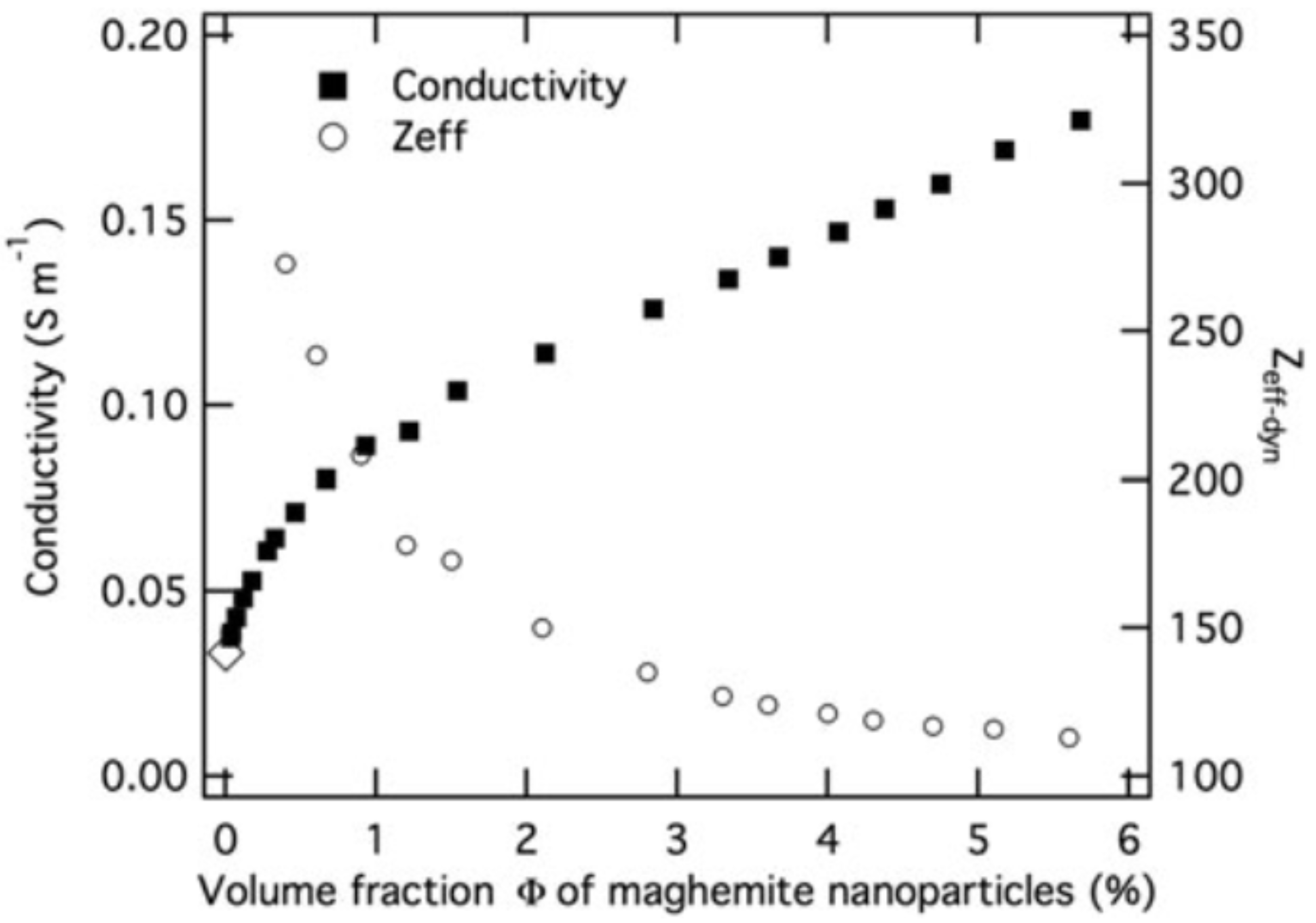
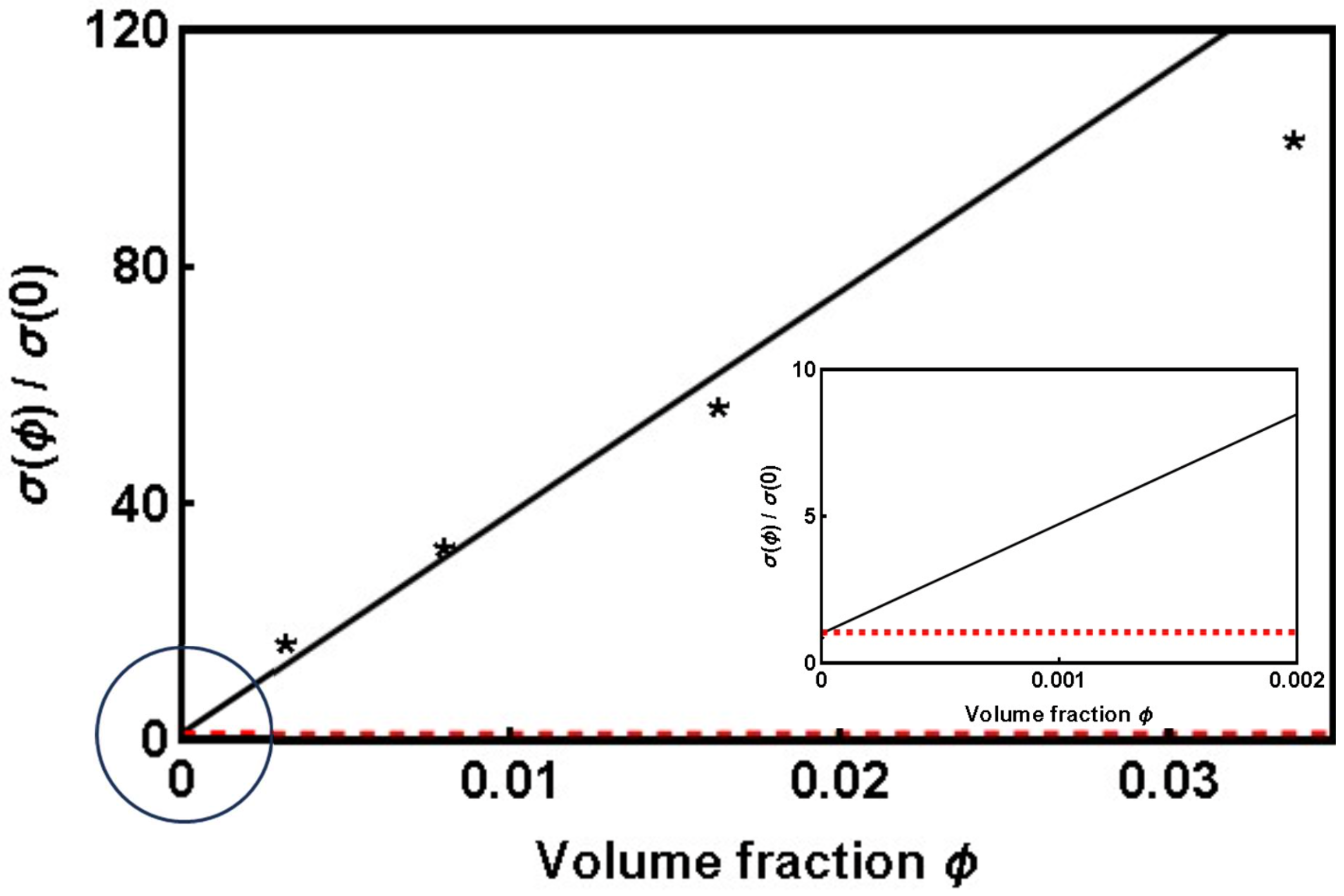
4. Analysis of the Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Minea, A. A Review on Electrical Conductivity of Nanoparticle-Enhanced Fluids. Nano Mater. 2019, 9, 1592–1613. [Google Scholar] [CrossRef] [PubMed]
- Geng, Y.; Khodadadi, H.; Karimipour, A.; Safaei, M.R.; Nguyen, T.K. A comprehensive presentation on nanoparticles electrical conductivity of nanofluids: Statistical study concerned effects of temperature, nanoparticles type and solid volume concentration. Physica A 2020, 542, 123432. [Google Scholar] [CrossRef]
- Poongavanam, G.; Duraisamy, S.; Vigneswaran, V.S.; Ramalingam, V. Review on the electrical conductivity of nanofluids: Recent developments. Mater. Today Proc. 2021, 39, 1532–1537. [Google Scholar] [CrossRef]
- Maxwell, J. A Treatise of Electricity and Magnetism, 3rd ed.; Part II; Oxford University Press: London, UK, 1892; Volume 1. [Google Scholar] [CrossRef]
- Lucas, I.T.; Durand-Vidal, S.; Bernard, O.; Dahirel, V.; Dubois, E.; Dufrêche, J.F.; Gourdin-Bertin, S.; Jardat, M.; Meriguet, G.; Roger, G. Influence of the volume fraction on the electrokinetic properties of maghemite nanoparticles in suspension. Mol. Phys. 2014, 112, 1463. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Landau, L.D. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Acta Phys. Chem. URSS 1941, 14, 633–662. [Google Scholar] [CrossRef]
- Verwey, E.; Overbeek, J. Theory of the Stability of Lyophobic Colloids; Elsevier: Amsterdam, The Netherlands, 1948. [Google Scholar]
- Heissenger, D.; Evers, M.; Palberg, T. Independent ion migration in suspensions of strongly interacting charged colloidal spheres. Phys. Rev. E 2000, 61, 5493. [Google Scholar] [CrossRef] [PubMed]
- Sommerfeld, A. Electrodynamics (Lectures on Theoretical Physics); N.Y Academic Press Inc.: New York, NY, USA, 1952; Volume 3. [Google Scholar]
- Chikina, I.; Nakamae, S.; Varlamov, A. On the ac Measurements of the Electrical Conductivity of Dilute Colloidal Electrolytes. Colloids Surfaces 2023, 7, 58. [Google Scholar] [CrossRef]
- Zyla, G.; Vallejo, J.P.; Fal, J.; Lugo, L. Nanodiamonds—Ethylene Glycol nanofluids: Experimental investigation of fundamental physical properties. Int. J. Heat Mass Transf. 2018, 121, 1201–1213. [Google Scholar] [CrossRef]
- Lewis, G.; Randall, M. Thermodynamics and the Free Energy of Chemical Substances; McGrow-Hill: New York, NY, USA; London, UK, 1923. [Google Scholar]
- Debye, P.; Hückel, E. The theory of electrolytes. I. Lowering of freezing point and related phenomena. Phys. Z. 1923, 24, 185–206. [Google Scholar]
- Shikin, V. Screening Properties of Pure Water and Dilute Aqueous Solutions. JETP Lett. 2023, 118, 343. [Google Scholar] [CrossRef]
- Robinson, R.; Stokes, R. Electrolyte Solutions; Butterworths Scientific Publications: London, UK, 1959. [Google Scholar]
- Butler, J. Ionic Equilibrium; Addison-Wesley: Reading, MS, USA, 1964. [Google Scholar]
- Levchenko, A.; Meghov-Deglin, L.; Chikina, I.; Shikin, V. Capacitance-voltage characteristics of metal-insulator-semiconductor structures (Review article). Low Temp. Phys. 2019, 45, 823. [Google Scholar] [CrossRef]
- Chikina, I. Phenomenological Statistics of Diluted Charge d Solutions. Low Temp. Phys. 2022, 48, 594–611. [Google Scholar] [CrossRef]
- Blakemore, J. Semiconductor Statistics; Pergamon Press: Oxford, UK; London, UK; New York, NY, USA; Paris, France, 1962. [Google Scholar]
- Onsager, L.; Samaras, N. The Surface Tension of Debye-Hückel Electrolytes. J. Chem. Phys. 1934, 2, 528–536. [Google Scholar] [CrossRef]
- Wagner, C. Die Oberflchenspannung verdnnter Elektrolytlsungen. Phys. Z. 1924, 25, 474–477. [Google Scholar]
- Ando, T.; Fauler, A.; Stern, F. Electronic properties of two-dimensional systems. Rev. Mod. Phys. 1982, 54, 437. [Google Scholar] [CrossRef]
- Shikin, V.; Monarcha, Y. Two-Dimensional Charged Systems in Helium; Nauka: Moscow, Russia, 1989. [Google Scholar]
- Martin, Z.B.; Thornton, K.; Ajdari, A. Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E 2004, 70, 021506. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Chikina, I.; Shikin, V. Accumulation layers in cryogenic electrolytes. Low Temp. Phys. 2020, 46, 1108–1113. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Kalpana Sarojini, K.G.; Manoj Siva, V.; Singh Pawan, K.; Pradeep, T.; Das Sarit, K. Electrical conductivity of ceramic and metallic nanofluids. Colloids Surfaces A Physicochem. Eng. Asp. 2013, 417, 39–46. [Google Scholar] [CrossRef]

| ND97-EG | ND87-EG | |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chikina, I.; Varlamov, A. The Role of Adsorption Phenomena in ac Conductivity Measurements of Dielectric Nanoparticle Suspensions. Colloids Interfaces 2024, 8, 34. https://doi.org/10.3390/colloids8030034
Chikina I, Varlamov A. The Role of Adsorption Phenomena in ac Conductivity Measurements of Dielectric Nanoparticle Suspensions. Colloids and Interfaces. 2024; 8(3):34. https://doi.org/10.3390/colloids8030034
Chicago/Turabian StyleChikina, Ioulia, and Andrey Varlamov. 2024. "The Role of Adsorption Phenomena in ac Conductivity Measurements of Dielectric Nanoparticle Suspensions" Colloids and Interfaces 8, no. 3: 34. https://doi.org/10.3390/colloids8030034
APA StyleChikina, I., & Varlamov, A. (2024). The Role of Adsorption Phenomena in ac Conductivity Measurements of Dielectric Nanoparticle Suspensions. Colloids and Interfaces, 8(3), 34. https://doi.org/10.3390/colloids8030034






