Rheological Behaviors and Fractional Viscoelastic Modeling of Glucopone (APG)/Water/Hydrocarbons Solutions
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Rheometer
3. Results and Discussions
3.1. Phase Diagram
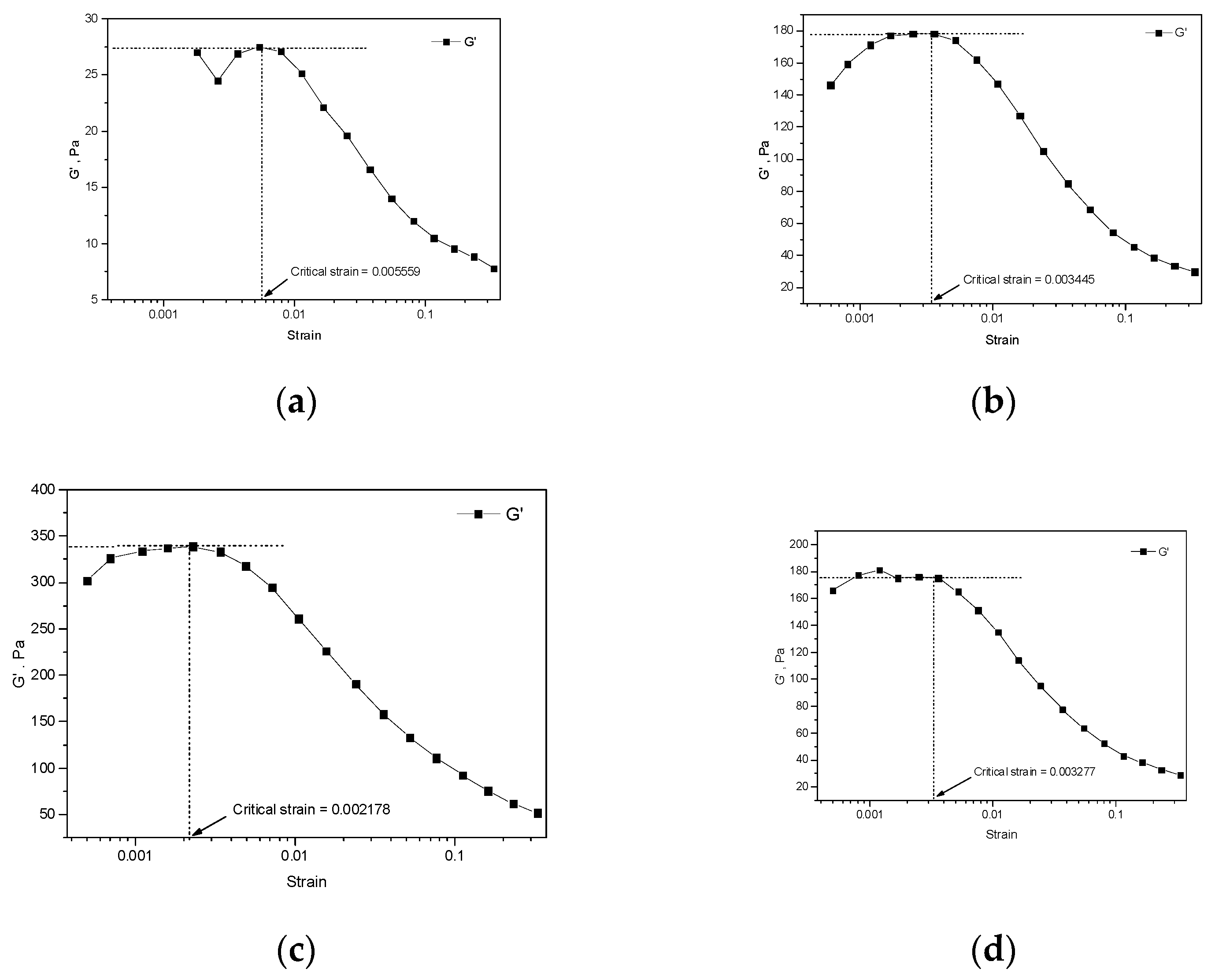
3.2. Strain Sweep
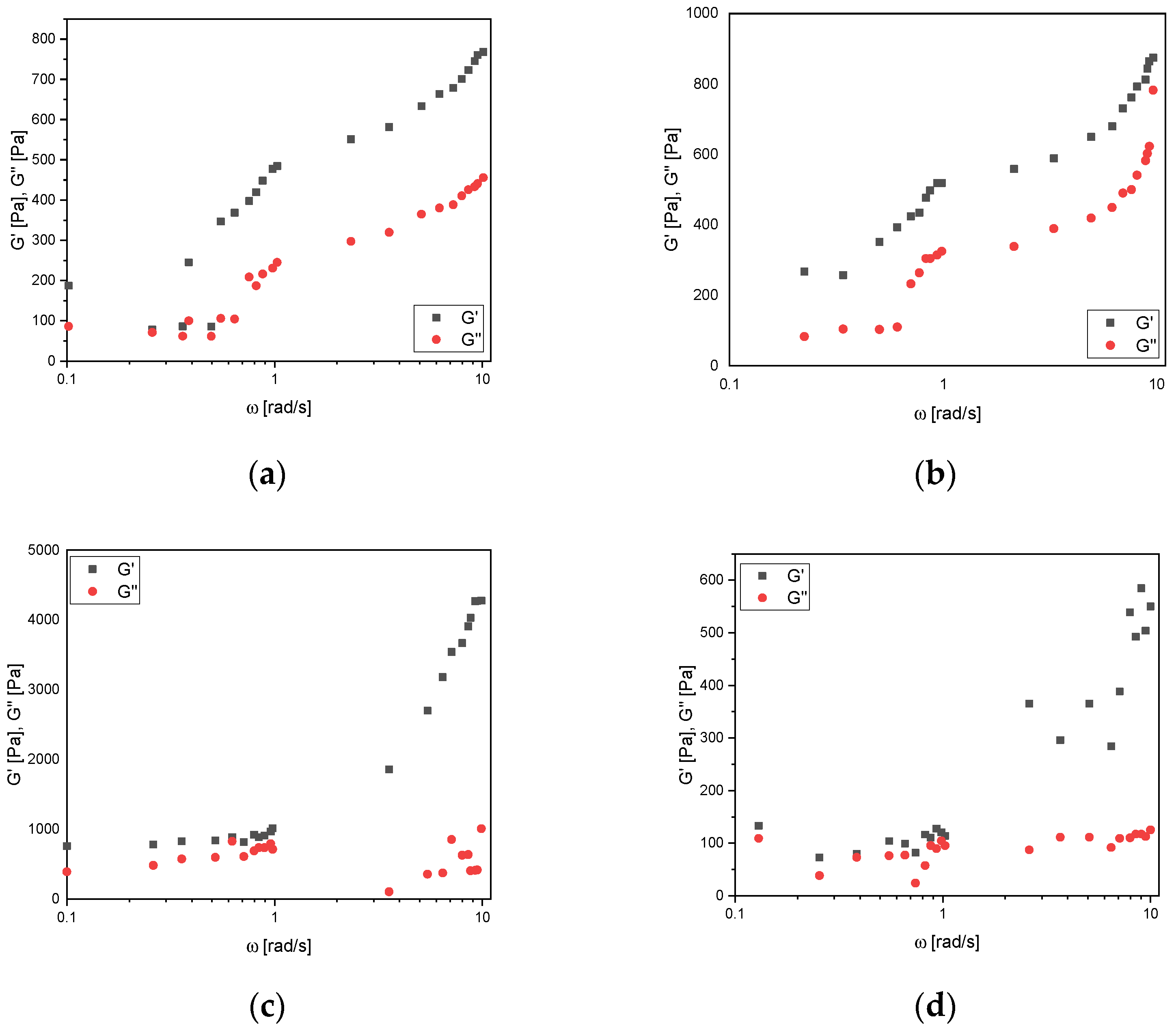
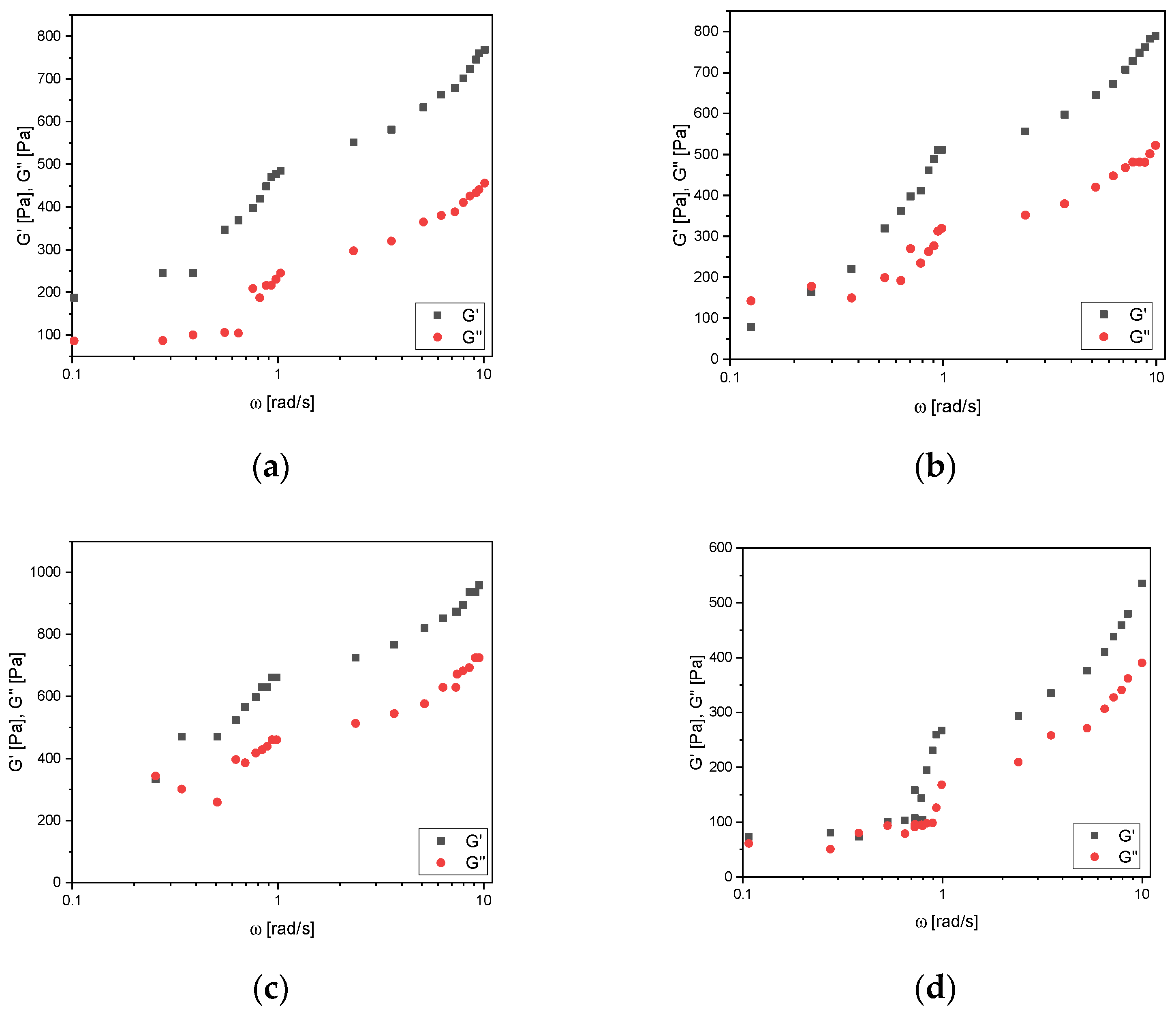
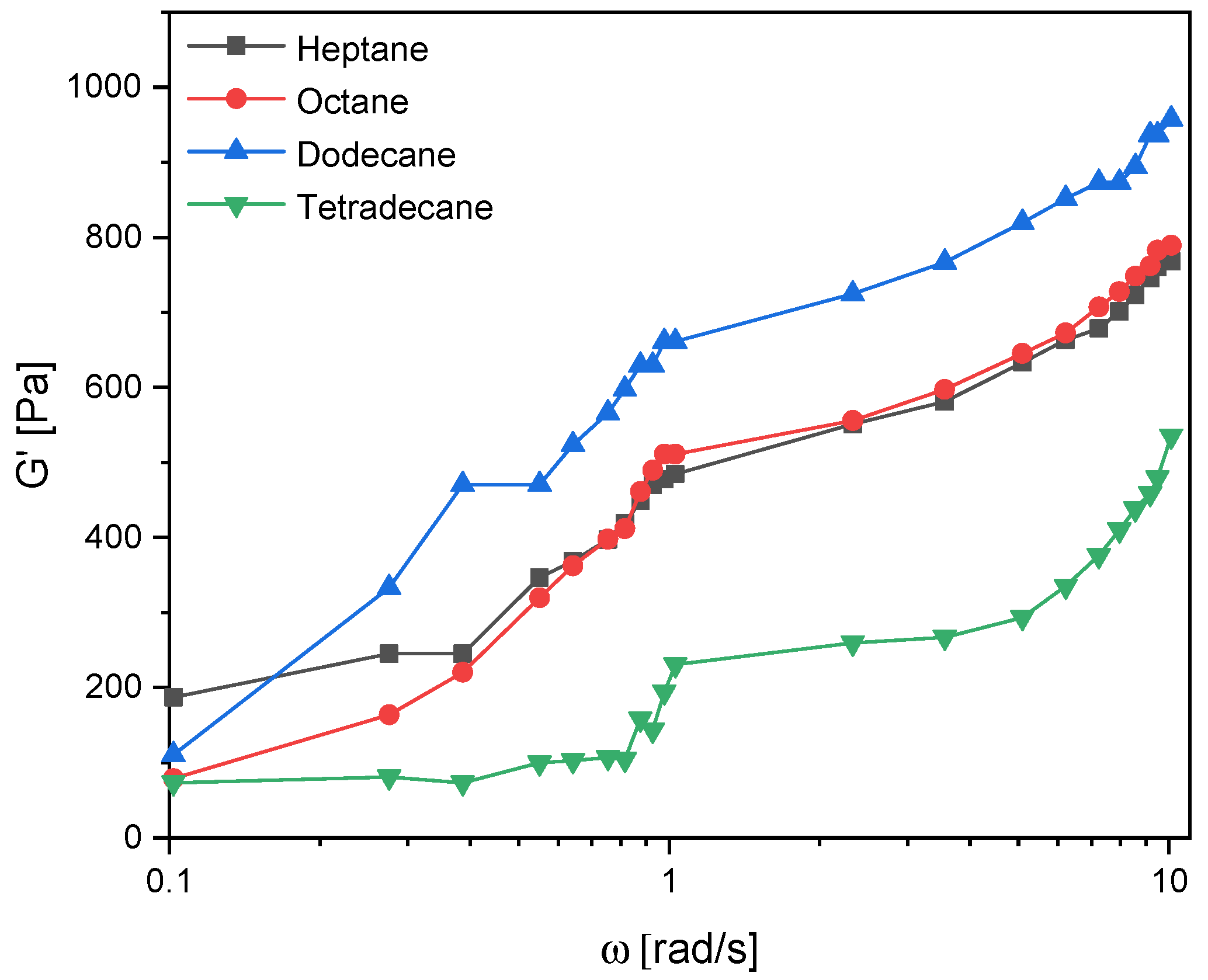
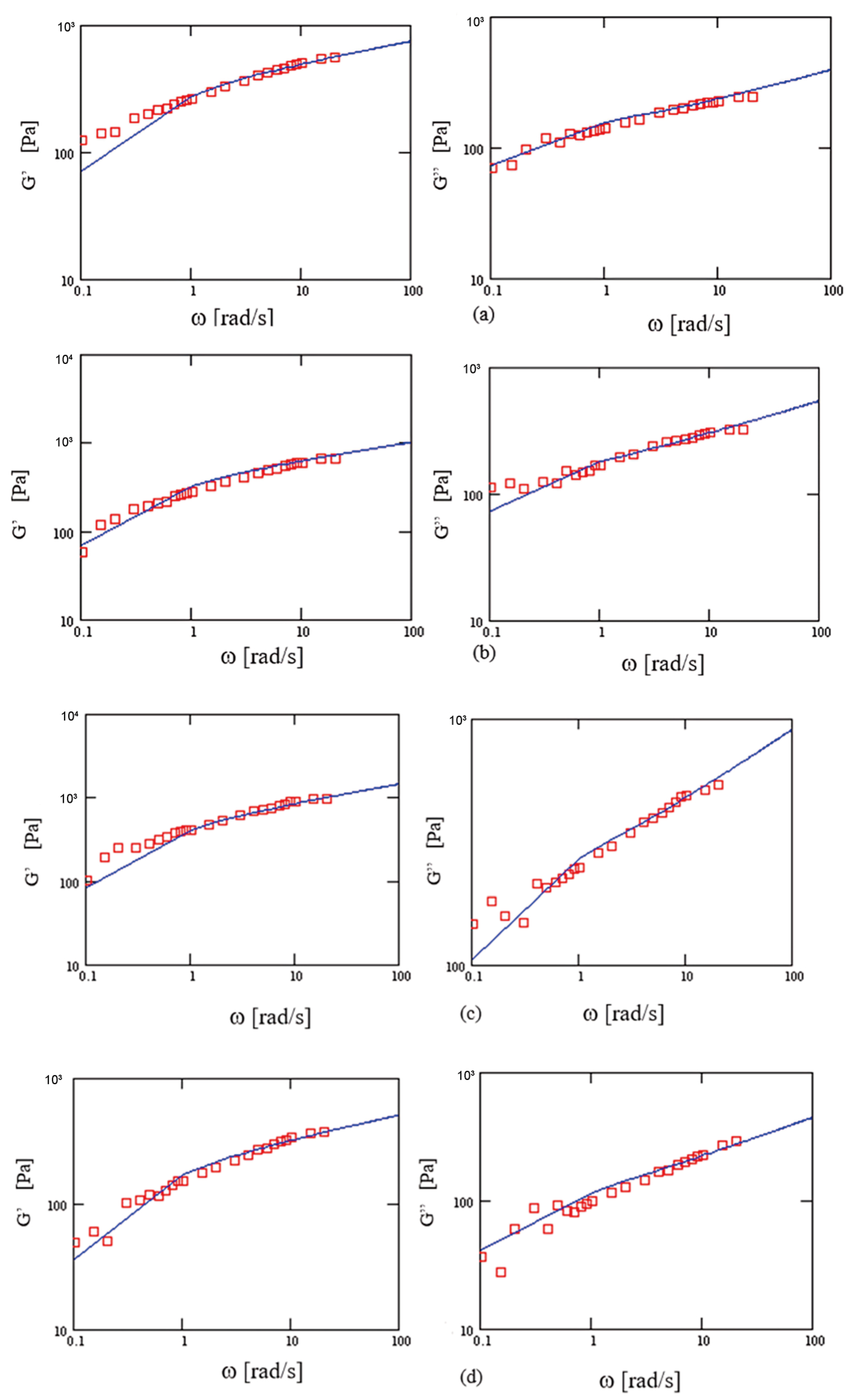
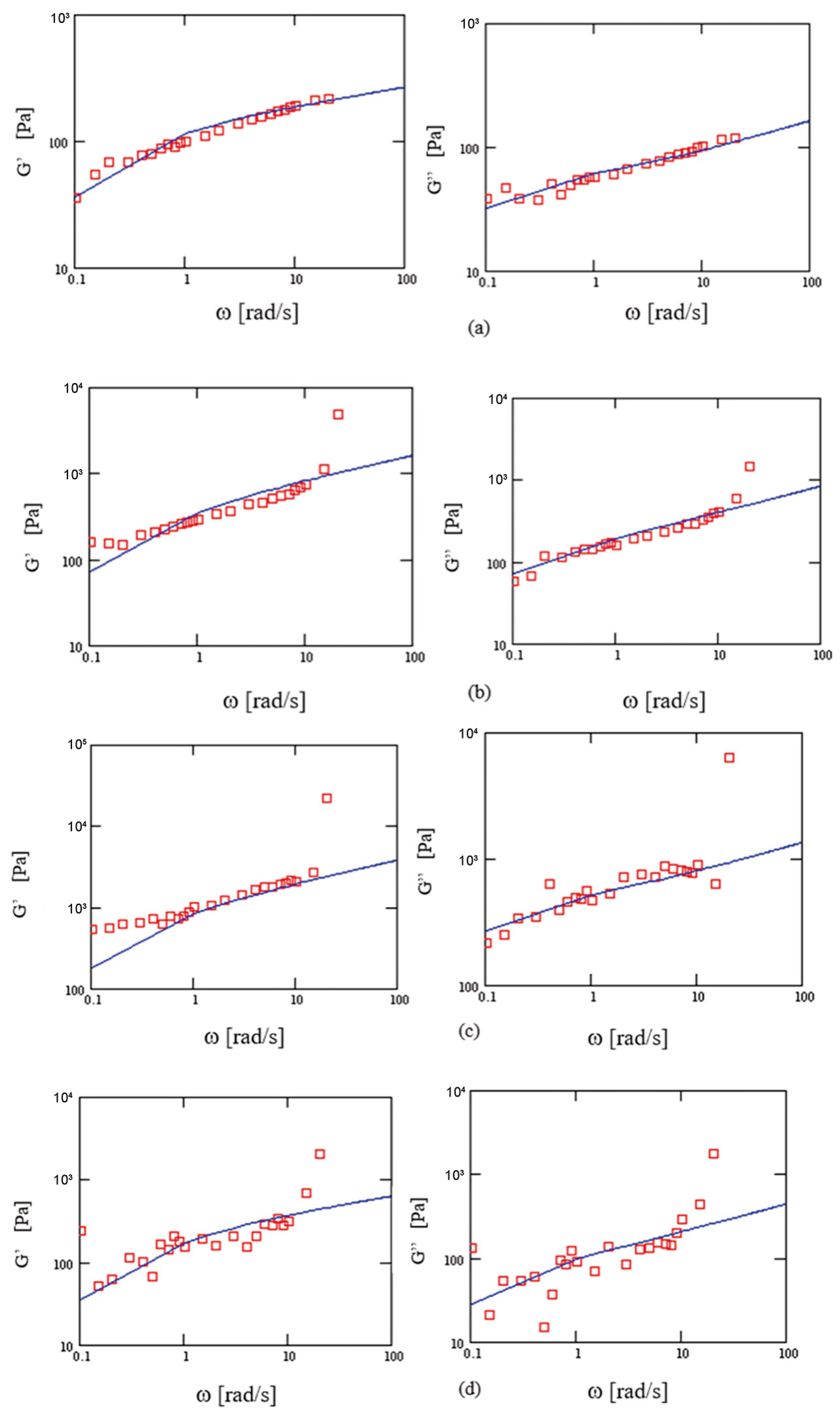
3.3. Frequency Sweep
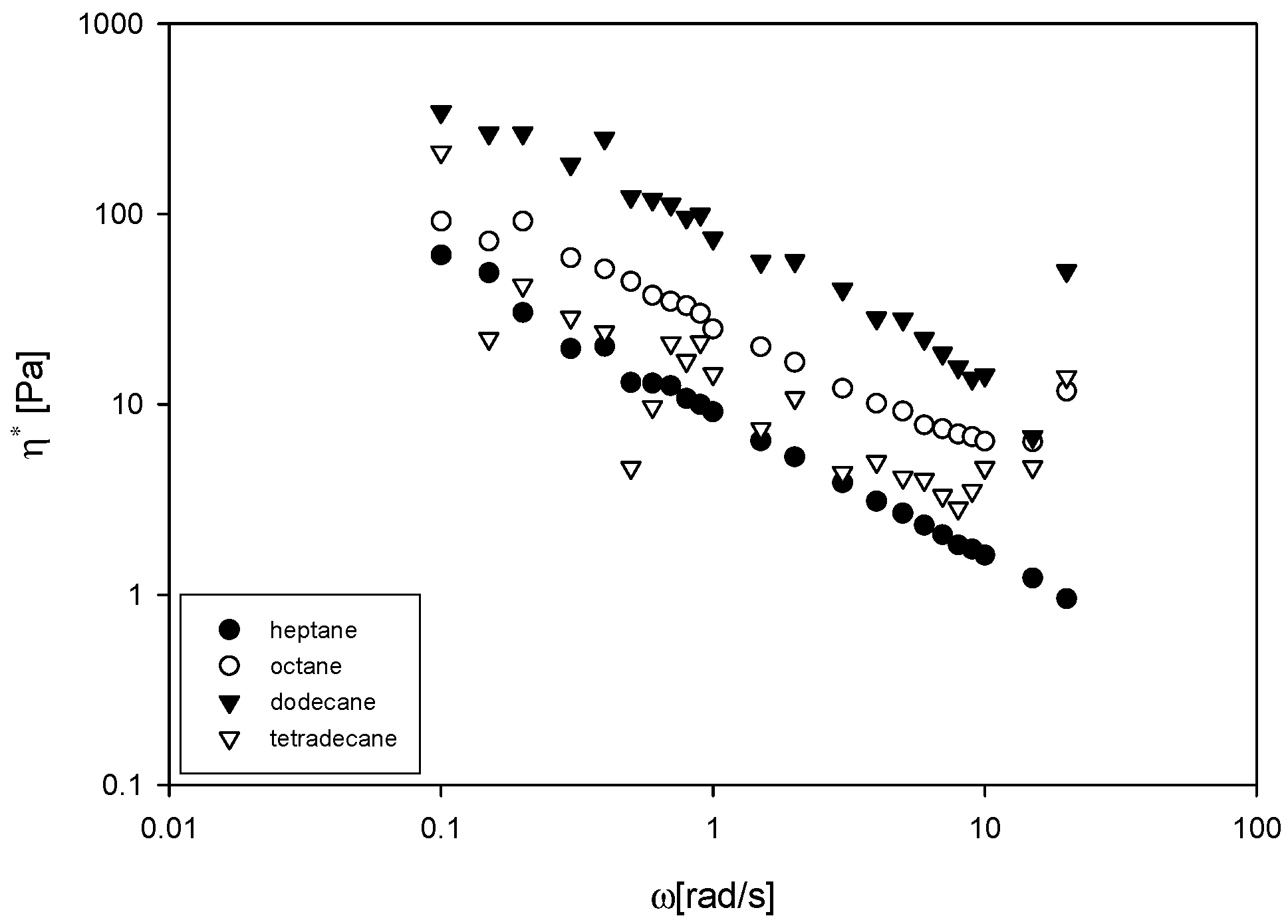
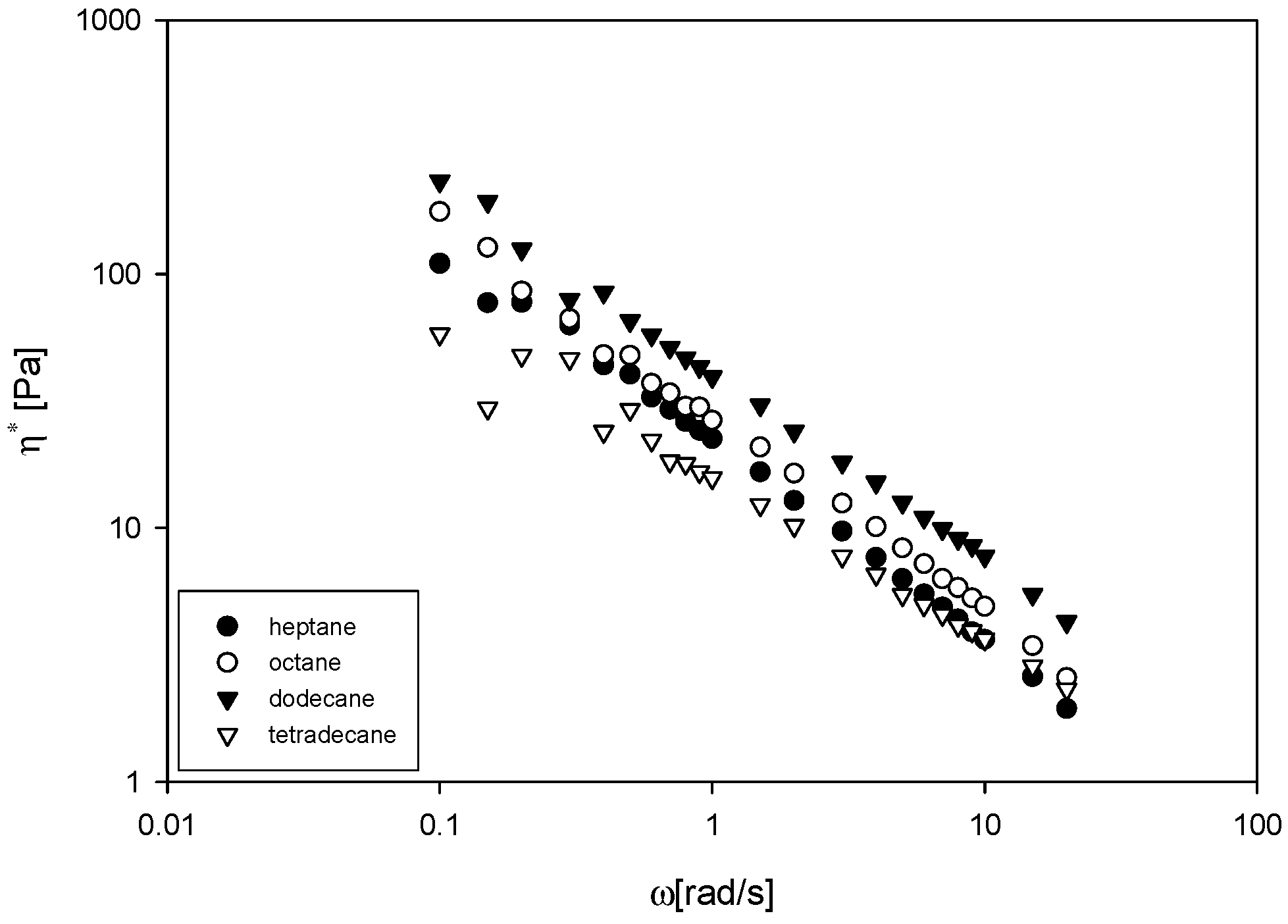
3.4. Complex Viscosity
4. Fractional Modeling
4.1. Friedrich–Braun Model
4.2. Modeling the Viscoelastic Solutions
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mahboob, A.; Kalam, S.; Kamal, M.S.; Hussain, S.S.; Solling, T. EOR Perspective of microemulsions: A review. J. Petrol. Sci. Eng. 2022, 208, 109312. [Google Scholar] [CrossRef]
- Ramos, D.M.; Sadtler, V.; Marchal, P.; Lemaitre, C.; Niepceron, F.; Benyahia, L.; Roques-Carmes, T. Particles’ Organization in Direct Oil-in-Water and Reverse Water-in-Oil Pickering Emulsions. Nanomaterials 2023, 13, 371. [Google Scholar] [CrossRef] [PubMed]
- Qu, J.; Wan, Y.; Tian, M.; Lv, W. Microemulsions Based on Diverse Surfactant Molecular Structure: Comparative Analysis and Mechanistic Study. Processes 2023, 11, 3409. [Google Scholar] [CrossRef]
- Hua, G. Review of the Microemulsion Flooding to Enhanced Oil Recovery. Shandong Chem. Ind. 2016, 9, 63–65. [Google Scholar]
- Wu, B.; Yang, C.; Xin, Q.; Kong, L.; Eggersdorfer, M.; Ruan, J.; Zhao, P.; Shan, J.; Liu, K.; Chen, D.; et al. Attractive Pickering Emulsion Gels. Adv. Mater. 2021, 33, 2102362. [Google Scholar] [CrossRef] [PubMed]
- Dai, X.; Zhang, J.; Bao, X.; Guo, Y.; Jin, Y.; Yang, C.; Zhang, H.; Liu, L.; Gao, Y.; Ye, C.; et al. Induction of Tumor Ferroptosis-Dependent Immunity via an Injectable Attractive Pickering Emulsion Gel. Adv. Mater. 2023, 35, e2303542. [Google Scholar] [CrossRef] [PubMed]
- Hematpur, H.; Abdollahi, R.; Safari-Beidokhti, M.; Esfandyari, H.; Yazdi, M. Experimental Microemulsion Flooding Study to Increase Low Viscosity Oil Recovery Using Glass Micromodel. Math. Probl. Eng. 2021, 2021, 5021868. [Google Scholar] [CrossRef]
- Siddig, M.A.; Radiman, S.; Jan, L.S.; Muniandy, S.V. Structure of cubic phases in ternary systems Glucopone/water/hydrocarbon. Colloids Surf. A Physicochem. Eng. Asp. 2004, 236, 57. [Google Scholar] [CrossRef]
- Veronico, L.; Colafemmina, G.; Gentile, L. Enhancing Oil-Uptake Efficiency with an Alkyl Polyglycoside–Dodecanol Formulation. Colloids Interfaces 2024, 8, 6. [Google Scholar] [CrossRef]
- Larry, D.R.; Kaler, E.W. Alkyl polyglucoside microemulsion phase behavior. Colloids Surf. A Physicochem. Eng. Asp. 2001, 176, 69. [Google Scholar]
- Ferrer, M.; Comelles, F.; Plou, F.J. Comparative surface activities of di-and trisaccharide fatty acid esters. Langmuir 2002, 18, 667. [Google Scholar] [CrossRef]
- Meral, F.C.; Royston, T.J.; Magin, R. Fractional calculus in viscoelasticity: An experimental study. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 939. [Google Scholar] [CrossRef]
- Caputo, M. Vibrations of an infinite viscoelastic layer with a dissipative memory. J. Acoust. Soc. Am. 1974, 56, 897–904. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. Fractional and Multivariable Calculus, Model Building and Optimization Problems; Springer International Publishing AG: Cham, Switzerland, 2017. [Google Scholar]
- Dalir, M.; Bashour, M. Applications of fractional calculus. Appl. Math. Sci. 2010, 4, 1021. [Google Scholar]
- Hilton, H.H. Generalized fractional derivative anisotropic viscoelastic characterization. Materials 2012, 5, 169. [Google Scholar] [CrossRef]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods, 2nd ed.; World Scientific Publishing: London, UK, 2017. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201. [Google Scholar] [CrossRef]
- Schiessel, H.; Blumen, A. Hierarchical analogues to fractional relaxation equations. J. Phys. A Math. Gen. 1993, 26, 5057. [Google Scholar] [CrossRef]
- Siddig, M.A.; Radiman, S.; Jan, L.S.; Muniandy, S.V. Rheological behaviours of the hexagonal and lamellar phases of glucopone (APG) surfactant. Colloids Surf. A Physicochem. Eng. Asp. 2006, 276, 15. [Google Scholar] [CrossRef]
- Scomoroscenco, C.; Teodorescu, M.; Nistor, C.L.; Gifu, I.C.; Petcu, C.; Banciu, D.D.; Banciu, A.; Cinteza, L.O. Preparation and In Vitro Characterization of Alkyl Polyglucoside-Based Microemulsion for Topical Administration of Curcumin. Pharmaceutics 2023, 15, 1420. [Google Scholar] [CrossRef]
- Abd Sisak, M.A.; Daik, R.; Ramli, S. Study on the effect of oil phase and co-surfactant on microemulsion systems. Malays. J. Anal. Sci. 2017, 21, 1409–1416. [Google Scholar]
- Torres, L.G.; Iturbe, R.; Snowden, M.J.; Chowdhry, B.Z.; Leharne, S.A. Preparation of o/w emulsions stabilized by solid particles and their characterization by oscillatory rheology. Colloids Surf. A Physicochem. Eng. Asp. 2007, 302, 439–448. [Google Scholar] [CrossRef]
- Numin, M.S.; Jumbri, K.; Ramli, A.; Borhan, N. Microemulsion Rheological Analysis of Alkaline, Surfactant, and Polymer in Oil-Water Interface. Processes 2020, 8, 762. [Google Scholar] [CrossRef]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional viscoelastic models for power-law Materials. Soft Matter 2020, 16, 6002–6020. [Google Scholar] [CrossRef] [PubMed]
- Bagley, R.L. Power law and fractional calculus model of viscoelasticity. AIAA J. 1989, 27, 1412. [Google Scholar] [CrossRef]
- Friedrich, C. Rheological material functions for associating comb-shaped or H-shaped polymers A fractional calculus approach. Phil. Mag. Lett. 1992, 66, 287. [Google Scholar] [CrossRef]
- Friedrich, C.; Braun, H.; Weese, J. Determination of relaxation time spectra by analytical inversion using a linear viscoelastic model with fractional derivatives. J. Polym. Eng. Sci. 1995, 35, 1661. [Google Scholar] [CrossRef]
- Carrera, Y.; Avila-de la Rosa, G.; Vernon-Carter, E.J.; Alvarez-Ramirez, J. A fractional-order Maxwell model for non-Newtonian fluids. Phys. A 2017, 482, 276–285. [Google Scholar] [CrossRef]
- Ramirez-Brewer, D.; Danilo Montoya, O.; Useche Vivero, J.; García-Zapateiro, L. Characterization and Modeling of the Viscoelastic Behavior of Hydrocolloid-Based Films Using Classical and Fractional Rheological Models. Fluids 2021, 6, 418. [Google Scholar] [CrossRef]
- Rathinaraj, J.D.J.; McKinley, G.H.; Keshavarz, B. Incorporating Rheological Nonlinearity into Fractional Calculus Descriptions of Fractal Matter and Multi-Scale Complex Fluids. Fractal Fract. 2021, 5, 174. [Google Scholar] [CrossRef]
- Hoffman, H.; Ebert, G. Surfactants, micelles and fascinating phenomena. Angew. Chem. Int. Ed. Engl. 1988, 27, 902. [Google Scholar] [CrossRef]
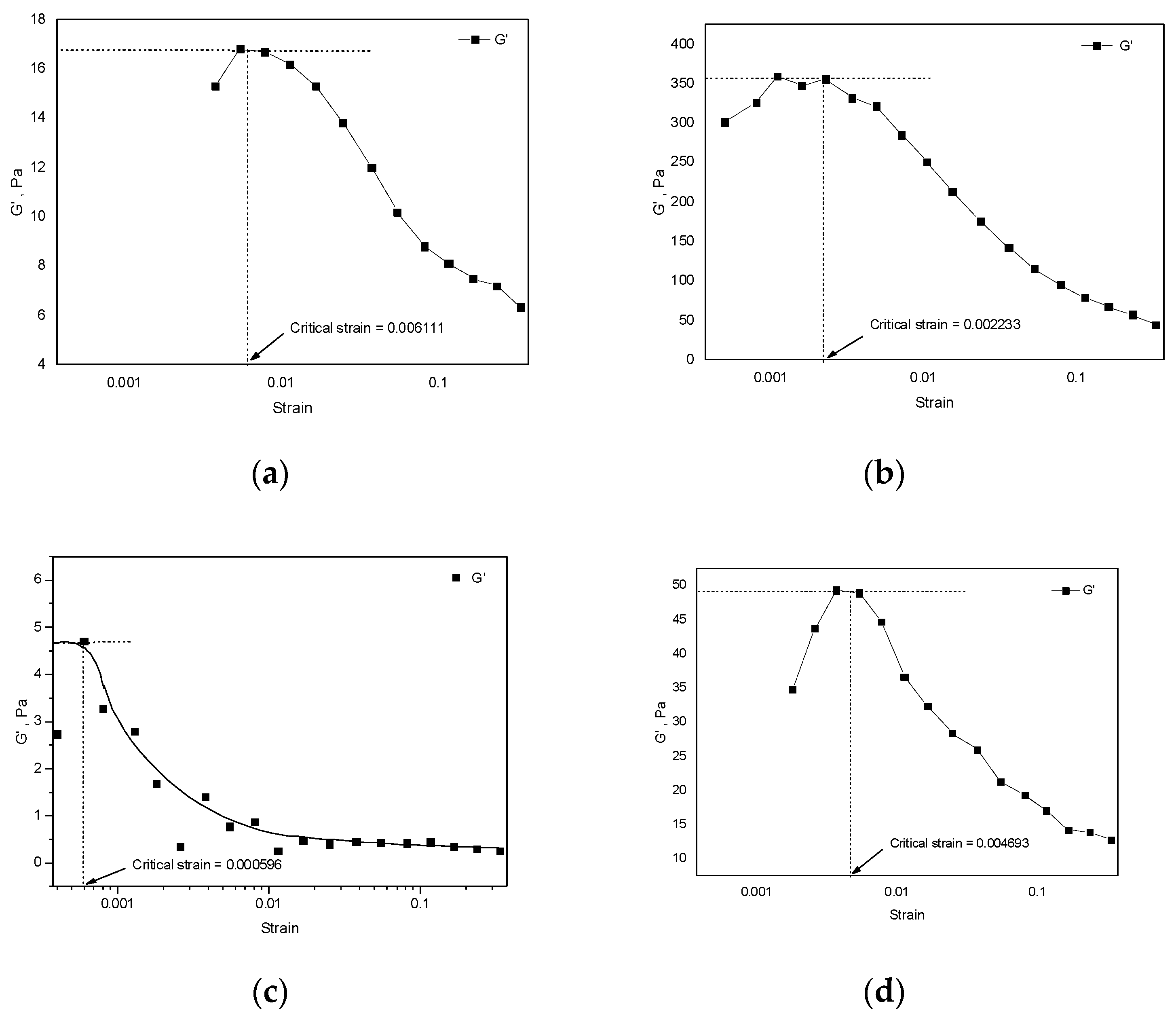


| Composition | Glucopone % | Hydrocarbon % | Water % |
|---|---|---|---|
| 1 | 45.00 | 4.60 | 50.40 |
| 2 | 55.00 | 4.60 | 40.40 |
| Composition 1 | Composition 2 | |||
|---|---|---|---|---|
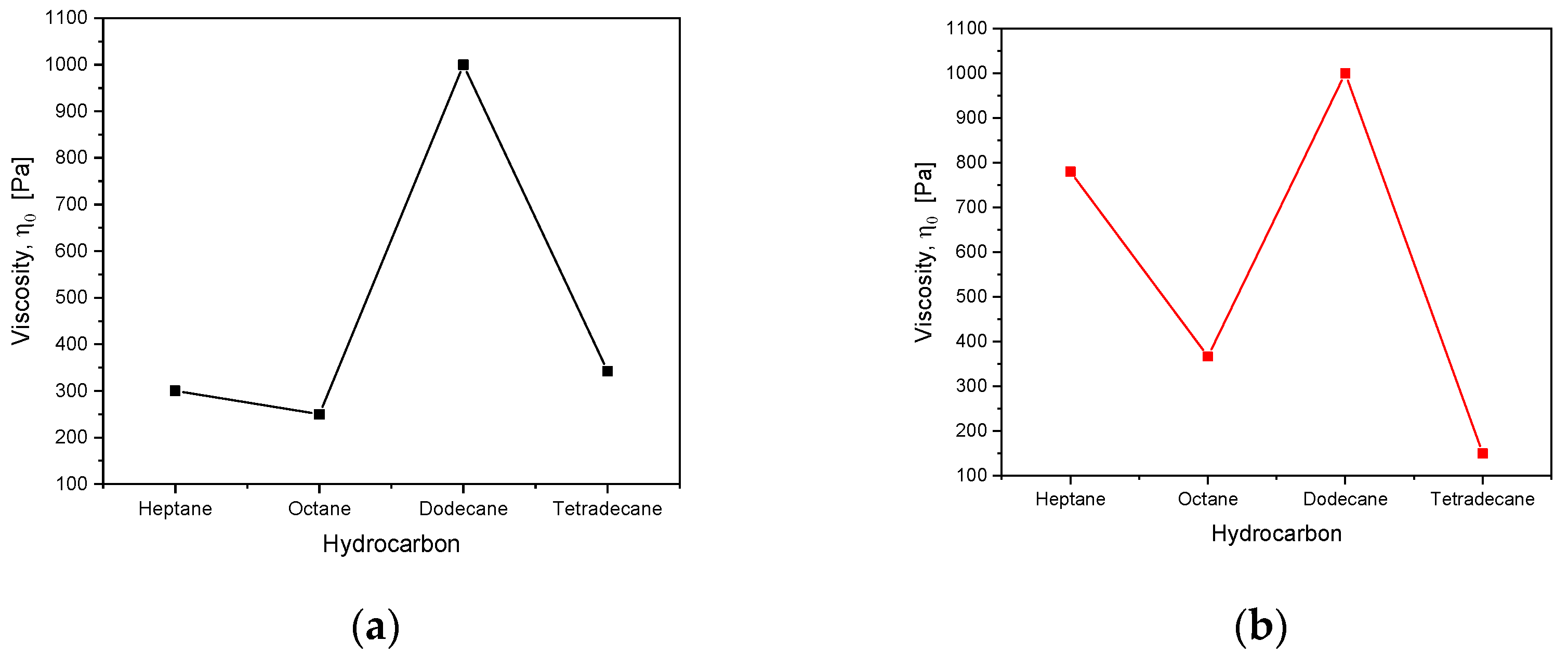
| Oil Type | Relaxation Time, τ/s | Viscosity, η0 Pa | Relaxation Time, τ/s | Viscosity, η0 Pa |
| Heptane | 5.00 | 300.00 ± 3.6 | 1.26 | 780.00 ± 8.4 |
| Octane | 2.50 | 250.00 ± 2.7 | 3.33 | 366.30 ± 6.3 |
| Dodecane | 2.00 | 1000.00 ± 8.3 | 5.00 | 1000.00 ± 11.8 |
| Tetradecane | 1.71 | 342.00 ± 3.8 | 1.66 | 149.40 ± 2.4 |
| Heptane | Octane | Dodecane | Tetradecane | |||||
|---|---|---|---|---|---|---|---|---|
| Parameter | G′ | G″ | G′ | G″ | G′ | G″ | G′ | G″ |
| ΔG [Pa] | 260 | 260 | 300 | 300 | 380 | 380 | 160 | 160 |
| λ [s] | 5.38 | 5.38 | 2.81 | 2.81 | 2.89 | 2.89 | 1.71 | 1.71 |
| q | 0.72 | 0.66 | 0.72 | 0.64 | 0.71 | 0.68 | 0.74 | 0.64 |
| μ | 0.89 | 0.91 | 0.93 | 0.98 | 0.93 | 0.98 | 0.93 | 0.96 |
| Heptane | Octane | Dodecane | Tetradecane | |||||
|---|---|---|---|---|---|---|---|---|
| Parameter | G′ | G″ | G′ | G″ | G′ | G″ | G′ | G″ |
| ΔG [Pa] | 100 | 100 | 280 | 280 | 640 | 640 | 190 | 190 |
| λ [s] | 7.53 | 7.53 | 4.64 | 4.64 | 5.53 | 5.53 | 2.2 | 2.2 |
| q | 0.73 | 0.72 | 0.66 | 0.64 | 0.67 | 0.66 | 0.65 | 0.63 |
| μ | 0.88 | 0.98 | 0.94 | 0.97 | 0.95 | 0.91 | 0.86 | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddig, M.A. Rheological Behaviors and Fractional Viscoelastic Modeling of Glucopone (APG)/Water/Hydrocarbons Solutions. Colloids Interfaces 2024, 8, 27. https://doi.org/10.3390/colloids8030027
Siddig MA. Rheological Behaviors and Fractional Viscoelastic Modeling of Glucopone (APG)/Water/Hydrocarbons Solutions. Colloids and Interfaces. 2024; 8(3):27. https://doi.org/10.3390/colloids8030027
Chicago/Turabian StyleSiddig, Mohamed A. 2024. "Rheological Behaviors and Fractional Viscoelastic Modeling of Glucopone (APG)/Water/Hydrocarbons Solutions" Colloids and Interfaces 8, no. 3: 27. https://doi.org/10.3390/colloids8030027
APA StyleSiddig, M. A. (2024). Rheological Behaviors and Fractional Viscoelastic Modeling of Glucopone (APG)/Water/Hydrocarbons Solutions. Colloids and Interfaces, 8(3), 27. https://doi.org/10.3390/colloids8030027





