Start-Up Rotation of a Porous Colloidal Sphere in a Cavity

Abstract

The starting rotation of a porous sphere induced by the sudden application of a continuous torque about its diameter at the center of a spherical cavity filled with an incompressible Newtonian fluid at low Reynolds numbers is analyzed. The unsteady Stokes and Brinkman equations governing the fluid velocities outside and inside the porous particle, respectively, are solved via the Laplace transform, and an explicit formula of its dynamic angular velocity as a function of the pertinent parameters is obtained. The behavior of the start-up rotation of an isolated porous particle and the cavity wall effect on the particle rotation are interesting. The angular velocity of the particle grows incessantly over time from an initial zero to its final value, while the angular acceleration declines with time continuously. In general, the transient angular velocity is an increasing function of the porosity of the particle. A porous sphere with higher fluid permeability rotates at higher angular velocity and acceleration relative to the reference particle at any elapsed time but lags behind the reference particle in the percentage growth of angular velocity towards the respective terminal values. The transient angular velocity decreases with increasing particle-to-cavity radius ratio, but it is not a sensitive function of the radius ratio when the resistance to fluid flow inside the porous particle or the radius ratio itself is small.

1. Introduction

The translation and rotation of solid particles in viscous fluids at low Reynolds numbers play important roles in a variety of technological and industrial processes such as sedimentation, centrifugation, agglomeration, microfluidics, suspension rheology, aerosol technology, and the motion of blood cells in arteries and veins. The analytical study of this topic grew out of the classic work of Stokes [1,2] on the steady motion of an isolated hard sphere in an incompressible Newtonian fluid.

Some small particles are porous, viz. permeable to fluids, such as macromolecules and flocs of fine particles. The translational and rotational motions of porous particles have been extensively studied for decades. An approach which comprises a second-order viscous term to Darcy’s equation for fluid flow through porous media was established by Brinkman [3]. Neale et al. [4] analyzed the translation of a porous sphere by using the Brinkman equation for the internal flow and the Stokes equation for the external flow with appropriate boundary conditions on the particle surface and the assumption that the effective viscosity inside the porous sphere equals the bulk fluid viscosity. Matsumoto and Suganuma [5] and Masliyah and Polikar [6] experimentally investigated the sedimentation of porous particles, the results of which agree well with the analytical formula obtained by Neale et al. [4].

The angular velocity of a porous sphere of radius $a$ rotating under an applied torque $T_{\mathrm{A}}$ about its diameter in an unbounded fluid of viscosity $\eta$ at the steady state of low Reynolds numbers has been obtained by solving the Brinkman and Stokes equations, with the result [7]

$${\Omega }_{\infty }=\frac{T_{\mathrm{A}}}{8\pi \eta a^3\omega },$$

(1)

$$\omega =1+\frac{3}{{(\lambda a)}^2}-\frac{3}{\lambda a}\coth (\lambda a),$$

(2)

where ${\lambda }^{-1}$ is the flow penetration length of the porous particle. In the limits $\lambda a=0$ (fully permeable in the porous particle) and $\lambda a\to \infty$ (impermeable), Equation (1) results in ${\Omega }_{\infty }\to \infty$ ($\omega =0$) and ${\Omega }_{\infty }=T_{\mathrm{A}}/8\pi \eta a^3$ ($\omega =1$, Stokes’ result for a hard sphere), respectively.

Particles move in bounded fluids in real situations, so it is important to know whether the proximity of a boundary affects the rotation of particles significantly [8,9,10,11,12,13]. In the operation of rotational viscometers and stirred vessels for high-viscosity liquids, it is necessary to determine the relationship between angular velocity and torque as the confining boundary is approached. The steady low-Reynolds-number rotation of a porous sphere about its diameter at the center of a spherical cavity was analytically studied, with the particle’s angular velocity given by [7,14]

$${\Omega }_{\infty }=\frac{T_{\mathrm{A}}}{8\pi \eta a^3\omega }(1-\frac{a^3}{b^3}\omega ),$$

(3)

where $b$ is the radius of the cavity. When $a/b=0$, the previous equation becomes Equation (1). Recently, the rotational motions of a porous sphere about its diameter at low Reynolds numbers within an approximate or eccentric spherical cavity [15,16,17,18] and near other boundaries [19,20] were also analyzed.

Although the basic formulation of slow particle rotation is mainly constructed in steady state, its transient behavior is also important for evaluating the validity of steady supposition [21,22]. The temporal evolution of a particle’s angular velocity is pertinent to particle dynamics in the sub-millisecond range [23,24]. The low-Reynolds-number response of the torques exerted by the fluid on isolated hard and soft particles to unsteady rotation has been studied to some extent [25,26,27]. Recently, the transient rotation of a hard particle caused by a suddenly applied torque in a confining cavity was also investigated [28]. However, the starting rotation of isolated or confined porous particles has not been examined. Knowledge of the start-up rotation in the proximity of confining boundaries may be important, for example, in the rotational viscometers and agitated vessels for highly viscous liquids. In this paper, the initial rotation of a porous sphere because of the sudden application of a continuous torque about its diameter at the center of a spherical cavity is analyzed. An explicit expression is obtained for the temporal Laplace transform of the transient angular velocity of the porous sphere.

2. Analysis

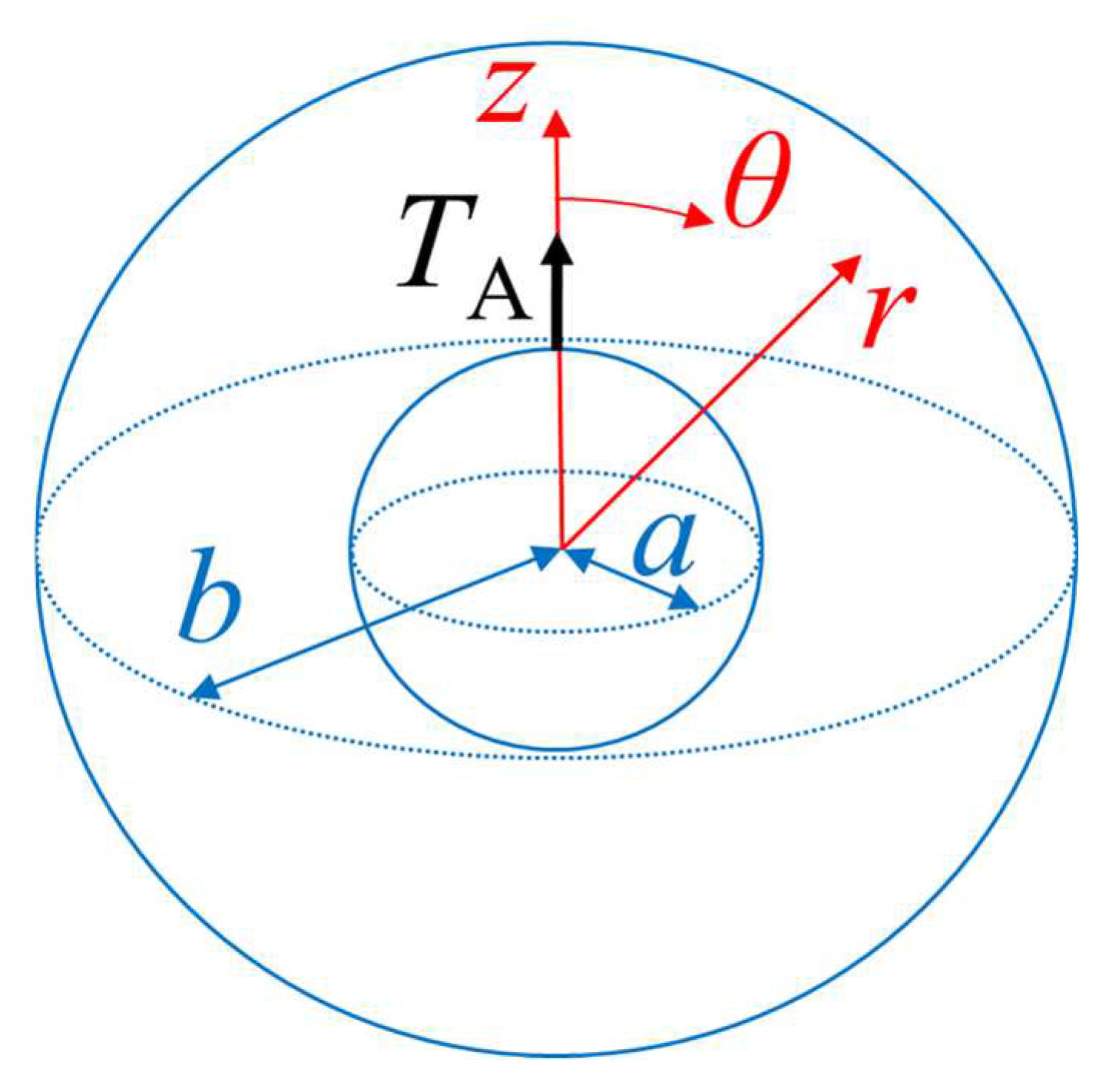
As shown in Figure 1, we consider the start-up rotation of a porous sphere of radius $a$ about its diameter in a viscous fluid within a concentric spherical cavity of radius $b$ in the spherical coordinate system $(r, \theta , \phi )$. At time $t=0$, the constant torque $T_{\mathrm{A}}$ in the $z$ direction (about the axis $\theta =0$) is suddenly applied to the originally motionless porous sphere and continues thereafter. The transient angular velocity $\Omega (t)$ (also in the $z$ direction) of the particle, which is zero at $t=0$ and equals the steady value ${\Omega }_{\infty }$ given by Equation (3) as $t\to \infty$, needs to be determined. The angular Reynolds number $Re={\Omega }_{\infty }{a}^2/\nu$ is vanishingly small, where $\nu$ is the kinematic viscosity of the fluid.

The velocity $v$ and hydrodynamic pressure $p$ of the fluid are governed by the transient Stokes and Brinkman equations [29],

$$[1-h(r)(1-\epsilon )]\rho \frac{𝜕v}{𝜕t}=-\nabla p+\eta {\nabla }^{2}v-h(r)\eta {\lambda }^2(v-\Omega \times r{e}_r),$$

(4)

where $\Omega =\Omega (t)e_z$ is the angular velocity of the porous sphere (equal to zero at $t=0$) to be determined, $e_r$ and $e_z$ are unit vectors in the $r$ and $z$ directions, respectively, $\rho$ and $\eta$ are the mass density and viscosity, respectively, of the fluid, $\epsilon$ and ${\lambda }^{-1}$ are the porosity and flow penetration length or square root of the fluid permeability, respectively, of the particle, $h(r)$ is a step function equal to unity if $r\le a$ and zero otherwise. ${\lambda }^{-1}$ is proportional to ${\epsilon }^{3/2}/(1-\epsilon )$ and the pore size according to the Blake–Kozeny equation [30]. In the Brinkman equation [i.e., Equation (4) for $r\le a$], $v$ is the superficial velocity averaged over a region of space of the solid plus fluid, large with respect to the pore size, but small with respect to the particle radius $a$; the last term relates to the friction force between internal sphere flow and the rigid sphere backbone, and the viscosity $\eta$ is assumed to be the bulk phase value [4].

For the transient rotation of a porous sphere about its diameter in a viscous fluid within a concentric spherical cavity, Equation (4) can be written as

$$[1-h(r)(1-\epsilon )]\frac{r^2}{\nu }\frac{𝜕v_{\varphi }}{𝜕t}=\frac{𝜕}{𝜕r}(r^2\frac{𝜕v_{\varphi }}{𝜕r})+\frac{𝜕}{𝜕\theta }[\frac{1}{\sin \theta }\frac{𝜕}{𝜕\theta }(v_{\varphi }\sin \theta )]-h(r){\lambda }^2{r}^2(v_{\varphi }-\Omega r\sin \theta ),$$

(5)

where $v_{\varphi }(r,\theta ,t)$ is the azimuthal (only nonzero) component of the fluid velocity satisfying the continuity equation and the hydrodynamic pressure is a constant throughout the space in the limit of a low Reynolds number. The initial and boundary conditions are

$$t=0:\hspace{1em}{v}_{\varphi }=0,$$

(6)

$$r=0:\hspace{1em}{v}_{\varphi } \mathrm{is\; finite},$$

(7)

$$r=a:\hspace{1em}{v}_{\varphi } \mathrm{and} {\tau }_{r\varphi } \mathrm{are\; continuous},$$

(8)

$$r=b:\hspace{1em}\hspace{1em}\hspace{1em}{v}_{\varphi }=0,$$

(9)

where ${\tau }_{r\varphi }$ is the only nonzero shear stress of the fluid at the particle surface. Equations (7)–(9) express the absence of any velocity field singularity, the continuity of velocity and hydrodynamic stress fields at the particle surface, and the stick (zero-slip) condition at the stationary inner container surface, respectively.

Equations (5)–(9) suggest the form of the fluid velocity to be

$$v_{\varphi }=g(r,t)\sin \theta .$$

(10)

The Laplace transform, which is defined by an over-bar for a function of time $f(t)$ as

$$\overline{f}(s)={\displaystyle {\int }_{ 0}^{ \infty }f(t)\exp (-st)\mathrm{d}t},$$

(11)

$$f(t)=\frac{1}{2\pi i}{\displaystyle {\int }_{ \gamma -i\infty }^{ \gamma +i\infty } \overline{f}(s)\exp (st)\mathrm{d}s},$$

(12)

will be used to solve for the flow field and particle’ angular velocity. Then, the transform of Equations (5) and (10) can be expressed as

$$\{\frac{{\mathrm{d}}^2}{\mathrm{d}{r}^2}+\frac{2}{r}\frac{\mathrm{d}}{\mathrm{d}r}-\frac{2}{r^2}-h(r){\lambda }^2-[1-h(r)(1-\epsilon )]\frac{s}{\nu }\}\overline{g}(r,s)=-h(r){\lambda }^{2}r\overline{\Omega }(s),$$

(13)

where $s$ is the transform variable.

The general solution of Equation (13) that satisfies the initial condition (6) is

$${\overline{v}}_{\varphi }=\overline{\Omega }a[C_1{I}_{3/2}(Ar)+C_2{I}_{-3/2}(Ar)]{(Ar)}^{-1/2}\sin \theta \hspace{1em}\hspace{1em}\mathrm{if} a\le r\le b,$$

(14)

$${\overline{v}}_{\varphi }=\overline{\Omega }r\{{(\frac{\lambda }{B})}^2+\left[\right(C_3+C_{4}Br)\cosh (Br)-(C_{3}Br+C_4)\sinh (Br)\left]{(\frac{a}{r})}^3\right\}\sin \theta \mathrm{if} r\le a,$$

(15)

where $A=\sqrt{s/\nu }$, $B=\sqrt{{\lambda }^2+\epsilon s/\nu }$, and $I_n$ are the modified Bessel functions of the first kind. The unknown constants (functions of $s$ actually) $C_1$, $C_2$, $C_3$, and $C_4$ are determined from the boundary conditions (7)–(9) as

$$C_1=\sqrt{\frac{\pi }{2}}{(\frac{\lambda }{B})}^2{L}_1{L}_{3}G,$$

(16)

$$C_2=\sqrt{\frac{\pi }{2}}{(\frac{\lambda }{B})}^2{L}_2{L}_{3}G,$$

(17)

$$C_3=0,$$

(18)

$$C_4={(\frac{\lambda }{B})}^2{L}_{4}G,$$

(19)

where

$$G={[L_5\sinh (Ba)-L_6\cosh (Ba)]}^{-1};$$

(20)

$$L_1=A^2{a}^2[Ab\sinh (Ab)-\cosh (Ab)],$$

(21)

$$L_2=A^2{a}^2[\sinh (Ab)-Ab\cosh (Ab)],$$

(22)

$$L_3=(3+B^2{a}^2)\sinh (Ba)-3Ba\cosh (Ba),$$

(23)

$$L_4=\cosh (Aa)[N_1\cosh (Ab)+N_2\sinh (Ab)]-\sinh (Aa)[N_2\cosh (Ab)+N_1\sinh (Ab)],$$

(24)

$$L_5=\cosh (Aa)[N_3\cosh (Ab)+N_4\sinh (Ab)]-\sinh (Aa)[N_4\cosh (Ab)+N_3\sinh (Ab)],$$

(25)

$$L_6=Ba[L_1\sinh (Aa)+L_2\cosh \left(Aa\right)];$$

(26)

$$N_1=Aa(3-A^{2}ab)-3Ab,$$

(27)

$$N_2=3-A^{2}a\left(3b-a\right),$$

(28)

$$N_3=A{B}^2{a}^2(b-a)-A^3{a}^{2}b,$$

(29)

$$N_4=A^2{a}^2(1+B^{2}ab)-B^2{a}^2.$$

(30)

The torque exerted by the fluid on the particle (in the $z$ direction) is negative and its Laplace transform is given by

$${\overline{T}}_{\mathrm{h}}=2\pi \eta {\lambda }^2{\displaystyle {\int }_0^{\pi }{\displaystyle {\int }_0^a({\overline{v}}_{\varphi }}}-\overline{\Omega }r\sin \theta )r^3{\sin }^2\theta \mathrm{d}r\mathrm{d}\theta ,$$

(31)

the magnitude of which increases monotonically with the elapsed time from naught at $t=0$ to $T_{\mathrm{A}}$ as $t\to \infty$. By using Equation (5) and the Gauss divergence theorem, Equation (31) can also be expressed as

$${\overline{T}}_{\mathrm{h}}=2\pi a^3{\displaystyle {\int }_0^{\pi }{\overline{\tau }}_{r\varphi }}(r=a){\sin }^2\theta \mathrm{d}\theta -2\pi \epsilon \rho s{\displaystyle {\int }_0^{\pi }{\displaystyle {\int }_0^a{\overline{v}}_{\varphi }}}{r}^3{\sin }^2\theta \mathrm{d}r\mathrm{d}\theta .$$

(32)

The substitution of Equations (14)–(19) into Equation (31) or (32) leads to

$${\overline{T}}_{\mathrm{h}}=\frac{8}{15}\pi \eta a^3\overline{\Omega }\{{\lambda }^2{a}^2[{(\frac{\lambda }{B})}^2-1]+5{(\frac{\lambda }{B})}^2{L}_3{L}_{4}G\},$$

(33)

where $\eta$ is the viscosity of the fluid. Note that $v_{\varphi }$ and $T_{\mathrm{h}}$ vanish in the limiting case of $\lambda a=0$.

The sum of the applied and hydrodynamic torques on the particle equals the angular acceleration multiplied by the moment of inertia,

$$T_{\mathrm{h}}+T_{\mathrm{A}}=\frac{8}{15}\pi a^5(1-\epsilon ){\rho }_{\mathrm{p}}\frac{\mathrm{d}\Omega }{\mathrm{d}t},$$

(34)

where ${\rho }_{\mathrm{p}}$ is the mass density of the solid part of the porous sphere. The substitution of Equation (33) into Equation (34) results in a formula for the transient angular velocity of the porous sphere in transform,

$$\overline{\Omega }=\frac{15T_{\mathrm{A}}}{8\pi \eta a^{3}s}{\{A^2{a}^2(1-\epsilon )\frac{{\rho }_{\mathrm{p}}}{\rho }-5{(\frac{\lambda }{B})}^4{L}_3{L}_{4}G+{\lambda }^2{a}^2[1-{(\frac{\lambda }{B})}^2]\}}^{-1},$$

(35)

where $\rho =\eta /\nu$ is the density of the fluid. This angular velocity can be obtained numerically using the inverse Laplace transform [31,32,33]. In the limiting case of $\lambda a\to \infty$ (the porous sphere becomes impermeable with $\epsilon =0$), Equation (35) is identical to the corresponding formula obtained for the transient rotation of a hard sphere inside a spherical cavity taking the surfaces to be nonslip [28].

If the applied torque $T_{\mathrm{A}}$ is suddenly taken away from a rotating porous sphere that is already at a steady state with angular velocity ${\Omega }_{\infty }$, the transient angular velocity of the porous sphere that stops rotating will decay from ${\Omega }_{\infty }$ to zero as ${\Omega }_{\infty }-\Omega$ decreases with time, calculated using the inverse transform of Equation (35).

In the limit $a/b=0$, $L_{4}G$ in Equation (35) reduces to that for the porous sphere rotating in an unbounded fluid:

$$L_{4}G=-\frac{3+3Aa+A^2{a}^2}{A^{2}B{a}^3\cosh (Ba)+(A{B}^{2}a-A^2+B^2)a^2\sinh (Ba)}.$$

(36)

In our linear problem, the transient translation of the porous sphere caused by an applied force can be considered separately [29].

3. Results and Discussion

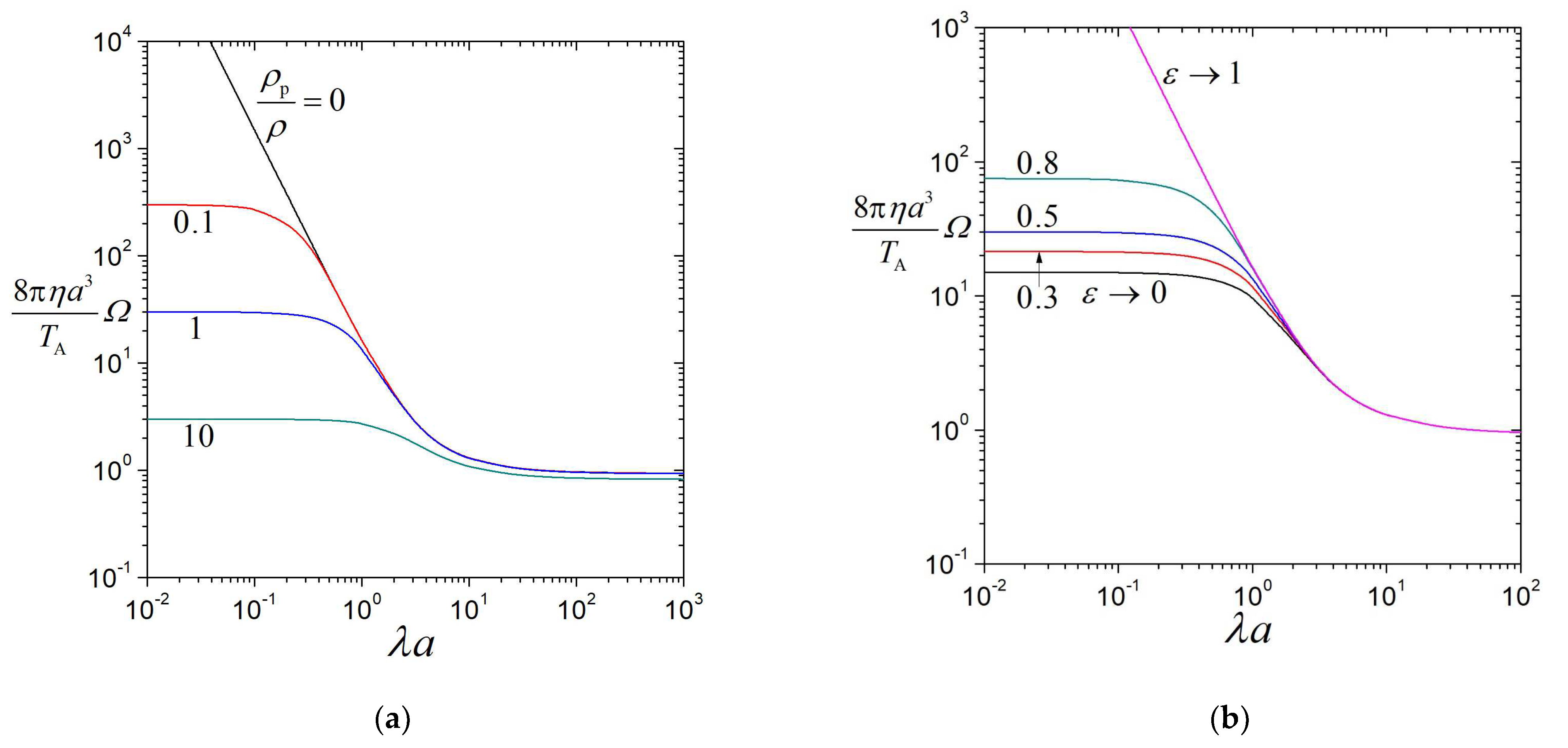
The nondimensionalized starting angular velocity $8\pi \eta a^3\Omega /T_{\mathrm{A}}$ of a porous sphere applied by constant torque $T_{\mathrm{A}}$ about a diameter in a boundless fluid ($a/b=0$), calculated from Equations (35) and (36) by means of numerical inverse transform, is plotted versus the dimensionless passed time $\nu t/a^2$, relative density ${\rho }_{\mathrm{p}}/\rho$, shielding parameter $\lambda a$, and porosity $\epsilon$ of the particle in Figure 2, Figure 3 and Figure 4. For fixed values of $\lambda a$, ${\rho }_{\mathrm{p}}/\rho$, and $\epsilon$, as expected, the particle’s angular velocity grows continuously with $\nu t/a^2$ from zero at $\nu t/a^2=0$ to the final rate given by Equation (1) (which does not depend on ${\rho }_{\mathrm{p}}/\rho$ or $\epsilon$) as $\nu t/a^2\to \infty$. In the limits of minimum density ${\rho }_{\mathrm{p}}/\rho =0$ and maximum porosity $\epsilon \to 1$ of the particle, as shown in Figure 2a,c, the initial value of $8\pi \eta a^3\Omega /T_{\mathrm{A}}$ may also be $15/{\lambda }^2{a}^2$ as singular situations at $t=0$.

For specified values of $\nu t/a^2$, ${\rho }_{\mathrm{p}}/\rho$, and $\epsilon$, as shown in Figure 2b, Figure 3 and Figure 4a, the dimensionless angular velocity $8\pi \eta a^3\Omega /T_{\mathrm{A}}$ of the porous sphere is a monotonic decreasing function of $\lambda a$ (relative resistance to fluid flow inside the porous particle) from infinity (as $\nu t/a^2\to \infty$, or ${\rho }_{\mathrm{p}}/\rho =0$, or $\epsilon \to 1$) or a finite value at $\lambda a=0$ (fully permeable particle) to a smaller value as $\lambda a\to \infty$ (impermeable particle), illustrating the reduction in the transient angular velocity of the porous particle with an increase in its internal resistance to fluid flow at any elapsed time. When the value of $\lambda a$ is small, interestingly, a porous particle with higher fluid permeability (smaller value of $\lambda a$) develops its angular velocity in percentage slower relative to the reference particle towards the respective terminal values (despite the greater value of its angular velocity at any elapsed time). In the limit $\lambda a=0$, the value of $8\pi \eta a^3\Omega /T_{\mathrm{A}}$ equals $15(\nu t/a^2)\rho /(1-\epsilon ){\rho }_{\mathrm{p}}$, as resulting from Equation (35).

For fixed values of $\nu t/a^2$, $\lambda a$, and $\epsilon$, as illustrated in Figure 2a, Figure 3a, and Figure 4, the angular velocity $8\pi \eta a^3\Omega /T_{\mathrm{A}}$ is a monotonic decreasing function of the density ratio ${\rho }_{\mathrm{p}}/\rho$ from a finite value (as $\lambda a>0$) or infinity (for the completely permeable case $\lambda a=0$) at ${\rho }_{\mathrm{p}}/\rho =0$, indicating the diminution in the transient angular velocity of the particle with an increase in its relative density. In the limit ${\rho }_{\mathrm{p}}/\rho \to \infty$, the angular velocity vanishes except for the steady state $\nu t/a^2\to \infty$. For the limiting case of maximum porosity $\epsilon \to 1$, the angular velocity does not depend on ${\rho }_{\mathrm{p}}/\rho$.

For given values of $\nu t/a^2$, ${\rho }_{\mathrm{p}}/\rho$, and $\lambda a$, as shown in Figure 2c, Figure 3b and Figure 4b, the angular velocity $8\pi \eta a^3\Omega /T_{\mathrm{A}}$ of the porous sphere in general is an increasing function of the porosity $\epsilon$ from a finite value as $\epsilon \to 0$ to a larger one as $\epsilon \to 1$, illustrating that a particle with smaller porosity lags behind that with greater porosity in the development of the angular velocity. However, $8\pi \eta a^3\Omega /T_{\mathrm{A}}$ may slightly decrease with an increase in $\epsilon$ when the value of ${\rho }_{\mathrm{p}}/\rho$ is relatively small.

The dimensionless angular acceleration $(8\pi \rho a^5/T_{\mathrm{A}})\mathrm{d}\Omega /\mathrm{d}t$ of a porous sphere starting to rotate under the application of a constant torque in a boundless fluid as a function of the dimensionless time $\nu t/a^2$ is presented in Figure 5 for various values of the shielding parameter $\lambda a$, density ratio ${\rho }_{\mathrm{p}}/\rho$, and porosity $\epsilon$. This angular acceleration decreases monotonically with an increase in $\nu t/a^2$ from a maximum equal to $15\rho /(1-\epsilon ){\rho }_{\mathrm{p}}$ (independent of finite values of $\lambda a$) or $15\rho /[(1-\epsilon ){\rho }_{\mathrm{p}}+\epsilon \rho ]$ (for the singular limit $\lambda a\to \infty$) at $\nu t/a^2=0$ and disappears as $\nu t/a^2\to \infty$. For given values of $\lambda a$ and $\epsilon$, the angular acceleration $(8\pi \rho a^5/T_{\mathrm{A}})\mathrm{d}\Omega /\mathrm{d}t$ decreases as ${\rho }_{\mathrm{p}}/\rho$ increases at the early stage, is not a monotonic function of ${\rho }_{\mathrm{p}}/\rho$ at the medium stage, and then increases with an increase in ${\rho }_{\mathrm{p}}/\rho$ at the late stage, but always vanishes in the limit ${\rho }_{\mathrm{p}}/\rho \to \infty$ (where $8\pi \eta a^3\Omega /T_{\mathrm{A}}=0$). This consequence reproduces the fact that a particle of higher relative density grows its angular velocity slower but has a terminal value independent of the relative density. In the limiting case of ${\rho }_{\mathrm{p}}/\rho \to \infty$, the angular acceleration of the particle vanishes (so does its angular velocity) regardless of the elapsed time. For any fixed values of $\nu t/a^2$, ${\rho }_{\mathrm{p}}/\rho$, and $\epsilon$, the quantity $(8\pi \rho a^5/T_{\mathrm{A}})\mathrm{d}\Omega /\mathrm{d}t$ decreases as $\lambda a$ increases from $15\rho /(1-\epsilon ){\rho }_{\mathrm{p}}$ at $\lambda a=0$ [where the angular acceleration of the porous sphere does not depend on the elapsed time and $8\pi \eta a^3\Omega /T_{\mathrm{A}}=15(\nu t/a^2)\rho /(1-\epsilon ){\rho }_{\mathrm{p}}$] to a smaller constant as $\lambda a\to \infty$. This outcome reflects again the behavior that a porous sphere with higher fluid permeability develops its angular velocity in percentage slower toward the terminal value. For specified values of ${\rho }_{\mathrm{p}}/\rho$ and $\lambda a$, $(8\pi \rho a^5/T_{\mathrm{A}})\mathrm{d}\Omega /\mathrm{d}t$ increases with an increase in $\epsilon$ at the early stage (reflecting that a particle with greater porosity develops its angular velocity faster), is not a monotonic function of $\epsilon$ at the medium stage, and then decreases with an increase in $\epsilon$ at the late stage (since the particle with greater porosity has already developed most of its terminal angular velocity).

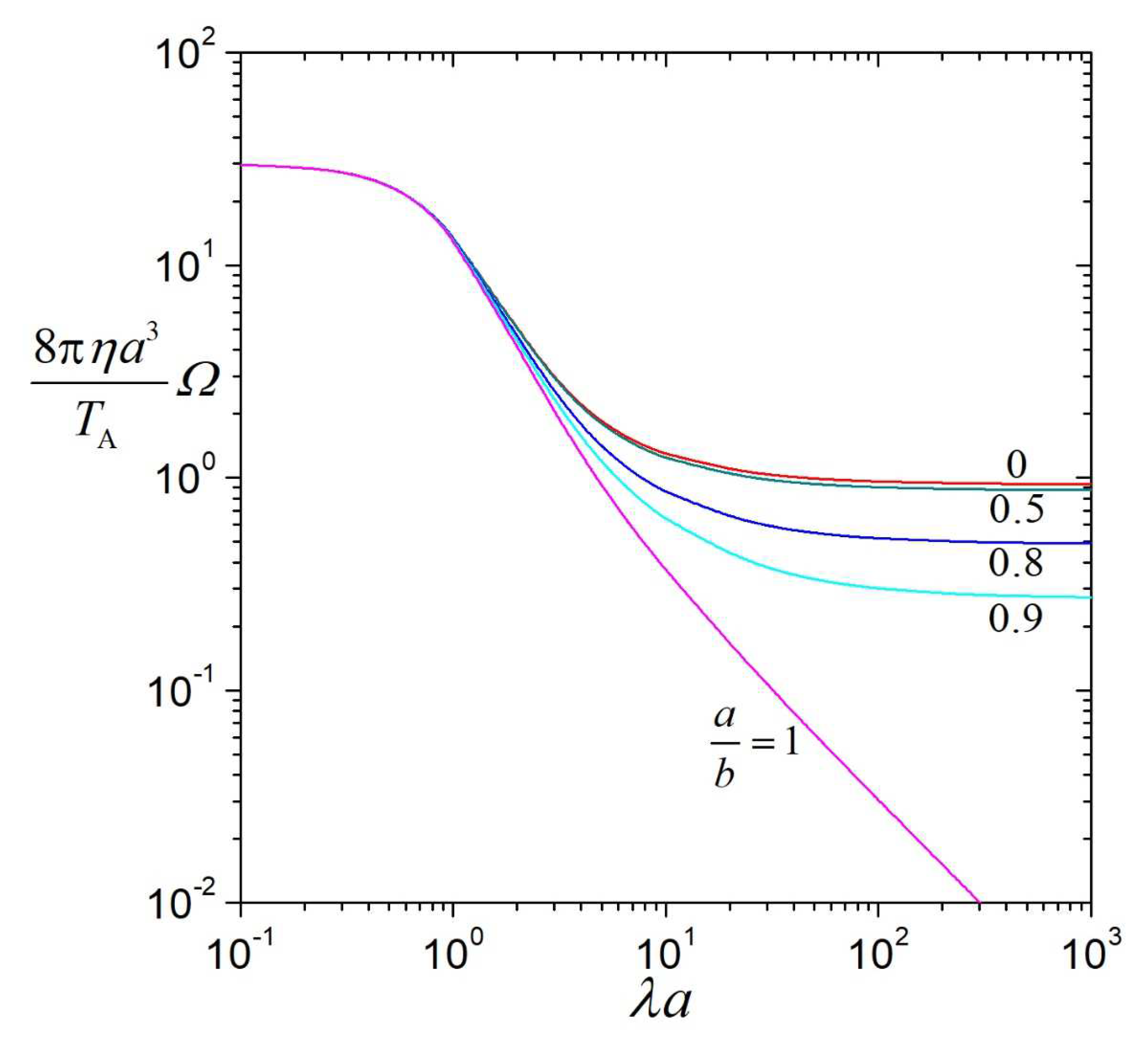
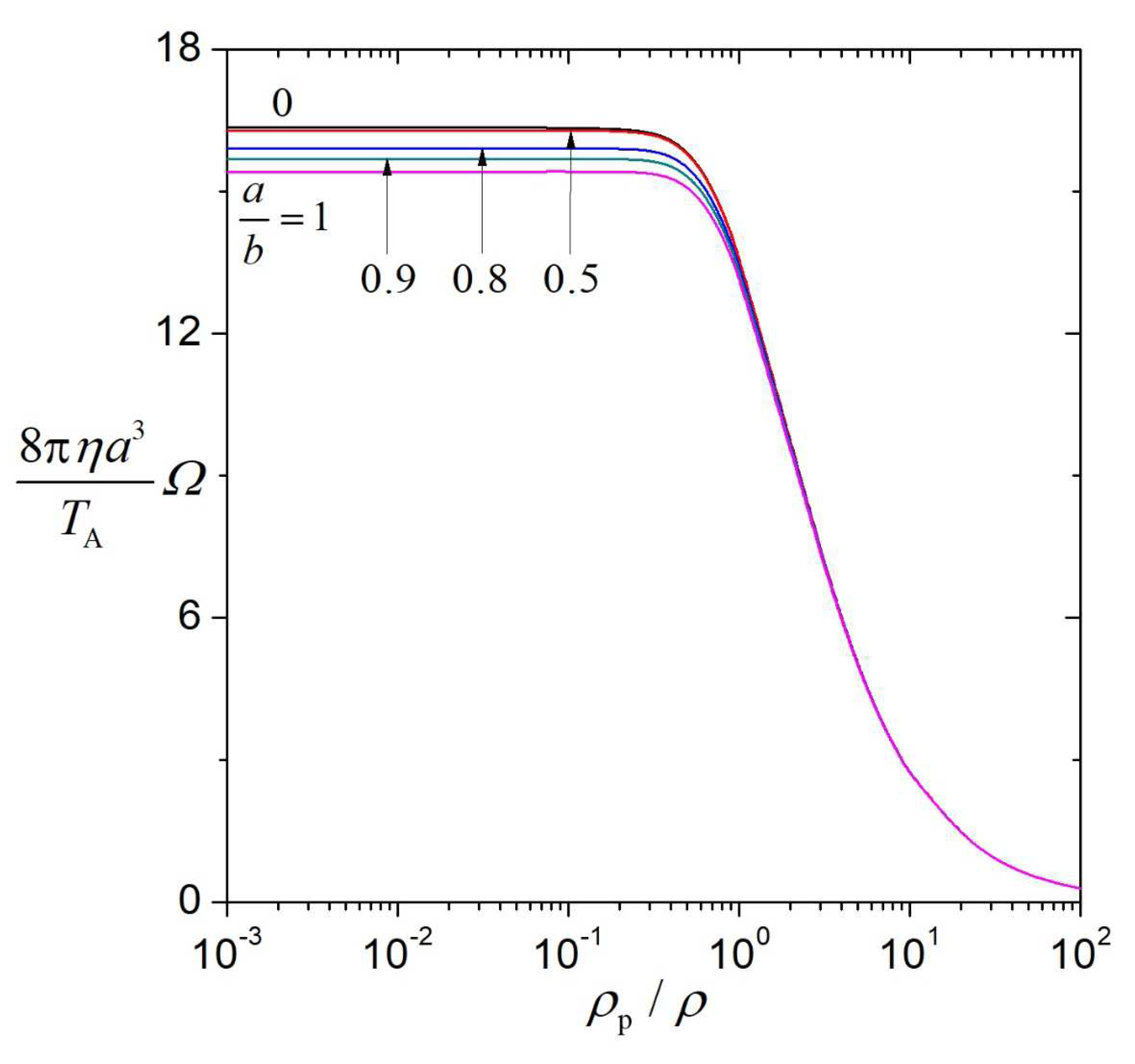
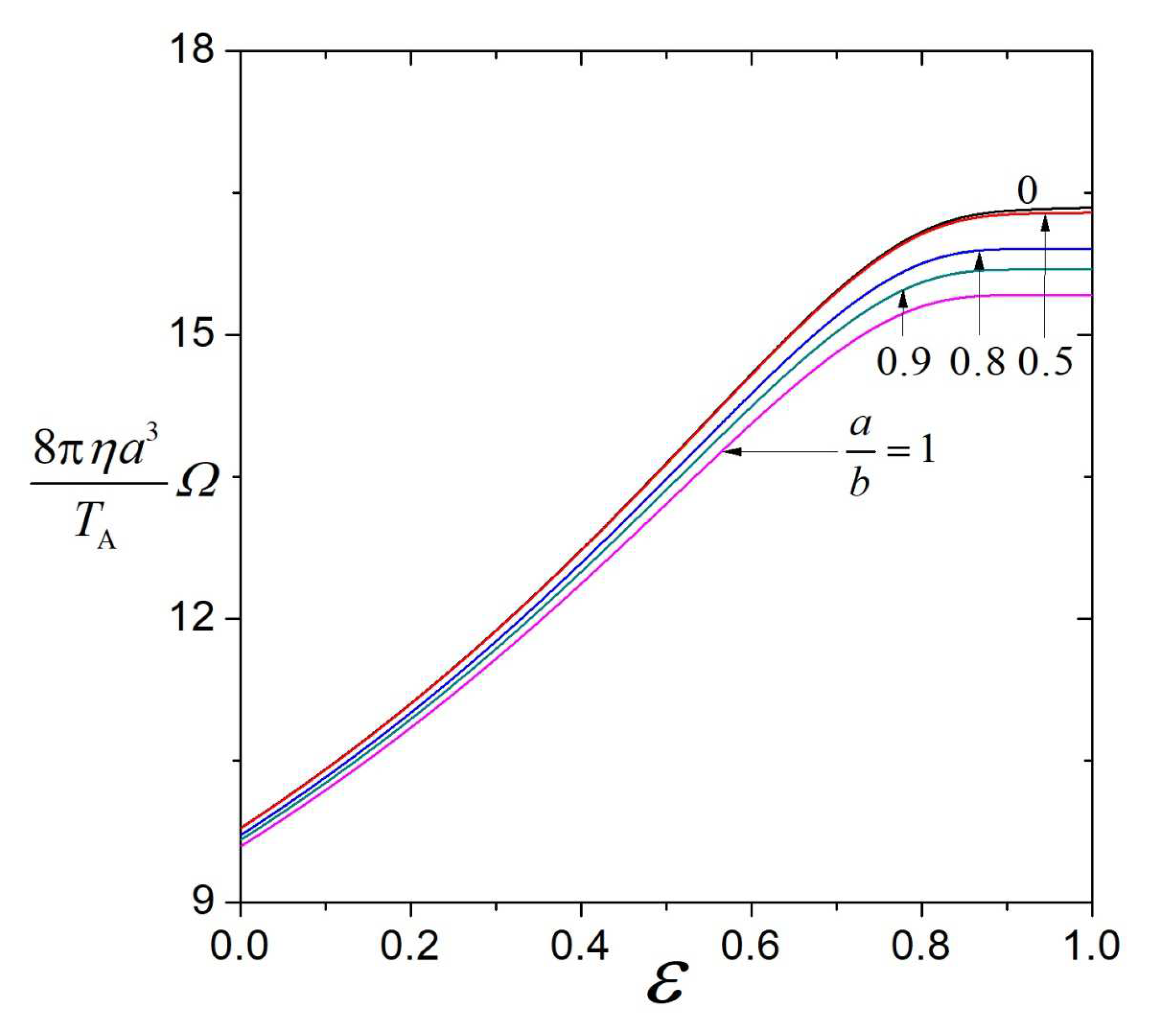
The dimensionless starting angular velocity $8\pi \eta a^3\Omega /T_{\mathrm{A}}$ of a porous sphere applied by a constant torque $T_{\mathrm{A}}$ about a diameter at the center of a spherical cavity, calculated from Equation (35) by means of numerical inverse transform, is plotted versus the dimensionless passed time $\nu t/a^2$, ratio of the particle radius to the permeation length $\lambda a$, particle-to-fluid density ratio ${\rho }_{\mathrm{p}}/\rho$, and particle porosity $\epsilon$ in Figure 6, Figure 7, Figure 8 and Figure 9, respectively, for several values of the particle-to-cavity radius ratio $a/b$. Again, $8\pi \eta a^3\Omega /T_{\mathrm{A}}$ grows continuously from zero at $\nu t/a^2=0$ to the final value (which does not depend on ${\rho }_{\mathrm{p}}/\rho$) given by Equation (3) as $\nu t/a^2\to \infty$, diminishes monotonically with increasing $\lambda a$ from a constant at $\lambda a=0$ to a smaller one as $\lambda a\to \infty$, is a monotonic decreasing function of ${\rho }_{\mathrm{p}}/\rho$ from a constant at ${\rho }_{\mathrm{p}}/\rho =0$ to zero as ${\rho }_{\mathrm{p}}/\rho \to \infty$, and in general is an increasing function of $\epsilon$, keeping the other parameters unchanged. For fixed values of $\nu t/a^2$, $\lambda a$, ${\rho }_{\mathrm{p}}/\rho$, and $\epsilon$, the angular velocity $8\pi \eta a^3\Omega /T_{\mathrm{A}}$ decreases monotonically with an increase in $a/b$ (the wall retardation effect on the particle rotation is an increasing function of the relative particle radius) but in general is not a sensitive function of $a/b$ when $\nu t/a^2$ is small (say, less than 1), $\lambda a$ is small (say, less than 1), ${\rho }_{\mathrm{p}}/\rho$ is large (say, greater than 1), or $a/b$ is small (say, less than 0.5). For a nonzero value of $\nu t/a^2$ and finite value of ${\rho }_{\mathrm{p}}/\rho$, the quantity $8\pi \eta a^3\Omega /T_{\mathrm{A}}$ remains finite in the limit $a/b=1$ (the cavity is filled up by the particle), except for the case of $\lambda a\to \infty$.

4. Conclusions

This work analyzes the start-up rotation of a porous sphere caused by a suddenly applied torque about its diameter in a concentric spherical cavity filled with a viscous fluid at low Reynolds numbers. The transient Stokes and Brinkman equations governing the fluid velocities outside and inside the porous particle, respectively, are solved by using Laplace transformation, and an explicit formula of its dynamic angular velocity as a function of the related parameters is obtained in Equation (35). The behavior of the starting rotation of an isolated porous particle and the effect of the confining cavity wall on the particle rotation are interesting. The angular velocity continuously increases over time from an initial zero to a terminal value and the angular acceleration continuously decays over time. A porous sphere with higher fluid permeability rotates at higher angular velocity and acceleration relative to the reference particle at any elapsed time, but it lags behind it in the percentage increase in angular velocity towards the respective final values. A particle with a higher relative density or smaller porosity rotates at a lower angular velocity in any elapsed time, and the angular velocity grows slower towards the terminal value. The transient angular velocity decreases with the increase in the particle-to-cavity radius ratio but is not a sensitive function of the radius ratio when the fluid flow resistance inside the porous particle is small, the particle-to-fluid density ratio is large, or the radius ratio itself is small. The insights gained from this theoretical research on the transient rotational motion of a porous particle at low Reynolds Numbers may hold significance in the design of micro/nanorobots [34,35].