Ballpoint/Rollerball Pens: Writing Performance and Evaluation
Abstract
1. Introduction
2. Experimental Section
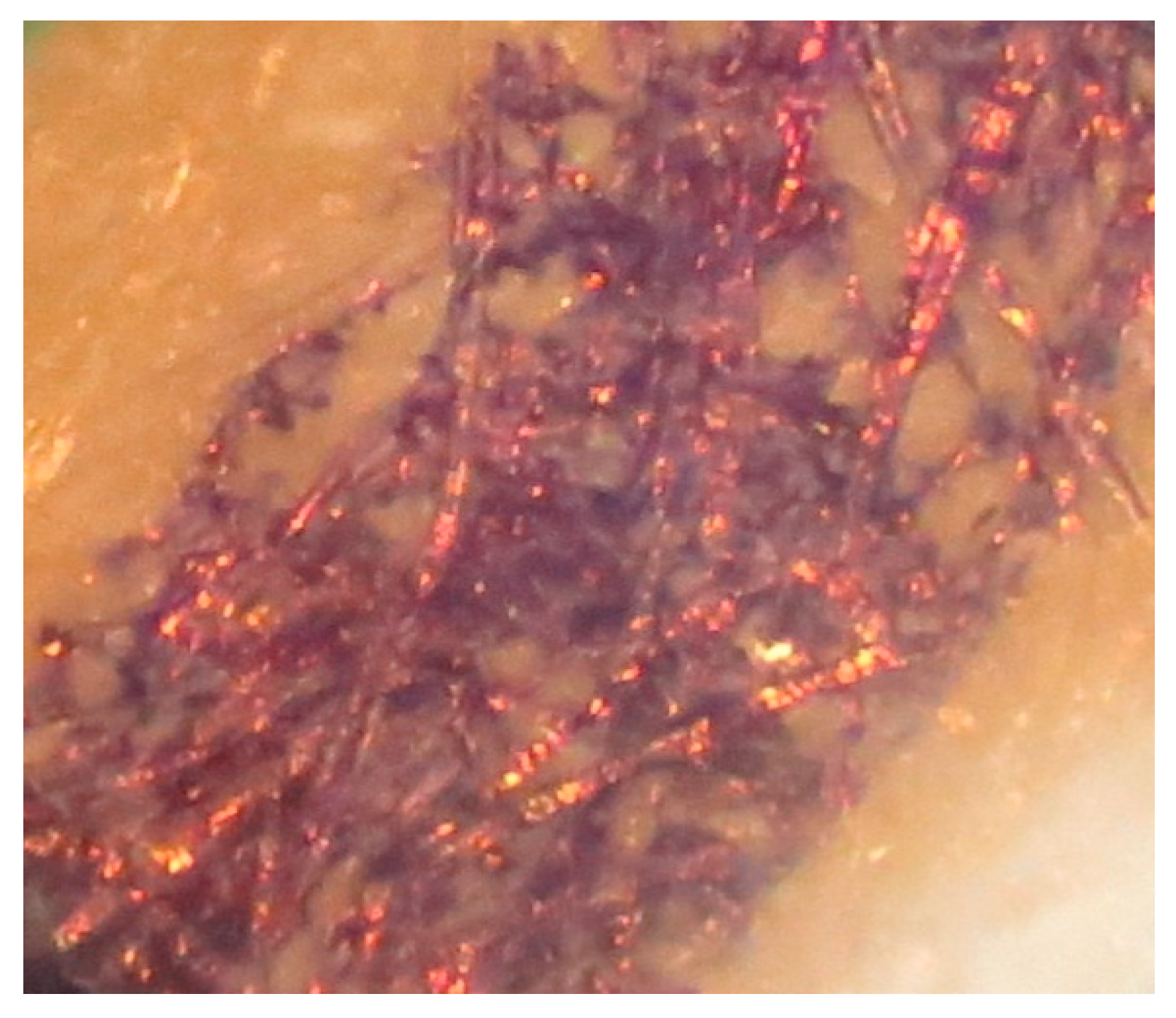
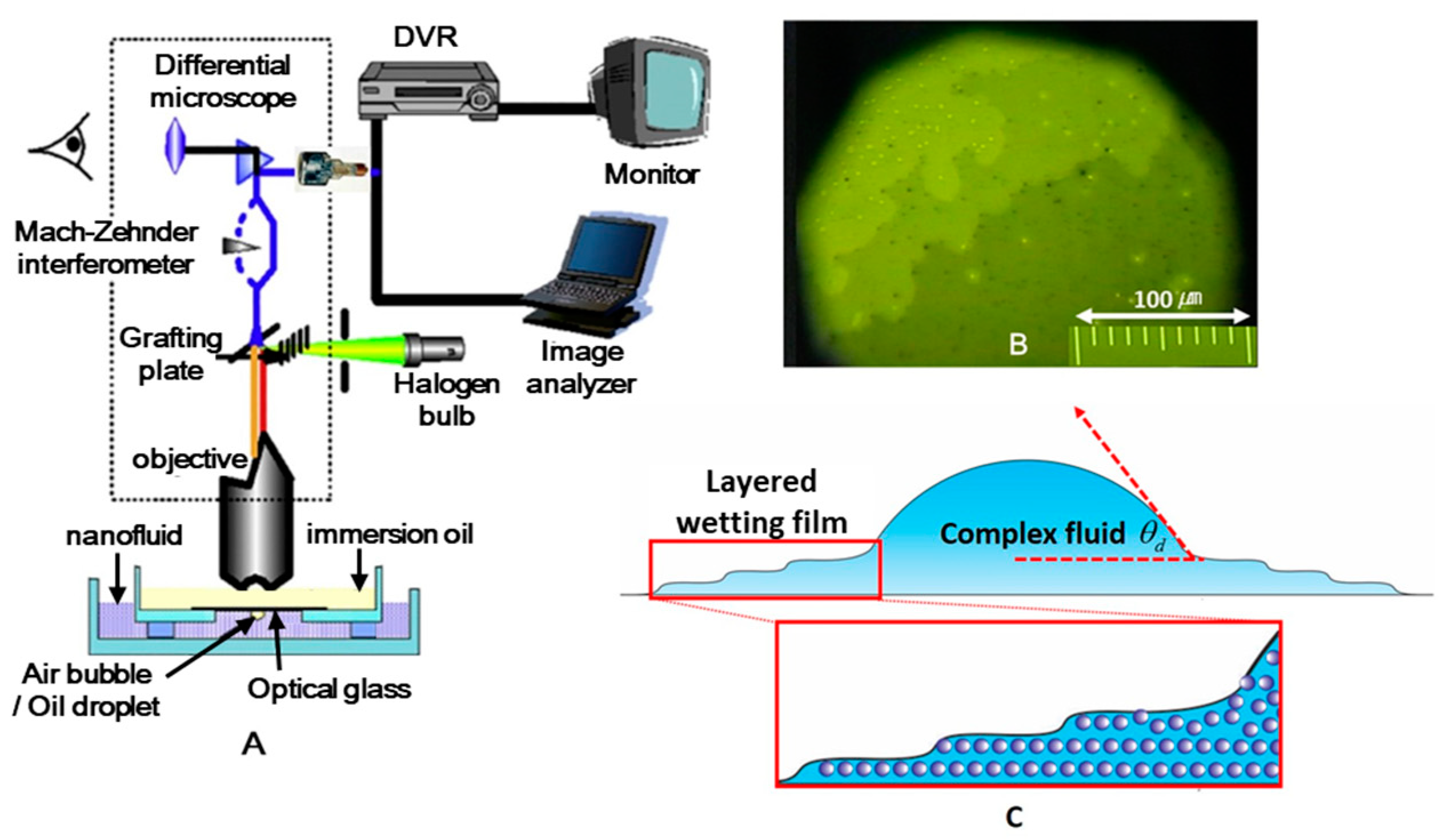
2.1. Monitoring Ballpoint Pen Writing Performance by Lens End Fiber Optics
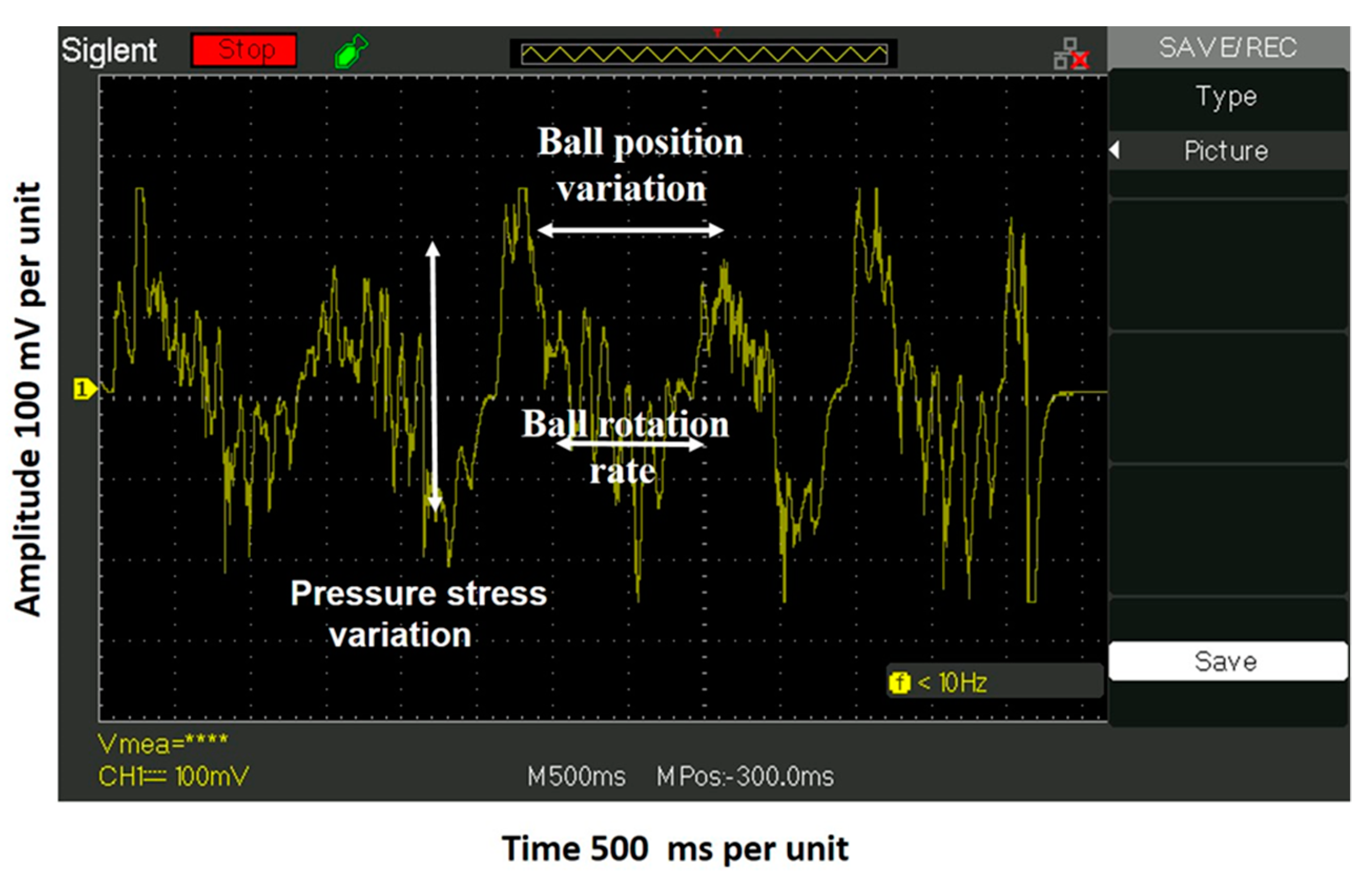
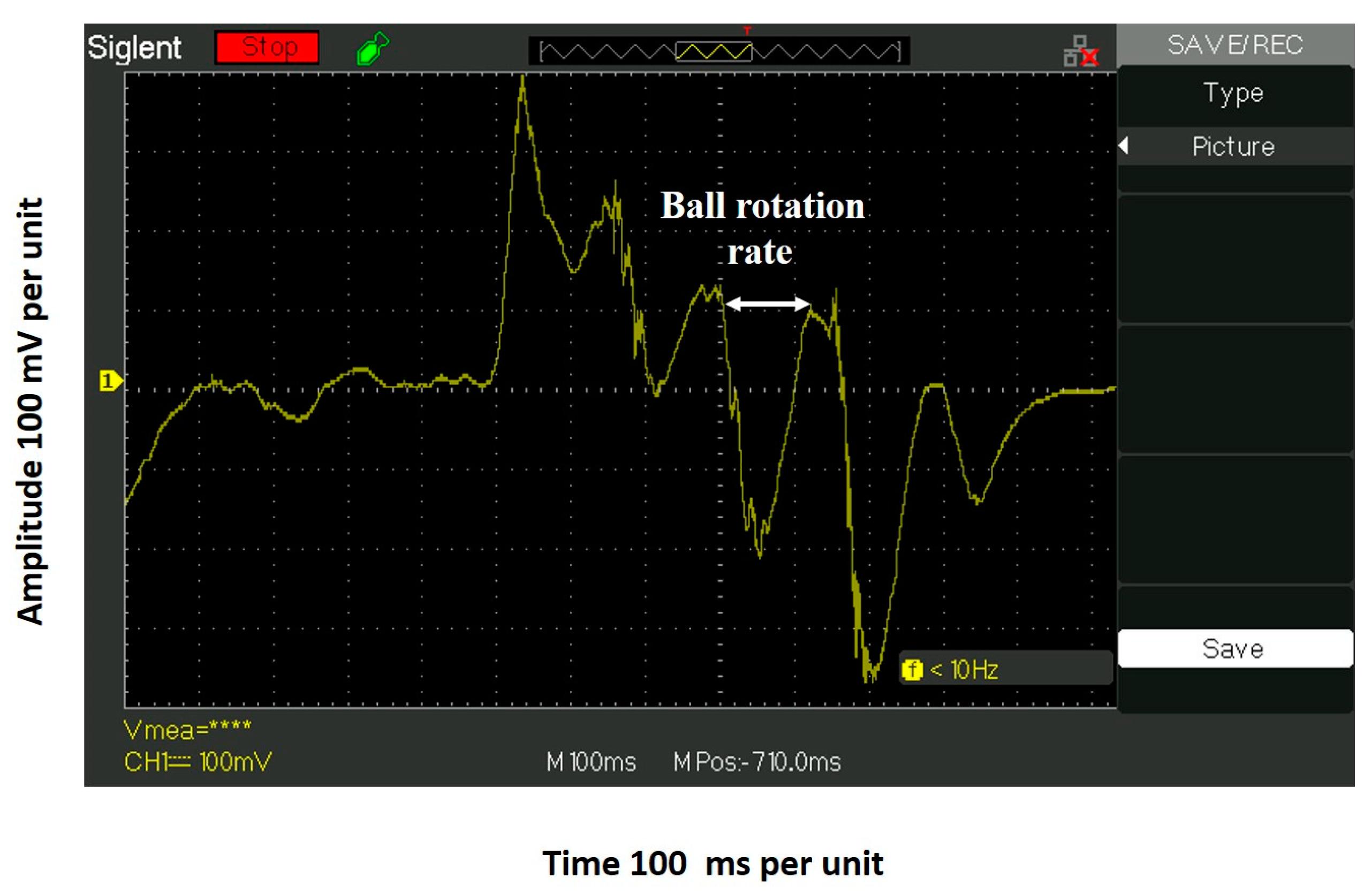
2.2. Monitoring Ballpoint Writing Using a Piezoelectric Disk Transducer (PEDT)
3. Fundamentals
3.1. Classical Concept of Fluid-Wetted Solid
3.2. Three-Phase Contact Angle Defined by the Force Balance Model
3.3. Complex Molecular Fluid Wetting Solid via the Hydrodynamic Model
3.4. Empirical Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Fischer, S.R. History of Writing; Reaktion Books: London, UK, 2001. [Google Scholar]
- da Vinci, L. Codex Leicester (A Collection of Scientific Writings); Manuscript; 1510; pp. 1504–1508. [Google Scholar]
- Nikolov, A.; Murad, S.; Wasan, D.; Wu, P. How the capillarity and ink-air flow govern the performance of a fountain pen. J. Colloid Interface Sci. 2020, 578, 660–667. [Google Scholar] [CrossRef]
- Fritz, I. Identification of fountain pen ink properties which determine the amount put on paper during handwriting. Mater. Des. 2022, 219, 110739. [Google Scholar] [CrossRef]
- Kim, J.; Moon, M.-W.; Lee, K.-R.; Mahadevan, L.; Kim, H.-Y. Hydrodynamics of writing with ink. Phys. Rev. Lett. 2011, 107, 264501. [Google Scholar] [CrossRef]
- Nikolov, A.; Wasan, D. Air bubble bursting phenomenon at the air-water interface monitored by the piezoelectric-acoustic method. Adv. Colloid Interface Sci. 2019, 272, 101998. [Google Scholar] [CrossRef]
- Nardo, S.D. How Do Ballpoint Pens Work. Available online: https://www.dayspringpens.com/blogs/the-jotted-line/how-do-ballpoint-pens-work (accessed on 10 February 2023).
- Cox, R. The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 1986, 168, 169–194. [Google Scholar] [CrossRef]
- Young, T., III. An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar]
- Laplace, P. Traité de mécanique céleste, Supplement to the 10th Book; Duprat: Paris, France, 1807. [Google Scholar]
- Dupré, A.; Dupré, P. Théorie Mécanique de la Chaleur; Gauthier-Villars: Paris, France, 1869. [Google Scholar]
- Huh, C.; Scriven, L.E. Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 1971, 35, 85–101. [Google Scholar] [CrossRef]
- Voinov, O. Hydrodynamics of wetting. Fluid Dyn. 1976, 11, 714–721. [Google Scholar] [CrossRef]
- Dussan, V. On the difference between a bounding surface and a material surface. J Fluid Mech 1976, 75, 609–623. [Google Scholar] [CrossRef]
- Brochard-Wyart, F.; De Gennes, P. Dynamics of partial wetting. Adv. Colloid Interface Sci. 1992, 39, 234501. [Google Scholar] [CrossRef]
- Cherry, B.W.; Holmes, C.M. Kinetics of wetting of surfaces by polymers. J. Colloid Interface Sci. 1969, 29, 174–176. [Google Scholar] [CrossRef]
- Blake, T.D. The physics of moving wetting lines. J. Colloid Interface Sci. 2006, 299, 1–13. [Google Scholar] [CrossRef]
- Blake, T.; Haynes, J. Kinetics of liquidliquid displacement. J. Colloid Interface Sci. 1969, 30, 421–423. [Google Scholar] [CrossRef]
- Katoh, K.; Wakimoto, T.; Yamamoto, Y.; Ito, T. Dynamic wetting behavior of a triple-phase contact line in several experimental systems. Exp. Therm. Fluid. Sci. 2015, 60, 354–360. [Google Scholar] [CrossRef]
- Shanahan, M.E.; Houzelle, M.-C.; Carré, A. Strange spreading behavior of tricresyl phosphate. Langmuir 1998, 14, 528–532. [Google Scholar] [CrossRef]
- Wu, P.; Nikolov, A.; Wasan, D. Capillary dynamics driven by molecular self-layering. Adv. Colloid Interface Sci. 2017, 243, 114–120. [Google Scholar] [CrossRef]
- Nikolov, A.; Wu, P.; Wasan, D. Structure and stability of nanofluid films wetting solids: An overview. Adv. Colloid Interface Sci. 2019, 264, 1–10. [Google Scholar] [CrossRef]
- Newman, S. Kinetics of wetting of surfaces by polymers; capillary flow. J. Colloid Interface Sci. 1968, 26, 209–213. [Google Scholar] [CrossRef]
- Jiang, T.-S.; Soo-Gun, O.; Slattery, J.C. Correlation for dynamic contact angle. J. Colloid Interface Sci. 1979, 69, 74–77. [Google Scholar] [CrossRef]
- Bracke, M.; De Voeght, F.; Joos, P. The kinetics of wetting: The dynamic contact angle. In Trends in Colloid and Interface Science III; Springer: Berlin/Heidelberg, Germany, 1989; pp. 142–149. [Google Scholar]
- Joos, P.; Vanremoortere, P.; Bracke, M. The Kinetics of Wetting in a Capillary. J. Colloid Interface Sci. 1990, 136, 189–197. [Google Scholar] [CrossRef]
- Vanremoortere, P.; Joos, P. The Kinetics of Wetting—the Motion of a 3 Phase Contactline in a Capillary. J. Colloid Interface Sci. 1991, 141, 348–359. [Google Scholar] [CrossRef]
- Beattie, D.A.; Espinosa-Marzal, R.M.; Ho, T.T.; Popescu, M.N.; Ralston, J.; Richard, C.l.J.; Sellapperumage, P.M.; Krasowska, M. Molecularly-thin precursor films of imidazolium-based ionic liquids on mica. J. Phys. Chem. C 2013, 117, 23676–23684. [Google Scholar] [CrossRef]
- Ausserré, D.; Picard, A.; Léger, L. Existence and role of the precursor film in the spreading of polymer liquids. Phys. Rev. Lett. 1986, 57, 2671. [Google Scholar] [CrossRef]
- Hoang, A.; Kavehpour, H.P. Dynamics of Nanoscale Precursor Film near a Moving Contact Line of Spreading Drops. Phys. Rev. Lett. 2011, 106, 254501. [Google Scholar] [CrossRef]
- Yuan, Q.Z.; Zhao, Y.P. Precursor Film in Dynamic Wetting, Electrowetting, and Electro-Elasto-Capillarity. Phys. Rev. Lett. 2010, 104, 246101. [Google Scholar] [CrossRef]
- Chibbaro, S.; Biferale, L.; Diotallevi, F.; Succi, S.; Binder, K.; Dimitrov, D.; Milchev, A.; Girardo, S.; Pisignano, D. Evidence of thin-film precursors formation in hydrokinetic and atomistic simulations of nano-channel capillary filling. EPL 2008, 84, 44003. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Christenson, H.; Gruen, D.; Horn, R.; Israelachvili, J. Structuring in liquid alkanes between solid surfaces: Force measurements and mean-field theory. J. Chem. Phys. 1987, 87, 1834–1841. [Google Scholar] [CrossRef][Green Version]
- Horn, R.G.; Israelachvili, J.N. Direct measurement of structural forces between two surfaces in a nonpolar liquid. J. Chem. Phys. 1981, 75, 1400–1411. [Google Scholar] [CrossRef]
- Chu, X.; Nikolov, A.; Wasan, D. Monte Carlo simulation of inlayer structure formation in thin liquid films. Langmuir 1994, 10, 4403–4408. [Google Scholar] [CrossRef]
- Wasan, D.T.; Nikolov, A.D. Spreading of nanofluids on solids. Nature 2003, 423, 156–159. [Google Scholar] [CrossRef]
- Nikolov, A.D.; Dimitrov, A.S.; Kralchevsky, P.A. Accuracy of the Differential-interferometric Measurements of Curvature. Opt. Acta Int. J. Opt. 1986, 33, 1359–1368. [Google Scholar] [CrossRef]
- Dimitrov, A.; Kralchevsky, P.; Nikolov, A.; Wasan, D.T. Contact angles of thin liquid films: Interferometric determination. Colloids Surf. 1990, 47, 299–321. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Murad, S.; Nikolov, A. Ballpoint/Rollerball Pens: Writing Performance and Evaluation. Colloids Interfaces 2023, 7, 29. https://doi.org/10.3390/colloids7020029
Lee J, Murad S, Nikolov A. Ballpoint/Rollerball Pens: Writing Performance and Evaluation. Colloids and Interfaces. 2023; 7(2):29. https://doi.org/10.3390/colloids7020029
Chicago/Turabian StyleLee, Jongju, Sohail Murad, and Alex Nikolov. 2023. "Ballpoint/Rollerball Pens: Writing Performance and Evaluation" Colloids and Interfaces 7, no. 2: 29. https://doi.org/10.3390/colloids7020029
APA StyleLee, J., Murad, S., & Nikolov, A. (2023). Ballpoint/Rollerball Pens: Writing Performance and Evaluation. Colloids and Interfaces, 7(2), 29. https://doi.org/10.3390/colloids7020029








