Electric Fields Enhance Ice Formation from Water Vapor by Decreasing the Nucleation Energy Barrier
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Equipment
2.3. Experimental Setup
2.4. Temperatures
3. Theory and Calculations
3.1. Ice Formation Enhancement by Decreasing Its Surface Tension: Application of the Classical Nucleation Theory
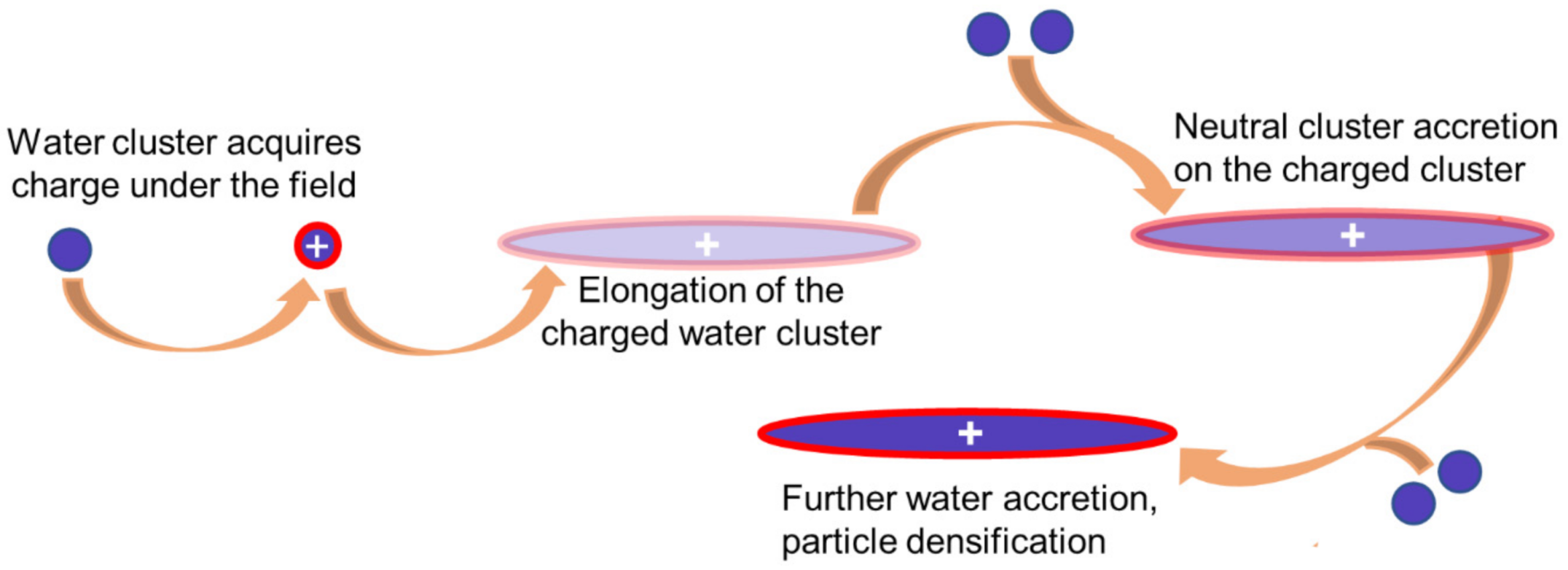
3.2. A Non-Classical Path for Ice Particle Formation Enhancement under an Electric Field
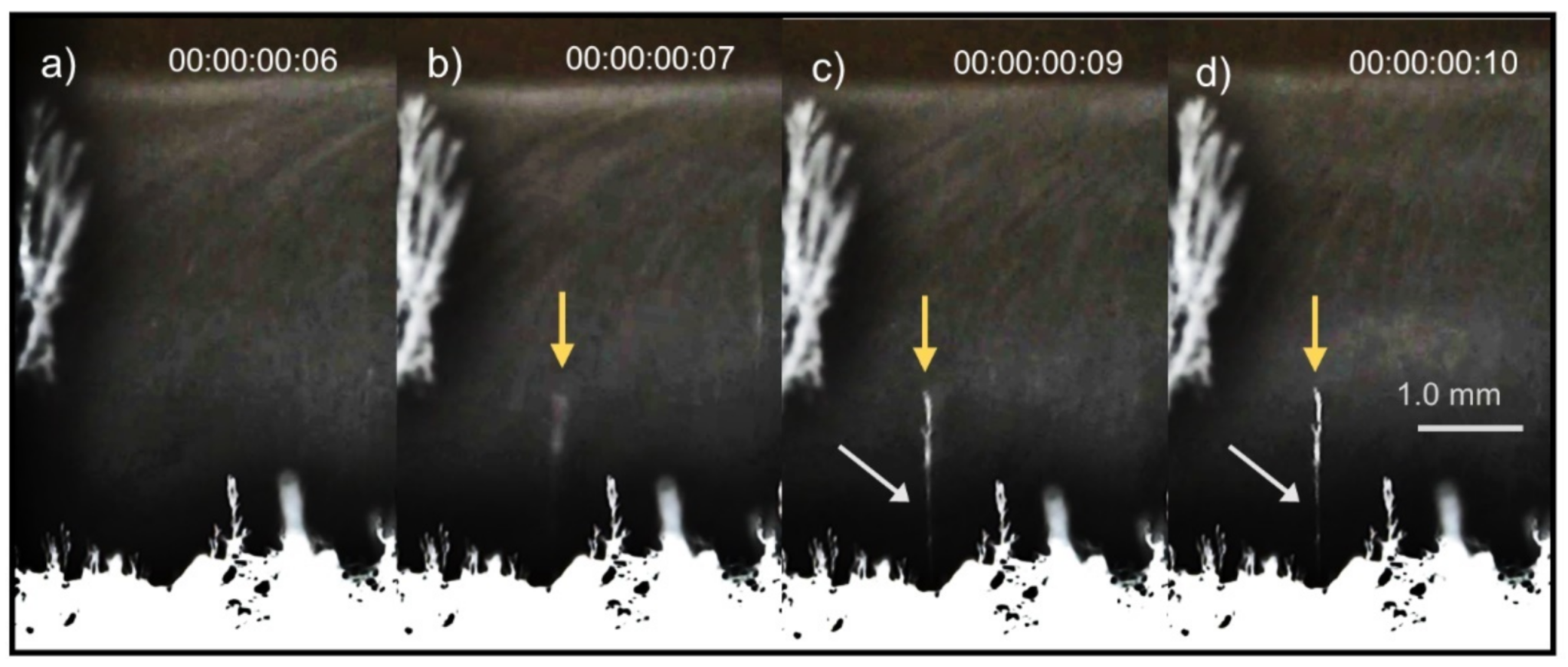
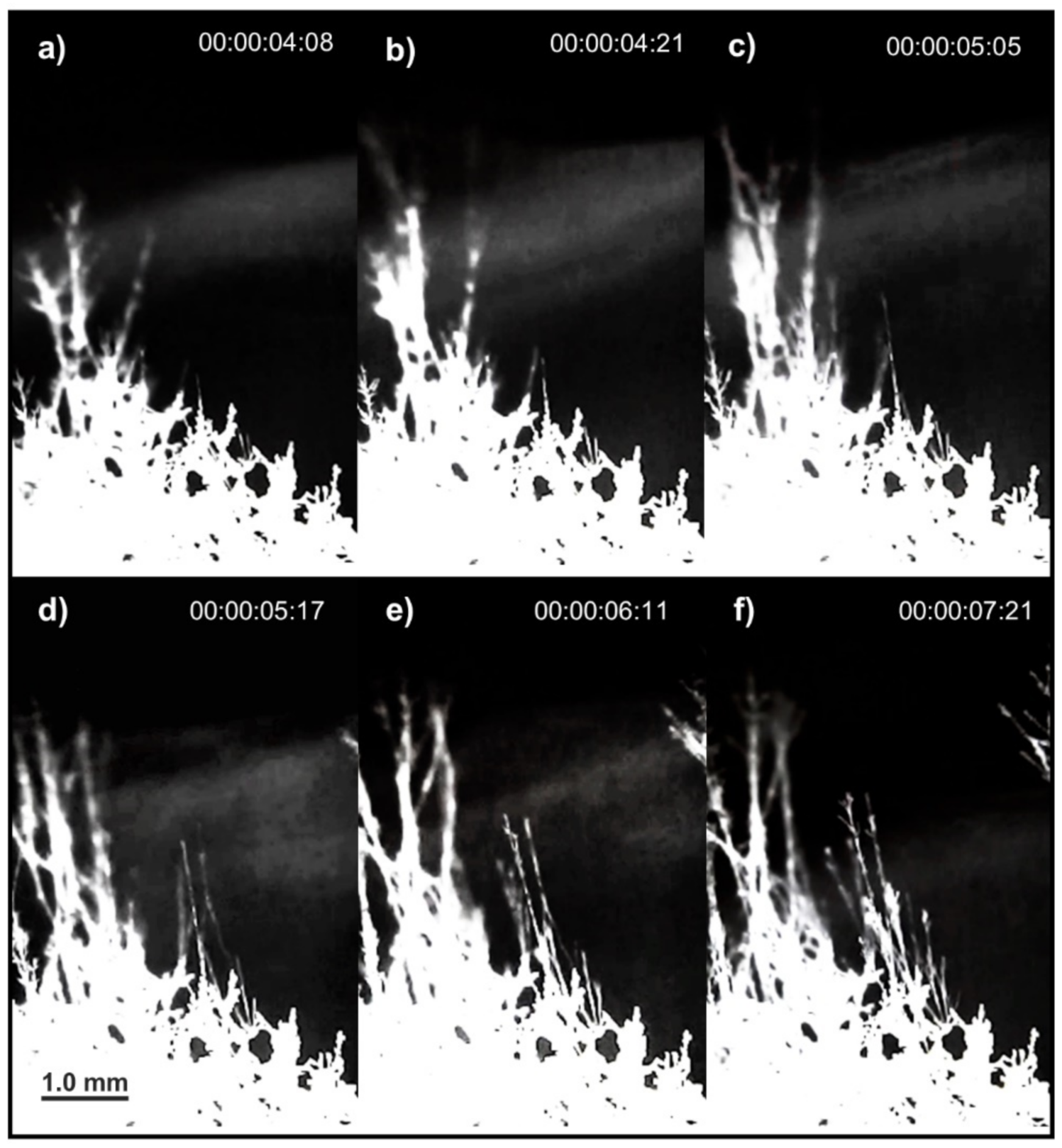
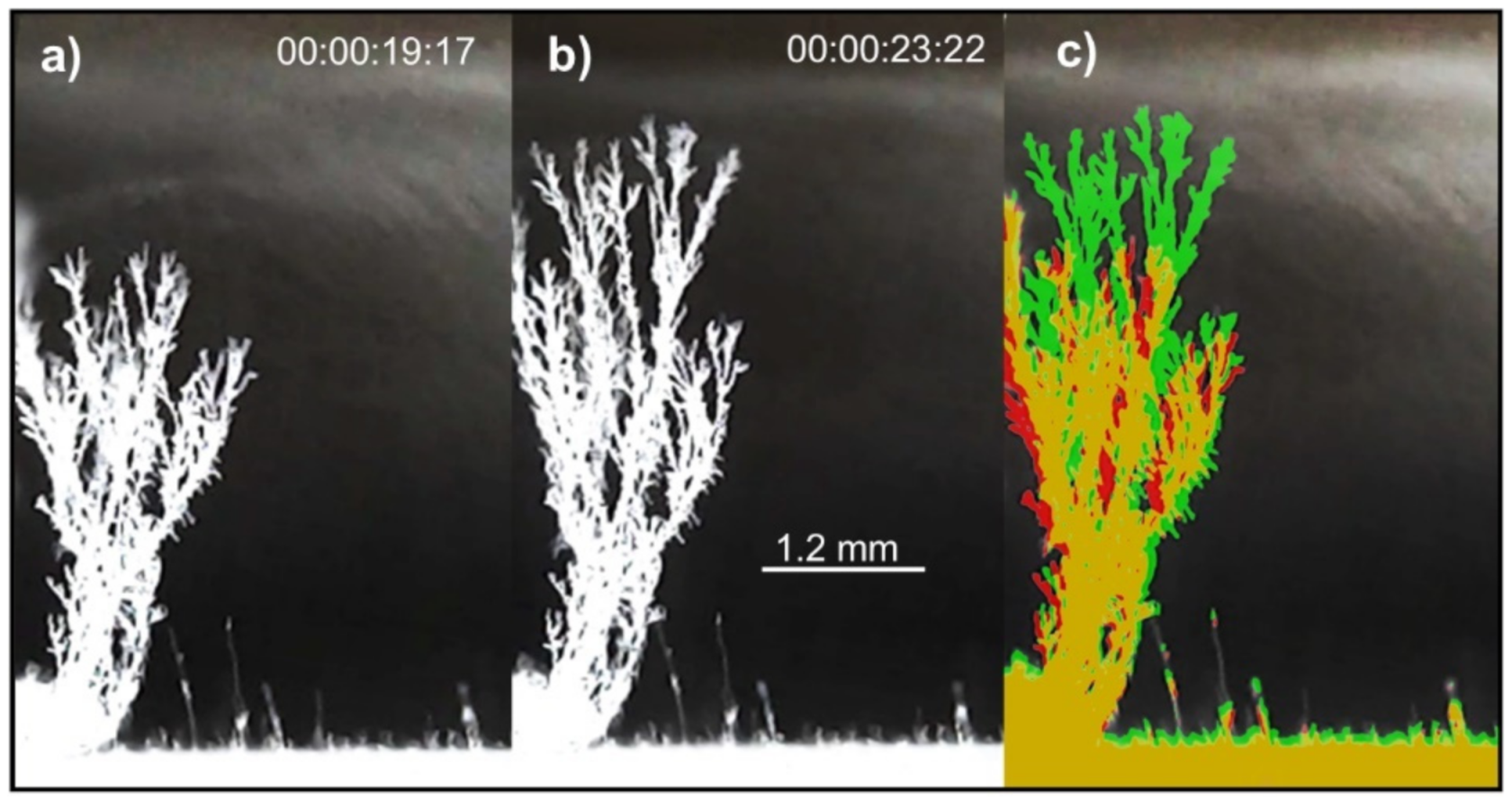
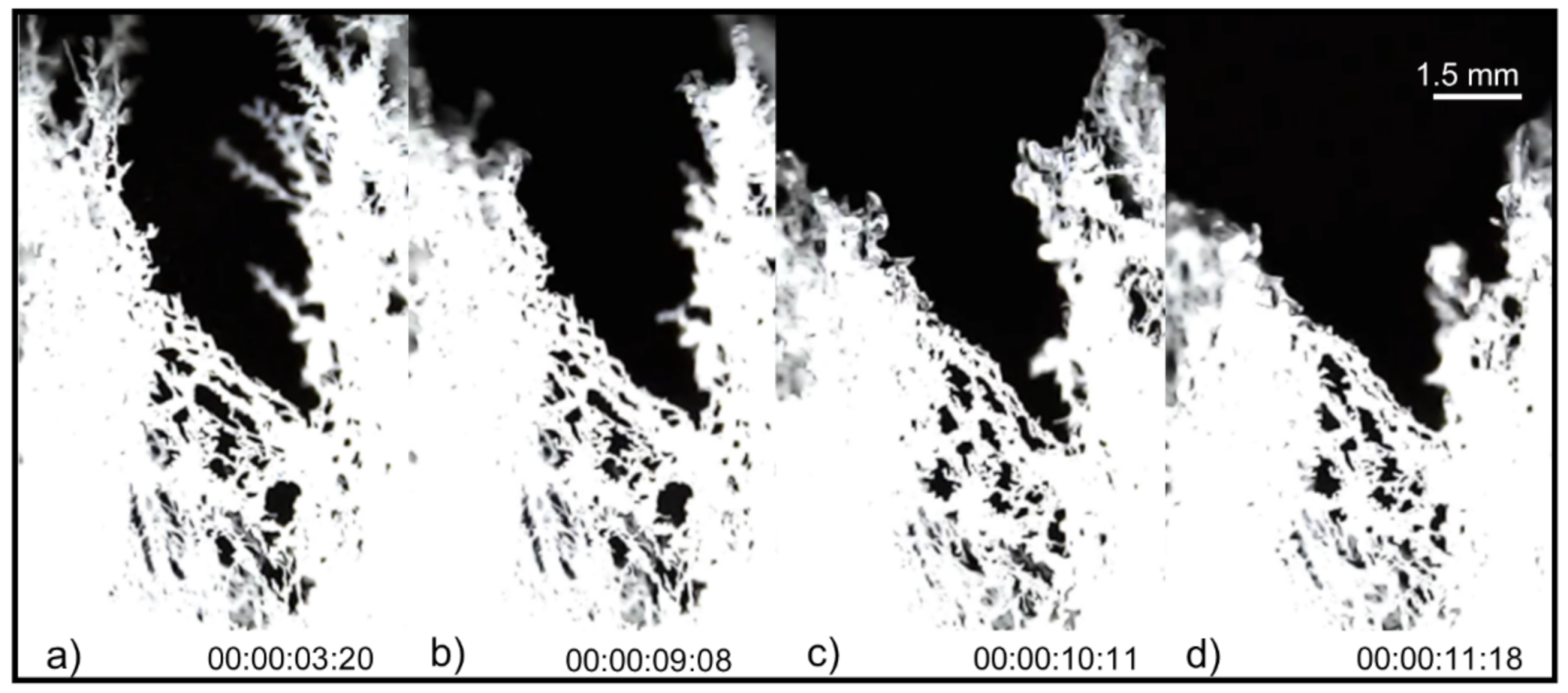
4. Results
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surfaces, 6th ed.; Wiley: New York, NY, USA, 1997; Chapter IX. [Google Scholar]
- Apfel, R.E. Water Superheated to 279.5 °C at Atmospheric Pressure. Nat. Phys. Sci. 1972, 238, 63–64. [Google Scholar] [CrossRef]
- Wölk, J.; Strey, R.; Heath, C.H.; Wyslouzil, B.E. Empirical function for homogeneous water nucleation rates. J. Chem. Phys. 2002, 117, 4954–4960. [Google Scholar] [CrossRef]
- Debenedetti, P.G. Metastable Liquids: Concepts and Principles; Princeton University Press: Princeton, NJ, USA, 1996. [Google Scholar]
- Carlson, M.T.; Green, A.J.; Richardson, H.H. Superheating Water by CW Excitation of Gold Nanodots. Nano Lett. 2012, 12, 1534–1537. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-Y.; Svensson, G.; Brandenburg, A.; Haugen, N.E.L. Cloud-droplet growth due to supersaturation fluctuations in stratiform clouds. Atmos. Chem. Phys. 2019, 19, 639–648. [Google Scholar] [CrossRef] [Green Version]
- Bakhtar, F.; Young, J.B.; White, A.; Simpson, D.A. Classical Nucleation Theory and Its Application to Condensing Steam Flow Calculations. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 2005, 219, 1315–1333. [Google Scholar] [CrossRef]
- Volmer, M.; Weber, A. Keimbildung in übersättigten Gebilden. Z. Für Phys. Chem. 1926, 119, 277–301. [Google Scholar] [CrossRef]
- Sear, R. Nucleation: Theory and applications to protein solutions and colloidal suspensions. J. Phys. Condens. Matter 2007, 19, 033101. [Google Scholar] [CrossRef]
- Liu, X.Y. Heterogeneous nucleation or homogeneous nucleation? J. Chem. Phys. 2000, 112, 9949–9955. [Google Scholar] [CrossRef]
- Cahn, J.W. Spinodal Decomposition. Trans. Met. Soc. AIME 1968, 242, 168–180. [Google Scholar]
- De Yoreo, J.J.; Gilbert, P.U.P.A.; Sommerdijk, N.A.J.M.; Penn, R.L.; Whitelam, S.; Joester, D.; Zhang, H.; Rimer, J.D.; Navrotsky, A.; Banfield, J.F.; et al. Crystallization by particle attachment in synthetic, biogenic, and geologic environments. Science 2015, 349, aaa6760. [Google Scholar] [CrossRef]
- Ivanov, V.K.; Fedorov, P.P.; Baranchikov, A.Y.; Osiko, V.V. Oriented attachment of particles: 100 years of investigations of non-classical crystal growth. Russ. Chem. Rev. 2014, 83, 1204–1222. [Google Scholar] [CrossRef]
- Li, M.; Schnablegger, H.; Mann, S. Coupled synthesis and self-assembly of nanoparticles to give structures with controlled organization. Nature 1999, 402, 393–395. [Google Scholar] [CrossRef]
- Cölfen, H.; Antonietti, M. Mesocrystals: Inorganic Superstructures Made by Highly Parallel Crystallization and Controlled Alignment. Angew. Chem. Int. Ed. 2005, 44, 5576–5591. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Böhm, C.F.; Harris, J.; Schodder, P.I.; Wolf, S.E. Bioinspired Materials: From Living Systems to New Concepts in Materials Chemistry. Materials 2019, 12, 2117. [Google Scholar] [CrossRef] [Green Version]
- Maeda, N. Brief Overview of Ice Nucleation. Molecules 2021, 26, 392. [Google Scholar] [CrossRef]
- Hakimian, A.; Mohebinia, M.; Nazari, M.; Davoodabadi, A.; Nazifi, S.; Huang, Z.; Bao, J.; Ghasemi, H. Freezing of few nanometers water droplets. Nat. Commun. 2021, 12, 1–8. [Google Scholar] [CrossRef]
- Han, G.; Hu, Q. Effects of Electric Field on Saturated Vapor Pressure. J. Phys. Chem. C 2019, 124, 1820–1826. [Google Scholar] [CrossRef]
- Jha, P.K.; Sadot, M.; Vino, S.A.; Jury, V.; Curet-Ploquin, S.; Rouaud, O.; Havet, M.; Le-Bail, A. A review on effect of DC voltage on crystallization process in food systems. Innov. Food Sci. Emerg. Technol. 2017, 42, 204–219. [Google Scholar] [CrossRef]
- Carpenter, K.; Bahadur, V. Electronucleation for Rapid and Controlled Formation of Hydrates. J. Phys. Chem. Lett. 2016, 7, 2465–2469. [Google Scholar] [CrossRef] [Green Version]
- Grabowska, J.; Kuffel, A.; Zielkiewicz, J. The accretion of the new ice layer on the surface of hexagonal ice crystal and the influence of the local electric field on this process. J. Chem. Phys. 2017, 147, 174502. [Google Scholar] [CrossRef]
- Budevski, E.; Staikov, G.; Lorenz, W. Electrocrystallization: Nucleation and growth phenomena. Electrochim. Acta 2000, 45, 2559–2574. [Google Scholar] [CrossRef]
- Yang, F.; Shaw, R.A.; Gurganus, C.W.; Chong, S.K.; Yap, Y.K. Ice nucleation at the contact line triggered by transient electrowetting fields. Appl. Phys. Lett. 2015, 107, 264101. [Google Scholar] [CrossRef]
- Peleg, Y.; Yoffe, A.; Ehre, D.; Lahav, M.; Lubomirsky, I. The Role of the Electric Field in Electrofreezing. J. Phys. Chem. C 2019, 123, 30443–30446. [Google Scholar] [CrossRef]
- Busch, S.; Dolhaine, H.; DuChesne, A.; Heinz, S.; Hochrein, O.; Laeri, F.; Podebrad, O.; Vietze, U.; Weiland, T.; Kniep, R. Biomimetic Morphogenesis of Fluorapatite-Gelatin Composites: Fractal Growth, the Question of Intrinsic Electric Fields, Core/Shell Assemblies, Hollow Spheres and Reorganization of Denatured Collagen. Eur. J. Inorg. Chem. 1999, 10, 1643–1653. [Google Scholar] [CrossRef]
- Santos, L.P.; da Silva, D.S.; Galembeck, A.; Galembeck, F. Ice Needle Nucleation and Dendrite Growth under an Electric Field. IEEE Trans. Ind. Appl. 2021. [Google Scholar] [CrossRef]
- Ferreira, E.S.; da Silva, D.S.; Burgo, T.A.L.; Batista, B.C.; Galembeck, F. Graphite exfoliation in cellulose solutions. Nanoscale 2017, 9, 10219–10226. [Google Scholar] [CrossRef]
- Santos, L.P.; da Silva, D.S.; Bertacchi, J.P.F.; Moreira, K.S.; Burgo, T.A.D.L.; Batista, B.C.; dos Santos, J.; de Paula, P.A.; Galembeck, F. Multifunctional coatings of exfoliated and reassembled graphite on cellulosic substrates. Faraday Discuss. 2020, 227, 105–124. [Google Scholar] [CrossRef] [Green Version]
- Job, G.; Rüffler, R. Physical Chemistry from a Different Angle, 1st ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Tolman, R.C. The Effect of Droplet Size on Surface Tension. J. Chem. Phys. 1949, 17, 333–337. [Google Scholar] [CrossRef] [Green Version]
- Benson, G.C.; Shuttleworth, R. The Surface Energy of Small Nuclei. J. Chem. Phys. 1951, 19, 130–131. [Google Scholar] [CrossRef]
- Courtney, W.G. Remarks on Homogeneous Nucleation. J. Chem. Phys. 1961, 35, 2249–2250. [Google Scholar] [CrossRef]
- Santos, L.P.; Ducati, T.R.D.; Balestrin, L.; Galembeck, F. Water with Excess Electric Charge. J. Phys. Chem. C 2011, 115, 11226–11232. [Google Scholar] [CrossRef]
- Djikaev, Y.S.; Ruckenstein, E. Self-Consistent Determination of the Ice–Air Interfacial Tension and Ice–Water–Air Line Tension from Experiments on the Freezing of Water Droplets. J. Phys. Chem. C 2017, 121, 16432–16439. [Google Scholar] [CrossRef]
- Karthika, S.; Radhakrishnan, T.; Kalaichelvi, P. A Review of Classical and Nonclassical Nucleation Theories. Cryst. Growth Des. 2016, 16, 6663–6681. [Google Scholar] [CrossRef]
- Bailey, M.P.; Hallett, J. A Comprehensive Habit Diagram for Atmospheric Ice Crystals: Confirmation from the Laboratory, AIRS II, and Other Field Studies. J. Atmos. Sci. 2009, 66, 2888–2899. [Google Scholar] [CrossRef] [Green Version]
- Nunes, S.P.; Inoue, T. Evidence for spinodal decomposition and nucleation and growth mechanisms during membrane formation. J. Membr. Sci. 1996, 111, 93–103. [Google Scholar] [CrossRef]
- Da Silva, A.K.; Ponge, D.; Peng, Z.; Inden, G.; Lu, Y.; Breen, A.; Gault, B.; Raabe, D. Phase nucleation through confined spinodal fluctuations at crystal defects evidenced in Fe-Mn alloys. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef]
- Priezjev, N.V.; Markev, M.A. Structural transformations and mechanical properties of porous glass under compressive loading. J. Non-Cryst. Solids 2018, 500, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Testard, V.; Berthier, L.; Kob, W. Influence of the Glass Transition on the Liquid-Gas Spinodal Decomposition. Phys. Rev. Lett. 2011, 106, 125702. [Google Scholar] [CrossRef]
- Sasidhar, K.; Meka, S. Spinodal decomposition during isothermal gas-solid equilibration—Its effects and implications. Acta Mater. 2018, 161, 266–272. [Google Scholar] [CrossRef]
- Schaefer, V.J.; Cheng, R.J. The production of ice crystal fragments by sublimation and electrification. J. Rech. Atmos. 1971, 5, 5–10. [Google Scholar]
- Oshika, Y.; Tsuchiya, Y.; Okumura, T.; Muramoto, Y. Alternating current breakdown voltage of ice electret. J. Phys. Conf. Ser. 2017, 897, 012006. [Google Scholar] [CrossRef]
- Buckley, J.R. A Study of Heterogeneous Nucleation and Electrostatic Charge in Steam Flows. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2003. [Google Scholar]
- Rydock, J.P.; Williams, E.R. Charge separation associated with frost growth. Q. J. R. Meteorol. Soc. 1991, 117, 409–410. [Google Scholar] [CrossRef]
- Mukherjee, R.; Ahmadi, S.F.; Zhang, H.; Qiao, R.; Boreyko, J.B. Electrostatic Jumping of Frost. ACS Nano 2021, 15, 4669–4677. [Google Scholar] [CrossRef] [PubMed]
- Santos, L.P.; da Silva, D.S.; Galembeck, A.; Galembeck, F. Ice Needle Nucleation and Dendrite Growth Under an Electric Field. In Proceedings of the 2020 IEEE Industry Applications Society Annual Meeting, Detroit, MI, USA, 10–16 October 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Hagopian, A.; Doublet, M.-L.; Filhol, J.-S. Thermodynamic origin of dendrite growth in metal anode batteries. Energy Environ. Sci. 2020, 13, 5186–5197. [Google Scholar] [CrossRef]
- Tohmfor, G.; Volmer, M. Die Keimbildung unter dem Einfluß elektrischer Ladungen. Ann. Der Phys. 1938, 425, 109–131. [Google Scholar] [CrossRef]
- Field, P.R.; Lawson, R.P.; Brown, P.R.A.; Lloyd, G.; Westbrook, C.; Moisseev, D.; Miltenberger, A.; Nenes, A.; Blyth, A.; Choularton, T.; et al. Chapter 7. Secondary Ice Production—Current state of the science and recommendations for the future. Meteorol. Monogr. 2016, 58, 7.1–7.20. [Google Scholar] [CrossRef] [Green Version]
- Martin, S.T. Phase Transitions of Aqueous Atmospheric Particles. Chem. Rev. 2000, 100, 3403–3454. [Google Scholar] [CrossRef]






| Particle Radius (m) | Temperature (°C) | = 0.09 N/m b | = 0.02 N/m c | = 5 × 10−3 N/m c | = 10−3 N/m c | |
|---|---|---|---|---|---|---|
| 3 × 10−10 | −5 | −35 | 17,965 | 3965 | 965 | 165 |
| 1 × 10−9 | 5365 | 1165 | 265 | 25 | ||
| 3 × 10−9 | 1765 | 365 | 65 | −15 | ||
| 1 × 10−8 | 505 | 85 | −5 | −29 | ||
| 3 × 10−8 | 145 | 5 | −25 | −33 | ||
| 1 × 10−7 | 19 | −23 | −32 | −34 | ||
| 3 × 10−7 | −17 | −31 | −34 | −35 | ||
| 1 × 10−6 | −30 | −34 | −35 | −35 | ||
| 3 × 10−10 | −15 | −285 | 17,715 | 3715 | 715 | −85 |
| 1 × 10−9 | 5115 | 915 | 15 | −225 | ||
| 3 × 10−9 | 1515 | 115 | −185 | −265 | ||
| 1 × 10−8 | 255 | −165 | −255 | −279 | ||
| 3 × 10−8 | −105 | −245 | −275 | −283 | ||
| 1 × 10−7 | −231 | −273 | −282 | −284 | ||
| 3 × 10−7 | −267 | −281 | −284 | −285 | ||
| 1 × 10−6 | −280 | −284 | −285 | −285 |
| Image Component | Measured Length or Height/μm | Growth Rate/μm s−1 |
|---|---|---|
| Top dendrite branches | 850 | 189 |
| 810 | 180 | |
| 850 | 189 | |
| 890 | 200 | |
| 1280 | 284 | |
| 850 | 189 | |
| 770 | 171 | |
| Lower dendrite branches | 150 | 33 |
| 230 | 51 | |
| 120 | 27 | |
| Needles | <40 | <9 |
| <40 | <9 | |
| <40 | <9 | |
| Lower ice layer | 40–80 | 9–18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, L.P.; da Silva, D.S.; Galembeck, A.; Galembeck, F. Electric Fields Enhance Ice Formation from Water Vapor by Decreasing the Nucleation Energy Barrier. Colloids Interfaces 2022, 6, 13. https://doi.org/10.3390/colloids6010013
Santos LP, da Silva DS, Galembeck A, Galembeck F. Electric Fields Enhance Ice Formation from Water Vapor by Decreasing the Nucleation Energy Barrier. Colloids and Interfaces. 2022; 6(1):13. https://doi.org/10.3390/colloids6010013
Chicago/Turabian StyleSantos, Leandra P., Douglas S. da Silva, André Galembeck, and Fernando Galembeck. 2022. "Electric Fields Enhance Ice Formation from Water Vapor by Decreasing the Nucleation Energy Barrier" Colloids and Interfaces 6, no. 1: 13. https://doi.org/10.3390/colloids6010013
APA StyleSantos, L. P., da Silva, D. S., Galembeck, A., & Galembeck, F. (2022). Electric Fields Enhance Ice Formation from Water Vapor by Decreasing the Nucleation Energy Barrier. Colloids and Interfaces, 6(1), 13. https://doi.org/10.3390/colloids6010013






