Interfacial Dilational Viscoelasticity of Adsorption Layers at the Hydrocarbon/Water Interface: The Fractional Maxwell Model
Abstract
1. Introduction
2. Materials and Method
2.1. Materials
2.2. Apparatus
2.3. Experimental Procedure
3. Brief Outline of the Applied Model
3.1. The Interfacial Dilational Viscoelastic Modulus
3.2. Maxwell Model
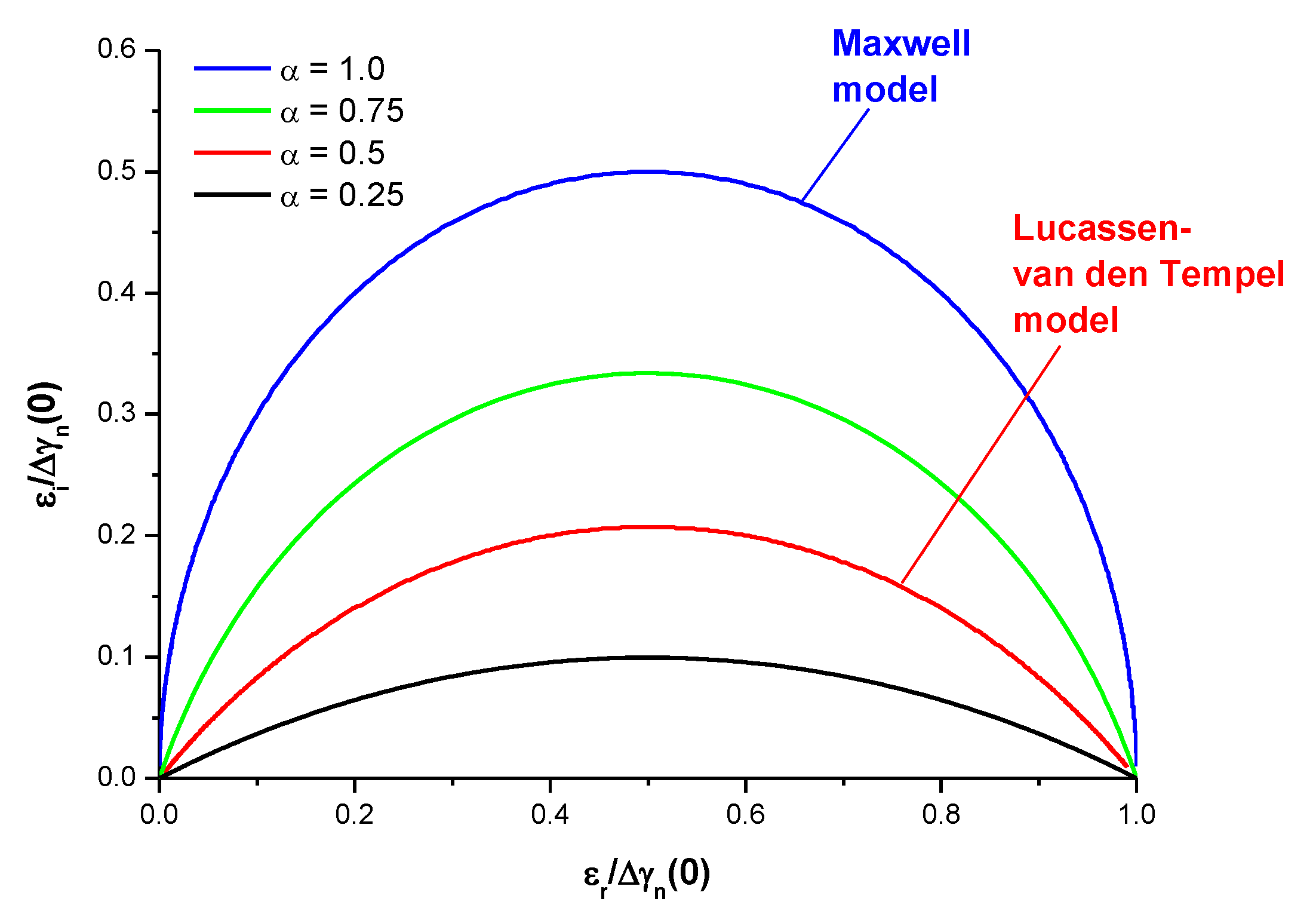
3.3. Fractional Maxwell Model
3.4. Lucassen–van den Tempel Model
4. Results and Discussion
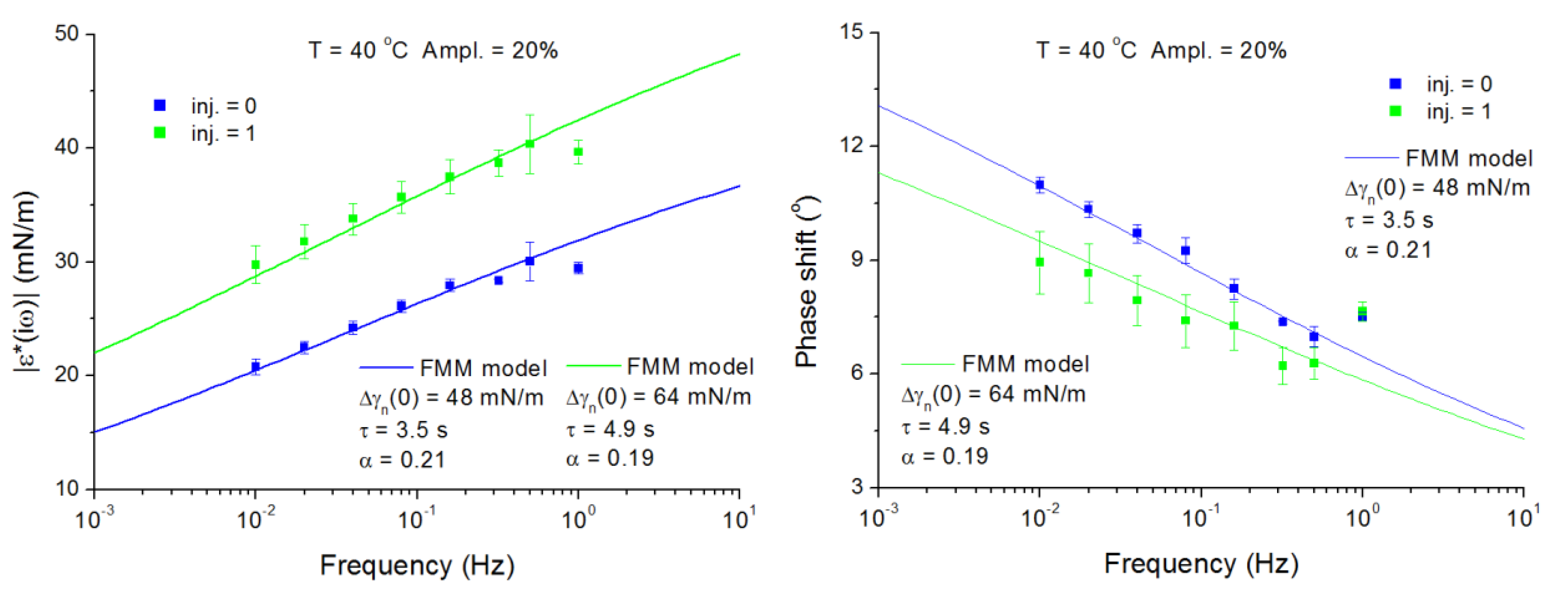
4.1. Span-80 Adsorption Layers at Paraffin–Oil/Water Interface
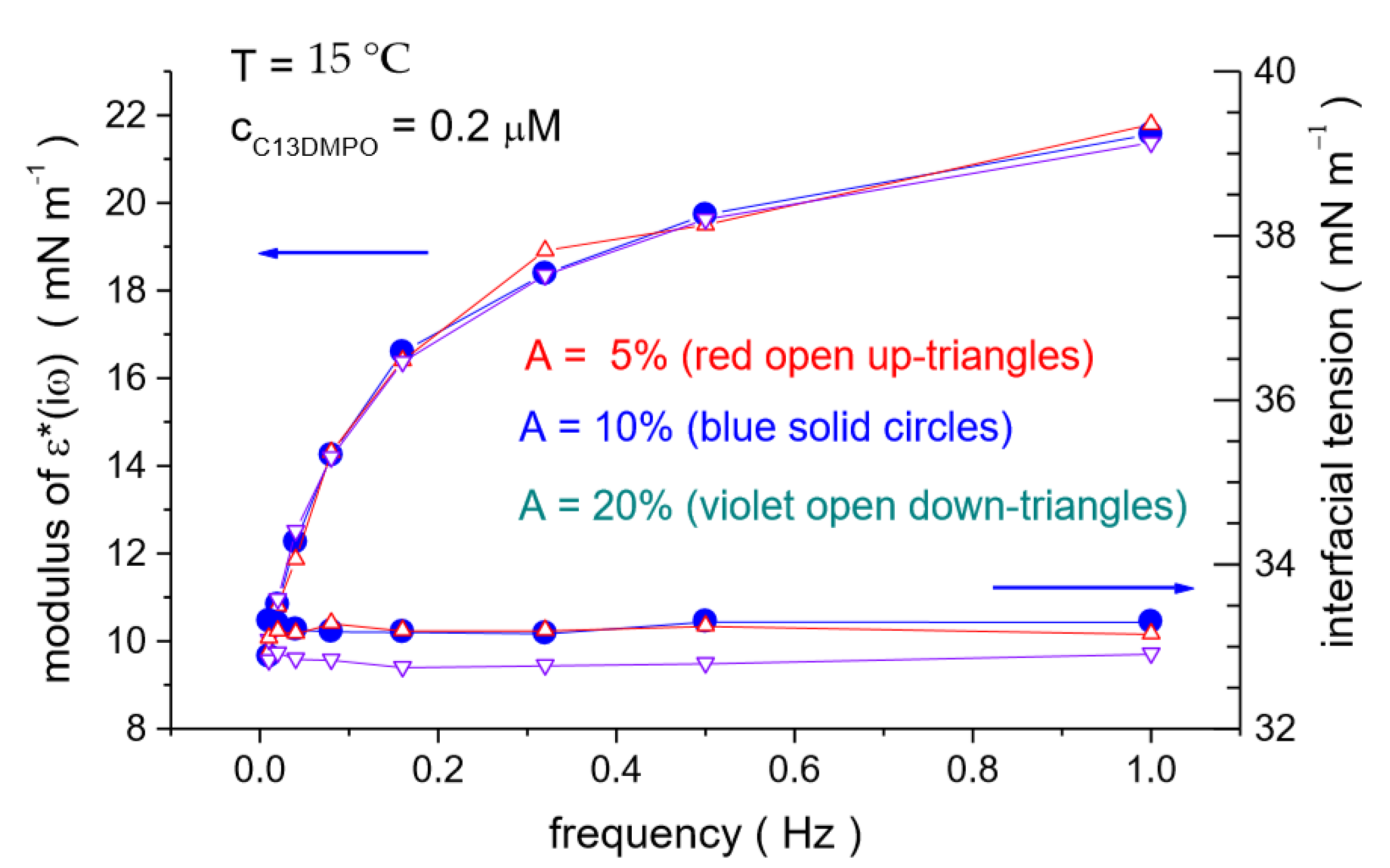
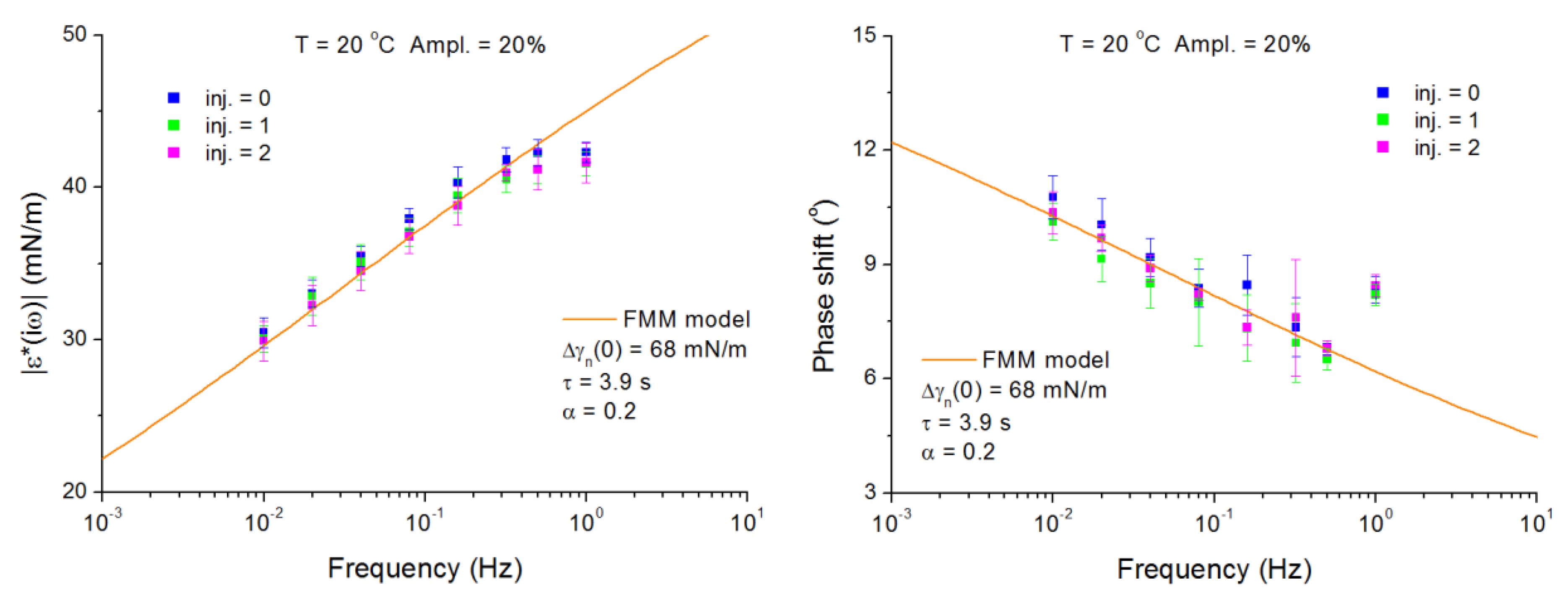
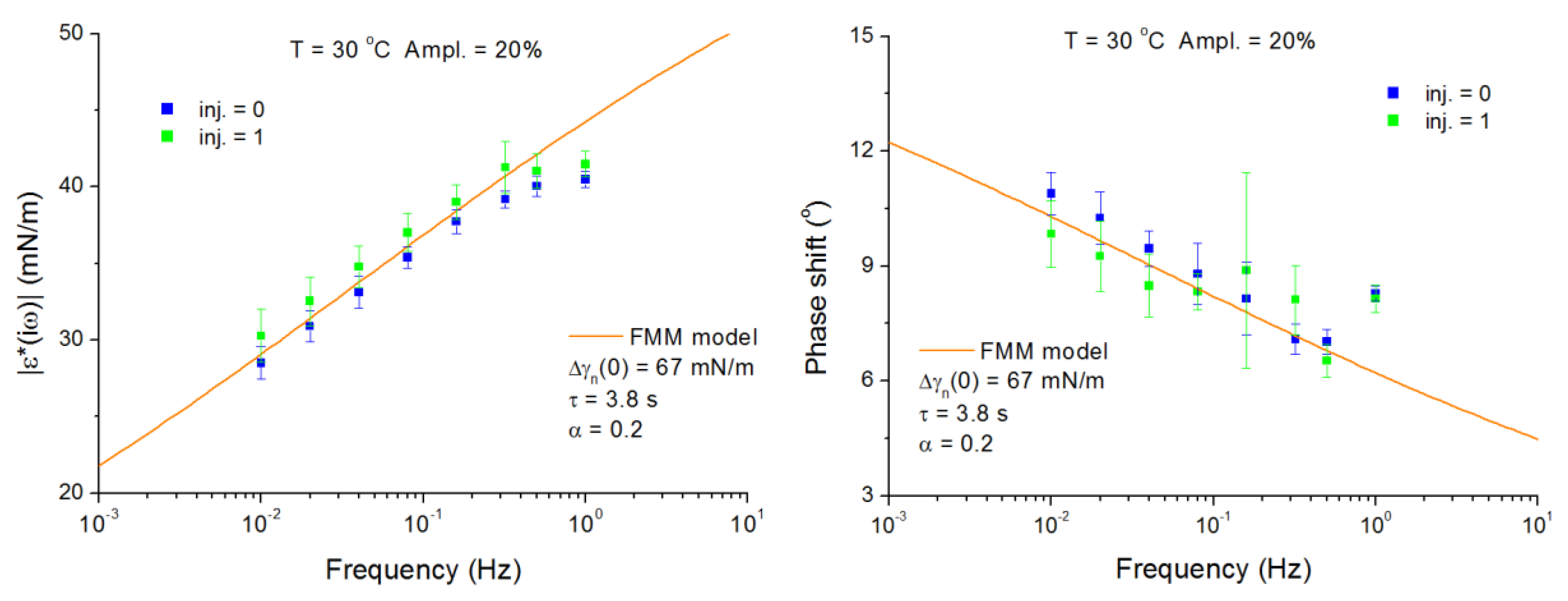
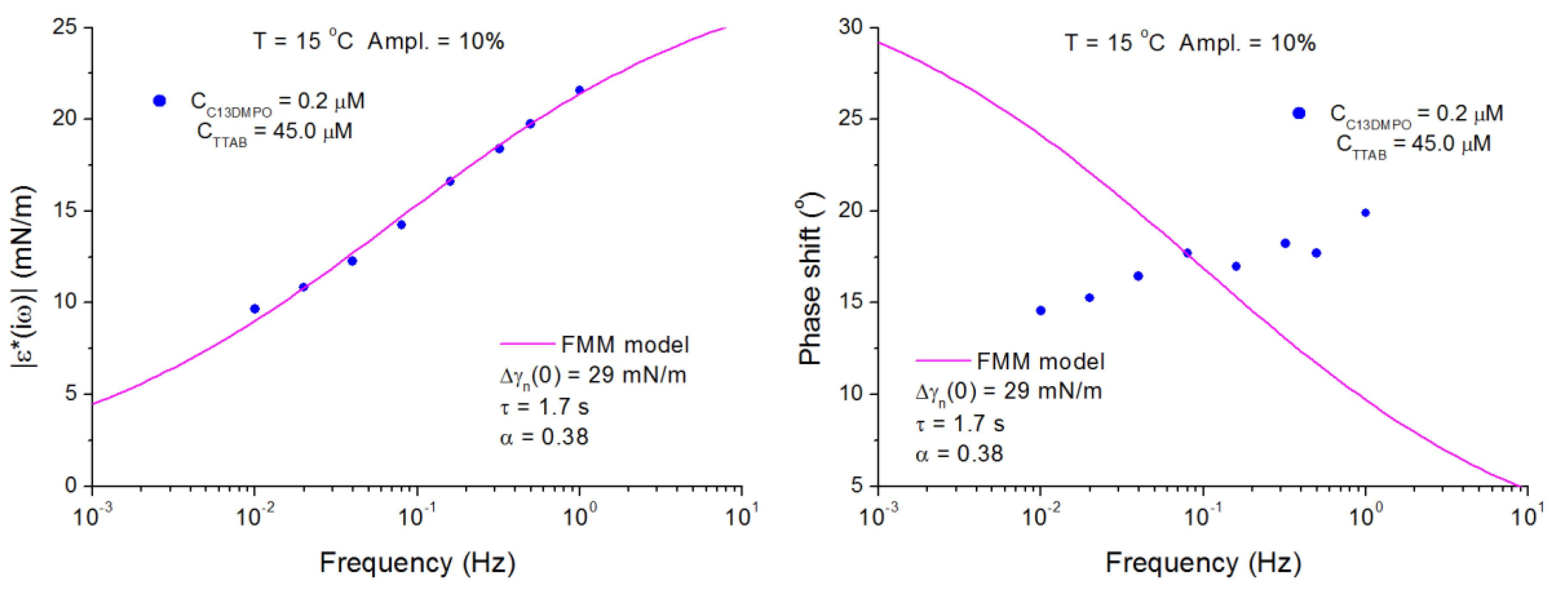
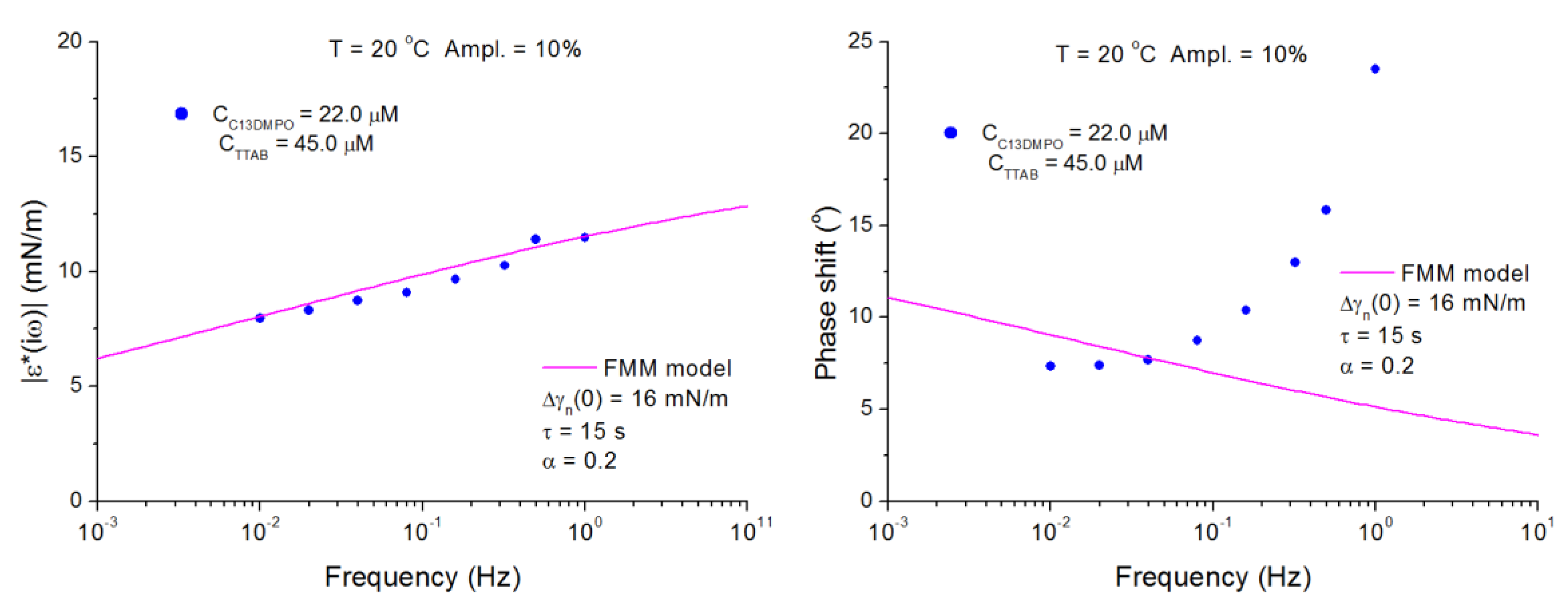
4.2. C13DMPO/TTAB Adsorption Layers at Water/Hexane Interface
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Francois, D.; Pineau, A.; Zaoui, A. Solid mechanics and its applications 180. In Viscoelasticity. Mechanical Behavior of Materials. Volume 1: Micro- and Macroscopic Constitutive Behavior; Springer Netherlands: Haarlem, The Netherlands, 2012; pp. 113, 283. [Google Scholar] [CrossRef]
- Herman, I.P. Physics of the Human Body, Biological and Medical Physics, Biomedical Engineering; Springer International Publishing: Basel, Switzerland, 2016; p. 247. [Google Scholar] [CrossRef]
- Rosales-Anzola, S.D.; García-Sucre, M.; Urbina-Villalba, G.; Lopez, E. Surface dilational viscoelasticity of surfactants. In Topics in the Colloidal Aggregation and Interfacial Phenomena; Garcia-Sucre, M., Loszan, A., Castellanos-Suarez, A.J., Toro-Mendoza, J., Eds.; Research Signpost: Kerala, India, 2012; ISBN 978-81-308-0491-0. [Google Scholar]
- Krotov, V.V. Basics of interfacial rheology. In Interfacial Rheology, 1st ed.; Miller, R., Liggieri, L., Eds.; CRC Press: Boca Raton, FL, USA, 2009; Volume 1, pp. 1–37. [Google Scholar]
- Geri, M.; Keshavarz, B.; Divoux, T.; Clasen, C.; Curtis, D.J.; McKinley, G.H. Time-resolved mechanical spectroscopy of soft materials via optimally windowed chirps. Phys. Rev. X 2018, 8, 041042. [Google Scholar] [CrossRef]
- Bouzid, M.; Keshavarz, B.; Geri, M.; Divoux, T.; Del Gado, E.; McKinley, G.H. Computing the linear viscoelastic properties of soft gels using an optimally windowed chirp protocol. J. Rheol. 2018, 62, 1037–1050. [Google Scholar] [CrossRef]
- Arikoglu, A. A new fractional derivative model for linearly viscoelastic materials and parameter identification via genetic algorithms. Rheol. Acta 2014, 53, 219–233. [Google Scholar] [CrossRef]
- Pritchard, R.H.; Terentjev, E.M. Oscillations and damping in the fractional Maxwell materials. J. Rheol. 2017, 61, 187–203. [Google Scholar] [CrossRef]
- Holmes, M.H. Texts in applied mathematics 56. In Introduction to the Foundations of Applied Mathematics; Springer Science and Business Media: Berlin, Germany, 2009; p. 311. [Google Scholar] [CrossRef]
- Meral, F.C.; Royston, T.J.; Magin, R. Fractional calculus in viscoelasicity: An experimental study. Commun. Nonlinear Sci. Numer. Simulat. 2010, 15, 939–945. [Google Scholar] [CrossRef]
- Costa, M.F.P.; Ribeiro, C. Generalized fractional Maxwell model: Parameter estimation of a viscoelastic material. AIP Conf. Proc. 2012, 1479, 790–793. [Google Scholar] [CrossRef]
- Costa, M.F.P.; Ribeiro, C. A modified fractional Zener model to describe the behavior of a carbon fibre reinforced polymer. AIP Conf. Proc. 2013, 1558, 606–609. [Google Scholar] [CrossRef]
- Yu, Y.; Perdikaris, P.; Karniadakis, G.E. Fractional modeling of viscoelasticity in 3D cerebral arteries and aneurysms. J. Comput. Phys. 2016, 323, 219–242. [Google Scholar] [CrossRef] [PubMed]
- Lei, D.; Liang, Y.; Xiao, R. A fractional model with parallel fractional Maxwell elements for amorphous thermoplastics. Physica A 2018, 490, 465–475. [Google Scholar] [CrossRef]
- Stankiewicz, A. Fractional Maxwell model of viscoelastic biological materials. BIO Web Conf. 2018, 10, 02032. [Google Scholar] [CrossRef]
- Povstenko, Y. Essentials of fractional calculus. In Fractional Thermoelasticity. In Fractional Thermoelasticity; Springer International Publishing: Basel, Switzerland, 2015; Volume 219. [Google Scholar] [CrossRef]
- Jaishankar, A.; Sharma, V.; MacKinley, G.H. Interfacial viscoelasticity, yielding and creep ringing of globulin protein-surfactant mixtures. Soft Matter 2011, 7, 7623–7634. [Google Scholar] [CrossRef]
- Jaishankar, A.; MacKinley, G.H. Power-law rheology in the bulk and at the interface: Quasi-properties and fractional constitutive equations. Proc. Roy. Soc. A 2012, 469, 20120484. [Google Scholar] [CrossRef]
- Sharma, V.; Jaishankar, A.; Wang, Y.-C.; MacKinley, G.H. Rheology of bulk protein, apparent yield stress, high shear rate viscosity and viscoelasticity of albumine serum solutions. Soft Matter 2011, 7, 5150–5160. [Google Scholar] [CrossRef]
- Pandolfini, P.; Loglio, G.; Ravera, F.; Liggieri, L.; Kovalchuk, V.I.; Javadi, A.; Karbaschi, M.; Krägel, J.; Miller, R.; Noskov, B.A.; et al. Dynamic properties of Span-80 adsorbed layers at paraffin–oil/water interface: Capillary pressure experiments under low gravity conditions. Colloids Surf. A Physicochem. Eng. Asp. 2017, 532, 228–243. [Google Scholar] [CrossRef]
- Loglio, G.; Kovalchuk, V.I.; Bykov, A.G.; Ferrari, M.; Krägel, J.; Liggieri, L.; Miller, R.; Noskov, B.A.; Pandolfini, P.; Ravera, F.; et al. Dynamic properties of mixed cationic/nonionic adsorbed layers at the n-hexane/water interface: Capillary pressure experiments under low gravity conditions. Colloids Interfaces 2018, 2, 53. [Google Scholar] [CrossRef]
- Lucassen, J.; Van den Tempel, M. Dynamic measurements of dilational properties of a liquid interface. Chem. Eng. Sci. 1972, 27, 1283–1291. [Google Scholar] [CrossRef]
- Loglio, G.; Tesei, U.; Cini, R. Spectral Data of Surface Viscoelastic Modulus Acquired via Digital Fourier Transformation. J. Colloid Interface Sci. 1979, 71, 316–320. [Google Scholar] [CrossRef]
- Noskov, B.A.; Loglio, G. Dynamic surface elasticity of surfactant solutions. Colloids Surf. A 1998, 143, 167–183. [Google Scholar] [CrossRef]
- Joos, P. Dynamic Surface Phenomena; VSP: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Ravera, F.; Ferrari, M.; Liggieri, L.; Miller, R.; Passerone, A. Measurement of the partition coefficient of surfactants in water/oil systems. Langmuir 1997, 13, 4817–4820. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loglio, G.; Kovalchuk, V.I.; Bykov, A.G.; Ferrari, M.; Krägel, J.; Liggieri, L.; Miller, R.; Noskov, B.A.; Pandolfini, P.; Ravera, F.; et al. Interfacial Dilational Viscoelasticity of Adsorption Layers at the Hydrocarbon/Water Interface: The Fractional Maxwell Model. Colloids Interfaces 2019, 3, 66. https://doi.org/10.3390/colloids3040066
Loglio G, Kovalchuk VI, Bykov AG, Ferrari M, Krägel J, Liggieri L, Miller R, Noskov BA, Pandolfini P, Ravera F, et al. Interfacial Dilational Viscoelasticity of Adsorption Layers at the Hydrocarbon/Water Interface: The Fractional Maxwell Model. Colloids and Interfaces. 2019; 3(4):66. https://doi.org/10.3390/colloids3040066
Chicago/Turabian StyleLoglio, Giuseppe, Volodymyr I. Kovalchuk, Alexey G. Bykov, Michele Ferrari, Jürgen Krägel, Libero Liggieri, Reinhard Miller, Boris A. Noskov, Piero Pandolfini, Francesca Ravera, and et al. 2019. "Interfacial Dilational Viscoelasticity of Adsorption Layers at the Hydrocarbon/Water Interface: The Fractional Maxwell Model" Colloids and Interfaces 3, no. 4: 66. https://doi.org/10.3390/colloids3040066
APA StyleLoglio, G., Kovalchuk, V. I., Bykov, A. G., Ferrari, M., Krägel, J., Liggieri, L., Miller, R., Noskov, B. A., Pandolfini, P., Ravera, F., & Santini, E. (2019). Interfacial Dilational Viscoelasticity of Adsorption Layers at the Hydrocarbon/Water Interface: The Fractional Maxwell Model. Colloids and Interfaces, 3(4), 66. https://doi.org/10.3390/colloids3040066








