Superspreading on Hydrophobic Substrates: Effect of Glycerol Additive

Abstract

The spreading of solutions of three trisiloxane surfactants on two hydrophobic substrates, polyethylene and polyvinylidenefluoride, was studied with the addition of 0–40 mass % of glycerol. It was found that all the surfactant solutions spread faster than silicone oil of the same viscosity, confirming the existence of a mechanism which accelerates the spreading of the surfactant solutions. For the non-superspreading surfactant, BT-233, addition of glycerol improved the spreading performance on polyvinylidenefluoride and resulted in a transition from partial to complete wetting on polyethylene. The fastest spreading was observed for BT-233 at a concentration of 2.5 g/L, independent of glycerol content. For the superspreading surfactants, BT-240 and BT-278, the concentration at which the fastest spreading occurs systematically increased with concentration of glycerol on both substrates from 1.25 g/L for solutions in water to 10 g/L for solutions in 40% glycerol/water mixture. Thus, the surfactant equilibration rate (and therefore formation of surface tension gradients) and Marangoni flow are important components of a superspreading mechanism. De-wetting of the solutions containing glycerol, once spread on the substrates, resulted in the formation of circular drop patterns. This is in contrast to the solely aqueous solutions where the spread film shrank due to evaporation, without any visible traces being left behind.

1. Introduction

Surfactants are broadly used to enhance spreading performance of aqueous formulations over hydrophobic substrates [1,2,3,4] with example applications in coating, painting, printing, agriculture and medicine. The contact angle of pure water on many polymeric materials of industrial importance and on biological surfaces is around or above 90°. Surfactants decrease the interfacial tension on the liquid/air and liquid/solid interfaces and, therefore, improve wetting.

It is not straightforward to find surfactants which can provide complete wetting on highly hydrophobic surfaces such as polyethylene or plant leaves. Even solutions of fluorosurfactants, which reduce the surface tension of water to very low values (17–20 mN/m) do not provide complete wetting of these surfaces due to low adsorption at the liquid/solid interface [5]. Branched surfactants, such as dioctyl sodium sulfosuccinate (Aerosol OT) [6,7] or synergetic surfactant mixtures are often used to facilitate spreading [8,9,10]. However, the best performance is achieved with trisiloxane surfactants, often called superspreaders [11,12,13].

Superspreaders are able to spread over large surfaces forming a film of micron thickness. They spread very fast, faster than pure liquids with similar properties. The spreading of pure liquids follows the power law S ~ t^0.2 [14,15] to S ~ t^2/7 [16,17], where S is the spread area and t is time, whereas for superspreaders S ~ t [11,12]. Another peculiarity in the behaviour of superspreading solutions is a maximum in the dependencies of spread area upon surfactant concentration and upon substrate hydrophobicity.

Several mechanisms have been proposed to explain superspreading and its regularities. It has been suggested that the fast spreading is due to “caterpillar motion” of the liquid reducing hydrodynamic resistance at the leading edge of spreading [18]. This idea is supported by the specific T-shape of superspreading trisiloxane surfactants (see Figure 1) which is a favourable configuration to promote the caterpillar motion and adsorption at the three-phase contact line [19,20,21]. Another hypothesis which is related to the surfactant structure is the facilitation of spreading by bi-layer aggregates adsorbing at the leading edge and promoting water suction in their hydrophilic interior [22,23].

One of the proposed mechanisms explains superspreading due to Marangoni flow at the leading edge [6,24,25,26]. When a surfactant solution spreads over a substrate surface, both liquid/air and liquid/solid interfacial areas expand. Surfactant from the bulk adsorbs onto both interfaces and can also adsorb at the solid/air interface. If the surfactant transfer to the leading edge of spreading is not fast enough to replenish its loss due to adsorption, the surface tension local to this position increases due to surfactant depletion. This results in Marangoni flow in the direction of spreading, with scaling S ~ t^α where the spreading exponent, α, is in the range 0.5–1 depending on the length scale over which surface tension gradients develop [6,24].

This mechanism explains why spreading slows down at large concentrations as surfactant transfer then becomes fast enough to avoid depletion at the leading edge of spreading. Consequently, the Marangoni flow no longer contributes noticeably to the spreading kinetics, see [17,24] for more detailed discussion. The diffusive flux of surfactant is proportional to both the concentration difference and diffusion coefficient. Therefore, if Marangoni flow provides a crucial contribution to superspreading, a decrease in the diffusion coefficient should result in the shift of the maximum spreading to the larger concentrations. Comparison of spreading performance of two surfactants with different properties has shown that the surfactant which equilibrates slower spreads faster [27] as confirmation of importance of Marangoni flow in superspreading. However, this confirmation was not entirely conclusive, because other properties of these surfactants can be more important than the equilibration rate.

Unfortunately, none of the proposed mechanisms has received general acceptance to date, because of lack of stringent experimental corroboration. In this paper, we isolate the effect of the Marangoni flow on superspreading by studying the effect of surfactant equilibration rate for the same surfactant as a function of diffusion coefficient. The diffusion coefficient was altered (reduced) by adding glycerol to surfactant solutions. Addition of glycerol does not noticeably change surface tension, but changes the solution viscosity and therefore the surfactant diffusion coefficient.

2. Materials and Methods

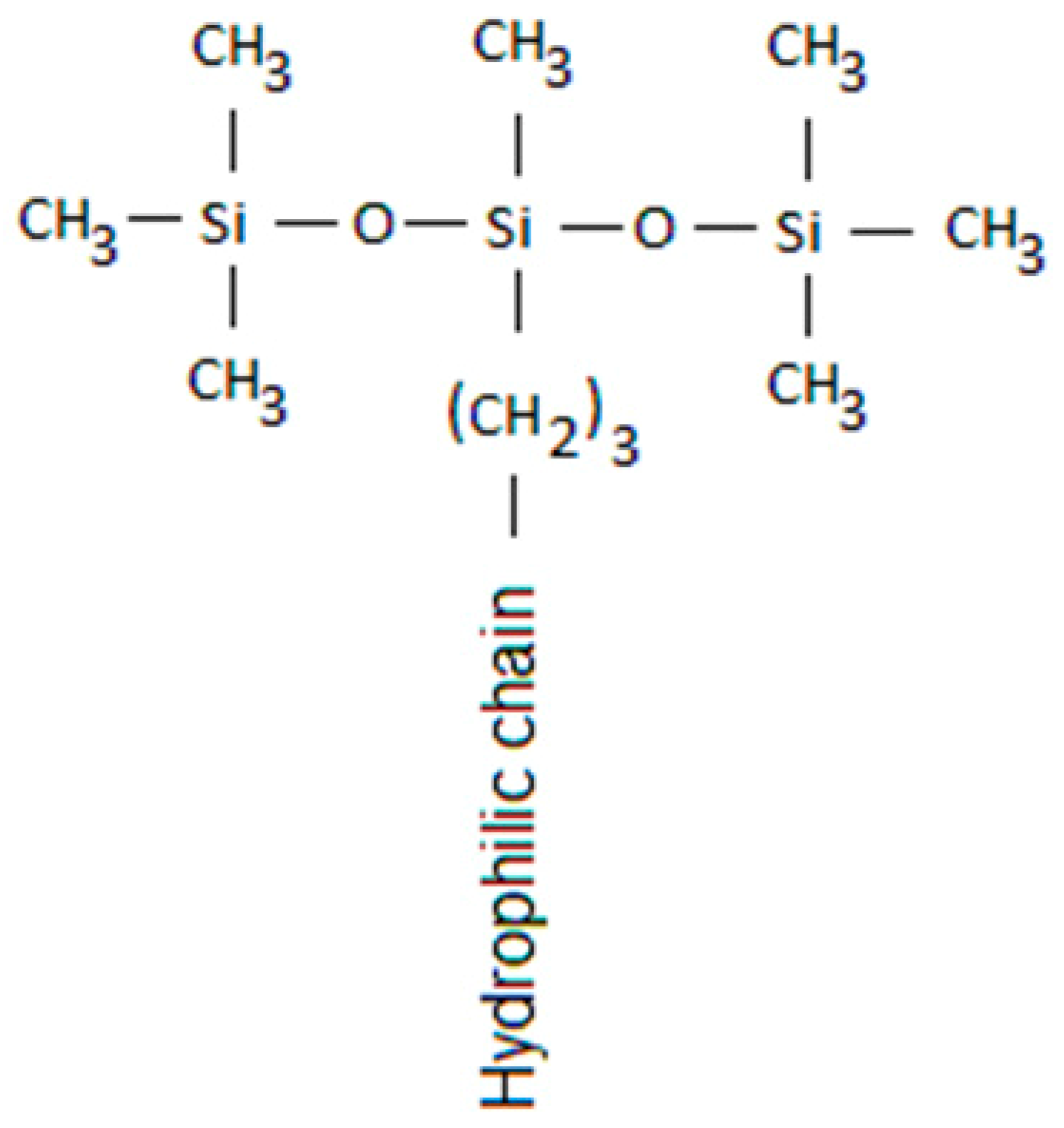
Study of spreading characteristics of solutions of three trisiloxane surfactants (Evonic), BREAK-THRU S 278 (BT-278), BREAK-THRU S 240 (BT-240) and BREAK-THRU S 233 (BT-233) was performed on two substrates, polyethylene (PE) and polyvinylidenefluoride (PVDF). The contact angle of water on these substrates was 102° and 84°, respectively. The trisiloxane surfactants used have similar structure shown in Figure 1. They have bulky hydrophobic part, exposing at the interface close packed CH₃ groups and therefore reducing water/air surface tension to considerably lower values than common unbranched hydrocarbon surfactants. The difference between the three surfactants used in this study is the composition of the hydrophilic part containing different numbers of ethylene oxide and propylene oxide groups. Due to differences in composition, the surfactant can form various self-assembled structures – micelles, vesicles and lamellae. The critical aggregation concentration (CAC) for these surfactants is CAC < 0.2 g/L [28]. The surface tension above CAC is 24.3 mN/m for BT-233, 22.5 mN/m for BT-240 and 21.7 mN/m for BT-278.

BT-278 and BT-240 are superspreaders, whereas BT-233 is not. Solutions of these surfactants at concentrations 0.625, 1.25, 2.5, 5 and 10 g/L (all above CAC) were prepared in double-distilled water and in 20, 30 and 40% glycerol/water (GL_W) mixtures. The properties of aqueous phases used are summarised in

Table 1. Physical properties of the aqueous phases used as solvents.

	Water	20% GL_W	30% GL_W	40% GL_W
Density*, kg/m3	1000	1049	1075	1101
Viscosity*, mPa·s	1.0	1.8	2.5	3.7
Surface tension, mN/m	73.0	72.3	72.1	71.8

* According to [30].

. According to Table 1 the addition of glycerol affects considerably the viscosity of aqueous phase whereas changes in the density and surface tension are quite small. Addition of glycerol reduced the surface tension of surfactant solutions by 0.2 – 0.5 mN/m. All solutions were used on the day when they were prepared to avoid hydrolysis and loss of surface activity [29].

PE and PVDF films, thickness 0.05 mm (GoodFellow) were cut into pieces of size ~ 4 × 4 cm and placed on glass microscope slides. After/before each experiment substrates were washed with isopropanol (>99.5%, Fisher), rinsed with plenty of double-distilled water, dried on hotplate at 40 °C for 20–25 min and conditioned at room temperature for 2–3 min.

All spreading experiments were performed at room temperature and humidity. The spreading of a 5 μL drop released from the Eppendorf micropipette close to the substrate surface was recorded using a Photron SA3 high speed camera at 60 fps with an exposure set to 0.5 ms The camera was equipped with AF NIKKOR 24–85 mm lens giving resolution 0.04 mm/pixel. The substrate was illuminated by cold light source KL 2500 LED (SHOTT) equipped with ring-light of 40 mm diameter. The videos were processed by ImageJ free software [31] to follow wetting and de-wetting process and find kinetics of spreading. For comparison, kinetics of spreading of two silicone oils (Sigma-Aldrich) with viscosities 1 mPa·s (similar to water) and 4.6 mPa·s (larger than the viscosity of 40% glycerol/water mixture) were studied. The surface tension of silicone oils was 18 and 19 mN/m respectively. The presented results are the average of 3–7 measurements. The experimental error for the spread area measurement did not exceeded 10% for silicone oils and 50% for surfactant solutions. The large experimental error is most probably related to the variation in the surface properties of the substrates used (mainly chemical composition), i.e., to the fact that the used films were not homogeneous. The performance of the individual samples of the same substrate, was however self-consistent (i.e., the sample that showed maximum (or minimum) spreading exhibited this behaviour for all solutions). Therefore, the experimental error was considerably smaller when experiments were repeated on the same sample. The experimental error is larger for surfactant solution than for silicone oils, because the substrate properties affect not only spreading itself, but also surfactant adsorption on the substrate.

The surfactant adsorption kinetics was followed by measurement of dynamic surface tension over the time scale 0.01–20 s, relevant to the spreading process, using Maximum Bubble Pressure tensiometer BPA-1S (Sinterface).

3. Results and Discussion

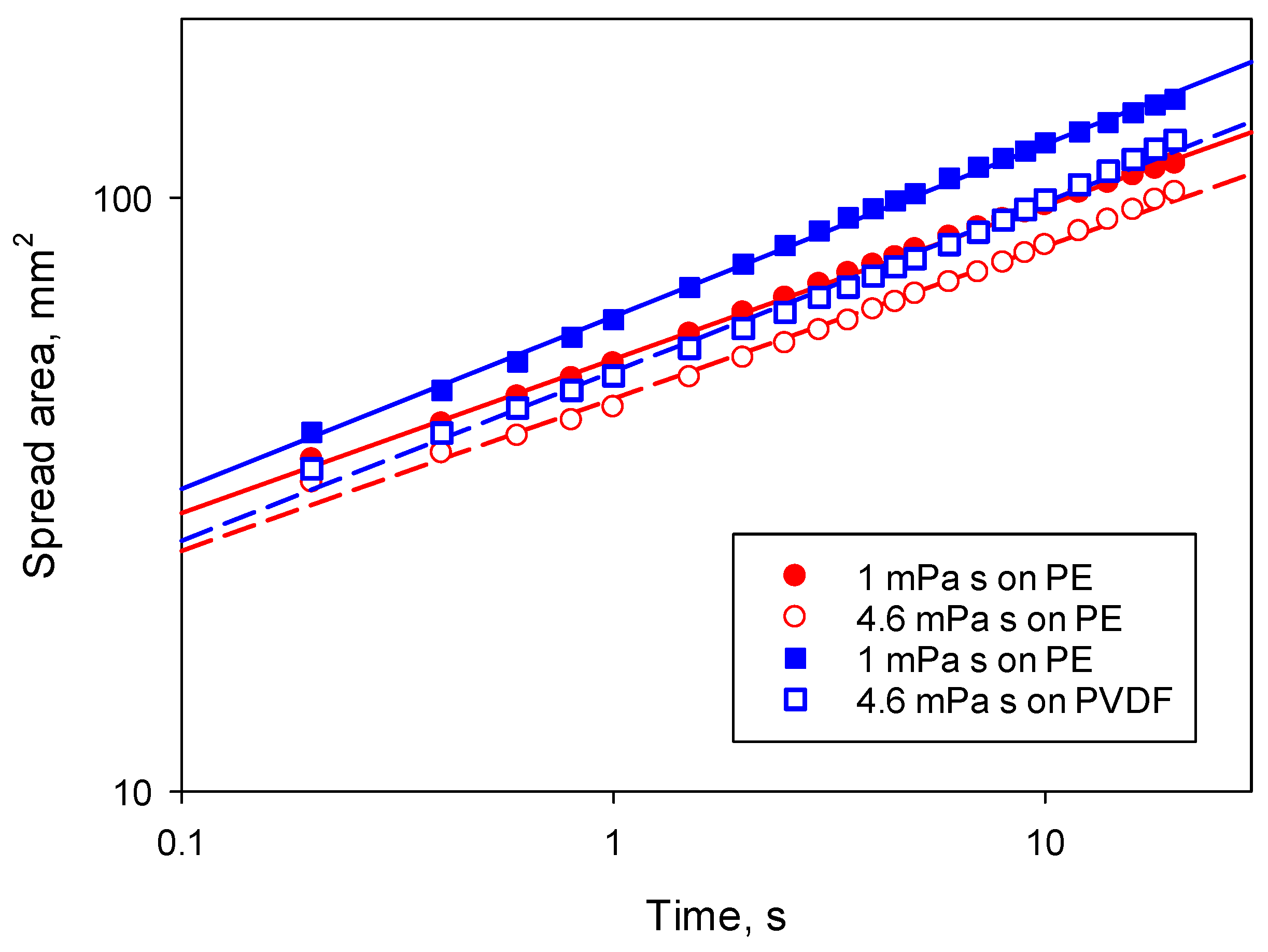
The spreading kinetics of the two silicone oils used was similar with a spreading exponent α = 0.26 on PE and α = 0.29 on PVDF (Figure 2). The spreading exponent was slightly higher than the theoretical prediction α = 0.2 expected for silicone oils [14,15]. The difference is possibly related to the substrate roughness, because PVDF has higher roughness than PE since the surface is micro-grooved. These micro-grooves can facilitate spreading by additional capillary suction. The pre-exponential factor is ~5% larger for the less viscous silicone oil, in agreement with [15], predicting a rather weak dependence of the spreading kinetics on liquid viscosity, μ, with a pre-exponential factor ~μ^−0.2. Based upon these results, it can be concluded that the variation in viscosity of surfactant solution, in the range used in this study, should not affect the spreading kinetics noticeably. Therefore, any changes in spreading kinetics should be related to the changes of diffusion coefficient, which is inversely proportional to viscosity according to the Stokes–Einstein relationship.

The spreading kinetics of surfactant solutions, were dependent upon concentration, as expected [11,12]. For the purely aqueous solutions, the fastest kinetics were observed at a concentration of 1.25 g/L for surfactants BT-240 and BT-278 on both substrates, and at a concentration of 2.5 g/L for BT-233 on PVDF. Only partial wetting was observed for solutions of BT-233 on PE with a contact angle of ~8° being estimated from the spread area assuming that the drop has a spherical cap shape. 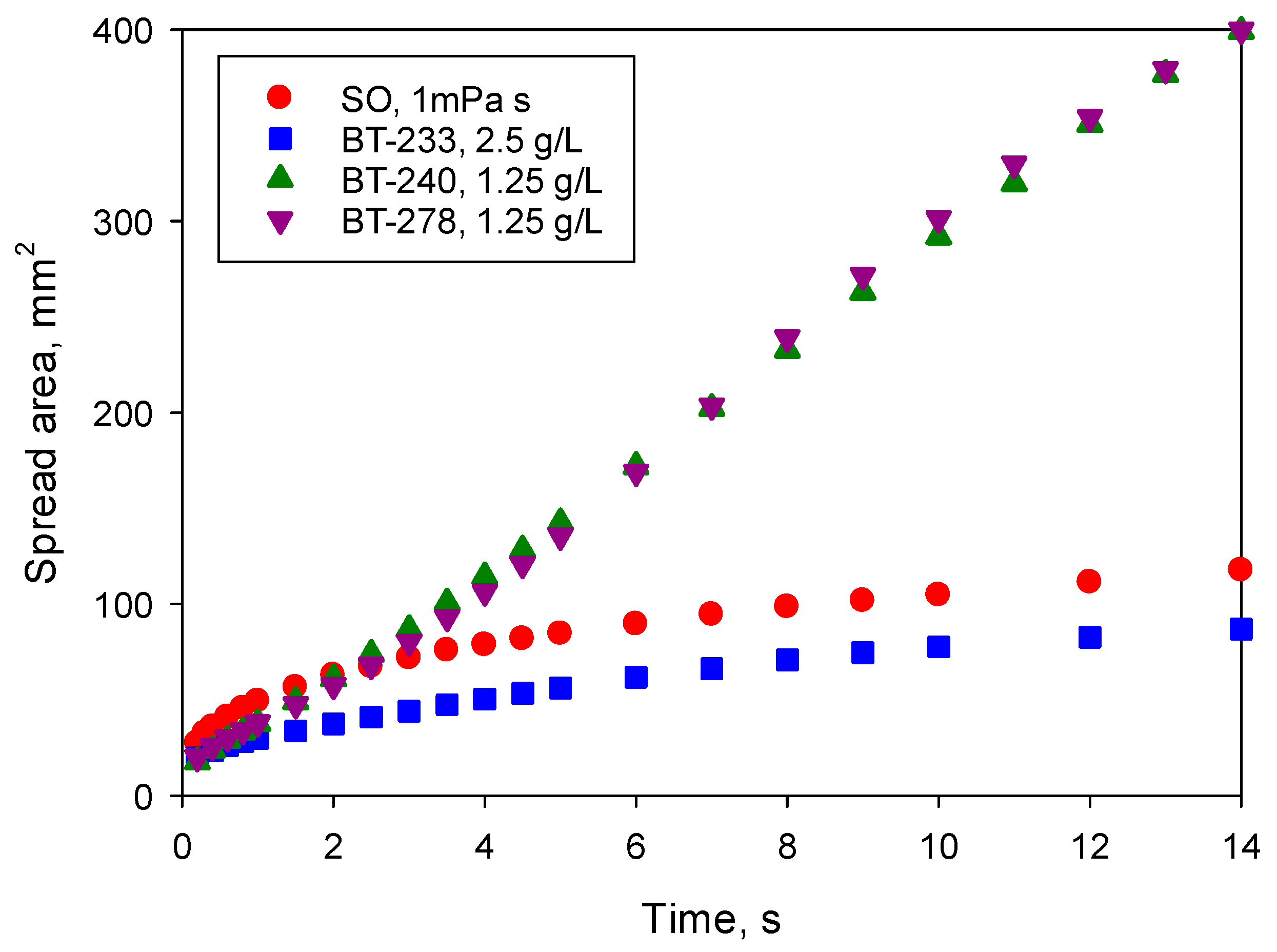Figure 3 compares the spreading kinetics of the less viscous silicone oil with surfactant solutions in water (which have the same viscosity) at the above concentrations which provided the best spreading. Spreading kinetics was studied over a relatively short time scale, 14 s, firstly, to minimise the effect of evaporation and secondly, to ensure the maximum image resolution within the capability of the camera. At the resolution used in this study, the spread area of solutions in water with maximum spreadability was in some cases outside of the field of view at t > 14 s. Figure 3 demonstrates the huge difference in behaviour between the superspreading and non-superspreading surfactants: although all three solutions provide complete wetting of the substrate, the area wetted by superspreaders was more than four-times larger on the time scale of observation. Redrawing Figure 3 on a log/log scale, similar to Figure 2, it can be seen that the spread area for the superspreaders within the first second increased proportionally to t^0.4 demonstrating the viscous stage of spreading [17] and later it increased linearly with time as superspreading occurred. For the non-superspreader BT-233 on the time scale ~1 s, the spreading exponent was slightly lower than that of silicone oils α₁ = 0.24, but later it increased to α₂ = 0.44 demonstrating appearance of an additional mechanism accelerating spreading when compared to the pure liquid. The observation of the smaller spreading exponent within the viscous stage for non-superspreading trisiloxane surfactant when compared with the superspreaders is in line with [17].

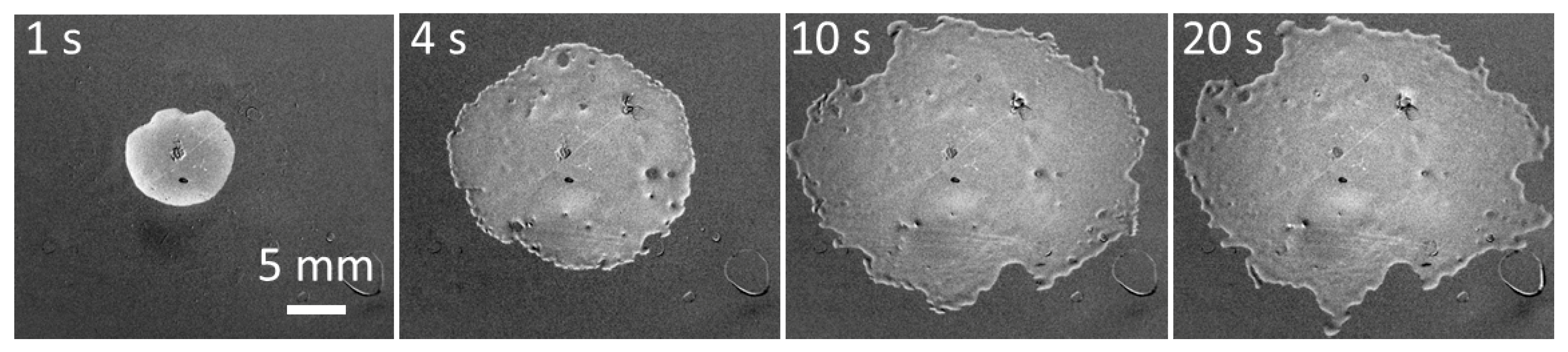
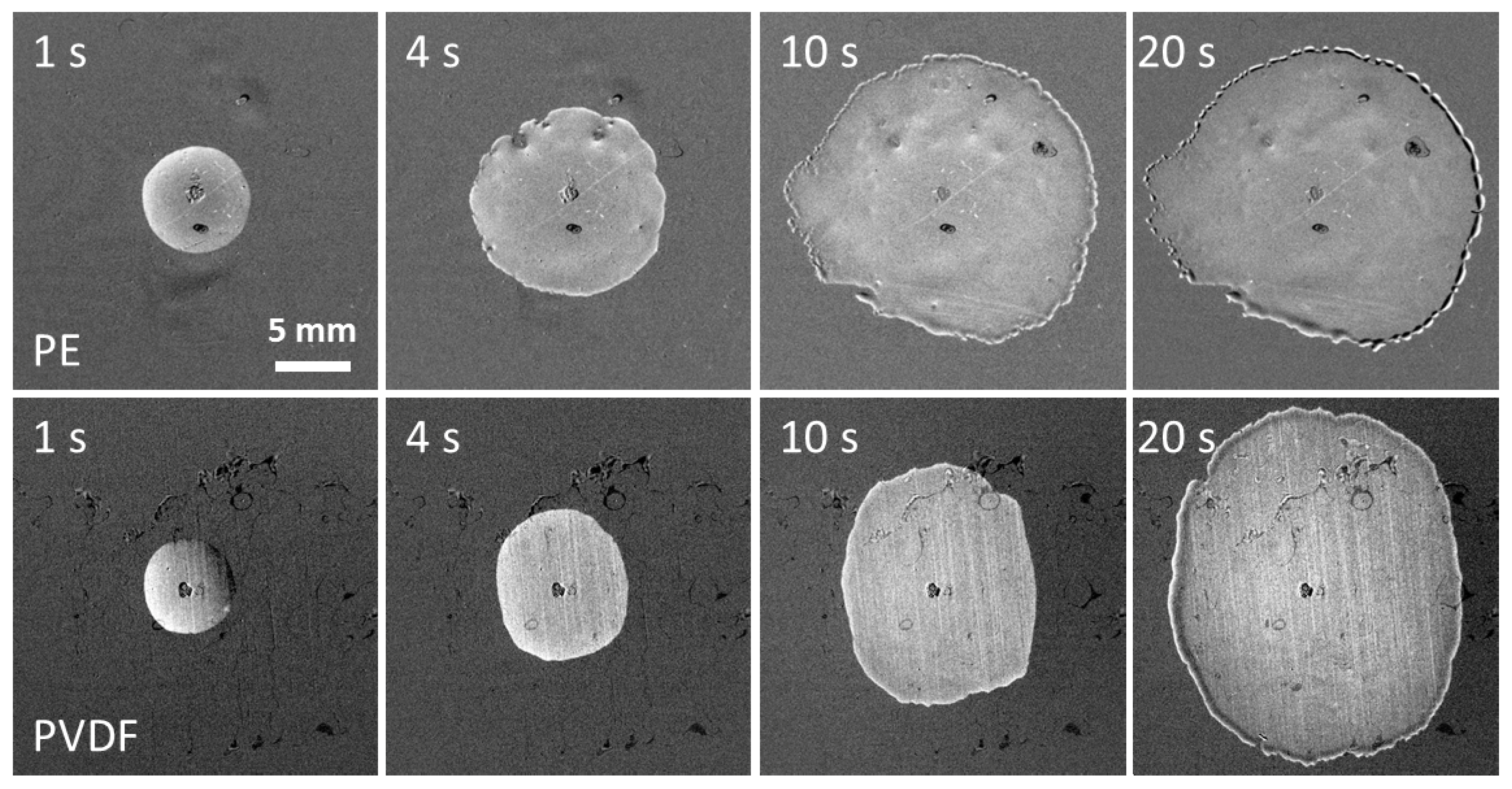
Spreading patterns on PE of a solution of the superspreading surfactant BT-278 in water at a concentration of 1.25 g/L corresponding to the maximum spread area are shown in Figure 4. The spread area can remain circular for a longer time than is shown in Figure 4, but within several seconds the protrusions (fingers) seen in Figure 4, at t = 1 s develop at the leading edge of spreading. Later, the protrusions split into more branches and sometimes form holes inside the spread area as seen on images for t > 1 s. The holes are later covered by the spreading solution. Note, the hole/spot visible in the centre of drops in Figure 4 and Figure 5 is a mark made on the reverse side of the substrate enabling the precise positioning of the drop in the centre of the camera field of view. When the spread area increases, a rim is formed at the leading edge of spreading (t = 10 and 20 s) which is characteristic of superspreading [6,25].

Addition of glycerol to the solutions does not change the spreading patterns significantly as shown in Figure 5 for solutions of BT-278 in 30% glycerol/water mixture. Opposite to silicone oil, for solutions of BT-278, faster spreading is observed on the PE substrate. For the solution shown in Figure 4, the maximum spread area on PE was reached after ~20 s whereas on PVDF it was reached after ~30 s. The rim at the leading edge of spreading is more pronounced for solutions in water/glycerol mixtures.

After the maximum spread area is reached, the behaviour of solutions in water/glycerol mixtures becomes different from those in water alone. For purely aqueous solutions, the three-phase contact line retracts leaving behind a visibly uniform dry surface during the evaporation process. A drop of water placed on the dried substrate within the area initially covered by surfactant solution demonstrates the contact angle close to zero, therefore it can be concluded that the whole area is covered by surfactant molecules.

For solutions in glycerol/water mixtures the rim disintegrates into separate drops when the maximum spread area is reached. The beginning of this process is already visible in Figure 5 for the spreading pattern on PE at t = 20s. As time increases, the evaporating film detaches and moves away from the drops at the edge of spread area while the drops remain in place and become circular. The film shrinks due to liquid evaporation leaving behind the patterns of circular drops shown in Figure 6. Most probably this distinctive de-wetting process is due to much faster evaporation of water when compared with glycerol. The de-wetting patterns are slightly different for two studied substrates: on PE the large drops form the external de-wetting ring, whereas on PVDF the large drops form the second ring inside the de-wetted area being surrounded from outside by the small drops. Drop formation by de-wetting was observed also for solutions BT-240 and BT-233 in water/glycerol mixtures.

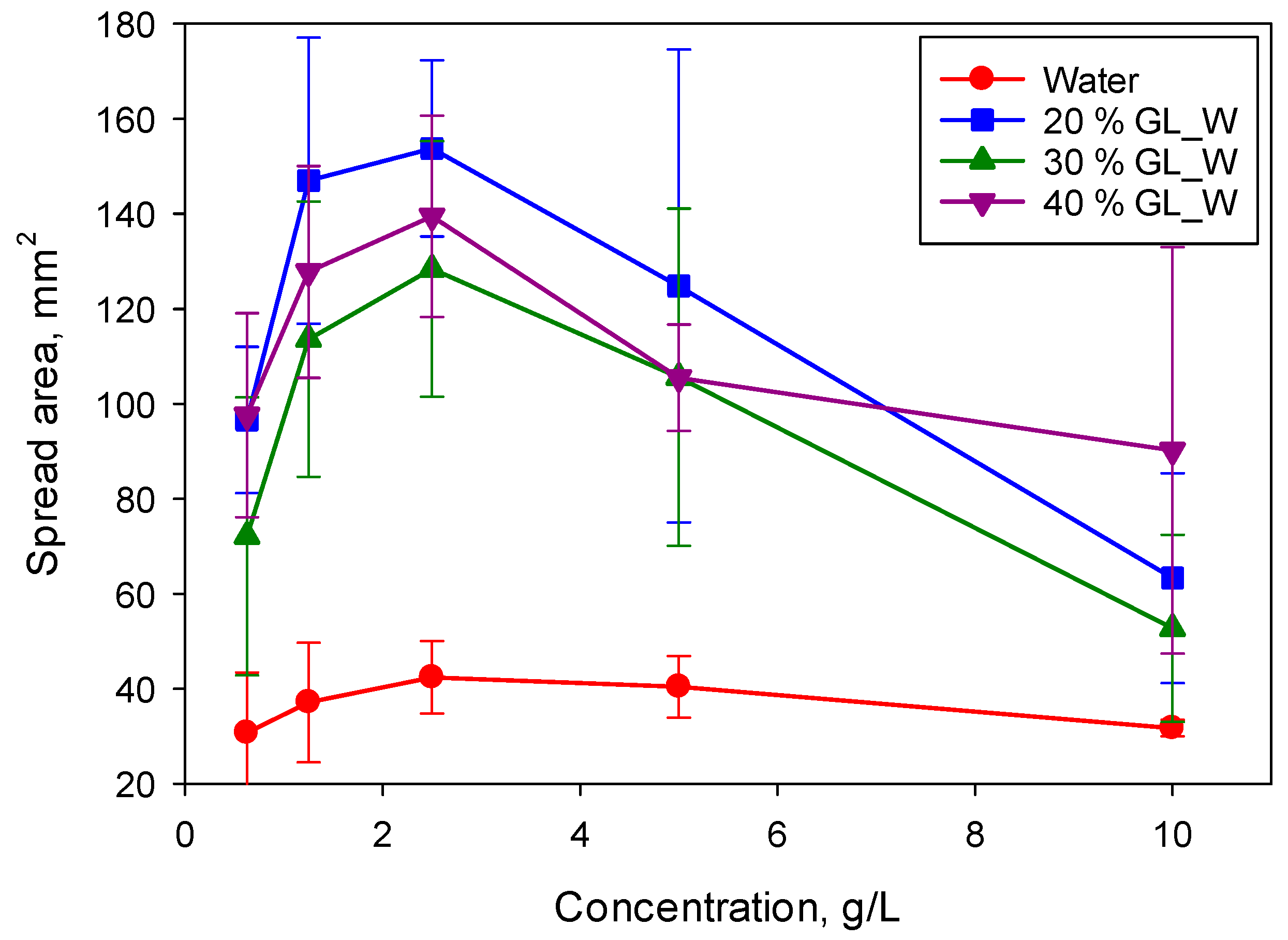
Besides the effect on the de-wetting patterns, addition of glycerol to solutions considerably affects the spreading kinetics. Figure 7 shows the values of spread area on the PE substrate at t = 14 s as a function of surfactant and glycerol concentration for the non-superspreading surfactant BT-233. As mentioned earlier, solutions of BT-233 in water only partially wet the PE substrate. Addition of 20% glycerol causes transition from partial to complete wetting resulting in a spread area which is more than three-times larger. This transition can be the result of decrease of equilibrium surface tension of BT-233 solutions from 24.3 to 23.9 mN/m, but also the addition of glycerol can affect the interfacial tension at the water/PE interface. For BT-233 the increase in the glycerol concentration does not change the concentration of the surfactant, 2.5 g/L, at which the maximum in spreading was observed on PE. Similar behaviour was observed for spreading on PVDF including the increased spread area of solutions in 20% glycerol/water mixture when compared to solutions in water. Addition of glycerol also resulted in an increase in power law exponent for the second stage of spreading to α₂ = 0.6 on both substrates.

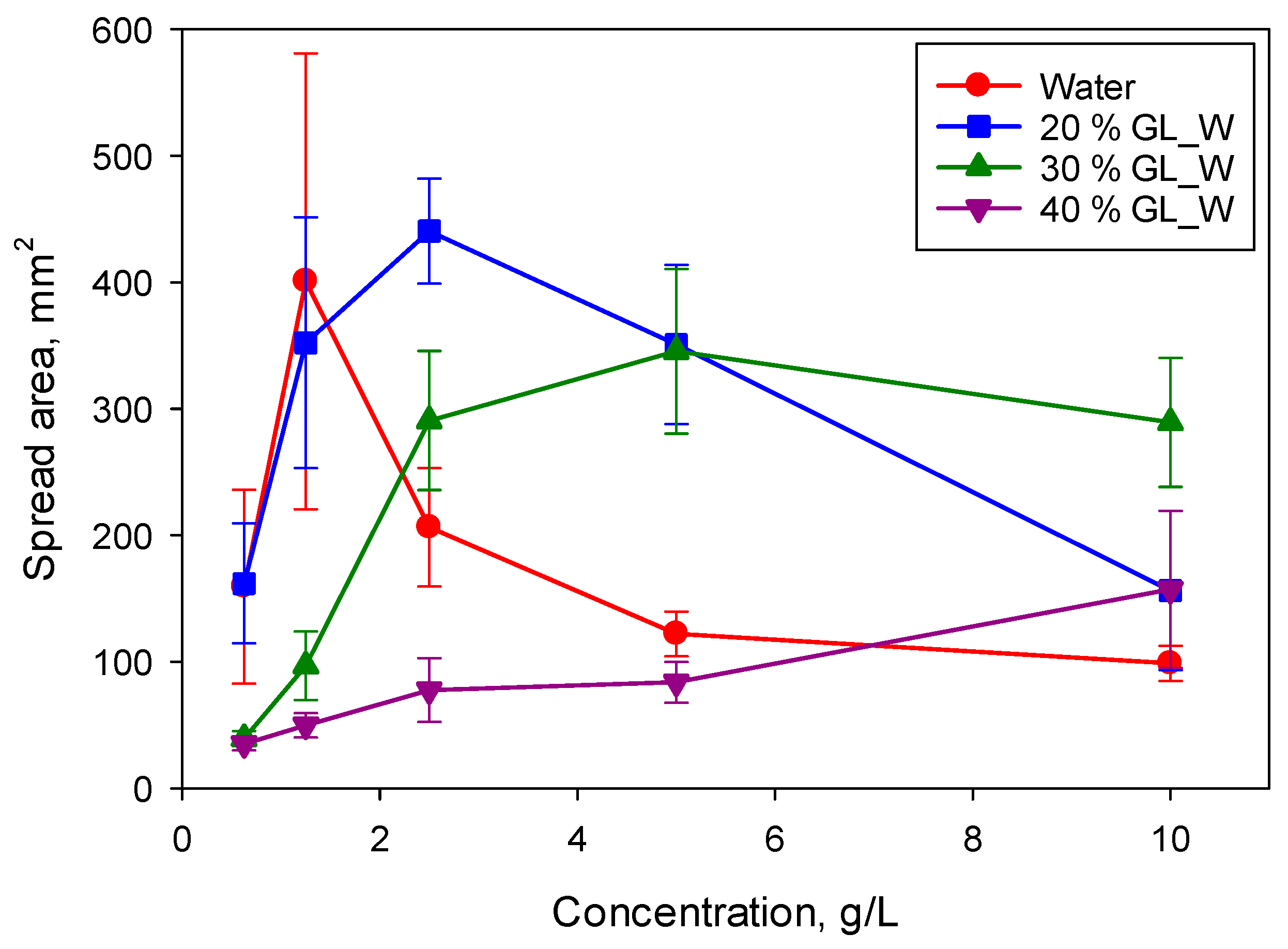
Figure 8 shows the spread area on the PE substrate after 14 s for the superspreader BT-278. For both studied superspreaders, a systematic increase of concentration corresponding to the maximum spreading on both substrates was observed, from 1.25 g/L for solutions in water to (at least) 10 g/L for solutions in 40% glycerol/water mixture. Therefore, the surfactant equilibration rate is of high importance to the superspreading mechanism.

Considering that the spreading exponent for BT-233 is higher than that for the silicone oil, but lower than that for superspreaders, it can be assumed that that there are several mechanisms contributing to the superspreading. One of those mechanisms occurs for both superspreading and non-superspreading trisiloxane surfactants, whereas other mechanisms occur only for the superspreaders. The mechanism related to the surfactant equilibration rate is responsible for the concentration shift presented in Figure 8.

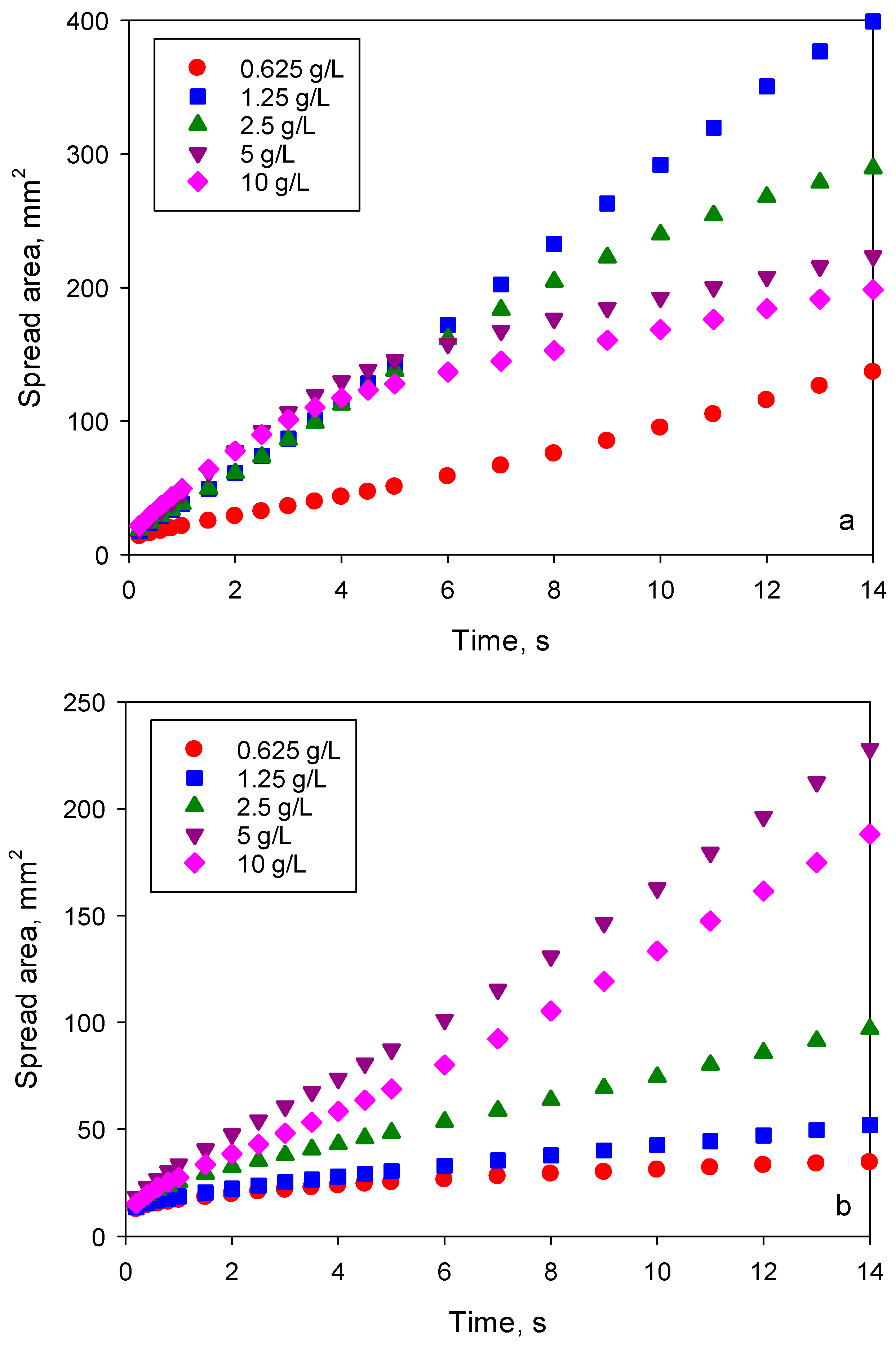
Figure 9 presents the spreading kinetics of solutions of superspreader BT-240 in water and in 30% water/glycerol mixture. Within the time of observation, 14 s, the kinetics for solutions in water can be divided into three stages, each with distinct spreading exponents. In the first stage corresponding to t < 1 s, α is in the range of 0.3–0.5 and increasing with an increase of the concentration. The second stage of fast spreading was observed at t > 1 s with the spreading exponent depending on the concentration as shown in

Table 2. Maximum spreading exponent for solutions of BT-240 on PVDF.

Solvent	Surfactant Concentration, g/L
	0.625	1.25	2.5	5	10
Water	0.8	1.0	0.9	0.8	0.7
30% GL_W	0.3	0.5	0.7	1.0	1.0

. This stage can be denoted as superspreading as the spreading exponent for all concentrations is higher than 0.5. The third stage occurs when the spreading slows down, with α in the range of 0.4–0.5, this was observed only for solutions in water at concentrations between 2.5–10 g/L within the time span. For these concentrations, the third stage begins at t > 5 s. The exponent for the third stage is close to the spreading exponent of the non-superspreading surfactant BT-233.

For solutions in 30% glycerol/water mixture, the fastest spreading was observed for concentrations larger than 1.25 g/L (Table 2). It is noticeable that the superspreading stage characterised by the exponent given in Table 2 for these solutions begins at t ~ 5 s (i.e., much later than for solutions in water (t ~ 1 s)). Between 1 s < t < 5 s, spreading with 0.5 < α < 0.7 was observed with α increasing with an increase of the surfactant concentration. The third stage, when the spreading slows down, was not observed for these solutions within the time span of observation.

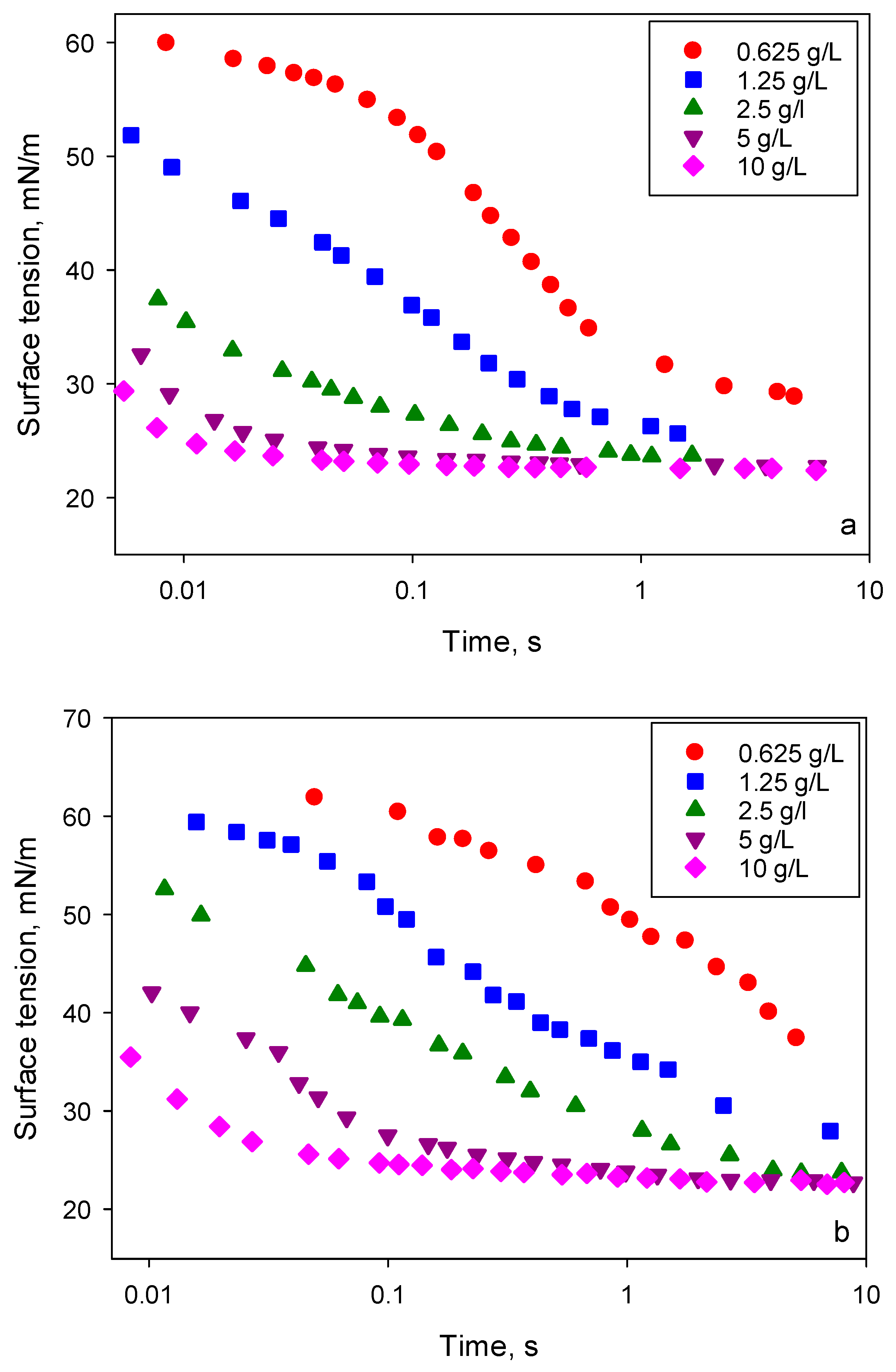
An increase of liquid viscosity due to addition of glycerol results in slower changes of dynamic interfacial tension due to a smaller diffusion coefficient as is seen from the comparison of dynamic surface tension for solutions of BT-240 in water and in 30% glycerol/water mixture presented in Figure 10. Therefore, it can be expected that surface tension gradients created inside the spreading surfactant solution are considerably affected by the surfactant diffusion coefficients.

Note, the dynamic surface tension does not provide enough data for a quantitative analysis because the local surface tension distribution during the spreading depends on the rate of surface deformation, on depletion of surfactant from the bulk phase on the leading edge of spreading and on the adsorption kinetics at solid/liquid interface. Nevertheless, it provides the characteristic time scales and the rates of change of surface tension involved. Comparing the spreading kinetics (Figure 9) with the data on dynamic surface tension of surfactant solutions shown in Figure 10, it can be suggested that the maximum spreading rate requires a moderate surfactant equilibration rate. The data suggest that, in solutions with the maximum spreading rate, the equilibrium surface tension should be established on the time scale of 1–2 s. It can be assumed that solutions with small concentrations in water/glycerol mixture do not have enough adsorbed surfactant to promote the fast spreading. On the other hand, the spreading of solutions in water slows down with an increase of concentration beyond 1.25 g/L. This correlates with the difference in surface tension between 0.01 and 0.1 s. The larger the difference, the faster the spreading is. This also agrees well with the observed spreading exponents for solutions in the 30% glycerol/water mixture. These results support the hypothesis of the critical role of Marangoni flows in the mechanism of superspreading.

4. Conclusions

A study of the spreading of trisiloxane surfactants BT-233 (non-superspreader), BT-240 and BT-278 (both superspreaders) on polyethylene and polyvinylidenefluoride and comparison with the spreading of silicone oils on the same substrates has shown the following.

1. Surfactant solutions spread faster than silicone oils of similar viscosity. The spread area for the two studied silicone oils was proportional to t^0.26−0.29, within the whole time of observation. For surfactant solutions, spreading began with the value of the spreading exponent being similar to that of silicone oils but it then increased to 0.4–0.6 for BT-233 and up to 1 for BT-240 and BT-278. The larger values of spreading exponent obtained for the surfactant solutions when compared with pure liquids of similar surface tension and viscosity demonstrates that there should be additional mechanisms accelerating the spreading of surfactant solutions, including both superspreaders and non-superspreaders.

2. Addition of glycerol accelerated spreading of BT-233 solutions, increasing the spreading exponent from 0.4 to 0.6. Solutions of BT-233 in water wet completely polyvinylidenefluoride, but provide only partial wetting on polyethylene. The addition of glycerol resulted in a transition from partial to complete wetting on this substrate. The maximum spreading rate for solutions of BT-233 on both substrates was observed at the same concentration, 2.5 g/L, and was independent of glycerol content.

3. Solutions of superspreaders BT-240 and BT-278 in water demonstrate a slowing down of the spreading kinetics for concentrations > 1.25 g/L. The concentration providing the maximum spreading rate (with spreading exponent equal to 1) increased with the increase of glycerol content from 1.25 g/L for purely aqueous solutions to at least 10 g/L for solutions in 40% glycerol/water mixture. Addition of glycerol to water has a minimum effect on the surface tension, but considerably increases viscosity and therefore decreases the surfactant diffusion coefficient. The study of spreading of silicone oils has shown that variations of viscosity itself in the studied range have negligible effect on spreading kinetics. Therefore, the only parameter responsible for the shift of concentration corresponding to the maximum spreading rate is the diffusion coefficient. The observed shift to the larger concentrations with a decrease of diffusion coefficient demonstrates clearly that there is an optimal rate of surfactant equilibration at which the fastest spreading is observed. That means that the formed surface tension gradients and resulting Marangoni flow are an important part of the superspreading mechanism.

4. The de-wetting due to evaporation of spread trisiloxane solutions in water does not leave any visible traces on the substrate. It can be assumed that the whole initially wetted area is covered by surfactant molecules, because the water drops placed inside this area spread much better than on the clean substrate. The de-wetting of solutions in glycerol for all three studied surfactants results in formation of circular patterns of small drops.