Measuring Inner Layer Capacitance with the Colloidal Probe Technique
Abstract
1. Introduction
2. Experimental Setup and Methods
2.1. Materials
2.2. Direct Force Measurements
2.3. DLVO Theory
2.4. Basic Stern Model
3. Results and Discussion
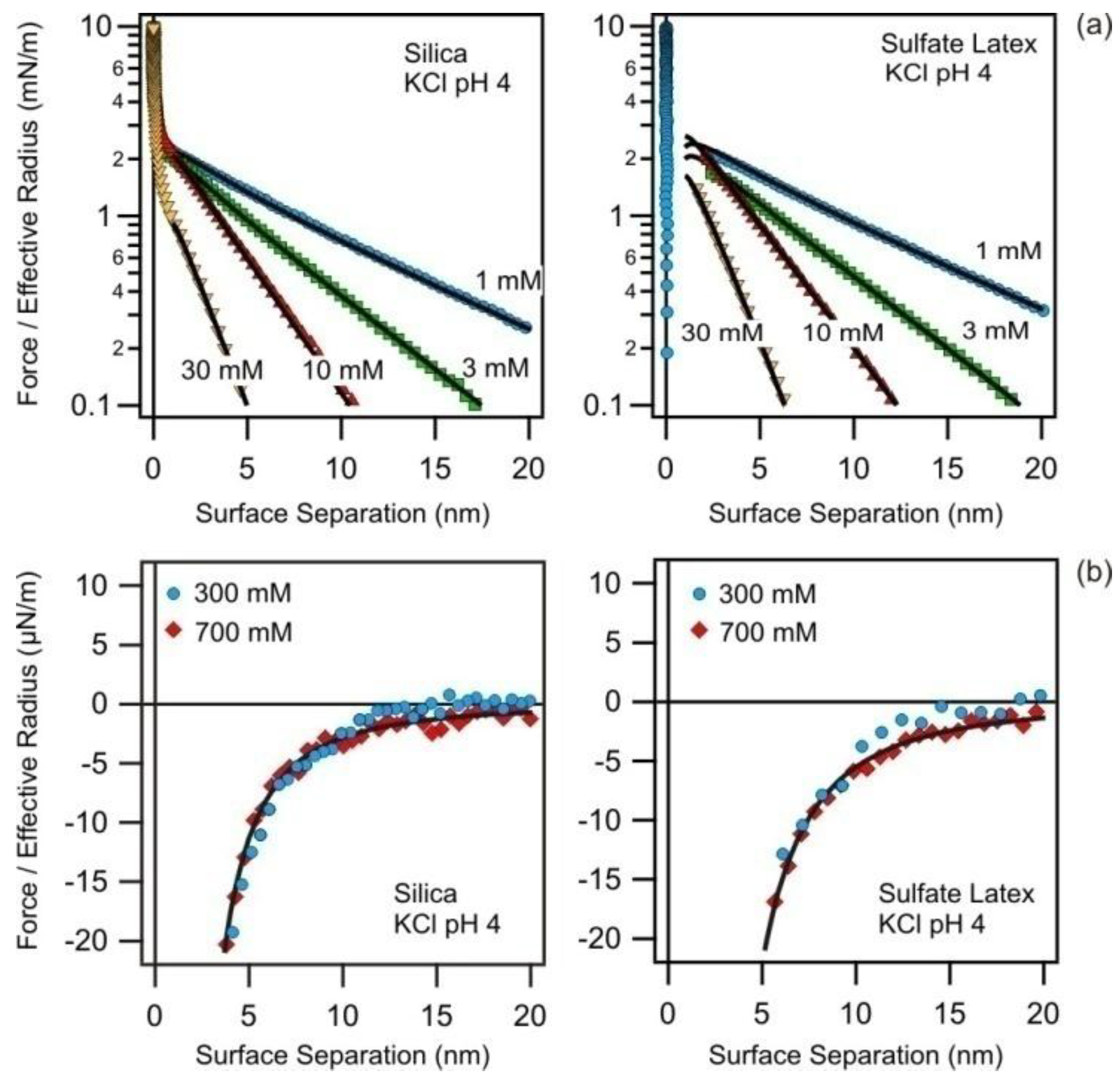
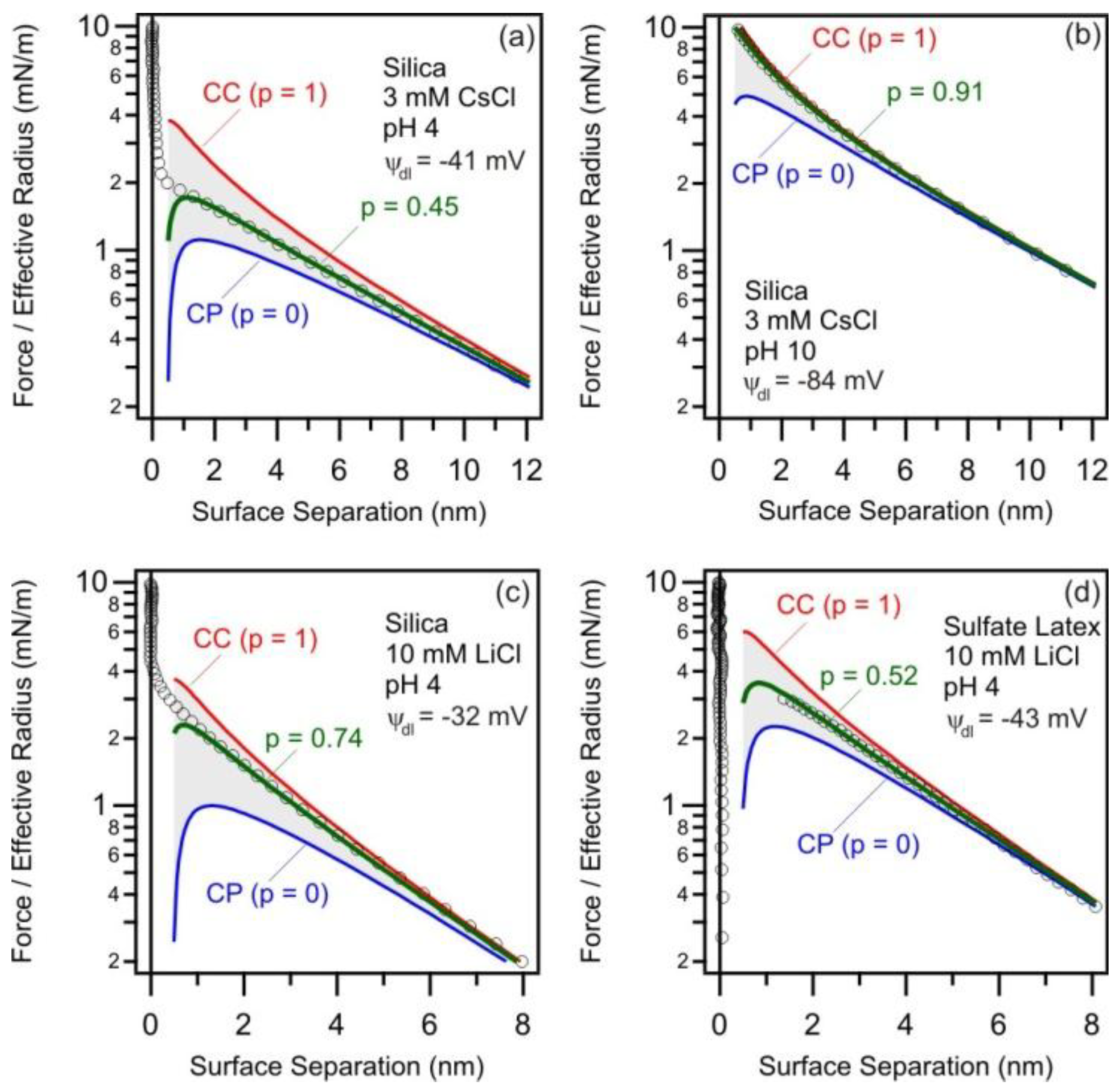
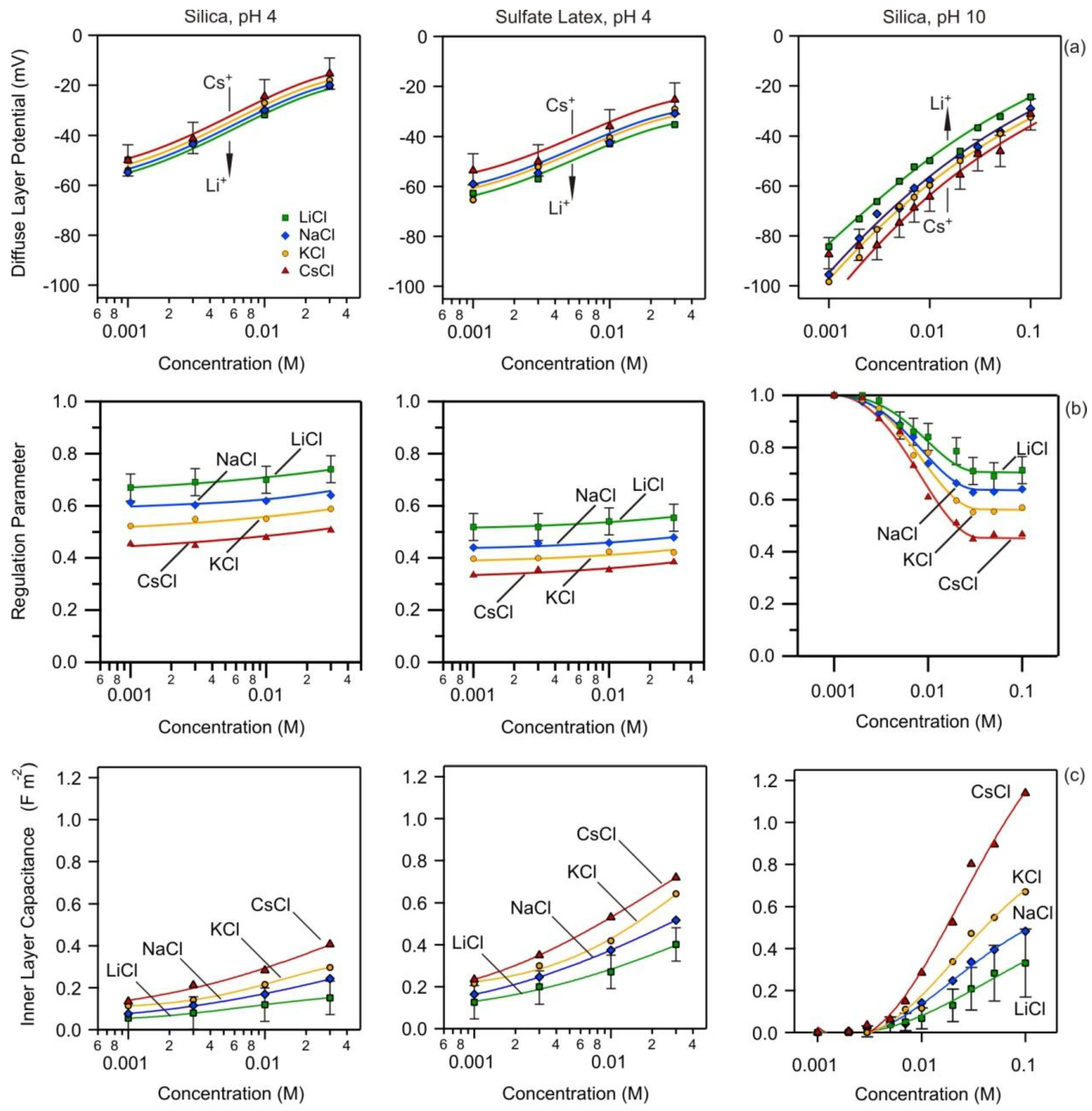
3.1. Quantification of Measured Forces Profiles by DLVO Theory
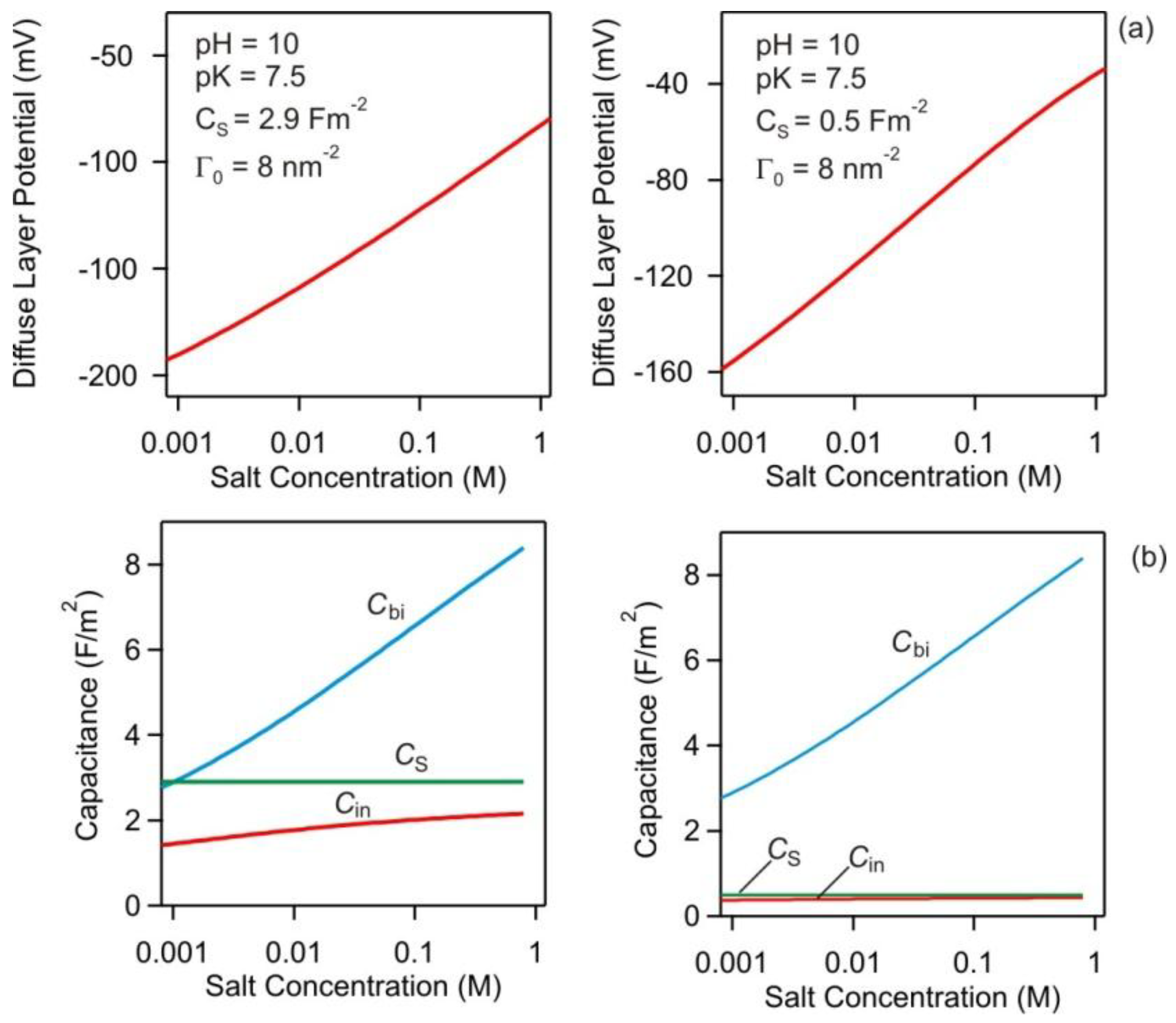
3.2. Charging and Regulation Behavior of Isolated Surfaces
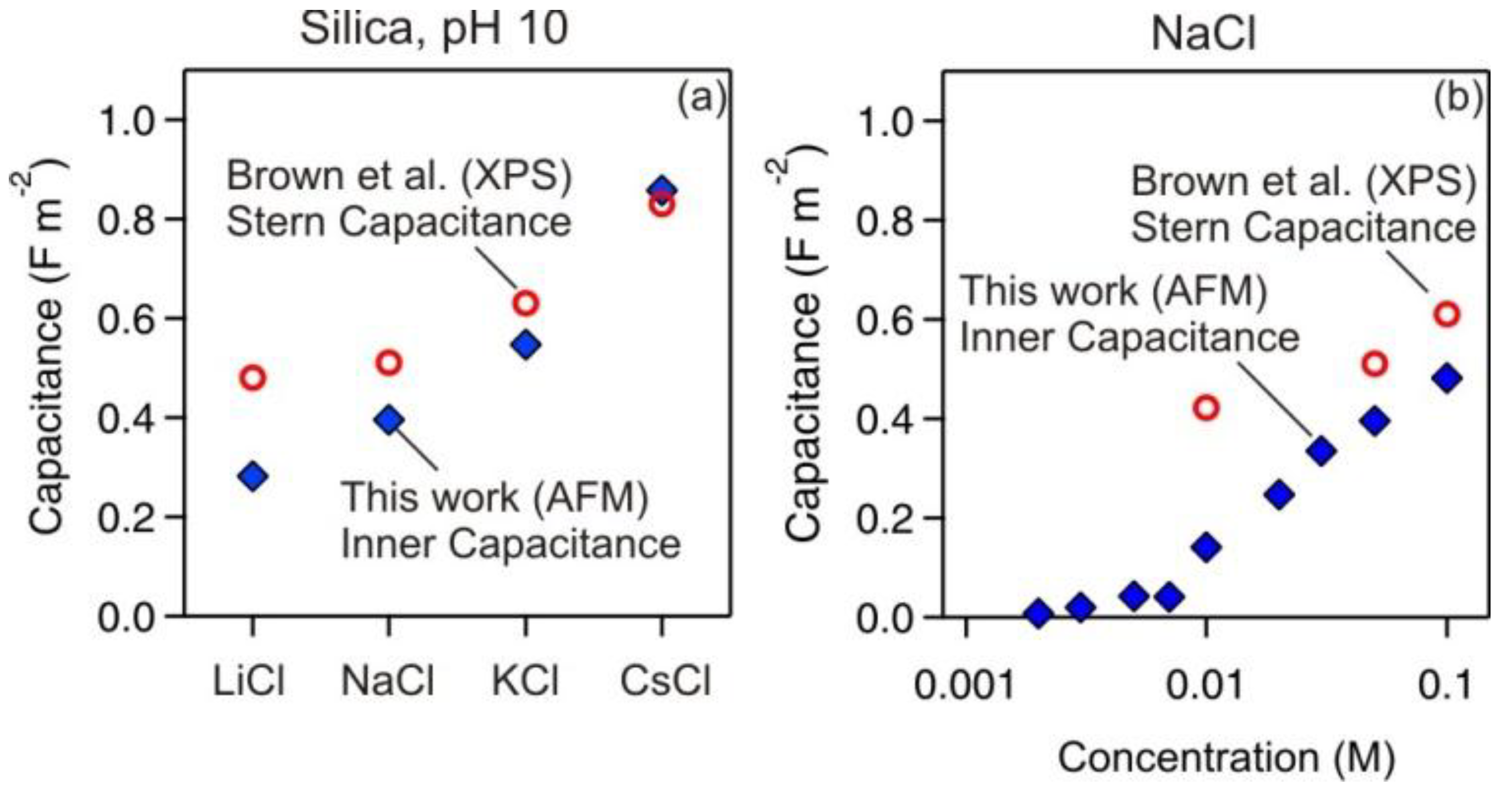
3.3. Comparison with X-Ray Photoelectron Spectroscopy (XPS)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Russel, W.B.; Saville, D.A.; Schowalter, W.R. Colloidal Dispersions; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Elimelech, M.; Gregory, J.; Jia, X.; Williams, R.A. Particle Deposition and Aggregation: Measurement, Modeling, and Simulation; Butterworth-Heinemann Ltd.: Oxford, UK, 1995. [Google Scholar]
- Bolto, B.; Gregory, J. Organic polyelectrolytes in water treatment. Water Res. 2007, 41, 2301–2324. [Google Scholar] [CrossRef] [PubMed]
- Iselau, F.; Restorp, P.; Andersson, M.; Bordes, R. Role of the aggregation behavior of hydrophobic particles in paper surface hydrophobation. Colloid Surf. A 2015, 483, 264–270. [Google Scholar] [CrossRef]
- Zanini, M.; Hsu, C.P.; Magrini, T.; Marini, E.; Isa, L. Fabrication of rough colloids by heteroaggregation. Colloid Surf. A 2017, 532, 116–124. [Google Scholar] [CrossRef]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977–1026. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications; John Wiley: New York, NY, USA, 2001. [Google Scholar]
- Naji, A.; Kanduc, M.; Forsman, J.; Podgornik, R. Perspective: Coulomb fluids - weak coupling, strong coupling, in between and beyond. J. Chem. Phys. 2013, 139, 150901. [Google Scholar] [CrossRef] [PubMed]
- Stern, O. Zur Theorie der elektrolytischen Doppelschicht. Z. Elektrochem. 1924, 30, 508–516. [Google Scholar]
- Hiemstra, T.; de Wit, J.C.M.; van Riemsdijk, W.H. Multisite proton adsorption modeling at the solid-solution interface of (hydr)oxides: A new approach 2. Application to various important (hydr)oxides. J. Colloid Interface Sci. 1989, 133, 105–117. [Google Scholar] [CrossRef]
- Machesky, M.L.; Wesolowski, D.J.; Palmer, D.A.; Ichiro-Hayashi, K. Potentiometric titrations of rutile suspensions to 250 degrees C. J. Colloid Interface Sci. 1998, 200, 298–309. [Google Scholar] [CrossRef]
- Kobayashi, M.; Skarba, M.; Galletto, P.; Cakara, D.; Borkovec, M. Effects of heat treatment on the aggregation and charging of Stöber-type silica. J. Colloid Interface Sci. 2005, 292, 139–147. [Google Scholar] [CrossRef] [PubMed]
- Dove, P.M.; Craven, C.M. Surface charge density on silica in alkali and alkaline earth chloride electrolyte solutions. Geochim. Cosmochim. Acta 2005, 69, 4963–4970. [Google Scholar] [CrossRef]
- Brown, M.A.; Abbas, Z.; Kleibert, A.; Green, R.G.; Goel, A.; May, S.; Squires, T.M. Determination of surface potential and electrical double-layer structure at the aqueous electrolyte-nanoparticle interface. Phys. Rev. X 2016, 6. [Google Scholar] [CrossRef]
- Boamah, M.D.; Ohno, P.E.; Geiger, F.M.; Eisenthal, K.B. Relative permittivity in the electrical double layer from nonlinear optics. J. Chem. Phys. 2018, 148, 222808. [Google Scholar] [CrossRef] [PubMed]
- Darlington, A.M.; Jarisz, T.A.; DeWalt-Kerian, E.L.; Roy, S.; Kim, S.; Azam, M.S.; Hore, D.K.; Gibbs, J.M. Separating the pH-dependent behavior of water in the Stern and diffuse layers with varying salt concentration. J. Phys. Chem. C 2017, 121, 20229–20241. [Google Scholar] [CrossRef]
- Myalitsin, A.; Urashirna, S.H.; Nihonyanagi, S.; Yamaguchi, S.; Tahara, T. Water structure at the buried silica/aqueous interface studied by heterodyne-detected vibrational sum-frequency generation. J. Phys. Chem. C 2016, 120, 9357–9363. [Google Scholar] [CrossRef]
- Bourg, I.C.; Lee, S.S.; Fenter, P.; Tournassat, C. Stern layer structure and energetics at mica-water interfaces. J. Phys. Chem. C 2017, 121, 9402–9412. [Google Scholar] [CrossRef]
- Brown, M.A.; Goel, A.; Abbas, Z. Effect of electrolyte concentration on the Stern layer thickness at a charged interface. Angew. Chem. Int. Ed. 2016, 55, 3790–3794. [Google Scholar] [CrossRef] [PubMed]
- Perkin, S.; Kampf, N.; Klein, J. Long-range attraction between charge-mosaic surfaces across water. Phys. Rev. Lett. 2006, 96, 038301. [Google Scholar] [CrossRef] [PubMed]
- Israelachvili, J.; Min, Y.; Akbulut, M.; Alig, A.; Carver, G.; Greene, W.; Kristiansen, K.; Meyer, E.; Pesika, N.; Rosenberg, K.; et al. Recent advances in the surface forces apparatus (SFA) technique. Rep. Prog. Phys. 2010, 73, 036601. [Google Scholar] [CrossRef]
- Helfricht, N.; Mark, A.; Dorwling-Carter, L.; Zambelli, T.; Papastavrou, G. Extending the limits of direct force measurements: Colloidal probes from sub-micron particles. Nanoscale 2017, 9, 9491–9501. [Google Scholar] [CrossRef] [PubMed]
- Gutsche, C.; Keyser, U.F.; Kegler, K.; Kremer, F. Forces between single pairs of charged colloids in aqueous salt solutions. Phys. Rev. E 2007, 76, 031403. [Google Scholar] [CrossRef] [PubMed]
- Crocker, J.C.; Grier, D.G. Microscopic measurement of the pair interaction potential of charge-stabilized colloid. Phys. Rev. Lett. 1994, 73, 352–355. [Google Scholar] [CrossRef] [PubMed]
- Derjaguin, B.; Landau, L.D. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Acta Phys. Chim. 1941, 14, 633–662. [Google Scholar] [CrossRef]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of Stability of Lyophobic Colloids; Elsevier: Amsterdam, The Netherlands, 1948. [Google Scholar]
- Labbez, C.; Jonsson, B.; Pochard, I.; Nonat, A.; Cabane, B. Surface charge density and electrokinetic potential of highly charged minerals: Experiments and Monte Carlo simulations on calcium silicate hydrate. J. Phys. Chem. B 2006, 110, 9219–9230. [Google Scholar] [CrossRef] [PubMed]
- Kanduc, M.; Naji, A.; Forsman, J.; Podgornik, R. Dressed counterions: Strong electrostatic coupling in the presence of salt. J. Chem. Phys. 2010, 132, 124701. [Google Scholar] [CrossRef] [PubMed]
- Hartley, P.G.; Larson, I.; Scales, P.J. Electrokinetic and direct force measurements between silica and mica surfaces in dilute electrolyte solutions. Langmuir 1997, 13, 2207–2214. [Google Scholar] [CrossRef]
- Dishon, M.; Zohar, O.; Sivan, U. From repulsion to attraction and back to repulsion: The effect of NaCl, KCl, and CsCl on the force between silica surfaces in aqueous solution. Langmuir 2009, 25, 2831–2836. [Google Scholar] [CrossRef] [PubMed]
- Ninham, B.W.; Parsegian, V.A. Electrostatic potential between surfaces bearing ionizable groups in ionic equilibrium with physiologic saline solutions. J. Theor. Biol. 1971, 31, 405–408. [Google Scholar] [CrossRef]
- Carnie, S.L.; Chan, D.Y.C. Interaction free energy between plates with charge regulation: A linearized model. J. Colloid Interface Sci. 1993, 161, 260–264. [Google Scholar] [CrossRef]
- Behrens, S.H.; Borkovec, M. Electrostatic interaction of colloidal surfaces with variable charge. J. Phys. Chem. B 1999, 103, 2918–2928. [Google Scholar] [CrossRef]
- Zhao, C.; Ebeling, D.; Siretanu, I.; van den Ende, D.; Mugele, F. Extracting local surface charges and charge regulation behavior from atomic force microscopy measurements at heterogeneous solid-electrolyte interfaces. Nanoscale 2015, 7, 16298–16311. [Google Scholar] [CrossRef] [PubMed]
- Trefalt, G.; Behrens, S.H.; Borkovec, M. Charge regulation in the electrical double layer: Ion adsorption and surface interactions. Langmuir 2016, 32, 380–400. [Google Scholar] [CrossRef] [PubMed]
- Borkovec, M.; Behrens, S.H. Electrostatic double layer forces in the case of extreme charge regulation. J. Phys. Chem. B 2008, 112, 10795–10799. [Google Scholar] [CrossRef] [PubMed]
- Popa, I.; Sinha, P.; Finessi, M.; Maroni, P.; Papastavrou, G.; Borkovec, M. Importance of charge regulation in attractive double-layer forces between dissimilar surfaces. Phys. Rev. Lett. 2010, 104, 228301. [Google Scholar] [CrossRef] [PubMed]
- Valmacco, V.; Elzbieciak-Wodka, M.; Herman, D.; Trefalt, G.; Maroni, P.; Borkovec, M. Forces between silica particles in the presence of multivalent cations. J. Colloid Interf. Sci. 2016, 472, 108–115. [Google Scholar] [CrossRef] [PubMed]
- Sader, J.E.; Larson, I.; Mulvaney, P.; White, L.R. Method for the calibration of atomic force microscope cantilevers. Rev. Sci. Instrum. 1995, 66, 3789–3798. [Google Scholar] [CrossRef]
- Morag, J.; Dishon, M.; Sivan, U. The governing role of surface hydration in ion specific adsorption to silica: An AFM-based account of the Hofmeister universality and its reversal. Langmuir 2013, 29, 6317–6322. [Google Scholar] [CrossRef] [PubMed]
- Trefalt, G.; Palberg, T.; Borkovec, M. Forces between colloidal particles in aqueous solutions containing monovalent and multivalent ions. Curr. Opin. Colloid Interf. Sci. 2017, 27, 9–17. [Google Scholar] [CrossRef]
- Ducker, W.A.; Senden, T.J.; Pashley, R.M. Direct measurement of colloidal forces using an atomic force microscope. Nature 1991, 353, 239–241. [Google Scholar] [CrossRef]
- Valle-Delgado, J.J.; Molina-Bolivar, J.A.; Galisteo-Gonzalez, F.; Galvez-Ruiz, M.J.; Feiler, A.; Rutland, M.W. Hydration forces between silica surfaces: Experimental data and predictions from different theories. J. Chem. Phys. 2005, 123, 034708. [Google Scholar] [CrossRef] [PubMed]
- Grabbe, A.; Horn, R.G. Double layer and hydration forces measured between silica sheets subjected to various surface treatments. J. Colloid Interface Sci. 1993, 157, 375–383. [Google Scholar] [CrossRef]
- Acuna, S.M.; Toledo, P.G. Nanoscale repulsive forces between mica and silica surfaces in aqueous solutions. J. Colloid Interface Sci. 2011, 361, 397–399. [Google Scholar] [CrossRef] [PubMed]
- Adler, J.J.; Rabinovich, Y.I.; Moudgil, B.M. Origins of the non-DLVO force between glass surfaces in aqueous solution. J. Colloid Interface Sci. 2001, 237, 249–258. [Google Scholar] [CrossRef] [PubMed]
- Montes Ruiz-Cabello, F.J.; Trefalt, G.; Oncsik, T.; Szilagyi, I.; Maroni, P.; Borkovec, M. Interaction forces and aggregation rates of colloidal latex particles in the presence of monovalent counterions. J. Phys. Chem. B 2015, 119, 8184–8193. [Google Scholar] [CrossRef] [PubMed]
- Moazzami-Gudarzi, M.; Trefalt, G.; Szilagyi, I.; Maroni, P.; Borkovec, M. Nanometer-ranged attraction induced by multivalent ions between similar and dissimilar surfaces probed by the atomic force microscope (AFM). Phys. Chem. Chem. Phys. 2016, 18, 8739–8751. [Google Scholar] [CrossRef] [PubMed]
- Valmacco, V.; Elzbieciak-Wodka, M.; Besnard, C.; Maroni, P.; Trefalt, G.; Borkovec, M. Dispersion forces acting between silica particles across water: Influence of nanoscale roughness. Nanoscale Horiz. 2016, 1, 325–330. [Google Scholar] [CrossRef]
- Ackler, H.D.; French, R.H.; Chiang, Y.M. Comparisons of Hamaker constants for ceramic systems with intervening vacuum or water: From force laws and physical properties. J. Colloid Interface Sci. 1996, 179, 460–469. [Google Scholar] [CrossRef]
- Bevan, M.A.; Prieve, D.C. Direct measurement of retarded van der Waals attraction. Langmuir 1999, 15, 7925–7936. [Google Scholar] [CrossRef]
- Elzbieciak-Wodka, M.; Popescu, M.; Montes Ruiz-Cabello, F.J.; Trefalt, G.; Maroni, P.; Borkovec, M. Measurements of dispersion forces between colloidal latex particles with the atomic force microscope and comparison with Lifshitz theory. J. Chem. Phys. 2014, 140, 104906. [Google Scholar] [CrossRef] [PubMed]
- Oncsik, T.; Trefalt, G.; Borkovec, M.; Szilagyi, I. Specific ion effects on particle aggregation induced by monovalent salts within the Hofmeister series. Langmuir 2015, 31, 3799–3807. [Google Scholar] [CrossRef] [PubMed]
- Montes Ruiz-Cabello, F.J.; Trefalt, G.; Maroni, P.; Borkovec, M. Accurate predictions of forces in the presence of multivalent ions by Poisson-Boltzmann theory. Langmuir 2014, 30, 4551–4555. [Google Scholar] [CrossRef] [PubMed]
- Tadros, T.F.; Lyklema, J. Adsorption of potential determining ions at silica-aqueous electrolyte interface and role of some cations. J. Electroanal. Chem. 1968, 17, 267–275. [Google Scholar] [CrossRef]
- Abendroth, R.P. Behavior of a pyrogenic silica in simple electrolytes. J. Colloid Interface Sci. 1970, 34, 591–596. [Google Scholar] [CrossRef]
- Bonthuis, D.J.; Gekle, S.; Netz, R.R. Profile of the static permittivity tensor of water at interfaces: Consequences for capacitance hydration interaction and ion adsorption. Langmuir 2012, 28, 7679–7694. [Google Scholar] [CrossRef] [PubMed]
- Redondo, A.B.; Jordan, I.; Ziazadeh, I.; Kleibert, A.; Giorgi, J.B.; Worner, H.J.; May, S.; Abbas, Z.; Brown, M.A. Nanoparticle-induced charge redistribution of the air-water interface. J. Phys. Chem. C 2015, 119, 2661–2668. [Google Scholar] [CrossRef]
- Schwierz, N.; Horinek, D.; Netz, R.R. Anionic and cationic Hofmeister effects on hydrophobic and hydrophilic surfaces. Langmuir 2013, 29, 2602–2614. [Google Scholar] [CrossRef] [PubMed]
- Montes Ruiz-Cabello, F.J.; Trefalt, G.; Maroni, P.; Borkovec, M. Electric double layer potentials and surface regulation properties measured by colloidal probe atomic force microcopy. Phys. Rev. E 2014, 90, 012301. [Google Scholar] [CrossRef] [PubMed]
- Uzelac, B.; Valmacco, V.; Trefalt, G. Interactions between silica particles in the presence of multivalent coions. Soft Matter 2017, 13, 5741–5748. [Google Scholar] [CrossRef] [PubMed]
- Sverjensky, D.A. Prediction of surface charge on oxides in salt solutions: Revisions for 1:1 (M+L−) electrolytes. Geochim. Cosmochim. Acta 2005, 69, 225–257. [Google Scholar] [CrossRef]
- Kielland, J. Individual Activity Coefficients of Ions in Aqueous Solutions. J. Am. Chem. Soc. 1937, 59, 1675–1678. [Google Scholar] [CrossRef]
- Marcus, Y. Ionic radii in aqueous solutions. Chem. Rev. 1988, 88, 1475–1498. [Google Scholar] [CrossRef]
- Persson, I. Hydrated metal ions in aqueous solution: How regular are their structures? Pure Appl. Chem. 2010, 82, 1901. [Google Scholar] [CrossRef]
- Kameda, Y.; Uemura, O. Neutron Diffraction Study on the Structure of Highly Concentrated Aqueous LiBr Solutions. Bull. Chem. Soc. Jpn. 1993, 66, 384–389. [Google Scholar] [CrossRef]
- Kay, R.L. The current state of our understanding of ionic mobilities. Pure Appl. Chem. 1991, 63, 1393. [Google Scholar] [CrossRef]
- Marcus, Y. Are Ionic Stokes Radii of Any Use? J. Solut. Chem. 2012, 41, 2082–2090. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smith, A.M.; Maroni, P.; Borkovec, M.; Trefalt, G. Measuring Inner Layer Capacitance with the Colloidal Probe Technique. Colloids Interfaces 2018, 2, 65. https://doi.org/10.3390/colloids2040065
Smith AM, Maroni P, Borkovec M, Trefalt G. Measuring Inner Layer Capacitance with the Colloidal Probe Technique. Colloids and Interfaces. 2018; 2(4):65. https://doi.org/10.3390/colloids2040065
Chicago/Turabian StyleSmith, Alexander M., Plinio Maroni, Michal Borkovec, and Gregor Trefalt. 2018. "Measuring Inner Layer Capacitance with the Colloidal Probe Technique" Colloids and Interfaces 2, no. 4: 65. https://doi.org/10.3390/colloids2040065
APA StyleSmith, A. M., Maroni, P., Borkovec, M., & Trefalt, G. (2018). Measuring Inner Layer Capacitance with the Colloidal Probe Technique. Colloids and Interfaces, 2(4), 65. https://doi.org/10.3390/colloids2040065