Abstract
Capillary pressure experiments are performed in microgravity conditions on board the International Space Station to quantify the dynamic interfacial behavior of mixed adsorption layers of TTAB and C13DMPO at the water/hexane interface. While the non-ionic surfactant C13DMPO is soluble in both bulk phases, water and hexane, the cationic surfactant TTAB is only soluble in the aqueous phase. The interfacial layer is thus formed by TTAB molecules adsorbing from the aqueous phase while the C13DMPO molecules adsorb from the aqueous phase, and transfer partially into the hexane phase until both the equilibrium of adsorption and the distribution between the two adjacent liquid phases is established. The experimental constrains as well as all possible influencing parameters, such as interfacial and bulk phase compressibility, interfacial curvature, calibration of pressure and absolute geometry size, are discussed in detail. The experimental results in terms of the dilational interfacial viscoelasticity of the mixed adsorption layers in a wide range of oscillation frequencies show that the existing theoretical background had to be extended in order to consider the effect of transfer of the non-ionic surfactant across the interface, and the curvature of the water/hexane interface. A good qualitative agreement between theory and experiment was obtained, however, for a quantitative comparison, additional accurate information on the adsorption isotherms and diffusion coefficients of the two studied surfactants in water and hexane, alone and in a mixed system, are required.
1. Introduction
Water/oil interfaces are of great relevance for many technological processes, such as oil recovery [1,2], food processing [3,4,5], production of cosmetics [6] and pharmaceutics [7]. In most of these cases mixtures of surfactants are applied, in order to reach required properties of the respective systems [8,9,10].
In particular, knowledge on the formation of mixed adsorption layers at water/oil interfaces is not quite advanced due to the complexity of the systems. Therefore, model surfactants are to be studied in order to get some important basic insights into the interfacial behavior. Interfacial rheology methods appeared to be very promising for studies of such systems as they bear important information about the relationships between the molecular properties of emulsifying agents and dynamics of the interfacial layers [11,12,13,14,15,16,17]. For this aim, also microgravity conditions are of great importance as they allow simplifying not only the experimental conditions but also the required theories for a quantitative description of the interfacial layer behavior. The microgravity environment first of all excludes convections due to density and temperature differences [18]. In addition, geometries are simplified, such as all drops have a spherical shape making the consideration of diffusional transport less complicated. This, however, entails also the disadvantage that only capillary pressure tensiometry is appropriate as experimental technique [19] while all other techniques fail due to the missing gravity.
As model surfactants we have selected the cationic surfactant tetradecyl trimethyl ammonium bromide (TTAB) and the non-ionic surfactant tridecyl dimethyl phosphine oxide (C13DMPO), which are well studied at the interface between their aqueous solutions and air and various oil phases [2,3,20,21,22] and references therein. Mixtures of these two surfactants have not been investigated yet, and also the number of adsorption studies for other surfactant mixtures at liquid interfaces are rather limited [23,24,25,26].
This manuscript reports on recent capillary pressure experiments performed in microgravity conditions on board the International Space Station, using a special designed capillary pressure tensiometer. Mixtures of TTAB and C13DMPO in water have been investigated at the water/hexane interface at different concentrations and compositions. A complication for the present mixed surfactant system is the solubility of the non-ionic C13DMPO in both bulk phases, water and hexane [20,27], while TTAB is only soluble in the aqueous phase. Thus, after formation of the interface, TTAB molecules only adsorb until equilibrium has been established while C13DMPO molecules adsorb from the aqueous phase, and transfer partially until not only the equilibrium of adsorption but also of the distribution in the two adjacent liquid phases is reached.
2. Experimental Technique and Procedure
2.1. Materials
Pure water (purity level MilliQ) was produced by a Millipore (Elix plus MilliQ, Merck, Kenilworth, NJ, USA) purification chain, provided with ultraviolet ray irradiation.
The hydrocarbon n-Hexane for spectroscopy Uvasol® (CAS 110-54-3) was purchased from Sigma-Aldrich (Merck) and used as received.
The non-ionic surfactant tridecyl dimethyl phosphine oxide, C13DMPO, (CAS 186953-53-7) was purchased from Gamma-Service, Berlin, Germany, with high purity and used as received.
The cationic surfactant tetradecyl trimethyl ammonium bromide, TTAB, (CAS 1119-97-7), with a purity higher than 98%, was purchased from Sigma-Aldrich (St. Louis, MO, USA) and used without further purification.
The multi-component two-phase liquid system is visualised in Figure 1.

Figure 1.
Mixed non-ionic/cationic surfactant components of the aqueous matrix solution (C13DMPO + TTAB) and of the adjoining hydrocarbon dispersed phase (pure n-hexane drop).
2.2. Measurement Cell
The instrument is a capillary pressure tensiometer, devised for exploring the adsorption layer behavior of a single n-hexane drop immersed in an aqueous solution of a surfactant mixture, i.e., TTAB and C13DMPO.
The measurement cell (structure and the functionality) is identical to the cell recently described for a similar microgravity experiment [28].
Essentially the measurement cell consists of two chambers (pure n-hexane reservoir and aqueous matrix-cell) connected through a capillary. The volume of the reservoir is about v = 5.6 cm3 and of the matrix-cell is about V = 68.2 cm3, gradually increasing after each injection of surfactant solution, up to a maximum of 70.0 cm3. During the instrument storage and transport the two chambers are separated by a closed main valve (positioned in the safe state).
The hydrocarbon/water interface is generated by withdrawing from the reservoir an appropriate amount of pure n-hexane into the aqueous matrix by means of a piezo-actuator, forming a drop at the tip of the capillary. The piezo-actuator also controls the drop dimensions (i.e., radius and interfacial area extension) according to pre-established time-functions.
Two syringes allow injection, into the matrix-cell, of exactly-dosed amounts of C13DMPO (concentration in the syringe#1 aqueous solution, c = 0.002 mol/dm3) and of TTAB (concentration in the syringe#2 aqueous solution, c = 0.45 mol/dm3), in a pre-established sequence, triggered by a built-in time line.
Two pressure sensors, a CCD-camera and other devices in synchronism acquire the values of Laplace-pressure, of geometrical properties of the drop and of temperature.
2.3. Measurement Sequence
The FASTER facility was operated by a ground-established built-in software, actuating a sequence of actions according to a given time-line (TL). Table 1 shows the conditions of surfactant injections and concentrations in the matrix cell throughout the overall TL.

Table 1.
Sequence of surfactant injections and concentrations in the matrix cell.
Actually the TL started on the day-of-year (DOY) 183, 2014 (i.e., 2 July 2014), operating continuously during the daily 24-hours and terminating on DOY 219 (i.e., 7 August 2014).
Initially, some small nitrogen bubbles, trapped in the closed main valve, were released into the capillary during the valve opening action, impeding any operation in the pure liquid sample and in the sample with the first injection of C13DMPO-surfactant (see Table 1). Then, the nitrogen bubbles were purged out from the capillary and subsequently the gas phase became dissolved in the aqueous matrix, as often visually ascertained by inspection of the telemetered images, up to the TL termination.
In a similar scheme as recently illustrated for an equivalent microgravity experiment [28], the drop interfacial area was subjected to different sequences of perturbations (harmonic oscillations, square pulses, ancillary ramp- and step-changes for calibration purpose), for each sample of aqueous surfactant solutions, as resulting from each injection (i.e., from injection 1-1 to 6-5).
Specific harmonic oscillation sequences involved 12 cycles for each of 8 frequencies in the low frequency range, f = 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.50, 1.0 Hz, and likewise 12 cycles for each of 12 frequencies in the high frequency range f = 1, 2, 3, 5, 10, 20, 40, 60, 80, 100, 150, 200 Hz.
For each sample, all experimental sequences (i.e., harmonic oscillations and square pulses) were performed at 3 different amplitudes (5%, 10%, 20% of the drop baseline area) and at 3 different temperatures (i.e., T = 15, 20 and 30 °C).
A minor part of the forecast above-mentioned 90 experimental sequences misses of complete integrity, for the on-ground availability, due to losses in the telemetered transmission.
The final concentration value of TTAB is assumed with an estimated uncertainty of about 5% less than the nominal value in Table 1, uncertainty ascribed to the TTAB adsorption on a few small n-hexane drops, detached into the aqueous matrix on DOY 206. Moreover, the C13DMPO concentration value is affected by a 0.3% uncertainty, in connection with the estimated 0.3% inaccurate knowledge of the aqueous-matrix volume. A more important uncertainty can be caused in the C13DMPO concentration due to its dissolution in hexane, as it is discussed in detail below.
2.4. Data Acquisition, Transmission and Pre-Processing
The operations of digital data acquisition, from analog output of the measurement sensors/actuators, and the operations for the telemetry transmission to ground, in the form of 1-second time-tagged digital-unit packets and digital-images, were executed with the same systematic procedure already described in Ref. [28].
In particular, each of the above-mentioned 1-second packets was constituted by drop radius data together with drop-height data (both properties being acquired at a 20-Hz frequency) and by pressure data (acquired at 60-Hz frequency), as well as by other complementary data. In intermittent mode, together with such 1-second packets, additional 1-second packets were also telemetered, containing 33-point drop profiles. Moreover, 1000 × 1000-pixel drop images, acquired at 35-second intervals, accompanied the downlink transmission stream.
On-ground, the telemetered data were first checked according to a step-by-step pre-processing protocol, aimed at granting reliability and consistence of the measurement values of all relevant physical quantities. In this protocol, the following essential elements were borne in mind and effectively operated prior to any data processing [28]:
- (a)
- noise filtering,
- (b)
- data misalignment check inside the telemetered digital-unit packets and, in case required, synchronization of pressure data with optical data,
- (c)
- selection of oscillation sequences, for each concentration sample, at each amplitude and at each temperature,
- (d)
- in flight check of calibration parameters and, in case required, calibration adjustment.
2.4.1. Optical Calibration In-Flight Check
The stability of ground optical calibration parameters was confirmed by the (internal reference) known length of capillary diameter, d = 0.984 mm, as seen in the example of Figure 1. The in-flight tests, conducted at intervals during the measurement time-line, gave a mean value of the micrometer/pixel ratio, that is the optical calibration factor, c = 2.624 μm/pix. This value appeared satisfactorily comparable with the on-ground result, c = 2.583 μm/pix, hence being 1.5% the incertitude concerning the geometrical properties (that is, the systematic error expressed as percentage of the measured value in the International System of Units). Note that a two-dimensional calibration factor was not necessary as the CCD-camera features square pixels.
Specific operations for the optical calibration and image characteristics are reported in the Supplementary Material: Appendix A.
2.4.2. Adjustment of Pressure Sensor Calibration
The in-flight checks showed that the stability of pressure-sensor calibration parameters was compromised during the long-term on-ground storage of the facility, before launch, or likely in consequence of mechanical and temperature stresses during the transfer of the facility from the factory to the ISS installation. In particular, the offset value of the pressure sensor devices (GE-Druck, Bad Nauheim, Germany, PDCR-4000 model) was altered, as it was manifested by the plot of the differential pressure vs. inverse radius in the course of a growing-drop experiment. In principle, this plot should result in a straight line intercepting the pressure axis at the origin, at constant interfacial tension, according to the Laplace equation. The slope parameter of the above-mentioned straight line, instead, resulted essentially stable, according to a (preliminary on-ground verified) specification of the used pressure sensors.
As the in-flight check showed that the vertical intercept zero-value was definitely altered, such an observed numeric value was used to adjust the pressure-sensor calibration-offset parameters. Considering the conformation of the cell, the adjustment value was operatively attributed just to the reference pressure sensor (inside the n-hexane reservoir chamber). Actually, the contribution of the altered offset of the working pressure sensor (inside the drop chamber) cannot be distinguished within the observed intercept value and anyway this distinction is irrelevant as the significant physical quantity is the difference between the signals of the two pressure sensors.
In the telemetered data, about 30 growing drop experiments were available with a suitable behavior for the required adjustment of the differential-pressure offset. Growing-drop experiments in the samples with the greatest surfactant concentration were preferentially selected for the in-flight calibration adjustment, because the fast adsorption process allowed the interfacial tension to be maintained at an almost constant value during the interfacial area expansion. Useful growing-drop experiments were also taken into account at the smallest available surfactant concentration. Albeit the condition of constant interfacial tension did not exist during the whole time interval of interfacial area expansion, however the fit of the upper part of the growing ramp provided a correct evaluation for the pressure-calibration adjustment, since the drop growth rate matched the rate of the surfactant adsorption process. A satisfactory agreement was observed between the offset values observed at the smallest concentration and at the greatest concentration, indicating a calibration stability during the entire microgravity-experiment time-line. In principle, the offset value obtained at the greatest concentration should be considered more reliable in respect to the dilute surfactant concentration, as the fitting is obtained along almost all the ramp interval extent.
The correction value of the calibration offset was obtained by the average of different growing-drop experiments, respectively at the cell temperatures T = 15, 20 and 30 °C. As usual, out-layer values were discarded. Telemetered data with scarce integrity were also discarded. The estimated uncertainty on the adjusted pressure values is about 1.5%, that is, the systematic error expressed as percentage of the measured value in the International System of Units.
The plot in Figure 2 illustrates an example of a growing drop experiment, selected for the pressure adjustment operation.
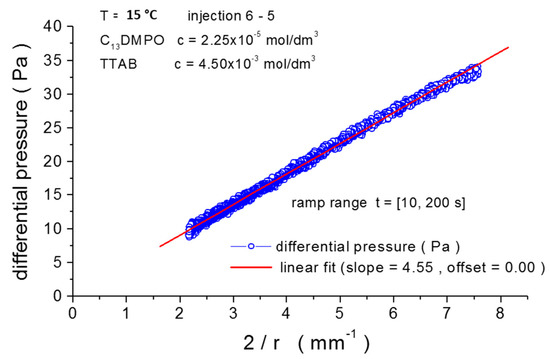
Figure 2.
Fitting of differential pressure vs. inverse radius, r, for injection 6-5 at T = 15 °C for a growing drop experiment, with filtered reference pressure and adjusted calibration parameters (linear fit, slope = 4.55 mNm−1, offset = 0.00 Pa).
Additional results for the adjustment operation of pressure-sensor calibration can be found in the Supplementary Material: Appendix B.
Technical details about the processing of the telemetered data are extensively outlined in Ref. [29] and in a note, available in the Supplementary Material: Appendix C.
3. Theory
3.1. Dilational Viscoelasticity of Mixed Adsorption Layers
The surface dilational viscoelasticity characterizes the response of an interfacial layer to a dilational deformation (i.e., expansion or compression) of the interface. Quantitatively the surface dilational viscoelasticity modulus is defined as the ratio of complex amplitudes of the interfacial tension variation, Δγ, to the respective relative interfacial area variation, ΔlnA,
In Equation (1) Δγ and ΔlnA are the complex amplitudes of harmonically varying interfacial tension and relative interfacial area , ΔlnA = ΔA/A0, with γ0 and A0 being the equilibrium interfacial tension and area, i the complex unit, ω = 2πf the angular frequency, and f the frequency of oscillations.
As a complex quantity the surface viscoelasticity modulus can be represented as
where is its magnitude and φ(ω) is the phase, which are usually specific functions of the oscillation frequency. The shapes of these functions depend on the properties of the interfacial layer and the relaxation processes induced by the deformations. Therefore, the studies of rheological interfacial characteristics can bear important information about the properties of interfacial layers in equilibrium and low-amplitude dynamic experiments.
In the simples case of an interfacial layer formed by a single surfactant, which is characterized by a diffusion limited adsorption mechanism, the complex viscoelasticity modulus can be described by the Lucassen and van den Tempel equation [30,31]
where is the limiting elasticity, Г = Г(c) is the adsorption, which is a function of the surfactant concentration c, D is the diffusion coefficient and T is the absolute temperature.
For mixed adsorption layers composed of two surfactants, both of them characterized by a diffusion limited adsorption mechanism, two analytical expressions for the surface viscoelasticity modulus where presented, one of them proposed by Jiang et al. [32] and the second one proposed by Joos [33]. These analytical expressions can be easily transformed one to another [34,35]. The corrected expression for the surface viscoelasticity of a mixture derived by Jiang et al. has the form [32,34,35]
where and are the partial elasticities [33], (i, j = 1, 2) are the partial derivatives of the adsorptions Г1 = Г1(c1, c2) and Г2 = Г2(c1, c2) by the surfactants concentrations c1 and c2, D1 and D2 are the diffusion coefficients, and . The expression Equation (4) transforms to the Lucassen and van den Tempel equation, Equation (3), in the case when one of the two surfactant concentrations, c1 or c2, turns to zero.
Equations (3) and (4) were derived for systems with an air/liquid interface, where the surfactants are dissolved in one contacting phase only. We are considering here a more complicated system with two contacting immiscible liquids, where the surfactants can partition between the two liquid phases. In this case, under equilibrium conditions the ratio of the surfactant concentrations in the two phases is given by the distribution coefficient
Here and below the lower indexes j = 1, 2 are related to the two surfactants, whereas the upper indexes α and β are related to the two contacting liquids.
In such systems, if the interface between the two liquids is expanded (or compressed), then adsorption (desorption) begins from (to) the both liquid phases to restore the equilibrium. The rate of the diffusional transfer in each of the liquids depends on the diffusion coefficients and concentrations of the surfactants in these two liquids. Thus, a more general theoretical model is necessary, which accounts for the surfactants partitioning and diffusion in the two contacting liquids.
The theoretical analysis presented in Supplementary Material: Appendix D shows that the expression for the surface viscoelasticity of a mixture, Equation (4), preserves its validity also in the case of two contacting liquids but with the substitution of the diffusion coefficients D1 and D2 by their effective counterparts
In the case of a single surfactant partitioning between two liquid phases, the viscoelasticity of the interfacial layer should be described by Equation (3), but with the effective diffusion coefficient given by Equation (6) [36,37]. The effective diffusion coefficient should enter also into the Ward-Tordai equation describing the dynamics of adsorption at the interface formed between two immiscible liquids [33,37].
As it is seen from Equation (6), the effective diffusion coefficients and depend on the diffusion coefficients of the surfactants in both phases and , as well as on the distribution coefficients Kj. Thus, to calculate the surface viscoelasticity modulus we have to know these parameters.
3.2. Equilibrium Equation of State and Adsorption Isotherms of the Mixed Adsorption Layer
Equation (4) contains additional 6 parameters: two partial elasticities, E01 and E02, and four coefficients ai,j. These 6 parameters should be determined from the surface equation of state and the adsorption isotherms and (or and ). Thus, to calculate the surface viscoelasticity modulus by using Equation (4) we have to know the equilibrium equation of state and adsorption isotherms of the mixed adsorption layers [34,35]. Unfortunately, for the mixed adsorption layers of TTAB and C13DMPO at hexane/water interface considered here, such equations are presently unknown. Therefore, for the analysis of the experimental data we will use a simplified approach assuming that the individual adsorption layers of TTAB and C13DMPO can be characterized by the Langmuir model with adsorptions and interfacial tension given by the equations
where γ0 is the interfacial tension of the pure hexane/water interface (which is about 51.1 mN/m [20,38]), are the limiting adsorptions, and are the equilibrium adsorption constants. Note, Equation (7) defines the adsorptions with respect to the concentrations in the phase α, but they can be also defined with respect to the concentrations in the phase β, as these concentrations are in equilibrium according to Equation (5). The parameters and for the individual adsorption layers of TTAB and C13DMPO at the hexane/water interface can be found in literature (e.g., in [20,38]).
In this case, the adsorptions and interfacial tension for the mixed layers can be described by the following approximate equations [33]
and
where and are the equilibrium surface coverages by the surfactants, and are their molar areas, and is the average molar area. Equations (9) and (10) can be used as an approximation only in the case of similar values for Г1∞ and Г2∞. In a general case, when Г1∞ and Г2∞ are different, these equations are inconsistent with thermodynamic requirements [33].
For the adsorption layer model described by Equations (9) and (10) one can obtain the required parameters as
3.3. Dilational Viscoelasticity of Curved Interfaces
Equations (3) and (4) were derived for flat interfacial layers. For a drop interface considered here, the effect of curvature can be significant. The effect of curvature on the dilational interfacial viscoelasticity was analyzed by Joos, who considered several confined geometries, such as thin liquid films, small drops and thin liquid cylinders [33]. In particular, he derived two expressions, which describe the viscoelasticity of curved interfaces of drops for the situations with the surfactant diffusion from either outside or inside the drop (Equations (8.63) and (8.68) in [33]). For large drops and large oscillation frequencies these expressions are reduced to the Lucassen and van den Tempel equation, Equation (3). However, with a decreasing drop radius and decreasing oscillation frequency the corrections introduced due to the curvature of the drop interface can become significant. The curvature influences the dilational viscoelasticity because, in contrast to flat interfaces, the surfactant diffusion to or from a curved interface occurs along the converging or diverging radial directions, and, therefore, the concentration profiles become different. Also, in the case of small drops, the surfactant diffusion from the drop leads to solution depletion in the drop (or enrichment in the case of diffusion from the interface to the bulk solution inside the drop).
Unfortunately, the expressions derived by Joos do not account for the possibility of surfactant partitioning between the external and internal liquids when the diffusion and adsorption are possible on both sides of the interface. For this particular case the expressions by Joos can be generalized and an equation combining both situations with surfactant diffusion from outside and inside the drop can be derived [39]
where and , r0 is the equilibrium drop radius, and cα is the surfactant concentration in the external liquid phase. With account for Equation (5) this expression can be easily transformed to the case when the adsorption is defined with respect to the concentration in the internal phase β, . In the limiting cases of a very small (K << 1) or very large (K >> 1) distribution coefficient Equation (14) is reduced to the respective expressions by Joos for the surfactant diffusion and adsorption from only one side of the drop interface. For large drop radii and large oscillation frequencies, when and , Equation (14) takes the form of the Lucassen and van den Tempel equation, Equation (3), with the effective diffusion coefficient . This corresponds to the case of a locally flat interface with adsorption of one surfactant from the both contacting liquids.
4. Results and Discussion
4.1. Experimental Results—Low Frequency Range
As it is stated above, all experimental sequences were performed at 3 different amplitudes (5%, 10%, 20% of the drop baseline area) and at 3 different temperatures (i.e., T = 15, 20 and 30 °C). In most cases, the results obtained at 3 different amplitudes practically coincide. This fact indicates a good linearity of the interfacial tension response to the interfacial area perturbations. Thus, the results obtained at different amplitudes can be used to check the repeatability of the measurements for the same temperature and concentration. The equilibrium value of the drop radius was r0 = 0.270 ± 0.004 mm, slightly larger than the inner capillary radius (0.25 mm).
Figure 3 and Figure 4 show the typical dependencies of the viscoelasticity modulus and phase shift φ(ω) versus frequency in the low frequency range at different C13DMPO and TTAB concentrations. These dependencies will be used here for the analysis of the dynamics of the mixed interfacial layers formed at the water/hexane interface under different experimental conditions.
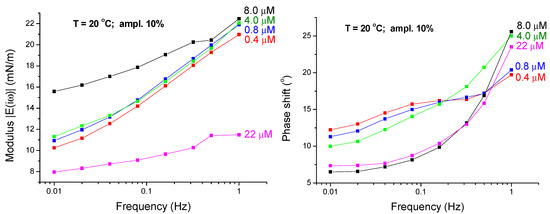
Figure 3.
Viscoelasticity modulus and phase shift φ(ω) as functions of the frequency for C13DMPO concentrations of 4.0 × 10−7, 8.0 × 10−7, 4.0 × 10−6, 8.0 × 10−6 and 2.2 × 10−5 mol/dm3 (injections 2-1 to 6-1) at a fixed TTAB concentration of 4.5 × 10−5 mol/dm3 (T = 20 °C; ampl. 10%); the lines are guides for the eye.
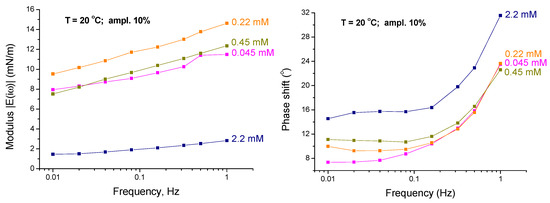
Figure 4.
Viscoelasticity modulus and phase shift φ(ω) as functions of frequency for TTAB concentrations of 4.5 × 10−5, 2.2 × 10−4, 4.5 × 10−4 and 2.2 × 10−3 mol/dm3 (injections 6-1 to 6-4) at a fixed C13DMPO concentration of 2.2 × 10−5 mol/dm3 (T = 20 °C; ampl. 10%); the lines are guides for the eye.
It is seen from Figure 3 and Figure 4 that similarly to the case of single surfactants adsorbed at flat interfaces, the viscoelasticity modulus of the mixed interfacial layers at drop interfaces increases with the frequency. However, in contrast to the situation with single surfactants at flat interfaces, the phase shift φ(ω) also increases with the frequency. Such behaviour of the phase shift is opposite to what we have in the case of single surfactants at flat interfaces, where the phase shift decreases with increasing frequency. We will return to this point further below.
Figure 3 and Figure 4 show also the effect of the surfactants concentrations on the viscoelasticity modulus and phase shift. It is seen from Figure 3 that for increasing C13DMPO concentration at a fixed TTAB concentration the viscoelasticity modulus initially increases (for the concentrations between 4.0 × 10−7 and 8.0 × 10−6 mol/dm3) and then decreases (for concentrations higher than 8.0 × 10−6 mol/dm3). Figure 4 shows a similar behavior of the viscoelasticity modulus with respect to the TTAB concentration at a fixed C13DMPO concentration: the modulus initially increases (for the concentrations between 4.5 × 10−5 and 2.2 × 10−4 mol/dm3) and then decreases (for concentrations higher than 2.2 × 10−4 mol/dm3). Such effect of concentration is typical also for individual surfactants solutions, as will be discussed further below.
For the highest TTAB concentrations of 2.2 × 10−3 and 4.5 × 10−3 mol/dm3 in the presence of 2.2 × 10−5 mol/dm3 C13DMPO (injections 6-4 and 6-5) the viscoelasticity modulus becomes very low, of the order of few mN/m only. It should be noted that the concentration of 2.2 × 10−3 mol/dm3 is close to and the concentration 4.5 × 10−3 mol/dm3 is above the CMC for aqueous TTAB solutions, which is of about 3.5 × 10−3 mol/dm3 [40]. Such small modulus values are typical for micellar surfactant solutions, where the exchange of monomers with the micelles supports to keep the monomer concentration at the interface almost constant (if the oscillation frequency is not very high), and, as consequence, the interfacial tension practically does not change [41]. At very small modulus values, the determination of the phase shift may become problematic because the relative errors in determining the real and imaginary parts of the modulus strongly increase. This can even cause some small negative phase shift values obtained for the injection 6-5. Therefore, these results are not analysed here.
4.2. Comparison with Model Calculations
4.2.1. Parameter Sets of the Model
To understand the experimental data for the viscoelasticity modulus and phase shift we performed some model calculations by using the theoretical approach formulated above. For these calculations, we have used the parameters for the individual adsorption layers of TTAB and C13DMPO presented in literature. The parameters of the Langmuir isotherm for adsorption layers of C13DMPO at the hexane/water interface are presented in [20]: 2.1 × 10−6 mol/m2 and 1.25 × 107 dm3/mol (for definiteness, phase α is water here). The diffusion coefficient of C13DMPO in water was obtained in [20,27] to be about = (0.9–2.2) × 10−9 m2/s. These values are several times higher than the typical values for surfactants in aqueous solutions, which can be probably explained by a certain contribution of a convective transfer. Such convective mixing is less probable under microgravity conditions, therefore, the correct diffusion coefficient of C13DMPO in water should be probably smaller. According to the results in [27], the diffusion coefficient of C13DMPO in hexane is smaller than in water. One could expect the opposite, as the viscosity of hexane is about three times lower than that of water. A strong solvent-surfactant interaction could probably explain this fact, according to the authors. In a recent study by Fainerman et al. [42] the diffusion coefficient of C13DMPO in hexane was found to be = (3.2–4.5) × 10−9 m2/s for a water drop in hexane, and = (2–3) × 10−9 m2/s for a hexane drop in water. The diffusion coefficient of C13DMPO in water was found to be = (1–2) × 10−9 m2/s, i.e., practically the same as in [27]. The distribution coefficient for C13DMPO between hexane and water was obtained to be of about K1 = 34 in [27] and of about K1 = 30 in [42], which is quite close to each other. With these values for the diffusion coefficients in hexane and water and the distribution coefficient, the effective diffusion coefficient of C13DMPO, , will be of the order of 10−6 m2/s. Such large value is explained by the high solubility of C13DMPO in hexane.
The parameters of the Langmuir isotherm for adsorption layers of TTAB at the hexane/water interface were obtained in [38]: 2.33 × 10−6 mol/m2 and 9.4 × 105 dm3/mol. It is seen that the difference between and is small, therefore the approximate Equations (9)–(13) can be applied. It is seen that the solubility of TTAB in water is much higher than the solubility of C13DMPO. At the same time the solubility of TTAB in hexane is practically negligible, which is typical for ionic surfactants. Therefore, the effective diffusion coefficient of TTAB is determined mainly by its diffusion coefficient in the aqueous phase, , which is about 1 × 10−10 mol/m2, according to [38].
4.2.2. Viscoelasticity Modeling for Mixed and Individual Solutions
With the set of parameters listed above, the viscoelasticity modulus and the phase shift φ(ω) were calculated according to Equations (4), (6) and (11)–(13) for several C13DMPO concentrations and a fixed TTAB concentration and are presented in Figure 5. The frequency range used for the calculations was much broader than in the experiments. It is seen that similarly to the experimental data the calculated viscoelasticity modulus increases with the frequency in the whole frequency range. In contrast, the phase shift versus frequency dependence is not monotonous, it also demonstrates an increase with the frequency, but only in a limited interval of intermediate frequencies. This is a typical behaviour for surfactants mixtures [34,35]. Hence, one of the possible explanations of the increasing phase shift with frequency is the presence of the second surfactant in the solution. It can be assumed that for the system considered here, that the applied frequencies related to the low frequency range approximately coincide with this limited frequency interval where both the viscoelasticity modulus and the phase shift are increasing. Another possible explanation of the increasing phase shift could be related to the curvature effect of the interface, as will be considered below.
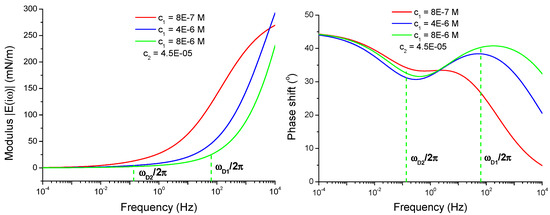
Figure 5.
Viscoelasticity modulus and phase shift φ(ω) of a mixed adsorption layer as functions of frequency calculated according to Equations (4), (6) and (11)–(13) for 8.0 × 10−7, 4.0 × 10−6 and 8.0 × 10−6 mol/dm3 at fixed 4.5 × 10−5 mol/dm3.
For comparison we have calculated also the viscoelasticity modulus and the phase shift φ(ω) for the individual solutions of C13DMPO and TTAB according to the Lucassen and van den Tempel model, Equation (3), by using the same adsorption parameter sets. The results are presented in Figure 6. The viscoelasticity modulus for individual solutions demonstrates a qualitatively similar behaviour as for the mixed solutions presented in Figure 5, i.e., the modulus increases with the frequency. In contrast, the phase shift does not have a frequency interval, where it increases with the frequency. For diffusion-limited adsorption of a single surfactant at a flat interface the phase shift should decrease continuously with increasing frequency from 45° at very small frequencies to zero at very high frequencies, as it follows from the Lucassen and van den Tempel model. Thus, the increasing phase shift with the frequency observed in our experiments can be an indication of the significance of the fact that the solutions studied here are surfactants mixtures.
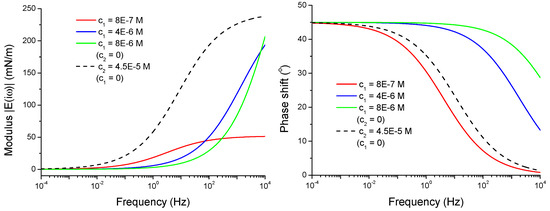
Figure 6.
Viscoelasticity modulus and phase shift φ(ω) of individual adsorption layers as functions of frequency calculated according to Equation (3) for 8.0 × 10−7, 4.0 × 10−6 and 8.0 × 10−6 mol/dm3 at 0 (full lines) and for 4.5 × 10−5 mol/dm3 at 0 (dashed line).
It should be noted that for diffusion-limited adsorption at a flat interface, also in the case of surfactants mixtures, the phase shift should not exceed the value of 45°, as predicted by Equation (4). The experimental values of the phase shift presented in Figure 3 and Figure 4 are below this value. This allows us to assume that the adsorption is limited by diffusion in the studied system here, and other relaxation processes are absent. The phase shift could exceed 45°, if the adsorption kinetics would be limited by an activation energy barrier, or if some other relaxation processes would be present in the system, e.g., aggregation of the surfactant molecules [43].
For the further analysis, Equation (4) can be transformed to a more convenient form
where and are dimensionless variables, and are the two characteristic relaxation frequencies and (Supplementary Material: Appendix D).
Thus, the surface dilational viscoelastic modulus of a surfactant mixture depends on two characteristic frequencies, ωD1 and ωD2, which characterize the rates of diffusional relaxation of the two surfactants in the mixture. These characteristic frequencies are determined by the effective diffusion coefficients and , which depend on the diffusion rate in both liquid phases. The effective diffusion coefficients depend also on the surfactants’ distribution coefficients Kj. The diffusion in the phase, where the surfactant is more soluble, is more significant for the surface dilational viscoelastic modulus. The surface dilational viscoelastic modulus of a mixture depends also on some equilibrium parameters: E0j, Г0j and the ratios a12/a22 and a21/a11.
The two characteristic frequencies, ωD1 and ωD2, are shown on the curve for the concentration 8.0 × 10−6 mol/dm3 in Figure 5. In this particular case, the difference between these two frequencies is large, their ratio is larger than two orders of magnitude. The limited frequency interval, where the phase shift increases with frequency, is located between these two frequencies. If we would decrease the effective diffusion coefficient for C13DMPO by two or three orders of magnitude, then the difference between the frequencies ωD1 and ωD2 will be much smaller, and a frequency interval with increasing phase shift would not be observed. This fact demonstrates that the apparently large value of the effective diffusion coefficient for C13DMPO discussed above is consistent with the observed system behavior. Note, the real diffusion coefficients of C13DMPO in the two liquids are by three orders of magnitude smaller than .
The adsorption equilibrium constant for TTAB obtained in [38] is about 7 times smaller than that obtained in [21]. If we take for our calculations a 7 times larger constant than we used, then the characteristic frequency ωD2 increases and the difference between the frequencies ωD1 and ωD2 becomes much smaller, i.e., the frequency interval with increasing phase shift becomes much shorter or disappears (for smaller C13DMPO concentrations). Thus, the smaller equilibrium constant obtained in Ref. [38] is more consistent with the experimental results presented above.
4.2.3. Effect of the Isotherm Parameters
As discussed above we are using here a simplified approach assuming that the individual and mixed adsorption layers of TTAB and C13DMPO can be characterized by the Langmuir model for which all necessary parameters are available. A detailed comparison of the experimental data with the results of the model calculations shows that the use of the Langmuir model is probably sufficient for a qualitative interpretation of the observed dynamic system behavior, however it is not sufficient for a more precise quantitative analysis. In particular, one has to pay attention to very high viscoelasticity modulus values for the individual and mixed adsorption layers, which exceed 100 mN/m for higher frequencies, as it is seen in Figure 5 and Figure 6. It was shown previously [44] and references therein] that such large viscoelasticity modulus values can be a consequence of neglecting the finite size of the adsorbing molecules in the Langmuir or Frumkin models. At high surface coverages one can improve formally the agreement of the models with experimental data by assuming that the molar areas can depend linearly on the surface pressure as
where Ω0j are the molar areas of the surfactants at zero surface pressure, εj are coefficients of the linear dependence, and ∏ = γ0 − γ is the surface pressure (γ0 and γ are the surface tensions of the interface in absence and in presence of surfactants, respectively). Sometimes, an alternative dependence is used [35,38]
The variation of the molar areas with surface pressure according to Equations (16) or (17) practically does not influence the surface pressure versus surfactant concentration dependencies but strongly influences the rheological characteristics of the interfacial layers [44]. If this effect is neglected then the calculations based on the standard Langmuir or Frumkin models give unphysically large values for the limiting elasticities and characteristic relaxation frequencies. With account for this effect, one obtains realistic values for the limiting elasticities and characteristic relaxation frequencies, which agree with the experimental data for rheological surface properties.
The calculations performed by using the model and the parameters listed above show that the surface coverages should be rather high for these surfactant concentrations. In particular, for the smallest concentrations 2.0 × 10−7 mol/dm3 and 4.5 × 10−5 mol/dm3 we obtained surface coverages of θ1 = 0.055 and θ2 = 0.924, respectively, with the total surface coverage θ1 + θ2 = 0.978. Note, the adsorption constants for oil/water interfaces are usually much larger than for the air/water interface, which for the studied concentrations results in large values (much larger than 1) and large θj values. Hence, even for the smallest concentrations the total surface coverage is close to unity, i.e., the studied adsorption layers are in a compressed state. For such compressed layers the effect of variation of the molar areas could be significant. Thus, the very high viscoelasticity modulus values seen in Figure 5 and Figure 6 could be a consequence of the neglected variation of the molar areas. Also, the characteristic frequencies, ωD1 and ωD2, could be incorrect for the same reason. Therefore, the calculations performed here based on the Langmuir model are not sufficient for a more detailed quantitative comparison with the experimental data.
Another important limitation of the Langmuir model is the neglected interaction between the adsorbed molecules. For surfactants with sufficiently long hydrocarbon chains (and at high surface coverages) the attractive interaction is usually significant. Moreover, in addition to the attractive interaction of the respective hydrocarbon chains, also an attraction can occur between the positive electrical charges of the TTAB cations and the negatively polarised oxygen in the PO group of C13DMPO. Thus, a more general model, which takes into account the surfactants interaction, would be more adequate for the considered system.
In Figure 6 of [38], the viscoelasticity modulus versus concentration dependencies are presented for the individual adsorption layers of TTAB at the water/hexane interface. It is seen that our TTAB concentration range corresponds to the descending branch of the dependencies, shown in this figure, i.e., the maximum is at a concentration smaller than our minimum TTAB concentration (4.50 × 10−5 mol/dm3). However, our results discussed above (Figure 4) show that there is obviously a maximum of the viscoelasticity modulus at the TTAB concentration of about 2.25 × 10−4 mol/dm3, i.e., the maximum is shifted to a higher TTAB concentration in the presence of C13DMPO. Also, the height of the maximum for mixed solutions is much smaller than in absence of C13DMPO. These differences could be an indication of the importance of interactions between the surfactants in the studied system.
Thus, it can be concluded from the discussion above, that for a proper comparison of the experimental data with the modeling results we need a more general model for the mixed adsorption layers than the simple Langmuir model. For this purposes the so-called Frumkin Ionic Compressibility adsorption model would be suitable [38]. However, the parameters included in this more general model are presently unknown for mixed adsorption layers of TTAB and C13DMPO.
Interpretation of the experimental results is also complicated by the uncertainty in the C13DMPO concentration, because of its dissolution in hexane. The volume of the hexane drop is much smaller than the volume of the aqueous matrix-cell, therefore, the amount of C13DMPO dissolved in the drop can be neglected. However, the drop is connected to the hexane reservoir, and a part of C13DMPO can diffuse to this reservoir though the capillary connecting it with the drop. This diffusion process is very slow, but the total time of the experiment is large, which may lead to a gradual decrease of the C13DMPO concentration in the matrix-cell. Nevertheless, this concentration decrease should not be large because the measurements for each subsequent concentration are performed shortly after the injection of a new portion of C13DMPO during the time, which is not sufficient for the diffusion of C13DMPO between the drop and the hexane reservoir. Moreover, the injected amounts are continuously increasing, therefore, the loss of small surfactant amounts from the previous injections should be insignificant.
4.2.4. Effect of Curvature of the Drop Interface
As it was discussed above, the curvature of the interface can influence the dilational viscoelasticity, especially at small drop radii and small oscillation frequencies. This effect can be neglected only if the parameters and are much larger than 1. For the drop radius r0 = 0.27 mm and diffusion coefficient D = 10−9 m2/s, one obtains = 2.2 × 10−3 s−1, which is not too far from the lower frequencies in this study. Therefore, the possibility of curvature effect should be also considered. In Figure 7, one can see the viscoelasticity modulus and phase shift φ(ω) of C13DMPO adsorption layers calculated according to Equation (14) for different drop radii with Dα = Dβ = 10−9 m2/s, cα = 8.0 × 10−7 mol/dm3 and the Langmuir isotherm parameters as presented above. At higher frequencies the curves for and φ(ω) for different drop radii approach those for the infinite radius. The larger is the drop radius, the closer is the respective curve to that for the infinite radius (flat surface). However, the dependencies for the finite radii have a plateau and the respective φ(ω) dependencies are not monotonous at smaller frequencies, in contrast to the case of infinite radius. It is important that there is a frequency range where the phase shift φ(ω) increases with frequency.
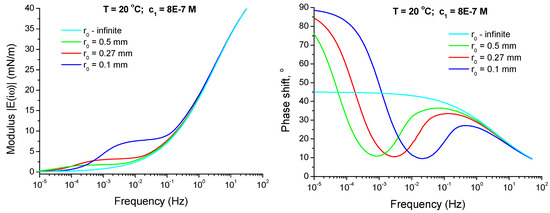
Figure 7.
Viscoelasticity modulus and phase shift φ(ω) of C13DMPO adsorption layers at the drop interfaces with radii r0 = 0.1, 0.27, 0.5 mm and infinite as functions of frequency, calculated according to Equation (14) for Dα = Dβ = 10−9 m2/s and cα = 8.0 × 10−7 mol/dm3 with the Langmuir isotherm parameters given in the text.
The specific shape of the curves in Figure 7 can be explained as follows. If the oscillation frequency is very large, the diffusion layer thickness is much smaller than the drop radius r0, and the interface behaves like locally flat. Accordingly, the phase shift decreases with increasing frequency in this case and the viscoelasticity modulus gradually increases up to its high-frequency limit (see Equation (3)). In contrast, if the oscillation frequency is very small and, additionally, the surfactant solubility in the external phase is also small or negligible (K >> 1), then the diffusion layer thickness is much larger than the drop radius r0, and the adsorption equilibrium between the interface and the drop volume establishes during a time much smaller than one oscillation period. In this case, the interface and the surfactant concentration within the drop oscillate with almost the same phase and the phase shift between the area oscillations and the interfacial tension oscillations becomes very small. Thus, the phase shift should decrease with the frequency decrease left from the local maximum. Also under these conditions, the amplitudes of the interfacial tension oscillations practically do not depend on the rate of interfacial area expansion or compression. This explains the appearance of a plateau on the viscoelasticity modulus versus frequency dependencies at intermediate frequencies. The level of this plateau is determined by the surfactant depletion in the drop due to its adsorption at the interface—the smaller is the drop the higher is the depletion [45].
If the surfactant solubility in the external phase is small but not negligible, then the diffusion can propagate within the external phase up to the distances much larger than the drop radius. This leads to an increase of the phase shift up to 90° with further frequency decrease, i.e., beyond the theoretical limit of 45° for flat interfaces. However, under these conditions, the viscoelasticity modulus becomes negligibly small and the phase shift becomes not determinable.
Thus, from the analysis presented in this subsection it follows that the effect of curvature of the drop interface can give a second explanation for the experimentally observed increase of the phase shift with frequency, alternative to the above discussed effect of surfactant mixtures. To discriminate between the relative contributions of these two effects, a more general theoretical model is necessary which describes co-adsorption of two partitioning surfactants at a curved interface. As well, a more precise information about the adsorption isotherms and diffusion coefficients of the surfactants is necessary. Such studies are the subject of future works.
4.3. Experimental Results and Analysis—High Frequency Range
For higher frequencies (1–200 Hz), the experimental protocol is significantly different compared to the low frequency range considered in the previous section. In the case of high-frequency oscillations, the direct determination of the instant geometric characteristics of the drop becomes difficult because of the limitations in the optical tools’ resolution and data transfer rate. Therefore, the drop volume and interfacial area variations should be determined in an indirect way via the piezo-actuator displacements by taking into account the compressibilities of the liquids in the two chambers of the measuring cell [28]. In addition, the pressure difference measured between the two chambers includes not only the Laplace pressure contribution at the drop interface but also some hydrodynamic contributions due to the oscillating flow in the capillary and around the drop. This leads to more complicated frequency dependencies, than in the case of low frequency oscillations.
In the frequency domain, the pressure variation in chamber A (aqueous matrix-cell) relative to the average pressure in this chamber is described by the equation [28,46]
where BA,B and VA,B are the effective bulk elasticities and volumes of chamber A and chamber B (n-hexane reservoir), respectively, δVAct is the volume variation produced by the piezo-actuator, and RC is the complex hydrodynamic resistance of the capillary with the attached meniscus and adjacent liquid. In the approximation of a quasi-stationary flow this resistance is given by the equation [28,46]
where G1 and G2 are the coefficients describing the viscous and inertia contributions due to the flow in the bulk of liquids, and are the geometric parameters—the derivatives of the drop radius r and the relative surface area lnA on the meniscus volume Vm, and γeq and r0 are the equilibrium interfacial tension and drop radius.
The pressure difference between the chambers A and B is described by the equation
For frequencies below 10 Hz the pressure variation in chamber B, δPB, is negligible, and the pressure difference, δPAB, is practically the same as the pressure variation in chamber A, δPA (see Equation (18)). However, for frequencies above 10 Hz the pressure variation in chamber B becomes also significant (due to resonance effects), and one has to take it into account.
It is seen from Equation (19) that the complex hydrodynamic resistance RC is determined not only by the hydrodynamic effects (viscosity and inertia) in the bulk of liquids but also by the properties of the drop interface—the equilibrium interfacial tension γeq and the interfacial viscoelasticity modulus E. This means that the oscillating flow through the capillary connecting the chambers A and B depends on the equilibrium (γeq) as well as on the dynamic (E = E(iω)) properties of the interfacial layer formed between the two contacting liquids. Accordingly, the measured pressure variations in the chambers A and B should also depend on these interfacial characteristics. However, the interfacial characteristics strongly depend on the composition of the interfacial layer, which is determined by the surfactants’ concentrations in the bulk solutions. As a result, the measured pressure signals strongly depend on the solutions’ composition.
In Figure 8 and Figure 9 one can see the amplitude- and phase-shift-frequency characteristics related to the pressure variation in chamber A for mixed solutions of C13DMPO and TTAB with different concentrations. As it is seen, these characteristics strongly depend on the surfactants’ concentrations. The relative amplitude of the pressure oscillations decreases with C13DMPO concentration and the minimum and maximum in the frequency characteristic gradually disappear (Figure 8). At the same time, the phase shift depends only slightly on the C13DMPO concentration. With increasing TTAB concentration the maximum in the amplitude-frequency characteristic becomes more pronounced and shifts to smaller frequencies (Figure 9). The phase shift decreases by its absolute value (i.e., increases with respect to −π) for the two highest TTAB concentrations at small frequencies.
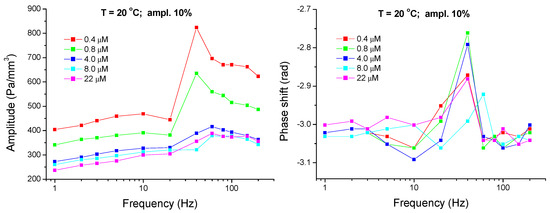
Figure 8.
Amplitude- and phase-shift-frequency characteristics for the pressure in chamber A (aqueous matrix-cell) measured for mixed solutions of C13DMPO with concentrations of 4.0 × 10−7, 8.0 × 10−7, 4.0 × 10−6, 8.0 × 10−6 and 2.2 × 10−5 mol/dm3 (injections 2-1 to 6-1) and TTAB with a fixed concentration of 4.5 × 10−5 mol/dm3 (T = 20 °C; ampl. 10%); the lines are guides for the eye.
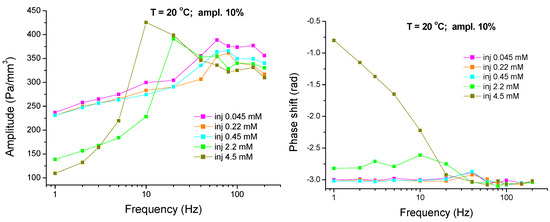
Figure 9.
Amplitude- and phase-shift-frequency characteristics for the pressure in chamber A (aqueous matrix-cell) measured for mixed solutions of TTAB with concentrations of 4.5 × 10−5, 2.2 × 10−4, 4.5 × 10−4, 2.2 × 10−3 and 4.5 × 10−3 mol/dm3 (injections 6-1 to 6-5) and C13DMPO with a fixed concentration of 2.2 × 10−5 mol/dm3 (T = 20 °C; ampl. 10%); the lines are guides for the eye.
For frequencies below 10 Hz the contribution of hydrodynamic effects is very small and the level of the plateau left from the amplitude maximum is determined mainly by the two last terms in Equation (19), i.e., by the properties of the drop interface [28,46]. The equilibrium interfacial tension γeq decreases with increasing surfactant concentrations what should lead to an increase of the plateau level. However, the effect of the interfacial viscoelasticity E(iω) is opposite in phase and is stronger in this concentration range and, therefore, the general trend is a decrease of the plateau level with increasing surfactant concentrations. The plateau level gradually rises up with increasing frequency which reflects an increase of the viscoelasticity modulus and an increase of the hydrodynamic contribution.
At higher frequencies a resonance maximum is observed in the amplitude-frequency characteristics, which is a consequence of compensation of the increased inertia contribution G2ω2 by the elastic contribution due to the bulk elasticity and the contribution of the interface in the denominator of Equation (18) [28,46]. The height of this maximum is determined by the dissipative processes in the system. With increasing C13DMPO concentration, the contribution of the dilational interfacial viscosity becomes larger, therefore, the resonance maximum decreases (see Figure 8). However, with a further increase in the TTAB concentration both real and imaginary parts of the interfacial viscoelasticity E(iω) become very small and, as a result, the resonance maximum moves toward smaller frequencies and slightly increases again (Figure 9). These results show that the viscoelastic characteristics of the interface can have a strong effect on the dynamic properties of the system as a whole.
5. Conclusions
The obtained results reveal that capillary pressure tensiometry is a suitable tool to study the equilibrium and dynamic properties of adsorption layers formed at the interface between two immiscible liquids under microgravity conditions. Such studies can provide, in particular, a consistent set of reliable data for the dynamic properties of mixed surfactant layers at the water/hydrocarbon interface. An important advantage of this method is that all operations, including the surfactant injections, drop size control, temperature and pressure control, etc. can be performed in a fully automatic regime according to a pre-established sequence, triggered by a built-in time line. In necessary cases, the pressure sensors’ calibration can be performed by using the growing drop procedure described here.
In these particular experiments, the dynamic properties of mixed adsorption layers formed by C13DMPO and TTAB surfactants at the interface between water and hexane at different surfactants’ concentrations were studied in a wide frequency range. The measured interfacial dilational viscoelasticity as a function of frequency and of temperature reveal that the water/hexane interface in contact with mixed C13DMPO/TTAB solutions exhibits a viscoelastic behavior and that the adsorption from both contacting liquids is important. The phase shift versus frequency dependences measured at different surfactants’ concentrations are rising up, in contrast to the decreasing curves usually obtained for single surfactant adsorption layers at flat interfaces. The possible explanations of the increasing phase shifts with the frequency of oscillations are: (i) the effect of mixture, when two surfactants in the mixture are characterized by different characteristic relaxation frequencies, and (ii) the effect of curvature of the interface, when the radius of curvature is comparable with the diffusion layer thickness. To quantify the relative contribution of each of these two effects, a more rigorous information about the adsorption isotherms is required.
The viscoelastic modulus versus frequency characteristics show a non-monotonous dependences on the surfactants concentrations, with a decrease of the modulus at higher concentrations. Such a behavior is an indication of insufficiency of the standard Langmuir or Frumkin models at high surface coverages, where the variation of the molar areas with the surface pressure should be taken into account. Also, the effects of interactions between the components of the mixed layers should be accounted for.
In the high frequency range it was shown that the pressure variations in the second chamber (n-hexane reservoir) can become significant and, as a result, the pressure difference between the two chambers can be different from the pressure variations in the first chamber (aqueous matrix-cell), where the volume oscillations are generated by means of a piezo-actuator. The measurements clearly show a dependence of the amplitude- and phase-shift-frequency characteristics of the system on the viscoelastic properties of the interface between the two liquids along with the hydrodynamic and bulk elasticity effect.
In summary, we can conclude that the obtained experimental data are in a good qualitative agreement with the theoretically predicted system behavior. However, for a more detailed comparison with the theory a more precise information about the adsorption isotherms and diffusion coefficients of the two studied surfactants at the water/hexane interface is necessary.
Supplementary Materials
The following are available online at http://www.mdpi.com/2504-5377/2/4/53/s1.
Author Contributions
All authors planned the work and designed the experiments; M.F., J.K., L.L., G.L., P.P. and R.M. conducted the microgravity experiments; V.I.K., G.L. and P.P. performed the elaboration of the telemetered data; V.I.K., R.M. and B.A.N. interpreted and discussed the data; V.I.K., G.L. and R.M. wrote the manuscript.
Funding
European Space Agency projects “Fundamental and Applied Studies in Emulsion Stability—FASES”, Contract no. 47702388027160000510 from the Russian Federation, “Soft Matter Dynamics”, “Particle Stabilized Emulsions—PASTA” from the European Space Agency (and the corresponding grants by the Italian Space Agency ASI n. 2013-028-R.O) are greatly acknowledged.
Acknowledgments
The authors are very thankful to V. B. Fainerman from SINTERFACE Technologies, Berlin, for many valuable discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Schramm, L.L. Surfactants: Fundamentals and Applications in the Petroleum Industry; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Sjöblom, J. Encyclopedic Handbook of Emulsion Technology; Marcel Dekker, Inc.: New York, NY, USA, 2001. [Google Scholar]
- McClements, D.J. Food Emulsions: Principles, Practices, and Techniques, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Murray, B.S. Interfacial rheology of food emulsifiers and proteins. Curr. Opin. Colloid Interface Sci. 2002, 7, 426–431. [Google Scholar] [CrossRef]
- Dickinson, E. Milk protein interfacial layers and the relationship to emulsion stability and rheology. Colloids Surf. B 2001, 20, 197–210. [Google Scholar] [CrossRef]
- Lin, J. Manufacturing Cosmetic Emulsions Pragmatic Troubleshooting and Energy Conservation; Allured Pub Corp.: Carol Stream, IL, USA, 2009. [Google Scholar]
- Powell, K.C.; Damitz, R.; Chauhan, A. Relating emulsion stability to interfacial properties for pharmaceutical emulsions stabilized by Pluronic F68 surfactant. Int. J. Pharm. 2017, 521, 8–18. [Google Scholar] [CrossRef] [PubMed]
- Rosen, M.J.; Kunjappu, J.T. Surfactants and Interfacial Phenomena, 4th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Böttchera, S.; Keppler, J.K.; Drusch, S. Mixtures of Quillaja saponin and beta-lactoglobulin at the oil/water-interface: Adsorption, interfacial rheology and emulsion properties. Colloids Surf. A 2017, 518, 46–56. [Google Scholar] [CrossRef]
- Cao, C.; Lei, J.; Zhang, L.; Du, F.-P. Equilibrium and Dynamic Interfacial Properties of Protein/Ionic-Liquid-Type Surfactant Solutions at the Decane/Water Interface. Langmuir 2014, 30, 13744–13753. [Google Scholar] [CrossRef] [PubMed]
- Dicharry, C.; Arla, D.; Sinquin, A.; Graciaa, A.; Bouriat, P. Stability of water/crude oil emulsions based on interfacial dilatational rheology. J. Colloid Interface Sci. 2006, 297, 785–791. [Google Scholar] [CrossRef] [PubMed]
- Arla, D.; Flesisnki, L.; Bouriat, P.; Dicharry, C. Influence of Alkaline pH on the Rheology of Water/Acidic Crude Oil Interface. Energy Fuels 2011, 25, 1118–1126. [Google Scholar] [CrossRef]
- Sun, H.-Q.; Zhang, L.; Li, Z.-Q.; Zhang, L.; Luo, L.; Zhao, S. Interfacial dilational rheology related to enhance oil recovery. Soft Matter 2011, 7, 7601–7611. [Google Scholar] [CrossRef]
- Benmekhbi, M.; Simon, S.; Sjöblom, J. Dynamic and Rheological Properties of Span-80 at Liquid–Liquid Interfaces. J. Dispers. Sci. Technol. 2014, 35, 765–776. [Google Scholar] [CrossRef]
- Angle, C.W.; Hua, Y. Dilational Interfacial Rheology for Increasingly Deasphalted Bitumens and n-C5 Asphaltenes in Toluene/NaHCO3 Solution. Energy Fuels 2012, 26, 6228–6239. [Google Scholar] [CrossRef]
- Zhou, H.; Luo, Q.; Gonga, Q.-T.; Liu, Z.-Y.; Liu, M.; Zhang, L.; Zhang, L.; Zhao, S. Interfacial dilational properties of di-substituted alkyl benzenesulfonates at kerosene/water and crude oil/water interfaces. Colloids Surf. A 2017, 520, 561–569. [Google Scholar] [CrossRef]
- Zhou, H.; Cao, X.-L.; Guo, L.-L.; Guo, Z.-Y.; Liu, M.; Zhang, L.; Zhang, L.; Zhao, S. Studies on the interfacial dilational rheology of films containing heavy oil fractions as related to emulsifying properties. Colloids Surf. A 2018, 541, 117–127. [Google Scholar] [CrossRef]
- Loglio, G.; Pandolfini, P.; Miller, R.; Makievski, A.V.; Krägel, J.; Ravera, F.; Liggieri, L. STS-107 OV-102 Mission FAST experiment: Slow surface relaxation at the solution-air interface. Microgravity Sci. Technol. J. 2005, 16, 205–209. [Google Scholar] [CrossRef]
- Passerone, A.; Liggieri, L.; Rando, N.; Ravera, F.; Ricci, E. A new experimental method for the measurement of the interfacial tension between immiscible fluids at zero bond number. J. Colloid Interface Sci. 1991, 146, 152–162. [Google Scholar] [CrossRef]
- Ferrari, M.; Liggieri, L.; Ravera, F.; Amodio, C.; Miller, R. Adsorption kinetics of alkyl phosphine oxides at the water/hexane interface 1. Pendant drop experiments. J. Colloid Interface Sci. 1997, 186, 40–45. [Google Scholar] [CrossRef] [PubMed]
- Pradines, V.; Fainerman, V.B.; Aksenenko, E.V.; Krägel, J.; Mucic, N.; Miller, R. Alkyltrimethylammonium bromides adsorption at liquid/fluid interfaces. Colloids Surf. A 2010, 371, 22–28. [Google Scholar] [CrossRef]
- Lyttle, D.J.; Lu, J.R.; Su, T.J.; Thomas, R.K.; Penfold, J. Structure of a Dodecyltrimethylammonium Bromide Layer at the Air/Water Interface Determined by Neutron Reflection: Comparison of the Monolayer Structure of Cationic Surfactants with Different Chain Lengths. Langmuir 1995, 11, 1001–1008. [Google Scholar] [CrossRef]
- Aksenenko, E.V.; Fainerman, V.B.; Petkov, J.T.; Miller, R. Dynamic surface tension of mixed oxyethylated surfactant solutions. Colloids Surf. A 2010, 365, 210–214. [Google Scholar] [CrossRef]
- Phan, C.M.; Nguyen, C.V.; Yusa, S.-I.; Yamada, N.L. Synergistic Adsorption of MIBC/CTAB Mixture at the Air/Water Interface and Applicability of Gibbs Adsorption Equation. Langmuir 2014, 30, 5790–5796. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Zhang, G.; Jiang, P.; Ge, J. Dilational Rheology at Air/Water Interface and Molecular Dynamics Simulation Research of Hydroxyl Sulfobetaine Surfactant. J. Dispers. Sci. Technol. 2014, 35, 448–455. [Google Scholar] [CrossRef]
- Negm, N.A.; Tawfik, S.M. Studies of Monolayer and Mixed Micelle Formation of Anionic and Nonionic Surfactants in the Presence of Adenosine-5-monophosphate. J. Solut. Chem. 2012, 41, 335–350. [Google Scholar] [CrossRef]
- Liggieri, L.; Ravera, F.; Ferrari, M.; Passerone, A.; Miller, R. Adsorption Kinetics of alkyl phosphine oxides at water/hexane interface 2. Theory of the adsorption with transport across the interface in finite systems. J. Colloid Interface Sci. 1997, 186, 46–52. [Google Scholar] [CrossRef] [PubMed]
- Pandolfini, P.; Loglio, G.; Ravera, F.; Liggieri, L.; Kovalchuk, V.I.; Javadi, A.; Karbaschi, M.; Krägel, J.; Miller, R.; Noskov, B.A.; et al. Dynamic properties of Span-80 adsorbed layers at paraffin-oil/water interface: Capillary pressure experiments under low gravity conditions. Colloids Surf. A Physicochem. Eng. Asp. 2017, 532, 228–243. [Google Scholar] [CrossRef]
- Loglio, G.; Pandolfini, P.; Liggieri, L.; Makievski, A.V.; Ravera, F. Determination of interfacial properties by the pendant drop tensiometry: Optimization of experimental and calculation procedures. In Bubble and Drop Interfaces; Progress in Colloid and Interface Science Series; Liggieri, L., Miller, R., Eds.; Brill: Leiden, The Netherlands, 2011; Volume 2, Chapter 2; pp. 7–38. [Google Scholar]
- Lucassen, J.; van den Tempel, M. Dynamic Measurements of Dilational Properties of a Liquid Interface. Chem. Eng. Sci. 1972, 27, 1283–1291. [Google Scholar] [CrossRef]
- Lucassen, J.; van den Tempel, M. Longitudinal waves on visco-elastic surfaces. J. Colloid Interface Sci. 1972, 41, 491–498. [Google Scholar] [CrossRef]
- Jiang, Q.; Valentini, J.E.; Chiew, Y.C. Theoretical models for dynamic dilational surface properties of binary surfactant mixtures. J. Colloid Interface Sci. 1995, 174, 268–271. [Google Scholar] [CrossRef]
- Joos, P. Dynamic Surface Phenomena; VSP: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Aksenenko, E.V.; Kovalchuk, V.I.; Fainerman, V.B.; Miller, R. Surface dilational rheology of mixed adsorption layers at liquid interfaces. Adv. Colloid Interface Sci. 2006, 122, 57–66. [Google Scholar] [CrossRef] [PubMed]
- Aksenenko, E.V.; Kovalchuk, V.I.; Fainerman, V.B.; Miller, R. Surface dilational rheology of mixed surfactants layers at liquid interface. J. Phys. Chem. C 2007, 111, 14713–14719. [Google Scholar] [CrossRef]
- Miller, R.; Loglio, G.; Tesei, U. Exchange of matter at the interface between two liquid phases. Colloid Polym. Sci. 1992, 270, 501–598. [Google Scholar] [CrossRef]
- Ravera, F.; Ferrari, M.; Liggieri, L. Adsorption and partitioning of surfactants in liquid-liquid systems. Adv. Colloid Interface Sci. 2000, 88, 129–177. [Google Scholar] [CrossRef]
- Mucic, N.; Kovalchuk, N.M.; Pradines, V.; Javadi, A.; Aksenenko, E.V.; Krägel, J.; Miller, R. Dynamic properties of CnTAB adsorption layers at the water/oil interface. Colloids Surf. A 2014, 441, 825–830. [Google Scholar] [CrossRef]
- Kovalchuk, V.I.; Aksenenko, E.V.; Makievski, A.V.; Fainerman, V.B.; Miller, R. Dilational interfacial rheology of tridecyl dimethyl phosphine oxide adsorption layers at the water/hexane interface. 2018. under preparation. [Google Scholar]
- Bergeron, V. Disjoining Pressures and Film Stability of Alkyltrimethylammonium Bromide Foam Films. Langmuir 1997, 13, 3474–3482. [Google Scholar] [CrossRef]
- Noskov, B.A. Dynamic surface properties of solutions of colloidal surfactants. Fluid Dyn. 1989, 24, 251–260. [Google Scholar] [CrossRef]
- Fainerman, V.B.; Sharipova, A.A.; Aidarova, S.B.; Kovalchuk, V.I.; Aksenenko, E.V.; Makievski, A.V.; Miller, R. Direct determination of the distribution coefficient of tridecyl dimethyl phosphine oxide between water and hexane. Colloids Interfaces 2018, 2, 28. [Google Scholar] [CrossRef]
- Ravera, F.; Ferrari, M.; Santini, E.; Liggieri, L. Influence of surface processes on the dilational visco-elasticity of surfactant solutions. Adv. Colloid Interface Sci. 2005, 117, 75–100. [Google Scholar] [CrossRef] [PubMed]
- Fainerman, V.B.; Kovalchuk, V.I.; Aksenenko, E.V.; Michel, M.; Leser, M.E.; Miller, R. Models of two-dimensional solution assuming the internal compressibility of adsorbed molecules: A comparative analysis. J. Phys. Chem. B 2004, 108, 13700–13705. [Google Scholar] [CrossRef]
- Fainerman, V.B.; Kovalchuk, V.I.; Aksenenko, E.V.; Miller, R. Dilational Viscoelasticity of Adsorption Layers Measured by Drop and Bubble Profile Analysis: Reason for Different Results. Langmuir 2016, 32, 5500–5509. [Google Scholar] [CrossRef] [PubMed]
- Kovalchuk, V.I.; Krägel, J.; Makievski, A.V.; Loglio, G.; Ravera, F.; Liggieri, L.; Miller, R. Frequency Characteristics of Amplitude and Phase of Oscillating Bubble Systems in a Closed Measuring Cell. J. Colloid Interface Sci. 2002, 252, 433–442. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).