Interfacial and Colloidal Forces Governing Oil Droplet Displacement: Implications for Enhanced Oil Recovery
Abstract
1. Introduction
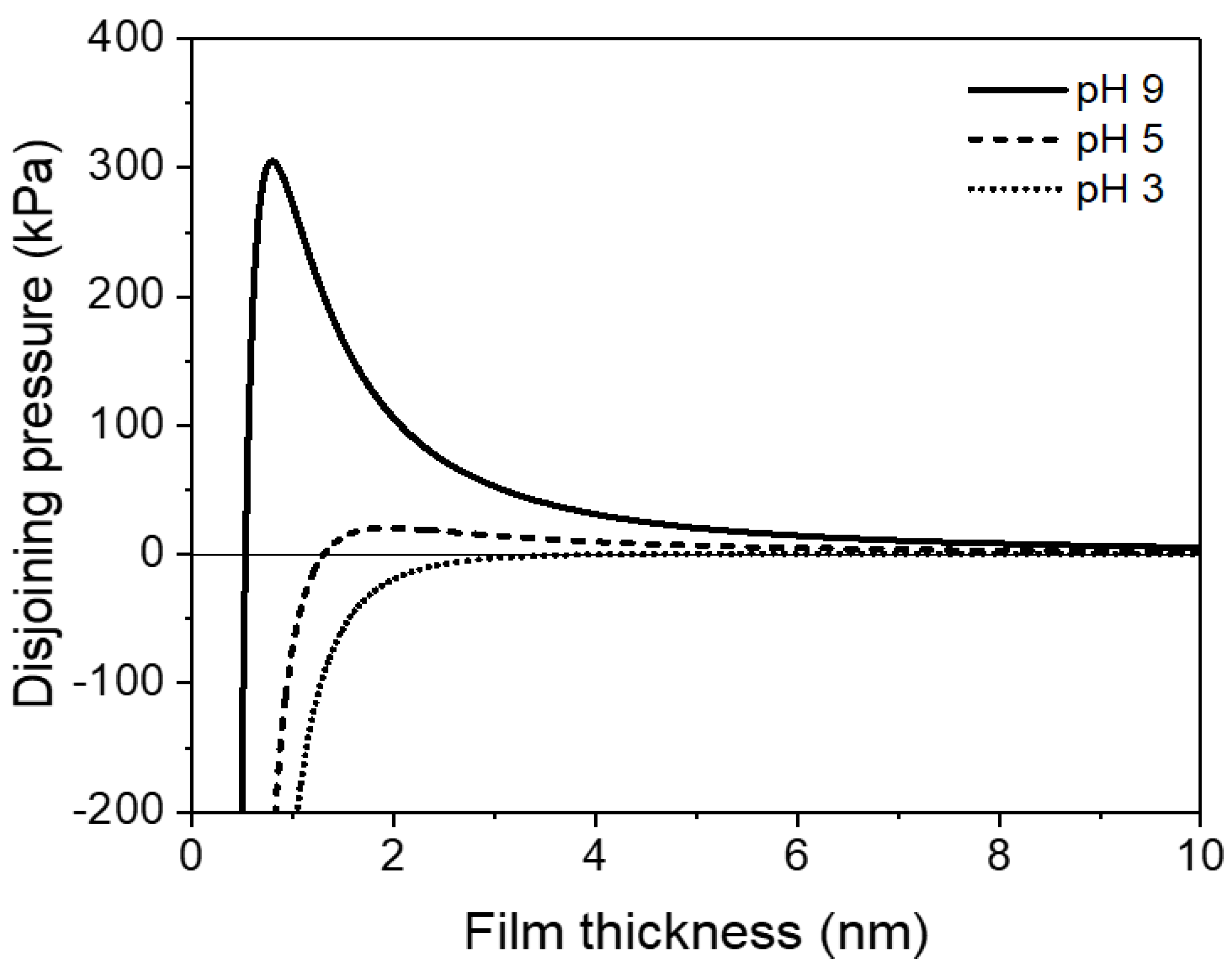
2. Background Science
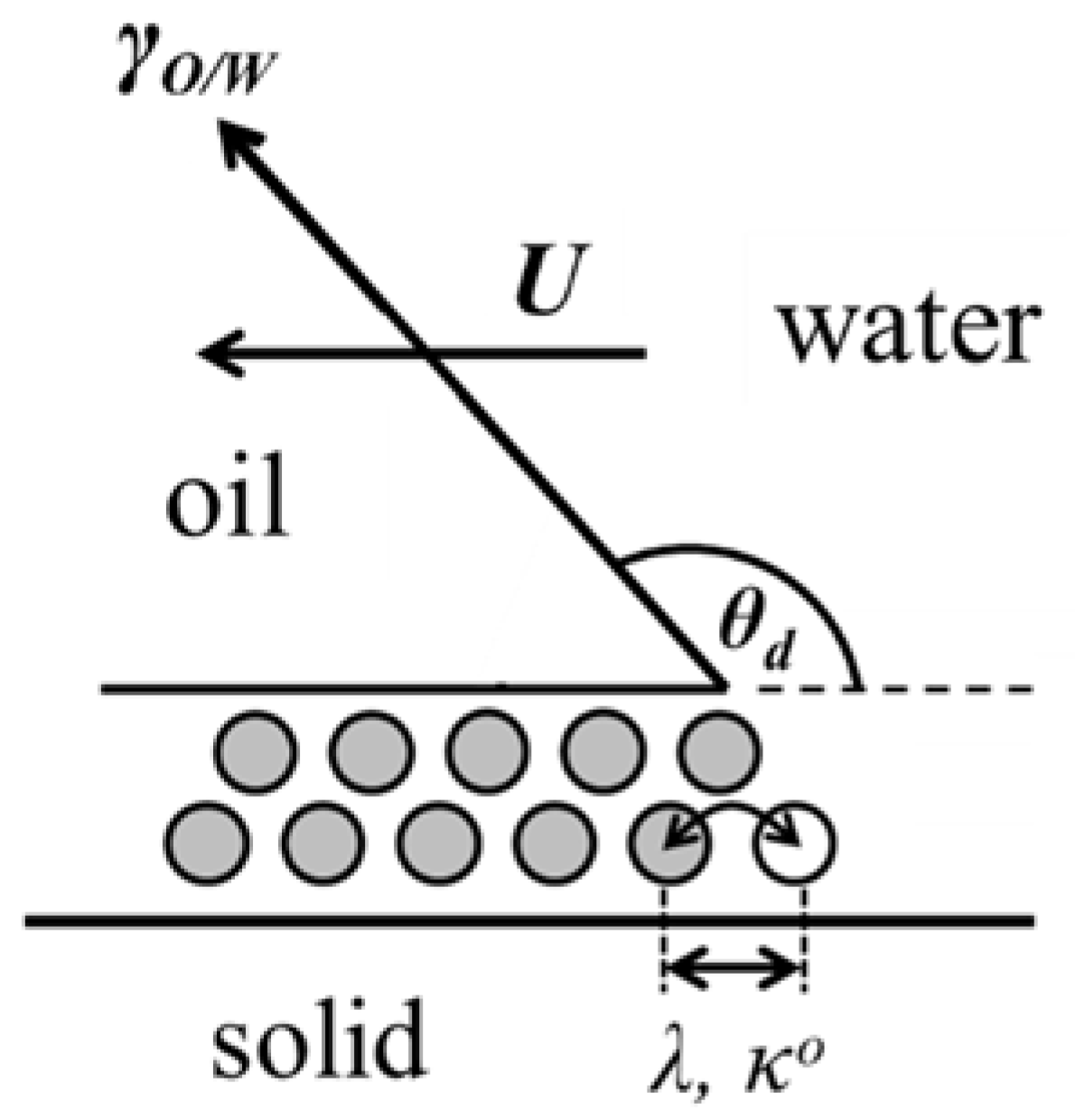
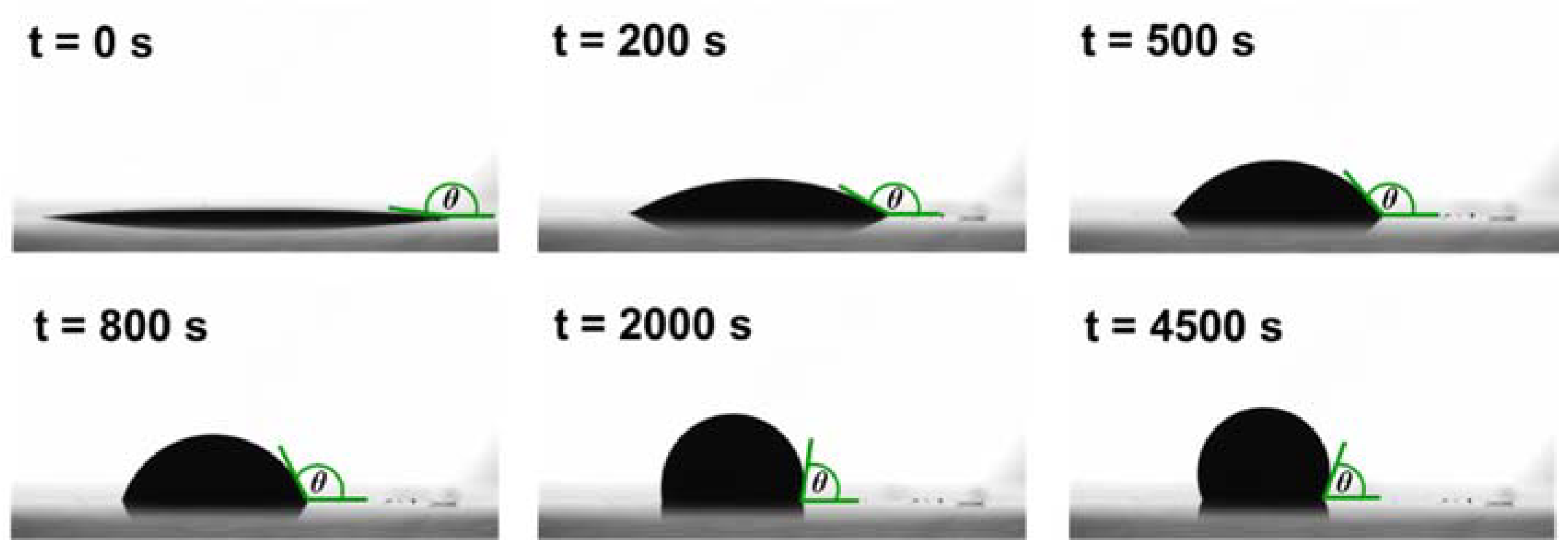
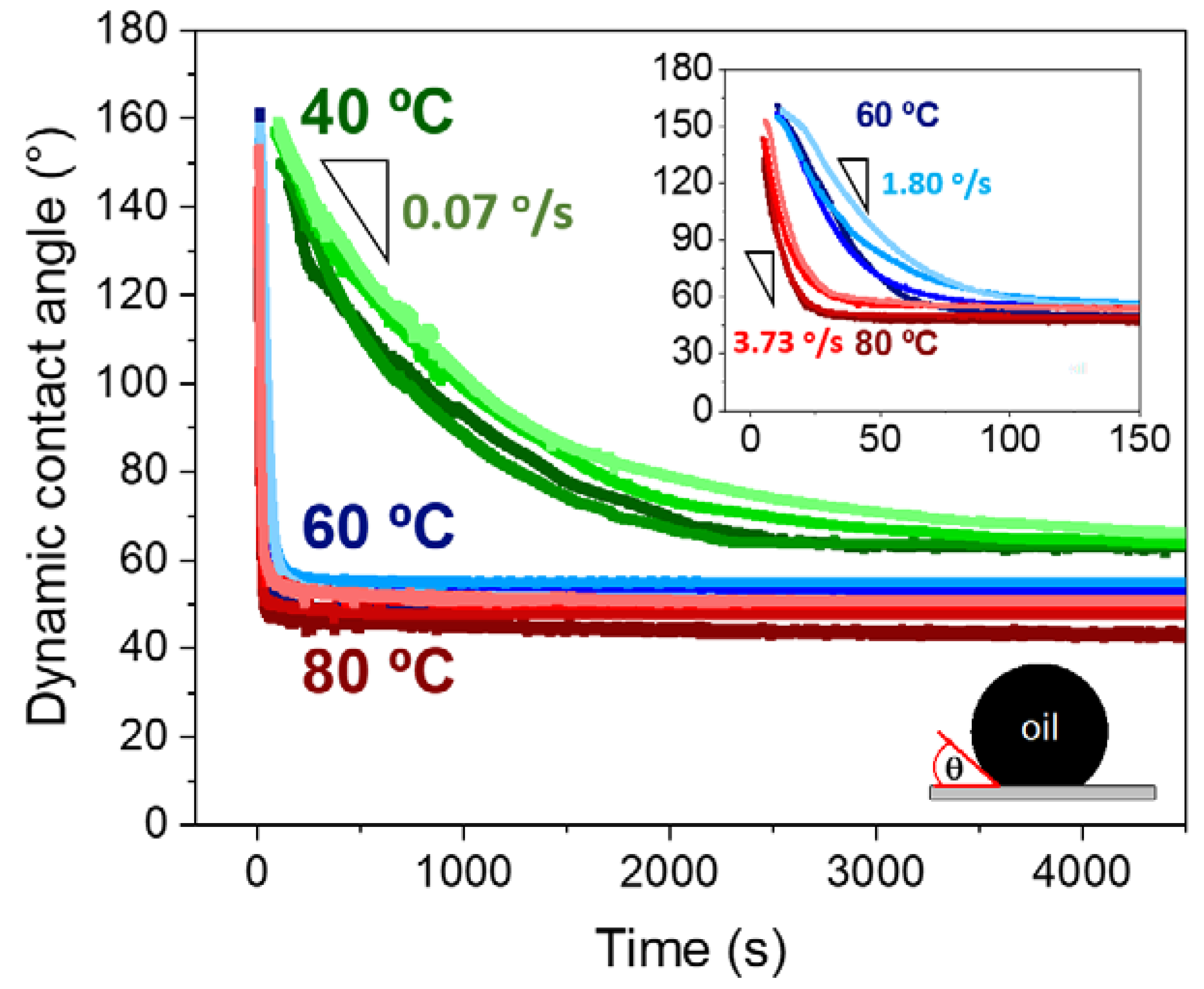
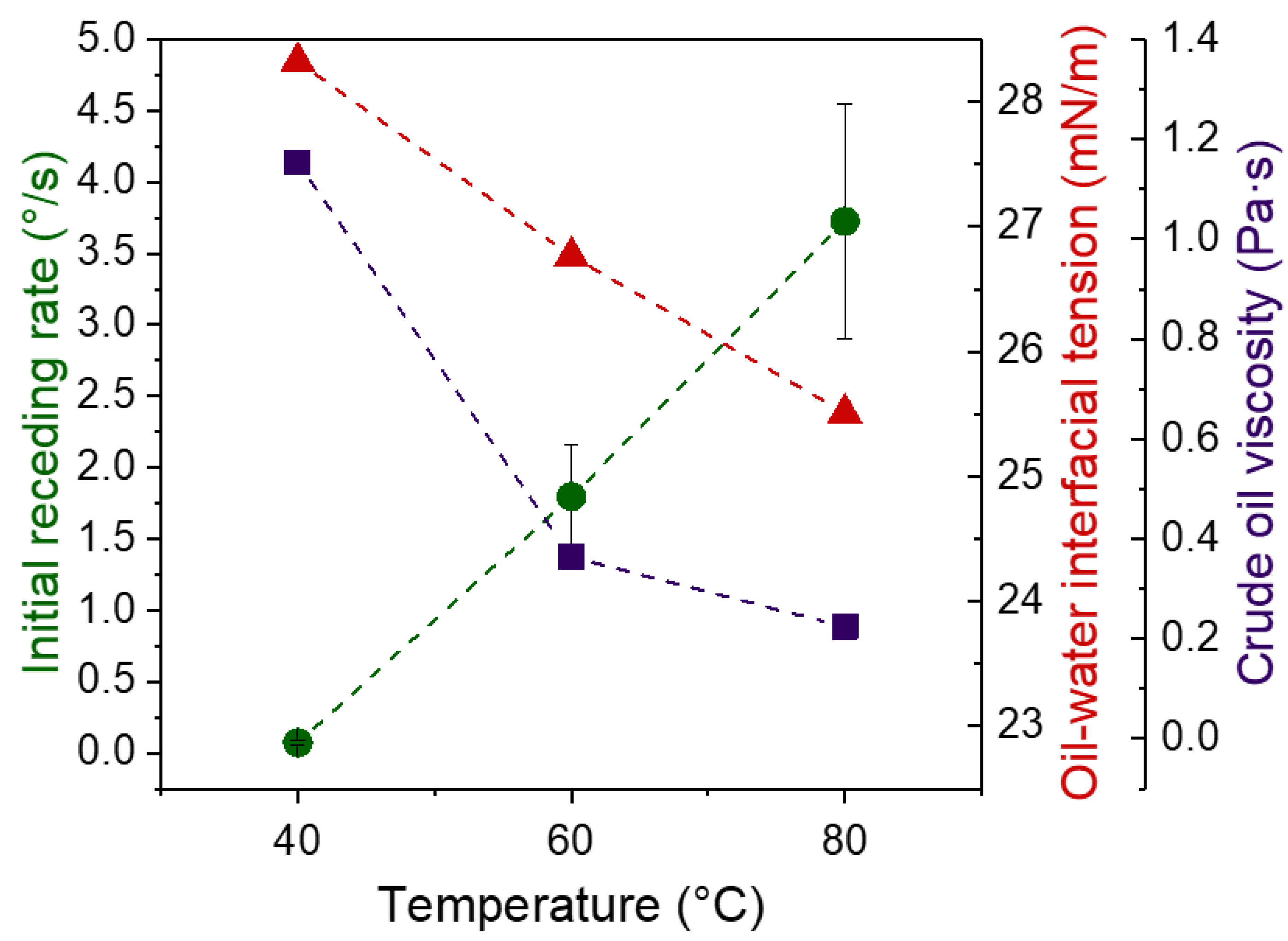
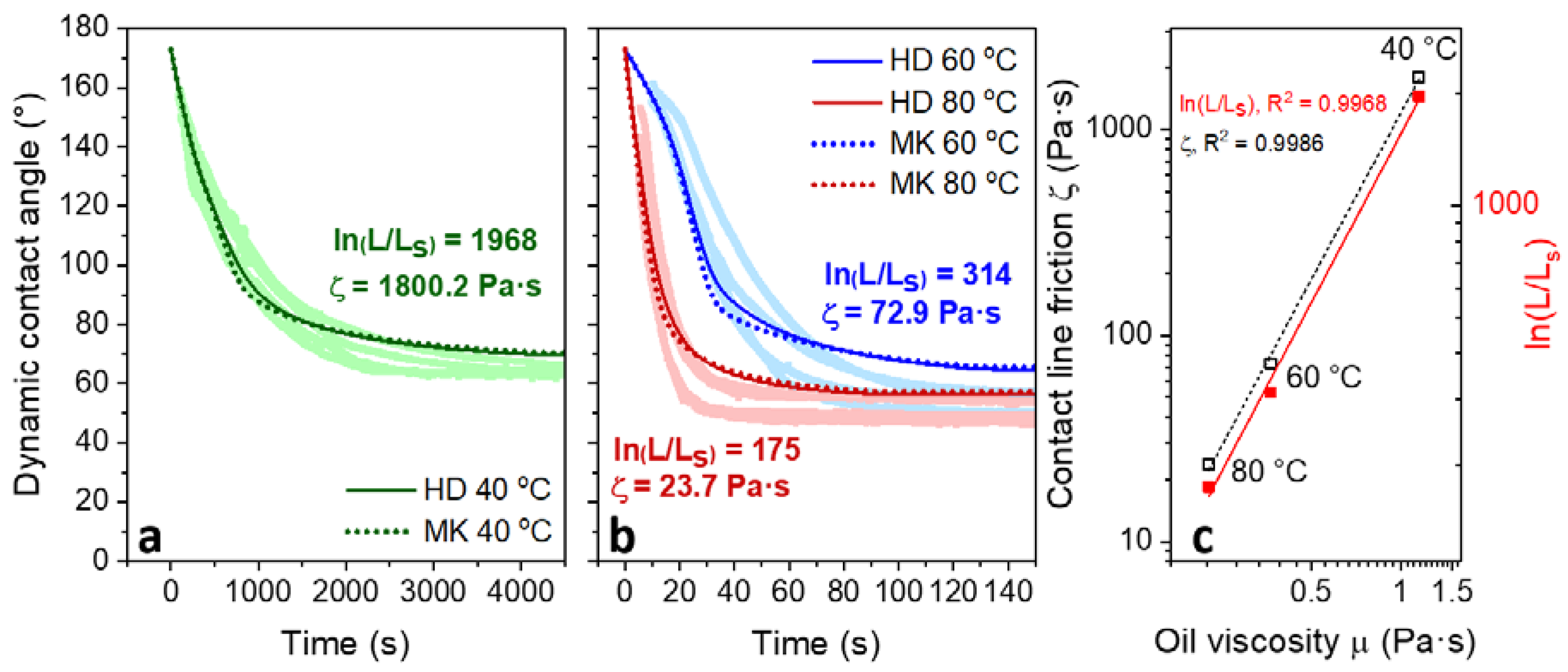
3. Dynamics of oil Film Recession
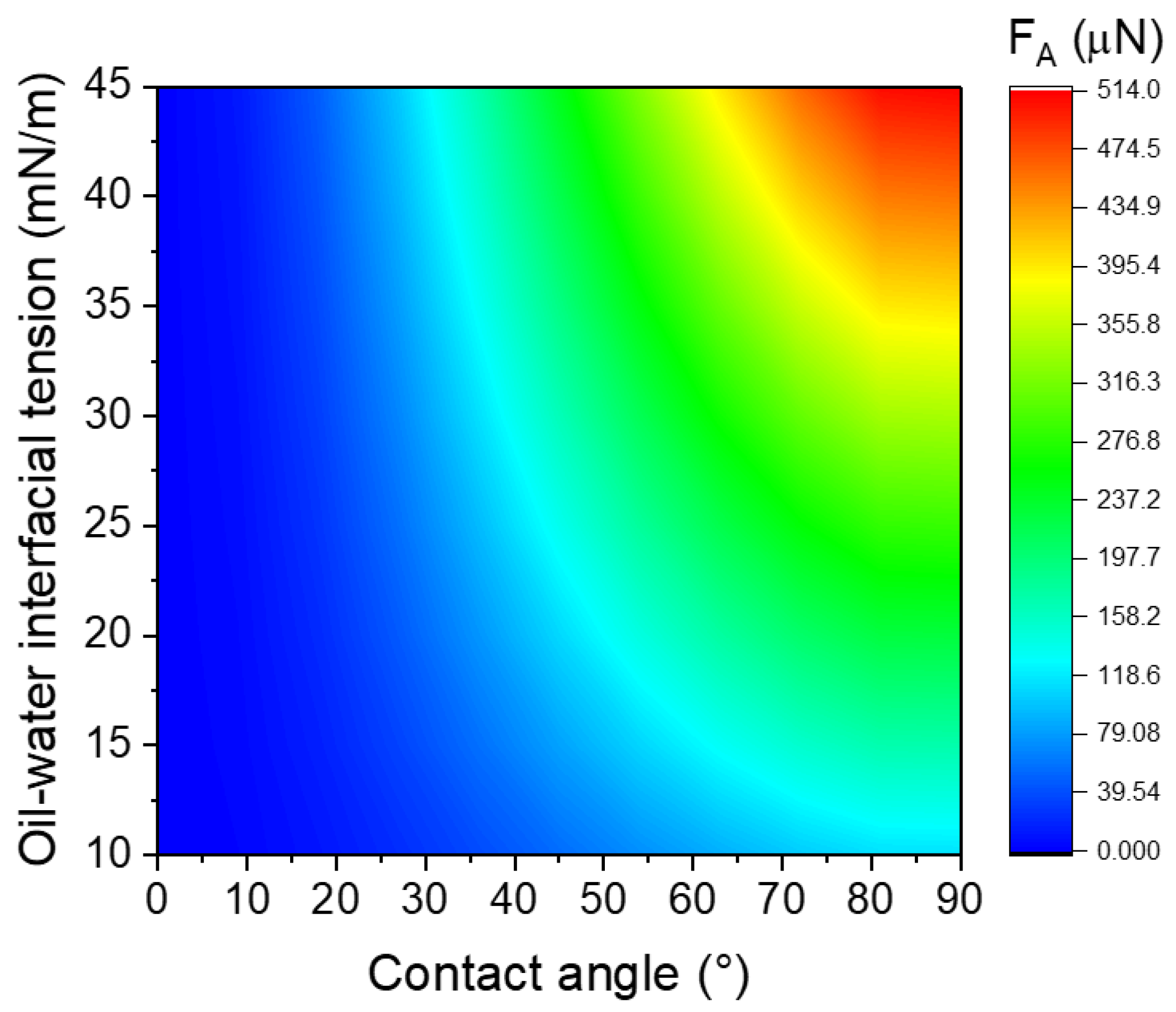
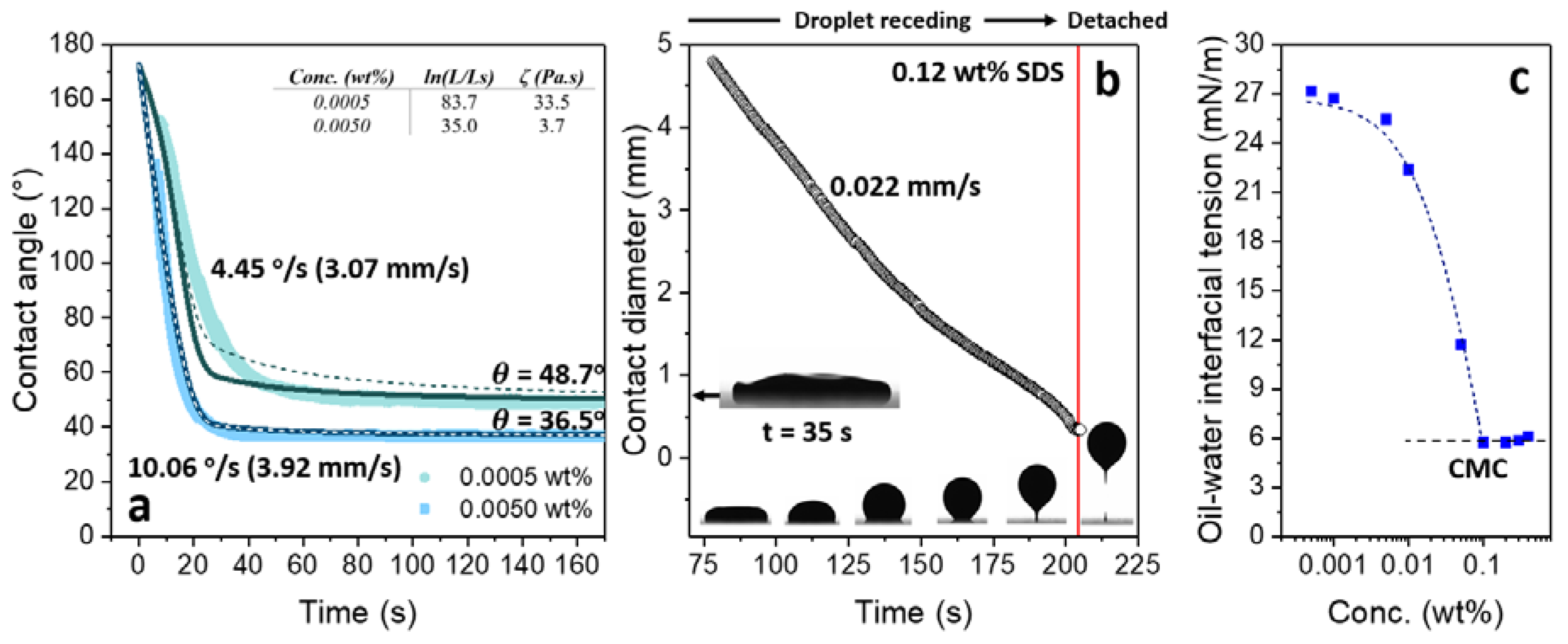
4. Surfactant Oil Droplet Displacement
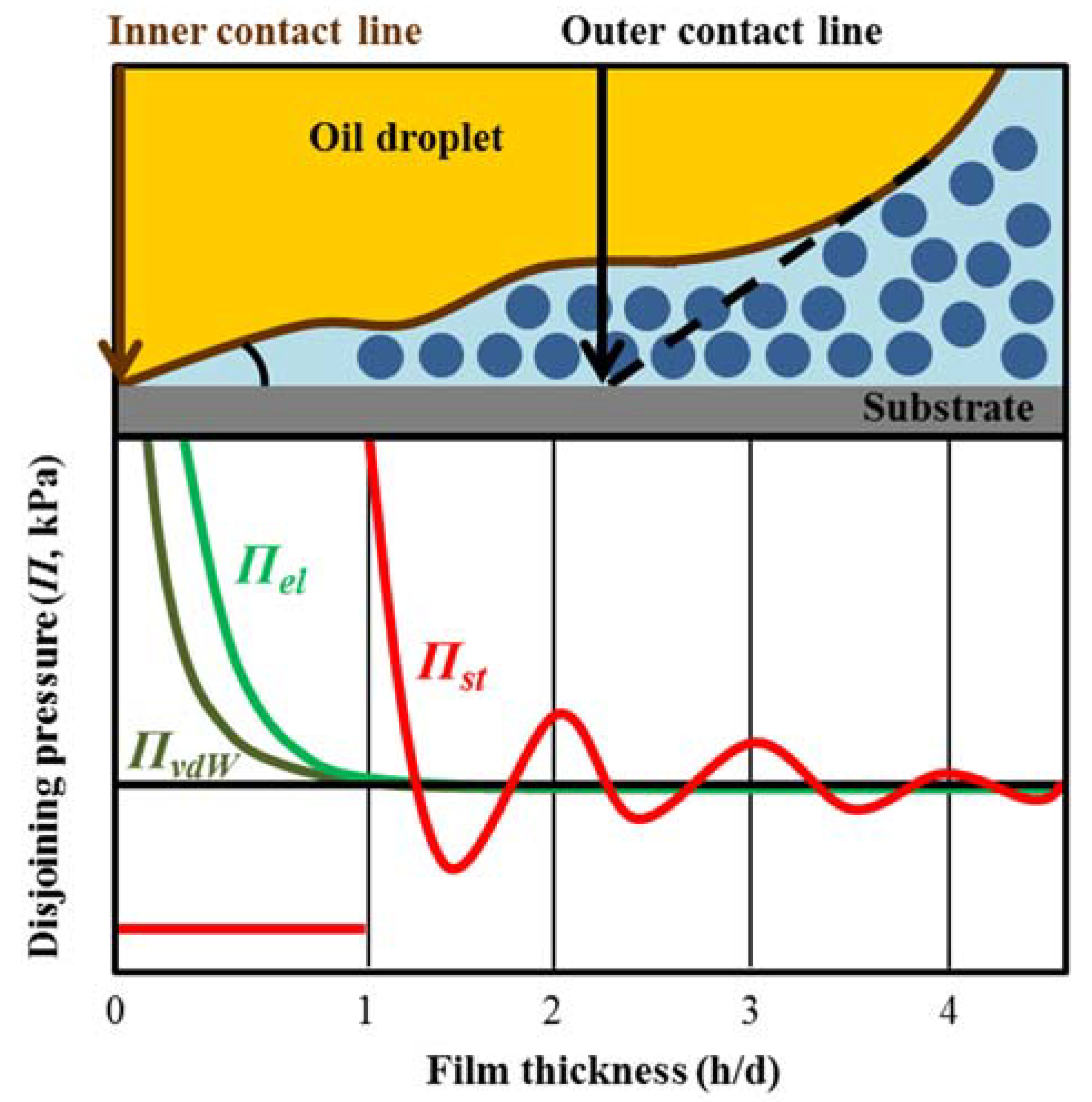
5. Nanoparticle Oil Droplet Displacement
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Surfactants | Conc. | Solid Surface | Oil Type | Remarks a | Ref. |
|---|---|---|---|---|---|
| Cationic surfactants | |||||
| n-C8-N(CH3)3Br (C8TAB) in brine | 4.0 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 57°, IFT b = 2.85 mN/m | [44] |
| n-C10-N(CH3)3Br (C10TAB) in water | 0.4 wt % | Calcite | Decane mixed with naphthenic acids | IFT = 2.67 mN/m | [45] |
| n-C12-N(CH3)3Br (C12TAB) in water | 0.4 wt % | Calcite | Decane mixed with naphthenic acids | IFT = 0.59 mN/m | [45] |
| n-C12-N(CH3)3Br (C12TAB) in brine | 5.0 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 12°, IFT = 0.81 mN/m | [44] |
| n-C16-N(CH3)3Br (C16TAB) in brine | 1.0 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 27°, IFT = 0.38 mN/m | [44] |
| Cetyltrimethylammonium bromide (CTAB) in brine | 0.3 wt % | Quartz | Crude oil | Contact angle = 57° | [76] |
| n-Decyl triphenylphosphonium bromide (C10TPPB) in water | 0.4 wt % | Calcite | Decane mixed with naphthenic acids | IFT = 3.56 mN/m | [45] |
| Cocoalkyltrimethyl ammonium chloride (CAC) in brine | 75–2620 ppm (0.0075–0.262 wt %) | Dolomite | Crude oil | [47] | |
| Dodecyltrimethylammonium bromide (DTAB) in brine | 0.5 wt % | Calcite | Crude oil | Contact angle = 69°, IFT = 4.8 mN/m | [77] |
| Dodecyltrimethylammonium bromide (DTAB) in brine | 0.06 wt % | Quartz | Crude oil | Contact angle = 95°, IFT = 2.49 mN/m | [78] |
| n-(C8-C18)-N(CH3)2(CH2-Ph)Cl (ADMBACl) in brine | 0.5 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 26°, IFT = 0.41 mN/m | [44] |
| n-C8-Ph-(EO)2-N(CH3)2(CH2-Ph)Cl (Hyamine) in brine | 0.2 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 21°, IFT = 0.48 mN/m | [44] |
| Coconut oil alkyl trimethylammonium chloride (ARQUAD C-50) in water | 0.4 wt % | Calcite | Decane mixed with naphthenic acids | IFT = 0.53 mN/m | [45] |
| Trimethyl tallowalky ammonium choride (ARQUAD T-50) in water | 0.4 wt % | Calcite | Decane mixed with naphthenic acids | IFT = 0.69 mN/m | [45] |
| Methyldodecylbis ammonium tribromide | 0.0001–1 mM | Mica | Kerosene mixed with n-decane | Contact angle = 87°, IFT = 0.18 mN/m | [79] |
| Anionic surfactants | |||||
| n-(C12-C15)-(EO)15-SO3Na (S-150) in brine | 0.5 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 63°, IFT = 2.29 mN/m | [44] |
| n-C13-(EO)8-SO3Na (B 1317) in brine | 0.5 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 40°, IFT = 0.78 mN/m | [44] |
| n-C8-(EO)3-SO3Na (S-74) in brine | 0.5 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 49°, IFT = 6.72 mN/m | [44] |
| n-(C12-C15)-(PO)4-(EO)2-OSO3Na (APES) in brine | 1.0 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 44°, IFT = 0.082 mN/m | [44] |
| n-(C8O2CCH2)(n-C8O2C)CH-SO3Na (Cropol) in brine | 0.5 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 55°, IFT = 8.77 mN/m | [44] |
| n-C8-(EO)8-OCH2-COONa (Akypo) in brine | 0.5 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 48°, IFT = 2.99 mN/m | [44] |
| n-C9-Ph-(EO)x-PO3Na (Gafac) in brine | 0.5 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 75°, IFT = 0.42 mN/m | [44] |
| Sodium dodecyl sulfate (SDS) in brine | 0.1 wt % | Chalk | Crude oil mixed with heptane | Contact angle = 39°, IFT = 2.95 mN/m | [44] |
| Sodium dodecyl sulfate (SDS) in water | 0.4 wt % | Calcite | Decane mixed with naphthenic acids | IFT = 4.77 mN/m | [45] |
| Sodium dodecyl 3EO sulfate in brine | 0.05 wt % | Calcite | Crude oil | Contact angle ~ 45°, IFT = 0.003 mN/m | [80] |
| Alkyldiphenyloxide disulfonate in Na2CO3/NaCl | 0.05 wt % | Calcite | Crude oil | Contact angle ~ 110°, IFT = 0.0011 mN/m | [50] |
| Polyether sulfonate in Na2CO3/NaCl | 0.30 wt % | Calcite | Crude oil | Contact angle ~ 80°, IFT = 0.00812 mN/m | [50] |
| Sodium nonyl phenol ethoxylated sulfate (4EO) in Na2CO3/NaCl | 0.05 wt % | Calcite | Crude oil | Contact angle ~ 60°, IFT = 0.003 mN/m | [50] |
| C12-C13 propoxy sulfate (8PO) in Na2CO3/NaCl | 0.05 wt % | Calcite | Crude oil | Contact angle ~ 40°, IFT = 0.0001 mN/m | [50] |
| Alkyldiphenyloxide disulphonate + C14T-isofol propoxy sulfate (8PO) in Na2CO3/NaCl | 0.075 wt % | Calcite | Crude oil | Contact angle ~ 70°, IFT = 0.116 mN/m | [50] |
| Methyl alcohol+Proprietary sulfonate in brine | 0.02–0.20 wt % | Shale (siliceous) | Crude oil | Contact angle = 38°, IFT = 0.4 mN/m) | [81] |
| Sodium laureth sulfate in brine | 0.02–0.05 wt % | Quartz | Crude oil | Contact angle ~ 110°, IFT = 2.007 mN/m | [76] |
| Sodium lauryl monoether sulfate in brine | 0.035 wt % | Quartz | Crude oil | Contact angle = 116.1°, IFT = 2.49 mN/m | [78] |
| Nonionic surfactants | |||||
| Poly-oxyethylene alcohol (POA) in brine | 750–1050 ppm (0.075–0.105 wt %) | Dolomite | Crude oil | IFT = 2.0 mN/m | [47] |
| Ethoxylated C11-C15 secondary alcohol (Tergitol 15-S-3) in water | 0.4 wt % | Calcite | Decane mixed with naphthenic acids | IFT = 4.44 mN/m | [45] |
| Ethoxylated C11-C15 secondary alcohol (Tergitol 15-S-7) in water | 0.4 wt % | Calcite | Decane mixed with naphthenic acids | IFT = 1.39 mN/m | [45] |
| Ethoxylated C11-C15 secondary alcohol (Tergitol 15-S-40) in water | 0.4 wt % | Calcite | Decane mixed with naphthenic acids | IFT = 11.5 mN/m | [45] |
| Nonylphenoxypoly(ethyleneoxy)ethanol (Igepal CO-530) in water | 0.4 wt % | Calcite | Decane mixed with naphthenic acids | IFT = 0.33 mN/m | [45] |
| C12-C15 linear primary alcohol ethoxylate (Neodol 25-7) in water | 0.4 wt % | Calcite | Decane mixed with naphthenic acids | IFT = 2.02 mN/m | [45] |
| Secondary alcohol ethoxylate in Na2CO3/NaCl | 0.10 wt % | Calcite | Crude oil | Contact angle ~ 20°, IFT = 0.0017 mN/m | [50] |
| Nonyl phenol ethoxylate in Na2CO3/NaCl | 0.10 wt % | Calcite | Crude oil | Contact angle ~ 80°, IFT = 0.0006 mN/m | [50] |
| Branched alcohol oxyalkylate in brine | 0.02–0.20 wt % | Shale (siliceous) | Crude oil | Contact angle = 60°, IFT = 9.8 mN/m | [81] |
| Polyoxyethylene octyl phenyl ether in brine | 0.04 wt % | Quartz | Crude oil | Contact angle = 95°, IFT = 4.05 mN/m | [76] |
| Alkylpolyglycosides in brine | 0.05 wt % | Quartz | Crude oil | Contact angle = 58.8°, IFT = 2.49 mN/m | [78] |
| Nanoparticles/Fluids | Solid Surface | Oil Type | Remarks a | Ref. |
|---|---|---|---|---|
| Metal oxides | ||||
| TiO2 (0.01–1 wt %) | Sandstone | Heavy oil | Contact angle = 90° | [82] |
| TiO2 (0.01–0.10 wt %) | Sandstone | Heavy crude oil | Slight IFT b reduction ~ 1 mN/m | [52] |
| TiO2 (0.01–0.05 wt %) | Sandstone | Heavy oil | Contact angle change from 127° to 81°, Slight IFT reduction | [53] |
| Al2O3 (0.01–0.10 wt %) | Sandstone | Heavy crude oil | Slight IFT reduction ~ 1 mN/m | [52] |
| NiO (0.01–0.10 wt %) | Sandstone | Heavy crude oil | Slight IFT reduction ~ 1 mN/m | [52] |
| Organic | ||||
| Janus nanoparticles (0.0025–0.0004 mM) | NA c | Hexane | IFT = 12 mN/m | [83] |
| Carbon nanotubes (0.05–0.50 wt %) | Glass | Crude oil | IFT reduction ~ 3 mN/m | [84] |
| Nanocellulose (0.2–1.0 wt %) | Glass | Crude oil | IFT = 0.7 mN/m | [85] |
| Inorganic | ||||
| SiO2 (0.1–0.6 wt %) | Carbonate | Crude oil | Contact angle = 51° | [86] |
| SiO2 (0.5–4.0 wt %) | Calcite (oil-wet) | n-decane | Contact angle = 20° | [87] |
| SiO2 (0.1–5 wt %) | Glass | Crude oil | Contact angle = 0° | [88] |
| SiO2 (0.025–0.2 wt %) | Calcite (oil-wet) | n-heptane | Contact angle = 41.7° | [89] |
| SiO2 (0.4 effective volume fraction) | Glass | Model oil | [60] | |
| SiO2 (0.01–0.10 wt %) | Sandstone | Crude oil | Contact angle = 22°, IFT = 7.9 mN/m | [57] |
| SiO2 (0.10 wt %) | Sandstone | Light crude oil | Contact angle change from 34° to 32°, IFT reduced from 20 to 10 mN/m | [58] |
| SiO2 (0.01–0.10 wt %) | Sandstone | Heavy crude oil | Slight IFT reduction ~ 1 mN/m | [52] |
| Hydrophilic silica (0.01–0.10 wt %) | Glass/Sandstone | Light crude oil | Contact angle ~ 20°, IFT ~ 8 mN/m | [59] |
| Hydrophilic, neutralized, and hydrophobic silica (0.2–0.3 wt %) | Sandstone | Crude oil | Contact angle ~ 35° | [57] |
| Hydrophobic silica (0.1–0.4 wt %) | Sandstone | Crude oil | Contact angle = 95.4°, IFT = 1.75 mN/m | [90] |
| Nanostructure particles (0.05–0.50 wt %) | Sandstone | Light crude oil | Wettability index = 0.36 (wettability index = 1 is water-wet) | [91] |
| Silica colloidal nanoparticles (0.05–0.50 wt %) | Sandstone | Light crude oil | Wettability index = 0.57 (wettability index = 1 is water-wet) | [91] |
| Composite Fluids | Solid Surface | Oil Type | Remarks a | Ref. |
|---|---|---|---|---|
| Blend systems | ||||
| SDS and SiO2 (Patented nanofluid—No reported concentration) | Glass | Crude oil | Contact angle = 1.2° | [62] |
| SDS and hydrophilic and hydrophobic SiO2 (Surfactant: 100–6000 ppm, particle: 1000–2000 ppm) | Sandstone | Kerosene | IFT b = 1.81 mN/m | [72] |
| SDS and ZrO2 (Surfactant: 0.001–5 CMC, particle: 0.001–0.050 wt %) | NA c | n-heptane | IFT = 10 mN/m | [92] |
| Composite nanoparticles | ||||
| Zwitterionic polymer and SiO2 (coated) (No reported concentration) | Sandstone | n-decane | IFT = 35 mN/m | [74] |
References
- BP. 2017 Energy Outlook; BP: London, UK, 2017. [Google Scholar]
- BP. BP Statistical Review of World Energy 2017; BP: London, UK, 2017. [Google Scholar]
- Treiber, L.E.; Owens, W.W. A Laboratory Evaluation of the Wettability of Fifty Oil-Producing Reservoirs; Society of Petroleum Engineers: Richardson, TX, USA, 1972. [Google Scholar]
- Chilingar, G.V.; Yen, T.F. Some Notes on Wettability and Relative Permeabilities of Carbonate Reservoir Rocks, II. Energy Sources 1983, 7, 67–75. [Google Scholar] [CrossRef]
- Pu, W.-F.; Yuan, C.-D.; Wang, X.-C.; Sun, L.; Zhao, R.-K.; Song, W.-J.; Li, X.-F. The Wettability Alteration and the Effect of Initial Rock Wettability on Oil Recovery in Surfactant-based Enhanced Oil Recovery Processes. J. Dispers. Sci. Technol. 2016, 37, 602–611. [Google Scholar] [CrossRef]
- Natarajan, A.; Kuznicki, N.; Harbottle, D.; Masliyah, J.; Zeng, H.; Xu, Z. Understanding Mechanisms of Asphaltene Adsorption from Organic Solvent on Mica. Langmuir 2014, 30, 9370–9377. [Google Scholar] [CrossRef] [PubMed]
- Standal, S.; Haavik, J.; Blokhus, A.M.; Skauge, A. Effect of polar organic components on wettability as studied by adsorption and contact angles. J. Pet. Sci. Eng. 1999, 24, 131–144. [Google Scholar] [CrossRef]
- Kupai, M.M.; Yang, F.; Harbottle, D.; Moran, K.; Masliyah, J.; Xu, Z.H. Characterising rag-forming solids. Can. J. Chem. Eng. 2013, 91, 1395–1401. [Google Scholar] [CrossRef]
- Zeng, H.; Zou, F.; Horvath-Szabo, G.; Andersen, S. Effects of Brine Composition on the Adsorption of Benzoic Acid on Calcium Carbonate. Energy Fuels 2012, 26, 4321–4327. [Google Scholar] [CrossRef]
- Jadhunandan, P.P.; Morrow, N.R. Effect of Wettability on Waterflood Recovery for Crude-Oil/Brine/Rock Systems; Society of Petroleum Engineers: Richardson, TX, USA, 1995. [Google Scholar]
- Chengara, A.; Nikolov, A.D.; Wasan, D.T.; Trokhymchuk, A.; Henderson, D. Spreading of nanofluids driven by the structural disjoining pressure gradient. J. Colloid Interface Sci. 2004, 280, 192–201. [Google Scholar] [CrossRef] [PubMed]
- Bakhtiari, M.T.; Harbottle, D.; Curran, M.; Ng, S.; Spence, J.; Siy, R.; Liu, Q.X.; Masliyah, J.; Xu, Z.H. Role of Caustic Addition in Bitumen-Clay Interactions. Energy Fuels 2015, 29, 58–69. [Google Scholar] [CrossRef]
- Flury, C.; Afacan, A.; Bakhtiari, M.T.; Sjoblom, J.; Xu, Z. Effect of Caustic Type on Bitumen Extraction from Canadian Oil Sands. Energy Fuels 2014, 28, 431–438. [Google Scholar] [CrossRef]
- Swiech, W.; Taylor, S.; Zeng, H. The Role of Water Soluble Species in Bitumen Recovery from Oil Sands. In Proceedings of the SPE Heavy Oil Conference-Canada, Society of Petroleum Engineers, Calgary, AB, Canada, 10–12 June 2014. [Google Scholar]
- Liu, J.; Zhou, Z.; Xu, Z.; Masliyah, J. Bitumen–Clay Interactions in Aqueous Media Studied by Zeta Potential Distribution Measurement. J. Colloid Interface Sci. 2002, 252, 409–418. [Google Scholar] [CrossRef] [PubMed]
- Czarnecki, J.; Radoev, B.; Schramm, L.L.; Slavchev, R. On the nature of Athabasca Oil Sands. Adv. Colloid Interface Sci. 2005, 114, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A. Disintegration of macroscopic fluid sheets on substrates—A singular perturbation approach. J. Colloid Interface Sci. 1993, 156, 96–103. [Google Scholar] [CrossRef]
- Srinivasa, S.; Flury, C.; Afacan, A.; Masliyah, J.; Xu, Z. Study of Bitumen Liberation from Oil Sands Ores by Online Visualization. Energy Fuels 2012, 26, 2883–2890. [Google Scholar] [CrossRef]
- Bertrand, E.; Blake, T.D.; de Coninck, J. Dynamics of dewetting. Colloids Surfaces A Physicochem. Eng. Asp. 2010, 369, 141–147. [Google Scholar] [CrossRef]
- Basu, S.; Nandakumar, K.; Masliyah, J.H. A Model for Detachment of a Partially Wetting Drop from a Solid Surface by Shear Flow. J. Colloid Interface Sci. 1997, 190, 253–257. [Google Scholar] [CrossRef] [PubMed]
- Cox, R.G. The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 1986, 168, 169–194. [Google Scholar] [CrossRef]
- Cox, R.G. The dynamics of the spreading of liquids on a solid surface. Part 2. Surfactants. J. Fluid Mech. 2006, 168, 195–220. [Google Scholar] [CrossRef]
- Blake, T.D.; Haynes, J.M. Kinetics of liquid/liquid displacement. J. Colloid Interface Sci. 1969, 30, 421–423. [Google Scholar] [CrossRef]
- Blake, T.D. The physics of moving wetting lines. J. Colloid Interface Sci. 2006, 299, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Blake, T.D.; de Coninck, J. The influence of solid–liquid interactions on dynamic wetting. Adv. Colloid Interface Sci. 2002, 96, 21–36. [Google Scholar] [CrossRef]
- De Gennes, P.G. Wetting: Statics and dynamics. Rev. Mod. Phys. 1985, 57, 827–863. [Google Scholar] [CrossRef]
- Brochard-Wyart, F.; de Gennes, P.G. Dynamics of partial wetting. Adv. Colloid Interface Sci. 1992, 39, 1–11. [Google Scholar] [CrossRef]
- Schramm, L.L.; Smith, R.G. The influence of natural surfactants on interfacial charges in the hot-water process for recovering bitumen from the athabasca oil sands. Colloids Surfaces 1985, 14, 67–85. [Google Scholar] [CrossRef]
- Drelich, J.; Miller, J.D. Surface and interfacial tension of the Whiterocks bitumen and its relationship to bitumen release from tar sands during hot water processing. Fuel 1994, 73, 1504–1510. [Google Scholar] [CrossRef]
- Drelich, J.; Bukka, K.; Miller, J.D.; Hanson, F.V. Surface Tension of Toluene-Extracted Bitumens from Utah Oil Sands as Determined by Wilhelmy Plate and Contact Angle Techniques. Energy Fuels 1994, 8, 700–704. [Google Scholar] [CrossRef]
- Long, J.; Drelich, J.; Xu, Z.; Masliyah, J.H. Effect of Operating Temperature on Water-Based Oil Sands Processing. Can. J. Chem. Eng. 2007, 85, 726–738. [Google Scholar] [CrossRef]
- Rogers, V.V.; Liber, K.; MacKinnon, M.D. Isolation and characterization of naphthenic acids from Athabasca oil sands tailings pond water. Chemosphere 2002, 48, 519–527. [Google Scholar] [CrossRef]
- Grewer, D.M.; Young, R.F.; Whittal, R.M.; Fedorak, P.M. Naphthenic acids and other acid-extractables in water samples from Alberta: What is being measured? Sci. Total Environ. 2010, 408, 5997–6010. [Google Scholar] [CrossRef] [PubMed]
- Masliyah, J.H.; Xu, Z.; Czarnecki, J.A. Handbook on Theory and Practice of Bitumen Recovery from Athabasca Oil Sands: Theoretical Basis; Kingsley Knowledge Pub.: Cochrane, AB, Canada, 2011. [Google Scholar]
- Schramm, L.L.; Stasiuk, E.N.; MacKinnon, M. Surfactants in Athabasca oil sands slurry conditioning, flotation recovery, and tailings processes. In Surfactants: Fundamentals and Applications in the Petroleum Industry; Schramm, L.L., Ed.; Cambridge University Press: Cambridge, UK, 2000; pp. 365–430. [Google Scholar]
- Kelesoglu, S.; Volden, S.; Kes, M.; Sjoblom, J. Adsorption of naphthenic acids onto mineral surfaces studied by quartz crystal microbalance with dissipation monitoring (QCM-D). Energy Fuels 2012, 26, 5060–5068. [Google Scholar] [CrossRef]
- Ding, L.; Rahimi, P.; Hawkins, R.; Bhatt, S.; Shi, Y. Naphthenic acid removal from heavy oils on alkaline earth-metal oxides and ZnO catalysts. Appl. Catal. A Gen. 2009, 371, 121–130. [Google Scholar] [CrossRef]
- Duvivier, D.; Seveno, D.; Rioboo, R.; Blake, T.D.; de Coninck, J. Experimental Evidence of the Role of Viscosity in the Molecular Kinetic Theory of Dynamic Wetting. Langmuir 2011, 27, 13015–13021. [Google Scholar] [CrossRef] [PubMed]
- Lin, F.; He, L.; Primkulov, B.; Xu, Z. Dewetting Dynamics of a Solid Microsphere by Emulsion Drops. J. Phys. Chem. C 2014, 118, 13552–13562. [Google Scholar] [CrossRef]
- Moeini, F.; Hemmati-Sarapardeh, A.; Ghazanfari, M.-H.; Masihi, M.; Ayatollahi, S. Toward mechanistic understanding of heavy crude oil/brine interfacial tension: The roles of salinity, temperature and pressure. Fluid Phase Equilib. 2014, 375, 191–200. [Google Scholar] [CrossRef]
- Basu, S.; Sharma, M.M. Measurement of Critical Disjoining Pressure for Dewetting of Solid Surfaces. J. Colloid Interface Sci. 1996, 181, 443–455. [Google Scholar] [CrossRef]
- Haagh, M.E.J.; Siretanu, I.; Duits, M.H.G.; Mugele, F. Salinity-Dependent Contact Angle Alteration in Oil/Brine/Silicate Systems: The Critical Role of Divalent Cations. Langmuir 2017, 33, 3349–3357. [Google Scholar] [CrossRef] [PubMed]
- Somasundaran, P.; Zhang, L. Adsorption of surfactants on minerals for wettability control in improved oil recovery processes. J. Pet. Sci. Eng. 2006, 52, 198–212. [Google Scholar] [CrossRef]
- Standnes, D.C.; Austad, T. Wettability alteration in chalk: 2. Mechanism for wettability alteration from oil-wet to water-wet using surfactants. J. Pet. Sci. Eng. 2000, 28, 123–143. [Google Scholar] [CrossRef]
- Wu, Y.; Shuler, P.J.; Blanco, M.; Tang, Y.; Goddard, W.A. An Experimental Study of Wetting Behavior and Surfactant EOR in Carbonates with Model Compounds; Society of Petroleum Engineers: Richardson, TX, USA, 2008. [Google Scholar]
- Jarrahian, K.; Seiedi, O.; Sheykhan, M.; Sefti, M.V.; Ayatollahi, S. Wettability alteration of carbonate rocks by surfactants: A mechanistic study. Colloids Surfaces A Physicochem. Eng. Asp. 2012, 410, 1–10. [Google Scholar] [CrossRef]
- Xie, X.; Weiss, W.W.; Tong, Z.; Morrow, N.R. Improved Oil Recovery from Carbonate Reservoirs by Chemical Stimulation; Society of Petroleum Engineers: Richardson, TX, USA, 2004. [Google Scholar]
- Curbelo, F.D.S.; Santanna, V.C.; Neto, E.L.B.; Dutra, T.V.; Dantas, T.N.C.; Neto, A.A.D.; Garnica, A.I.C. Adsorption of nonionic surfactants in sandstones. Colloids Surfaces A Physicochem. Eng. Asp. 2007, 293, 1–4. [Google Scholar] [CrossRef]
- Park, S.; Lee, E.S.; Sulaiman, W.R.W. Adsorption behaviors of surfactants for chemical flooding in enhanced oil recovery. J. Ind. Eng. Chem. 2015, 21, 1239–1245. [Google Scholar] [CrossRef]
- Gupta, R.; Mohanty, K. Temperature Effects on Surfactant-Aided Imbibition into Fractured Carbonates; Society of Petroleum Engineers: Richardson, TX, USA, 2010. [Google Scholar]
- Vafaei, S.; Borca-Tasciuc, T.; Podowski, M.Z.; Purkayastha, A.; Ramanath, G.; Ajayan, P.M. Effect of nanoparticles on sessile droplet contact angle. Nanotechnology 2006, 17, 2523–2527. [Google Scholar] [CrossRef] [PubMed]
- Alomair, O.A.; Matar, K.M.; Alsaeed, Y.H. Nanofluids Application for Heavy Oil Recovery; Society of Petroleum Engineers: Richardson, TX, USA, 2014. [Google Scholar]
- Ehtesabi, H.; Ahadian, M.M.; Taghikhani, V. Enhanced Heavy Oil Recovery Using TiO2 Nanoparticles: Investigation of Deposition during Transport in Core Plug. Energy Fuels 2015, 29, 1–8. [Google Scholar] [CrossRef]
- Binks, B.P. Particles as surfactants—Similarities and differences. Curr. Opin. Colloid Interface Sci. 2002, 7, 21–41. [Google Scholar] [CrossRef]
- Fan, H.; Striolo, A. Nanoparticle effects on the water-oil interfacial tension. Phys. Rev. E 2012, 86, 051610. [Google Scholar] [CrossRef] [PubMed]
- Chinnam, J.; Das, D.K.; Vajjha, R.S.; Satti, J.R. Measurements of the surface tension of nanofluids and development of a new correlation. Int. J. Therm. Sci. 2015, 98, 68–80. [Google Scholar] [CrossRef]
- Hendraningrat, L.; Li, S.; Torsæter, O. A coreflood investigation of nanofluid enhanced oil recovery. J. Pet. Sci. Eng. 2013, 111, 128–138. [Google Scholar] [CrossRef]
- Parvazdavani, M.; Masihi, M.; Ghazanfari, M.H. Monitoring the influence of dispersed nano-particles on oil–water relative permeability hysteresis. J. Pet. Sci. Eng. 2014, 124, 222–231. [Google Scholar] [CrossRef]
- Li, S.; Hendraningrat, L.; Torsaeter, O. Improved Oil Recovery by Hydrophilic Silica Nanoparticles Suspension: 2-Phase Flow Experimental Studies. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2013. [Google Scholar]
- Wasan, D.T.; Nikolov, A.D. Spreading of nanofluids on solids. Nature 2003, 423, 156–159. [Google Scholar] [CrossRef] [PubMed]
- Kondiparty, K.; Nikolov, A.; Wu, S.; Wasan, D. Wetting and Spreading of Nanofluids on Solid Surfaces Driven by the Structural Disjoining Pressure: Statics Analysis and Experiments. Langmuir 2011, 27, 3324–3335. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Nikolov, A.; Wasan, D. Enhanced Oil Recovery (EOR) Using Nanoparticle Dispersions: Underlying Mechanism and Imbibition Experiments. Energy Fuels 2014, 28, 3002–3009. [Google Scholar] [CrossRef]
- Trokhymchuk, A.; Henderson, D.; Nikolov, A.; Wasan, D.T. A Simple Calculation of Structural and Depletion Forces for Fluids/Suspensions Confined in a Film. Langmuir 2001, 17, 4940–4947. [Google Scholar] [CrossRef]
- Winkler, K.; Paszewski, M.; Kalwarczyk, T.; Kalwarczyk, E.; Wojciechowski, T.; Gorecka, E.; Pociecha, D.; Holyst, R.; Fialkowski, M. Ionic Strength-Controlled Deposition of Charged Nanoparticles on a Solid Substrate. J. Phys. Chem. C 2011, 115, 19096–19103. [Google Scholar] [CrossRef]
- Darlington, T.K.; Neigh, A.M.; Spencer, M.T.; Guyen, O.T.N.; Oldenburg, S.J. Nanoparticle characteristics affecting environmental fate and transport through soil. Environ. Toxicol. Chem. 2009, 28, 1191–1199. [Google Scholar] [CrossRef] [PubMed]
- Bayat, A.E.; Junin, R.; Samsuri, A.; Piroozian, A.; Hokmabadi, M. Impact of Metal Oxide Nanoparticles on Enhanced Oil Recovery from Limestone Media at Several Temperatures. Energy Fuels 2014, 28, 6255–6266. [Google Scholar] [CrossRef]
- Li, Y.V.; Cathles, L.M.; Archer, L.A. Nanoparticle tracers in calcium carbonate porous media. J. Nanopart. Res. 2014, 16, 2541. [Google Scholar] [CrossRef]
- Li, Y.V.; Cathles, L.M. Retention of silica nanoparticles on calcium carbonate sands immersed in electrolyte solutions. J. Colloid Interface Sci. 2014, 436, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Nwidee, L.N.; Al-Anssari, S.; Barifcani, A.; Sarmadivaleh, M.; Lebedev, M.; Iglauer, S. Nanoparticles influence on wetting behaviour of fractured limestone formation. J. Pet. Sci. Eng. 2017, 149, 782–788. [Google Scholar] [CrossRef]
- Zargartalebi, M.; Barati, N.; Kharrat, R. Influences of hydrophilic and hydrophobic silica nanoparticles on anionic surfactant properties: Interfacial and adsorption behaviors. J. Pet. Sci. Eng. 2014, 119, 36–43. [Google Scholar] [CrossRef]
- Ahualli, S.; Iglesias, G.R.; Wachter, W.; Dulle, M.; Minami, D.; Glatter, O. Adsorption of Anionic and Cationic Surfactants on Anionic Colloids: Supercharging and Destabilization. Langmuir 2011, 27, 9182–9192. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.K.; Son, H.A.; Kim, H.T.; Kim, J.W. Nanofluid Enhanced Oil Recovery Using Hydrophobically Associative Zwitterionic Polymer-Coated Silica Nanoparticles. Energy Fuels 2017, 31, 7777–7782. [Google Scholar] [CrossRef]
- ShamsiJazeyi, H.; Miller, C.A.; Wong, M.S.; Tour, J.M.; Verduzco, R. Polymer-coated nanoparticles for enhanced oil recovery. J. Appl. Polym. Sci. 2014, 131. [Google Scholar] [CrossRef]
- Hou, B.; Wang, Y.; Cao, X.; Zhang, J.; Song, X.; Ding, M.; Chen, W. Surfactant-Induced Wettability Alteration of Oil-Wet Sandstone Surface: Mechanisms and Its Effect on Oil Recovery. J. Surfactants Deterg. 2016, 19, 315–324. [Google Scholar] [CrossRef]
- Karimi, M.; Al-Maamari, R.S.; Ayatollahi, S.; Mehranbod, N. Wettability alteration and oil recovery by spontaneous imbibition of low salinity brine into carbonates: Impact of Mg2+, SO42− and cationic surfactant. J. Pet. Sci. Eng. 2016, 147, 560–569. [Google Scholar] [CrossRef]
- Hou, B.; Wang, Y.; Cao, X.; Zhang, J.; Song, X.; Ding, M.; Chen, W. Mechanisms of Enhanced Oil Recovery by Surfactant-Induced Wettability Alteration. J. Dispers. Sci. Technol. 2016, 37, 1259–1267. [Google Scholar] [CrossRef]
- Zhang, R.; Qin, N.; Peng, L.; Tang, K.; Ye, Z. Wettability alteration by trimeric cationic surfactant at water-wet/oil-wet mica mineral surfaces. Appl. Surf. Sci. 2012, 258, 7943–7949. [Google Scholar] [CrossRef]
- Hirasaki, G.; Zhang, D.L. Surface Chemistry of Oil Recovery from Fractured, Oil-Wet, Carbonate Formations; Society of Petroleum Engineers: Richardson, TX, USA, 2004. [Google Scholar]
- Alvarez, J.O.; Schechter, D.S. Wettability Alteration and Spontaneous Imbibition in Unconventional Liquid Reservoirs by Surfactant Additives; Society of Petroleum Engineers: Richardson, TX, USA, 2017. [Google Scholar]
- Ehtesabi, H.; Ahadian, M.M.; Taghikhani, V.; Ghazanfari, M.H. Enhanced Heavy Oil Recovery in Sandstone Cores Using TiO2 Nanofluids. Energy Fuels 2014, 28, 423–430. [Google Scholar] [CrossRef]
- Glaser, N.; Adams, D.J.; Böker, A.; Krausch, G. Janus Particles at Liquid−Liquid Interfaces. Langmuir 2006, 22, 5227–5229. [Google Scholar] [CrossRef] [PubMed]
- Soleimani, H.; Baig, M.K.; Yahya, N.; Khodapanah, L.; Sabet, M.; Demiral, B.M.R.; Burda, M. Impact of carbon nanotubes based nanofluid on oil recovery efficiency using core flooding. Results Phys. 2018, 9, 39–48. [Google Scholar] [CrossRef]
- Wei, B.; Li, Q.; Jin, F.; Li, H.; Wang, C. The potential of a novel nanofluid in enhancing oil recovery. Energy Fuels 2016, 30, 2882–2891. [Google Scholar] [CrossRef]
- Roustaei, A.; Bagherzadeh, H. Experimental investigation of SiO2 nanoparticles on enhanced oil recovery of carbonate reservoirs. J. Pet. Explor. Prod. Technol. 2015, 5, 27–33. [Google Scholar] [CrossRef]
- Al-Anssari, S.; Barifcani, A.; Wang, S.; Maxim, L.; Iglauer, S. Wettability alteration of oil-wet carbonate by silica nanofluid. J. Colloid Interface Sci. 2016, 461, 435–442. [Google Scholar] [CrossRef] [PubMed]
- Maghzi, A.; Mohammadi, S.; Ghazanfari, M.H.; Kharrat, R.; Masihi, M. Monitoring wettability alteration by silica nanoparticles during water flooding to heavy oils in five-spot systems: A pore-level investigation. Exp. Therm. Fluid Sci. 2012, 40, 168–176. [Google Scholar] [CrossRef]
- Monfared, A.D.; Ghazanfari, M.H.; Jamialahmadi, M.; Helalizadeh, A. Potential Application of Silica Nanoparticles for Wettability Alteration of Oil–Wet Calcite: A Mechanistic Study. Energy Fuels 2016, 30, 3947–3961. [Google Scholar] [CrossRef]
- Shahrabadi, A.; Bagherzadeh, H.; Roostaie, A.; Golghanddashti, H. Experimental Investigation of HLP Nanofluid Potential to Enhance Oil Recovery: A Mechanistic Approach; Society of Petroleum Engineers: Richardson, TX, USA, 2012. [Google Scholar]
- Li, S.; Genys, M.; Wang, K.; Torsæter, O. Experimental Study of Wettability Alteration during Nanofluid Enhanced Oil Recovery Process and Its Effect on Oil Recovery; Society of Petroleum Engineers: Richardson, TX, USA, 2015. [Google Scholar]
- Esmaeilzadeh, P.; Hosseinpour, N.; Bahramian, A.; Fakhroueian, Z.; Arya, S. Effect of ZrO2 nanoparticles on the interfacial behavior of surfactant solutions at air–water and n-heptane–water interfaces. Fluid Phase Equilib. 2014, 361, 289–295. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tangparitkul, S.; Charpentier, T.V.J.; Pradilla, D.; Harbottle, D. Interfacial and Colloidal Forces Governing Oil Droplet Displacement: Implications for Enhanced Oil Recovery. Colloids Interfaces 2018, 2, 30. https://doi.org/10.3390/colloids2030030
Tangparitkul S, Charpentier TVJ, Pradilla D, Harbottle D. Interfacial and Colloidal Forces Governing Oil Droplet Displacement: Implications for Enhanced Oil Recovery. Colloids and Interfaces. 2018; 2(3):30. https://doi.org/10.3390/colloids2030030
Chicago/Turabian StyleTangparitkul, Suparit, Thibaut V. J. Charpentier, Diego Pradilla, and David Harbottle. 2018. "Interfacial and Colloidal Forces Governing Oil Droplet Displacement: Implications for Enhanced Oil Recovery" Colloids and Interfaces 2, no. 3: 30. https://doi.org/10.3390/colloids2030030
APA StyleTangparitkul, S., Charpentier, T. V. J., Pradilla, D., & Harbottle, D. (2018). Interfacial and Colloidal Forces Governing Oil Droplet Displacement: Implications for Enhanced Oil Recovery. Colloids and Interfaces, 2(3), 30. https://doi.org/10.3390/colloids2030030





