Effect of Polysorbates on Solids Wettability and Their Adsorption Properties

Abstract

The wettability of solids is important from both practical and theoretical viewpoints. In this study, we measured the contact angle of aqueous solutions of polysorbates (Tween 20, Tween 60, and Tween 80) on polytetrafluoroethylene (PTFE), polyethylene (PE), polymethyl methacrylate (PMMA), polyamide (nylon 6), and quartz. Based on the obtained results, the adsorption of Tween 20 (T20), Tween 60 (T60), and Tween 80 (T80) at the solid-water interface was determined based on the structure and size of their molecules. Next, the tendency of polysorbates to adsorb at the solid-water interface was considered based on the Gibbs standard free energy of adsorption ($\Delta G_{ads}^o$). This energy was evaluated using various methods, including a method we propose based on the critical micelle concentration (CMC) and the contact angle of water and solution at the CMC, as well as their surface tension. The $\Delta G_{ads}^o$ values obtained by this method were comparable to those calculated from the Langmuir equation. Taking into account the Tweens tendency to adsorb at the solid-water interface, the measured contact angle, the components and parameters of surface tension of Tweens solutions and solids, and the surface tension of water and its Lifshitz-van der Waals component that we determined, the wetting process in the solid-solution drop-air system was analyzed. The results based on the mentioned parameters showed that it is possible to predict the wettability of apolar, monopolar, and bipolar solids using the aqueous Tweens solution and their solution adhesion.

1. Introduction

Polysorbates are extensively used in food, cosmetic, pharmaceutical preparations, bioresearch, and chemical compounds detection owing to their nontoxicity, easy accessibility, emulsification, and solubilisation [1,2,3,4]. Polysorbates such as Tween 20 and Tween 60 were found to be capable of enhancing drug transport across biological membranes [5]. Tween 80 has been widely used in various drug dosage forms to control wetting, stability, and solubilisation of hydrophobic drugs [6]. Despite their wide range of applications, the adsorption and wetting properties of these surfactants have not yet been fully explained [7]. Moreover, some discrepancies exist in the literature concerning polysorbates [8,9,10,11,12,13,14,15,16,17,18,19].

Adsorption of surfactants at the water-air, solid-air, and solid-water interfaces is directly connected to their wetting properties [20,21,22]. Wettability of the solid by the aqueous surfactant solutions depends on the solution and solid surface tension, as well as the solid-solution interface tension. The addition of surfactants to water causes a decrease in its surface tension to a minimal value, which depends on the kind of surfactant used. However, with the addition of surfactant, the solid-water interface tension can decrease, increase, or remain constant. Practically, for the homologous series of surfactants with a given hydrophilic group, the decrease in water surface tension at the same surfactant concentration is proportional to the hydrophobic chain length but packing of the molecules at their perpendicular orientation in the saturated monolayers at the water-air interface is similar [20]. With parallel orientation of the surfactant molecules at the solid-water interface, packing of the surfactant molecules depends on the length of the hydrophobic chain with the same hydrophilic part [20]. The solid-water interface tension changes that are due to surfactants adsorption depend not only on the length of hydrophobic chain of surfactant molecules but also on their orientation toward the water phase. The orientation toward the water phase by the hydrophobic part of molecules causes the increase of the solid-water interface tension but the reverse orientation can result in its decrease [20].

Notably, the polysorbate head is composed of many oxyethylene groups in four hydrophilic chains. Apart from these groups, the heterocyclic ring and –OH group are present in the hydrophilic part of polysorbates [20]. Likely depending on the environmental conditions, these hydrophilic chains can transform into a different form. Therefore, studies reported different results for Tween 20 (T20), Tween 60 (T60), and Tween 80 (T80) [23,24]. Different forms of the surfactant molecules at the water-air and solid-water interfaces significantly influence their wetting properties. In the literature, few studies have addressed the wetting properties of T20, T60, and T80 in the light of their adsorption at the water-air and solid-water interfaces. Therefore, the main aim of our study was to determine the wettability of apolar (polytetrafluoroethylene (PTFE) and polyethylene (PE)), monopolar (polymethyl methacrylate (PMMA)), and bipolar (nylon 6 and quartz) solids by the aqueous solutions of T20, T60 and T80 depending on their adsorption at the water-air and solid-water interfaces. This aim was achieved using the literature data on the surface tension of the aqueous solutions of T20, T60, and T80, their contact angle measured on the PTFE, PE, PMMA, nylon 6, and quartz surfaces, and on the thermodynamic analysis of the adsorption and wetting processes.

2. Materials and Methods

2.1. Materials

In this study, polyethylene glycol sorbitan monolaurate, Tween 20 (T20) (Sigma-Aldrich, St. Louis, MO, USA), polyethylene glycol sorbitan monostearate, Tween 60 (T60) (Sigma-Aldrich) and polyethylene glycol sorbitan monooleate, Tween 80 (T80) (Sigma-Aldrich) were used. The plates of polymer solids (50 × 30 mm) were cut from large plates obtained from Mega-Tech (Tomaszow Mazowiecki, Poland) and quartz solids obtained from Conductance (Warszawa, Poland). The procedure of polishing and cleaning the polymer plates before the contact angle measurements was described previously [25]. The quartz plates were cleaned with the aqueous solution of commercial detergent, washed many times in distilled water, and placed in an ultrasonic bath for 15 min. The quality of the surface of each plate was controlled by a polarizing microscope (Nikon, Tokyo, Japan, ECLIPSE E 600 POL). Next, the selected plates without cracks and roughness were additionally controlled by measurements of the contact angle of the water drop settled on the solid surfaces. The water used for solution preparation and contact angle measurements was doubly distilled and deionized (Destamat Bi18E) and its resistance was equal to 18.2 × 10⁶ Ω m. The purity of water was also checked by contact angle on the PTFE surface and surface tension measurements.

2.2. Contact Angle Measurements

Measurements of the advancing contact angle for the aqueous solutions of T20, T60, and T80 on the PTFE, PE, PMMA, nylon 6, and quartz surfaces were recorded using recorded using the sessile drop method with a DSA30 measuring system (Krüss, Hamburg, Germany) in a thermostated chamber at 293 ± 0.1 K. The apparatus chamber was saturated with a solution vapor at a given concentration of surfactant whose contact angle was measured by placing a cell filled with this solution in the chamber for a few hours prior to measurements. The contact angles for the aqueous solution of Tweens at a given concentration were measured for at least 30 drops whose volume was equal to 6 μL and good reproducibility was found. This drop volume was estimated based on the influence of size drop on the contact angle values [26]. The standard deviation of the contact angle values depends on the solution concentration of Tweens being in the range from ±1 to ±2°.

3. Results and Discussion

The wettability of a solid depends on the surface tension of the liquid or solution and the solid as well as the solid-liquid (solution) interface tension. However, if the solid surface tension and solid-water interface tension change due to the adsorption of liquid vapour or solution film formation, solid wetting depends on the film pressure. If the liquid is not spread completely over the solid surface, solid wetting can be described by the modified Young equation [27]:

$${\gamma }_S-{\pi }_1-\left({\gamma }_{SL}-{\pi }_2\right)={\gamma }_L\cos \theta$$

(1)

where ${\gamma }_S$ is the solid surface tension, ${\gamma }_L$ is the liquid or solution surface tension, ${\gamma }_{SL}$ is the solid-liquid (solution) interface tension, ${\pi }_1$ is the film pressure behind the liquid or solution drop settled on the solid surface, ${\pi }_2$ is the film pressure under the liquid or solution drop settled on the solid surface, and $\theta$ is the contact angle.

Assuming that $\pi ={\pi }_2-{\pi }_1$, we obtain [27]:

$${\gamma }_S-\pi -{\gamma }_{SL}={\gamma }_L\cos \theta$$

(2)

In the cases where ${\pi }_2={\pi }_1$ or ${\pi }_2=0$ and ${\pi }_1=0$, Equation (2) assumes the form commonly used for the discussion of the wetting process:

$${\gamma }_S-{\gamma }_{SL}={\gamma }_L\cos \theta$$

(3)

The addition of surfactants to water causes the reduction in its surface tension and changes the solid-water interface tension because of their adsorption at the water-air and solid-water interfaces. In many cases, the behavior of the surfactant molecules at the solid-water interface is quite different from that at the solid-water interface. Changes in the solid surface tension affected by the surfactant film behind the solution drop settled on the solid surface were observed. Therefore, Equation (2) should generally be applied for the solid wetting by the aqueous solution of surfactants.

3.1. Wetting and Surfactant Adsorption at the Solid-Water Interface

The isotherms of the contact angle of aqueous solutions of T20, T60, and T80 for PTFE, PE, PMMA, nylon 6, and quartz (Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5) are similar to that of surface tension [28]. However, complete spreading over the solid surface was not observed. Small discrepancies were recorded in the values of the contact angle of T20, T60, and T80 aqueous solutions on a given solid at the same concentration of Tweens.

The minimum values of the surface tension of the studied aqueous solutions of Tweens [28] were higher than those of PTFE and PE, but lower than those of PMMA, nylon 6, and quartz [29]. The minimum contact angle values of the aqueous solution of Tweens on the surface of these solids were higher than those of the other nonionic surfactants whose minimum values of their aqueous solution surface tensions were close to those of Tweens [30].

Conversely, similar to both the nonionic and ionic surfactants, a straight linear dependence was observed between the adhesion and surface tension for the studied Tweens (Figures S1 and S2, respectively). The slope of this dependence for PTFE and PE was close to −1 and did not depend on the kind of Tween. However, for PMMA, nylon 6, and quartz, the slope depended on the kind of Tween; for nylon 6 and quartz, the slope of this dependence was positive. Notably, the value of the solution surface tension corresponding strictly to zero contact angle, called the critical surface tension of solid wetting (${\gamma }_c$), was higher than that of the PTFE surface tension, ${\gamma }_S$ (${\gamma }_S$ = 20.24 mN/m; ${\gamma }_c$= 23.15 mN/m) and lower than that of PE (${\gamma }_S$ = 33.71 mN/m; ${\gamma }_c$ = 30.21 mN/m), but it was nearly the same as those obtained for classical surfactants [31]. In the case of monopolar PMMA, bipolar nylon 6, and quartz, the values of ${\gamma }_c$ were even lower than that of the Lifshitz-van der Waals component of these solid surface tensions (Figure S2). In contrast to the findings of Zisman and colleagues [32,33,34], no linear dependence was observed between the cosine of the contact angle and the surface tension of the Tweens solution (Figures S3 and S4). For hydrophobic solids, only in the case of a solution whose Lifshitz-van der Waals component of its surface tension was close to the surface tension of solids, would the value of the critical surface tension of solids wetting be equal to their surface tension if the surface tension of the solid behind the solution drop settled on the solid surface does not depend on the concentration of the surfactant in solution. In the case of monopolar and bipolar solids, this is practically impossible [31].

To confirm this suggestion, the contact angle values of the aqueous solution on PTFE, PE, PMMA, nylon 6, and quartz were calculated using the concept introduced by van Oss et al. [35,36,37,38]. According to them, the following equation can be used to calculate the contact angle of the surfactant solution [35,36,37,38]:

$${\gamma }_L\cos \theta =-{\gamma }_L+2\sqrt{{\gamma }_L^{LW}{\gamma }_S^{LW}}$$

(4)

where ${\gamma }_L$ is the aqueous solution of surfactant surface tension, and ${\gamma }_L^{LW}$ and ${\gamma }_S^{LW}$ are the Lifshitz-van der Waals components of the surfactant solution and solid surface tension, respectively. Because the value of the Lifshitz-van der Waals component of the water surface tension, ${\gamma }_W^{LW}$ (26.85 mN/m), is close to that of the surface tension of most hydrocarbons, as they are the hydrophobic part of surfactant molecules, it is possible to assume that ${\gamma }_L^{LW}\approx {\gamma }_W^{LW}=26.85$ mN/m [29]. In this case, the decrease in the water surface tension due to the adsorption of the surfactant at the water-air interface results only from the decrease in the acid-base component of the water surface tension.

The contact angle values of the aqueous solutions of T20, T60, and T80 on the PTFE and PE surface calculated from Equation (4) are close to those measured (Figure 6 and Figure S5–S7). This indicates that the PTFE and PE surface tension is constant in the range of studied Tweens concentrations and that the orientation and packing of the Tweens molecules at the polymer-water interface are similar to those at the water-air interface.

In the case of polar solids, the van Oss et al. equation can be written as [35,36,37,38]:

$${\gamma }_L\cos \theta =-{\gamma }_L+2\left(\sqrt{{\gamma }_L^{LW}{\gamma }_S^{LW}}+\sqrt{{\gamma }_L^{+}{\gamma }_S^{-}}+\sqrt{{\gamma }_L^{-}{\gamma }_S^{+}}\right)$$

(5)

where ${\gamma }_L^{+}$ and ${\gamma }_S^{+}$ are the electron-acceptor parameters of the acid-base component of the aqueous solution of the surfactant and the solid surface tension, respectively; and (${\gamma }_L^{AB}$), ${\gamma }_L^{-}$, and ${\gamma }_S^{-}$ are the electron-donor parameters of the acid-base component of surfactant solution and solid surface tension, respectively.

Taking into account the values of the components and parameters of PMMA, nylon 6, and quartz surface tension determined in our previous study [29] and assuming that the Lifshitz-van der Waals component of the solution surface tension is equal to that of water surface tension, and the electron-acceptor and electron-donor parameters have the same values, the contact angle values were calculated. The values of the contact angle of the aqueous solutions of Tweens calculated from Equation (5) were considerably different from those measured and they are not presented here. This indicates that, in the case of monopolar PMMA, bipolar nylon 6, and quartz, the values of $\pi$ in (Equation (2) are different from zero and depend on the surfactant concentration. Therefore, Equation (5) can be modified by adding $\pi$. Thus:

$${\gamma }_L\cos \theta =-{\gamma }_L+2\left(\sqrt{{\gamma }_L^{LW}{\gamma }_S^{LW}}+\sqrt{{\gamma }_L^{+}{\gamma }_S^{-}}+\sqrt{{\gamma }_L^{-}{\gamma }_S^{+}}\right)-\pi$$

(6)

In this case, confirming the above-mentioned suggestion is possible by calculating the solid surface tension using the equation presented by Neumann et al. [39,40,41,42]:

$$\frac{\cos \theta +1}{2}=\sqrt{\frac{{\gamma }_S}{{\gamma }_L}}\exp \left[-\beta {\left({\gamma }_L-{\gamma }_S\right)}^2\right]$$

(7)

where $\beta$ is the constant that does not depend on the kind of solid and is assumed to be equal to 0.000115 (m²/mJ)².

The values of ${\gamma }_S$ calculated from Equation (7) were proven to decrease as a function of Tween concentration in the solution. Thus, we assumed that the difference between the solid surface tension determined from the contact angle for water and surfactant solution at a given concentration at the first approximation is equal to $\pi$. The van Oss et al. [35,36,37,38] and Neumann et al. [39,40,41,42] concepts provide different results in the calculation of solid surface tension in many cases. However, the contact angle values calculated from Equation (6), using the $\pi$ values determined from the Neumann et al. concept [39,40,41,42], are close to those of the measured values in many cases (Figures S8–S16). The analysis of the obtained results of the contact angle and surface tension of the aqueous solution of Tweens shows that, at first, the $\pi$ values are equal to $\frac{{\gamma }_W-{\gamma }_L}{2}$. Using the $\pi$ values determined using Equation (6), we calculated the $\theta$ values (${\gamma }_W$ is the water and ${\gamma }_L$ is the aqueous solution of surfactant surface tension). These values were closer to the measured ones than those calculated on the basis of the $\pi$ values determined by means of the Neumann et al. concept [39,40,41,42,43] (Figures S8–S16).

The calculations of the contact angle of the aqueous solutions of Tweens on the PTFE and PE surfaces confirm the suggestion drawn from the linear dependence between the adhesion and surface tension, that the adsorption and orientation of Tweens molecules at the water-air and PTFE/PE-water interfaces are the same. However, calculation of $\theta$ values of the aqueous solution of Tweens on PMMA, nylon 6, and quartz indicated that the adsorption and orientation of the Tweens molecules at the solid-water interface are different from those at the water-air interface [28]. This conclusion can be confirmed by calculating the Gibbs surface excess concentration at the solid-water interface. If $\pi =0$, then the Gibbs equation is [43]:

$$\Gamma =\frac{-C}{RT}{\left[\frac{\partial \left(-{\gamma }_L\cos \theta \right)}{\partial C}\right]}_{T,p}=\frac{-1}{2.303RT}{\left[\frac{\partial \left(-{\gamma }_L\cos \theta \right)}{\partial \log C}\right]}_{T,p}$$

(8)

If $\pi$ is not zero [43]:

$$\Gamma =\frac{-C}{RT}{\left[\frac{\partial \left({\gamma }_{SL}\right)}{\partial C}\right]}_{T,p}=\frac{-1}{2.303RT}{\left[\frac{\partial \left({\gamma }_{SL}\right)}{\partial \log C}\right]}_{T,p}$$

(9)

The calculated values of for T20, T60, and T80 at the PTFE-water and PE-water interfaces from Equation (8) (Figures S17 and S18) were close to those at the water-air interface [28].This means that the packing of the Tweens molecules in the surface layer at the hydrophobic polymer-water interface is the same as in the layer at the water-air interface [28] and the molecules are oriented perpendicularly or at an angle close to 90° toward the polymer-water-interface. The tails of the surfactant molecules in the surface layer should be directed toward the polymer surface. In the case of PMMA, nylon 6, and quartz, considerable differences were observed between the Gibbs surface excess concentration at the PMMA(nylon 6, quartz)-water interface compared to their adsorption at the water-air interface [28] (Figures S19–S21,

Table 1. The values of the Gibbs surface excess concentration ($\Gamma$, ×10⁻⁶ m²/mol) in the saturated monolayer and area occupied by one molecule (A, Ų) at the water-air (W-A) [28], polytetrafluoroethylene-water (PTFE-W), polyethylene-water (PE-W), polymethyl methacrylate-water (PMMA-W), nylon 6-water (nylon 6-W), and quartz-water (Quartz-W) interfaces calculated using different methods.

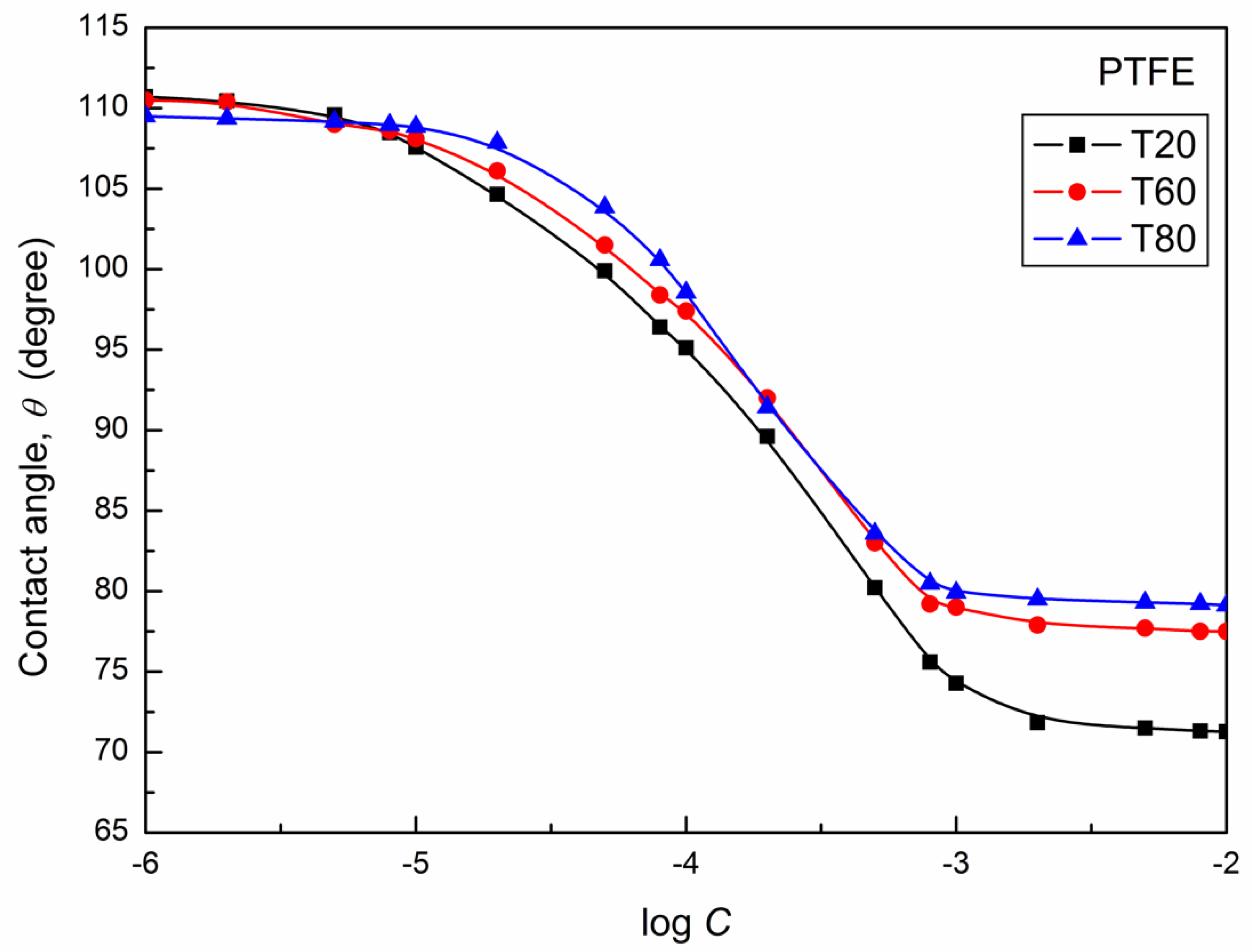
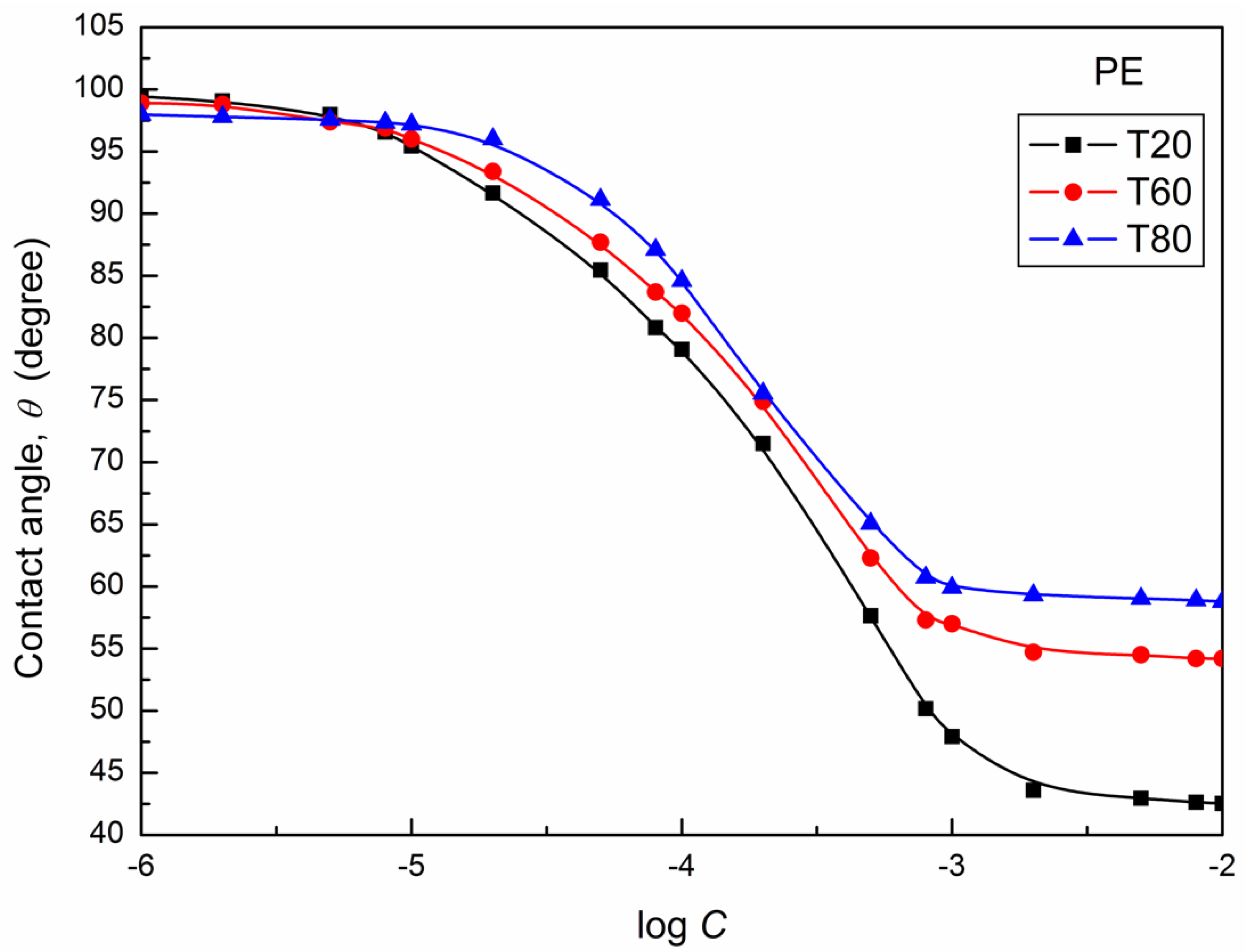
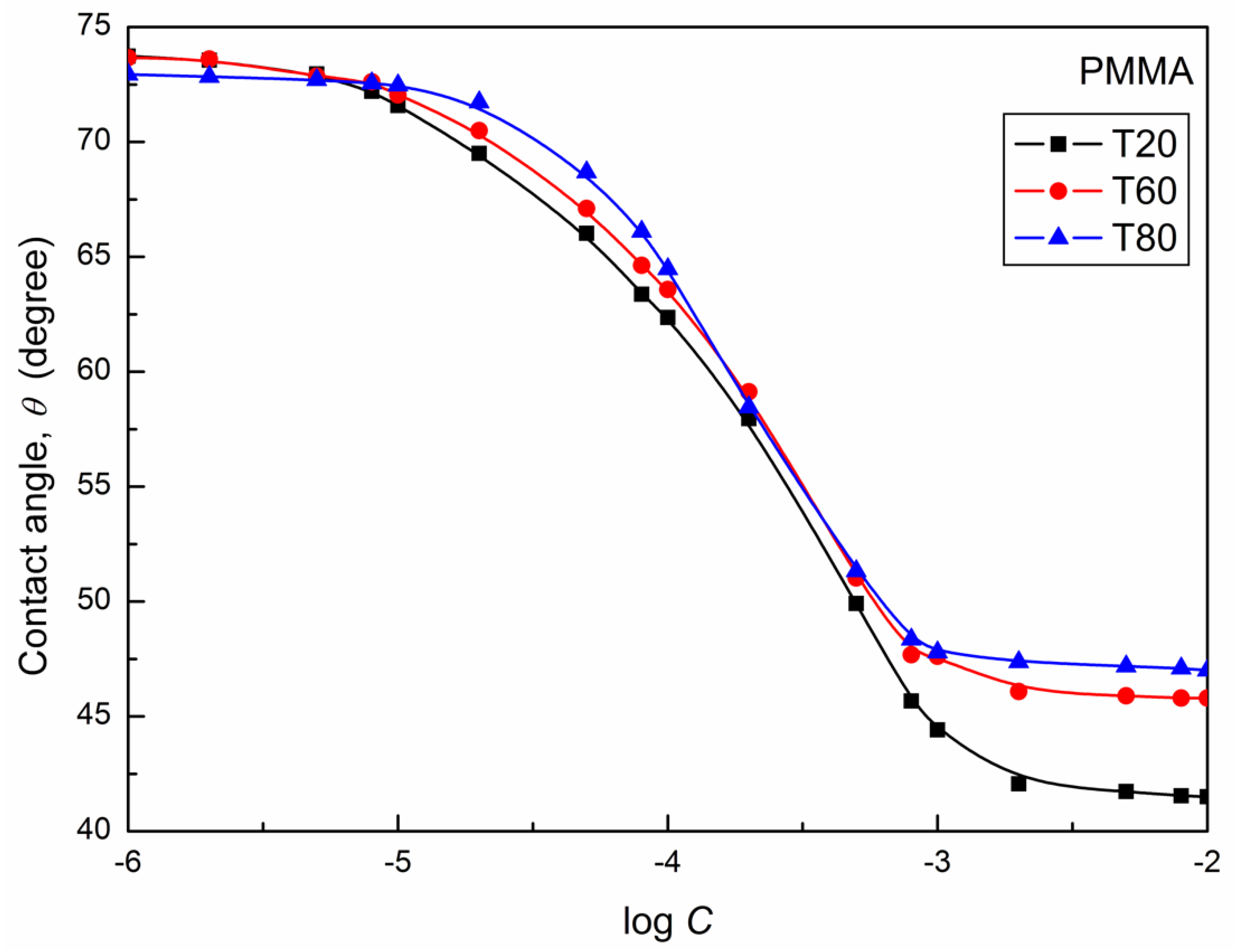
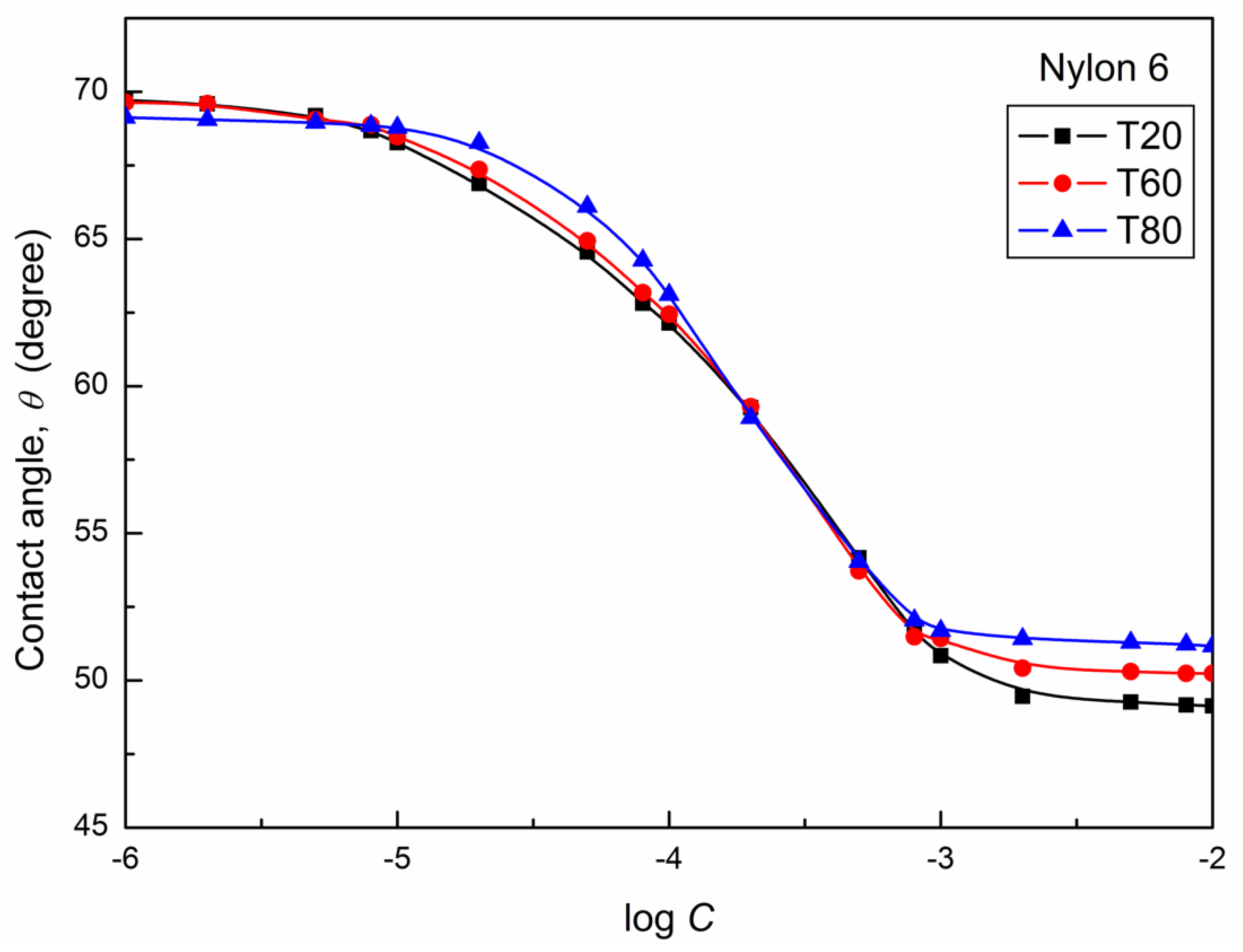
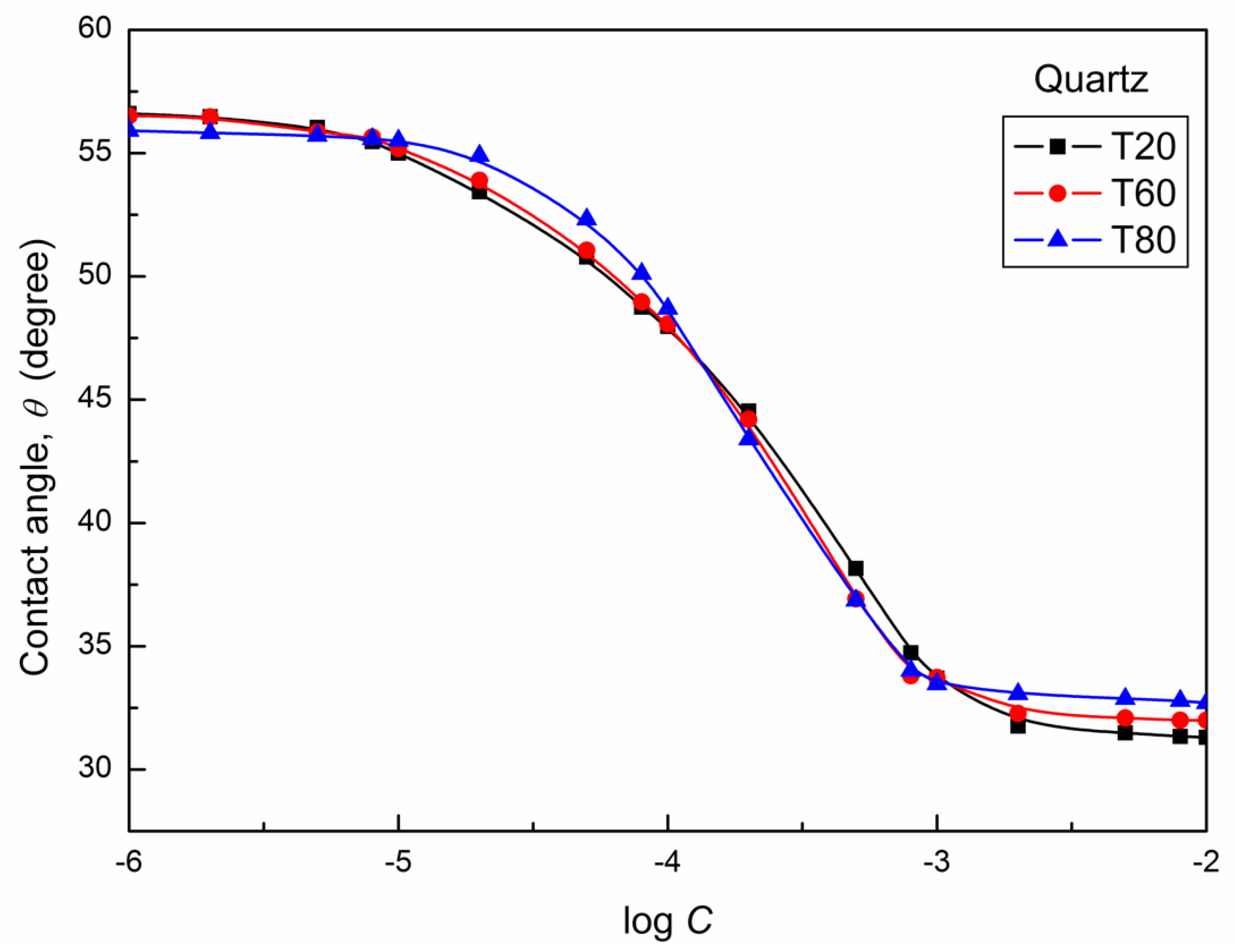
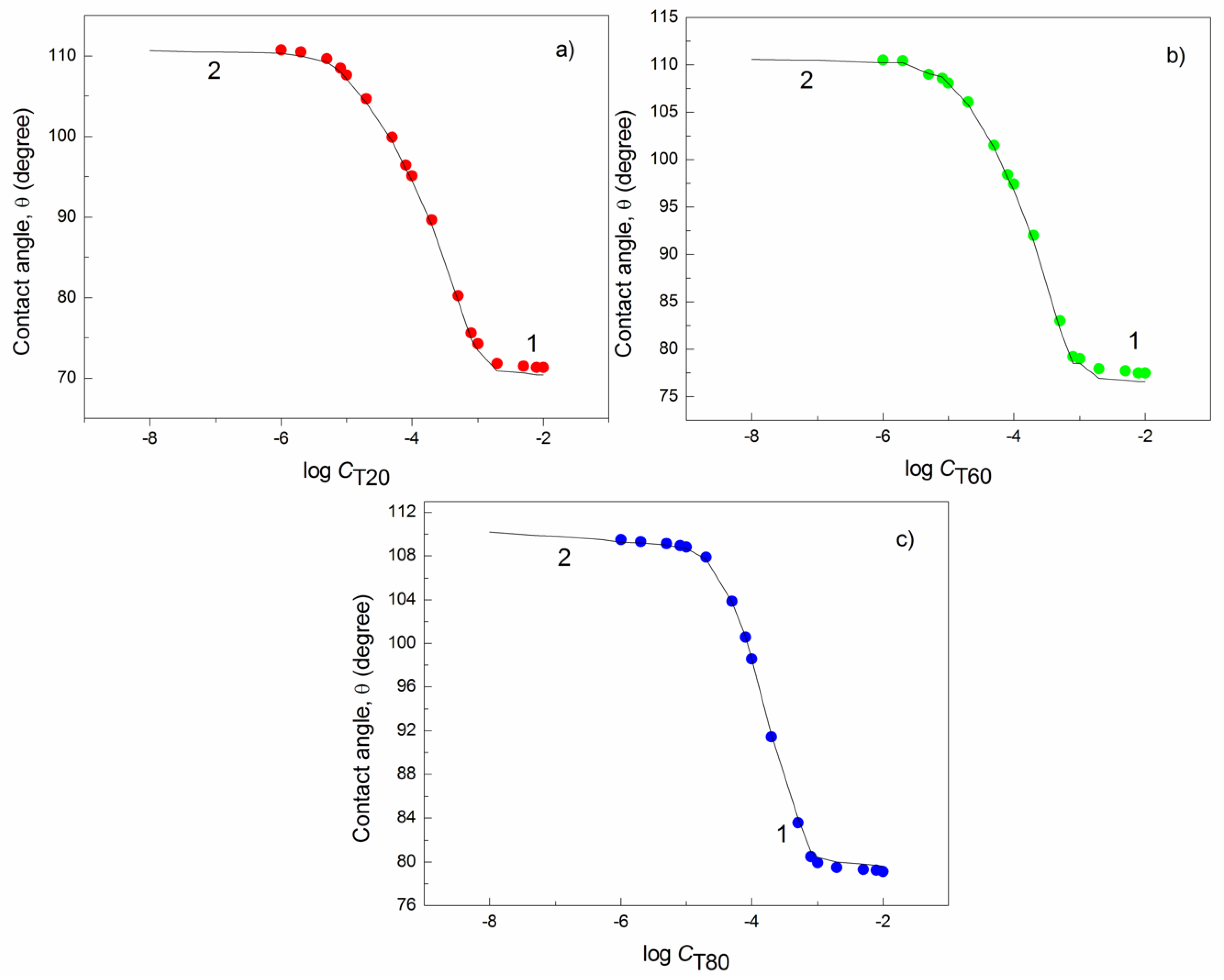
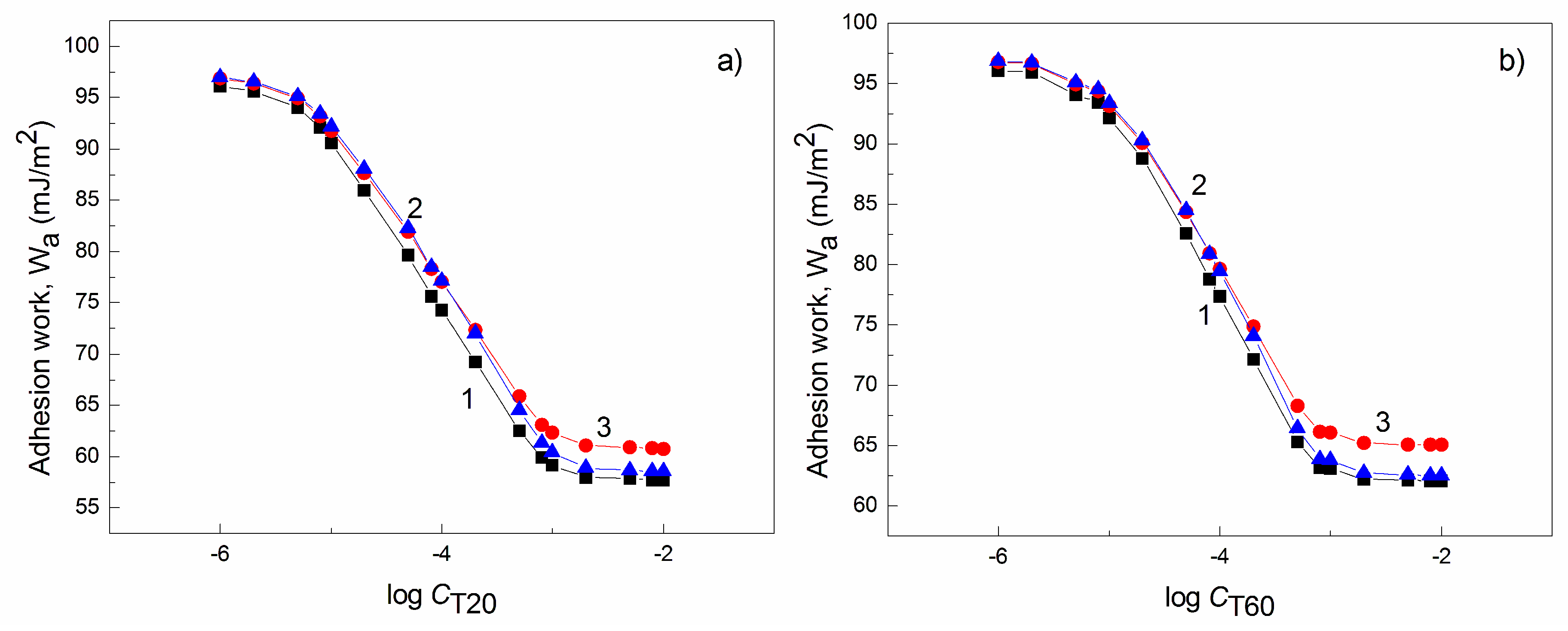
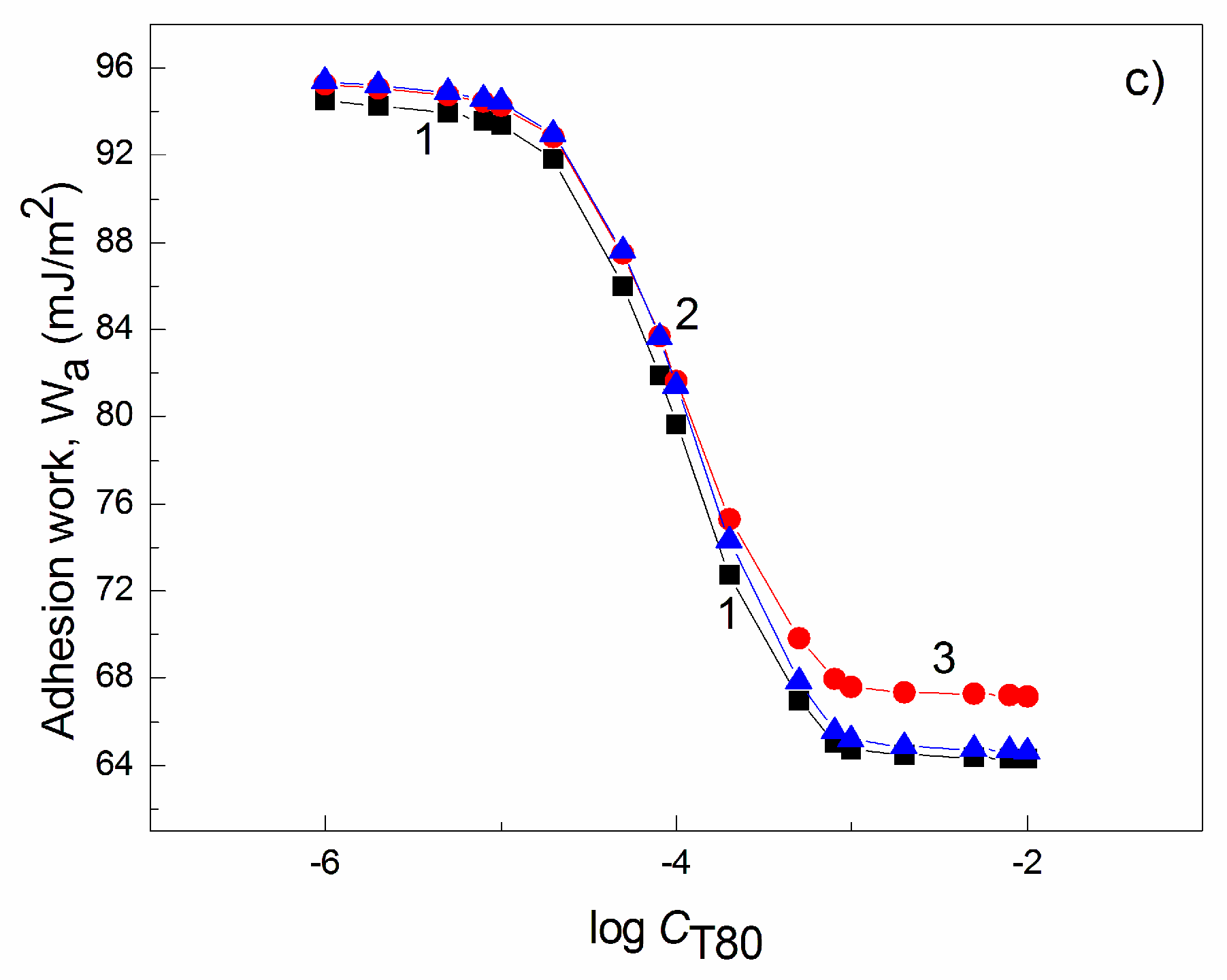
	W-A		PTFE-W		PE-W		PMMA-W		Nylon 6-W		Quartz-W
	$\mathbf{\Gamma }$	A	$\mathbf{\Gamma }$	A	$\mathbf{\Gamma }$	A	$\mathbf{\Gamma }$	A	$\mathbf{\Gamma }$	A	$\mathbf{\Gamma }$	A
T20	2.79 a	59.62	2.87	57.85	2.94	56.4	1.92	86.47	1.29	129.11	0.69	241.67
	3.63 b	45.74	3.73	44.5	3.83	43.40	2.53	65.70	1.74	95.20	0.97	172.05
	$\Gamma$ = 2.45–4.84 c A = 34.30–67.64 c						$\Gamma$ = 2.55–2.27 c1 A = 65.19–73.09 c1 $\Gamma$ = 0.44–0.43 c2 A = 378.66–386.36 c2 $\Gamma$ = 0.37–0.36 c3 A = 443.85–459.45 c3 $\Gamma$ = 0.59 c4 A = 283.91 c4
T60	3.00	55.38	2.94	56.45	2.97	55.88	2.08	79.82	1.454	114.19	0.86	193.96
	3.61	45.99	3.73	44.57	3.69	45.03	2.69	61.81	1.93	85.98	1.17	141.66
	$\Gamma$ = 2.45–4.84 c A = 34.30–67.64 c						$\Gamma$ = 1.720–1.54 c1 A = 96.55–108.15 c1 $\Gamma$ = 0.44–0.43 c2 A = 378.66–386.36 c2 $\Gamma$ = 0.35–0.34 c3 A = 475.22–494.50 c3 $\Gamma$ = 0.52 c4 A = 318.97 c4
T80	3.94	42.14	3.41	48.65	3.35	49.58	2.40	69.21	1.67	99.42	1.03	161.04
	4.04	41.10	4.14	40.10	4.06	40.89	3.48	47.76	2.51	66.17	1.60	103.83
	$\Gamma$ = 2.45–4.84 c A = 34.30–67.64 c						$\Gamma$ = 1.73–1.55 c1 A = 96.05–107.32 c1 $\Gamma$ = 0.44–0.43 c2 A = 378.66–386.36 c2 $\Gamma$ = 0.35–0.34 c3 A = 474.72–493.68 c3 $\Gamma$ = 0.52 c4 A = 318.14 c4

^a Determined from the surface tension isotherm; ^b Calculated from the Joos equation in Equation (10); ^c Calculated based on the bond length and angle between them; ^c1 Tail; ^c2 Head; and ^c3 Total molecule in the flat position; ^c4 Total molecule if tail, heterocyclic ring and only one hyddophilic chain are contacted with the solid surface.

). This suggests that the packing and orientation of Tweens molecules in the surface layer at the PMMA (nylon 6, quartz)-water interface are different from those at the water-air interface [28]. The knowledge about the limiting area occupied by the Tweens molecules at their parallel and perpendicular orientations toward the given interface can provide a more comprehensive explanation of the structure of the surface layer at the solid-water interface. Among others, the limiting area occupied by the surfactant molecules at the interfaces can be calculated from the molecule size using the Joos equation [44]:

$$\exp \left(\frac{-\Pi }{RT{\Gamma }_W^{\infty }}\right)+\exp \left(\frac{-\Pi }{RT{\Gamma }_S^{\infty }}\right)\frac{C}{a_S}=1$$

(10)

where $\Pi ={\gamma }_W-{\gamma }_L$ for the surfactant solution-air interface or $\Pi ={\gamma }_{SW}-{\gamma }_{SL}$ for the solid-surfactant solution interface.${\gamma }_W$ is the water surface tension, ${\gamma }_L$ is the aqueous solution of surfactant surface tension, ${\gamma }_{SW}$ is the solid-water interface tension, and ${\gamma }_{SL}$ is the solid-surfactant solution interface tension, ${\Gamma }_W^{\infty }$ is the maximum possible Gibbs surface excess concentration of water and ${\Gamma }_S^{\infty }$ of surfactant at the interfaces, and $a_S=\exp \left(\frac{{\mu }_S^{0S}-{\mu }_S^{0B}}{RT}\right)\omega$ (${\mu }_S^{0S}$ and ${\mu }_S^{0B}$ are the standard potentials of surfactant in the surface layer and bulk phase).

Using the Joos equation in Equation (10) [44] for the solid-water interface, the limiting Gibbs surface excess concentration (${\Gamma }_S^{\infty }$) of the Tweens molecules was determined. Next, the limiting area occupied by these molecules ($A_0$) was established ($A_0=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\Gamma }_S^{\infty }N$}\right.$).

In the case of the PTFE (PE)-water interface, the values of this area were similar to those at the water-air interface [28]. However, the values of this area at the PMMA (nylon 6 and quartz)-water interface were considerably higher than those at the water-air interface. The limiting area occupied by the Tween molecules at the PMMA (nylon 6, quartz)-water interface calculated from the Joos equation for each Tween was lower than that of the minimum area calculated from the Gibbs isotherm adsorption.

The considerably lower adsorption of Tweens at the PMMA (nylon 6, quartz)-water interface compared to water-air [28] should be reflected in the orientation and conformation of Tween molecules in the layer at the solid-water interface. The adsorption of Tween at the PMMA-water, nylon 6-water, and quartz-water interfaces appeared to fulfill the straight linear form of the Langmuir equation. This indicates that, at these interfaces, a Tweens monolayer is formed. To confirm this suggestion, the possible areas of hydrophilic and hydrophobic parts of Tweens contact with the solid surface were calculated based on the bonds lengths, the angle between them, and the average distance between molecules given the parallel orientation of Tween molecules at the interfaces. Similar to the calculation of Tweens volume [28], different average distances between the molecules was assumed. Thus, the minimum and maximum contactable areas at a given conformation of Tweens molecules were obtained (Table 1). In the calculation of contactable area of Tween molecules in parallel orientation at the solid-water interface, two possible conformations of their molecules were considered. The first conformation take places when in the flat position of the molecules their which is hydrophobic part and all hydrophilic chains were in contact with the solid surface. The second, when the hydrophobic part, heterocyclic ring and only one oxyethylene chain are in contact with the solid surface. In each case the contactable area of Tweens molecules determined in such ways is larger than the limiting area calculated from the Joos equation [44] and that the minimal area corresponding to the maximal Gibbs surface excess concentration. In the case of PMMA, the minimum area occupied by the molecules of T60 and T80 was smaller than even the minimum contactable area of the tail. This comparison shows that there is no parallel orientation of Tween molecules at the saturated monolayer at the PMMA (nylon 6, quartz)-water interface. The saturated monolayer of the Tween molecules is most probably contacted by the tail or is partially parallel to the solid surface, but the hydrophilic part is directed toward the water phase and is probably rolled to a large extent.

3.2. Gibbs Standard Free Energy of Adsorption at the Solid Water Interface

The Gibbs standard free energy of surfactants adsorption ($\Delta G_{ads}^o$) at a given interface measures the adsorption efficiency of a given surfactant and indicates whether the adsorption is spontaneous.

In the literature, many different methods to calculate $\Delta G_{ads}^o$ have been presented [20,45]; however, the method proposed by Langmuir is often used [20,46]. The Langmuir equation modified by de Boer [46] is:

$$\frac{A_0}{A-A_0}\exp \frac{A_0}{A-A_0}=\frac{C}{\omega }\exp \left(\frac{-\Delta G_{ads}^0}{RT}\right)$$

(11)

where A₀ is the limiting area occupied by the surface active agent at the interface and A is the area occupied by the surface active agent at the given concentration in the bulk phase.

$\Delta G_{ads}^o$ can be also calculated from the linear form of the Langmuir isotherm equation as [20,46]:

$$\frac{C}{\Gamma }=\frac{C}{{\Gamma }^{\max }}+\frac{a}{{\Gamma }^{\max }}$$

(12)

where a is constant.

The constant a can be expressed as:

$$a=\omega \exp \frac{\Delta G_{ads}^o}{RT}$$

(13)

where $\omega$ is the number of water moles at 1 dm³.

For all studied systems, Equation (12) was satisfied. Thus, calculating $\Delta G_{ads}^o$ from Equation (13) was possible.

The values of $\Delta G_{ads}^o$ calculated from Equation (11) for a given system were somewhat higher than those calculated from Equation (13) (Figures S22–S26,

Table 2. The values of standard Gibbs free energy of Tweens adsorption ($\Delta G_{ads}^o$, kJ/mol) calculated from Equations (11) and (13)–(15) at the water-air (W-A) [28], PTFE-water (PTFE-W), PE-water (PE-W), PMMA-water (PMMA-W), nylon 6-water (nylon 6-W), and quartz-water (Quartz-W) interfaces.

Surfactant	Equation	W-A	PTFE-W	PE-W	PMMA-W	Nylon 6-W	Quartz-W
T20	(11)	−37.16	−37.33	−37.33	−36.55	−37.67	−37.45
	(13)	−39.68	−40.83	−40.83	−40.03	−41.32	−41.23
	(14)	−39.61	−39.71	−39.69	−39.41	−39.37	−39.38
	(14)	−	−	−	−29.88	−25.17	−12.79
	(15)	−	−39.71	−39.70	−29.99	−25.12	−12.36
T60	(11)	−35.99	−37.49	−36.47	−36.83	−36.15	−36.34
	(13)	−38.06	−39.77	−39.41	−39.81	−39.37	−39.55
	(14)	−38.53	−39.02	−39.01	−38.41	−38.45	−38.34
	(14)	−	−	−	−30.36	−26.91	−18.87
	(15)	−	−39.01	−39.02	−30.50	−26.89	−18.49
T80	(11)	−32.32	−34.32	−34.62	−33.95	−32.79	−33.23
	(13)	−33.28	−35.57	−35.36	−37.03	−37.50	−36.47
	(14)	−35.89	−37.81	−37.84	−37.24	−37.24	−37.28
	(14)	−	−	−	−30.76	−27.93	−22.07
	(15)	−	−37.83	−37.85	−30.95	−27.93	−21.75

). There are some discrepancies among the values of $\Delta G_{ads}^o$ for T20, T60 and T80 for the given system. For the given Tween, the $\Delta G_{ads}^o$ values did not depend on the kind of interface. Notably, the $\Delta G_{ads}^o$ values calculated from Equation (13) for T20 and T80 were close to those reported in the literature [18].

To explain the lack of differences between $\Delta G_{ads}^o$ for the given Tween for all studied solids, $\Delta G_{ads}^o$ was calculated from the Rosen equation, which, for the nonionic surfactants is [20]:

$$\Delta G_{ads}^o=RT\ln \frac{CMC}{\omega }-\frac{{\pi }_e}{{\Gamma }^{\max }}$$

(14)

where CMC is the critical micelle concentration and π_e is the difference between the solid-water interface tension and the solid-solution tension at CMC.

If the ${\pi }_e$ values determined above were applied in Equation (14), the $\Delta G_{ads}^o$ values determined from this equation were considerably different from those calculated from Equation (11) and depended not only on the kind of Tween but also on the solid. ${\pi }_e$ was determined based on the Young equation with the assumption that γ_S was constant in the studied range of surfactant concentration.

If we applied the value of ${\pi }_e$ equal to $\frac{{\gamma }_W-{\gamma }_L}{2}$ (${\gamma }_W$ is the water and ${\gamma }_L$ is the aqueous solution of surfactant surface tension, respectively), then the values of $\Delta G_{ads}^o$ calculated from Equation (11) were similar to those obtained from Equation (14) and did not depend on the kind of solid for the given Tween. In our previous paper, we proposed a new method for the calculation of $\Delta G_{ads}^o$ adsorption at the solid-water interface. This equation is [47]:

$$\Delta G_{ads}^o=RT\ln \frac{CMC}{\omega }-\frac{{\gamma }_W\cos {\theta }_W-{\gamma }_L^{\min }\cos {\theta }_{\min }}{{\Gamma }^{\max }}$$

(15)

where ${\gamma }_W$ is the water surface tension, ${\gamma }_L^{\min }$ is the minimum surface tension of aqueous solution of surfactant, ${\theta }_W$ is the contact angle for water, and ${\theta }_{\min }$ is the minimum contact angle of the solution.

The values of $\Delta G_{ads}^o$ for the PTFE-water and PE-water interfaces calculated from Equation (15) were the same as those calculated from Equations (11) and (14). However, the $\Delta G_{ads}^o$ values calculated from Equation (15) for PMMA, nylon 6, and quartz were close to those calculated from Equation (14) with the assumption that ${\gamma }_S$ was constant in the studied range of surfactant concentrations. The differences between $\Delta G_{ads}^o$ for these solids calculated from Equations (11) and (15) were probably connected with the standard free energy of Tween film formation at the PMMA (nylon 6, quartz)-water interfaces.

3.3. Work of Adhesion of Aqueous Solution of Tweens to the Solid Surface

The work of adhesion ($W_a$) of the aqueous solution of surfactants on the solid surface is important in the wetting process because the difference between the adhesion and cohesion work determines the spreading of the solution over the solid surface.

According to the thermodynamic rule, the adhesion work satisfies the equation [46]:

$$W_a={\gamma }_S+{\gamma }_L-{\gamma }_{SL}$$

(16)

If the liquid does not spread completely over the solid surface, the Young equation and Equation (16) transform into the Young-Dupre equation [20,46]:

$$W_a={\gamma }_L\left(\cos \theta +1\right)$$

(17)

From Equation (17):

$${\gamma }_L\cos \theta =-{\gamma }_L+W_a$$

(18)

From this equation, if there is a linear dependence between the adhesion and surface tension of surfactant solution at a slope equal to -1, then the second constant in Equation (18) is equal to the work of adhesion of the liquid on the solid surface. As it was mentioned above, these dependences exist in the PTFE-aqueous solution of Tweens and PE-aqueous solution of the surfactants system. The $W_a$ values resulting from Equation (18) for PTFE and PE were equal to 46.3 mJ/m² and 60.42 mJ/m², respectively. However, from the dependence between the cosine of the contact angle and the reciprocal of the solution surface tension, the results showed that the work of adhesion of the Tween solutions was 46.21 mJ/m² and 60.50 mJ/m² for PTFE and PE, respectively. These values were almost the same as those calculated from the following equation [35]:

$$W_a=2\sqrt{{\gamma }_L^{LW}{\gamma }_S^{LW}}$$

(19)

For calculations of $W_a$, values from Equation (19), the values of the Lifshitz-van der Waals component of the water surface tension (26.85 mN/m), and the surface tension of PTFE and PE (20.24 and 33.71 mN/m, respectively) were applied. These values of $W_a$ for PTFE and PE were 46.62 and 60.17 mJ/m², respectively.

The adhesion work of the aqueous solution of T20, T60, and T80 to PMMA, nylon 6, and quartz surface was calculated from Equation (17) and from the following equation:

$$W_a=2\left(\sqrt{{\gamma }_L^{LW}{\gamma }_S^{LW}}+\sqrt{{\gamma }_L^{+}{\gamma }_S^{-}}+\sqrt{{\gamma }_L^{-}{\gamma }_S^{+}}\right)-\pi$$

(20)

For the calculation of $W_a$ from Equation (20), the π values determined from the equation introduced by Neumann et al. [39,40,41,42] and the water and surfactant solution surface tension values were used.

The $W_a$ values calculated from Equation (20) based on $\pi$ obtained from the difference between the surface of water and solution were very close to those calculated from Equation (17) from the surface tension of water and solution (Figure 7 and Figure S27–S32). In fact, $W_a$ depends on the kind of solid and Tween. Notably, for PMMA, nylon 6, and quartz, a straight linear dependence was observed between the adhesion work of the solution to their surface calculated from Equation (17) and the solution surface tension (Figures S33–S35).

4. Conclusions

From the data reported in the literature on the adsorption of T20, T60, and T80 at the water-air interface, and the analysis of the isotherms of the contact angle of the aqueous solution of these surfactants on the PTFE and PE, our results showed that the adsorption of Tweens at the water-air interface is comparable to that at the PTFE-water and PE-water interfaces. This indicates that the Tweens molecules in the saturated monolayer at the water-air interface are oriented with their tail toward the air phase, and are oriented toward the polymer phase at the PTFE/PE-water interface. The orientation of the Tween molecules is probably perpendicular or almost perpendicular toward both interfaces. In the case of PMMA, nylon 6, and quartz, we found from the isotherms of the surface tension and the contact angle of Tweens solution that the adsorption of Tweens at the solid-water interface is lower than at the water-air interface. The Tweens molecules at the solid-water interface are oriented parallel to this interface and their head is directed toward the water phase. The efficiency of Tweens adsorption was deduced based on the standard Gibbs free energy of Tweens adsorption at the water-air and solid-water interfaces calculated by applying different methods. The methods used include one previously proposed in our work, and methods based on the CMC value, surface tension of solution at the CMC, surface tension of water, contact angle of water, solution at the CMC and the maximal Gibbs surface excess concentration of surfactant at the solid-water interface. The values of the standard Gibbs free energy of adsorption that were calculated by applying our method were comparable to those obtained using the Langmuir method. The standard Gibbs free energy of Tweens adsorption at the water-air and PTFE/PE-water interfaces as a measure of adsorption was lower than that of classical nonionic surfactants, such as Tritons.

The efficiency and effectiveness of surfactant adsorption at the solid-water interface were analysed in terms of the wettability of PTFE, PE, PMMA, nylon 6, and quartz. Based on our analysis, we proved that using the values of PTFE and/or PE surface tension, the values of surface tension of aqueous solutions of Tweens, and the Lifshitz-van der Waals component of water surface tension, predicting the contact angle of this solution on the PTFE and/or PE surface, and the adhesion work of the solution to those polymers was possible. In the case of PMMA, nylon 6, and quartz, it was also possible to predict their wettability by aqueous solutions of Tweens and the adhesion work of this solution to their surface, if the pressure of the Tweens film on the solid surface was considered.

However, except for the components and parameters of these solids’ surface tensions, the Lifshitz-van der Waals component and parameters of the solution surface tension and the pressure of the Tweens layer must be used. This proved that the Tweens layer pressure can be established from the water and surfactant solution surface tension.