Learning to Balance Mixed Adversarial Attacks for Robust Reinforcement Learning

Abstract

Reinforcement learning agents are highly susceptible to adversarial attacks that can severely compromise their performance. Although adversarial training is a common countermeasure, most existing research focuses on defending against single-type attacks targeting either observations or actions. This narrow focus overlooks the complexity of real-world mixed attacks, where an agent’s perceptions and resulting actions are perturbed simultaneously. To systematically study these threats, we introduce the Action and State-Adversarial Markov Decision Process (ASA-MDP), which models the interaction as a zero-sum game between the agent and an adversary attacking both states and actions. Using this framework, we show that agents trained conventionally or against single-type attacks remain highly vulnerable to mixed perturbations. Moreover, we identify a key challenge in this setting: a naive mixed-type adversary often fails to effectively balance its perturbations across modalities during training, limiting the agent’s robustness. To address this, we propose the Action and State-Adversarial Proximal Policy Optimization (ASA-PPO) algorithm, which enables the adversary to learn a balanced strategy, distributing its attack budget across both state and action spaces. This, in turn, enhances the robustness of the trained agent against a wide range of adversarial scenarios. Comprehensive experiments across diverse environments demonstrate that policies trained with ASA-PPO substantially outperform baselines—including standard PPO and single-type adversarial methods—under action-only, observation-only, and, most notably, mixed-attack conditions.

1. Introduction

Deep reinforcement learning (DRL) algorithms [1] enable agents to learn optimal policies through interaction and achieve superhuman performance in domains ranging from game play [2,3,4] to robotics [5,6,7]. Despite successes in various domains, policies learned by DRL algorithms are often brittle because of neural network parameterization. As first demonstrated in image classification tasks [8], neural networks are vulnerable to adversarial perturbations. These perturbations, typically imperceptible to humans, can lead to erroneous predictions with high confidence [9]. Similarly, trained DRL agents can fail catastrophically when deployed in environments slightly different from training settings or when subjected to noise or adversarial perturbations [10,11]. This lack of robustness limits the deployment of agents in real-world scenarios where model misspecification, inherent environmental stochasticity, and the potential for malicious adversarial interventions are prevalent. Addressing this susceptibility to perturbations and modeling differences remains a critical challenge in the field.

Numerous techniques have been proposed to address the vulnerabilities of trained policies in DRL. By integrating safety constraints [12,13], domain randomization [14], and adversarial training frameworks [15], researchers have developed methods to improve agent robustness while maintaining its performance in dynamic environments [16,17]. Among these techniques, adversarial reinforcement learning (ARL) enhances the standard training process by exposing the agent to worst-case (or near worst-case) perturbations during training, thereby improving its robustness [18]. In ARL, two agents typically compete with each other: an adversary agent and a protagonist agent. The adversary is trained alongside the protagonist rather than being held fixed. The core idea is to formulate a minimax optimization problem in which the protagonist aims to maximize the cumulative reward, while the adversary seeks to minimize it through perturbations [19].

Adversarial attacks in DRL can be broadly categorized according to which aspect of the process they target [20]: the state observations received by the agent [21,22], the actions taken by the agent [23], the reward function that guides the learning process [24], or the dynamics of the environment [25]. Existing methods typically focus on a single attack type, neglecting their interactions and mutual effects [26]. Some studies have shown that adversarial training with an action-disrupting adversary improves the resilience of the agent to parametric variations during training, while the impact of such training on other factors remains largely unexplored [27]. However, in practical scenarios, multiple disruptions occur simultaneously and influence each other. For example, an autonomous vehicle utilizes sensors (e.g., cameras and LiDAR) for environmental perception and controls its steering and speed through actuation. Both the sensing and actuation processes are susceptible to noise and uncertainties at any time during the operation [28]. There remains a significant gap in the literature regarding the extent to which an agent, trained to be robust to a specific type of disturbance through such adversarial training, can effectively generalize its robustness to novel and distinct forms of disruption.

In this study, we investigate the limitations of various adversarial training methods, with a particular focus on their inability to achieve robustness across mixed-attack scenarios simultaneously. To address these shortcomings, we introduce the Adversarial Synthesis and Adaptation (ASA) framework. It integrates and balances mixed adversarial attack strategies to achieve robustness against both observational and action-based attacks simultaneously. Our method adaptively learns to scale diverse attack types during training to effectively balance the trade-offs between them. The results in Mujoco Playground environments [29] demonstrate the ability of ASA to adaptively balance adversarial attacks, leading to improved performance over baseline methods in default settings, as well as under single-type and mixed adversarial attacks. In summary, our study offers the following key contributions:

1.

Empirical Evidence of Asymmetric Robustness: We are the first to empirically demonstrate that robustness to observation perturbations does not imply robustness to action perturbations and vice versa. This distinction is often overlooked in prior work, which typically focuses on single-type adversarial attacks in isolation. Our results highlight the critical need to address mixed perturbations that simultaneously target multiple components of the decision-making pipeline.

2.

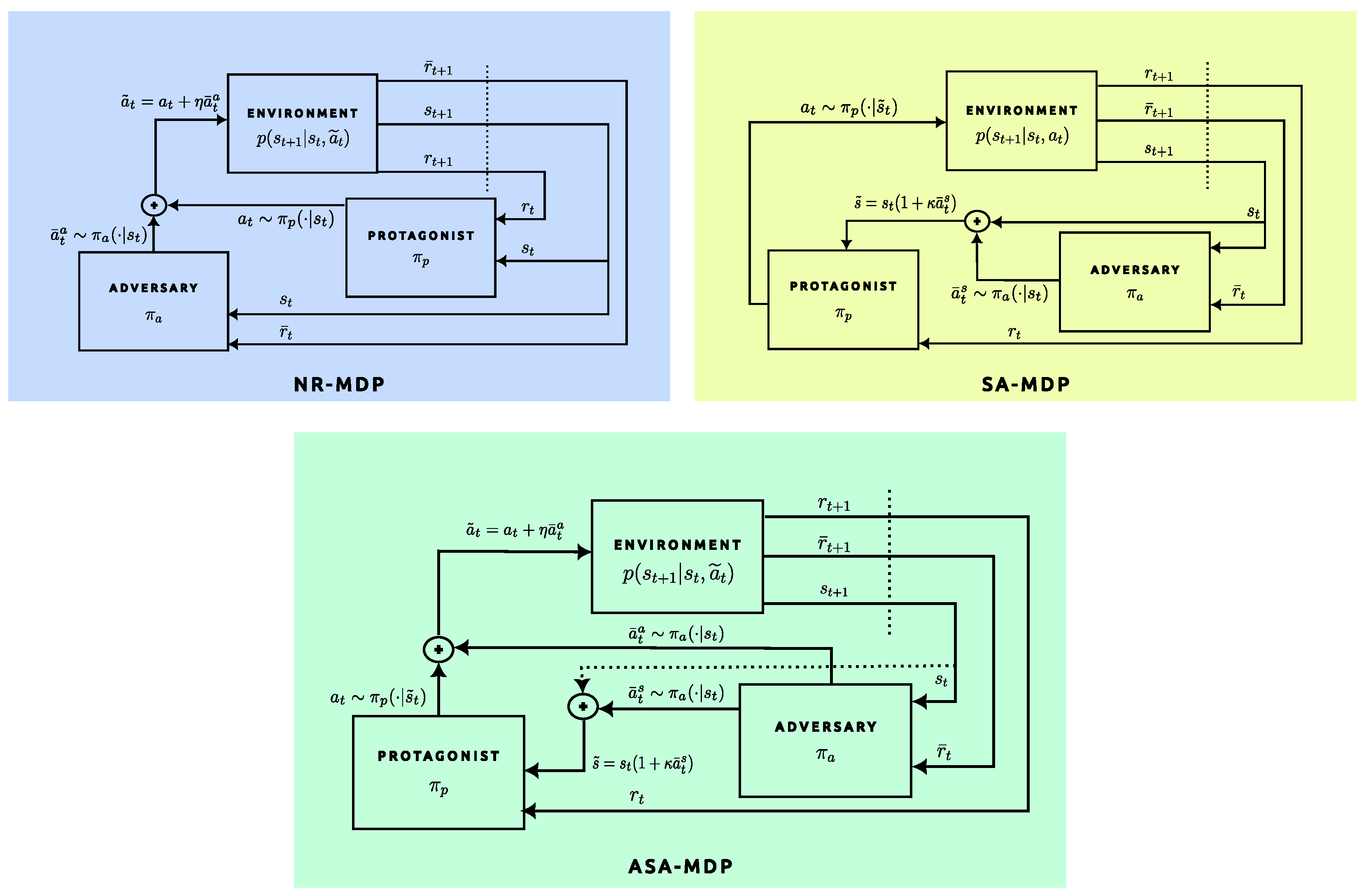
A Generalized Framework for Mixed Adversarial Attacks: We introduce Action and State-Adversarial Markov Decision Process (ASA-MDP), a novel game-theoretic extension of the standard MDP. Unlike prior formulations such as NR-MDP [23] and SA-MDP [21], ASA-MDP formally models mixed adversarial attacks involving simultaneous perturbations to both the actions and observations. In  particular, ASA-MDP subsumes MDP, NR-MDP, and SA-MDP as special cases through the appropriate parameterization of adversarial strengths, providing a unified and flexible framework for studying adversarial robustness.

3.

Balanced Adversarial Training via ASA-PPO: We propose ASA-PPO, a hybrid adversarial training algorithm in which the adversary dynamically balances its perturbation budget in both the state and action spaces. Unlike naive unbalanced mixed-attack strategies, ASA-PPO promotes the learning of protagonist policies that are significantly more robust across a spectrum of attack modalities, including single-type and mixed perturbations. Extensive experiments validate the superiority of ASA-PPO over the existing baselines.

The remainder of this paper is organized as follows. Section 2 reviews related works, providing a comprehensive overview of the existing research in the field. Section 3 introduces the notation and background necessary to understand this study. Section 4 presents the formulation of the problem and the proposed solution framework, detailing its components and methodology. Section 5 evaluates the framework through simulations and discusses the results, highlighting the key findings and implications. Finally, Section 6 concludes the paper by summarizing the contributions and outlining potential directions for future work.

2. Related Works

Adversarial learning originates from early findings in deep learning, which revealed that small perturbations to input data can cause models to produce incorrect classifications [8,9]. Building on adversarial attacks in deep learning, a wide range of attack strategies have been proposed for different problem domains [30,31]. Specifically in DRL, early studies by Huang et al. [10] and Kos et al. [15] demonstrated that minor perturbations to the observed states of an agent can significantly degrade the performance of the learned policy, often resulting in failures in the control tasks. Subsequent research has shown that trained agents are also vulnerable to action-space perturbations [32], reward poisoning [24,25], and model attacks [33], causing similar performance failures. All of these findings underscored the critical need for robust learning strategies in DRL [21], especially for safety-critical applications.

Beyond direct manipulation of MDP aspects, the concept of adversarial policies emerged, where an adversary agent in a multi-agent setting learns to specifically exploit the weaknesses of a DRL agent, leading it into undesirable states or forcing suboptimal actions, even without directly altering agent’s sensory inputs [34]. Adversarial reinforcement learning (ARL) incorporates manipulated samples into the training process as a defense mechanism, preventing performance degradation in the presence of adversarial or natural noise [23,35]. Attacks in ARL can be classified into three settings: white-box, gray-box, and black-box based on the level of knowledge available to the attacker. In the white-box setting, gradient-based methods, such as the Fast Gradient Sign Method (FGSM) [9] and Projected Gradient Descent (PGD) [36], exploit gradients of the loss function to perturb control policies, causing significant performance degradation [35,37]. In the gray-box setting, adversaries with limited knowledge of the target policy employ man-in-the-middle strategies [38]. In the black-box setting, attacks can reduce the performance of the agent without access to model parameters [33].

Despite the initial successes of adversarial training, robustness evaluation often suffered from a static perspective. This led to a critical understanding that robust evaluation requires considering adaptive attacks that are specifically designed to overcome particular defenses [39]. After all, a protagonist that is aware of the static attack mechanism can often devise strategies to bypass it, leading to a false sense of security. A foundational approach in this area is Robust Adversarial Reinforcement Learning (RARL), proposed by Pinto [19]. RARL formalizes the problem as a zero-sum game between a protagonist agent and an adversarial agent, where the adversary actively learns to apply destabilizing forces on the predetermined joints. The protagonist, in turn, learns a policy that is robust to the optimal disruptive strategies employed by the adversary. Later, Pan et al. extended RARL by proposing the Risk-Averse Robust Adversarial Reinforcement Learning (RARARL) algorithm in which the risk-averse protagonist and the risk-seeking adversary alternate control of the executed actions [40]. The introduction of risk-averse behavior significantly reduced test-time catastrophes for protagonist agents trained with a learned adversary, compared to those trained without one. Building on their previous work in [21], Zhang et al. uses the same zero-sum formulation under the ARL framework to train an agent that is robust to perturbations in the observation space [41]. This coadaptation process forces the agent to learn to perform well even under worst-case (or near worst-case) conditions generated during training, thereby improving its generalization to previously unforeseen disturbances.

Even though co-adaptation has advantages over static attacks, Gleave [34] showed that the protagonist trained with an adversary via DRL is not robust to replacement of the adversarial policy at a test time in multi-agent reinforcement learning (MARL) settings [42]. In order to improve robustness in this case, some researchers used a population of adversaries and randomly picked an adversary from the pool to use it to train the protagonist in the min–max formulation [43]. They also showed that using a single adversary does not provide robustness against different adversaries. In a more theoretical study, He et.al. proposed a robust multi-agent Q-learning algorithm (RMAQ) and robust multi-agent actor–critic (RMAAC) algorithms to provide robustness in MARL [44].

As DRL agents are increasingly deployed in complex real-world scenarios, they often process information from multiple sources or modalities. This introduces the challenge of mixed attacks, where adversaries can craft perturbations across one or more input modalities simultaneously. Mandelekar et al. analyzed the individual effect of perturbations on performance: model parameter uncertainty, process noise, and observation noise using probabilistic and gradient-based attacks [45]. Rakhsha et al. also investigated optimal poisoning reward and transition attacks to force the agent to executing a target policy [25]. However, in these studies, the authors did not investigate the collaborative effects of the attacks on agents. More recently, Liu and Lai [46] analyzed attacks in MARL, where an exogenous adversary injects perturbations into the actions and rewards of the agents. They show that combined action and reward poisoning can drive agents toward behaviors selected by the attacker, even without access to the environment. Although recent studies have explored various strategies for attacking and improving the robustness of DRL algorithms, the impact of mixed attacks on the learned policy, as well as their potential use for enhancing robustness, remains an open problem—one that is addressed in this work.

3. Preliminaries

This section introduces the notation and essential concepts required to understand our contribution.

3.1. Notation and Background

A Markov Decision Process (MDP) is a mathematical framework to model decision-making in situations where outcomes are stochastic and/or deterministic under the control of a decision-maker. An MDP is formally defined as a tuple $<S,A,P,R,\gamma >$ where S and A represent the state and action space, and $P:S\times A\to \Delta \left(S\right)$ is the set of probability distribution ($\Delta \left(X\right)$: distributions over the X) over the state space S. $R:S\times A\to \mathbb{R}$ is the reward function, where $r_t=R(s,a)$ is the immediate reward received after taking the action a in state s. The discount factor $\gamma \in (0,1)$ weighs the importance of future rewards against immediate ones. Starting from the initial state $s_0$, the goal of the agent is to find a policy $\pi :S\to A$ that maximizes the expected discounted cumulative reward, known as the state value function, which is given by Equation (1).

$$V_{\pi }\left(s\right):={\mathbb{E}}_{P,a_t\sim \pi }\left[\sum _{t=0}^{\infty }{\gamma }^{t}R(s_t,a_t)|s_0=s\right]$$

(1)

The action–value function, which measures the expected return of taking a specific action in a given state, is defined as in Equation (2).

$$Q_{\pi }(s,a):={\mathbb{E}}_{P,a_t\sim \pi }\left[\sum _{t=0}^{\infty }{\gamma }^{t}R(s_t,a_t)|s_0=s,a_0=a\right]$$

(2)

Similarly, the advantage function that estimates the benefit of choosing a particular action over other actions available to the agent is given by Equation (3).

$$A^{\pi }(s,a):=Q_{\pi }(s,a)-V_{\pi }\left(s\right)$$

(3)

3.2. Zero-Sum Game

A zero-sum Markov game models strategic interaction in which the total payoff across all players always sums to zero. A zero-sum game between two agents, referred to as the protagonist and the adversary, is defined by the tuple $\langle S,A_p,A_a,P,R,\gamma \rangle$, where $A_p$ and $A_a$ denote the action spaces of the protagonist and the adversary, respectively. Since it is a multi-agent game, the transition dynamics P and the reward R depend both on the protagonist policy ${\pi }_p\in {\Pi }_p$ and the adversary policies ${\pi }_a\in {\Pi }_a$. At any time during the interaction, the reward of the adversary is defined as $R(s,\overline{a})=-R(s,a)$, where $\overline{a}$ is the action taken by the adversary, and $R(s,a)$ is the reward received by the protagonist. Equation (4) formalizes a two-player zero-sum game between the protagonist and the adversary in which the protagonist aims to maximize the expected discounted cumulative reward, whereas the adversary seeks to minimize it.

$$R=\arg \underset{{\pi }_p}{max}\underset{{\pi }_a}{min}{\mathbb{E}}_{P,{\pi }_a,{\pi }_p}\left[\sum _{t=0}^{\infty }{\gamma }^{t}R(s_t,a_t,{\overline{a}}_t)\right]$$

(4)

A minimax equilibrium in a two-player zero-sum Markov game exists under the following conditions: the state and action spaces are finite (or compact and convex), the reward functions are bounded, and the presence of a discount factor below one or a finite horizon ensures convergence. Additionally, the transition probabilities must be well defined and the game must satisfy the zero-sum property, which allows stationary policies, depending only on the current state, to achieve equilibrium [47].

3.3. Robust Markov Decision Process (RMDP)

A Robust Markov Decision Process (RMDP) [48] generalizes the standard MDP by incorporating uncertainty in the transition dynamics, aiming to derive policies that optimize performance under worst-case scenarios within a defined uncertainty set. Formally, an RMDP is defined as a tuple $<S,A,P,r,\gamma >$ for small- to mid-sized problems, where $P:S\times A\to \mathcal{U}$ maps each state–action pair to an uncertainty set $\mathcal{U}\subseteq \Delta \left(S\right)$. Here, $P(s_t,a_t,s_{t+1})$ denotes the transition probability of moving from $s_t$ to $s_{t+1}$ under action $a_t$, with the exact value varying within $\mathcal{U}$. The objective is to optimize the policy by maximizing the worst-case expected discounted return, expressed as a minimax optimization problem in Equation (5).

$$V_{\pi }\left(s\right):=\underset{\pi }{max}\underset{P\in \mathcal{P}}{min}{\mathbb{E}}_{a_t\sim \pi }\left[\sum _{t=0}^{\infty }{\gamma }^{t}R(s_t,a_t)|s_0=s\right]$$

(5)

This formulation frames the problem as a zero-sum stochastic game between the agent (protagonist) and an adversary (nature), which selects the worst-case dynamics from the uncertainty set $\mathcal{P}$. Uncertainty sets $\mathcal{U}$ (or globally $\mathcal{P}$) specify the range of possible transition probabilities and are essential for ensuring both tractability and modeling realism [49]. A crucial assumption for the uncertainty set is ($s,a$)-rectangularity, as defined in Equation (6). It states that the uncertainty set can be decomposed into independent uncertainty sets for each state–action pair.

$$\mathcal{P}=\underset{s\in S,a\in A}{⨂}{\mathcal{U}}_{s,a}$$

(6)

This means that the adversary can choose the worst-case transition distribution $P(·|s_t,a_t)$ for each $(s_t,a_t)$ pair independently of the choices made for other pairs [26]. The RMDP formulation presented here inherits the equilibrium existence conditions established for zero-sum games.

3.4. Adversarial Attacks

The Noisy Action Robust Markov Decision Process (NR-MDP) is an extension of the standard MDP framework that accounts for uncertainties or adversarial perturbations during the execution of the action. In an NR-MDP, the action selected by the agent is modified by an adversary before being applied to the environment. This setting can be modeled as a zero-sum game between a protagonist and an adversary, where the protagonist selects action $a_t\sim {\pi }_p(·|s_t)$, and the adversary chooses a perturbation action ${\overline{a}}_t\sim {\pi }_a(·|s_t)$. The action applied in the environment is given by ${\tilde{a}}_t=a_t+\eta {\overline{a}}_t$, where $\eta$ controls the strength of the adversary.

The State-Adversarial Markov Decision Process (SA-MDP) is another type of extension of the standard MDP, where an adversary perturbs the state observation of the protagonist, while the underlying true state of the environment remains unchanged. The SA-MDP models scenarios where sensors are noisy or susceptible to adversarial attacks. In this framework, at each time step t, after the environment transitions to a new state $s_t$, the adversary modifies the observation of the protagonist to a different state ${\tilde{s}}_t\sim {\pi }_a(·|s_t)$ from a set of possible perturbed states $B\left(s_t\right)$, which is typically a ball of a certain size $ϵ$ around the true state $s_t$. The agent then selects an action $a_t\sim {\pi }_p(·\mid {\tilde{s}}_t)$ based on the perturbed state.

Each distinct value of $\eta$ and $\kappa$ defines a different NR-MDP and SA-MDP. The upper row of Figure 1 presents the compact structures of these frameworks.

3.5. Proximal Policy Optimization (PPO)

Proximal Policy Optimization (PPO) [50] is a policy gradient-based optimization algorithm that uses on-policy updates. It employs a clipped objective function to constrain policy updates, promoting stable learning. The standard objective function used in PPO is defined as follows:

$$\begin{array}{cc}\hfill {\mathcal{L}}^{CLIP}\left(\theta \right)=\underset{\left(s_t,a_t,r_t\right)}{\mathbb{E}}& [min(r_t\left(\theta \right)A_t,\hfill \\ \hfill & clip\left(r_t\left(\theta \right),1-\zeta ,1+\zeta \right)A_t\left)\right]\hfill \end{array}$$

(7)

Here, $A_t$ denotes the advantage estimate, $\zeta$ is a clipping parameter, and $r_t\left(\theta \right)$ is the probability ratio defined in Equation (8).

$$r_t\left(\theta \right)={\displaystyle \frac{\pi \left(a_t\mid s_t;\theta \right)}{\pi \left(a_t\mid s_t;{\theta }_{\mathrm{old}}\right)}}$$

(8)

In [50], the original objective function is enhanced with a loss term of the value function, ${\mathcal{L}}^{VF}$, as defined in Equation (9), to improve the estimation of advantage, and an entropy bonus term, $\mathcal{H}$, as given in Equation (10), to encourage exploration.

$${\mathcal{L}}^{VF}\left(\theta \right)={\left(V^{\theta }\left(s_t\right)-V_t^{target}\right)}^2$$

(9)

$$\mathcal{H}\left[\pi (·\mid s)\right]=-\sum _a\pi (a\mid s)log\pi (a\mid s)$$

(10)

The resulting PPO objective is defined as follows:

$$L\left(\theta \right)=\mathbb{E}\left[L^{CLIP}\left(\theta \right)-v_c{L}^{VF}\left(\theta \right)+e_c\mathcal{H}\left[{\pi }_p\left(·|s\right)\right]\right]$$

(11)

Here, $v_c$ and $e_c$ are hyperparameters that weight the value error and entropy objectives, respectively.

4. Methodology

4.1. Problem Formulation

Our framework models mixed adversarial attacks as a zero-sum game between a protagonist and an adversary. In this setting, the adversary operates in a black-box setting, with no access to the model architecture or parameters of the protagonist when generating attacks. The only feedback available to the adversary to evaluate the effectiveness of its attacks is the negative of the reward obtained by the protagonist from the environment. While the protagonist aims to maximize its cumulative reward, the adversary seeks to minimize it, resulting in an adversarial optimization process over the reward function, as in Equation (4).

The ultimate goal of our study is to train a protagonist policy that not only maximizes the reward but also demonstrates robustness against mixed adversarial perturbations. In the framework, the adversarial agent is trained dynamically instead of being fixed or heuristic-based. The adversary receives the state of the environment $s_t$ and selects an action ${\overline{a}}_t\sim {\pi }_a(·|s_t)$, which is used to perturb both the observation and the action of the protagonist before they are perceived or applied, as in the NR-MDP and SA-MDP frameworks.

To study the decision problem under mixed attacks, we define Action and State-Adversarial Markov Decision Process (ASA-MDP) as a tuple ($S,A_p,A_a,P,R,\gamma ,{\mathcal{B}}_s,{\mathcal{B}}_a$). ASA-MDP is a version of RMDP in which perturbations applied by the adversary to states and actions are constrained by predefined sets ${\mathcal{B}}_s\subseteq {\mathbb{R}}^{d_s}$ and ${\mathcal{B}}_a\subseteq {\mathbb{R}}^{d_a}$, where $d_s$ and $d_a$ denote the dimensions of the state and action spaces, respectively. This extension preserves the equilibrium existence properties established in [47] while enabling the study of hybrid attack effects. In an RMDP, the ground-truth transition dynamics are altered by the adversary, while the agent continues to observe the true environmental states and acts accordingly. In contrast, our ASA-MDP formulation allows the adversary to manipulate only the agent’s observations and actions—without altering the ground-truth states—by mapping the protagonist’s current state–action pair to their perturbed counterparts as defined in Equations (12) and (13).

$${\tilde{s}}_t:=s_t·(1+\kappa {\overline{a}}_t^s)\mathrm{where}{\tilde{s}}_t\in {\mathcal{B}}_s$$

(12)

$${\tilde{a}}_t:=a_t+\eta {\overline{a}}_t^a\mathrm{where}{\tilde{a}}_t\in {\mathcal{B}}_a$$

(13)

Here, ${\overline{a}}_t=({\overline{a}}_t^a,{\overline{a}}_t^s)$ denotes the perturbation actions applied to the action and state spaces of the protagonist agent, and the parameters $\eta$ and $\kappa$ control the strength of these perturbations. We employ multiplicative perturbations for states and additive perturbations for actions to reflect their distinct semantic roles and attack characteristics. States represent environmental observations that are naturally subject to proportional distortions (e.g., sensor scaling attacks and lighting variations), where multiplicative perturbations preserve the relative structure of information while testing robustness to scaling-based adversarial manipulations. In contrast, actions represent control commands that are typically corrupted through direct signal injection or bias addition, making additive perturbations more representative of realistic actuator-level attacks. This distinction ensures that perturbations align with domain-specific noise characteristics, enhancing the realism of adversarial attacks. To define the sets of perturbations and limit the perturbation magnitudes (${ϵ}_a,{ϵ}_s$), clipping is applied to the output of the adversarial policy.

$${\mathcal{B}}_s\left(s\right)=\tilde{s}\in \mathcal{S}:\left|\right|\tilde{s}-s{\left|\right|}_{\infty }\le {ϵ}_s$$

(14)

$${\mathcal{B}}_a\left(s\right)=\tilde{a}\in \mathcal{A}:\left|\right|\tilde{a}-a{\left|\right|}_{\infty }\le {ϵ}_a$$

(15)

It is important to note that the reward and transition functions depend directly on the perturbed action ${\tilde{a}}_t$ and the true state $s_t$ and indirectly on the perturbed state ${\tilde{s}}_t$. This indirect dependency arises because the protagonist selects the action $a_t$ based solely on the perturbed state ${\tilde{s}}_t$, which in turn influences both the reward and transition dynamics through ${\tilde{a}}_t$. The explicit forms of the reward and transition functions are provided in Equations (16) and (17).

$$\begin{array}{cc}\hfill r(s_t,{\tilde{a}}_t)& :=r(s_t,a_t+\eta {\overline{a}}_t^a)\hfill \\ \hfill & :=r(s_t,{\pi }_p\left(a_t\right|{\tilde{s}}_t)+\eta {\overline{a}}_t^a)\hfill \\ \hfill & :=r(s_t,{\pi }_p\left(a_t\right|s_t·(1+\kappa {\overline{a}}_t^s))+\eta {\overline{a}}_t^a)\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill P\left(s_{t+1}\right|s_t,{\tilde{a}}_t)& :=P\left(s_{t+1}\right|s_t,a_t+\eta {\overline{a}}_t^a)\hfill \\ \hfill & :=P\left(s_{t+1}\right|s_t,{\pi }_p\left(a_t\right|{\tilde{s}}_t)+\eta {\overline{a}}_t^a)\hfill \\ \hfill & :=P\left(s_{t+1}\right|s_t,{\pi }_p\left(a_t\right|s_t·(1+\kappa {\overline{a}}_t^s))+\eta {\overline{a}}_t^a)\hfill \end{array}$$

(17)

The ASA-MDP simplifies to the NR-MDP when $\kappa =0$, to the SA-MDP when $\eta =0$, and to the classical MDP when both $\kappa =0$ and $\eta =0$. We define the ASA-MDP for tasks with continuous state and action spaces. Instead of solving the intractable minimax optimization problem exactly, our approach focuses on approximating a Nash equilibrium by learning stationary policies ${\pi }_p^{*}$ and ${\pi }_a^{*}$ [51]. The bottom row of Figure 1 illustrates the compact structure of the ASA-MDP framework, which incorporates a learning-based adversary.

4.2. Adversarial Synthesis and Adaptation (ASA)

ASA extends classical adversarial attacks on actions and observations by introducing a mixed-attack approach. As discussed in previous sections, existing studies have typically focused on adversarial attacks targeting a single aspect of the decision-making process. However, in realistic scenarios, noise or uncertainty can simultaneously affect multiple components of the system. Instead of using a single-type adversary, we design the adversarial training framework so that the adversarial agent applies perturbations to both the action and observation spaces. This design encourages the agent to develop robustness against a range of mixed perturbations. The min–max high-level problem of the ASA framework is explicitly formulated in Equation (18), which illustrates the objective function reformulated in three steps: starting from the general form, then incorporating the protagonist and adversary policies, and finally introducing explicit scaling factors.

$$\begin{array}{cc}\hfill & \underset{\theta }{max}\underset{\varphi }{min}\mathbb{E}\left[\sum _{t=0}^T{\gamma }^{t}r\left(s_t,{\tilde{a}}_t\right)\right]\hfill \\ \hfill & \underset{\theta }{max}\underset{\varphi }{min}\mathbb{E}\left[\sum _{t=0}^T{\gamma }^{t}r\left(s_t,{\pi }_p\left(a_t\right|\tilde{s};\theta )+\eta {\pi }_a\left({\overline{a}}_t^a\right|s_t;\varphi )\right)\right]\hfill \\ \hfill & \underset{\theta }{max}\underset{\varphi }{min}\mathbb{E}\left[\sum _{t=0}^T{\gamma }^{t}r\right(s_t,{\pi }_p\left(a_t|s_t·(1+\kappa {\pi }_a\left({\overline{a}}_t^s\right|s_t;\varphi ));\theta \right)\hfill \\ & +\eta {\pi }_a\left({\overline{a}}_t\right|s_t;\varphi )\left)\right]\hfill \end{array}$$

(18)

Here, $\theta$ and $\varphi$ represent the neural network parameters of the protagonist and adversary policies, respectively. In this practical implementation of the Markov game, we approximate the full policy spaces using parameterized policies. Due to the non-convex nature of deep neural networks, the existence of a global minimax equilibrium in the parameter space is not guaranteed. Instead, our adversarial training algorithm seeks to find a local saddle point. This is a common approach in deep reinforcement learning and generative adversarial networks, where algorithms have been shown to empirically find high-quality local solutions despite the lack of global convergence guarantees.

A constant or heuristic-based adversary can be exploited by the protagonist, thereby reducing the effectiveness of adversarial training. To address this limitation, ASA employs an alternate optimization procedure (similar to RARL [19]) in which the protagonist and adversary policies are updated iteratively but not simultaneously. Specifically, during optimization, the parameters of the adversary are held fixed while updating the protagonist policy, and vice versa. This alternating process continues until either an approximate equilibrium is reached or a predefined maximum number of timesteps is exceeded, at which point, the protagonist is considered robust to the adversarial strategies learned during training.

At each time step, the adversary first observes the state $s_t$ and determines the perturbation actions ${\overline{a}}_t^a$ and ${\overline{a}}_t^s$. According to Equation (12), the perturbed state ${\tilde{s}}_t$ is then computed and provided to the protagonist. Based on this perturbed state, the protagonist selects an action $a_t$, which is subsequently perturbed by ${\overline{a}}_t^a$ using Equation (13). The resulting perturbed action ${\tilde{a}}_t$ is applied to the environment, and the corresponding reward $r_t$ is received.

A naive approach to applying mixed perturbations is to assume that the action and observation spaces are uncoupled and to define the adversary’s action space as the sum of the protagonist’s state and action space dimensions, i.e., $d_s+d_a$. Then, at each time step, the sampled perturbation action of the adversary is split into two components corresponding to the perturbations applied to the observation and action spaces, respectively. However, this naive approach overlooks the dependency between the state and action of the protagonist agent, which may cause the adversary to apply excessive or suboptimal perturbations. In the absence of any regularization on the choice or intensity of attacks, the adversary may maximize perturbations to their full extent, potentially leading the protagonist to fail the task entirely.

The PPO algorithm is adopted to guide the parameter updates of both policies. The extended objective function of PPO, as defined in Equation (11), is used to optimize the protagonist policy. The primary challenge in achieving robustness within the adversarial training framework lies in balancing the distinct strengths of different attacks and in regularizing the adversarial policy to manage the associated trade-offs during training. Since PPO is inherently modular, structural constraints or regularization terms can, in principle, be directly integrated into the adversary’s objective, provided that the objective function remains differentiable and compatible with policy gradient updates. However, our preliminary investigations showed that standard regularization approaches designed for black-box scenarios were insufficient to achieve balanced mixed attacks. Although theoretically sound, these methods failed to capture the intricate coupling between state and action perturbations necessary for realistic adversarial settings. The key challenge lies in enabling the adversary to coordinate attacks across both domains, rather than simply maximizing perturbations independently, which ultimately motivated our development of the coupled multi-head architecture.

In order to achieve balanced attacks, we modified the adversary’s PPO policy network by incorporating an intrinsic regularization mechanism that constrains the magnitude of the perturbations and balances their distribution in the state and action spaces. Following the shared feature extraction layers, the ASA-PPO policy network employs two separate action heads: one for generating state perturbations and the other for action perturbations. Since the perturbed state is fed into the protagonist and influences the resulting action, the output of the state-perturbation head is also provided as input to the action-perturbation head, allowing the adversary to account for this dependency. Figure 2 illustrates the multi-head adversarial PPO network structure, which represents a modified version of the classical PPO architecture.

The objective function for the adversary is similar to that in Equation (11). In practice, the policy ratio $r_t\left(\varphi \right)$ is approximately calculated with log probabilities as follows:

$$r_t\left(\varphi \right)={\displaystyle \frac{{\pi }_a\left({\overline{a}}_t\right|s_t;\varphi )}{{\pi }_a\left({\overline{a}}_t\right|s_t;{\varphi }_{old})}}\approx log\left({\pi }_a\left({\overline{a}}_t\right|s_t;\varphi )\right)-log\left({\pi }_a\left({\overline{a}}_t\right|s_t;{\varphi }_{old})\right)$$

(19)

In the two-head PPO actor network used by the adversary agent, the log probability is computed separately for each head, and their mean is then taken, as shown in Equation (20).

$$log\left({\pi }_a\left({\overline{a}}_t\right|s_t)\right)={\displaystyle \frac{log\left({\pi }_a\left({\overline{a}}_t^s\right|s_t)\right)+log\left({\pi }_a\left({\overline{a}}_t^a\right|s_t)\right)}{2}}$$

(20)

Similarly, we approximate the entropy bonus with using sampled minibatches for both action spaces and take the mean of it as follows:

$$\mathcal{H}\left[{\pi }_a(·\mid s_t)\right]={\displaystyle \frac{\left(-{\sum }_{{\overline{a}}^s}{\pi }_a({\overline{a}}_t^s\mid s)log{\pi }_a({\overline{a}}_t^s\mid s_t),-{\sum }_{{\overline{a}}^a}{\pi }_a({\overline{a}}_t^a\mid s)log{\pi }_a({\overline{a}}_t^a\mid s_t)\right)}{2}}$$

(21)

Since the value function depends only on the current state, the value loss is included only once in the adversary objective function (as in Equation (9)), consistent with the original PPO objective in Equation (11). To stabilize the algorithm, the generalized advantage estimation is computed as follows:

$$A^{\pi }(s_t,a_t)={\delta }_t+\gamma \lambda {\delta }_{t+1}+\dots +{\left(\gamma \lambda \right)}^{T-t+1}{\delta }_{T-1}={\delta }_t+\gamma \lambda A^{\pi }(s_{t+1},a_{t+1})$$

(22)

Here, T denotes the trajectory horizon, and the ${\delta }_t=r_t+\gamma V\left(s_{t+1}\right)-V\left(s_t\right)$.

Within the proposed framework, the adversary policy functions as an end-to-end attacker, directly learning optimal perturbations to both states and actions in order to minimize the value of the policy followed by the protagonist. Algorithm 1 outlines the ASA framework in detail. In practice, it is crucial to carefully define and constrain the perturbation budgets ${ϵ}_a$ and ${ϵ}_o$ to ensure convergence to optimal policies. Excessively high budgets may hinder the ability of the protagonist to learn an effective policy for completing the task, while budgets that are too low may fail to induce meaningful robustness. The impact of varying perturbation budget values was empirically evaluated, highlighting the benefits they offer in the context of adversarial learning.

Algorithm 1: Adversarial Synthesis and Adaptation

We train and evaluate the proposed ASA-PPO algorithm on three distinct tasks, comparing its performance with algorithms designed to attack and train robust reinforcement learning agents. These include NR-PPO, a framework for developing policies robust to action attacks; ATLA-PPO, which focuses on robustness to observation attacks; and N-HYBRID-PPO, which employs naive mixed attacks but does not account for state–action dependency, aiming to develop policies robust against combined perturbations.

5. Experiments

In this section, we present experiments conducted on the Mujoco Playground [29], using environments from the DeepMind Control Suite [52] and the MuJoCo physics simulator [53]. As baselines, we selected the random hybrid noise-augmented PPO algorithm (NA-PPO), the PPO implementation of NR-MDP [23] (NR-PPO) for action-based adversarial attacks, and ATLA-PPO [41] for observation-based adversarial attacks. Also, N-HYBRID-PPO, a naive version of our proposed algorithm ASA-PPO, is included as baselines for comparison. All baselines, except NA-PPO, employ learned perturbation strategies, rather than fixed attack patterns, consistent with the approach used in our proposed framework. We train and compare all methods on three continuous control tasks: PendulumSwingup, FingerSpin, and CheetahRun. We normalize the environment’s state $s_t$ and reward $r_t$ to the range [−1.0, 1.0], and we also clip the actions of both the adversarial and protagonist agents to the same range. Continuous perturbations are discretized into five levels with $\eta ,\kappa \in [0.05,0.10,0.15,0.20,0.25]$. The PPO implementation is adapted from the codebase provided in [54], which we modified to integrate the baselines and our proposed algorithm. Our setup enables vectorized PPO training on GPU using JAX [55]. In the simulations, we optimized the hyperparameters of the PPO algorithm in a non-robust setting and applied the same values during the training of adversarial methods.

Table 1. PPO hyperparameters for all methods.

Hyperparameters	Default	Environment-Specific
learning rate	1 × ${10}^{-3}$
discount factor	0.995	FingerSpin: 0.95
entropy cost coefficient	1 × ${10}^{-2}$
value cost coefficient	0.5
max gradient norm	0.5
normalize observation	True
action repeat	1	PendulumSwingup: 4
unroll length	25
# of minibatches	32
# of updates per batch	4	PendulumSwingup: 8
# of environments	2048
# of timesteps	2 × ${10}^8$	FingerSpin: 1 × ${10}^8$

provides a list of these parameters, with some having environment-specific values. In all baseline methods and for all agents (both protagonist and adversary), the neural network architecture is identical: two hidden layers with 256 nodes each, followed by an output layer whose size matches the dimensionality of the corresponding output. The activation function used in all layers is tanh.

We investigate a diverse set of adversarial attacks and their effectiveness in training robust policies. Specifically, our aim is to address the following research questions:

• Question 1: Does robustness to action perturbation attacks imply robustness to observation-perturbation attacks, and vice versa?
• Question 2: Which type of adversarial attack leads the reinforcement learning agent to (near) worst-case performance?
• Question 3: Can training with a mixed adversarial attack enable the protagonist agent to develop simultaneous robustness against action, observation, and mixed perturbations?

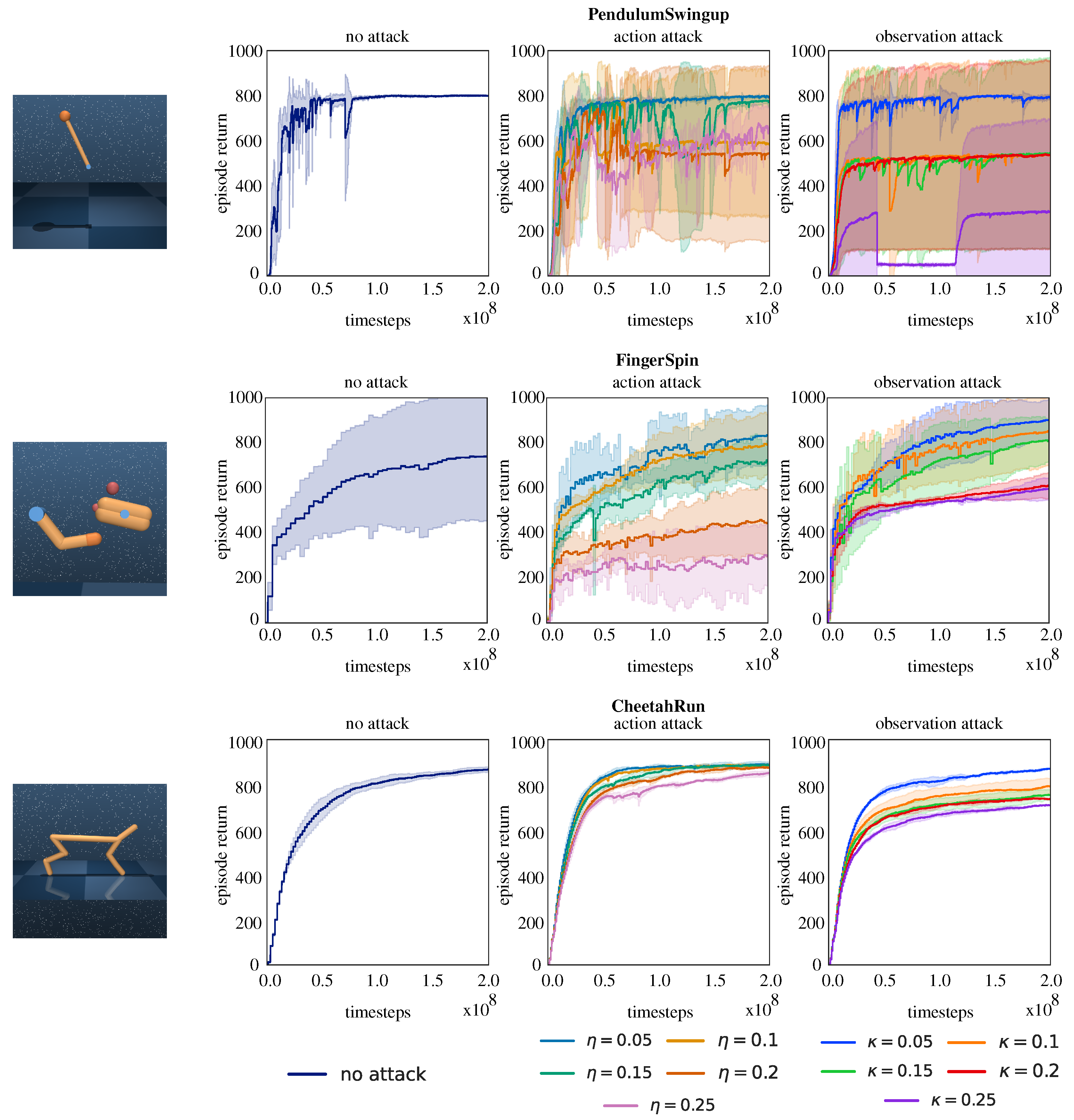
We first trained the baseline action and state-adversarial agents alongside a non-robust agent for each environment and compared their performance. Each training was repeated with five different random seeds. Figure 3 illustrates the training curves, where the solid lines represent the mean performance across all seeds, and the shaded areas indicate the standard deviations. We repeat the trainings for all perturbation levels ($\eta$ and $\kappa$) of the adversaries. The lower performance variability observed in CheetahRun is due to its more stable dynamics, as reported in previous studies [22,56]. Its high-dimensional state–action space and complex multi-joint dynamics provide natural robustness, allowing the agent to compensate for perturbations through alternative movement patterns. In contrast, PendulumSwingup and FingerSpin require precise control and timing, resulting in greater variability under different adversarial attacks.

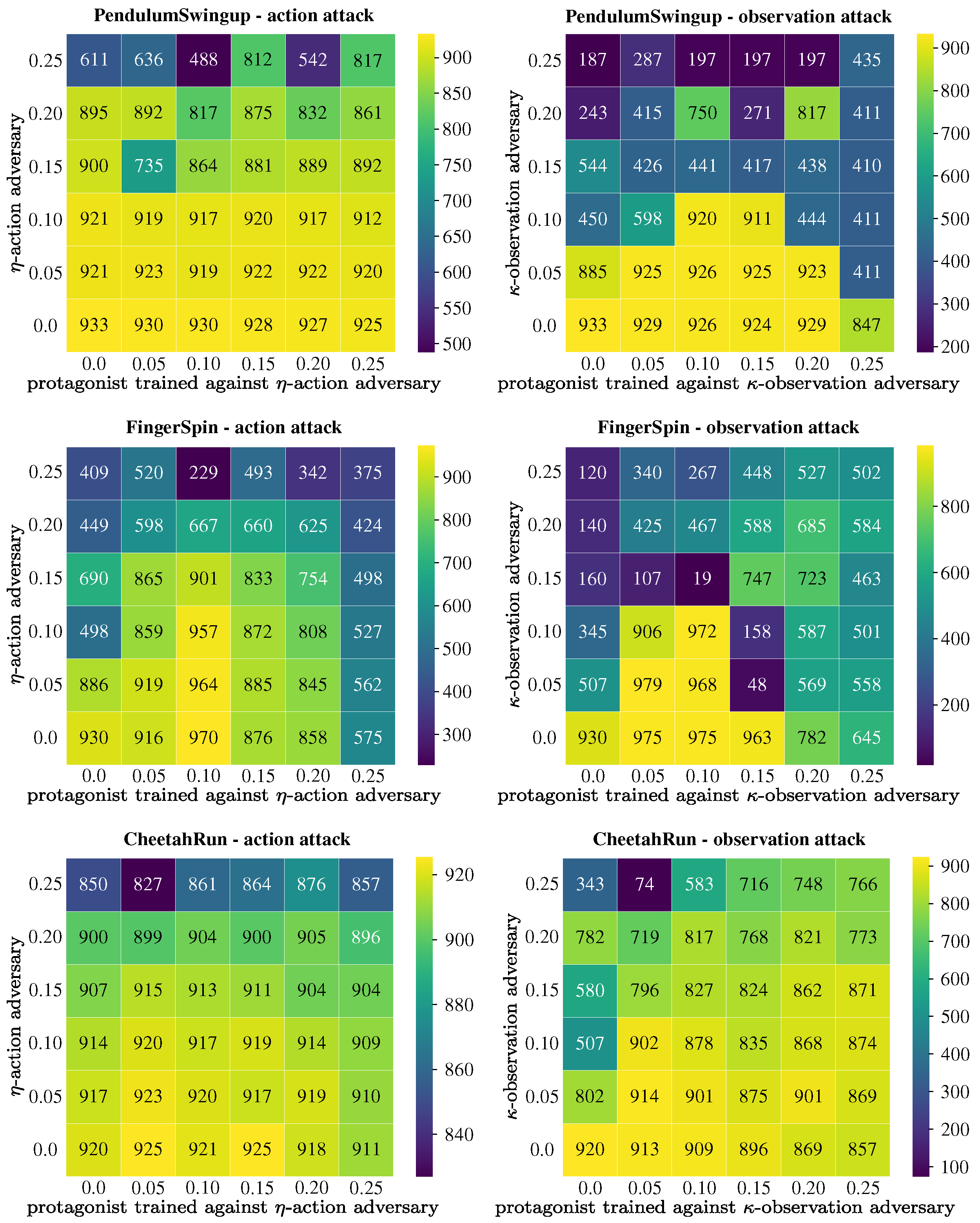
After training was completed, we evaluated the robustified protagonist agents under various perturbation levels, including levels that differed from those used by the adversary during training. Additionally, to evaluate the transferability of robustness, we tested action-robust agents against observation-based adversaries and vice versa. In all cases, the reported scores correspond to the performance of the median-performing agent, evaluated over 20 episodes. These results are presented in Figure 4 and Figure 5, where the horizontal axis indicates the perturbation strength of the adversary used during the training of the protagonist, and the vertical axis represents the perturbation strength of the adversary used during evaluation. The values in the grid represent the test performance of the protagonist when evaluated against the corresponding adversary.

The existing literature in ARL highlights the importance of perturbation magnitude in training robust agents. Excessive perturbation can destabilize the training process, although it may lead to better performance in highly challenging environments. On the other hand, very small perturbations may fail to yield any significant improvements in robustness. An analysis of Figure 4 supports this observation, showing that the average performance of the protagonist agent tends to deteriorate when facing adversaries stronger than those it was trained against, although the resulting performance gap does not exhibit a strictly monotonic pattern. The results also indicate that average performance on certain tasks, such as FingerSpin, degrades more significantly under strong perturbations. In contrast, methods trained with weaker perturbations are better able to preserve performance levels comparable to those achieved under unperturbed conditions.

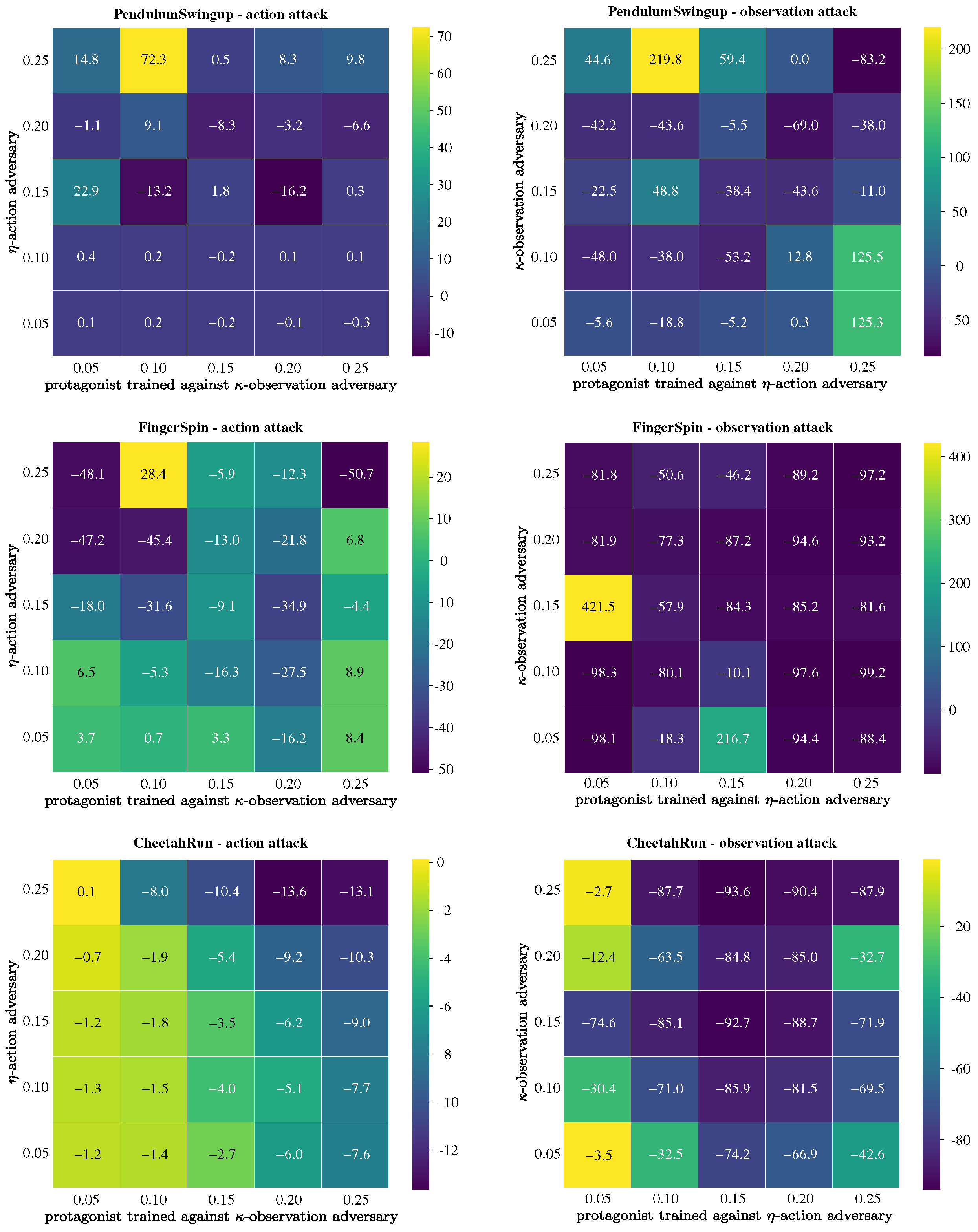
To address the first research question, we evaluate the protagonist agents against different types of adversaries from those against which they were trained to be robust. In Figure 5, we present the relative change in test performance, expressed as percentages, relative to the performance against the original adversary encountered during training. With a few exceptions, performance declines in most test cases, indicating that robustness to action attacks does not necessarily translate to robustness against observation attacks. This highlights the necessity of training robust policies against both types of attack, particularly in real-world scenarios where uncertainties and perturbations simultaneously impact both action and observation spaces.

To address the second research question, we evaluated our adversarial attacks on trained non-robust PPO protagonist agents and shared the results in Figure 6. As shown in the figure, non-robust agents across all environments are most vulnerable to hybrid attacks—especially under large perturbation budgets—and are least sensitive to random and action-based attacks. This indicates that both naive and balanced hybrid attacks are more effective than single-type attacks, highlighting the importance of taking into account such threats when training robust agents.

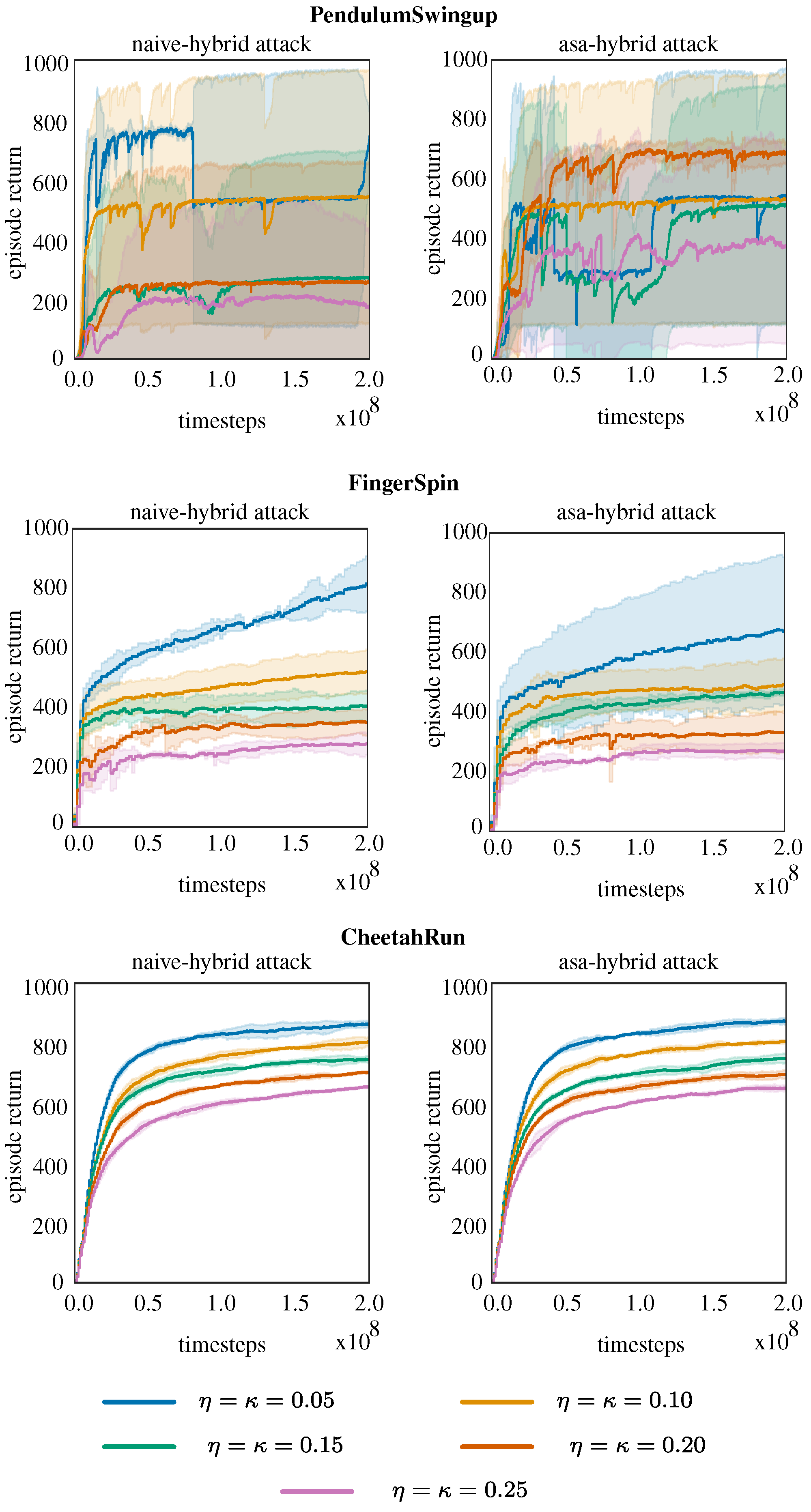
To address the final question, we trained hybrid agents. Figure 7 presents the training curves of the protagonist agents when trained against both a learning naive adversary and an ASA-HYBRID adversary. Without loss of generality, we selected specific perturbation levels for each environment to compare the robustness performance of the baseline methods with their hybrid counterparts. The perturbation levels selected for the experiments are as follows:

• PendulumSwingup and FingerSpin: $\eta =\kappa =0.05$;
• CheetahRun: $\eta =\kappa =0.10$.

Before addressing the final question, we examined the performance trade-off associated with robustness, as shown in

Table 2. Test performance comparison of baselines and hybrid attackers on the vanilla environment without adversary/perturbation. Scores are reported as mean ± standard deviation over 20 independent evaluation episodes (higher is better).

Environment	PendulumSwingup	FingerSpin	CheetahRun
Non-Robust	932.5 ± 41.6	930.9 ± 8.9	919.2 ± 2.6
NA-PPO	759.6 ± 380.2	873.3 ± 13.3	826.7 ± 3.2
NR-PPO	930.2 ± 43.0	916.6 ± 32.1	921.1 ± 2.1
ATLA-PPO	929.1 ± 49.4	975.1 ± 10.9	909.1 ± 3.6
N-HYBRID-PPO	926.1 ± 51.0	961.0 ± 20.5	905.8 ± 5.0
ASA-PPO	931.8 ± 42.0	885.5 ± 15.9	907.6 ± 5.8

. Although N-HYBRID-PPO and ASA-PPO were trained under more severe perturbations compared to other baselines, their performance in non-adversarial environments remains competitive.

To evaluate robustness against hybrid perturbations, we replaced the adversaries used during training with hybrid attackers. The results presented in

Table 3. Test performance comparison of baselines against naive hybrid attacker. Scores are reported as mean ± standard deviation over 20 independent evaluation episodes (higher is better).

Method—Environment	PendulumSwingup	FingerSpin	CheetahRun
NA-PPO	733.9 ± 367.0	248.8 ± 14.6	731.4 ± 27.4
NR-PPO	196.8 ± 393.6	31.0 ± 46.4	592.9 ± 294.0
ATLA-PPO	913.2 ± 65.7	485.5 ± 26.2	786.5 ± 75.4
N-HYBRID-PPO	920.4 ± 59.3	877.4 ± 14.7	906.1 ± 1.9

and

Table 4. Test performance comparison of baselines against ASA-HYBRID attacker. Scores are reported as mean ± standard deviation over 20 independent evaluation episodes (higher is better).

Method—Environment	PendulumSwingup	FingerSpin	CheetahRun
NA-PPO	193.0 ± 386.0	14.5 ± 20.6	518.0 ± 136.6
NR-PPO	792.6 ± 269.5	16.8 ± 15.9	880.1 ± 30.8
ATLA-PPO	440.6 ± 397.0	12.0 ± 11.5	720.2 ± 118.9
ASA-PPO	922.4 ± 61.4	797.6 ± 32.0	915.2 ± 2.8

demonstrate that NR-PPO and ATLA-PPO trained protagonists remain vulnerable to hybrid attacks, underscoring the necessity of a dedicated framework for training against such hybrid adversaries. It is also important to note that the N-HYBRID-PPO algorithm applies unbalanced attacks, primarily targeting observations, causing the agent trained with NR-PPO to perform worse than the agent trained with ATLA-PPO when evaluated against these attacks. Against balanced hybrid attacks, the performance of NR-PPO and ATLA-PPO is more comparable than under unbalanced attacks, yet both remain inferior to that of ASA-PPO.

Finally, we evaluated the protagonist trained against hybrid attacks by testing it against adversaries applying perturbations solely to actions or observations. As shown in

Table 5. Test performance comparison of protagonist trained with hybrid attackers against action-only or observation-only attacker. Scores are reported as mean ± standard deviation over 20 independent evaluation episodes (higher is better).

Environment	PendulumSwingup		FingerSpin		CheetahRun
Method—Attack	Action	Observation	Action	Observation	Action	Observation
N-HYBRID-PPO	921.3 ± 57.4	679.0 ± 401.2	816.7 ± 9.2	806.0 ± 23.1	854.5 ± 7.7	832.7 ± 10.0
ASA-PPO	921.5 ± 57.9	932.2 ± 43.0	875.4 ± 26.3	833.1 ± 24.1	889.9 ± 6.9	868.1 ± 6.3

, across all environments and attack scenarios, the protagonist trained against a balanced adversary consistently outperforms the one trained against a naive-HYBRID adversary.

The N-HYBRID-PPO adversary applies strong perturbations to observations, causing the protagonist agent trained against it to underperform when evaluated against adversaries that perturb only actions or only observations. In contrast, the ASA-PPO adversary learns to balance and diversify its attacks across both modalities, resulting in a protagonist that is more resilient to individual perturbation types. This highlights the importance of balancing mixed adversarial attacks to achieve a realistic and comprehensive measure of robustness. Furthermore, despite being trained under hybrid and stronger adversarial conditions, the proposed ASA-PPO method maintains robust performance across natural (unperturbed), action-only, and observation-only attack scenarios.

As a complementary experiment, we evaluate the robustness of the trained agents under parametric variations in the environment. Figure 8 shows the performance of the agents, including our proposed ASA-HYBRID and N-HYBRID approaches, under changes in environment dynamics—specifically mass and damping scales—in the CheetahRun, PendulumSwingup, and FingerSpin tasks. At the nominal scale of 1.0, all methods attain comparable high episode returns, reflecting effective baseline performance. As the scales deviate from 0.25 to 2.0, returns generally degrade. Our hybrid methods, designed to counter both action and observation perturbations, show moderate resilience at mild deviations but experience sharper declines at extreme values compared to baselines such as NR-PPO and ATLA-PPO. This limited transfer of robustness arises from the distinction between adversarial perturbations, which our methods are trained to mitigate, and parametric changes, which introduce out-of-distribution dynamics not explicitly addressed in the framework.

Notably, the adversarial attack budgets used during training were randomly predetermined to enhance the robustness of our agents. Since the hybrid agents were trained against a stronger adversary—entailing larger budgets for mixed action and observation perturbations—this focus on defending against targeted adversarial threats may reduce their effectiveness in handling parametric variations as it prioritizes adversarial robustness over adaptation to changes in environmental dynamics. While ASA-HYBRID and N-HYBRID excel against malicious attacks, their sensitivity to environment parameter shifts highlights the orthogonality of these robustness dimensions and motivates future work combining adversarial training with domain randomization or explicit parameter adaptation to achieve broader resilience.

6. Conclusions and Future Works

This work addresses the open problem of mixed adversarial attacks on the performance of a learned policy and their use in enhancing robustness. The proposed ASA-PPO algorithm was trained and evaluated on three distinct tasks, showing its effectiveness compared with algorithms designed for single-type attacks. The results indicate that while methods trained with weaker perturbations maintain performance levels comparable to unperturbed conditions, they falter against stronger adversaries. We also demonstrated that robustness to action perturbations does not guarantee robustness to observation attacks and vice versa, highlighting the necessity of training against mixed attacks. Non-robust agents were found to be most vulnerable to hybrid attacks, underscoring the effectiveness of the balanced hybrid attack models. The ASA-PPO method, despite being trained for more severe hybrid attacks, showed robust performance in non-adversarial settings, as well as in action-only and observation-only attack scenarios.

In this work, we employ multiplicative perturbations for states and additive perturbations for actions. Although this separation provides stable and interpretable adversarial settings, aligning perturbation metrics across states and actions would enable more direct comparisons and fairer benchmarking. We view the development of such a unified metric as a valuable avenue for future research. Beyond this, several broader limitations merit discussion, highlighting the areas for further improvement. For instance, the observed sensitivity to parameter variations likely arises because adversarial training against action and observation perturbations does not inherently confer robustness to changes in the underlying system dynamics, highlighting the need for complementary approaches that explicitly account for parametric uncertainty during training.

While the approach is effective, it relies on access to a simulator and currently lacks theoretical guarantees. The framework assumes that the adversary can observe the true state, which may not be feasible in a partially observable setting. Future work could extend this framework to Partially Observable Markov Decision Processes (POMDPs) [57] by incorporating history-based policies into the framework. Furthermore, the balance between the strengths of the state perturbation $\eta$ and the action perturbation $\kappa$ requires a task-specific hyperparameter adjustment as their relative impacts vary significantly. The increased computational load from dual perturbations necessitates efficient implementations, such as parallel rollouts. Another direction is the development of an adaptive adversarial training framework that dynamically adjusts perturbation strength based on the agent’s progress, which could better balance robustness and task performance, as proposed in [27].