Machine Unlearning for Robust DNNs: Attribution-Guided Partitioning and Neuron Pruning in Noisy Environments
Abstract
1. Introduction
- Attribution-guided Data Partitioning: We utilize gradient-based attribution scores to reliably distinguish high-quality samples from noisy samples. Leveraging Gaussian mixture models allows for probabilistic clustering without imposing restrictive assumptions about the noise distributions.
- Discriminative Neuron Pruning via Sensitivity Analysis: We introduce a novel methodology for quantifying neuron sensitivity to noise as a linear regression problem based on neuron activations. This strategy enables precise identification and removal of neurons primarily influenced by noisy samples. This regression-based sensitivity analysis for targeted pruning of noise-sensitive neurons represents a key methodological novelty not explored in prior attribution or pruning studies.
- Targeted Fine-Tuning: After pruning, the network is fine-tuned exclusively on high-quality data subsets, effectively recovering and enhancing its generalization capability without incurring substantial computational costs.
2. Preliminaries
2.1. Supervised Learning
2.2. Attribution Methods
2.3. Neural Network Pruning
2.4. Fine-Tuning
2.5. Machine Unlearning for Robustness
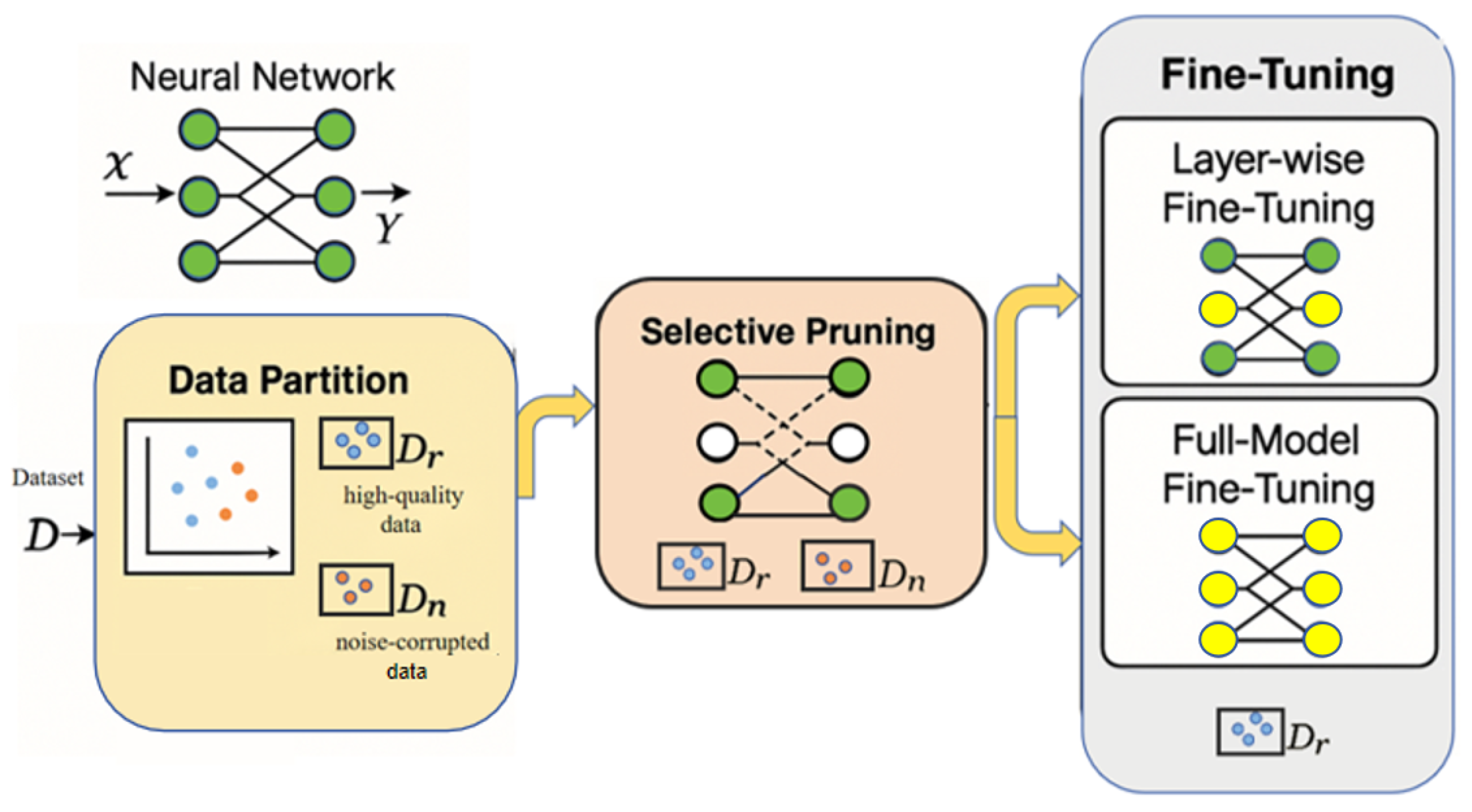
3. Method
3.1. Problem Setup
3.2. Data Partition
3.2.1. Attribution Computation
3.2.2. Attribution-Based Clustering via a Gaussian Mixture Model
3.3. Selective Pruning
3.4. Fine-Tuning
| Algorithm 1: Robust learning via attribution-based pruning (RLAP) |
|
4. Experiment
4.1. Computer Vision
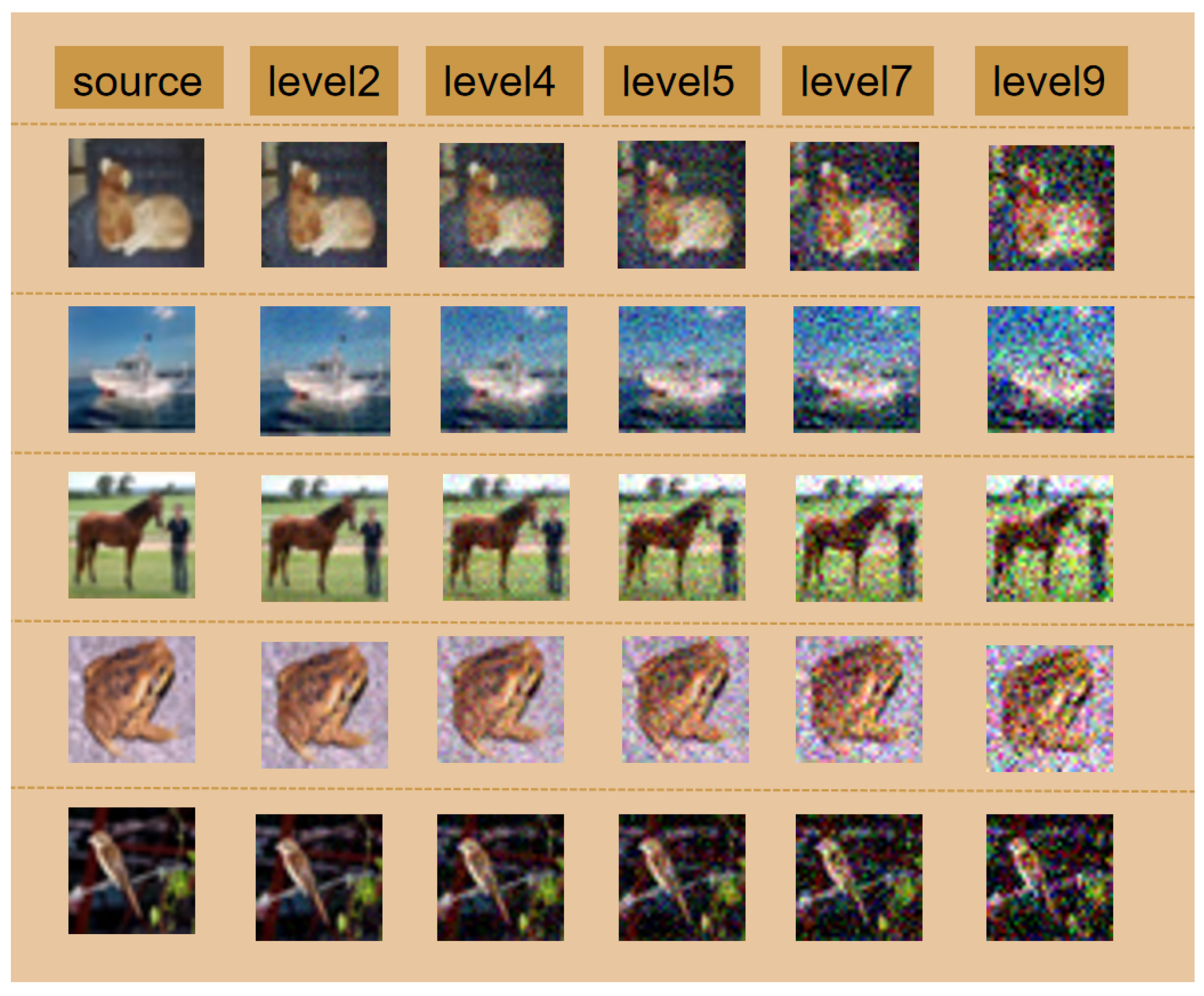
4.1.1. Dataset and Experimental Setup
4.1.2. Results and Analysis
| Train Size | Metric | Method | |||
|---|---|---|---|---|---|
| Initial Model | L-FT | F-FT | Retrain Model | ||
| 50 k | Accuracy | 0.6944 | 0.7508 | 0.8020 | 0.7299 |
| Precision | 0.6962 | 0.7546 | 0.8075 | 0.7450 | |
| F1-score | 0.6962 | 0.7500 | 0.8024 | 0.7298 | |
| Time (s) | 20.48 | 7.98 | 14.44 | 15 | |
| 25 k | Accuracy | 0.6196 | 0.6818 | 0.7253 | 0.6616 |
| Precision | 0.6710 | 0.6835 | 0.7257 | 0.6879 | |
| F1-score | 0.6129 | 0.6812 | 0.7228 | 0.6569 | |
| Time (s) | 11.68 | 3.1 | 5.55 | 5.43 | |
| 12.5 k | Accuracy | 0.5619 | 0.6067 | 0.6124 | 0.5828 |
| Precision | 0.5857 | 0.6112 | 0.6226 | 0.6238 | |
| F1-score | 0.5525 | 0.6070 | 0.6108 | 0.5884 | |
| Time (s) | 6.87 | 2.02 | 3.63 | 4.77 | |
| Size | Metric | Method | Abs | Rms | Freq | Std | Ours |
|---|---|---|---|---|---|---|---|
| 50 k | Acc. | Pruned | 0.4707 | 0.5073 | 0.5480 | 0.4139 | 0.2423 |
| L-FT | 0.7353 | 0.7586 | 0.7742 | 0.7526 | 0.7508 | ||
| F-FT | 0.7966 | 0.7894 | 0.7853 | 0.7988 | 0.8020 | ||
| Prec. | Pruned | 0.4874 | 0.6498 | 0.7284 | 0.5801 | 0.3610 | |
| L-FT | 0.7360 | 0.7579 | 0.7729 | 0.7547 | 0.7546 | ||
| F-FT | 0.7976 | 0.7984 | 0.7867 | 0.7896 | 0.8075 | ||
| F1 | Pruned | 0.4140 | 0.4449 | 0.5425 | 0.4139 | 0.1388 | |
| L-FT | 0.7443 | 0.7579 | 0.7731 | 0.7526 | 0.7500 | ||
| F-FT | 0.7966 | 0.7894 | 0.7827 | 0.7965 | 0.8024 | ||
| 25 k | Acc. | Pruned | 0.5492 | 0.5737 | 0.6169 | 0.5587 | 0.1771 |
| L-FT | 0.2731 | 0.6759 | 0.4683 | 0.6755 | 0.6818 | ||
| F-FT | 0.1285 | 0.6872 | 0.2738 | 0.7073 | 0.7253 | ||
| Prec. | Pruned | 0.6647 | 0.6908 | 0.6808 | 0.6151 | 0.0800 | |
| L-FT | 0.3199 | 0.6742 | 0.5747 | 0.6772 | 0.6835 | ||
| F-FT | 0.4678 | 0.6878 | 0.4358 | 0.7216 | 0.7257 | ||
| F1 | Pruned | 0.6294 | 0.5565 | 0.6203 | 0.5148 | 0.0938 | |
| L-FT | 0.2029 | 0.6741 | 0.4382 | 0.6753 | 0.6812 | ||
| F-FT | 0.0757 | 0.6857 | 0.1942 | 0.7077 | 0.7228 | ||
| 12.5 k | Acc. | Pruned | 0.5567 | 0.5104 | 0.2552 | 0.4735 | 0.1000 |
| L-FT | 0.5859 | 0.5939 | 0.5515 | 0.5704 | 0.6067 | ||
| F-FT | 0.6216 | 0.6040 | 0.6104 | 0.6296 | 0.6124 | ||
| Prec. | Pruned | 0.5929 | 0.5468 | 0.1738 | 0.5442 | 0.0100 | |
| L-FT | 0.5911 | 0.5930 | 0.5574 | 0.5660 | 0.6112 | ||
| F-FT | 0.6223 | 0.6093 | 0.5531 | 0.6345 | 0.6266 | ||
| F1 | Pruned | 0.5490 | 0.5133 | 0.1213 | 0.4416 | 0.0182 | |
| L-FT | 0.5859 | 0.5924 | 0.5531 | 0.5666 | 0.6070 | ||
| F-FT | 0.6196 | 0.6035 | 0.6104 | 0.6309 | 0.6108 |
| Noise Level | Metric | Method | |||
|---|---|---|---|---|---|
| Initial Model | L- FT | F- FT | Retrain Model | ||
| level = 2 | Accuracy | 0.7128 | 0.7741 | 0.7934 | 0.7127 |
| Precision | 0.7309 | 0.7749 | 0.7969 | 0.7499 | |
| F1-score | 0.7126 | 0.7735 | 0.7945 | 0.7123 | |
| Time (s) | 20.48 | 12.28 | 21.86 | 22.72 | |
| level = 3 | Accuracy | 0.7220 | 0.7754 | 0.7966 | 0.6855 |
| Precision | 0.7442 | 0.7749 | 0.7968 | 0.7257 | |
| F1-score | 0.7237 | 0.7746 | 0.7951 | 0.6806 | |
| Time (s) | 20.48 | 12.16 | 21.53 | 22.84 | |
| level = 4 | Accuracy | 0.7079 | 0.7761 | 0.7904 | 0.7058 |
| Precision | 0.7269 | 0.7796 | 0.7932 | 0.7468 | |
| F1-score | 0.7062 | 0.7758 | 0.7902 | 0.7086 | |
| Time (s) | 20.48 | 10.35 | 18.55 | 18.12 | |
| level = 5 | Accuracy | 0.6818 | 0.7754 | 0.7954 | 0.7074 |
| Precision | 0.7370 | 0.7742 | 0.7969 | 0.7448 | |
| F1-score | 0.6857 | 0.7743 | 0.7952 | 0.7131 | |
| Time (s) | 20.45 | 6.94 | 12.69 | 12.45 | |
| level = 6 | Accuracy | 0.6992 | 0.7654 | 0.7923 | 0.7039 |
| Precision | 0.7033 | 0.7672 | 0.7934 | 0.7301 | |
| F1-score | 0.6923 | 0.7656 | 0.7915 | 0.7053 | |
| Time (s) | 20.48 | 8.71 | 15.59 | 18.0 | |
| level = 7 | Accuracy | 0.7292 | 0.7575 | 0.7925 | 0.6307 |
| Precision | 0.7360 | 0.7585 | 0.7946 | 0.6770 | |
| F1-score | 0.7295 | 0.7568 | 0.7922 | 0.6192 | |
| Time (s) | 20.48 | 6.60 | 12.12 | 14.78 | |
| level = 8 | Accuracy | 0.6944 | 0.7508 | 0.8020 | 0.7299 |
| Precision | 0.6962 | 0.7546 | 0.8075 | 0.7450 | |
| F1-score | 0.6962 | 0.7500 | 0.8024 | 0.7298 | |
| Time (s) | 20.48 | 7.98 | 14.44 | 15 | |
| level = 9 | Accuracy | 0.7150 | 0.7657 | 0.8006 | 0.6986 |
| Precision | 0.7482 | 0.7648 | 0.8034 | 0.7562 | |
| F1-score | 0.7183 | 0.7643 | 0.8012 | 0.6945 | |
| Time (s) | 20.61 | 6.67 | 12.21 | 12.02 | |
| Attack Level | Metric | Method | |||
|---|---|---|---|---|---|
|
Initial Model |
L- FT |
F- FT |
Retrain Model | ||
| Attacked Rate = 0.2 | Accuracy | 0.7322 | 0.8135 | 0.8358 | 0.7744 |
| Precision | 0.7658 | 0.8126 | 0.8404 | 0.7936 | |
| F1-score | 0.7338 | 0.8128 | 0.8362 | 0.7733 | |
| Time (s) | 20.14 | 9.32 | 17.21 | 16.89 | |
| Attacked Rate = 0.4 | Accuracy | 0.6991 | 0.7859 | 0.8154 | 0.7410 |
| Precision | 0.7440 | 0.7869 | 0.8177 | 0.7611 | |
| F1-score | 0.7050 | 0.7857 | 0.8154 | 0.7435 | |
| Time (s) | 20.33 | 12.06 | 21.56 | 21.05 | |
| Attacked Rate = 0.5 | Accuracy | 0.7128 | 0.7741 | 0.7934 | 0.7127 |
| Precision | 0.7309 | 0.7749 | 0.7969 | 0.7499 | |
| F1-score | 0.7126 | 0.7735 | 0.7945 | 0.7123 | |
| Time (s) | 20.48 | 12.28 | 21.86 | 22.72 | |
| Attacked Rate = 0.7 | Accuracy | 0.5923 | 0.7100 | 0.7475 | 0.6668 |
| Precision | 0.6582 | 0.7165 | 0.7461 | 0.7095 | |
| F1-score | 0.5990 | 0.7092 | 0.7448 | 0.6672 | |
| Time (s) | 21.06 | 9.23 | 16.19 | 15.92 | |
| Attacked Rate = 0.9 | Accuracy | 0.4896 | 0.5705 | 0.5924 | 0.5184 |
| Precision | 0.5252 | 0.5688 | 0.5875 | 0.5388 | |
| F1-score | 0.4827 | 0.5661 | 0.5838 | 0.5148 | |
| Time (s) | 21.61 | 7.29 | 12.63 | 12.59 | |
| Attack Level | Metric | Method | |||
|---|---|---|---|---|---|
|
Initial Model |
L- FT |
F- FT |
Retrain Model | ||
| Attacked Rate = 0 | Accuracy | 0.7401 | 0.7972 | 0.8292 | 0.7782 |
| Precision | 0.7622 | 0.7952 | 0.8259 | 0.8019 | |
| F1-score | 0.7412 | 0.7955 | 0.8264 | 0.7822 | |
| Attacked Rate = 0.2 | Accuracy | 0.6272 | 0.6842 | 0.6836 | 0.6417 |
| Precision | 0.6870 | 0.6893 | 0.6897 | 0.7362 | |
| F1-score | 0.6340 | 0.6828 | 0.6827 | 0.6603 | |
| Attacked Rate = 0.4 | Accuracy | 0.5159 | 0.5766 | 0.5771 | 0.5054 |
| Precision | 0.6442 | 0.5984 | 0.5999 | 0.7147 | |
| F1-score | 0.5306 | 0.5751 | 0.5757 | 0.5465 | |
| Attacked Rate = 0.6 | Accuracy | 0.4023 | 0.4650 | 0.4642 | 0.3692 |
| Precision | 0.6109 | 0.5148 | 0.5114 | 0.6863 | |
| F1-score | 0.4152 | 0.4609 | 0.4599 | 0.4124 | |
| Attacked Rate = 0.8 | Accuracy | 0.2861 | 0.3549 | 0.3574 | 0.2361 |
| Precision | 0.5767 | 0.4302 | 0.4326 | 0.6693 | |
| F1-score | 0.2750 | 0.3422 | 0.3445 | 0.2487 | |
4.2. Speech Recognition
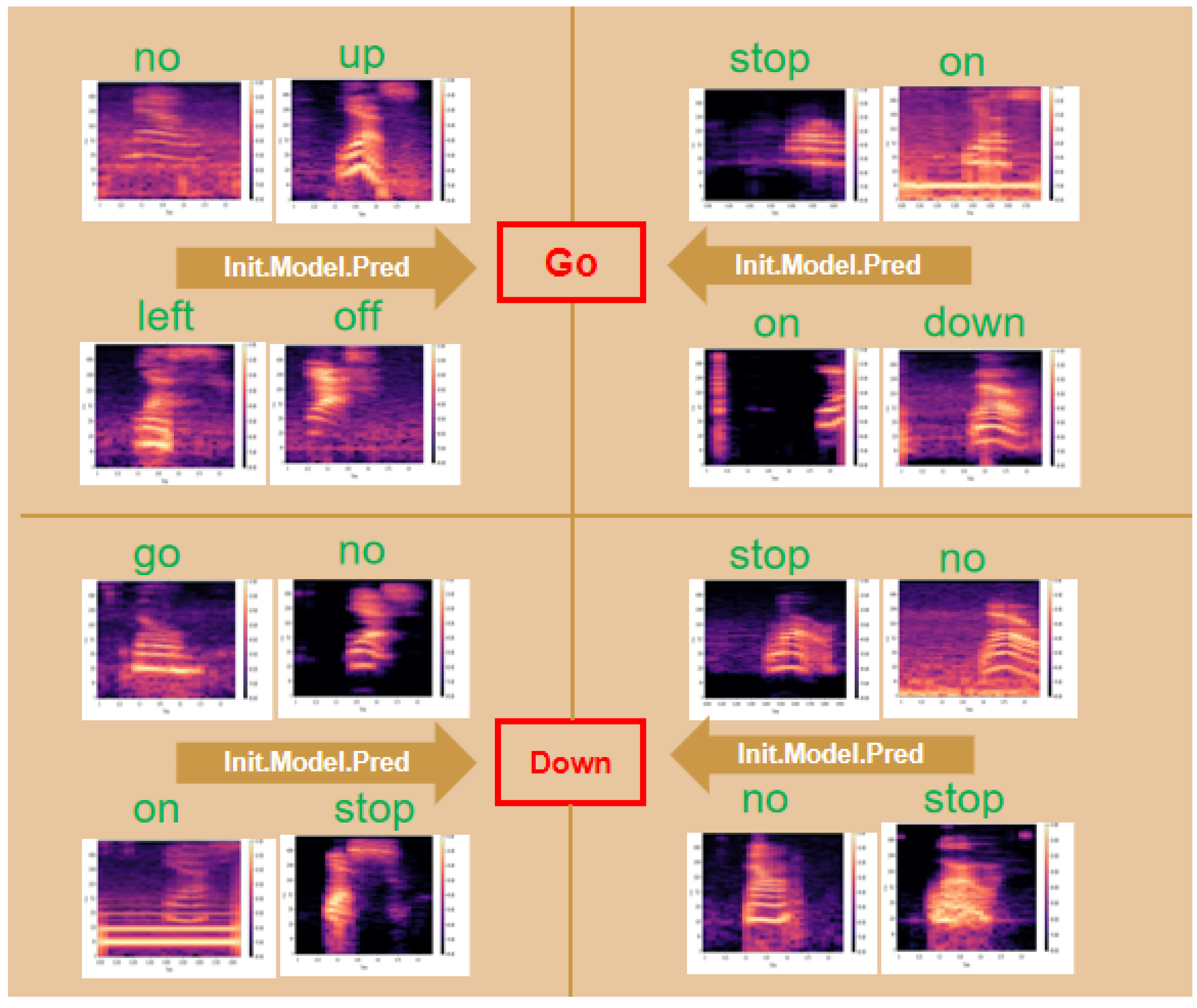
4.2.1. Dataset and Experimental Setup
4.2.2. Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics (NAACL), Minneapolis, MN, USA, 28 July–2 August 2019; pp. 4171–4186. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All You Need. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Graves, A.; Mohamed, A.r.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.r.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N.; et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Hannun, A.; Case, C.; Casper, J.; Catanzaro, B.; Diamos, G.; Elsen, E.; Prenger, R.; Satheesh, S.; Sengupta, S.; Coates, A.; et al. Deep speech: Scaling up end-to-end speech recognition. arXiv 2014, arXiv:1412.5567. [Google Scholar]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Van Der Laak, J.A.; Van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Biggio, B.; Corona, I.; Maiorca, D.; Nelson, B.; Šrndić, N.; Laskov, P.; Giacinto, G.; Roli, F. Evasion attacks against machine learning at test time. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases (ECML-PKDD), Prague, Czech Republic, 23–27 September 2013; pp. 387–402. [Google Scholar]
- Frénay, B.; Verleysen, M. Classification in the presence of label noise: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2013, 25, 845–869. [Google Scholar]
- Northcutt, C.G.; Athalye, A.; Mueller, J. Pervasive label errors in test sets destabilize machine learning benchmarks. arXiv 2021, arXiv:2103.14749. [Google Scholar] [CrossRef]
- Song, H.; Han, B.; Liu, Y.; Sugiyama, M. SELFIE: Refurbishing Unclean Samples for Robust Deep Learning. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 10–15 June 2019; pp. 5907–5915. [Google Scholar]
- Rolnick, D.; Veit, A.; Belongie, S.; Shavit, N. Deep learning is robust to massive label noise. arXiv 2017, arXiv:1705.10694. [Google Scholar]
- Johnson, A.E.; Pollard, T.J.; Shen, L.; Lehman, L.w.H.; Feng, M.; Ghassemi, M.; Moody, B.; Szolovits, P.; Anthony Celi, L.; Mark, R.G. MIMIC-III, a freely accessible critical care database. Sci. Data 2016, 3, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Arpit, D.; Jastrzębski, S.; Ballas, N.; Krueger, D.; Bengio, E.; Kanwal, M.S.; Maharaj, T.; Fischer, A.; Courville, A.; Bengio, Y.; et al. A closer look at memorization in deep networks. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, NSW, Australia, 6–11 August 2017; pp. 233–242. [Google Scholar]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning requires rethinking generalization. arXiv 2016, arXiv:1611.03530. [Google Scholar] [CrossRef]
- Belkin, M.; Hsu, D.; Ma, S.; Mandal, S. Reconciling modern machine-learning practice and the classical bias–variance trade-off. Proc. Natl. Acad. Sci. USA 2019, 116, 15849–15854. [Google Scholar] [CrossRef]
- Amodei, D.; Olah, C.; Steinhardt, J.; Christiano, P.; Schulman, J.; Mané, D. Concrete problems in AI safety. arXiv 2016, arXiv:1606.06565. [Google Scholar] [CrossRef]
- Lee, K.H.; He, X.; Zhang, L.; Yang, L. Cleannet: Transfer learning for scalable image classifier training with label noise. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 5447–5456. [Google Scholar]
- Lai, K.H.; Zha, D.; Wang, G.; Xu, J.; Zhao, Y.; Kumar, D.; Chen, Y.; Zumkhawaka, P.; Wan, M.; Martinez, D.; et al. Tods: An automated time series outlier detection system. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Online, 2–9 February 2021; Volume 35, pp. 16060–16062. [Google Scholar]
- Brodley, C.E.; Friedl, M.A. Identifying mislabeled training data. J. Artif. Intell. Res. 1999, 11, 131–167. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, X.; Chen, Z.; Luo, Y.; Yi, J.; Bailey, J. Symmetric cross entropy for robust learning with noisy labels. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 322–330. [Google Scholar]
- Zhang, Z.; Sabuncu, M. Generalized cross entropy loss for training deep neural networks with noisy labels. Adv. Neural Inf. Process. Syst. 2018, 31, 8792–8820. [Google Scholar]
- Ma, X.; Wang, Y.; Houle, M.E.; Zhou, S.; Erfani, S.; Xia, S.; Wijewickrema, S.; Bailey, J. Dimensionality-driven learning with noisy labels. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 3355–3364. [Google Scholar]
- Han, B.; Yao, Q.; Yu, X.; Niu, G.; Xu, M.; Hu, W.; Tsang, I.; Sugiyama, M. Co-teaching: Robust training of deep neural networks with extremely noisy labels. Adv. Neural Inf. Process. Syst. 2018, 31, 8536–8546. [Google Scholar]
- Jiang, L.; Zhou, Z.; Leung, T.; Li, L.J.; Fei-Fei, L. Mentornet: Learning data-driven curriculum for very deep neural networks on corrupted labels. In Proceedings of the International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 2304–2313. [Google Scholar]
- Patrini, G.; Rozza, A.; Krishna Menon, A.; Nock, R.; Qu, L. Making deep neural networks robust to label noise: A loss correction approach. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1944–1952. [Google Scholar]
- Ren, M.; Zeng, W.; Yang, B.; Urtasun, R. Learning to reweight examples for robust deep learning. In Proceedings of the International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 4334–4343. [Google Scholar]
- Liu, T.; Tao, D. Classification with noisy labels by importance reweighting. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 447–461. [Google Scholar] [CrossRef]
- Xia, X.; Liu, T.; Wang, N.; Han, B.; Gong, C.; Niu, G.; Sugiyama, M. Are anchor points really indispensable in label-noise learning? Adv. Neural Inf. Process. Syst. 2019, 32, 6838–6849. [Google Scholar]
- Li, J.; Wong, Y.; Zhao, Q.; Kankanhalli, M.S. Learning to learn from noisy labeled data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 5051–5059. [Google Scholar]
- Shu, J.; Xie, Q.; Yi, L.; Zhao, Q.; Zhou, S.; Xu, Z.; Meng, D. Meta-weight-net: Learning an explicit mapping for sample weighting. Adv. Neural Inf. Process. Syst. 2019, 32, 1919–1930. [Google Scholar]
- Cao, Y.; Yang, J. Towards making systems forget with machine unlearning. In Proceedings of the IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 17–21 May 2015; pp. 463–480. [Google Scholar]
- Bourtoule, L.; Chandrasekaran, V.; Choquette-Choo, C.A.; Jia, H.; Travers, A.; Zhang, B.; Lie, D.; Papernot, N. Machine unlearning. In Proceedings of the IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021; pp. 141–159. [Google Scholar]
- Graves, L.; Nagisetty, V.; Ganesh, V. Amnesiac machine learning. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Online, 2–9 February 2021; Volume 35, pp. 11516–11524. [Google Scholar]
- Thudi, A.; Jia, H.; Shumailov, I.; Papernot, N. On the necessity of auditable algorithmic definitions for machine unlearning. In Proceedings of the USENIX Security 22, Boston, MA, USA, 10–12 August 2022; pp. 4007–4022. [Google Scholar]
- Golatkar, A.; Achille, A.; Soatto, S. Eternal sunshine of the spotless net: Selective forgetting in deep networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 9304–9312. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 3319–3328. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W.J. Learning both weights and connections for efficient neural networks. Adv. Neural Inf. Process. Syst. 2015, 28, 1135–1143. [Google Scholar]
- Louizos, C.; Welling, M.; Kingma, D.P. Learning sparse neural networks through L0 regularization. arXiv 2017, arXiv:1712.01312. [Google Scholar]
- Howard, J.; Ruder, S. Universal language model fine-tuning for text classification. arXiv 2018, arXiv:1801.06146. [Google Scholar] [CrossRef]
- Ruder, S. Neural Transfer Learning for Natural Language Processing. Ph.D. Thesis, NUI Galway, Galway, Ireland, 2019. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 818–833. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar]
- Ghorbani, A.; Abid, A.; Zou, J. Interpretation of neural networks is fragile. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3681–3688. [Google Scholar]
- Wachter, S.; Mittelstadt, B.; Russell, C. Counterfactual explanations without opening the black box: Automated decisions and the GDPR. Harv. JL Tech. 2017, 31, 841. [Google Scholar] [CrossRef]
- Kindermans, P.J.; Hooker, S.; Adebayo, J.; Alber, M.; Schütt, K.T.; Dähne, S.; Erhan, D.; Kim, B. The (un) reliability of saliency methods. In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Springer: Cham, Switzerland, 2019; pp. 267–280. [Google Scholar]
- Sixt, L.; Granz, M.; Landgraf, T. When explanations lie: Why many modified bp attributions fail. In Proceedings of the International Conference on Machine Learning (ICML), Online, 13–18 July 2020; pp. 9046–9057. [Google Scholar]
- Geva, M.; Schuster, R.; Berant, J.; Levy, O. Transformer Feed-Forward Layers Are Key-Value Memories. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing (EMNLP), Punta Cana, Dominican Republic, 7–11 November 2021; pp. 5484–5495. [Google Scholar]
- Alain, G.; Bengio, Y. Understanding intermediate layers using linear classifier probes. In Proceedings of the International Conference on Learning Representations (ICLR) Workshop, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Morcos, A.S.; Barrett, D.G.; Rabinowitz, N.C.; Botvinick, M. On the importance of single directions for generalization. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Hooker, S.; Erhan, D.; Kindermans, P.J.; Kim, B. A benchmark for interpretability methods in deep neural networks. Adv. Neural Inf. Process. Syst. 2019, 32, 9737–9748. [Google Scholar]
- Agarwal, C.; D’souza, D.; Hooker, S. Estimating example difficulty using variance of gradients. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 10368–10378. [Google Scholar]
- Sanh, V.; Wolf, T.; Rush, A. Movement pruning: Adaptive sparsity by fine-tuning. Adv. Neural Inf. Process. Syst. 2020, 33, 20378–20389. [Google Scholar]
- Frankle, J.; Carbin, M. The lottery ticket hypothesis: Finding sparse, trainable neural networks. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Molchanov, P.; Mallya, A.; Tyree, S.; Frosio, I.; Kautz, J. Importance estimation for neural network pruning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 11264–11272. [Google Scholar]
- Theis, L.; Korshunova, I.; Tejani, A.; Huszár, F. Faster gaze prediction with dense networks and fisher pruning. arXiv 2018, arXiv:1801.05787. [Google Scholar] [CrossRef]
- Pearson, K. Contributions to the mathematical theory of evolution. Philos. Trans. R. Soc. Lond. A 1894, 185, 71–110. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. k-Means++: The Advantages of Careful Seeding; Technical Report; Stanford: Stanford, CA, USA, 2006. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Fraley, C.; Raftery, A.E. Model-based clustering, discriminant analysis, and density estimation. J. Am. Stat. Assoc. 2002, 97, 611–631. [Google Scholar] [CrossRef]
- Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv 2015, arXiv:1510.00149. [Google Scholar]
- Pochinkov, N.; Schoots, N. Dissecting language models: Machine unlearning via selective pruning. arXiv 2024, arXiv:2403.01267. [Google Scholar] [CrossRef]

| Stage | Performance Metrics | Time (s) | |||
|---|---|---|---|---|---|
| Accuracy (%) | Precision (%) | F1 (%) | Top-3 Acc (%) | ||
| Initial Model | 64.20 | 64.03 | 64.02 | 89.92 | 6.90 |
| L-FT | 66.94 | 76.34 | 77.01 | 90.45 | 1.32 |
| F-FT | 71.21 | 72.90 | 71.92 | 93.41 | 2.85 |
| Retrain Model | 65.37 | 65.31 | 65.27 | 90.38 | 3.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, D.; Chen, G.; Feng, S.; Ling, Y.; Zhu, H. Machine Unlearning for Robust DNNs: Attribution-Guided Partitioning and Neuron Pruning in Noisy Environments. Mach. Learn. Knowl. Extr. 2025, 7, 95. https://doi.org/10.3390/make7030095
Jin D, Chen G, Feng S, Ling Y, Zhu H. Machine Unlearning for Robust DNNs: Attribution-Guided Partitioning and Neuron Pruning in Noisy Environments. Machine Learning and Knowledge Extraction. 2025; 7(3):95. https://doi.org/10.3390/make7030095
Chicago/Turabian StyleJin, Deliang, Gang Chen, Shuo Feng, Yufeng Ling, and Haoran Zhu. 2025. "Machine Unlearning for Robust DNNs: Attribution-Guided Partitioning and Neuron Pruning in Noisy Environments" Machine Learning and Knowledge Extraction 7, no. 3: 95. https://doi.org/10.3390/make7030095
APA StyleJin, D., Chen, G., Feng, S., Ling, Y., & Zhu, H. (2025). Machine Unlearning for Robust DNNs: Attribution-Guided Partitioning and Neuron Pruning in Noisy Environments. Machine Learning and Knowledge Extraction, 7(3), 95. https://doi.org/10.3390/make7030095






