A Novel Prediction Model for Multimodal Medical Data Based on Graph Neural Networks

Abstract

Multimodal medical data provides a wide and real basis for disease diagnosis. Computer-aided diagnosis (CAD) powered by artificial intelligence (AI) is becoming increasingly prominent in disease diagnosis. CAD for multimodal medical data requires addressing the issues of data fusion and prediction. Traditionally, the prediction performance of CAD models has not been good enough due to the complicated dimensionality reduction. Therefore, this paper proposes a fusion and prediction model—EPGC—for multimodal medical data based on graph neural networks. Firstly, we select features from unstructured multimodal medical data and quantify them. Then, we transform the multimodal medical data into a graph data structure by establishing each patient as a node, and establishing edges based on the similarity of features between the patients. Normalization of data is also essential in this process. Finally, we build a node prediction model based on graph neural networks and predict the node classification, which predicts the patients’ diseases. The model is validated on two publicly available datasets of heart diseases. Compared to the existing models that typically involve dimensionality reduction, classification, or the establishment of complex deep learning networks, the proposed model achieves outstanding results with the experimental dataset. This demonstrates that the fusion and diagnosis of multimodal data can be effectively achieved without dimension reduction or intricate deep learning networks. We take pride in exploring unstructured multimodal medical data using deep learning and hope to make breakthroughs in various fields.

1. Introduction

Advancements in medical technology are making disease detection more scientific and refined, providing crucial data that accurately reflects the true and direct state of diseases [1,2]. This is particularly important for diagnosing complex diseases with multiple pathogenic factors. In cases where complex diseases with multiple contributing factors and high pathogenic hazards are involved, combining multiple detection methods is essential to ensuring a safe and accurate diagnosis process [3]. By leveraging the strengths of each detection method and avoiding their potential limitations, healthcare professionals can achieve more reliable and comprehensive diagnostic results, reducing the risk of misdiagnosis or overlooking critical information. Inevitably, numerous multimodal medical data will be generated by various aspects of this medical process, such as intelligent decision support systems [4], Clinical Concept [5], oncology [6], medical imageology [7], and so on.

Multimodal medical data refers to medical data from two or more sources or storage formats, such as clinical data, imaging, genetics, pathology, molecular biology, etc. [8]. Some researchers have studied the characteristics of multimodal medical data. Kline et al. [9] described the diversity of forms and modalities of multimodal medical data in their study. Stahlschmidt et al. [10] discussed the complexity and multidimensionality of multimodal medical data. Azam et al. [11] and Guo et al. [12] also emphasized the diversity of formats of multimodal medical data in medical imageology research. The processing of multimodal medical data faces challenges, such as data fusion, dimensionality reduction, and feature complexity reduction [13]. Chen et al. [14] proposed a prediction model for breast cancer prognosis based on the clinical and gene expression data. This model combines multiple feature selection with an attention mechanism to extract features and reduce feature complexity, then builds a deep neural network to predict the breast cancer prognosis. Yang et al. [15] proposed a multimodal medical data diagnosis model for clinical and breast cancer medical image data. The model design reduces the complexity of clinical data through feature selection and logical regression classification based on a random forest, and combines a multi-level deep neural network to extract the medical image features to finally predict the recurrence and metastasis risk of HER2-positive breast cancer. Alizadehsani et al. [16] used a paradigm of “feature selection + dimensionality reduction + prediction” to study multimodal data fusion and diagnosis of coronary artery disease, which represents the mainstream approach in the current research. In a 2018 study [16], Alizadehsani et al. firstly extracted features from ultrasound and echo data and then used a “dimensionality reduction + prediction” approach to sort the important features to achieve the goal of reducing complexity. Based on the sorting results, the important feature combinations were selected and input into a machine learning classifier for coronary artery disease classification. Golovenkin et al. [17] developed an intelligent evaluation system for predicting early complications of myocardial infarction. After feature selection, the system reduced the dimensionality of high-dimensional and multimodal cardiovascular detection data, and built a classification model based on multi-layer deep networks. Finally, the classification of complications of myocardial infarction was achieved, with an average accuracy of over 90%. In a 2022 study [18], Yavru et al. also used a paradigm of “feature selection + dimensionality reduction + prediction” to study the classification of complications on the same dataset used by Golovenkin et al. They designed a multimodal data fusion and disease classification model based on deep learning. The overall accuracy of the model classification was improved to 92%. In addition, Hu et al. [19] developed an Enterprise Service Bus (ESB) integration platform for multimodal medical data fusion from the perspective of hardware research on multimodal medical data fusion. This platform starts from the interface and data format standardization of various medical data platforms, builds a unified data output integration platform at the source of data generation, realizes the fusion of multimodal diagnosis and treatment data, and thus builds an intelligent decision-making system that improves the utilization of medical resources. This approach requires large-scale upgrades and iterations of existing hardware devices, which will face significant challenges in terms of economic cost and operability.

To summarize, the current methods for processing multimodal medical data typically involve initially extracting features from all the data, followed by applying traditional machine learning algorithms or deep learning networks for tasks such as classification and clustering. These methods can be summarized as following a pattern of “feature selection + dimensionality reduction + prediction”. However, these methods present several issues. Traditional machine learning algorithms or neural network models often exhibit poor classification performance when applied to high-dimensional data that has undergone feature selection, necessitating the need for data dimensionality reduction. The outcome of the dimensionality reduction process possesses a certain degree of randomness and is influenced by the final classification result. As a result, the interpretability of the dimensionality reduction result is limited when evaluated in reverse based on the final disease classification result. Additionally, the dimensionality reduction may lead to the loss of critical information within the data. Furthermore, the data’s dimension is often overlooked during processing, potentially resulting in the loss of physical information within the data. In addition, complex deep learning networks require a large amount of model training data and training resources (time resources, computing power resources) to support them. This paper proposes a new algorithm based on a graph neural network (GNN) for processing multimodal medical data. Compared to traditional methods, it can leverage the expressive advantage of graph data to preserve the information in the data as much as possible without a dimensionality reduction, and achieves the fusion and disease prediction of multimodal medical data.

2. Materials and Methods

As mentioned above, we need to solve the problems of diverse data modalities and complex data structures, while trying to avoid the loss of useful information as much as possible. We will introduce graph-structured data theory for solving the above problems.

2.1. Graph Data Structure for Feature Expression

Conventional AI algorithms, including traditional neural networks and machine learning algorithms, usually process Euclidean space data with typical spatial structures. In Euclidean space data, for example, text and speech data are one-dimensional sequence data structures [20], and image data [21,22] are typically rectangular structures. However, in reality, much data do not have the typical spatial structures belonging to non-Euclidean spaces, namely a graph data structure (GDS), for example, knowledge maps, sensor networks in communications, regulatory networks in genetics, and so on. In a GDS, the connections between nodes may not be fixed, forming a complex topology without a fixed node order, or the data present a dynamic multimodal structure.

A GDS typically consists of two important components, i.e., nodes and edges, which are used to represent the relationships between objects (or entities). The graph structure contains a set of nodes and edges that connect these nodes (the edges here can be directional or undirected). Graph structures have a stronger ability to express features [23,24,25]. A node can serve as a unit for storing entity information; that is to say, the stored information contains the feature description of the entity. And edges can also store information; the storage method is represented by the direction and thickness of the edges. Taking an undirected graph as an example, the feature expression ability of the GDS is shown in Equation (1). Specifically, the undirected graph $\mathrm{G}=(V,E)$, where V and E represent the nodes and the edges in the graph, respectively. V_n describes the n-th node in the GDS with n nodes, $v_{fn}$ describes the n-th feature of n-th node, $e_{mn}$ describes the edge between the m-th and n-th nodes, and $w_{mn}$ describes the connection weight between the m-th and n-th nodes.

$$\begin{gathered} \mathrm{G}=(V,E) \\ V=\{V_1,V_2,\dots ,V_n\} \\ E=\{E_1,E_2,\dots ,E_n\} \\ {V}_n=\{v_{f1},v_{f2},\dots ,v_{fn}) \\ {E}_n=\left(\begin{array}{ccc}{e}_{11}& \dots & e_{1m}\\ ⋮& \ddots & ⋮\\ e_{n1}& \dots & e_{\mathrm{nm}}\end{array}\right)\left(\begin{array}{ccc}{w}_{11}& \dots & w_{1m}\\ ⋮& \ddots & ⋮\\ w_{n1}& \dots & w_{nm}\end{array}\right) \end{gathered}$$

(1)

2.2. GDS Construction Based on Similarity Measurement

In this paper, we propose a GDS construction method based on a similarity measurement, which constructs a GDS where each patient is represented as a node, and the similarity between patients is described by the edges, as shown in Figure 1. All patients exist in a GDS as the nodes. However, the GDS is not fully connected, and whether a node has neighbors, that is, whether there are edges between the nodes, is based on their similarity measure. If they have a strong correlation, edges between them exist; otherwise, they do not exist.

In statistics, a similarity measure (or similarity function) is crucial for quantifying the similarity between different samples or sets [26]. Common methods include the Pearson correlation coefficient, Euclidean Distance [27], Manhattan Distance, Chebyshev Distance, and Information Entropy [28]. The Pearson correlation coefficient assesses the degree of correlation between two variables and is widely used across various fields, such as machine learning, statistics, and data analysis, for evaluating similarity. The range of the Pearson correlation coefficient r is $r\in [-\mathrm{1,1}]$. When $r=-1$, it indicates that the two variables (sets) are completely negatively correlated. When the Pearson correlation coefficient $r=1$, it indicates that the two variables (sets) are completely positively correlated. The Pearson correlation is shown in Equation (2), where X and Y represent two variables, and $\overline{X}$ and $\overline{Y}$, respectively, represent the standard deviation of variable X and variable Y.

$$r={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{(X_i-\overline{X})}^2}}\sqrt{{\displaystyle {\sum }_{i=1}^n{(Y_i-\overline{Y})}^2}}}}$$

(2)

2.3. The Learning of GDS Using a Graph Neural Network

A GNN is a type of neural network proposed by Gori et al. in 2005 [29]. Compared with conventional neural networks, its advantage is its ability to process a GDS. A GNN can collect and extract the features from nodes and edges in a GDS, and construct a corresponding feature expression model. A GNN can achieve model learning tasks [30], including classification [31], prediction [32], segmentation [33,34], etc. GNNs have been proven to be effective for disease prediction. Mohanraj et al. [35] proposed a new method for weighted feature extraction and GNN classification based on a Graph Wavelet Transform. By calculating the weighted correlation between the data and utilizing machine learning algorithms, it can effectively predict the severity of Parkinson’s disease and significantly improve the prediction accuracy. Hossain et al. [36] introduced a comorbidity network approach to assess the risk of cardiovascular disease in patients with type 2 diabetes, utilizing features derived from foundational networks. Meanwhile, the research by Xuan et al. [37] and Lee et al. [38] suggests that GNNs can be applied to analyze medical images, such as X-rays, CT scans, and MRIs, to detect potential abnormalities or diseases.

GraphSAGE (Graph Sample and aggreGatE) is a type of spatial-based GCN [39] with a strong generalization ability and aggregation operation. A GraphSAGE model mainly completes three stages of learning tasks, namely, sampling, aggregation, and node embedding. Object node(s) are determined through multi-level sampling and aggregating of adjacent nodes, then the features are captured and fused through the aggregate function. The sampling task collects the node information and connection information between the nodes. The aggregation function performs the aggregation task with a certain rule and generates a feature vector. Finally, the feature vector is processed as the node embedding, and input into the downstream classifiers to achieve the learning task. Figure 2 depicts the node classification task of GraphSAGE, and the following is an introduction to the detailed learning process of the model.

• Sampling: The model first samples the neighborhood node information of the original object node. The rule of sampling is as follows: firstly, set one is the original object node, and the remaining n nodes are the neighboring nodes. Set m as a fixed number of nodes for each sampling, and if n > = m, perform sampling without dropout; otherwise, perform sampling with dropout until m nodes are sampled. It is worth noting that GraphSage can achieve significant generalization of non-adjacent nodes without the involvement of the whole graph structure during the sampling process.
• Aggregation: For the sampled information, the next step is to aggregate it according to a specific rule. This process involves combining the feature vectors of a node and its neighbors, along with their respective weights, to capture the graph’s structure and generate new neighborhood embeddings. The aggregator function is described by Equation (3). In a GraphSAGE model, there are three primary types of aggregators: the mean aggregator, LSTM aggregator, and pooling aggregator. Additionally, convolution-based GCN operators can also be utilized as aggregators.

  $$h_v^k=\sigma [W^{(k)}\cdot concat(h_v^{k-1},AGGREGAT{E}_k(h_u^{k-1}\forall u\in N(v)))]$$

  (3)

  where σ represents the non-linear activation function, $W^k$ represents the weight matrix of $k$ aggregators, $\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}(·)$ represents vector concatenation, and $h_v^k$ represents the feature vector of the node.

• Prediction: The results will be input into the downstream machine learning classifiers for training, enabling node prediction.

2.4. Disease Prediction Model Based on GraphSAGE

A new algorithm, EPGC (feature Extraction, Pretreatment, Generate graph, and node Classification), is proposed in this paper for the fusion and disease prediction of multimodal medical data. The EPGC consists of two parts: multimodal data fusion and prediction, as shown in Figure 3. Firstly, fusing the multimodal data, the model preprocesses the diverse modalities and complex structures of data, and is mainly responsible for feature selection and quantification of non-numerical data. The preprocessing method effectively addresses the challenges related to unstructured data processing and inconsistent format standardization, and the purpose is to convert the multimodal data or its features into numerical data for the next step of constructing the GDS. The constructed GDS can better preserve the feature information of multimodal medical data. The feature extraction is based on AI algorithms to extract the effective features. For example, whether there are abnormal bands in an ECG, whether there are regions of interest in the image data, etc. Meanwhile, normalization is also essential. Then, the preprocessed data is used to construct a GDS using the patients as the nodes and the similarity between the patients as the edges, thereby fusing the multimodal data into the GDS, that is, merging some scattered multimodal data into one gathered GDS. Finally, a graph neural network learning task based on node classification is applied to the fused graph data to achieve the diagnosis of patient diseases.

EPGC algorithm described in Algorithm 1. For multimodal medical data $N\left(X_i\right)=\left\{X_1,X_2\dots {,\mathrm{X}}_{\mathrm{m}}\right\}$ (m samples), as the graph can only process numerical data, the EPGC first needs to convert the non-numerical multimodal medical data $\mathrm{N}\left({\mathrm{X}}_{\mathrm{i}}\right)$ into numerical data, which requires AI-based feature extraction algorithms to obtain the numerical data $N_i$. Then, $N_i$ is normalized to avoid inaccurate classification caused by inconsistent dimensions. Next, calculate the Pearson coefficient between each sample in $N_i$, and determine whether there are edges between the samples based on the value of Pearson coefficient $r_{ij}$ to construct the GDS. Next, select any target node in the GDS for sampling; collect information on the nodes and edges in the GDS; generate a feature vector $h_v^k$, aggregate and embed the feature vectors; and finally use the downstream classifiers to predict the node types, i.e., patient disease prediction.

Algorithm 1: EPGC algorithm

Input: Multimodal data $N\left(X_i\right)=\{X_1,X_2,\dots X_m\}$; the depth of graph; weight matrix $W^k,\forall k\in \{\mathrm{1,2},\dots ,K\}$; non-linear activation function $\mathsf{\sigma }$; aggregator. Adjacency function: $N:\upsilon \to 2^{\upsilon }$. Output: ${\mathit{z}}_v,v\in V$, the result of the following prediction: 1: Extract features from non-numerical data in $N\left(X_i\right)$ to obtain numerical data $N_i$. 2: Normalize $N_i$, $N_i\to {\tilde{N}}_i$. 3: Calculate the Pearson correlation coefficient ${\mathit{r}}_{ij}$ between each sample in ${\tilde{N}}_i$ according to Equation (2). 4: Construct the graph $G=(V,E)$. 5: Sample the node information of $G=(V,E)$ and generate feature vector ${\mathit{h}}_v^k$. 6: Aggregate feature information, $h_{\tilde{N}\left(v\right)}^k\leftarrow AGGREGAT{E}_k\left(\right\{h_v^{k-1},\forall v\in \tilde{N}(v)\left\}\right)$, and generate new feature vectors. 7: Normalize feature vectors, $h_v^k\leftarrow \raisebox{1ex}{$h_v^k$}\!\left/ \!\raisebox{-1ex}{${\Vert h_v^k\Vert }_2$}\right.,\forall v\in V$. 8: Generate new node embedding, $z_v\leftarrow h_v^k,\forall v\in V$. 9: Classify feature vectors and output the prediction result of diseases.

The advantages and innovations of the EPGC lie in introducing a GDS into the fusion of multimodal medical data, leveraging the feature expression advantages of GDS’s nodes and edges to solve the problem of multi-source heterogeneous and high-dimensional multimodal medical data fusion. It establishes a classification model based on graph learning using the fused multimodal data to achieve the classification and diagnosis of patient disease types. Compared to existing multimodal medical data processing models, the EPGC model preserves the association rule information of features in the data samples as far as possible and does not require redundant work in dimensionality reduction.

3. Experimental Section

3.1. Experimental Data

In this paper, we evaluate the model’s performance using a cardiovascular diseases dataset. Cardiovascular diseases are the leading cause of death globally, taking an estimated 17.9 million lives each year. Cardiovascular diseases include disorders of the heart and blood vessels and include coronary heart disease, cerebrovascular disease, rheumatic heart disease, and other conditions [40]. This paper focuses on the prediction of two types of diseases from the data, namely coronary artery disease and myocardial infarction.

Coronary artery disease, also known as coronary heart disease or ischemic heart disease, is the most prevalent type of cardiovascular disease. In some developed countries, its incidence among individuals over 65 can reach up to 20%, with even higher rates in developing nations. Coronary artery disease is a disease with a complex etiology; it is typically diagnosed using invasive coronary angiography, which offers a high accuracy exceeding 90%. However, this method carries certain risks, as it involves injecting a contrast agent into the body. Such procedures can lead to complications, including bleeding, infection, hematoma, and, in rare cases, death [41]. In contrast, traditional diagnostic methods, a combined medical examination with an electrocardiogram (ECG), electroencephalogram (EEG), and laboratory tests, are safer and more widely used [42]. These methods provide a comprehensive assessment of a patient’s condition and can be effectively used even in regions with less developed medical infrastructure, offering patients a safer and more accessible diagnostic experience.

Myocardial infarction is a prevalent and highly detrimental cardiac condition, typically resulting from myocardial ischemia due to coronary artery occlusion [43]. Myocardial infarction can lead to severe complications, such as atrial fibrillation, arrhythmia [44], cardiogenic shock, and congestive heart failure, with the potential for fatal outcomes in severe cases [45]. Even experienced clinicians may struggle with accurately predicting these complications. Therefore, it is crucial to reliably predict potential complications to implement timely and appropriate interventions. In clinical practice, multimodal data are collected from patients, including demographic information, blood test results, and diagnosis and treatment details during hospitalization.

The two experimental datasets are sourced from UCI. The first dataset is an extension of the Z-Alizadeh Sani dataset, specifically designed for coronary artery disease detection [46]. It comprises the examination records from 303 patients, with each patient’s data including 54 features. This dataset encompasses five types of data—demographic information, symptoms and related disease screening, electrocardiogram data, blood test results, and cardiac echo characteristics—along with the disease types. It includes numerical data, sequential data, and textual data, with complete data and balanced positive and negative samples. A detailed description of the data is provided in

Table 1. Introduction of coronary artery disease datasets.

Feature	Details
Demographic	Age, Weight, Sex, BMI (Body Mass Index), DM (Diabetes Mellitus), Current Smoker, Ex-Smoker, FH (Family History), CRF (Chronic Renal Failure), CVA (Cerebrovascular Accident), Thyroid Disease, CHF (Congestive Heart Failure), DLP (Dyslipidemia), etc.
Symptoms and examination	BP (Blood Pressure), PR (Pulse Rate), Edema, Weak Peripheral Pulse, Lung Rales, Systolic Murmur, Diastolic Murmur, Typical Chest Pain, Dyspnea, Function Class, Atypical, Nonanginal CP, Exertional CP (Exertional Chest Pain), Low Th Ang (Low Threshold angina).
ECG and vectorcardiogram	Rhythm, Q Wave, ST Elevation, ST Depression, T Inversion, LVH (Left Ventricular Hypertrophy), Poor R Progression (Poor R Wave Progression), LAD (Left Anterior Descending), LCX (Left Circumflex), RCA (Right Coronary Artery).
Laboratory and echo	FBS (Fasting Blood Sugar), Cr (Creatine) (mg/dl), TG (Triglyceride), LDL (Low-Density Lipoprotein), HDL (High-Density Lipoprotein), BUN (Blood Urea Nitrogen), ESR (Erythrocyte Sedimentation Rate), HB (Hemoglobin), K (Potassium), Na (Sodium), WBC (White Blood Cell), Lymph (Lymphocyte), Neut (Neutrophil), PLT (Platelet), EF (Ejection Fraction), Region with RWMAa (Regional Wall Motion Abnormality), VHD (Valvular Heart Disease).
Type of coronary artery disease	Yes or No

. The dataset has undergone comprehensive feature extraction, including the electrocardiogram, vector electrocardiogram, and echocardiographic data. It is of high quality, with no missing values and clearly labeled data.

The second dataset selected for this paper study is the myocardial infarction complications dataset [47], which comprises examination records of 1700 myocardial infarction patients. Each patient’s examination record has 124 feature attributes, of which 1 attribute is the patient’s ID, 111 feature attributes are the clinical descriptions of myocardial infarction, and 12 feature attributes are the complications of myocardial infarction. The data are presented in

Table 2. Introduction of myocardial infarction complications dataset.

Feature	Details
The clinical description of myocardial infarction.	Demography, electrocardiogram, laboratory data, hospitalization records, medication records, etc.
The types of myocardial infarction complications.	Atrial fibrillation (AF), supraventricular tachycardia (ST), ventricular tachycardia (VT), ventricular fibrillation (VF), third-degree AV block (TA), pulmonary edema (PE), myocardial rupture (MR), Dressler syndrome (DS), chronic heart failure (CH), relapse of the myocardial infarction (RM), post-infarction angina (PA), lethal outcome (LO).

. It includes numerical data, time-series data, and textual data. The dataset has undergone the feature extraction steps, mainly for the electrocardiogram data. The data quality of this dataset is poor, with numerous missing data points and inconsistent data labels. We selected 202 complete data samples from it to form the experimental data, with balanced positive and negative samples.

3.2. Experimental Design

During the construction of a diagnostic model for multimodal medical data, we designed the following experimental steps: data fusion and disease prediction, model evaluation, and control group experimental design.

3.2.1. Data Fusion and Disease Prediction

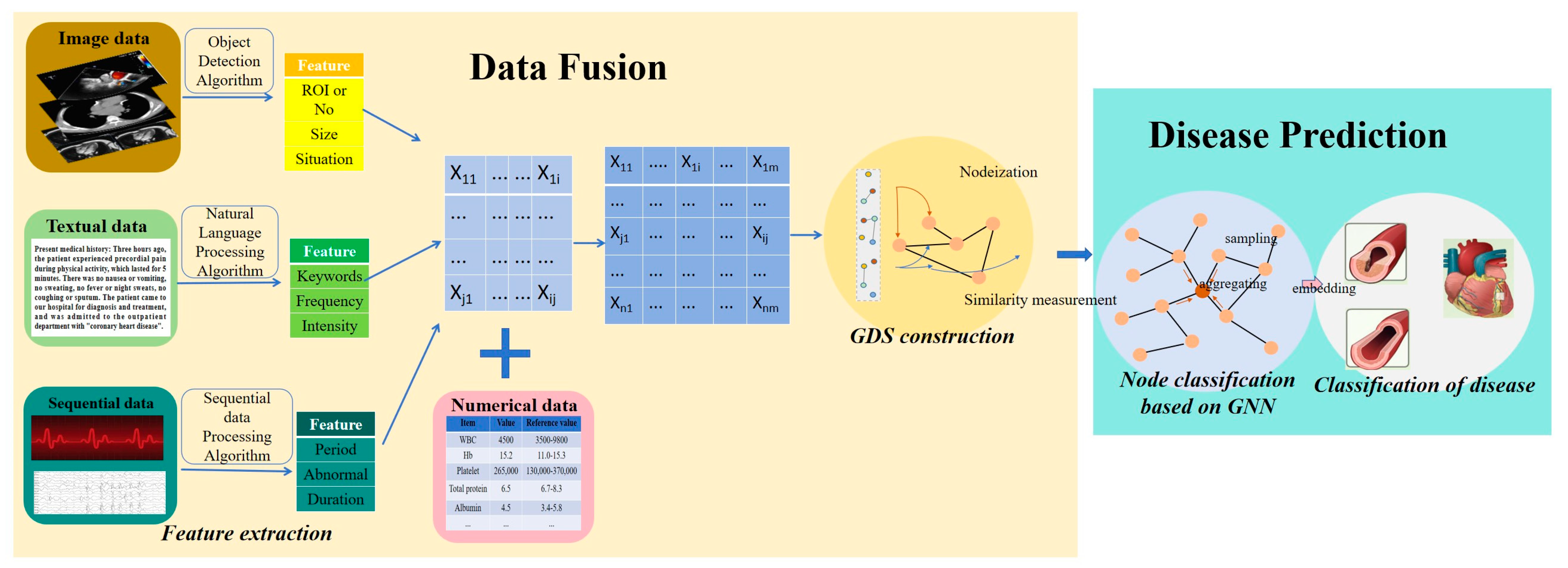
• Data preprocessing: This mainly involves standardizing the format and dimensions of experimental data and converting the multimodal data into numerical data. We use AI-based feature extraction to convert these multimodal data into numerical data. This needs to be implemented based on AI algorithms, as shown in Figure 3. It mainly focuses on image data (CT, MRI, etc.), textual data (symptom description, etc.), and sequential data (electrocardiogram, electroencephalogram, etc.). The ECG data describe the features of a patient’s ECG-related bands and was preprocessed by the dataset provider. Additionally, some individual features in the original data include descriptive text data, such as the severity of heart valve disease, which is categorized as N, Mild, Moderate, and Severe to describe the patient’s condition. For consistency and to perform a numerical analysis, we convert these descriptive categories into numerical values: 0 for N, 1 for Mild, 2 for Moderate, and 3 for Severe. In addition, the multimodal medical data are characterized by dimensional inconsistency. To address this, we apply mean normalization to the original data. This step helps to mitigate the impact of varying dimensions on model learning and ensures that the classifier accuracy is not adversely affected by these differences.
• GDS construction: Each patient is represented as a node, and the similarity between patients is represented as an edge. The edges are determined using the Pearson correlation coefficient. According to the Pearson correlation coefficient, an edge is drawn between two nodes if their correlation coefficient is greater than or equal to 0.5, i.e., $r\ge 0.5$, indicating a strong similarity and thus a connection between them. Conversely, if the coefficient is 0.5 or less, i.e., $r<0.5$, this indicates a weak similarity and no connection edge is drawn between the nodes.
• Disease prediction—designing the network learning models: The constructed GDS is undirected. We propose using a GraphSAGE network, which samples the node information with random walks on the graph and generates the node features. Given that the types and sizes of experimental data are relatively simple, we propose using a two-layer GNN network, utilizing a GCN aggregator and mean aggregator, respectively. This design approach enhances the extraction of features from the graph structure. The expression of the GCN aggregator is shown in Equation (4), where $h^k$ represents the feature vector of node, $\sigma$ represents the non-linear activation function, $W^{k-1}$ represents the adjacency weight matrix of node, and ${\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$ is the normalized Laplacian matrix. The mean aggregator is shown in Equation (5), where $h_i^{\left(k\right)}$ represents the feature vector of node $N\left(v\right)$, and g represents the $i$, which is the adjacent point of the node.

$$h^k=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{h}^{k-1}{W}^{k-1})$$

(4)

$$h_v^k\leftarrow \sigma (W\cdot mean(\left\{h_v^{k-1}\right\}\cup \{h_u^{k-1},\forall u\in N(v)\})$$

(5)

In addition, we also add a control group for the experiment, which comes from the experimental results in the references. The experimental results are currently the best-known classification model for this dataset. The result is a disease classification model using feature selection and machine learning algorithms on the same dataset.

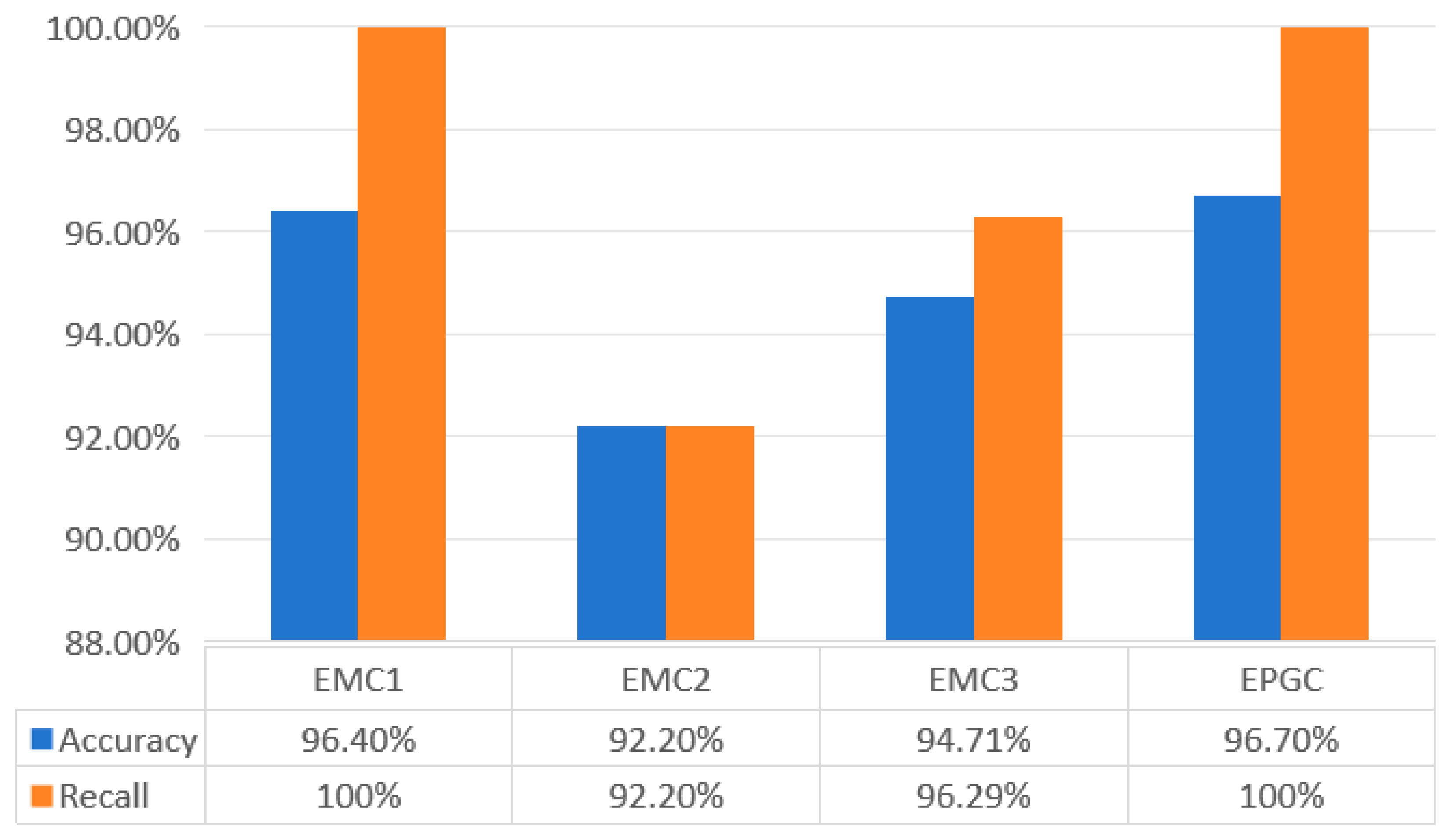
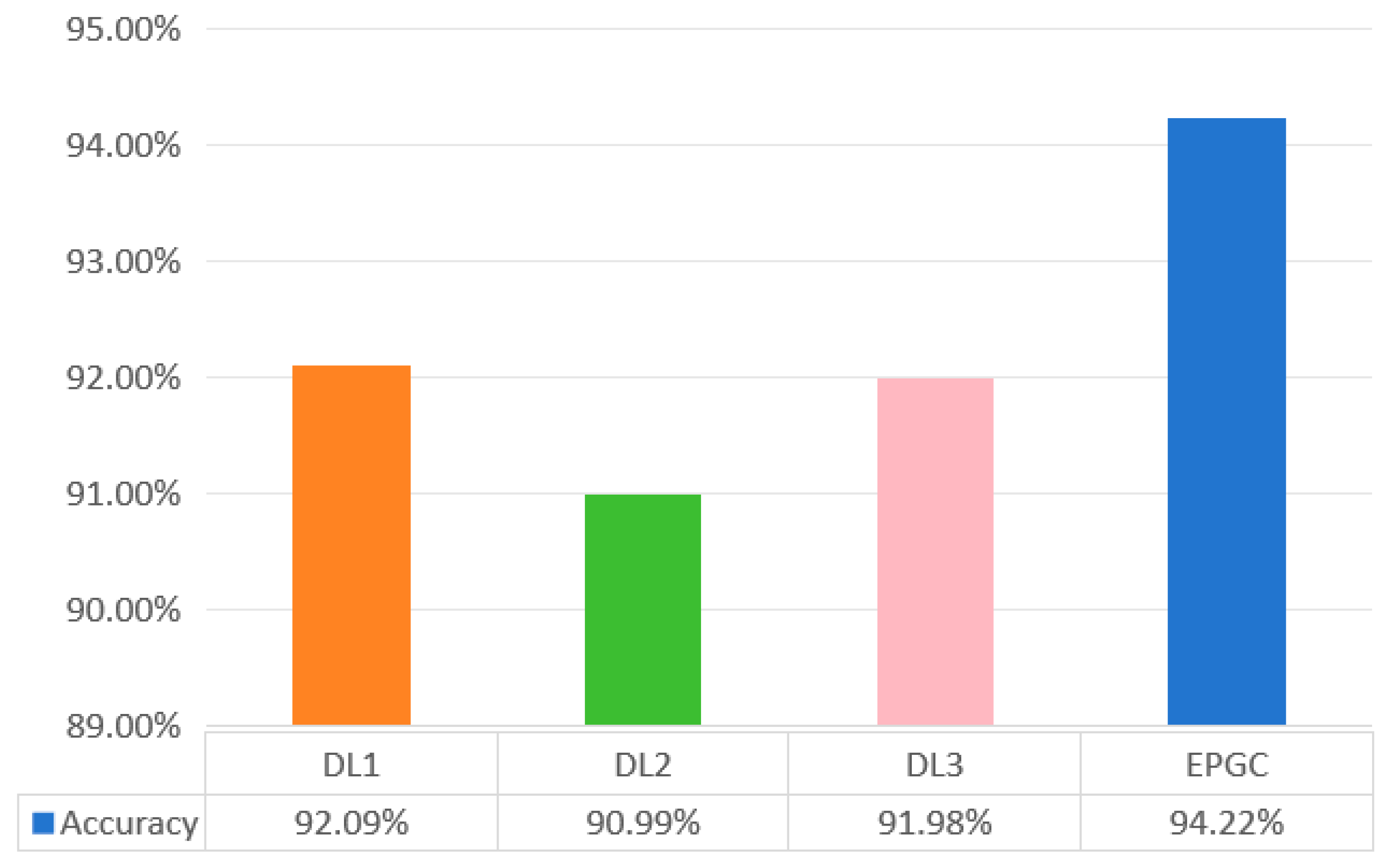
3.2.2. Control Group Experiment

In order to highlight the generalization ability of the model, two datasets were used for model validation, i.e., the coronary artery disease detection dataset and the myocardial infarction complication dataset.

The dataset on coronary artery disease detection is openly available from researchers’ papers. Some researchers have conducted extensive studies on disease prediction based on this dataset. We selected the results with the best classification performance as the control group for the EPGC model experiment. Meanwhile, in order to demonstrate the comparability of our experimental results, we referred to the reported experimental results for the existing best-in-class methods for comparison with ours, and used the same evaluation indicators. This model uses the traditional “feature selection + dimensionality reduction + prediction” approach, referred to as the “EMC” (Feature Extraction, Dimensionality Reduction, Classification) method. Specifically, reference [16] proposed a feature engineering method to select, rank, and combine the features in the dataset to predict coronary artery disease using the optimal feature combination. This model is referred to as EMC1. Reference [48] conducted a study using the BESO (Bald Eagle Search Optimization) for dimensionality reduction. Ten optimal features were selected from the original data, then combined with a random forest to predict coronary artery disease. This model is referred to as EMC2. Reference [49] proposed a combination of genetic algorithms and neural networks for feature selection in their research, obtaining an optimal prediction combination containing 24 features through various parameter settings. This model is referred to as EMC3.

The myocardial infarction complications dataset is openly available from researchers’ papers too. We referred to the dataset on myocardial infarction complications selected the reported experimental results for the existing best-in-class methods for comparison with ours, and used the same evaluation indicators. The control group included models developed by three different research groups. All the groups utilized deep neural network frameworks and dimensionality reduction techniques. Specifically, reference [18] introduced a five-layer deep neural network model, which included three hidden layers for feature extraction and complexity reduction. This model is termed the DL1 (Deep Learning 1) method. Reference [17] initially performed dimensionality reduction on the high-dimensional data and then designed a four-layer deep neural network model with two hidden layers for feature learning and extraction. This model is referred to as the DL2 (Deep Learning 2) method. Reference [50] presented a multitask deep learning model to predict myocardial infarction complications. This model is referred to as DL3 (Deep Learning 3).

3.2.3. Model Evaluation

In terms of model evaluation, this study was based on a control group experiment. In the model validation experiment using the coronary artery disease data, the same evaluation indicators as in references [16,48,49] were used, and the results were evaluated using two indicators: accuracy and recall. The equations for accuracy and recall are shown in Equations (6) and (7), respectively.

In the model validation experiment using the myocardial infarction complications dataset, we used the same accuracy evaluation index as in references [17,18,50] to ensure consistency with the same dataset. The accuracy served as the index for assessing model performance.

$$Accuracy={\displaystyle \frac{TP+TN}{TP+TN+FN+FP}}$$

(6)

$$\mathrm{R}\mathrm{e}call={\displaystyle \frac{TP}{TP+FN}}$$

(7)

where TP (True Positive) represents the number of originally positive samples correctly identified as positive, TN (True Negative) represents the number of originally negative samples correctly identified as negative, FN (False Negative) represents the number of originally positive samples incorrectly classified as negative, and FP (False Positive) represents the number of negative samples correctly identified as positive.

4. Results

The experimental design used a two-layer GNN network structure, utilizing a GCN aggregator and a mean aggregator for aggregating the sampling information. The model’s loss function was the entropy loss function. In the experiment, 303 samples from the coronary artery disease dataset were divided into training, validation, and testing sets at an 8:1:1 ratio. The 10-fold cross-validation method was implemented in model training, which means that at each compromise, the data was divided into a ratio of 80% (training), 10% (validation), and 10% (testing), and the experiment was repeated for all folds to ensure the minimization of the risk of insufficient single division and resulting randomness. The training set and validation set were used to train the model, and optimize and adjust the parameters, while the test set was used to test the performance of the model. We conducted numerous repeated experiments, and the model had the best convergence performance when the learning rate for the model was set to 0.1. Given the advantages of GraphSage in small sample learning [51], 202 available samples from the myocardial infarction complications dataset samples underwent the same operation.

The experimental results for the coronary artery disease dataset are displayed in Figure 4. As illustrated in Figure 4, the EPGC model proposed in this study achieved <Accuracy, Recall> = <96.70%, 100%>. In contrast, the EMC1 model achieved performance indexes for <Accuracy, Recall> = <96.40%, 100%>. The EMC2 model achieved performance indexes for <Accuracy, Recall> = <92.20%, 92.20%>. The EMC3 model achieved performance indexes for <Accuracy, Recall> = <94.71%, 96.29%>. The results demonstrate that the EPGC model provides superior prediction performance for the multimodal coronary artery disease data, as reflected in the accuracy and recall.

The experimental results for the myocardial infarction complications dataset are displayed in Figure 5. The prediction accuracies of DL1, DL2, and DL3 are 92.09%, 90.99%, and 91.98%, respectively. The prediction accuracy of EPGC model proposed in this study is 94.22%. The results demonstrate that the EPGC model outperforms the DL1, DL2, and DL3 methods, which are based on complex deep neural network frameworks, on the myocardial infarction complications dataset. The prediction accuracy is improved by 2.13%, 3.23%, and 2.24%, respectively.

5. Discussion

In this study, we propose a data fusion approach to design a GDS construction method based on sample similarity. The model avoids conventional dimensionality reduction processes, such as complex feature selection or extraction during the fusion of multimodal medical data, and helps to preserve the integrity of the data as much as possible. Subsequently, a GraphSAGE network is employed to sample and aggregate the information from the nodes and edges within the GDS, ultimately allowing for the prediction of a patient’s disease type. The proposed model, the EPGC, demonstrates strong applicability to high-dimensional data, and in the disease prediction experiments on two different multimodal medical datasets, the model outperformed the existing control group models.

The fusion and intelligent decision-making of multimodal medical data face challenges, such as diverse data formats, high dimensionality, and data complexity. The data format of multimodal medical data is both multi-source and complex. To address this, data format transformation and feature extraction are essential. In this paper, we have drawn on the experience of other researchers, converting multimodal data into numerical data in preprocessing, to meet the requirements of deep algorithms that require a large number of iterations and computational power to converge a model. Therefore, transforming data formats and extracting features are crucial for effective learning and model training.

Meanwhile, multimodal medical data often has high dimensionality, which can reduce the accuracy of disease prediction when using traditional machine learning or deep neural network classifiers due to the curse of dimensionality. Most existing research on this topic has attempted disease prediction by constructing complex networks or using a “feature selection + dimensionality reduction + prediction” approach. These methods require lots of dimensionality reduction work, which can be result-oriented, blind, and random, increasing a model’s complexity and leading to information loss. For example, researchers have often tried various dimensionality reduction methods and then evaluated them based on the final predicted results, using a reverse approach to identify the best method. This undoubtedly impacts the prediction performances of the models. Compared with the existing research, our method does not require dimensionality reduction, which preserves as much information as possible in the original data. It reduces the loss of useful information and improves the performance of subsequent model training. This is demonstrated by the experimental results on the two datasets. At the same time, leveraging the powerful feature expression capability of a GDS, dispersed multimodal medical data is fused into one GDS, which not only solves the problem of high data dimensionality and complexity but also addresses the fusion issue of multimodal medical data. In addition, GraphSage has been proven to have an excellent learning ability on massive transactional network data [52] and large-scale multi-entity heterogeneous graph data [53], which also provides support for the EPGC to deal with the complexity of multimodal medical data.

6. Conclusions

Intelligent diagnosis using multimodal medical data represents a significant trend in the development of medical big data. In this paper, we propose a fusion and disease prediction model for multimodal medical data; the construction of a GDS is innovatively introduced into the fusion of multimodal medical data. The multimodal medical data initially undergoes preprocessing steps, including format transformation and feature extraction. Meanwhile, normalization is applied to address the dimensional inconsistencies and improve the classifier accuracy. Subsequently, each patient sample is represented as a node, and the similarities between the samples are represented as edges, constructing a GDS. Following the construction of the GDS, node sampling and aggregation are employed to generate the feature vectors associated with the nodes. Node embedding is subsequently applied to these feature vectors. Finally, the machine learning classifier utilizes the embedded features to predict the node labels, thus enabling disease prediction. In the experiment, we compared the proposed EPGC model with the current mainstream and best-performing methods on the same datasets. The results reveal that the EPGC shows strong applicability to high-dimensional data and outperforms the reference models at disease prediction on various multimodal medical datasets.

As shown in Figure 3, there are some AI-based feature extraction modules in the EPGC model that handle multimodal data, such as image data, textual data, sequential data, etc. These modules can address the challenges of common medical data modalities. However, during this process, the AI-based feature extraction may be biased due to the performance of AI algorithms themselves, which can affect the subsequent prediction performance. In addition, constructing the GDS based on the Pearson coefficient (hyperparameters) ($r\ge 0.5$), may also lead to bias in the results. The above are all limitations of the EPGC. Correspondingly, with an improvement in the AI algorithm’s performance and the optimization of selection of hyperparameters, the performance of the EPGC model will also be further improved. In future research, the EPGC will be applied to other areas by adding feature extraction modules, such as video stream data and sensor data.