A Novel Spatio-Temporal Graph Convolutional Network with Attention Mechanism for PM2.5 Concentration Prediction
Abstract
1. Introduction
- The Spatio-Temporal Graph Convolutional Network with Attention Mechanism (STGCA) model is proposed, which is designed based on a seq2seq framework, and is able to effectively capture the complex dependencies of PM2.5 concentration in both spatial and temporal dimensions by combining GCN and GRU. GCN processes the non-Euclidean spatial features for accurately modeling spatial correlations among different regions, while the GRU models time series information to capture the long-term and short-term temporal dynamics.
- A spatio-temporal attention mechanism for air pollution prediction is designed, which is used to extract features in the temporal and spatial dimensions. By learning the distribution of attention weights, this mechanism can effectively extract important information to improve the prediction of air pollutant concentrations.
- To objectively and comprehensively evaluate the proposed model, we design extensive experiments utilizing multi-source data, including air pollutant data, meteorological data and other relevant data. These experiments encompass multi-step regional prediction tasks of PM2.5 concentrations at high spatial resolution in Beijing and compare the model performance against baseline methods using various accuracy and robustness metrics.
2. Study Area and Dataset Analysis
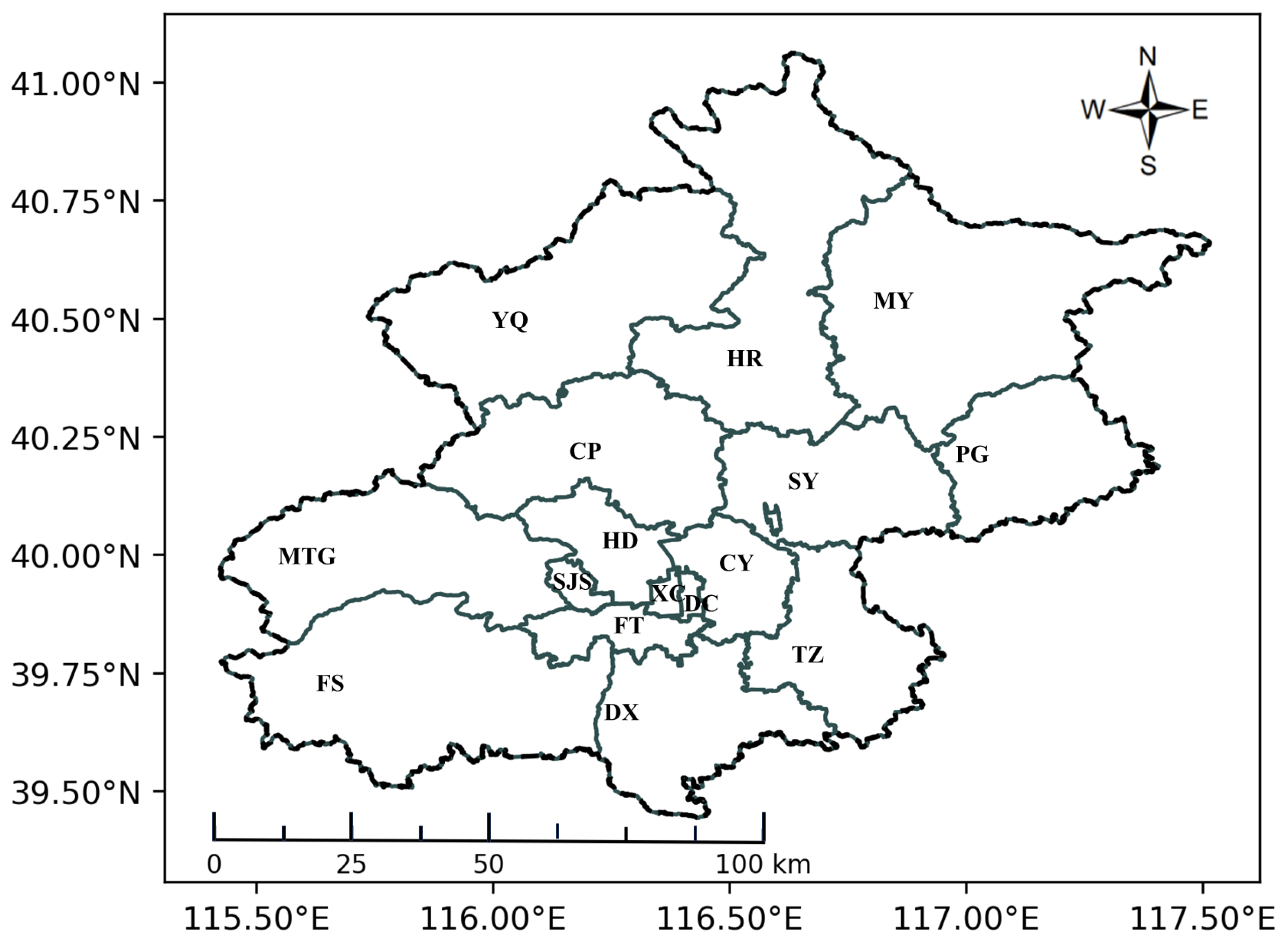
2.1. Study Area
2.2. Dataset Description
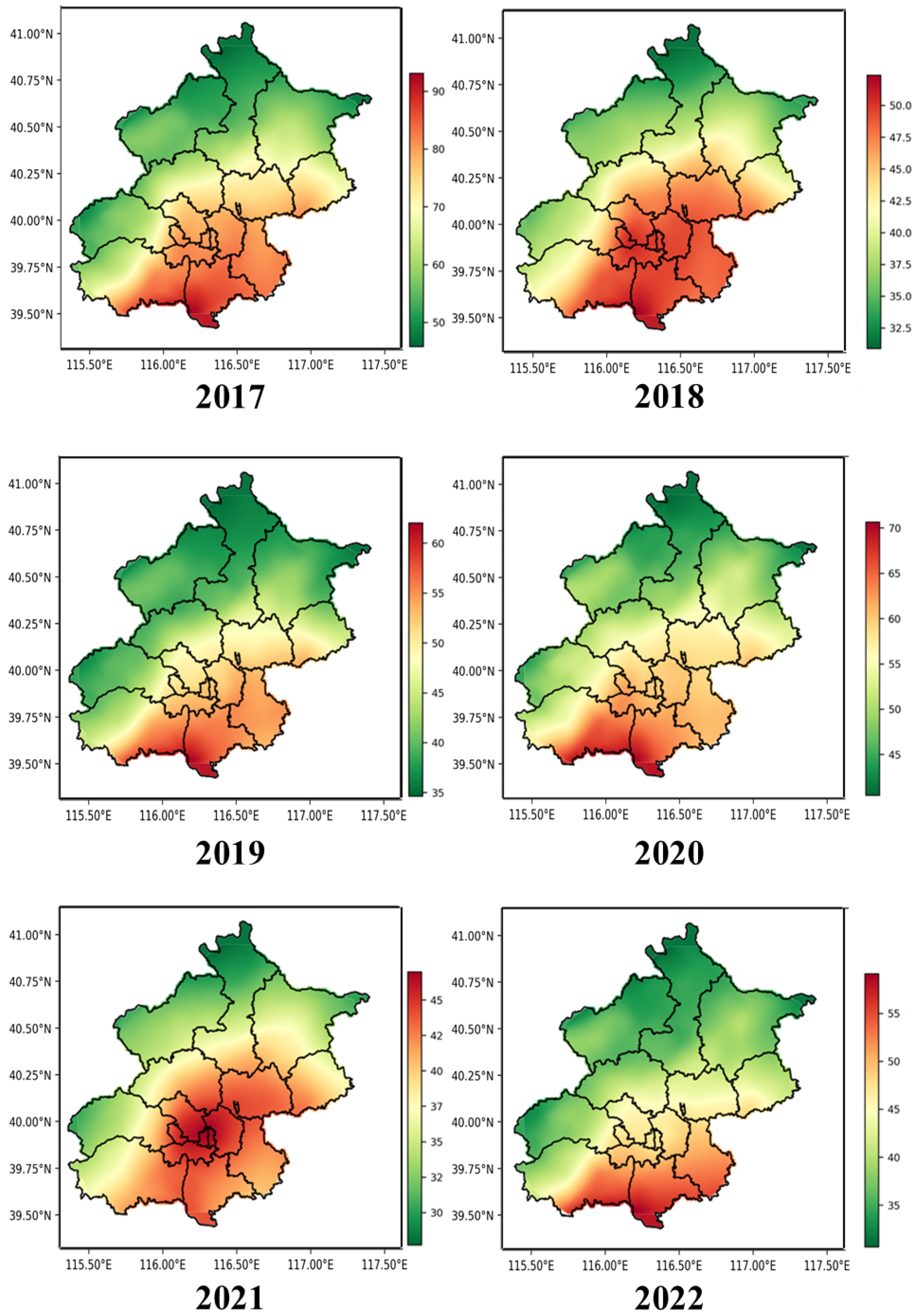
2.3. Analysis of Temporal and Spatial Correlation
2.3.1. Analysis of Temporal Correlation
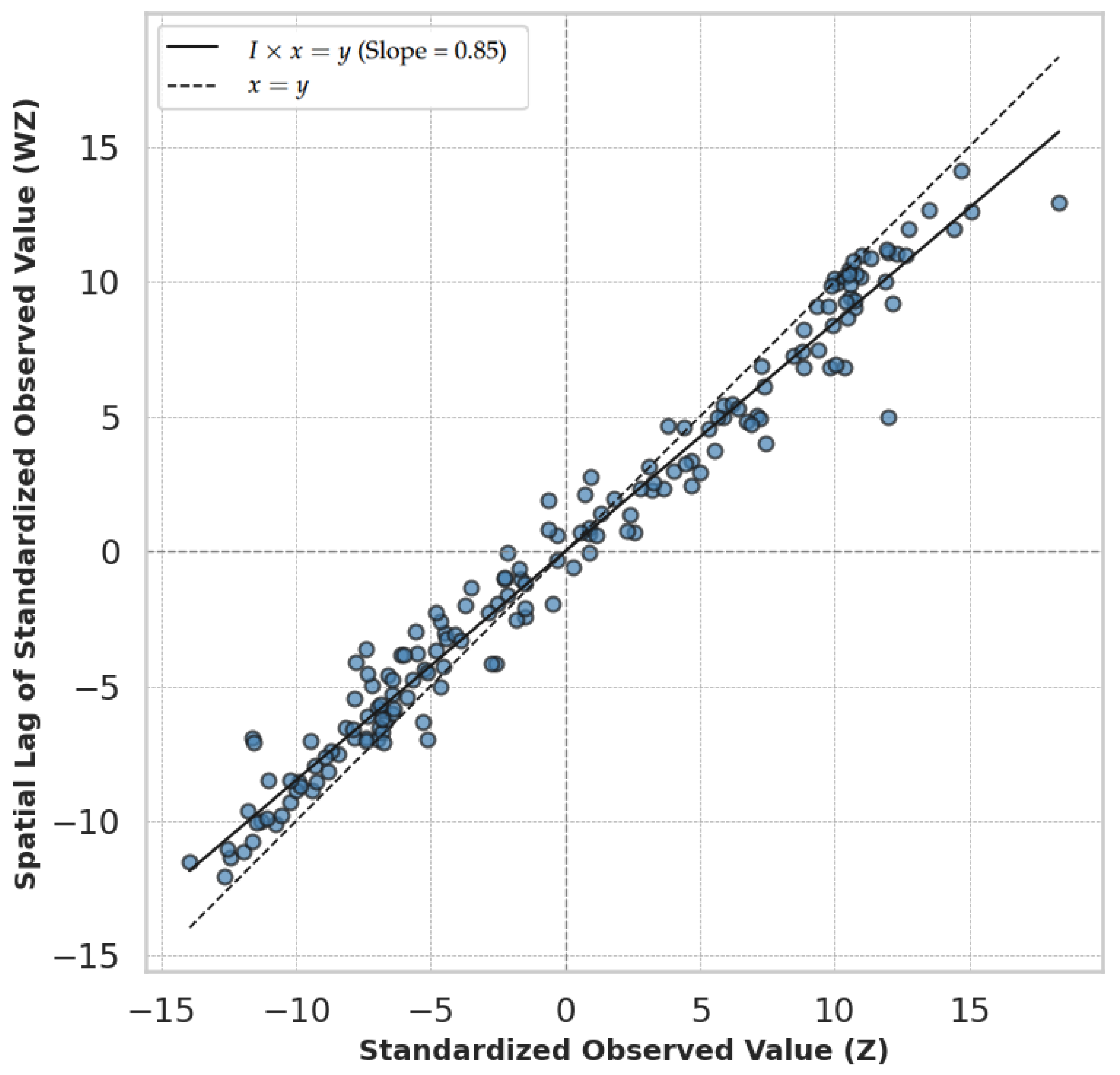
2.3.2. Analysis of Spatial Correlation
Global Spatial Autocorrelation
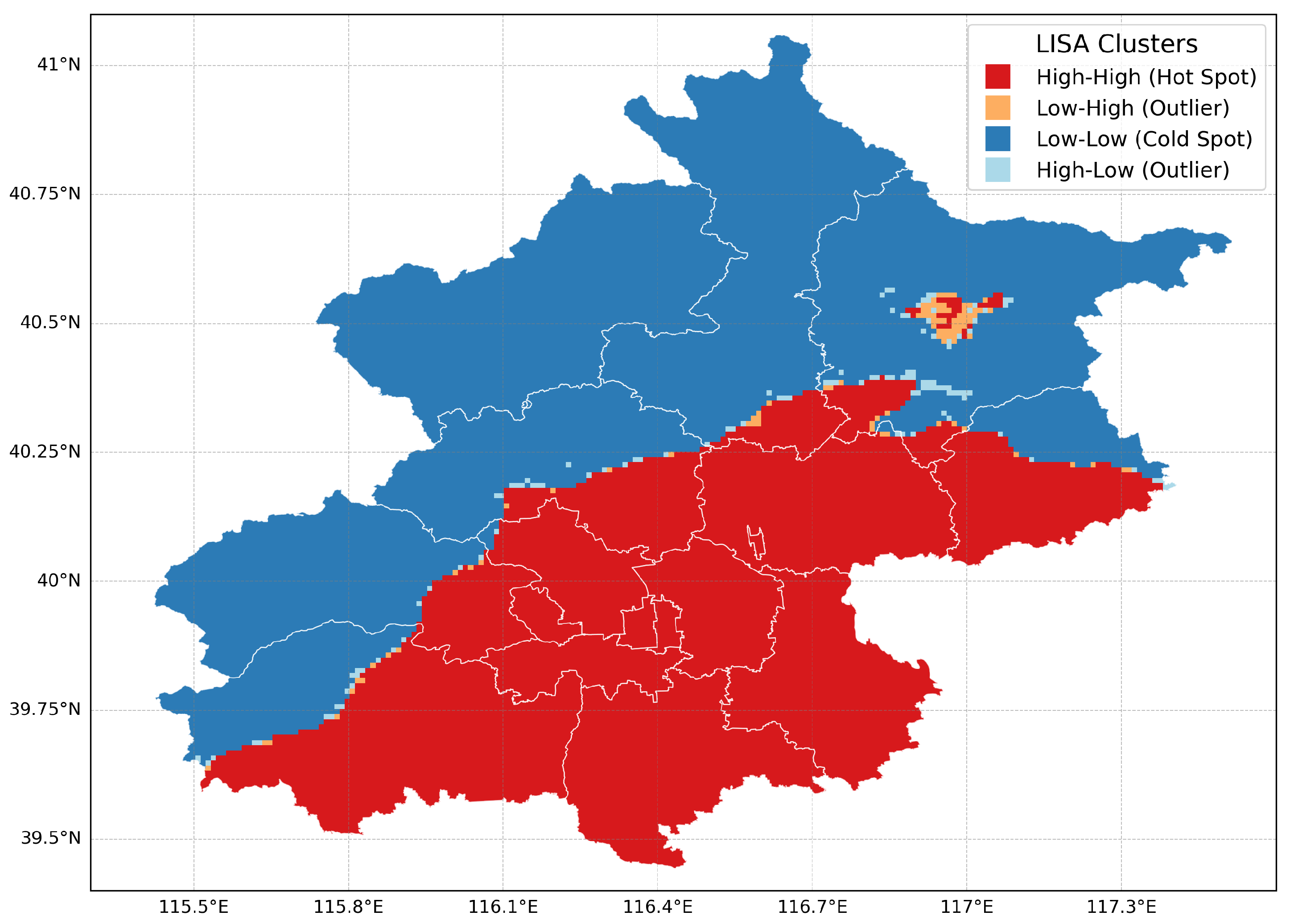
Local Spatial Autocorrelation (LISA)
2.4. Evaluation Metrics
3. Research Methodology
3.1. Prediction Model
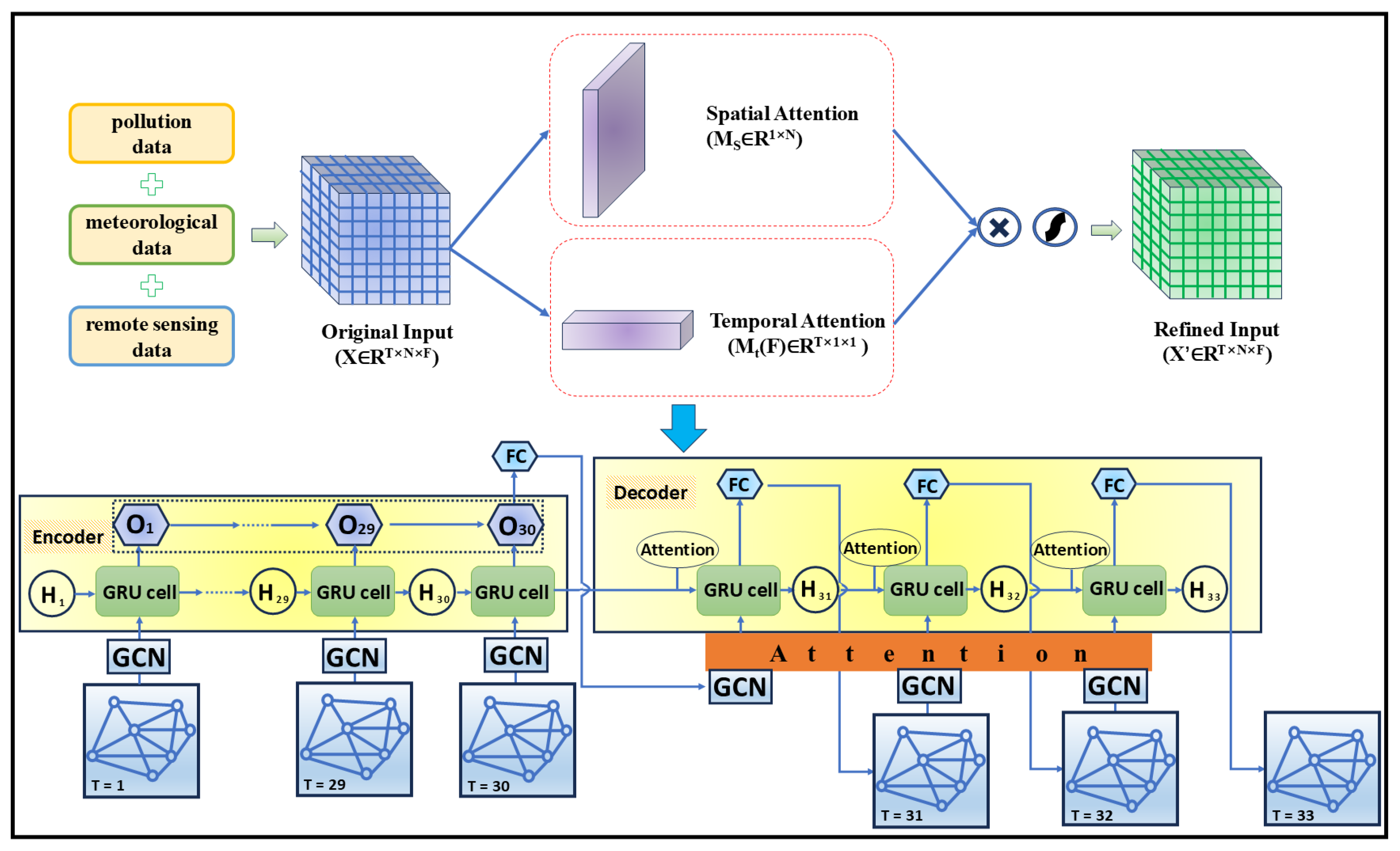
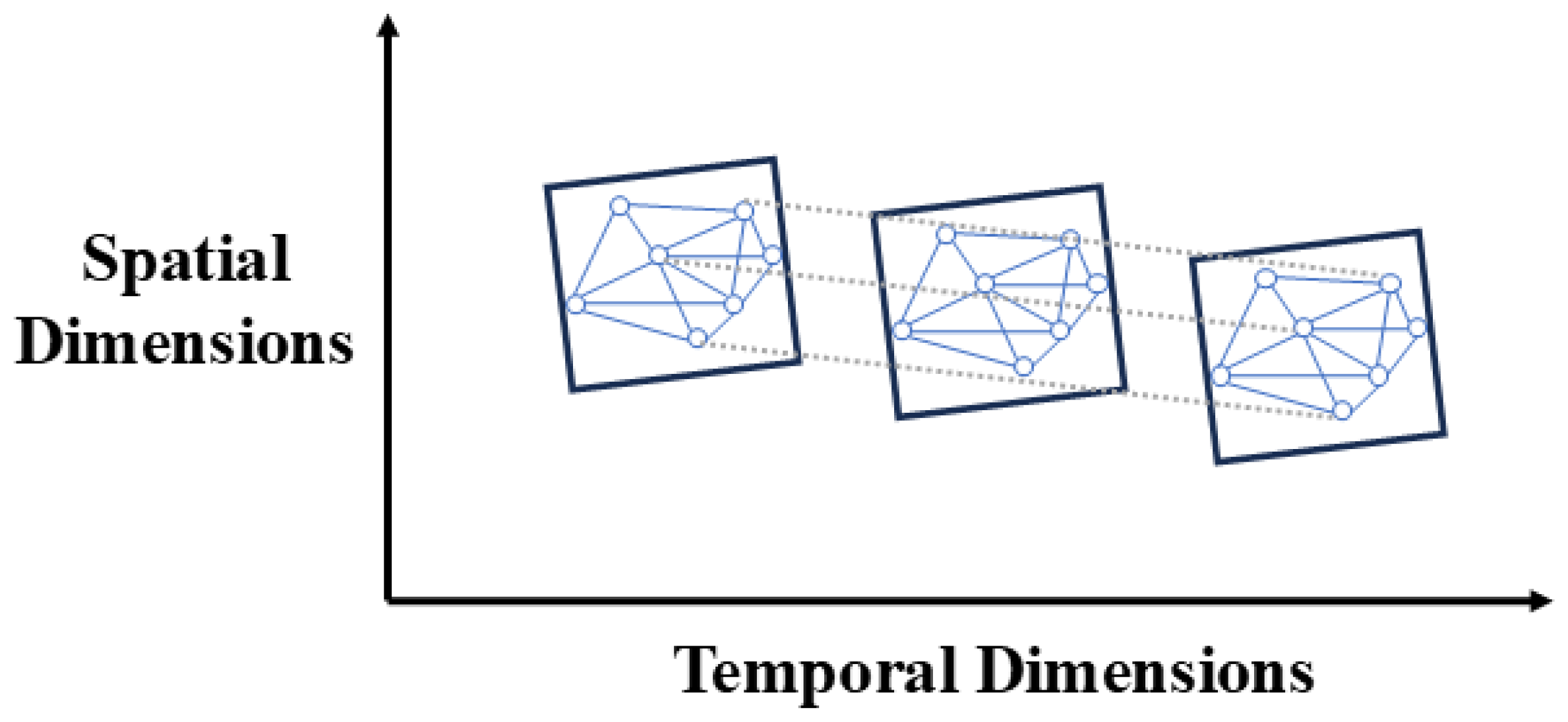
- We integrate and preprocess the multi-source data required for PM2.5 concentration prediction. These data include air pollutants, meteorological elements, and other environmental factors from remote sensing for Beijing. To effectively represent the spatio-temporal characteristics, the data for the 173 raster cells are structured into a tensor containing three dimensions: a temporal dimension representing the sequence of historical time steps, a spatial dimension corresponding to the raster cells, and a feature dimension. This results in a unified three-dimensional (3D) spatio-temporal matrix that provides high-precision input for the proposed model, ensuring that the model absorbs rich spatio-temporal information.
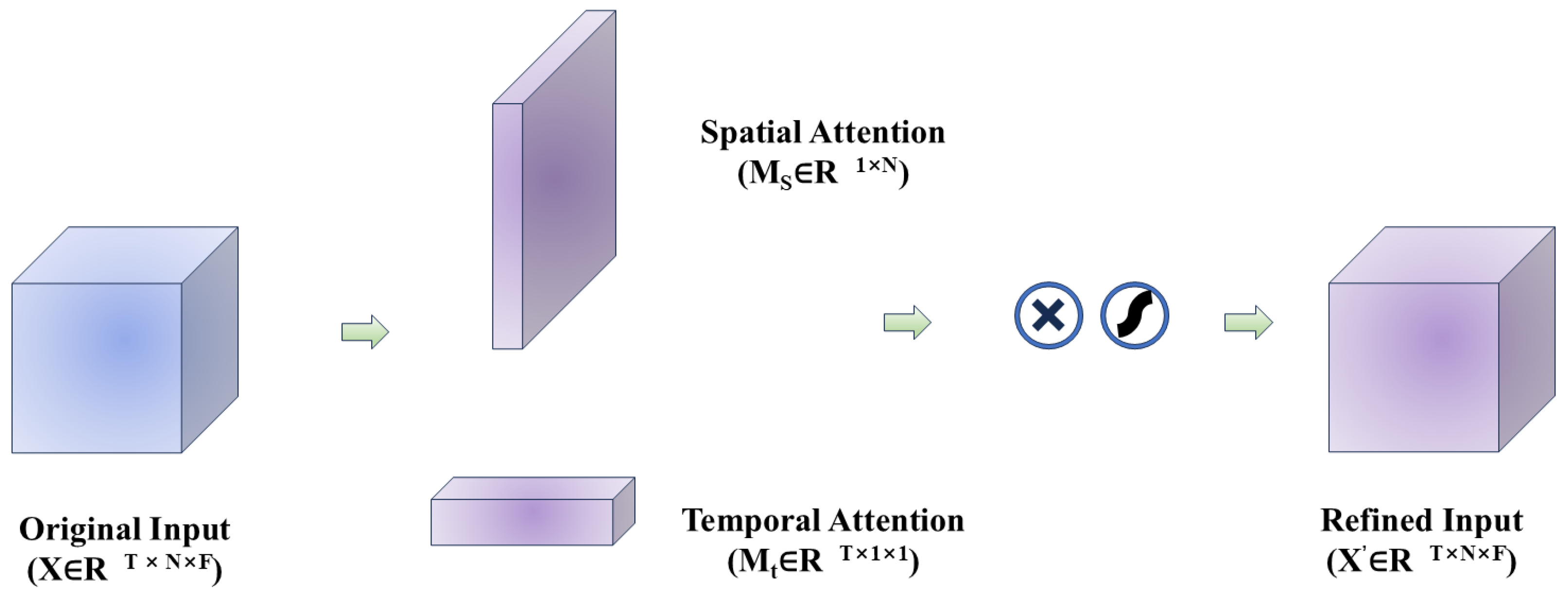
- The spatio-temporal matrix is then processed by the attention module. This module contains two parts, spatial attention and temporal attention, which are used to assign spatial and temporal weights to the data.
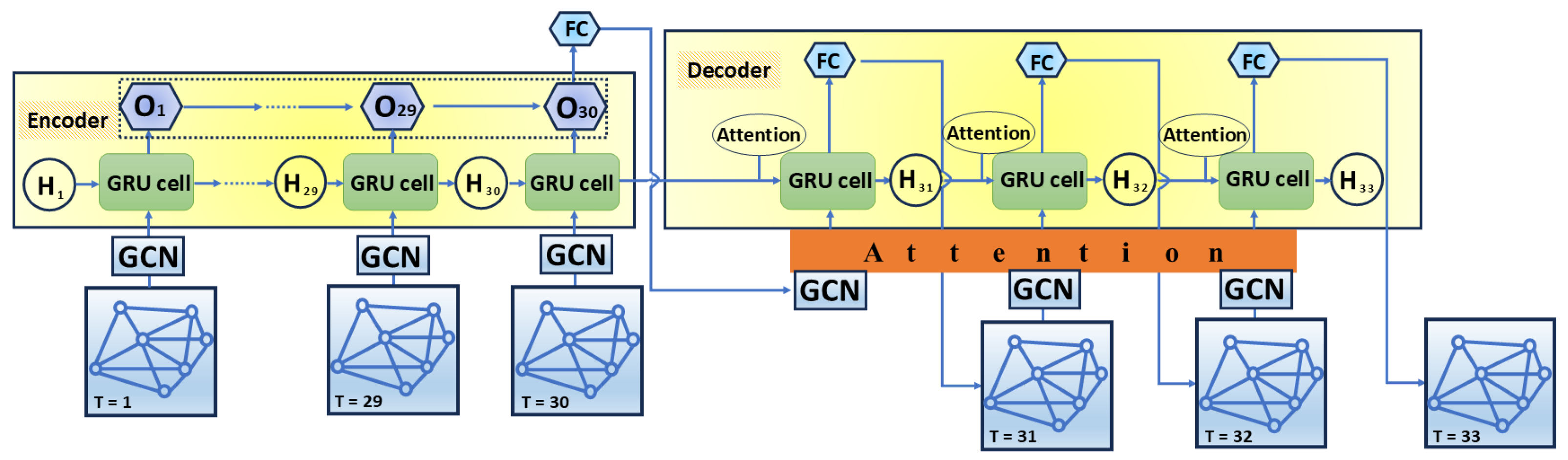
- The refined input data are passed to the proposed STGCA prediction model. The model utilizes a seq2seq architecture that combines GCN and GRU. In the encoder, the GCN is tasked with modeling intricate spatial relationships among raster cells, while the GRU is used to process time-series information to capture dynamic patterns of PM2.5 concentrations over time. The hidden representation generated by the encoder is passed to the decoder, which realizes multi-step prediction through the GRU and GCN layers and enhances the time-dependent representation through the attention layer to generate PM2.5 concentration values at future moments. This structure effectively integrates the spatio-temporal features, which makes the model highly accurate in capturing the spatial and temporal dependence of PM2.5 concentration changes in the Beijing area [38].
3.2. Spatio-Temporal Attention Mechanism
3.2.1. Spatial Attention Module
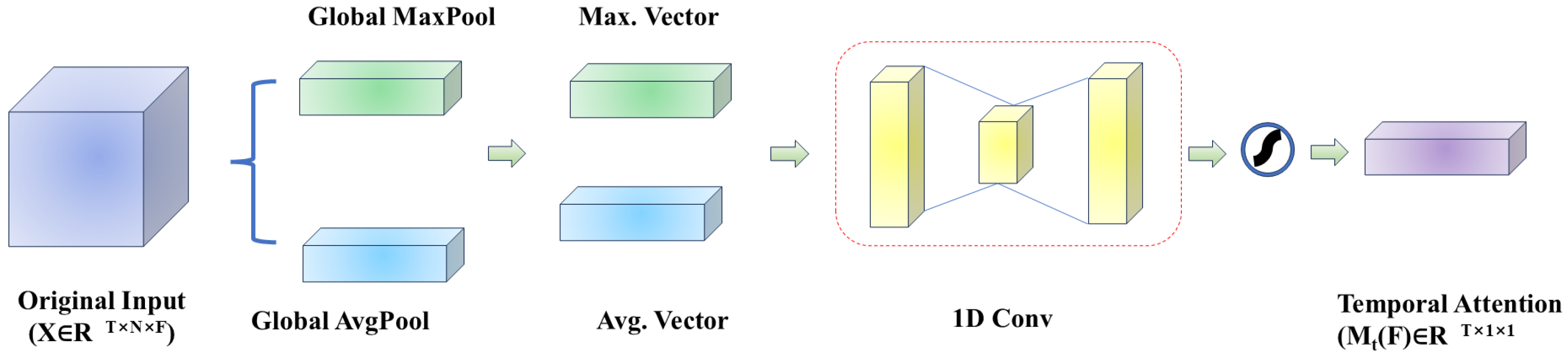
3.2.2. Temporal Attention Module
3.2.3. Spatio-Temporal Attention Module
3.3. GCA Module
3.3.1. Graph Convolutional Neural Network
3.3.2. The Improved GCN
- (1)
- To mitigate over-smoothing, where node features become indistinguishable after many layers, we adjust the weight of self-loops by introducing a parameter [47]. By re-distributing weights between a node and its neighbors, we can explicitly control the amount of information retained from the node itself in each layer. The modified adjacency matrix is defined asWhen p approaches 1, the contribution of a node’s neighbors is emphasized, whereas a p value closer to 0 increases the weight of its self-information. After extensive testing, we found that the optimal value of p is approximately , which effectively balances these influences for our task.
- (2)
- To expand the receptive field of the graph convolution without excessively deepening the model, we incorporate multi-hop neighborhood connections. By applying the normalized adjacency matrix K times, the model can directly capture information from up to K-hop neighbors in a single layer. This approach theoretically enhances the model’s ability to capture larger-scale spatial dependencies, which are crucial for regional pollution modeling [44].
3.3.3. GC-GRU
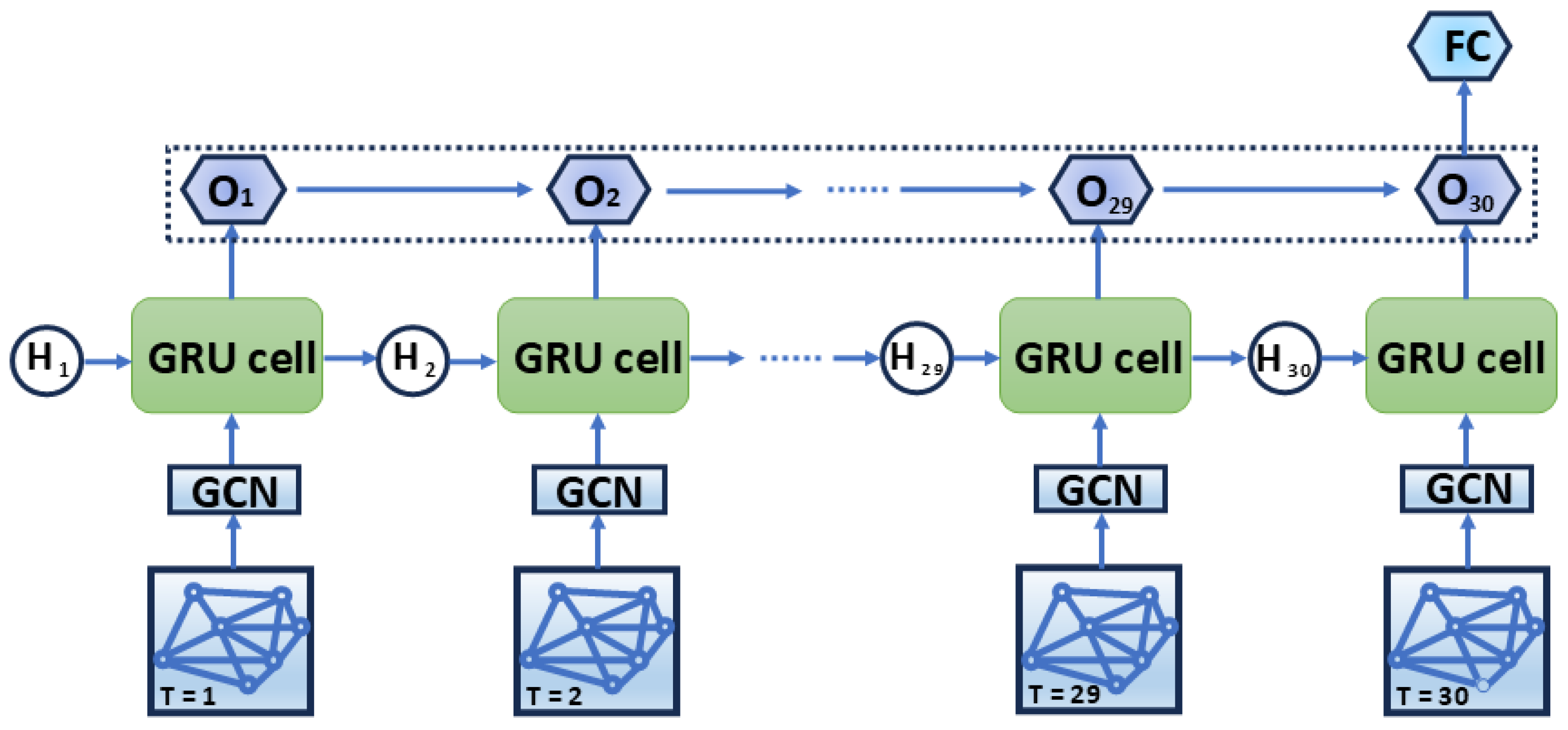
- The core of our temporal modeling component is the GC-GRU cell. This module enhances the conventional GRU structure by making its gating mechanisms spatially aware. Instead of standard matrix multiplications, graph convolution operations () are integrated into the update and reset gates. This modification allows each GRU to aggregate information not only from its own past state but also from its spatial neighbors at the current time step, thereby learning a unified spatio-temporal representation.The candidate hidden state is then calculated using the reset gate to modulate the influence of the previous hidden state:Finally, the new hidden state is produced by the update gate, which balances information from the previous state and the current candidate state:where is the input feature matrix at time t, and is the hidden state from the previous time step. The symbol denotes the graph convolution operation [50], is the Sigmoid activation function, and ⊙ represents the element-wise (Hadamard) product. The terms are the learnable weight matrices for their respective gates.
- Series connection of loop units: all GC-GRU cells are connected in series in chronological order, and the output of each unit is used as the input of the next unit to ensure the temporal continuity. With this structural design, the model is able to process inputs from different time steps and gradually establish global temporal dependencies. Figure 11 illustrates the architecture of the GC-GRU network.
- Multi-Layer Architecture: To enhance the model’s capacity for learning complex patterns, multiple GC-GRU layers can be stacked. A ReLU activation function is applied between each layer to improve the model’s nonlinear representation capabilities. Finally, the output from the last GC-GRU layer is processed by a fully connected layer to generate the final predictions.
3.3.4. Seq2Seq
3.3.5. Attention Mechanism
3.4. STGCA Model
- Initialization: The hidden state of the decoder is initialized with the final hidden state vector from the encoder’s last time step. A special start-of-sequence token is used as the initial input to begin the generation process.
- Decoder Self-Attention: At each decoding step t, the decoder first employs a self-attention mechanism. It uses its current state to attend to the sequence of all previously generated outputs (). This step allows the decoder to consider the context of its own predictions so far.
- Encoder–Decoder Attention: Subsequently, the decoder uses an attention mechanism to consult the source information. The decoder’s current hidden state is used as the “query” to attend to the entire sequence of the encoder’s output vectors. This produces a context vector that captures the most relevant input information needed for the current prediction.
- Prediction and Iteration: The context vector obtained from the previous step is combined with the decoder’s current hidden state. This combined vector is then passed through a final fully connected layer to generate the prediction for the current time step, . This new output, , will then be used as the input for the next decoding step.
3.5. Experimental Configurations
4. Experimental Design and Validation
4.1. Experimental Design
Ablation Experiments
- Comparison between GC-LSTM and GC-GRUTo explore the differences between LSTM and GRU in prediction accuracy, we compare the GC-LSTM with GC-GRU models. Table 5 presents the performance comparison between the GC-LSTM and GC-GRU models for PM2.5 prediction tasks. The results demonstrate that the GC-GRU model outperforms the GC-LSTM model across all metrics. Specifically, GC-GRU achieves lower RMSE, MAPE, TIC and higher IA values indicating better accuracy in predicting PM2.5 concentrations. This indicates that the GC-GRU has shown superior accuracy over GC-LSTM in prediction tasks.
- Convolution methodsIn the graph convolution module, we test Chebyshev polynomial convolution (CConv) [54], diffusion convolution (DConv) [55], and our proposed IConv, which is detailed in Section 3.3.2. Our improved convolution method achieved the best performance across all metrics (Table 6).
- Graph Convolution filterWe further investigated three types of graph convolution filters to understand their effect on capturing spatial dependencies: the standard Laplacian Filter (LF), the Random Walk Filter (RWF), and DRWF. The RWF and DRWF are based on the diffusion process defined in [56]. The DRWF extends the standard random walk by considering both forward and backward diffusion directions, allowing more comprehensive modeling of spatial dependencies across the graph [56]. The DRWF demonstrated superior performance, highlighting its better ability to capture spatial dependencies (Table 7).
- Attention mechanismFinally, we assess the effect of the attention mechanism by comparing the STGCA model with STGC, without the attention mechanism. The attention-enhanced STGCA model demonstrated improved accuracy by dynamically weighting important historical data, as shown in Table 8.The ablation experiments demonstrate that all the introduced IConv, DRWF and attention mechanisms significantly contribute to enhancing the proposed STGCA model’s predictive accuracy for PM2.5 concentrations. By jointly improving the model’s capacity to capture complex spatial and temporal dependencies, our proposed strategies achieve high performance in spatio-temporal prediction tasks.
4.2. Comparative Experiments
Performance Comparisons Among Prediction Models
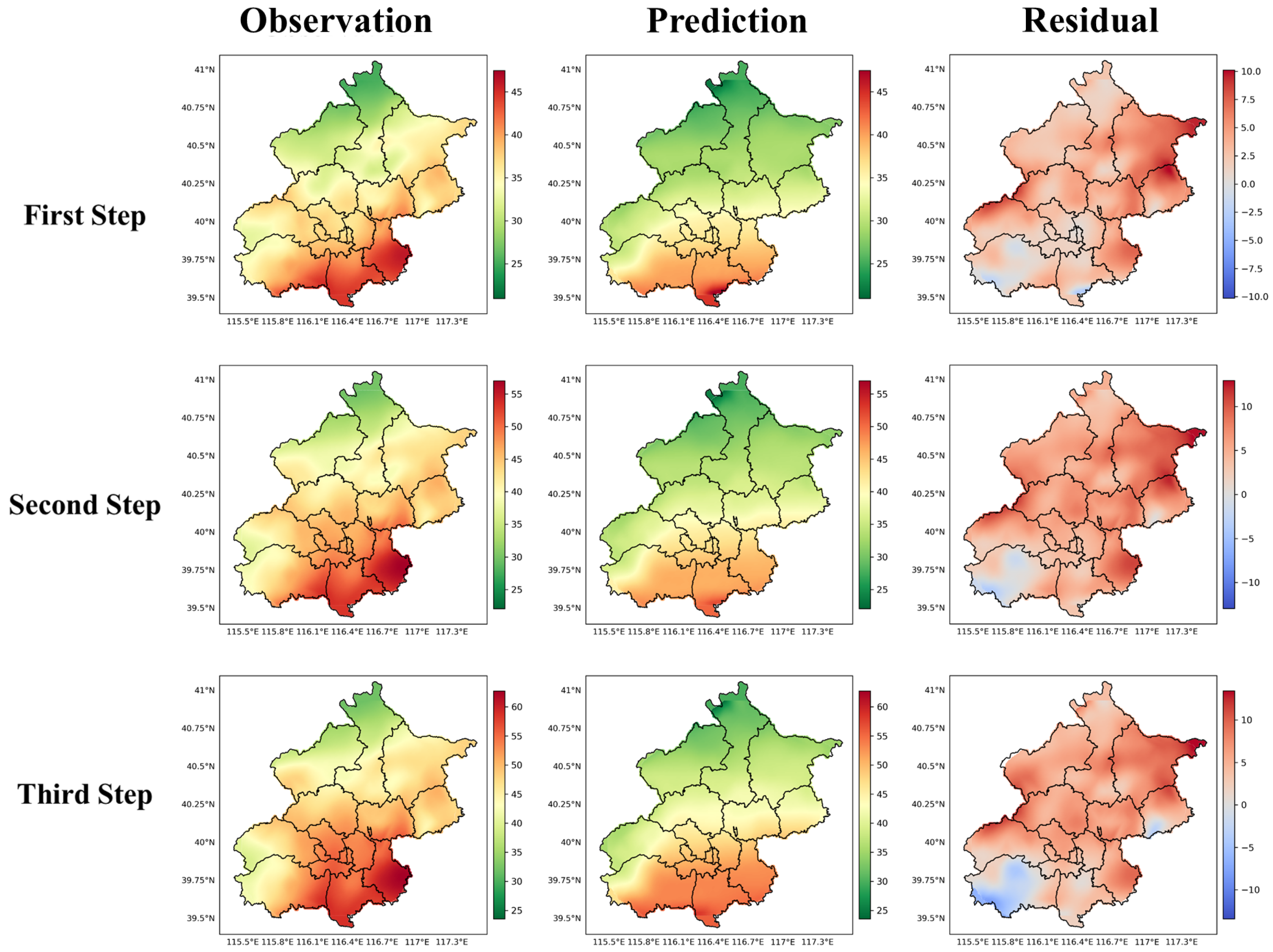
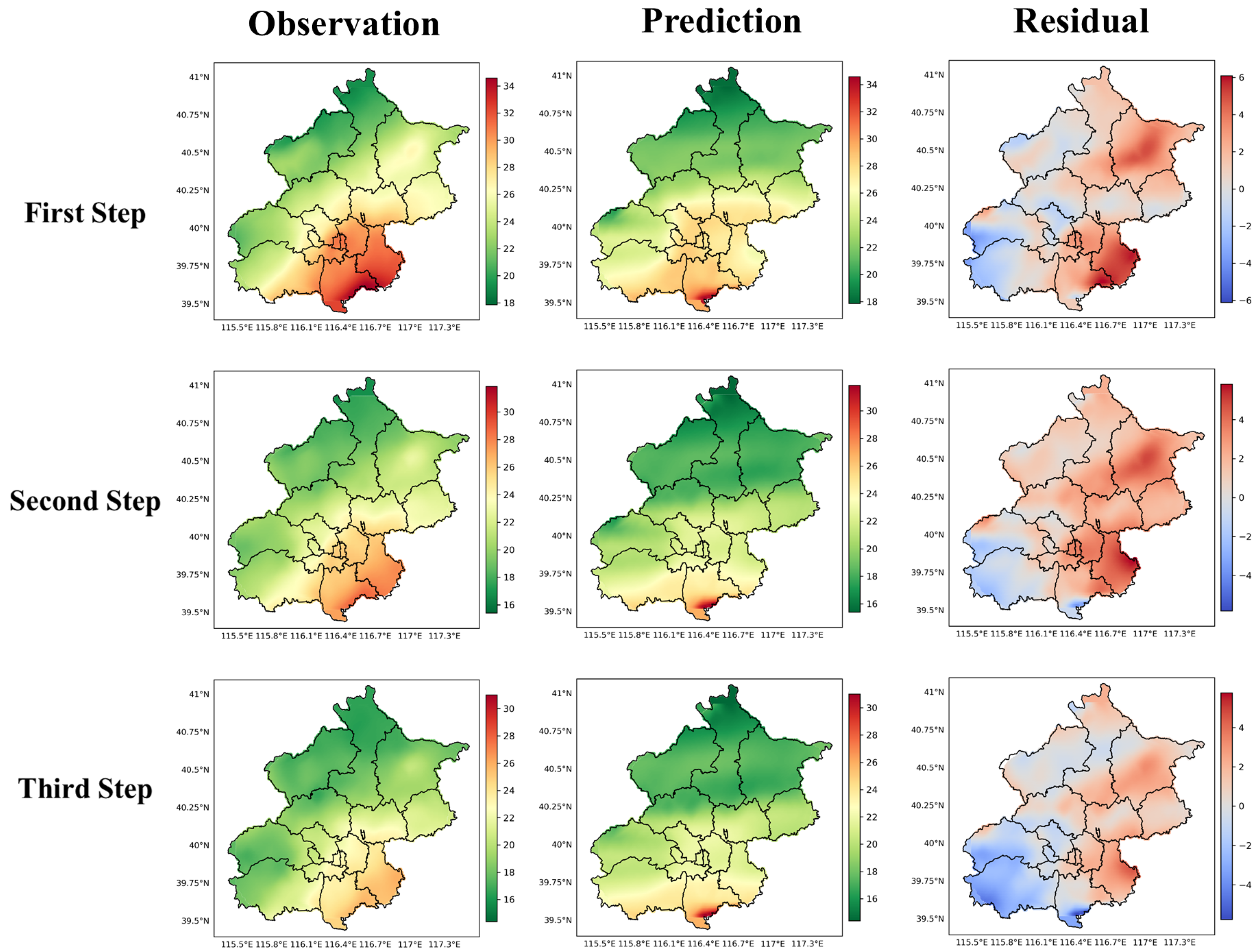
4.3. Comparisons Between Prediction and Observation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Hill, W.; Lim, E.L.; Weeden, C.E.; Lee, C.; Augustine, M.; Chen, K.; Kuan, F.C.; Marongiu, F.; Evans, E.J., Jr.; Moore, D.A.; et al. Lung adenocarcinoma promotion by air pollutants. Nature 2023, 616, 159–167. [Google Scholar] [CrossRef] [PubMed]
- Mo, X.; Li, H.; Zhang, L.; Qu, Z. Environmental impact estimation of PM2.5 in representative regions of China from 2015 to 2019: Policy validity, disaster threat, health risk, and economic loss. Air Qual. Atmos. Health 2021, 14, 1571–1585. [Google Scholar] [CrossRef]
- Fann, N.L.; Nolte, C.G.; Sarofim, M.C.; Martinich, J.; Nassikas, N.J. Associations between simulated future changes in climate, air quality, and human health. JAMA Netw. Open 2021, 4, e2032064. [Google Scholar] [CrossRef] [PubMed]
- Yarragunta, Y.; Francis, D.; Fonseca, R.; Nelli, N. Evaluation of the WRF-Chem performance for the air pollutants over the United Arab Emirates. Atmos. Chem. Phys. 2025, 25, 1685–1709. [Google Scholar] [CrossRef]
- Bhatti, U.A.; Yan, Y.; Zhou, M.; Ali, S.; Hussain, A.; Qingsong, H.; Yu, Z.; Yuan, L. Time series analysis and forecasting of air pollution particulate matter (PM2.5): An SARIMA and factor analysis approach. IEEE Access 2021, 9, 41019–41031. [Google Scholar] [CrossRef]
- Abdullah, S.; Napi, N.N.L.M.; Ahmed, A.N.; Mansor, W.N.W.; Mansor, A.A.; Ismail, M.; Abdullah, A.M.; Ramly, Z.T.A. Development of multiple linear regression for particulate matter (PM10) forecasting during episodic transboundary haze event in Malaysia. Atmosphere 2020, 11, 289. [Google Scholar] [CrossRef]
- Xu, X.; Tong, T.; Zhang, W.; Meng, L. Fine-grained prediction of PM2.5 concentration based on multisource data and deep learning. Atmos. Pollut. Res. 2020, 11, 1728–1737. [Google Scholar] [CrossRef]
- Masood, A.; Ahmad, K. A model for particulate matter (PM2.5) prediction for Delhi based on machine learning approaches. Procedia Comput. Sci. 2020, 167, 2101–2110. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, X.; Wang, X. PM2.5 prediction based on modified whale optimization algorithm and support vector regression. Sci. Rep. 2024, 14, 23296. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Do, K.; Li, Z.; Jiang, X.; Maji, K.J.; Ivey, C.E.; Russell, A.G. Predicting PM2.5 levels and exceedance days using machine learning methods. Atmos. Environ. 2024, 323, 120396. [Google Scholar] [CrossRef]
- Pan, B. Application of XGBoost algorithm in hourly PM2.5 concentration prediction. IOP Conf. Ser. Earth Environ. Sci. 2018, 113, 012127. [Google Scholar] [CrossRef]
- Maleki, H.; Sorooshian, A.; Goudarzi, G.; Baboli, Z.; Tahmasebi Birgani, Y.; Rahmati, M. Air pollution prediction by using an artificial neural network model. Clean Technol. Environ. Policy 2019, 21, 1341–1352. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wang, J.; Li, R.; Lu, H. Novel analysis–forecast system based on multi-objective optimization for air quality index. J. Clean. Prod. 2019, 208, 1365–1383. [Google Scholar] [CrossRef]
- Kow, P.Y.; Chang, L.C.; Lin, C.Y.; Chou, C.C.K.; Chang, F.J. Deep neural networks for spatiotemporal PM2.5 forecasts based on atmospheric chemical transport model output and monitoring data. Environ. Pollut. 2022, 306, 119348. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Cao, H.; Thé, J.; Yu, H. A hybrid model for multi-step coal price forecasting using decomposition technique and deep learning algorithms. Appl. Energy 2022, 306, 118011. [Google Scholar] [CrossRef]
- Zhang, K.; Thé, J.; Xie, G.; Yu, H. Multi-step ahead forecasting of regional air quality using spatial-temporal deep neural networks: A case study of Huaihai Economic Zone. J. Clean. Prod. 2020, 277, 123231. [Google Scholar] [CrossRef]
- Lim, B.; Zohren, S. Time-series forecasting with deep learning: A survey. Philos. Trans. R. Soc. A 2021, 379, 20200209. [Google Scholar] [CrossRef]
- Abirami, S.; Chitra, P. Regional air quality forecasting using spatiotemporal deep learning. J. Clean. Prod. 2021, 283, 125341. [Google Scholar] [CrossRef]
- Acikgoz, H. A novel approach based on integration of convolutional neural networks and deep feature selection for short-term solar radiation forecasting. Appl. Energy 2022, 305, 117912. [Google Scholar] [CrossRef]
- Sayeed, A.; Choi, Y.; Eslami, E.; Lops, Y.; Roy, A.; Jung, J. Using a deep convolutional neural network to predict 2017 ozone concentrations, 24 hours in advance. Neural Netw. 2020, 121, 396–408. [Google Scholar] [CrossRef] [PubMed]
- Mo, X.; Li, H.; Zhang, L. Design a regional and multistep air quality forecast model based on deep learning and domain knowledge. Front. Earth Sci. 2022, 10, 995843. [Google Scholar] [CrossRef]
- Ehteram, M.; Ahmed, A.N.; Khozani, Z.S.; El-Shafie, A. Graph convolutional network–Long short term memory neural network-multi layer perceptron-Gaussian progress regression model: A new deep learning model for predicting ozone concertation. Atmos. Pollut. Res. 2023, 14, 101766. [Google Scholar] [CrossRef]
- Chen, Q.; Ding, R.; Mo, X.; Li, H.; Xie, L.; Yang, J. An adaptive adjacency matrix-based graph convolutional recurrent network for air quality prediction. Sci. Rep. 2024, 14, 4408. [Google Scholar] [CrossRef] [PubMed]
- Bai, H.; Shi, Y.; Seong, M.; Gao, W.; Li, Y. Influence of spatial resolution on satellite-based PM2.5 estimation: Implications for health assessment. Remote Sens. 2022, 14, 2933. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z. China High Resolution High Quality PM2.5 Dataset (2000–2021); National Tibetan Plateau/Third Pole Environment Data Center: Beijing, China, 2023. [Google Scholar]
- Mathias, S.; Wayland, R. Fine Particulate Matter (PM2.5) Precursor Demonstration Guidance; Office of Air Quality Planning and Standards, United States Environmental Protection Agency: Washington, DC, USA, 2019. [Google Scholar]
- Muñoz Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Cai, W.; Li, K.; Liao, H.; Wang, H.; Wu, L. Weather conditions conducive to Beijing severe haze more frequent under climate change. Nat. Clim. Change 2017, 7, 257–262. [Google Scholar] [CrossRef]
- Bai, K.; Li, K.; Ma, M.; Li, K.; Li, Z.; Guo, J.; Chang, N.B.; Tan, Z.; Han, D. LGHAP: A Long-term Gap-free High-resolution Air Pollutants concentration dataset derived via tensor flow based multimodal data fusion. Earth Syst. Sci. Data Discuss. 2021, 2021, 1–39. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Kahn, R.; Levy, R.; Verduzco, C.; Villeneuve, P.J. Global estimates of ambient fine particulate matter concentrations from satellite-based aerosol optical depth: Development and application. Environ. Health Perspect. 2010, 118, 847–855. [Google Scholar] [CrossRef]
- Gong, C.; Xian, C.; Wu, T.; Liu, J.; Ouyang, Z. Role of urban vegetation in air phytoremediation: Differences between scientific research and environmental management perspectives. npj Urban Sustain. 2023, 3, 24. [Google Scholar] [CrossRef]
- Yao, R.; Wang, L.; Huang, X.; Sun, L.; Chen, R.; Wu, X.; Zhang, W.; Niu, Z. A robust method for filling the gaps in MODIS and VIIRS land surface temperature data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10738–10752. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar] [PubMed]
- Wang, W.; Zhao, S.; Jiao, L.; Taylor, M.; Zhang, B.; Xu, G.; Hou, H. Estimation of PM2.5 concentrations in China using a spatial back propagation neural network. Sci. Rep. 2019, 9, 13788. [Google Scholar] [CrossRef] [PubMed]
- Getis, A.; Aldstadt, J. Constructing the spatial weights matrix using a local statistic. Geogr. Anal. 2004, 36, 90–104. [Google Scholar] [CrossRef]
- Yang, H.; Zhu, Z.; Li, C.; Li, R. A novel combined forecasting system for air pollutants concentration based on fuzzy theory and optimization of aggregation weight. Appl. Soft Comput. 2020, 87, 105972. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, X.; Cao, H.; Thé, J.; Tan, Z.; Yu, H. Multi-step forecast of PM2.5 and PM10 concentrations using convolutional neural network integrated with spatial–temporal attention and residual learning. Environ. Int. 2023, 171, 107691. [Google Scholar] [CrossRef]
- Bahdanau, D. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Wang, H.; Chen, Z.; Zhang, P. Spatial Autocorrelation and Temporal Convergence of PM2.5 Concentrations in Chinese Cities. Int. J. Environ. Res. Public Health 2022, 19, 13942. [Google Scholar] [CrossRef]
- Chae, S.; Shin, J.; Kwon, S.; Lee, S.; Kang, S.; Lee, D. PM10 and PM2.5 real-time prediction models using an interpolated convolutional neural network. Sci. Rep. 2021, 11, 11952. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Wu, F.; Souza, A.; Zhang, T.; Fifty, C.; Yu, T.; Weinberger, K. Simplifying graph convolutional networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6861–6871. [Google Scholar]
- Chen, Z.M.; Wei, X.S.; Wang, P.; Guo, Y. Multi-label image recognition with graph convolutional networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5177–5186. [Google Scholar]
- Marino, R.; Buffoni, L.; Chicchi, L.; Giambagli, L.; Fanelli, D. Stable attractors for neural networks classification via ordinary differential equations (SA-nODE). Mach. Learn. Sci. Technol. 2024, 5, 035087. [Google Scholar] [CrossRef]
- Gasteiger, J.; Bojchevski, A.; Günnemann, S. Predict then propagate: Graph neural networks meet personalized pagerank. arXiv 2018, arXiv:1810.05997. [Google Scholar]
- Cho, K. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Sutskever, I. Sequence to Sequence Learning with Neural Networks. arXiv 2014, arXiv:1409.3215. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inf. Process. Syst. 2016, 29, 1386–1394. [Google Scholar]
- Atwood, J.; Towsley, D. Diffusion-convolutional neural networks. Adv. Neural Inf. Process. Syst. 2016, 29, 1993–2001. [Google Scholar]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. arXiv 2017, arXiv:1707.01926. [Google Scholar]
- Gholamzadeh, F.; Bourbour, S. Air pollution forecasting for Tehran city using Vector Auto Regression. In Proceedings of the 2020 6th Iranian Conference on Signal Processing and Intelligent Systems (ICSPIS), Mashhad, Iran, 23–24 December 2020; pp. 1–5. [Google Scholar]
- Yu, W.; Li, J.; Liu, Q.; Zhao, J.; Dong, Y.; Wang, C.; Lin, S.; Zhu, X.; Zhang, H. Spatial–Temporal Prediction of Vegetation Index With Deep Recurrent Neural Networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 922–929. [Google Scholar]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the dots: Multivariate time series forecasting with graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 23–27 August 2020; pp. 753–763. [Google Scholar]
- Jin, M.; Zheng, Y.; Li, Y.F.; Chen, S.; Yang, B.; Pan, S. Multivariate time series forecasting with dynamic graph neural odes. IEEE Trans. Knowl. Data Eng. 2022, 35, 9168–9180. [Google Scholar] [CrossRef]




| Data Type | Variable | Unit | Source |
|---|---|---|---|
| Pollutant | PM2.5 | µg/m3 | CHAP |
| Concentration | PM10 | µg/m3 | CHAP |
| NO2 | µg/m3 | CHAP | |
| CO | mg/m3 | CHAP | |
| O3 | µg/m3 | CHAP | |
| SO2 | µg/m3 | CHAP | |
| Meteorological | D2m | °C | ECMWF ERA5 |
| Factor | T2m | °C | ECMWF ERA5 |
| TP | mm | ECMWF ERA5 | |
| UW | m/s | ECMWF ERA5 | |
| VW | m/s | ECMWF ERA5 | |
| SP | hPa | ECMWF ERA5 | |
| SSR | MJ/m2 | ECMWF ERA5 | |
| Others | AOD | CHAP | |
| NDVI | NEO |
| ADF Statistic | 1% | 5% | 10% | p-Value |
|---|---|---|---|---|
| −5.9135 | −3.4314 | −2.8620 | −2.5670 |
| Metric | Calculation Formula |
|---|---|
| RMSE | |
| MAE | |
| MAPE | |
| IA | |
| TIC |
| Training Parameters | Method/Value |
|---|---|
| Observation window | 30 days |
| Prediction window | 3 days |
| Number of hidden layer neurons | 64 |
| Activation function of convolutional | Tanh |
| Activation function of fully connected layers in decoder | ReLU |
| Dropout ratio | 30% |
| Loss function | MAE |
| Optimization algorithm | Adam |
| Initial learning rate | 0.001 |
| Batch size | 128 |
| Training epochs | 300 |
| Time Step | Model | RMSE | MAE | MAPE | IA | TIC |
|---|---|---|---|---|---|---|
| First Step | GC-LSTM | 5.63 | 3.94 | 13.12 | 0.81 | 0.09 |
| GC-GRU | 4.21 | 3.11 | 11.41 | 0.98 | 0.06 | |
| Second Step | GC-LSTM | 6.21 | 4.51 | 14.20 | 0.78 | 0.11 |
| GC-GRU | 5.08 | 3.69 | 13.34 | 0.97 | 0.08 | |
| Third Step | GC-LSTM | 7.02 | 5.13 | 15.89 | 0.73 | 0.13 |
| GC-GRU | 6.54 | 4.61 | 16.62 | 0.95 | 0.10 |
| Time Step | Model | RMSE | MAE | MAPE | IA | TIC |
|---|---|---|---|---|---|---|
| First Step | CConv | 7.33 | 5.47 | 19.93 | 0.92 | 0.12 |
| DConv | 7.73 | 5.27 | 16.37 | 0.90 | 0.13 | |
| IConv | 4.21 | 3.11 | 11.41 | 0.98 | 0.06 | |
| Second Step | CConv | 8.89 | 6.15 | 20.10 | 0.90 | 0.13 |
| DConv | 8.10 | 6.32 | 19.88 | 0.89 | 0.11 | |
| IConv | 5.08 | 3.69 | 13.34 | 0.97 | 0.08 | |
| Third Step | CConv | 9.40 | 7.63 | 21.34 | 0.88 | 0.15 |
| DConv | 9.65 | 7.71 | 20.41 | 0.87 | 0.13 | |
| IConv | 6.54 | 4.61 | 16.62 | 0.95 | 0.10 |
| Time Step | Model | RMSE | MAE | MAPE | IA | TIC |
|---|---|---|---|---|---|---|
| First Step | LF | 5.57 | 4.34 | 17.31 | 0.95 | 0.09 |
| RWF | 6.90 | 5.35 | 22.33 | 0.93 | 0.10 | |
| DRWF | 4.21 | 3.11 | 11.41 | 0.98 | 0.06 | |
| Second Step | LF | 6.80 | 5.50 | 18.00 | 0.94 | 0.10 |
| RWF | 7.20 | 5.60 | 23.00 | 0.92 | 0.11 | |
| DRWF | 5.08 | 3.69 | 13.34 | 0.97 | 0.08 | |
| Third Step | LF | 7.00 | 5.70 | 20.50 | 0.93 | 0.13 |
| RWF | 7.50 | 5.80 | 25.50 | 0.90 | 0.12 | |
| DRWF | 6.54 | 4.61 | 16.62 | 0.95 | 0.10 |
| Time Step | Model | RMSE | MAE | MAPE | IA | TIC |
|---|---|---|---|---|---|---|
| First Step | STGC | 4.70 | 4.22 | 13.89 | 0.93 | 0.09 |
| STGCA | 4.21 | 3.11 | 11.41 | 0.98 | 0.06 | |
| Second Step | STGC | 5.31 | 4.38 | 14.26 | 0.92 | 0.10 |
| STGCA | 5.08 | 3.69 | 13.34 | 0.97 | 0.08 | |
| Third Step | STGC | 6.83 | 4.89 | 17.02 | 0.91 | 0.11 |
| STGCA | 6.54 | 4.61 | 16.62 | 0.95 | 0.10 |
| Time Step | Model | RMSE | MAE | MAPE | IA | TIC | Time (s) |
|---|---|---|---|---|---|---|---|
| VAR | 8.13 | 4.98 | 16.19 | 0.98 | 0.08 | 221.5 | |
| FCLSTM | 8.10 | 5.97 | 13.93 | 0.93 | 0.13 | 1480.7 | |
| First Step | ASTGCN | 7.46 | 4.72 | 9.00 | 0.84 | 0.17 | 1855.2 |
| MTGNN | 7.54 | 5.42 | 18.72 | 0.91 | 0.12 | 2160.4 | |
| MTGODE | 4.38 | 3.22 | 10.68 | 0.98 | 0.07 | 2450.9 | |
| STGCA | 4.21 | 3.11 | 11.41 | 0.98 | 0.06 | 1602.0 | |
| VAR | 11.51 | 7.06 | 21.42 | 0.96 | 0.12 | 221.5 | |
| FCLSTM | 9.50 | 6.60 | 15.50 | 0.91 | 0.14 | 1480.7 | |
| Second Step | ASTGCN | 9.62 | 6.36 | 12.00 | 0.88 | 0.16 | 1855.2 |
| MTGNN | 7.77 | 2.33 | 19.10 | 0.91 | 0.12 | 2160.4 | |
| MTGODE | 6.98 | 5.03 | 16.43 | 0.94 | 0.10 | 2450.9 | |
| STGCA | 5.08 | 3.69 | 13.34 | 0.97 | 0.08 | 1602.0 | |
| VAR | 14.55 | 9.15 | 26.54 | 0.93 | 0.15 | 221.5 | |
| FCLSTM | 10.00 | 7.20 | 16.00 | 0.90 | 0.14 | 1480.7 | |
| Third Step | ASTGCN | 11.03 | 7.58 | 21.00 | 0.70 | 0.28 | 1855.2 |
| MTGNN | 9.47 | 6.90 | 23.21 | 0.85 | 0.15 | 2160.4 | |
| MTGODE | 10.23 | 7.79 | 28.56 | 0.82 | 0.15 | 2450.9 | |
| STGCA | 6.54 | 4.61 | 16.62 | 0.95 | 0.10 | 1602.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, X.; Mo, X.; Li, H. A Novel Spatio-Temporal Graph Convolutional Network with Attention Mechanism for PM2.5 Concentration Prediction. Mach. Learn. Knowl. Extr. 2025, 7, 88. https://doi.org/10.3390/make7030088
Guan X, Mo X, Li H. A Novel Spatio-Temporal Graph Convolutional Network with Attention Mechanism for PM2.5 Concentration Prediction. Machine Learning and Knowledge Extraction. 2025; 7(3):88. https://doi.org/10.3390/make7030088
Chicago/Turabian StyleGuan, Xin, Xinyue Mo, and Huan Li. 2025. "A Novel Spatio-Temporal Graph Convolutional Network with Attention Mechanism for PM2.5 Concentration Prediction" Machine Learning and Knowledge Extraction 7, no. 3: 88. https://doi.org/10.3390/make7030088
APA StyleGuan, X., Mo, X., & Li, H. (2025). A Novel Spatio-Temporal Graph Convolutional Network with Attention Mechanism for PM2.5 Concentration Prediction. Machine Learning and Knowledge Extraction, 7(3), 88. https://doi.org/10.3390/make7030088






