Multilayer Perceptron Mapping of Subjective Time Duration onto Mental Imagery Vividness and Underlying Brain Dynamics: A Neural Cognitive Modeling Approach
Abstract
1. Introduction
- Very short durations (90 ms to 234–252 ms)
- Short durations (234–252 ms to 585–630 ms)
- Intermediate durations (585–630 ms to 1080–1170 ms)
- Long durations (1080–1170 ms to 2070 ms)
- Very long durations (>2070 ms)
1.1. Neural Networks
1.2. Analysis
1.3. Test and Evaluation
2. Materials and Methods
2.1. Dataset and Preprocessing
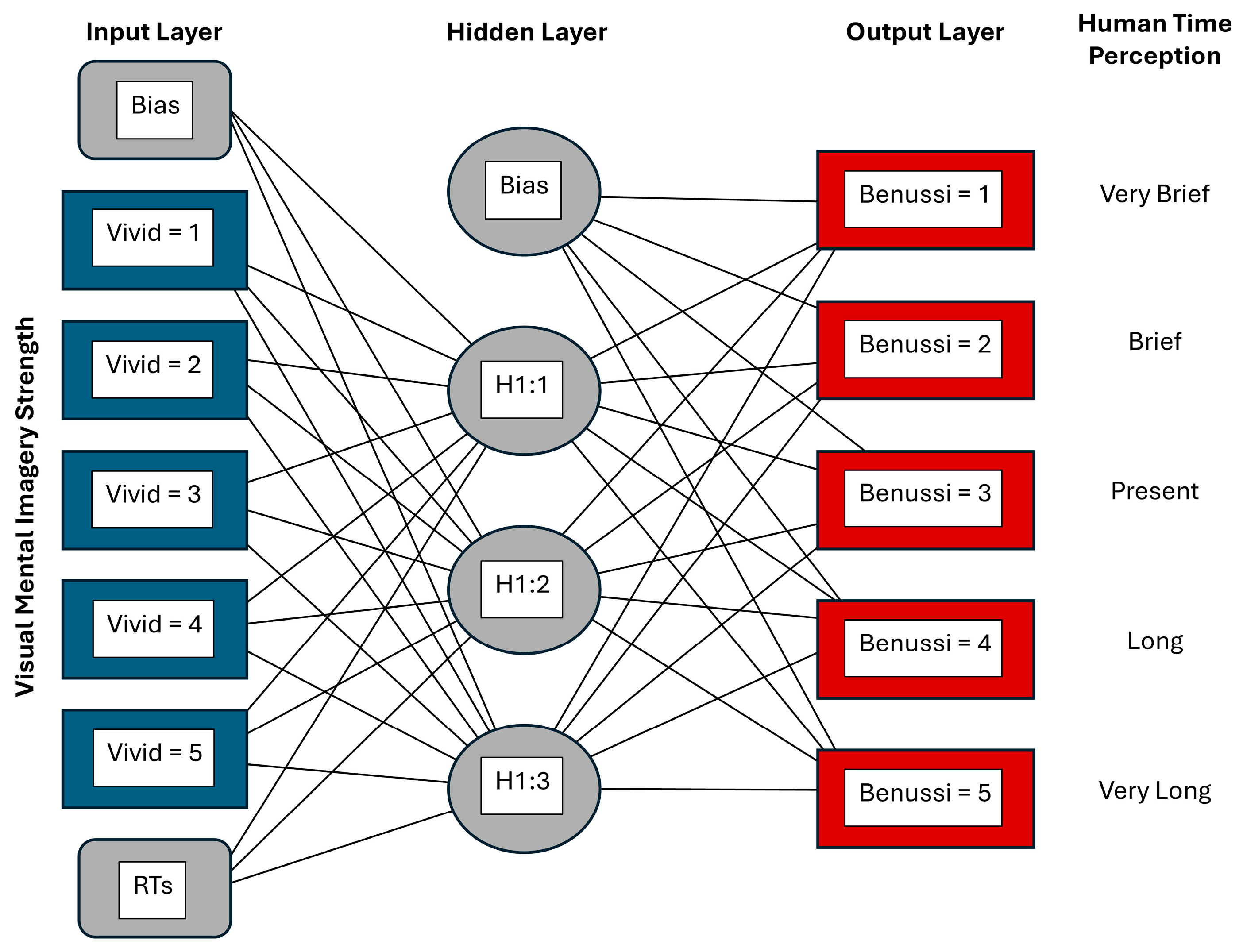
2.2. Multilayer Perceptron Model
- Input Layer: Five nodes representing factors of vividness levels (1 = No Image to 5 = Very Vivid), one standardized (z-score normalized) reaction time covariate node, and an additional bias node. The five vividness inputs were one-hot encoded so that for each trial, only one vividness node carried a value of 1 and the remaining four carried a value of 0. The standardized reaction time covariate node would typically pass a non-zero value, except in cases where it equalled the sample mean;
- Hidden Layer: A single layer comprising three nodes with sigmoid activation and an additional bias node;
- Output Layer: Five nodes corresponding to the Benussi categories (1 = very short durations to 5 = very long durations) using a softmax activation function with categorical cross-entropy as the loss measure. As the Benussi categories were encoded as distinct classes (through one-hot encoding), there was no need to numerically rescale the dependent variables.
2.3. Analysis of Hidden Node Weights
3. Results
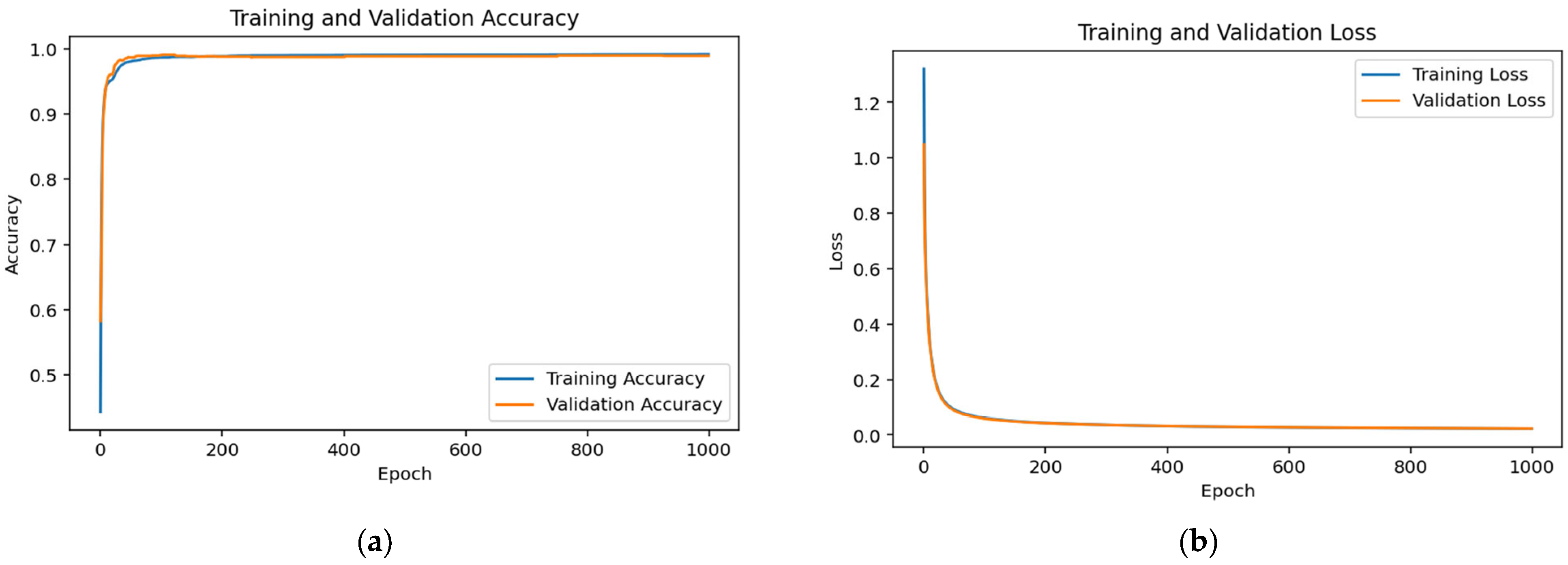
3.1. Accuracy and Loss
3.2. Precision, Recall, and F1-Score
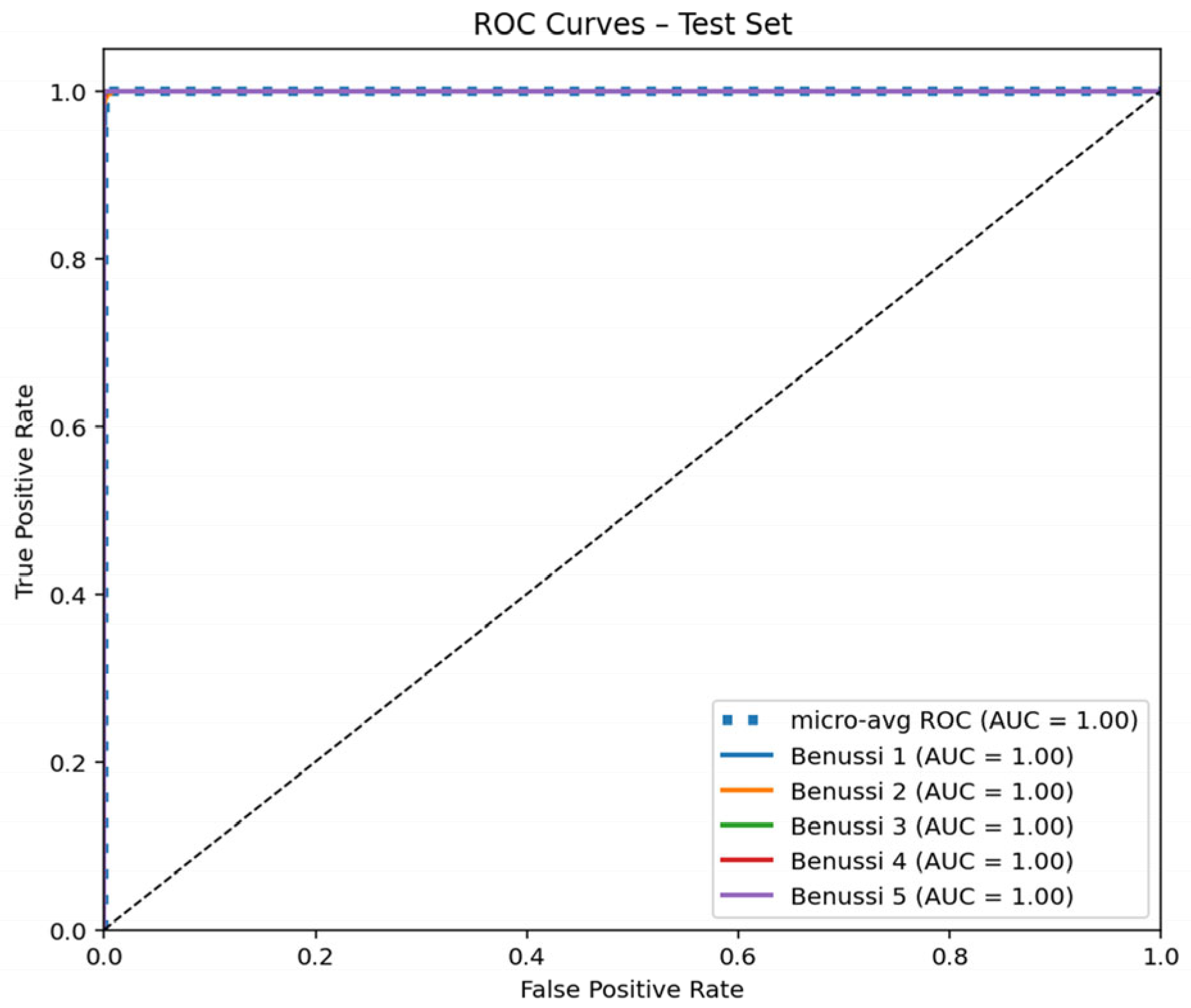
3.3. ROC Curve
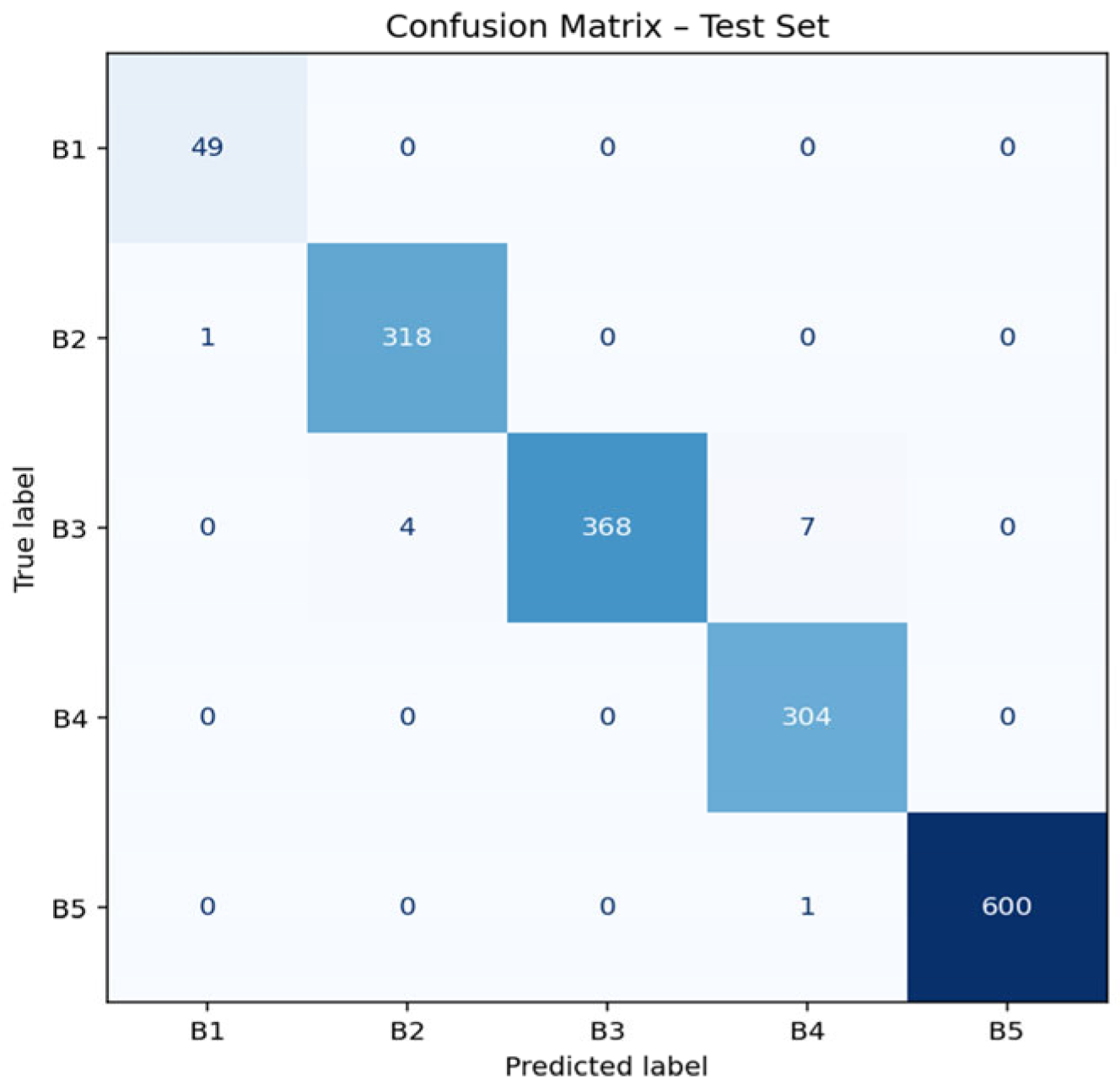
3.4. Confusion Matrix
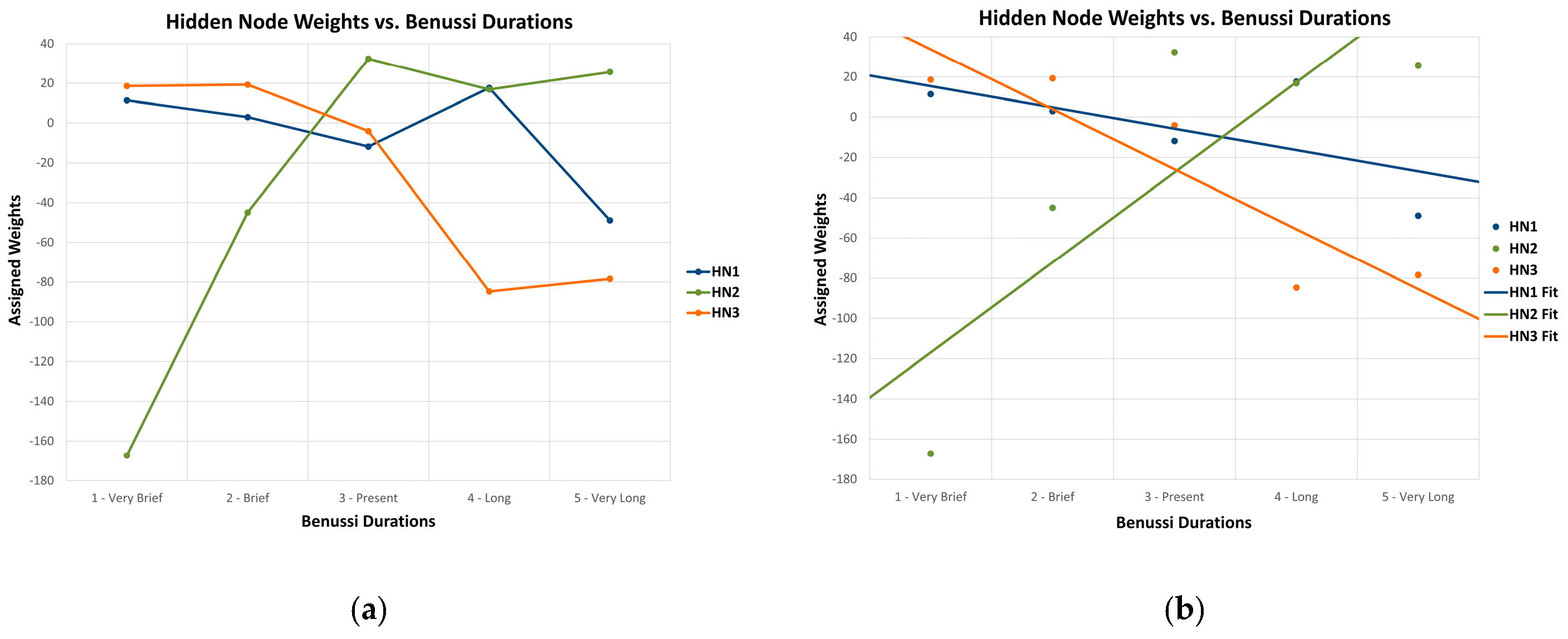
3.5. Correlation Analysis of Hidden Node Weights
4. Discussion
4.1. Multilayer Perceptron
4.2. Task Positive Network
4.3. Default Mode Network
4.4. Salience Network
4.5. Future Research Directions
4.6. Limitations to Methodology
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HDC | Hierarchical decomposition constraint |
| MLP | Multilayer perceptron |
| TPN | Task positive network |
| DMN | Default mode network |
| SN | Salience network |
| ROC | Receiver operating characteristic |
| AUC | Area under the curve |
Appendix A
Appendix A.1. MLP Python Script
import os
# <<< NEW: define seed and set env vars BEFORE any TF import
seed = 42
os.environ[“PYTHONHASHSEED”] = str(seed) # Python hash seed
os.environ[“TF_DETERMINISTIC_OPS”] = “1” # TF deterministic ops (>=TF2.13)
os.environ[“TF_ENABLE_ONEDNN_OPTS”] = “0” # disable oneDNN non-determinism
os.environ[‘TF_CPP_MIN_LOG_LEVEL’] = ‘2’ # only show errors, hide INFO and WARNING
# Standard libs
import random
random.seed(seed) # seed Python RNG
import time
import datetime
# Data libs
import pandas as pd
import numpy as np
np.random.seed(seed) # seed NumPy RNG
# TensorFlow import & determinism setup
# Note: Requires using tf.keras; ensure you’ve uninstalled standalone ‘keras’ package
# pip uninstall keras
import tensorflow as tf # MUST follow env vars & RNG seeds
try:
tf.keras.utils.set_random_seed(seed) # TF >=2.11
except (AttributeError, ModuleNotFoundError, ImportError):
# Fallback for TF2.10 or missing keras.api
tf.random.set_seed(seed) # fallback for TF2.10
# fallback for TF2.10
# limit parallelism to avoid non-determinism
tf.config.threading.set_inter_op_parallelism_threads(1)
tf.config.threading.set_intra_op_parallelism_threads(1)
# Other imports (using standalone Keras for model building)
import dingsound
import matplotlib.pyplot as plt
import seaborn as sns
from itertools import cycle
from sklearn.metrics import (
roc_curve, auc, confusion_matrix,
ConfusionMatrixDisplay, classification_report
)
from sklearn.model_selection import train_test_split, StratifiedKFold
from sklearn.preprocessing import StandardScaler, LabelEncoder
# Use standalone Keras
from keras.models import Sequential
from keras.layers import Dense, Input
from keras.optimizers import Adam
from keras.callbacks import EarlyStopping, Callback
# -----------------------------------------------------------------------------
# Utility Callbacks (unchanged)
# ----------------------------------------------------------------------------- (unchanged)
# -----------------------------------------------------------------------------
def get_callbacks():
early_stopping = EarlyStopping(
monitor = “val_loss”, patience = 30,
restore_best_weights = True, verbose = 1
)
relative_early_stopping = EarlyStopping(
monitor = “val_loss”, min_delta = 1 × 10−4,
patience = 20, restore_best_weights = True,
verbose = 1
)
class TimeStopping(Callback):
def __init__(self, seconds = None, verbose = 0):
super().__init__()
self.seconds = seconds
self.verbose = verbose
self.start_time = None
def on_train_begin(self, logs = None):
self.start_time = time.time()
def on_epoch_end(self, epoch, logs = None):
if time.time()-self.start_time > self.seconds:
if self.verbose:
print(f”\nTimeStopping: training stopped after {self.seconds} seconds.”)
self.model.stop_training = True
return [early_stopping, relative_early_stopping, TimeStopping(seconds = 900, verbose = 1)]
# -------- Load & preprocess data --------
file_path = “Benussi Data.xlsx”
df = pd.read_excel(file_path)
label_encoder = LabelEncoder()
df[“Vivid”] = label_encoder.fit_transform(df[“Vivid”])
vivid_dummies = pd.get_dummies(df[“Vivid”], prefix = “Vivid”)
X = pd.concat([vivid_dummies, df[[“RTs”]]], axis = 1).astype(np.float32).values
y = pd.get_dummies(df[“Benussi”]).astype(np.float32).values
y_labels = np.argmax(y, axis = 1)
# -----------------------------------------------------------------------------
# Independent Train/Test split BEFORE cross-validation (no test leakage)
# -----------------------------------------------------------------------------
X_remain, X_test, y_remain, y_test = train_test_split(
X, y, test_size = 0.15, stratify = y_labels, random_state = seed
)
y_remain_labels = np.argmax(y_remain, axis = 1)
print(f”Hold-out Test Set: {len(X_test)} samples held aside”)
# -----------------------------------------------------------------------------
# Stratified K-Fold Cross-Validation on the remaining data (no test leakage)
# -----------------------------------------------------------------------------
print(“Running Stratified K-Fold Cross-Validation…”)
k = 5
skf = StratifiedKFold(n_splits = k, shuffle = True, random_state = seed)
fold_acc, fold_loss, fold_time, fold_early = [], [], [], []
for fold, (train_idx, val_idx) in enumerate(skf.split(X_remain, y_remain_labels), start = 1):
# reproducible initialization per fold
random.seed(seed + fold)
np.random.seed(seed + fold)
try:
tf.random.set_seed(seed + fold)
except Exception:
pass
print(f”\nTraining fold {fold}/{k}...”)
# 1) Build fold-specific datasets
X_train_fold = X_remain[train_idx].copy()
y_train_fold = y_remain[train_idx]
X_val_fold = X_remain[val_idx].copy()
y_val_fold = y_remain[val_idx]
# 2) Scale RT feature on TRAIN only, then apply to VAL
scaler_cv = StandardScaler().fit(
X_train_fold[:, −1].reshape(−1, 1)
)
X_train_fold[:, −1] = scaler_cv.transform(
X_train_fold[:, −1].reshape(−1, 1)
).ravel()
X_val_fold[:, −1] = scaler_cv.transform(
X_val_fold[:, −1].reshape(−1, 1)
).ravel()
# 3) Instantiate a fresh model for this fold
model_cv = Sequential([
Dense(3, activation = “sigmoid”,
input_shape = (X_train_fold.shape[1],)),
Dense(y.shape[1], activation = “softmax”),
])
model_cv.compile(
optimizer = Adam(learning_rate = 0.01),
loss = “categorical_crossentropy”,
metrics = [“accuracy”],
)
# 4) Train & time it
cb = get_callbacks()
t0 = time.time()
hist = model_cv.fit(
X_train_fold, y_train_fold,
epochs = 1000, batch_size = 32,
validation_data = (X_val_fold, y_val_fold),
callbacks = cb,
shuffle = False,
verbose = 0,
)
t1 = time.time()
# 5) Record metrics
fold_time.append(t1 − t0)
fold_loss.append(hist.history[“val_loss”][−1])
fold_acc.append(hist.history[“val_accuracy”][−1])
fold_early.append(len(hist.history[“loss”]) < 1000)
# Summarize CV results
print(
f”\nStratified K-Fold Results on Remain Set: “
f”avg acc = {np.mean(fold_acc):.4f}, “
f”avg loss = {np.mean(fold_loss):.4f}, “
f”avg time = {np.mean(fold_time):.2f}s, “
f”early stops = {sum(fold_early)}/{k}”
)
# -----------------------------------------------------------------------------
# Final Training on Remaining -> Validation and Evaluate on Hold-out Test
# -----------------------------------------------------------------------------
# Split remaining into train/val
X_train, X_val, y_train, y_val = train_test_split(
X_remain, y_remain,
test_size = 0.17647, stratify = y_remain_labels, random_state = seed
)
# scale RT on X_train only
scaler = StandardScaler().fit(X_train[:, −1].reshape(−1,1))
X_train[:, −1] = scaler.transform(X_train[:, −1].reshape(−1,1)).ravel()
X_val[:, −1] = scaler.transform(X_val[:, −1].reshape(−1,1)).ravel()
X_test[:, −1] = scaler.transform(X_test[:, −1].reshape(−1,1)).ravel()
print(f”Dataset sizes → Train: {X_train.shape[0]}, Validation: {X_val.shape[0]}, Test: {X_test.shape[0]}”)
# -----------------------------------------------------------------------------
# Build & compile model using tf.keras exclusively
# -----------------------------------------------------------------------------
model = Sequential([
Dense(3, activation = “sigmoid”, input_shape = (X_train.shape[1],)), # specify input shape here instead of Input layer
Dense(y.shape[1], activation = “softmax”),
])
model.compile(
optimizer = Adam(learning_rate = 0.01),
loss = “categorical_crossentropy”,
metrics = [“accuracy”],
)
# -----------------------------------------------------------------------------
# Train with deterministic batches
# -----------------------------------------------------------------------------
callbacks = get_callbacks()
start_time = time.time()
history = model.fit(
X_train, y_train,
epochs = 1000, batch_size = 32,
validation_data = (X_val, y_val),
callbacks = callbacks,
shuffle = False,
verbose = 0,
)
elapsed = time.time()-start_time
train_acc_last = history.history[“accuracy”][−1]
val_acc_last = history.history[“val_accuracy”][−1]
train_loss_last = history.history[“loss”][−1]
val_loss_last = history.history[“val_loss”][−1]
print(f”\nFinal Training Accuracy (last epoch): {train_acc_last:.4f}”)
print(f”Final Validation Accuracy (last epoch): {val_acc_last:.4f}”)
print(f”Final Training Loss: {train_loss_last:.4f}”)
print(f”Final Validation Loss: {val_loss_last:.4f}”)
print(f”Total Training Time: {elapsed:.2f} s”)
# -----------------------------------------------------------------------------
# Evaluate on all three splits
# -----------------------------------------------------------------------------
train_loss_eval, train_acc_eval = model.evaluate(X_train, y_train, verbose = 0)
val_loss_eval, val_acc_eval = model.evaluate(X_val, y_val, verbose = 0)
test_loss_eval, test_acc_eval = model.evaluate(X_test, y_test, verbose = 0)
print(“\nFinal Performance:”)
print(f” • Training –loss: {train_loss_eval:.4f}, acc: {train_acc_eval:.4f}”)
print(f” • Validation–loss: {val_loss_eval:.4f}, acc: {val_acc_eval:.4f}”)
print(f” • Test –loss: {test_loss_eval:.4f}, acc: {test_acc_eval:.4f}”)
# -----------------------------------------------------------------------------
# Confusion Matrix & Classification Report (Test Set)
# -----------------------------------------------------------------------------
print(“\nClassification Report (Test Set):”)
y_test_labels = np.argmax(y_test, axis = 1)
y_pred_prob = model.predict(X_test, verbose = 0)
y_pred_labels = np.argmax(y_pred_prob, axis = 1)
print(
classification_report(
y_test_labels,
y_pred_labels,
target_names = [f”Benussi {i + 1}” for i in range(y.shape[1])],
)
)
cm = confusion_matrix(y_test_labels, y_pred_labels)
cmd = ConfusionMatrixDisplay(
cm,
display_labels = [f”B{i + 1}” for i in range(y.shape[1])],
)
fig_cm, ax_cm = plt.subplots(figsize = (6, 6))
cmd.plot(ax = ax_cm, cmap = “Blues”, colorbar = False)
ax_cm.set_title(“Confusion Matrix–Test Set”)
plt.tight_layout()
plt.show()
# -----------------------------------------------------------------------------
# ROC Curves (Multi-class, One-vs-Rest)
# -----------------------------------------------------------------------------
print(“\nPlotting ROC curves…”)
fpr = {}
tpr = {}
roc_auc = {}
for i in range(y.shape[1]):
fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_pred_prob[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# Micro-average
fpr[“micro”], tpr[“micro”], _ = roc_curve(y_test.ravel(), y_pred_prob.ravel())
roc_auc[“micro”] = auc(fpr[“micro”], tpr[“micro”])
colors = cycle([“#1f77b4”, “#ff7f0e”, “#2ca02c”, “#d62728”, “#9467bd”])
plt.figure(figsize = (7, 6))
plt.plot(
fpr[“micro”],
tpr[“micro”],
linestyle = “:”,
linewidth = 4,
label = f”micro-avg ROC (AUC = {roc_auc[‘micro’]:.2f})”,
)
for i, color in zip(range(y.shape[1]), colors):
plt.plot(
fpr[i],
tpr[i],
color = color,
lw = 2,
label = f”Benussi {i + 1} (AUC = {roc_auc[i]:.2f})”,
)
plt.plot([0, 1], [0, 1], “k--”, lw = 1)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel(“False Positive Rate”)
plt.ylabel(“True Positive Rate”)
plt.title(“ROC Curves–Test Set”)
plt.legend(loc = “lower right”)
plt.tight_layout()
plt.show()
# ————————————————————————————————————————————————————————————————
# Plot training & validation accuracy
# ————————————————————————————————————————————————————————————————
plt.figure() # new figure for accuracy
plt.plot(history.history[‘accuracy’], label = ‘Training Accuracy’)
plt.plot(history.history[‘val_accuracy’], label = ‘Validation Accuracy’)
plt.title(‘Training and Validation Accuracy’)
plt.xlabel(‘Epoch’)
plt.ylabel(‘Accuracy’)
plt.legend(loc = ‘best’)
plt.tight_layout()
plt.show()
# ————————————————————————————————————————————————————————————————
# Plot training & validation loss
# ————————————————————————————————————————————————————————————————
plt.figure() # new figure for loss
plt.plot(history.history[‘loss’], label = ‘Training Loss’)
plt.plot(history.history[‘val_loss’], label = ‘Validation Loss’)
plt.title(‘Training and Validation Loss’)
plt.xlabel(‘Epoch’)
plt.ylabel(‘Loss’)
plt.legend(loc = ‘best’)
plt.tight_layout()
plt.show()
# -----------------------------------------------------------------------------
# Record & Export Network Weights (including bias nodes)
# -----------------------------------------------------------------------------
print(“\nExporting weight matrix …”)
input_nodes = [f”Vivid {i + 1}” for i in range(5)] + [“RTs”]
hidden_nodes = [“H1_1”, “H1_2”, “H1_3”]
output_nodes = [f”Benussi {i + 1}” for i in range(y.shape[1])]
W1, bias_hidden, W2, bias_output = model.get_weights()
connections = []
# Input → Hidden
for i in range(W1.shape[0]):
for j in range(W1.shape[1]):
connections.append([f”[{input_nodes[i]}] --> [{hidden_nodes[j]}]”, W1[i, j]])
# Bias to Hidden
for j, b in enumerate(bias_hidden):
connections.append([f”[Bias (Input)] --> [{hidden_nodes[j]}]”, b])
# Hidden → Output
for i in range(W2.shape[0]):
for j in range(W2.shape[1]):
connections.append([f”[{hidden_nodes[i]}] --> [{output_nodes[j]}]”, W2[i, j]])
# Bias to Output
for j, b in enumerate(bias_output):
connections.append([f”[Bias (Hidden)] --> [{output_nodes[j]}]”, b])
weights_df = pd.DataFrame(connections, columns = [“Connection”, “Weight”])
output_dir = “New_Attempts”
timestamp = datetime.datetime.now().strftime(“%Y%m%d_%H%M%S”)
file_name = f”MLP_Assigned_Weights_{timestamp}.xlsx”
file_path = os.path.join(output_dir, file_name)
weights_df.to_excel(file_path, index = False)
print(f”Weights saved → {file_path}”)
# -----------------------------------------------------------------------------
# Save final trained model
# -----------------------------------------------------------------------------
model.save(“mlp_benussi_model_final.keras”)
dingsound.ding()
Appendix A.2. Python Script for Regression, Welch's t-Test, and Pearson's Correlation Analysis
# -*- coding: utf-8 -*-
import pandas as pd, numpy as np
import statsmodels.api as sm
from scipy.stats import pearsonr, t, norm
# ------------------------------------------------------------------
# Helper functions
# ------------------------------------------------------------------
def bf_upper_bound(p_val):
“““Sellke–Bayarri–Berger upper bound BF₀₁ (null/alt).”““
return -np.e * p_val * np.log(p_val) if p_val <= 1 / np.e else 1.0
def z_score(r_coeff, p_two):
“““Large-sample z associated with two-tailed p and sign(r).”““
p_two = max(p_two, np.finfo(float).tiny)
return np.sign(r_coeff) * norm.isf(p_two)
# ------------------------------------------------------------------
# Load data and collapse to Benussi–level means
# ------------------------------------------------------------------
FILE_PATH = “Correlation Analysis data NEW.xlsx”
df = pd.read_excel(FILE_PATH)
BEN = “Output_Benussi_Level” # predictor
HN = [
“Hidden_Node_1_Weight”,
“Hidden_Node_2_Weight”,
“Hidden_Node_3_Weight”,
]
collapsed = (df[[BEN] + HN]
.groupby(BEN, as_index = False)
.mean()
.sort_values(BEN)) # five rows
n_rows = len(collapsed) # 5
# ------------------------------------------------------------------
# Simple linear regressions: weight ~ Benussi
# ------------------------------------------------------------------
slopes = []
for col in HN:
y = collapsed[col]
X = sm.add_constant(collapsed[BEN])
fit = sm.OLS(y, X).fit()
# Basic estimates
beta = fit.params[BEN]
se_beta = fit.bse[BEN]
t_beta = fit.tvalues[BEN]
p_beta = fit.pvalues[BEN] # two-tailed
df_resid = int(fit.df_resid) # n-2
# 95 % CI
ci_low, ci_high = fit.conf_int().loc[BEN]
# Standardised β = β * (SD_x / SD_y)
sd_x = collapsed[BEN].std(ddof = 0)
sd_y = y.std(ddof = 0)
beta_std = beta * sd_x / sd_y if sd_y else np.nan
# Model-level stats
r2 = fit.rsquared
f_val = float(fit.fvalue)
f_p = float(fit.f_pvalue)
slopes.append({
“Node”: col,
“beta”: beta,
“SE”: se_beta,
“t”: t_beta,
“df”: df_resid,
“p_two”: p_beta,
“CI_low”: ci_low,
“CI_high”: ci_high,
“beta_std”: beta_std,
“R2”: r2,
“Adj_R2”: fit.rsquared_adj,
“F”: f_val,
“F_p”: f_p,
})
slopes_df = pd.DataFrame(slopes)
# ------------------------------------------------------------------
# Pair-wise slope contrasts (df = 6) – adds 95 % CI and Cohen’s d
# ------------------------------------------------------------------
contr = []
for i in range(3):
for j in range(i + 1, 3):
b1, se1, name1 = slopes_df.loc[i, [“beta”, “SE”, “Node”]]
b2, se2, name2 = slopes_df.loc[j, [“beta”, “SE”, “Node”]]
diff = b1 − b2
se_diff = np.sqrt(se1 ** 2 + se2 ** 2)
t_stat = diff / se_diff
df_con = (n_rows-2) * 2 # 6
p_two = 2 * t.sf(abs(t_stat), df_con)
bf01 = bf_upper_bound(p_two)
# 95 % confidence interval for the slope difference
t_crit = t.ppf(0.975, df_con)
ci_low = diff-t_crit * se_diff
ci_high = diff + t_crit * se_diff
# Cohen’s d from t (independent groups, unequal variances)
# d = 2t / sqrt(df)
cohen_d = 2 * t_stat / np.sqrt(df_con)
contr.append({
“contrast”: f”{name1} vs. {name2}”,
“beta_diff”: diff,
“SE_diff”: se_diff,
“t”: t_stat,
“df”: df_con,
“p_two”: p_two,
“CI_low”: ci_low,
“CI_high”: ci_high,
“Cohen_d”: cohen_d,
“BF10_upper”: 1.0 / bf01,
“Posterior_Odds”: 1.0 / bf01, # prior odds = 1:1 so posterior odds = BF10
})
contr_df = pd.DataFrame(contr)
# ------------------------------------------------------------------
# Main correlation loop
# ------------------------------------------------------------------
N_full = len(df)
z_crit = norm.ppf(0.975) # 1.96 for 95% CI
corr_rows = []
for i, c1 in enumerate(HN):
for j, c2 in enumerate(HN):
if j <= i:
continue
r_val, p_two = pearsonr(df[c1], df[c2])
z = np.arctanh(r_val)
se = 1 / np.sqrt(N_full-3)
delta = z_crit * se
# 2) back-transform to r-space
ci_low_r = np.tanh(z-delta)
ci_high_r = np.tanh(z + delta)
corr_rows.append({
“var1”: c1,
“var2”: c2,
“n”: N_full,
“Pearson_r”: r_val,
“CI_low_r”: ci_low_r,
“CI_high_r”: ci_high_r,
})
corr_df = pd.DataFrame(corr_rows)
# ------------------------------------------------------------------
# Export to Excel
# ------------------------------------------------------------------
OUT = “Hidden_Node_Analysis_Full.xlsx”
with pd.ExcelWriter(OUT) as writer:
collapsed.to_excel(writer, sheet_name = “Collapsed_means”, index = False)
slopes_df.to_excel(writer, sheet_name = “Slopes”, index = False)
contr_df.to_excel(writer, sheet_name = “Slope_tests”, index = False)
corr_df.to_excel(writer, sheet_name = “Pearson_corr”, index = False)
print(“✓ Analyses complete–results saved to”, OUT)
References
- Wearden, J.; O’Donoghue, A.; Ogden, R.; Montgomery, C. Subjective Duration in the Laboratory and the World Outside. In Subjective Time: The Philosophy, Psychology, and Neuroscience of Temporality; Arstila, V., Lloyd, D., Eds.; The MIT Press: Cambridge, MA, USA, 2014; pp. 287–306. ISBN 978-0-262-32274-4. [Google Scholar]
- Dainton, B. Temporal Consciousness. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Nodelman, U., Eds.; Metaphysics Research Lab, Stanford University: California, CA, USA, 2024; Available online: https://plato.stanford.edu/archives/fall2024/entries/consciousness-temporal/ (accessed on 4 June 2025).
- Albertazzi, L. Forms of Completion. Grazer Philos. Stud. 1995, 50, 321–340. [Google Scholar] [CrossRef]
- Benussi, V. Psychologie Der Zeitauffassung; C. Winter; 1913; Volume 6, Available online: https://onlinebooks.library.upenn.edu/webbin/book/lookupid?key=ha005762281 (accessed on 4 June 2025).
- Albertazzi, L. Vittorio Benussi (1878–1927). In The School of Alexius Meinong; Routledge: London, UK, 2017; pp. 99–134. ISBN 978-1-315-23717-6. [Google Scholar]
- Fulford, J.; Milton, F.; Salas, D.; Smith, A.; Simler, A.; Winlove, C.; Zeman, A. The Neural Correlates of Visual Imagery Vividness—An fMRI Study and Literature Review. Cortex 2018, 105, 26–40. [Google Scholar] [CrossRef]
- D’Angiulli, A.; Reeves, A. Generating Visual Mental Images: Latency and Vividness Are Inversely Related. Mem. Cognit. 2002, 30, 1179–1188. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, E.; D’Angiulli, A. Imagery-Mediated Verbal Learning Depends on Vividness–Familiarity Interactions: The Possible Role of Dualistic Resting State Network Activity Interference. Brain Sci. 2019, 9, 143. [Google Scholar] [CrossRef] [PubMed]
- Buckner, R.L.; Andrews-Hanna, J.R.; Schacter, D.L. The Brain’s Default Network. Ann. N. Y. Acad. Sci. 2008, 1124, 1–38. [Google Scholar] [CrossRef]
- Raichle, M.E.; MacLeod, A.M.; Snyder, A.Z.; Powers, W.J.; Gusnard, D.A.; Shulman, G.L. A Default Mode of Brain Function. Proc. Natl. Acad. Sci. USA 2001, 98, 676–682. [Google Scholar] [CrossRef]
- Andrews-Hanna, J.R.; Smallwood, J.; Spreng, R.N. The Default Network and Self-Generated Thought: Component Processes, Dynamic Control, and Clinical Relevance. Ann. N. Y. Acad. Sci. 2014, 1316, 29–52. [Google Scholar] [CrossRef]
- Astafiev, S.V.; Shulman, G.L.; Stanley, C.M.; Snyder, A.Z.; Van Essen, D.C.; Corbetta, M. Functional Organization of Human Intraparietal and Frontal Cortex for Attending, Looking, and Pointing. J. Neurosci. 2003, 23, 4689–4699. [Google Scholar] [CrossRef]
- Corbetta, M.; Shulman, G.L. Control of Goal-Directed and Stimulus-Driven Attention in the Brain. Nat. Rev. Neurosci. 2002, 3, 201–215. [Google Scholar] [CrossRef]
- Seeley, W.W.; Menon, V.; Schatzberg, A.F.; Keller, J.; Glover, G.H.; Kenna, H.; Reiss, A.L.; Greicius, M.D. Dissociable Intrinsic Connectivity Networks for Salience Processing and Executive Control. J. Neurosci. 2007, 27, 2349–2356. [Google Scholar] [CrossRef]
- Menon, V.; Uddin, L.Q. Saliency, Switching, Attention and Control: A Network Model of Insula Function. Brain Struct. Funct. 2010, 214, 655–667. [Google Scholar] [CrossRef]
- Kim, H. Dissociating the Roles of the Default-Mode, Dorsal, and Ventral Networks in Episodic Memory Retrieval. NeuroImage 2010, 50, 1648–1657. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Yuan, Y.; Wang, Y.; Wang, R. Neural Antagonistic Mechanism between Default-Mode and Task-Positive Networks. Neurocomputing 2020, 417, 74–85. [Google Scholar] [CrossRef]
- Kim, H.; Daselaar, S.M.; Cabeza, R. Overlapping Brain Activity between Episodic Memory Encoding and Retrieval: Roles of the Task-Positive and Task-Negative Networks. NeuroImage 2010, 49, 1045–1054. [Google Scholar] [CrossRef] [PubMed]
- Mancuso, L.; Cavuoti-Cabanillas, S.; Liloia, D.; Manuello, J.; Buzi, G.; Cauda, F.; Costa, T. Tasks Activating the Default Mode Network Map Multiple Functional Systems. Brain Struct. Funct. 2022, 227, 1711–1734. [Google Scholar] [CrossRef]
- Sridharan, D.; Levitin, D.J.; Menon, V. A Critical Role for the Right Fronto-Insular Cortex in Switching between Central-Executive and Default-Mode Networks. Proc. Natl. Acad. Sci. USA 2008, 105, 12569–12574. [Google Scholar] [CrossRef]
- Levine, D.S. Introduction to Neural and Cognitive Modeling; Psychology Press: New York, NY, USA, 2000. [Google Scholar]
- Kosslyn, S.M. Seeing and Imagining in the Cerebral Hemispheres: A Computational Approach. Psychol. Rev. 1987, 94, 148. [Google Scholar] [CrossRef]
- Farah, M.J.; McClelland, J.L. A Computational Model of Semantic Memory Impairment: Modality Specificity and Emergent Category Specificity. J. Exp. Psychol. Gen. 1991, 120, 339–357. [Google Scholar] [CrossRef]
- Farah, M.J.; O’Reilly, R.C.; Vecera, S.P. Dissociated Overt and Covert Recognition as an Emergent Property of a Lesioned Neural Network. Psychol. Rev. 1993, 100, 571–588. [Google Scholar] [CrossRef]
- Cohen, J.D.; Romero, R.D.; Servan-Schreiber, D.; Farah, M.J. Mechanisms of Spatial Attention: The Relation of Macrostructure to Microstructure in Parietal Neglect. J. Cogn. Neurosci. 1994, 6, 377–387. [Google Scholar] [CrossRef]
- Kosslyn, S.M.; Van Kleeck, M. Broken Brains and Normal Minds: Why Humpty-Dumpty Needs a Skeleton. In Computational Neuroscience; Schwartz, E.L., Ed.; MIT Press: Cambridge, MA, USA, 1990; pp. 390–402. [Google Scholar]
- Farah, M.J. Neuropsychological Inference with an Interactive Brain: A Critique of the “Locality” Assumption. In Cognitive Modeling; Polk, T.A., Seifert, C.M., Eds.; A Bradford Book; MIT Press: Cambridge, MA, USA, 2002; pp. 1149–1192. ISBN 978-0-262-66116-4. [Google Scholar]
- Beniaguev, D.; Segev, I.; London, M. Single Cortical Neurons as Deep Artificial Neural Networks. Neuron 2021, 109, 2727–2739.e3. [Google Scholar] [CrossRef] [PubMed]
- Stelzer, F.; Röhm, A.; Vicente, R.; Fischer, I.; Yanchuk, S. Deep Neural Networks Using a Single Neuron: Folded-in-Time Architecture Using Feedback-Modulated Delay Loops. Nat. Commun. 2021, 12, 5164. [Google Scholar] [CrossRef]
- Kasabov, N.K. NeuCube: A Spiking Neural Network Architecture for Mapping, Learning and Understanding of Spatio-Temporal Brain Data. Neural Netw. Off. J. Int. Neural Netw. Soc. 2014, 52, 62–76. [Google Scholar] [CrossRef] [PubMed]
- Cybenko, G. Approximation by Superpositions of a Sigmoidal Function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Aleksander, I. Impossible Minds: My Neurons, My Consciousness (Revised Edition); World Scientific: Singapore, 2014; ISBN 1-78326-571-X. [Google Scholar]
- Albantakis, L.; Hintze, A.; Koch, C.; Adami, C.; Tononi, G. Evolution of Integrated Causal Structures in Animats Exposed to Environments of Increasing Complexity. PLoS Comput. Biol. 2014, 10, e1003966. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Ji, J.; Liu, J.; Han, L.; Wang, F. Estimating Effective Connectivity by Recurrent Generative Adversarial Networks. IEEE Trans. Med. Imaging 2021, 40, 3326–3336. [Google Scholar] [CrossRef]
- Dai, P.; He, Z.; Ou, Y.; Luo, J.; Liao, S.; Yi, X. Estimating Brain Effective Connectivity from Time Series Using Recurrent Neural Networks. Phys. Eng. Sci. Med. 2025, 48, 785–795. [Google Scholar] [CrossRef]
- Abbasvandi, Z.; Nasrabadi, A.M. A Self-Organized Recurrent Neural Network for Estimating the Effective Connectivity and Its Application to EEG Data. Comput. Biol. Med. 2019, 110, 93–107. [Google Scholar] [CrossRef]
- Pulvermüller, F.; Tomasello, R.; Henningsen-Schomers, M.R.; Wennekers, T. Biological Constraints on Neural Network Models of Cognitive Function. Nat. Rev. Neurosci. 2021, 22, 488–502. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, D.; Lian, C.; Wang, L.; Wu, Z.; Shao, W.; Lin, W.; Shen, D.; Li, G. Topological Correction of Infant White Matter Surfaces Using Anatomically Constrained Convolutional Neural Network. NeuroImage 2019, 198, 114–124. [Google Scholar] [CrossRef]
- Goulden, N.; Khusnulina, A.; Davis, N.J.; Bracewell, R.M.; Bokde, A.L.; McNulty, J.P.; Mullins, P.G. The Salience Network Is Responsible for Switching between the Default Mode Network and the Central Executive Network: Replication from DCM. NeuroImage 2014, 99, 180–190. [Google Scholar] [CrossRef]
- Reeves, A.; D’Angiulli, A. What Does the Visual Buffer Tell the Mind’s Eye? Abstr. Psychon. Soc. 2003, 8, 82. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ho, Y. The Real-World-Weight Cross-Entropy Loss Function: Modeling the Costs of Mislabeling. IEEE Access 2020, 8, 4806–4813. [Google Scholar] [CrossRef]
- Wang, R.; Li, J. Bayes Test of Precision, Recall, and F1 Measure for Comparison of Two Natural Language Processing Models. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; Korhonen, A., Traum, D., Màrquez, L., Eds.; Association for Computational Linguistics: Florence, Italy, 2019; pp. 4135–4145. [Google Scholar]
- Calders, T.; Jaroszewicz, S. Efficient AUC Optimization for Classification. In Proceedings of the Knowledge Discovery in Databases: PKDD 2007, Warsaw, Poland, 17–21 September 2007; Kok, J.N., Koronacki, J., Lopez de Mantaras, R., Matwin, S., Mladenič, D., Skowron, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 42–53. [Google Scholar]
- Benjamin, D.J.; Berger, J.O. Three Recommendations for Improving the Use of p-Values. Am. Stat. 2019, 73, 186–191. [Google Scholar] [CrossRef]
- Nahm, F.S. Receiver Operating Characteristic Curve: Overview and Practical Use for Clinicians. Korean J. Anesthesiol. 2022, 75, 25–36. [Google Scholar] [CrossRef]
- Trujillo-Barreto, N.J. Bayesian Model Inference. In Brain Mapping; Toga, A.W., Ed.; Academic Press: Waltham, MA, USA, 2015; pp. 535–539. ISBN 978-0-12-397316-0. [Google Scholar]
- Sneve, M.H.; Grydeland, H.; Amlien, I.K.; Langnes, E.; Walhovd, K.B.; Fjell, A.M. Decoupling of Large-Scale Brain Networks Supports the Consolidation of Durable Episodic Memories. NeuroImage 2017, 153, 336–345. [Google Scholar] [CrossRef]
- Fox, M.D.; Snyder, A.Z.; Vincent, J.L.; Corbetta, M.; Van Essen, D.C.; Raichle, M.E. The Human Brain Is Intrinsically Organized into Dynamic, Anticorrelated Functional Networks. Proc. Natl. Acad. Sci. USA 2005, 102, 9673–9678. [Google Scholar] [CrossRef]
- Marks, D.F. Phenomenological Studies of Visual Mental Imagery: A Review and Synthesis of Historical Datasets. Vision 2023, 7, 67. [Google Scholar] [CrossRef]
- James, W. The Principles of Psychology; Henry Holt and Co.: New York, NY, USA, 1890; Volume I. [Google Scholar]
- Li, X.; Wong, D.; Gandour, J.; Dzemidzic, M.; Tong, Y.; Talavage, T.; Lowe, M. Neural Network for Encoding Immediate Memory in Phonological Processing. Neuroreport 2004, 15, 2459–2462. [Google Scholar] [CrossRef][Green Version]
- Marek, S.; Dosenbach, N.U.F. The Frontoparietal Network: Function, Electrophysiology, and Importance of Individual Precision Mapping. Dialogues Clin. Neurosci. 2018, 20, 133–140. [Google Scholar] [CrossRef]
- Cole, M.W.; Braver, T.S.; Meiran, N. The Task Novelty Paradox: Flexible Control of Inflexible Neural Pathways during Rapid Instructed Task Learning. Neurosci. Biobehav. Rev. 2017, 81, 4–15. [Google Scholar] [CrossRef]
- Lee, S.; Parthasarathi, T.; Kable, J.W. The Ventral and Dorsal Default Mode Networks Are Dissociably Modulated by the Vividness and Valence of Imagined Events. J. Neurosci. Off. J. Soc. Neurosci. 2021, 41, 5243–5250. [Google Scholar] [CrossRef] [PubMed]
- Addis, D.R.; Pan, L.; Vu, M.-A.; Laiser, N.; Schacter, D.L. Constructive Episodic Simulation of the Future and the Past: Distinct Subsystems of a Core Brain Network Mediate Imagining and Remembering. Neuropsychologia 2009, 47, 2222–2238. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro da Costa, C.; Soares, J.M.; Oliveira-Silva, P.; Sampaio, A.; Coutinho, J.F. Interplay between the Salience and the Default Mode Network in a Social-Cognitive Task toward a Close Other. Front. Psychiatry 2022, 12, 718400. [Google Scholar] [CrossRef] [PubMed]
- Menon, V. Large-Scale Brain Networks and Psychopathology: A Unifying Triple Network Model. Trends Cogn. Sci. 2011, 15, 483–506. [Google Scholar] [CrossRef]
| Benussi Level | Precision | Recall | F1-Score | Support 1 |
|---|---|---|---|---|
| 1 | 0.98 | 1.00 | 0.99 | 49 |
| 2 | 0.99 | 1.00 | 0.99 | 319 |
| 3 | 1.00 | 0.97 | 0.99 | 379 |
| 4 | 0.97 | 1.00 | 0.99 | 304 |
| 5 | 1.00 | 1.00 | 1.00 | 601 |
| Accuracy | - | - | 0.99 | 1652 |
| Macro Mean | 0.99 | 0.99 | 0.99 | 1652 |
| Weighted Mean | 0.99 | 0.99 | 0.99 | 1652 |
| Hidden Node | β | SE | t-Statistic (n = 5, df = 3) | p-Value | 95% CI | Adjusted R2 |
|---|---|---|---|---|---|---|
| 1 | −10.576 | 7.514 | −1.407 | 0.254 | −34.490, 13.338 | 0.197 |
| 2 | 44.750 | 16.510 | 2.710 | 0.073 | −7.792, 97.293 | 0.613 |
| 3 | −29.805 | 7.816 | −3.813 | 0.032 | −54.680, −4.930 | 0.772 |
| Hidden Node Contrast | ∆β | SE(∆β) | t-Statistic (n1 = n2 = 5, df = 6) | p-Value | 95% CI | Cohen’s d | BF10 |
|---|---|---|---|---|---|---|---|
| 1 vs. 2 | −55.326 | 18.140 | −3.050 | 0.023 | −99.712, −10.940 | −2.490 | 4.307 |
| 1 vs. 3 | 19.229 | 10.842 | 1.774 | 0.127 | −7.301, 45.760 | 1.448 | 1.407 |
| 2 vs. 3 | 74.555 | 18.267 | 4.081 | 0.006 | 29.858, 119.252 | 3.332 | 11.250 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheculski, M.; D’Angiulli, A. Multilayer Perceptron Mapping of Subjective Time Duration onto Mental Imagery Vividness and Underlying Brain Dynamics: A Neural Cognitive Modeling Approach. Mach. Learn. Knowl. Extr. 2025, 7, 82. https://doi.org/10.3390/make7030082
Sheculski M, D’Angiulli A. Multilayer Perceptron Mapping of Subjective Time Duration onto Mental Imagery Vividness and Underlying Brain Dynamics: A Neural Cognitive Modeling Approach. Machine Learning and Knowledge Extraction. 2025; 7(3):82. https://doi.org/10.3390/make7030082
Chicago/Turabian StyleSheculski, Matthew, and Amedeo D’Angiulli. 2025. "Multilayer Perceptron Mapping of Subjective Time Duration onto Mental Imagery Vividness and Underlying Brain Dynamics: A Neural Cognitive Modeling Approach" Machine Learning and Knowledge Extraction 7, no. 3: 82. https://doi.org/10.3390/make7030082
APA StyleSheculski, M., & D’Angiulli, A. (2025). Multilayer Perceptron Mapping of Subjective Time Duration onto Mental Imagery Vividness and Underlying Brain Dynamics: A Neural Cognitive Modeling Approach. Machine Learning and Knowledge Extraction, 7(3), 82. https://doi.org/10.3390/make7030082







