Significance of Time-Series Consistency in Evaluating Machine Learning Models for Gap-Filling Multi-Level Very Tall Tower Data

Abstract

Machine learning modeling is a valuable tool for gap-filling or prediction, and its performance is typically evaluated using standard metrics. To enable more precise assessments for time-series data, this study emphasizes the importance of considering time-series consistency, which can be evaluated through amplitude—specifically, the interquartile range and the lower bound of the band in gap-filled time series. To test this hypothesis, a gap-filling technique was applied using long-term (~6 years) high-frequency flux and meteorological data collected at four different levels (1.5, 60, 140, and 300 m above sea level) on a ~300 m tall flux tower. This study focused on turbulent kinetic energy among several variables, which is important for estimating sensible and latent heat fluxes and net ecosystem exchange. Five ensemble machine learning algorithms were selected and trained on three different datasets. Among several modeling scenarios, the stacking model with a dataset combined with derivative data produced the best metrics for predicting turbulent kinetic energy. Although the metrics before and after gap-filling reported fewer differences among the scenarios, large distortions were found in the consistency of the time series in terms of amplitude. These findings underscore the importance of evaluating time-series consistency alongside traditional metrics, not only to accurately assess modeling performance but also to ensure reliability in downstream applications such as forecasting, climate modeling, and energy estimation.

1. Introduction

Micrometeorology involves the study of atmospheric processes at small spatial scales, typically within the atmospheric boundary layer where turbulent motion is dominant. Turbulence kinetic energy (TKE) is a measure of the intensity of turbulence in a fluid flow, characterized by the mean kinetic energy per unit mass and the Root Mean Square of velocity fluctuations. The TKE is generated by wind shear, buoyancy, and other forces and is transferred through the turbulence energy cascade before eventually dissipating. This process is crucial for understanding various atmospheric phenomena such as weather patterns, pollutant dispersion, and ecosystem exchanges. The TKE can modify the thermal and moisture structures of the boundary layer. Sensible heat flux can increase the buoyancy and enhance turbulence, thereby increasing TKE. Similarly, latent heat flux affects TKE through the release or absorption of energy during phase changes in water [1,2,3,4].

Flux tower measurements allow for continuous monitoring of turbulence profiles and intensity. Over the past few decades, a global network of flux measurements in micrometeorology has emerged [5,6]. This network uses the eddy covariance (EC) method to measure turbulence and combines it with infrared gas analyzers (IRGAs) to monitor carbon dioxide (CO₂) and water vapor fluxes. This approach allows researchers to estimate the net ecosystem exchange, providing valuable insights into the carbon cycle of the terrestrial biosphere, which is associated with climate change. Therefore, accurate and predictive analyses are crucial. Integrating these measurements with other meteorological data will help develop comprehensive models that can predict the behavior of turbulent flows under different environmental conditions. The data obtained from these measurements are crucial for addressing challenges in fields such as aviation, air quality management, renewable energy, and CO₂ and other atmospheric greenhouse gas cycles.

In the field, researchers usually set up an EC system at a single level on a tower or mast, mainly for cost and labor efficiency. The measurement height is typically determined based on the target footprint area; the wider the footprint area, the higher the measurement height. In vegetation-dominated regions, flux measurement equipment is installed at the canopy level to observe ecosystem exchange [7,8,9,10]. In heterogeneous urban areas, the equipment should also be set to a level as high as the tower allows for the acquisition of the maximum footprint [11,12,13,14,15], and more QA/QC is required compared to homogeneous regions.

Accurate data collection at high frequencies (>10 Hz) is essential for understanding micrometeorological processes. However, missing or gapped data frequently occur because of instrument malfunction, maintenance, or adverse weather conditions. A previous study [3] noted that approximately 30% of EC flux measurements were missing, leading to errors or biases in the analysis and modeling studies and reduced accuracy and reliability. Therefore, gap-filling techniques have been employed to fill in missing data points, which are crucial for accurate modeling and reliable forecasting [16,17]. Many studies have emphasized the importance of gap-filling. For example, Gandin [18] introduced foundational concepts using objective analysis and Kalman filtering. Griffith [19] explored spatial statistical methods, particularly kriging, for spatially correlated data. Stull [1] provided the fundamental knowledge and statistical techniques for micrometeorology, including various approaches to addressing missing data. Gap-filling techniques such as marginal distribution sampling and multihead deep attention networks have demonstrated their effectiveness in improving the accuracy and reliability of micrometeorological datasets [20,21,22,23].

Recently, as computational costs have decreased and machine learning (ML) and deep learning (DL) algorithms have been developed, many studies have attempted to use these methods to fill the gaps in flux tower observations [17,24,25,26,27,28,29]. All these previous studies used data measured with single-layer flux towers and primarily evaluated model performance using traditional metrics such as Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and R-squared (R²), which offer insights into accuracy. However, this study argues that the existing methods are generally inadequate for accurately assessing the reliability and overall temporal characteristics of gap-filled time-series data. To address this limitation, in this study, a novel evaluation metric is introduced, termed “time-series consistency,” which focuses on amplitude—defined by the difference of average, interquartile range (IQR), and the lower bound of the data band within the reconstructed time series. To the author’s present knowledge, this is the first attempt to use multilayer data for gap-filling, likely because of the rarity of multilayer tall tower equipment.

The methodological approach of this study integrates a tower-based measurement system with ML modeling to evaluate the time-series consistency of gap-filling tall tower TKE data. Section 2 outlines the measurement setup, training datasets tailored to each modeling scenario, and the selection of ML algorithms. Section 3 details the modeling performance, key metrics, feature importance, and temporal coherence of the model outputs, which is the central finding. Finally, Section 4 summarizes the results and discusses the broader implications.

2. Methods

2.1. Flux Measurement Site

The National Institute of Meteorological Research (NIMR) of the Korea Meteorological Administration (KMA) manages a tall (~300 m) tower observation system in Boseong-gun, on the edge of the southern coastal area of the Korean Peninsula. The location and land-use information around the Boseong Global Standard Meteorological Observation Station (34°45′48″ N, 127°12′53″ E; hereafter, BOS) are shown in Figure 1. The flux measurement tower is situated in a flat, homogeneous, barley-rice double-crop paddy field. The site lies approximately 1.5 km southeast of the coast, while mountains reaching ~0.6 km and ~0.1 km in height are located to the north and west, respectively.

Net radiation sensors (CNR4; Kipp & Zonen, Deflt, The Netherlands) were installed at heights of 60 m, 140 m, and 300 m on the tower. Additionally, 3D sonic anemometers (CSAT3A; Campbell Scientific, Logan, UT, USA) were installed at these heights on the tower and combined with infrared gas analyzers (IRGAs) for CO₂/H₂O measurements. An enclosed system (Li-7200RS; Li-Cor, Bad Homburg, Germany) was installed at the 60 m level, and two closed systems (EC-155; Campbell Scientific) were set up at 140 and 300 m and installed in three directions (south, northwest, and northeast) at 120° intervals. An open-path system gas analyzer (EC-150; Campbell Scientific) was also installed 1.5 m above the ground on the east and west outer sides at the edge of the observation field. All anemometers carried temperature sensors (5628; Fluke Corp., Everett, WA, USA) and humidity sensors (HMP155A; Vaisala Corp., Louisville, CO, USA) housed in radiation shields, along with 2D sonic anemometers (Thies Clima UA-2d; Adolf Thies GmbH & Co. KG, Göttingen, Germany).

At the ground level, soil moisture probes (CS616-L and CS-655L; Campbell Scientific) were installed 20 cm below the surface to measure the soil water content (SWC). The soil heat flux (SHF) and temperature were measured 20 cm below the surface using an SHF plate (HFP01-L; Hukseflux Thermal Sensors B.V., Delft, the Netherlands) and a thermocouple probe (TCAV-L; Campbell Scientific), respectively. Data from the KMA Automated Synoptic Observation System (ASOS) were acquired from the ground stations.

To produce 30 min averaged data from 20 Hz raw data from the CSTA3-IGRA, EddyPro software (Version 7.0.4; Li-Cor) was used, following the methods of Lee et al. [30]. De-spiking, drop-out, skewness, and kurtosis tests [31], steady-state and well-developed turbulence tests [32], and low- and high-spectral correction [33,34] were performed. Further information on flux measurements and data processing can be found in a previously published study [35].

2.2. Data Processing

2.2.1. Input Data Interpolation

For six years, from 2015 to 2020, 30 min averaged flux data were collected from the multi-level tower EC system. The total number of variables (features) was 333, and the number of records was 105,216. In this study, 41 features were selected based on their relationships with TKE. Some features, such as wind speed and temperature, showed correlations with TKE. Other factors such as date, time, wind direction, soil temperature, soil heat, soil water content, ground temperature, and radiation had weak or no clear correlations.

Before conducting gap-filling or prediction, the missing values in the input weather data were treated as follows:

• Removing Outliers: First, outliers determined by the 4-sigma standard based on the q–q plot were removed.
• Solar Radiation Correction: The solar radiation data used had several values missing, particularly at night. The accurate sunrise and sunset times based on the solar angle according to latitude and longitude were calculated and the missing nighttime values replaced with zero. Because there were many missing radiation data points at the four levels of the tower, the short- and long-wave radiation from the four measurement levels was merged into one standard level (140 m), which had the least number of missing values and no significant differences in radiation data among the levels (<1%).
• Replacing with Alternative Measurement: When alternative observation data were available at the same measurement level, they were replaced with the 30 min averaged values from the other measurements. For example, when there were no T/RH data measured by the 3D sonic anemometer at the 60 m level, the data from the 2D sonic anemometer at the same level was used.
• Temporal Interpolation: For short-term missing periods, a linear or spline function was applied and an appropriate time window set based on the length of the missing data. For sequentially missing data of less than 6 h, a simple linear interpolation was used. For periods longer than 6 h and shorter than 12 h, a spline function was used to interpolate the missing values. For missing periods longer than 12 h and less than 72 h, the three-day average values for the same time period were used.
• Averaged Substitution: If data were still missing after Step 4, the missing values were substituted with averaged values at the same hour of each day in each season using data from the closest two years. Altered data can represent local climate conditions. We did not interpolate the wind data in order to preserve the original characteristics of the wind, as alterations could affect the ML modeling results. This decision was made because TKE is primarily governed by wind speeds. Potential impacts resulting from not interpolating the data will be discussed in Section 4. The numbers of missing WS and TKE values were 848 and 18,191 (1.5 m); 22,133 and 22,133 (60 m); 24,514 and 39,257 (140 m); and 9819 and 9819 (300 m), respectively.
• Miscellaneous: Soil temperature, heat flux, and water content had missing long-term data, although an attempt was made to fill in their coupled data as a backup. In this case, the average substitution was also used because of the relatively slow seasonal variations. This indicates that the completed dataset reflects the local climatological variations over six years.

2.2.2. Data Expansion

Although deep learning models such as Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) are effective for capturing temporal dependencies, they require continuous data sequences. Owing to the significant temporal discontinuities in our wind dataset, the application of such models is not feasible. To overcome this limitation, an alternative approach was used that directly incorporated temporal variations into the training dataset by adding time-aware features. Additionally, the formulation was extended to include vertical variation, which is especially valuable when working with multi-level flux tower data. Unlike single-layer towers, multi-level towers allow the derivation of physically meaningful features, such as vertical gradients of temperature or wind, that capture turbulence-related dynamics across heights. This strategy enabled the modeling of both temporal and vertical dependencies without relying on sequence-based deep learning models.

The number of features were expanded by creating second-order-derived variables for the vertical differences in wind speed and air temperature at each level using Equations (1) and (2):

$${\displaystyle \frac{\mathrm{d}U\left(z,t\right)}{\mathrm{d}\mathrm{z}}}=U\left(z,t\right)-U\left(z-1,t\right)$$

(1)

$${\displaystyle \frac{\mathrm{d}\mathrm{T}(z,t)}{\mathrm{d}\mathrm{z}}}=T\left(z,t\right)-T\left(z-1,t\right)$$

(2)

where $U\left(z,t\right)$ and $T\left(z,t\right)$ represent the wind speed and air temperature at level z and time t, respectively. The $z-1$ level refers to the measurement level immediately below $z$.

The temporal gradient of the air temperature at each level was calculated as follows:

$${\displaystyle \frac{\mathrm{d}T(z,t)}{\mathrm{d}\mathrm{t}}}=\mathrm{T}\left(z,t-1\right)-\mathrm{T}\left(z,t\right)$$

(3)

Here, the $t-1$ time refers to an hour earlier than the time of $t$. Note that the wind speed gradient was not filled to avoid harming the original characteristics of the wind data and affecting the TKE prediction modeling because of the large amount of missing data and the difficulty in filling in missing data.

2.2.3. Scenarios of Training Datasets

For ML modeling, three sets of training data were created from measured weather data. First, common features were selected that could be used in all the datasets. This dataset consisted of 16 features: month, day, hour, soil temperature, heat flux, water content, dew point temperature, surface and ground temperatures, air temperature (0.5 m), short- and long-wave radiation, and net radiation at 140 m. These common features were selected based on brute-force testing using various ML algorithms.

In addition to the common features, air temperature, wind speed, and wind direction from each level of measurement were added, including at ground level (1.5 m) and at 60, 140, and 300 m to create a single-level dataset called L1. To create the second dataset, in addition to L1, air temperature and wind data from all four levels were added because air temperature and winds are the main factors in the TKE equation, as described in Section 1, and the TKEs at each level are strongly correlated under the same environmental conditions. This dataset was called L4. The final dataset, designated L4E, was produced by adding newly expanded data to the L4 dataset.

The L1 dataset was used as the comparison group, and L4 and L4E as the experimental groups. The selected ML algorithm learned from each training dataset (L1, L4, and L4E) targeted the measured TKE and predicted the missing TKE at each level. All input data are listed in

Table 1. Input features of data used in this study.

Number	Features	Explanation	Number of 30 Min Averaged Raw Data	Number of Input Data After Interpolation
1	MM	Month	105,216	105,216
2	DD	Day	105,216	105,216
3	HH	Hour	105,216	105,216
4	T_soil	Soil temperature @ 20 cm	77,379	105,216
5	H_soil	Soil heat @ 20 cm	77,359	105,216
6	W_soil	Soil water contents @ 20 cm	77,121	105,216
7	Td	Dew point temperature @ 1.5 m	105,217	105,216
8	Ts	Surface temperature	105,115	105,216
9	Tg5	Ground temperature below 5 cm	104,605	105,216
10	Ta0.5	Air temperature @ 0.5 m	1,098,742	105,216
11	Kdn	Downward shortwave radiation @ 140 m	102,966	105,216
12	Kup	Upward shortwave radiation @ 140 m	102,967	105,216
13	Ldn	Downward longwave radiation @ 140 m	102,964	105,216
14	Lup	Upward longwave radiation @ 140 m	102,964	105,216
15	netrad	Net radiation @ 140 m	102,964	105,216
16	Ta0	Air temp @ 1.5 m	105,216	105,216
17	Ta60	Air temp @ 60 m	105,216	105,216
18	Ta140	Air temp @ 140 m	105,216	105,216
19	Ta300	Air temp @ 300 m	105,216	105,216
20	WS0	Wind speed @ 1.5 m	105,214	105,214
21	WS60	Wind speed @ 60 m	84,668	84,668
22	WS140	Wind speed @ 140 m	97,149	97,149
23	WS300	Wind speed @ 300 m	92,835	92,835
24	WD0	Wind direction @ 1.5 m	105,214	105,214
25	WD60	Wind direction @ 60 m	83,083	83,083
26	WD140	Wind direction @ 140 m	80,702	80,702
27	WD300	Wind direction @ 300 m	92,331	92,331
28	TKE0	TKE @ 1.5 m	87,025	87,025
29	TKE60	TKE @ 60 m	83,083	83,083
30	TKE140	TKE @ 140 m	65,960	65,960
31	TKE300	TKE @ 300 m	92,331	92,331

. While stacking (STK) models can enhance predictive performance by integrating multiple learners, a large number of features can increase the computational cost, both in terms of training time and memory usage. This trade-off to balance model complexity with efficiency must be acknowledged. The model performance under reduced feature subsets (via feature selection or dimensionality reduction) was assessed, and it was found that marginal gains in accuracy beyond a certain feature threshold did not justify the added computational burden. Therefore, the final model setup represents a carefully considered balance between these competing priorities.

2.3. Machine Learning Framework

Figure 2 shows a flowchart of the ML modeling used in this study, which includes five ensemble models and three different training datasets.

Table 2. Workflow of modeling process.

Step	Description
1. Data Import and Inspection	- Load raw dataset and perform exploratory data analysis. - Check for missing values, data types, and outliers.
2. Data Preprocessing	- Remove outliers and handle missing values, and interpolate missing data, except winds and TKE (Section 2.2.1).
3. Feature Engineering	- Produce three input datasets, including the expansion of new features for dataset L4E (Section 2.2.2).
4. Initialize PyCaret Environment	- Use setup() to configure PyCaret: 5-fold CV.
5. Model Selection and Comparison	- Use compare_models() to evaluate multiple algorithms using cross-validation. - Select 3 top-performing models based on a key metric (R2).
6. Model Tuning	- Apply tune_model() on selected model(s) to optimize a hyperparameter in 10 iterations. - Use stack_models() and blend_models() with 3 top-performing tuned models to build stacked and voting models, respectively.
7. Finalize Models	- Check out the feature importance of models. - Finalize models using finalize_model() to lock in parameters. - Finalize the stacking and voting models.
8. Evaluation and Interpretation	- Evaluate model performance on validation data with metrics (MAE, RMSE, and R2).
9. Gap-fill and Predict	- Use predict_model() on missing data and gap-fill. - Compare the results before and after gap-filling.

lists the modeling process. To select the ML models, the PyCaret package (ver. 3.3.2) was used, which supports efficient model development by automating data preprocessing, model training, hyperparameter tuning, and evaluation, employing a cross-validation strategy that performs k-fold cross-validation, specifically employing 5-fold CV. The modeling performance of 20 ML algorithms was compared, including the random forest regressor, LASSO least angle regression, decision tree regressor, and K-neighbor regressor, as listed on the official website.

Twenty algorithms were tested with dataset L1 using hyperparameter tuning to maximize the performance of each model by employing grid and random search methods to determine the best combination of hyperparameters. During this process, model performance was evaluated using cross-validation to prevent overfitting. Three high-performance models were selected: extremely randomized tree regressor (ET), Extreme Gradient Boosting (XGB), and Light Gradient Boosting Machine (LGM), each with a coefficient of determination (R²) greater than 0.7. These models are classified as ensemble models, which generally perform better because they combine the predictions of multiple models, resulting in reduced overfitting, improved bias–variance trade-off, error reduction, and increased robustness. The performance of the selected ensemble algorithms was compared under similar ensemble conditions.

The ET model is an ensemble learning method that builds multiple decision trees and averages their predictions to improve accuracy and control overfitting. Unlike traditional decision trees, ET introduces additional randomness, which helps reduce variance and makes the model less likely to overfit the training data [36]. The XGB model builds an ensemble of decision trees sequentially, where each new tree corrects errors made by the previous tree. It uses a level-wise tree growth strategy to ensure that the tree remains balanced with all leaves at the same depth [37]. The LGM model also builds an ensemble of decision trees sequentially but uses a leaf-wise growth strategy in which the leaf (node) that reduces the error the most is split. This method resulted in the formation of deep trees. The LGM model is generally faster and more memory-efficient than XGB [38].

To further improve the modeling performance, a second set of ensemble models were applied, including voting and stacking methods (VOT and STK, respectively), to the first individual ensemble models (ET, XGB, and LGM). STK involves training multiple base models (level-1 models) and using their outputs to create a metamodel (level-2 models). The metamodel makes the final predictions by learning from the outputs of the base models. In contrast, VOT aggregates the predictions of multiple models to provide a more stable and reliable final prediction. Both techniques leverage the strengths of each model to mitigate individual weaknesses and improve overall prediction capabilities [39].

The three individual models provide feature importance scores, which help us understand why each model makes certain predictions. ET uses impurity-based importance to measure the reduction in the Gini coefficient or entropy when a feature is used [36]. XGB provides multiple importance types, including Gain (average loss reduction), Split (how often a feature is used), and Cover (how many samples are affected) [37]. LGM computes feature importance based on either the Split count or Gain, with the latter reflecting the total contribution to the information gain [38].

2.4. Standard Metrics for Evaluation

As the key performance metrics for ML regression analysis, to check the performance accuracy and suitability of the prediction models, three evaluation metrics were used: Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and R-squared (R²), expressed as follows:

$$\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{\mathsf{\Sigma }\left(\right|{\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}}\left|\right)}{N}}$$

(4)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{\surd {\left(\mathsf{\Sigma }\right({\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}})}^2}{N}}$$

(5)

$$R^2=1-{\displaystyle \frac{\Sigma {\left(y_{\mathrm{i}}-\widehat{y_i}\right)}^2}{\Sigma {\left(y_{\mathrm{i}}-\overline{y}\right)}^2}}$$

(6)

Here, y_i and ${\widehat{y}}_i$_i represent the real and predicted values, respectively. $N$ indicates the number of measured data points. Root Mean Squared Error is relatively less sensitive to outliers because it uses the square of errors but can reduce sensitivity by taking the root mean. The MAE and RMSE share the same unit, making their interpretation relatively easy compared to other metrics. R-squared (R²) is a statistical measure used in regression analysis that represents the proportion of variance in the dependent variable that can be predicted from the independent variables. This indicates how well the developed model fit the measured data [40].

Among general regression metrics (such as MAE, RMSE, MAPE, MSLE, R², and AIC/BIC), MAE, RMSE, and R² were selected because the main purpose of this study was to supplement traditional metrics by adding the novel metric of time-series consistency for a more precise evaluation of ML models. Other metrics, such as MAPE, MSLE, and Adjusted R², were also checked, but no significant differences were found.

2.5. Novel Time-Series Consistency

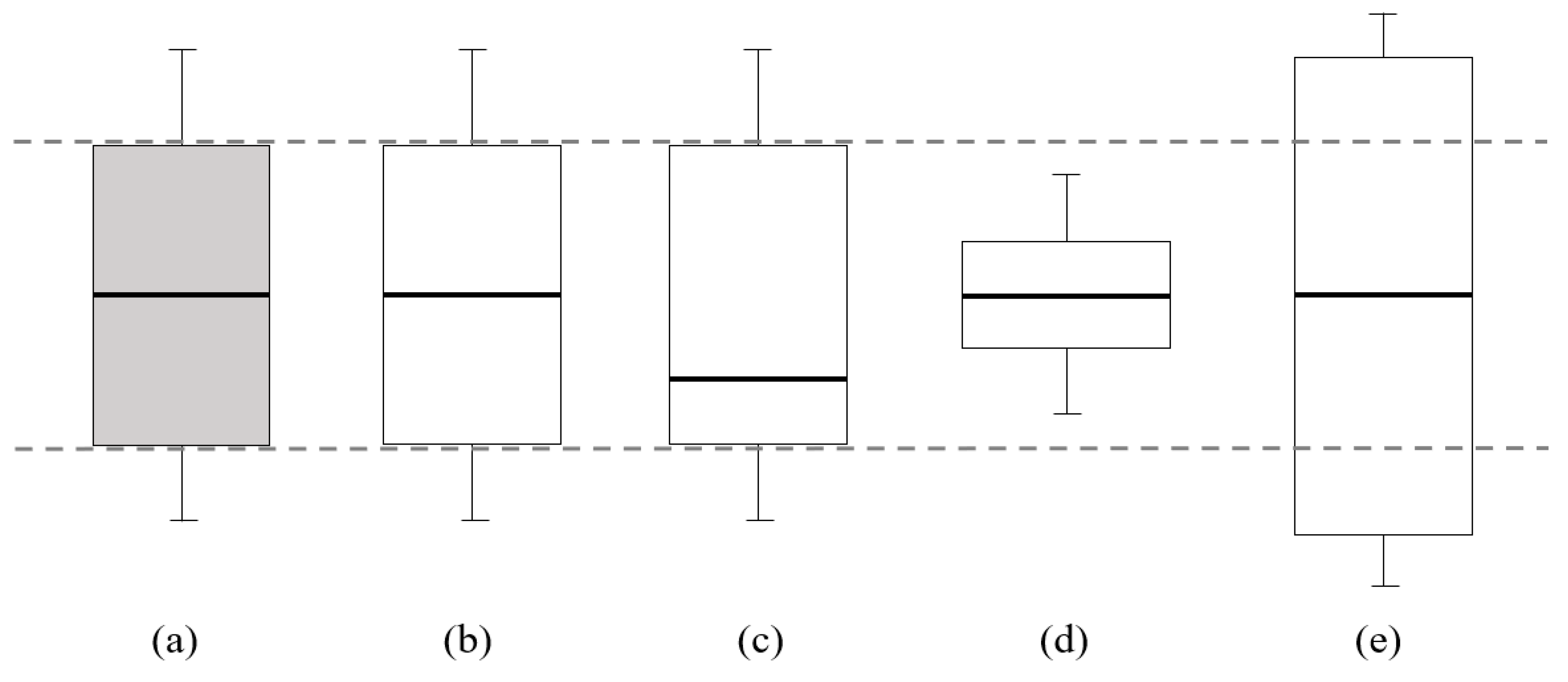
In addition to traditional metrics, this study proposes new metrics to evaluate the modeling performance in gap-filling (or predicting) time-series data. This novel metric is based on the amplitude of temporal variation, incorporating the IQR and lower bound of the time series, such as the averaged minimum values. It is proposed that after gap-filling, the predicted datasets should exhibit a temporal range, that is, amplitude, comparable to that of the original time series. Figure 3 illustrates the definition of this metric. Although many conceptual examples are possible, only four representative types of predicted boxplots, each combining different averages and IQRs, are shown in Figure 3b–e. A visual comparison suggests that Figure 3b demonstrates substantially greater consistency with the original data than Figure 3c–e. Although this is a qualitative definition, it can support more informed decisions when identifying the best-performing model through inter-comparisons across all simulated results. The time-series consistency discussed in Section 3 and Section 4 is consistently grounded in this concept.

3. Results

The results of the five models simulated by ET, XGB, LGM, VOT, and STK using different datasets, L1, L4, and L4E, are described in this section. First, the metrics and important features of each model are reported. The consistency of the predicted time series based on the difference in the average and IQR before and after the gap-filling modeling is then discussed.

3.1. Gap-Filling with Single-Level Features (L1)

In most studies on gap-filling data such as TKE and CO₂ fluxes, researchers typically use flux data measured at a single level. To predict or fill gaps in missing TKE values under similar circumstances, L1 was used at a single level, including 1.5, 60, 140, and 300 m. The modeling results are listed in

Table 3. Modeling performance with L1.

	ET	XGB	LGM	VOT	STK
0 m
MAE	0.2112	0.2151	0.2437	0.2099	0.2038
RMSE	0.4146	0.3974	0.4499	0.3949	0.3904
R2	0.7751	0.7933	0.7351	0.7959	0.8005
60 m
MAE	0.4113	0.4128	0.4542	0.4074	0.3970
RMSE	0.7233	0.7100	0.7690	0.7074	0.6968
R2	0.7442	0.7535	0.7108	0.7553	0.7626
140 m
MAE	0.4009	0.4023	0.4555	0.3995	0.3858
RMSE	0.7459	0.7030	0.8046	0.7187	0.6895
R2	0.7772	0.7974	0.7347	0.7883	0.8051
300 m
MAE	0.4746	0.4918	0.5370	0.4749	0.4648
RMSE	0.8488	0.8406	0.8894	0.8226	0.8119
R2	0.7843	0.7885	0.7632	0.7974	0.8026

.

At ground level (1.5 m), STK showed the best performance among the five models, with the lowest MAE and RMSE and the highest R², followed by ET, VOT, XGB, and LGM. At the upper levels (60, 140, and 300 m), STK also produced the best metrics: the MAE and RMSE were 2.3–3.0% and 1.3–2.6% lower than those of L1, respectively, whereas R² was 0.7–2.5% higher than the metrics of VOT, the second top-performing model. Overall, the MAE and RMSE tended to increase with measurement height as the wind speed increased.

Feature importance was investigated, which indicated the extent to which each feature affects the model performance. The output is shown in Figures S1–S3. ET calculates feature importance by averaging the decrease in impurities (e.g., Gini impurity or entropy) across all the trees in a forest. It is less prone to overfitting and provides a more robust measure of the feature importance. XGB calculates the feature importance based on the number of times a feature is used to split the data across all trees in the model. This is often referred to as “gain” or “split importance.” This provides a clear indication of the most influential features for making predictions [38]. LGM also uses split importance, similar to XGB, but handles large datasets more efficiently, with higher speeds and lower memory usage. VOT and STK do not provide feature importance; therefore, the focus for feature importance was on the results of ET, XGB, and LGM. The feature importance analysis showed that wind speed was the most important feature for ET and XGB at the ground level (importance > 0.4) and upper level (>0.3), respectively, followed by wind direction. This is because the equation for TKE consists of the square root of the wind speed components. In contrast, in LGM, wind speed and wind direction were the top features at both the ground and upper levels.

3.2. Gap-Filling with Multi-Level Features (L4)

To improve ML modeling performance, one can generally increase the number of features and/or the number of data records and perform hyperparameter tuning. Modeling with L4 was conducted, in which the number of input features was increased by adding features from other levels, including temperature and wind data, to L1 (Section 2.2.2). There were 26 features in L4.

Table 4. Modeling performance with L4.

	ET	XGB	LGM	VOT	STK
0 m
MAE	0.1996	0.2018	0.222	0.198	0.1938
RMSE	0.3856	0.3771	0.4258	0.3837	0.3681
R2	0.8046	0.8131	0.7617	0.8065	0.8219
60 m
MAE	0.3857	0.3769	0.4085	0.3748	0.368
RMSE	0.7058	0.6837	0.7318	0.6872	0.6768
R2	0.7735	0.7874	0.7565	0.7853	0.7917
140 m
MAE	0.3812	0.3754	0.4183	0.3723	0.3638
RMSE	0.8063	0.8134	0.8505	0.7989	0.7903
R2	0.7526	0.7482	0.7246	0.7572	0.7623
300 m
MAE	0.4714	0.4642	0.496	0.4565	0.4463
RMSE	0.8747	0.8372	0.8873	0.8378	0.8236
R2	0.7867	0.8046	0.7805	0.8043	0.8109

lists the modeling results obtained for L4. The MAE and RMSE tended to increase with measurement height as the variation in TKE increased with wind speed; however, R² did not show a clear measurement height dependency.

Among the five models, STK exhibited the best performance. At ground level, the MAE (0.1938) and RMSE (0.3681) decreased by 8.0% and 12.3%, respectively, compared to previous results with L1. R² increased by 1.5%. At the upper levels, the MAE and RMSE decreased by 1.3–15.2% and 7.3–36.1%, respectively, and R² increased by 3.1–20.9%, compared to the results using L1. The highest improvement appeared at the 140 m level, which was mainly caused by the larger amount of missing data compared to the other levels.

The results of the feature importance analysis are shown in Figures S1–S3. At the ground level, WS60 was the most important feature (importance ≥ 0.25) for both ET and XGB, followed by WS1 (~0.23) and WS300 (<0.10). Although WS60 was the most significant feature, the difference in importance compared with WS1 was negligible (<0.02). LGM identified WS1 as the most important feature.

At the upper level, wind speed was the most important feature. However, the details varied: the two most important features were WS1 and WS60 (>0.12) at 60 m, WS140 and WS1 (>0.10) at 140 m, and WS300 and WS1 (>0.12) at 300 m. Clearly, WS1 predominantly affected the gap-filling results at all the upper levels. Considering that turbulence originates from friction near the ground, the higher impact of WS1 on the other levels is reasonable. The flipped rank of feature importance at 60 m was likely due to topography, which will be discussed in a later section.

In summary, STK exhibited the best performance among the five models at both the ground and upper levels. However, R² at 60 and 140 m still displayed values of <0.8; therefore, an attempt was made to further improve the model performance, as described in the next section.

3.3. Gap-Filling with Expanded Features (L4E)

As mentioned in the previous section, increasing the number of input features and/or data records is a general method for improving model performance. To further enhance the modeling performance, the expanded feature dataset L4E was used, which included the entire time series of weather data and expanded datasets, such as the temporal gradient of temperature and the vertical gradient of temperature and winds (Section 2.2.2). Brute-force tests were conducted using various combinations of training data to determine the model with the best performance. A rain filter for this modeling scenario was applied; when the 30 min total precipitation exceeded 0.5 mm, the entire row was removed from the training features. Setting a 0.5 mm cut-off for rainfall data is standard practice to distinguish meaningful precipitation from noise, which comes from instrument sensitivity and resolution, or trace amounts that may result from measurement errors or non-rain events. A <0.5 mm cut-off is typically used to filter out noise and non-significant rainfall, ensuring that only meteorologically meaningful precipitation events are included in modeling and analysis [41,42,43].

The metrics of the best model, STK, using L4E are listed in

Table 5. Modeling performance with L4E.

	ET	XGB	LGM	VOT	STK
0 m
MAE	0.1868	0.1857	0.1999	0.1822	0.1782
RMSE	0.3303	0.3331	0.3523	0.3265	0.3227
R2	0.8267	0.8237	0.8029	0.8307	0.8346
60 m
MAE	0.3723	0.3642	0.3869	0.3591	0.3513
RMSE	0.6619	0.0633	0.6701	0.6334	0.6226
R2	0.7868	0.805	0.7814	0.8047	0.8114
140 m
MAE	0.3726	0.3694	0.3959	0.3591	0.3534
RMSE	0.7247	0.6737	0.7197	0.6757	0.6659
R2	0.7858	0.8149	0.7888	0.8138	0.8192
300 m
MAE	0.4193	0.4242	0.4541	0.4092	0.403
RMSE	0.736	0.7241	0.7675	0.7128	0.7021
R2	0.8106	0.8166	0.794	0.8223	0.8276

. As shown in the results in Section 3.2, the model produced the highest R² at both the ground and upper levels, followed by VOT, XGB, ET, and LGM. At ground level, the metrics significantly improved. The MAE, RMSE, and R² improved by 8.0%, 12.3%, and 1.5%, respectively, compared to the previous results for L4. At the upper levels, MAE and RMSE improved by 4.2% (60 m), 11.2% (300 m), 2.8% (60 m), and 10.0% (300 m). R² also increased by 1.3% (60 m) and 1.7% (300 m). At 140 m, MAE decreased by 2.8%. In contrast, RMSE and R² showed worse results: a 1.0% increase and 1.4% decrease, respectively, compared to the modeling results using L4, respectively, likely due to the lack of input data, as previously explained.

In the ET, XGB, and LGM models, the most important feature was WS60 at ground level, followed by WS1, WS140, and WS300. The greater importance of WS60 compared to WS1 is likely due to topographical factors. The measurement site is surrounded by mountains (with heights of approximately 400 m) in three directions (W, N, and E), and there is a valley between the lower mountains (<100 m in height and approximately 500 m in width) from W to NW. The tops of the valley and lower mountains are <100 m above ground level with average heights and widths of approximately 50 and 500 m, respectively (Figure 1). This topography coincides with the dominant wind direction (NW; ~45% frequency). The average wind speed from the valley was calculated as 4.9 m/s (60 m), 4.1 m/s (140 m), and 6.1 m/s (300 m), where WS60 was higher than WS140. Therefore, winds at 60 m may have affected the turbulence around the site, particularly at the 60 m level. This is reasonable considering the frequent appearance of WS60 as an important feature at all levels. In the case of the LGM model, several features such as wind speed, wind direction, and vertical temperature gradient were ranked as highly important (importance > 150).

The improvement in modeling performance from L1 to L4E could be mainly due to an increase in the number of features. To elucidate this possibility, various other features, such as relative humidity, vapor pressure, visibility, and soil moisture, were tested in the preliminary modeling study. No further improvements in the modeling performance were observed with these added features. The Richardson number was also used, which is expressed by thermal and mechanical turbulence, and represents turbulence motion well; however, it resulted in worse performance. Therefore, it was concluded that the importance of the modeling performance with L4E was not simply the result of an increased number of input features.

These gap-filling methods, such as interpolation and averaging, may introduce biases into the input variables, potentially affecting model performance. These methods, which are necessary for data continuity, can smooth out important fluctuations relevant to flux dynamics.

3.4. Time-Series Consistency

Traditional metrics are generally used when discussing the modeling performance of ML. In this section, other factors are suggested that should be considered when evaluating the modeling performance more precisely. In addition to these metrics, a novel evaluation metric is introduced, termed “time-series consistency,” which focuses on amplitude—defined by the IQR and the lower bound of the data band within the gap-filled data (Section 2.5). The results at 140 m were not analyzed because of the uncertainty caused by the relatively large amount of missing data.

Table 6. Descriptive statistics of TKE from the modeling of STK with L1, L4, and L4E training data.

Feature Dataset	Level (m)	(a) Whole Data Before Gap-Filling		(b) Predicted Data Gap-Filled Only		(c) Whole Data After Gap-Filling		$\frac{\left(\mathit{a}\right)-\left(\mathit{c}\right)}{\left(\mathit{a}\right)}\times 100$ (%)
		Avg ± s.d.	IQR	Avg ± s.d.	IQR	Avg ± s.d.	IQR	Avg	IQR
L1	0	0.748 ± 0.926	0.736	0.640 ± 0.672	0.683	0.729 ± 0.888	0.683	−2.5	7.3
	60	1.137 ± 1.401	1.112	2.270 ± 0.513	0.038	1.375 ± 1.348	1.692	−20.9	−52.2
	140	1.193 ± 1.586	1.211	2.246 ± 1.197	1.107	1.586 ± 1.539	2.188	−32.9	−80.7
	300	1.301 ± 1.770	1.368	3.834 ± 1.155	0.541	1.611 ± 1.898	2.240	−23.8	−63.7
L4	0	The same as above.		0.8096 ± 0.659	0.5762	0.759 ± 0.886	0.750	−1.5	−1.8
	60			2.180 ± 1.439	0.667	1.356 ± 1.472	1.528	−19.3	−37.4
	140			2.168 ± 1.507	1.255	1.557 ± 1.627	1.893	−30.5	−56.3
	300			3.406 ± 1.150	0.301	1.558 ± 1.840	2.077	−19.8	−51.8
L4E	0	The same as above.		0.673 ± 0.595	0.639	0.735 ± 0.878	0.878	1.7	−19.1
	60			1.863 ± 1.419	1.339	1.290 ± 1.419	1.337	−13.5	−20.2
	140			2.431 ± 2.338	1.284	1.655 ± 1.994	1.700	−38.7	−40.4
	300			2.602 ± 1.202	0.249	1.459 ± 1.758	1.813	−12.1	−33.8

reports the average and IQR of TKE before and after gap-filling and the predicted TKE, which were missing in the original dataset. After gap-filling, the average TKE increased at all levels because of the higher values of the predicted TKE. At the ground level, compared to the original time series, the mean values of the entire TKE time series increased by <1% (L1) and 1.5% (L4) and decreased by 1.7% (L4E), whereas the IQR decreased by 7.3% (L1) and 4.5% (L4E) and increased by 1.8% (L4). There was no significant change in the gap-filling results depending on the datasets. At the upper levels (60 m and 300 m), in contrast, the mean TKE increased by 19.4–21.0% (L1), 19.3–19.8% (L4), and 12.3–13.4% (L4E), with STK using L4E producing the smallest deviation compared to the original observation data. At 140 m, there was a >30% offset in the average, likely because of the large amount of missing data. The relatively large offsets at the upper levels were mainly caused by the higher predicted values of TKE. Further investigation is needed to understand the reason for the larger offsets between L1 and L4 in the time series after gap-filling.

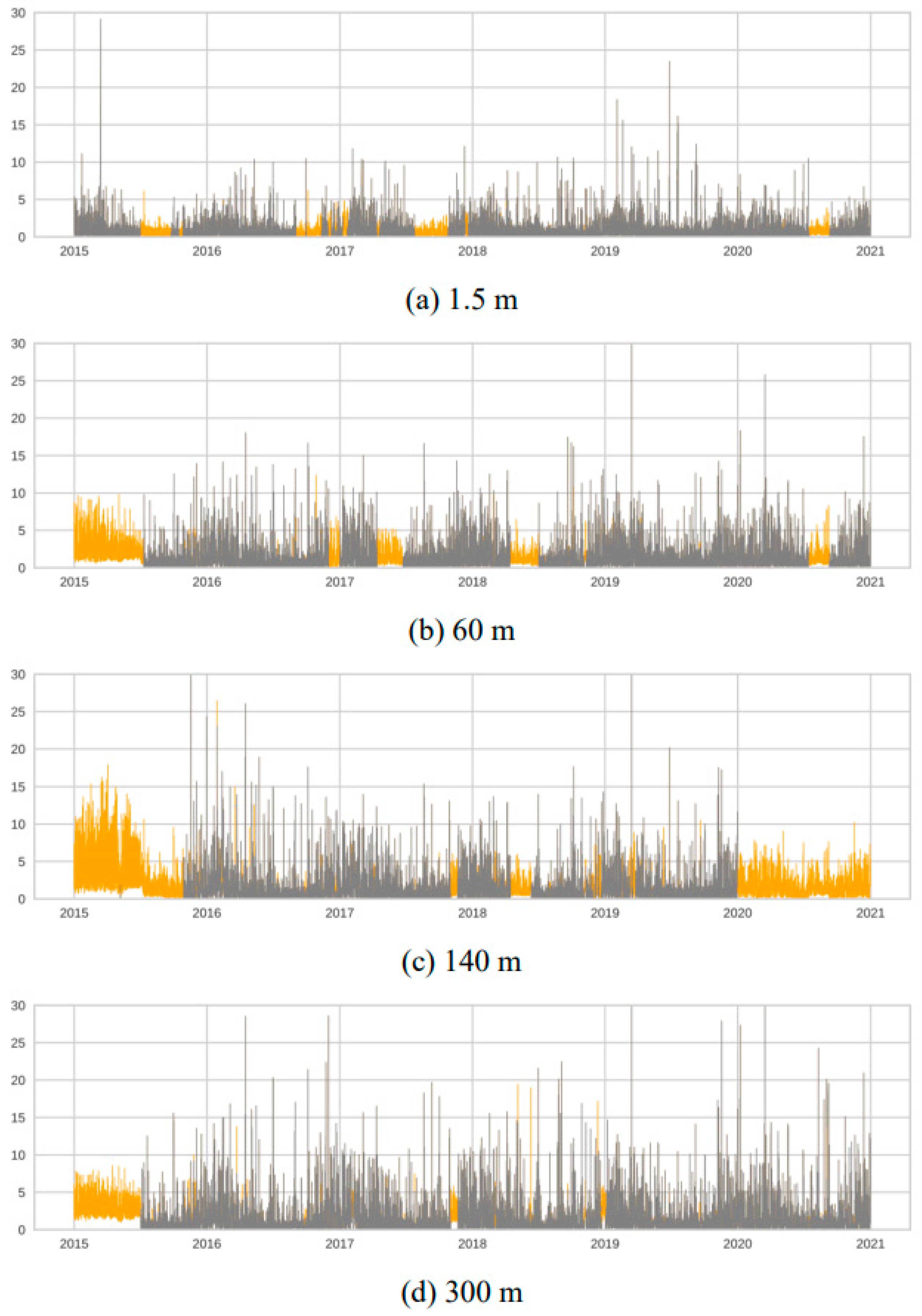
The TKE time series before and after gap-filling using L1 were compared. The entire time series of the TKE simulated with L4E is shown in Figure 4 and is overplotted with the original time series. TKE at upper levels showed significantly higher minimum values, ~2.2 m²/s² (60 m), ~4.5 m²/s² (140 m), and ~2.5 m²/s² (300 m), along with narrow bands, indicating lower amplitudes. The offsets of the average and IQR ranged from 19% to 33% and 52% to 65%, respectively, compared with the original data. Therefore, the TKE prediction using L1 failed to achieve time-series consistency. With the L4 dataset, while displaying better consistency than L1 with a relatively broader band, the average TKE offset remained at approximately 20% and the IQR was still significantly reduced, ranging from 37% to 52% at 60 and 300 m, respectively. This persistent reduction in IQR, despite the addition of multi-level features, implies that the model suppresses important turbulent fluctuations.

The STK and L4E results significantly improved. The entire TKE time series simulated using L4E is shown in Figure 5. The minimum predicted values were higher than those of the original time series before gap-filling. The average of the minimum values showed ~0.47 m²/s² (60 m), ~0.35 m²/s² (140 m), and ~0.74 m²/s² (300 m), which are much lower than the modeling results with L1 and L4. The largest offset of the minimum TKE appeared in the period of long-term missing data, such as in the first half of 2015, where the average minimum values were approximately twice as high, yet still lower than the two previous modeling results using L1 and L4. The mean values decreased by 13.4% and 12.3% at 60 m and 300 m, respectively, and the IQR with L4E also decreased. Overall, the gap-filling modeling of STK with L4E resulted in much better consistency in the time series, showing the lowest amplitude offset in terms of the average, IQR, and minimum values. This closer alignment with the original TKE is vital because it ensures that the gap-filled data accurately preserve the full range of turbulent intensities, which is indispensable for climate modeling, energy estimation, and pollutant dispersion studies, where the amplitude of TKE directly influences simulated atmospheric processes.

Differences in average TKE between the original and gap-filled data across 16 wind directions were also examined to assess whether gap-filling was influenced by wind directions related to specific data gaps. Figure 6 shows the directional difference in TKE before and after gap-filling. The gap-filling technique significantly increased the TKE by approximately 19% compared with the original time series, particularly in the direction from W to N. One might argue that this wind direction-dependent offset in TKE was caused by missing data. However, when the number of missing data points depending on wind direction was counted, the offset was not primarily due to the large amount of missing data in the same direction.

3.5. Dependency on Stability and Season

As TKE is governed by atmospheric stability in the planetary boundary layer, it is valuable to assess the modeling performance under varying atmospheric stability conditions. The L4E dataset was classified into stable and unstable regimes using both the Monin–Obukhov (M-O) stability parameters and atmospheric profiles. The M-O stability parameter ($\zeta )$, derived from the flux measurements, is defined as

$$\zeta ={\displaystyle \frac{z-d}{L}}$$

(7)

where $z$ is the measurement height, $d$ is the displacement height, and $L$ is the M-O length [44]. A positive $\zeta$ indicates stable conditions, while a negative $\zeta$ indicates unstable conditions. The atmospheric stability based on vertical temperature profiles was determined using the temperature difference ($∆T=T_{300m}-T_{1.5m}$): $∆T>0$ indicates stability, and $∆T<0$ indicates instability.

The performance of the STK model was evaluated using a subset of L4E data, and the time series produced is shown in Figures S4 and S5. Regardless of whether $\zeta$ or $∆T$ was used as the stability criterion, the results showed that, as expected, MAE and RMSE were significantly lower under stable conditions and higher under unstable conditions across all measurement heights, compared to the results using the full L4E dataset in Section 3.4. Under $\zeta$-defined stable conditions, MAE and RMSE ranged from 0.0865 (1.5 m) to 0.4259 (300 m) and from 0.1309 (1.5 m) to 0.8269 (300 m), respectively, with R² values ranging from 0.6047 to 0.7587. Under unstable conditions, the MAE and RMSE ranged from 0.1757 to 0.4046 and 0.3258 to 0.7184, respectively, with R² values between 0.7508 and 0.8073. When using $∆T$ as the stability criterion, the results were consistent with those based on $\zeta$, except for a higher R² value (0.8332) at the level of 140 m than the results with the full L4E dataset. Modeling with subset data did not reveal a clear change in time-series consistency dependent on atmospheric stability. The gap-filled results from the STK model using the L1 subset under stable conditions still exhibited a narrow and higher minima band, whereas those using the L4E subset demonstrated higher consistency, aligning with previous results using L4E.

The seasonal dependency of the STK modeling performance was also investigated using the L4E dataset for summer and winter, and the results are presented in Figures S6. In summer, the RMSE ranged from 0.3363 (1.5 m) to 0.4711 (300 m), and the R² values ranged from 0.6673 to 0.8315. In winter, the RMSE ranged from 0.3363 (1.5 m) to 0.4711 (300 m), with R² values between 0.7902 and 0.8126. There was no improvement in the amplitude and minima compared to the whole set of L4E.

The overall findings revealed that the best performance was achieved with the STK model using the expanded L4E dataset, achieving the highest R² and notable improvements in MAE and RMSE. In addition, this combination produced improved time-series consistency, exhibiting the lowest amplitude offsets (average, IQR, and minima) compared with the other datasets. Implications include the necessity for future research that considers both traditional metrics and time-series consistency.

4. Discussion

Notwithstanding the successful demonstration of the effectiveness of ML models, especially stacking ensembles combined with an expanded feature dataset for gap-filling TKE data, it is important to recognize the study’s limitations and the potential for future improvement.

At the early stage of preprocessing, to ensure data continuity, spline interpolation or temporal averaging was used, which can distort high-frequency variability or flatten extremes, thereby introducing bias. For instance, spline interpolation may overestimate intermediate values under rapidly changing conditions, whereas averaging can dampen extremes, leading to underrepresentation of peak events. These artifacts can affect the model accuracy and physical realism; therefore, validation and sensitivity analyses are essential when using imputed data. Careful validation of gap-filled data and sensitivity analyses are essential for assessing the robustness of model predictions under varying imputation strategies.

It was decided not to interpolate the wind data to preserve their original properties. As wind includes both direction and magnitude, it is highly sensitive to interpolation. Although this makes direct comparisons more difficult, recent studies have shown that ML models can predict wind speed accurately without spatial or temporal interpolation [45,46]. One study even reported an R² of 0.84 with a 30-day gap and only a 19.7% increase in RMSE with a 120-day gap [47]. These study results suggest that not applying interpolation may also be acceptable in this study.

At the stage of selecting ML models, the level of R² < 0.8 from STK with L1 appears somewhat low. In meteorology, predicting wind speed, which plays a dominant role in determining the TKE, is particularly challenging. Previous studies have reported R² values for wind speed prediction ranging from 0.57 to 0.69 using the Weather Research and Forecasting (WRF) meteorological model [48,49] and from 0.63 to 0.91 using ML models [50,51]. Compared with these studies, the R² > 0.83 achieved with STK using L4E (Section 3.3) can be considered a reasonably strong outcome.

Although stacking models can enhance predictive performance by integrating multiple learners, a large number of features can increase the computational cost in terms of training time and memory usage. This trade-off is acknowledged, and a balance between model complexity and efficiency was sought. Specifically, model performance was evaluated under reduced feature subsets using feature selection in the setup function of the Pycaret package. It was found that marginal gains in accuracy beyond a certain feature threshold did not increase the computational burden.

Unlike single models, it is difficult to trace how input features influence the final prediction in stacking modeling. This black-box nature can be a limitation in scientific- and policy-driven domains, where understanding the influence of input features is essential. To maximize transparency in feature influence, an interpretable metamodel, linear regression, was employed in this study. However, balancing performance with transparency remains a key consideration, and future work may use explainable tools such as SHAP [52] to assess the feature contributions.

In this study, a stacking model improves the time-series consistency, not by the metamodel in STK simply smoothing out the averaged prediction but rather by learning complex relationships from the outputs of multiple base models, which themselves have been trained on an exceptionally rich dataset (L4E) that explicitly encodes temporal and vertical dependencies. This combination allows STK with L4E to overcome the limitations of models trained on less comprehensive datasets, leading to more accurate TKE amplitude and variability predictions, which are critical for robust flux-based climate modeling and other atmospheric applications.

5. Conclusions and Summary

Missing values are inevitable in high-frequency flux measurements, making gap-filling techniques crucial for accurate analysis and prediction of weather phenomena. Gap-filling or prediction of missing data is essential for the accuracy and reliability of statistical results in boundary meteorology, particularly concerning the interaction of mass, energy, and momentum between the surface and atmosphere. Among the several techniques, in this study, gap-filling was achieved using ML algorithms with a few flux measurement datasets acquired by the EC system at a multi-level tall flux tower.

Weather and flux data at four different measurement levels (1.5, 60 m, 140 m, and 300 m) were collected at a tall flux tower in the southern part of the Korean Peninsula over approximately six years. To fill gaps in this data and predict the TKE, ML modeling was conducted using different input training datasets. Modeling with five ML algorithms, ET, XGB, LGM, VOT, and STK, was performed using three different training feature datasets. Basic meteorological data, including air, surface, and ground temperatures; relative humidity; and wind speed at each tower level were used as input for the ML technique. Combined, multi-level, and expanded data were also produced, including the vertical and temporal differences in wind speed and temperature between two nearby measurement levels. Among the five models tested, STK exhibited the best performance in terms of MAE, RMSE, and R².

Based on traditional metrics, there were no significant differences between the STK results for L1, L4, and L4E. However, a large discrepancy was found in the time-series consistency in terms of amplitude. The amplitude of the time series can be represented by the difference between the average, IQR, and minima before and after gap-filling. Interestingly, the difference in amplitude before and after gap-filling was large, particularly at the upper levels, which displayed a narrow band. The minimum TKE gap-filled values were significantly larger than those of the original time series for L1 and L4. The gap-filled values from STK with L4E were much closer to the original time series, indicating a higher consistency than the original time series.

The STK model with the L4E dataset achieved much better time-series consistency, exhibiting the lowest offset of amplitude in terms of the average, IQR, and minimum TKE values. The minimum predicted L4E value is much closer to that of the original time series, representing a substantial improvement over the higher minima produced by L1 and L4. This rigorous assessment of temporal consistency is essential for the accurate evaluation of ML prediction models. Considering this result, it is evident that the evaluation of ML modeling performance should use not only traditional metrics but also time-series consistency when attempting to gap-fill or predict time-series data, as it provides critical additional insights into model reliability.

These findings may be generalizable to other time-series prediction studies at other sites with distinct characteristics such as surface roughness, land use, and atmospheric conditions. Although the STK model demonstrated robust performance for TKE reconstruction, further validation across diverse regions, such as urban areas, and other variables, including sensible heat flux and CO₂ flux, is necessary. The consistency-based evaluation approach can serve as a foundation for similar applications in other environments: The proposed modeling framework also holds strong potential for climate modeling. In agricultural meteorology, this approach may enhance the prediction of climatic variables that are critical for crop growth and irrigation. Urban climatology is well-suited for the accurate modeling of complex turbulence, which is essential for estimating air pollution emissions, mitigating urban heat islands, and informing urban planning. The results of this study are vital for ensuring reliability in downstream applications such as forecasting or climate modeling. Future plans involve the use of consistent TKE data to improve meteorological models.