A Simple Yet Powerful Hybrid Machine Learning Approach to Aid Decision-Making in Laboratory Experiments

Abstract

High-dimensional experimental spaces and resource constraints challenge modern science. We introduce a hybrid machine-learning (ML) framework that combines Ordinary Least Squares (OLS) for global surface estimation, Gaussian Process (GP) regression for uncertainty modelling, expected improvement (EI) for active learning, and K-means clustering for diversifying conditions. We applied this approach to published growth-rate data of the diatom Thalassiosira pseudonana, originally measured across 25 phosphate–temperature conditions. Using the nutrient–temperature model as a simulator, our ML framework located the optimal growth conditions in only 25 virtual experiments—matching the original study’s outcome. Sensitivity analyses further revealed that fewer iterations and controlled batch sizes maintain accuracy even with higher data variability. This demonstrates that ML-guided experimentation can achieve expert-level decision-making without extensive prior data, reducing experimental burden while preserving rigour. Our results highlight the promise of algorithm-assisted experimentation in biology, agriculture, and medicine, marking a shift toward smarter, data-driven scientific workflows.

1. Introduction

Scientific knowledge, as we understand it today, is the result of centuries of methodological refinement, evolving from philosophical speculation into systematic experimentation. The transformation of observational inquiry into controlled scientific experimentation during the Renaissance and Enlightenment periods was one of the most important milestones for the development of the scientific method and was marked by several key methodological innovations. Francis Bacon’s concept of “experimental natural history” introduced a new philosophy of experimentation and practice-based classification systems [1]. Bacon’s approach involved constraining nature through “the violence of impediments” [2] and emphasized the productive role of experiments in generating new effects and conceptual innovations [3]. The period saw a shift from individual observations to socially established experimental facts [4], and a growing emphasis on experience and the experimental method [5]. This era also witnessed the emergence of the mathematization of nature, corpuscularian natural philosophy, and empiricist experimental science [6]. The 18th century further refined these approaches, distinguishing between exploratory and demonstrative experimentation and embracing diverse methodologies [7].

Fast forward to the 21st century, and the scientific method is used globally at an unprecedented scale, resulting in millions of research publications annually. This high output of scientific knowledge is in part due to the number of active researchers worldwide, which has increased from 4 million in 1980 to 13.1 million in 2018 [8]. Nonetheless, one of the greatest innovations of the 20th century, the internet, has significantly contributed to this high output and transformed scientific research and communication. It has increased access to data, facilitated collaboration across distances, and accelerated information sharing [9,10,11]. Building on that foundation, we now find ourselves in the year 2025 at a pivotal milestone in the evolution of the scientific method: the integration of advanced data analytics and computational tools, broadly encompassed by the term artificial intelligence. Machine learning (ML) and artificial intelligence (AI) are already transforming scientific research across disciplines, revolutionizing data analysis, simulation, and hypothesis generation [12]. These technologies are accelerating discovery processes by enabling sophisticated analysis of complex datasets and developing predictive models [13]. Notably, for the first time, the 2024 Nobel Prize in Chemistry recognized advances in artificial intelligence, awarding David Baker for “computational protein design” and Demis Hassabis and John Jumper for “protein structure prediction” through the development of AlphaFold [14,15]. This landmark recognition signals not just a shift in scientific capability but also a broader acceptance of AI as an essential tool in modern discovery.

Yet, despite these recent advances, experimental research in the life sciences still largely depends on traditional, trial-and-error methods—approaches that are often slow, costly, and inefficient when navigating complex, high-dimensional experimental spaces [16,17]. This raises an important question: can machine learning (ML) meaningfully assist researchers in making more informed and statistically sound experimental decisions? If so, the implications could be profound—accelerating discovery, improving reproducibility, and enabling scientists to do more with fewer resources [18]. At the same time, as ML systems grow more autonomous and complex, ensuring effective human oversight becomes both a technical and ethical challenge, particularly in sensitive domains like biotechnology and agriculture. It has been argued that oversight must be proactive, embedding interpretability, auditability, and domain-informed collaboration into system design from the outset [19]. In this study, we explore that vision through a focused case study using published biological data to evaluate whether hybrid ML models can guide experimental design as effectively as expert intuition. Our aim is to foster a more collaborative, transparent, and trustworthy approach to scientific discovery, where artificial intelligence enhances rather than replaces human expertise.

Active learning methods—such as uncertainty sampling, query-by-committee, and margin-based strategies—have been shown to iteratively focus experimental efforts on the most informative perturbations, thereby dramatically reducing the total number of wet-lab assays required to uncover complex biological networks [20,21]. Furthermore, embedding a lab-in-the-loop paradigm—where ML-generated hypotheses guide wet-lab experiments and their outcomes are subsequently used to retrain and refine the surrogate model—ensures continual human oversight and robustness, which is critical for high-stakes applications in biology, agriculture, and medicine [22]. Gaussian Process Regression (GP) is a powerful foundational ML model with great potential for active learning. Recent work in Bayesian optimization has introduced several techniques that extend beyond classic Gaussian Process. For example, deep Gaussian processes (deep GPs) [23] and deep kernel learning embed neural networks within GP covariance functions to capture complex, nonlinear structure in high-dimensional spaces, enabling scalable surrogate modelling and richer uncertainty estimates [24]. At the same time, probabilistic programming frameworks have made it possible to specify highly expressive priors and bespoke likelihoods—allowing surrogate models to incorporate domain knowledge (e.g., mechanistic constraints or structured noise models) directly into the optimization loop [25,26]. By leveraging these advances (including entropy-based acquisition functions and multi-fidelity or multi-task extensions), our hybrid approach can be seen as one instantiation within a rapidly evolving toolbox of methods for data-efficient, robust experimental design.

Building on these state-of-the-art active-learning and surrogate-modelling techniques, we focus here on two foundational methods—Gaussian Process Regression (GP) and Ordinary Least Squares (OLS)—that serve complementary roles in our hybrid framework. These methods can quantify uncertainty, make precise predictions, and systematically explore parameter spaces [25]. The key benefit of integrating ML into experimentation is its ability to shift experimental designs from exhaustive or arbitrary sampling toward targeted, knowledge-driven exploration. OLS modelling has been widely used due to its computationally inexpensive means, interpretability, and robustness in capturing global trends within experimental data [27]. However, while OLS excels in identifying broad patterns, it assumes linear relationships or polynomial transformations, potentially missing complex local interactions [28]. Complementary to OLS, GP regression addresses this limitation by modelling the data through flexible, probabilistic functions that quantify uncertainty explicitly [18]. By combining both methods, OLS for global approximation and GP for local exploration, experimenters can significantly enhance the precision and efficiency of the discovery process. This combination of foundational machine learning algorithms creates a unique hybrid machine learning approach, which we demonstrate that it can guide experimentation as effectively as senior scientists.

2. Materials and Methods

To explore whether artificial intelligence can support more efficient and statistically informed experimental decisions, we revisited a well-characterized biological dataset from [29]. In their study, the marine diatom Thalassiosira pseudonana was grown under 25 unique combinations of phosphate and temperature, each replicated three times, resulting in a total of 75 data points. This full-factorial design allowed them to accurately resolve a two-dimensional response surface describing the organism’s growth rate across nutrient (phosphate) and temperature gradients.

Here, we ask a forward-looking question: Could a machine learning-assisted experimental strategy have achieved the same scientific outcome with fewer experiments? More specifically:

• Would the AI-guided method converge on the same optimum growth conditions?
• Could it do so more efficiently by performing fewer total experimental experiments?

To address these questions, we designed a hybrid machine learning framework that combines global trend modelling with adaptive local exploration. This strategy integrates:

• Ordinary Least Squares (OLS) regression model to fit the observed growth rate data adding a second-order polynomial that includes both quadratic and interaction terms (Phosphate², Temperature², and Phosphate*Temperature) to help capture nonlinear relationships between the predictor variables and the response variable;
• Gaussian Process (GP) regression model with a Matern (ν = 2.5) kernel trained on residuals $r_i=y_i-{\widehat{f}}_{OLS}(x_i)$ to capture uncertainty across the parameter space. The combine predictive mean at a new point x is ${\widehat{f}}_{OLS}(x)+{\mu }_{GP}(x)$, and the perspective variance ${\sigma }_{GP}^2(x)$. Hyperparameters for the GP model were optimized using maximum likelihood estimation via scikit-learn’s internal routines. A small noise term (alpha = 10⁻⁶) was added to improve numerical stability;
• Expected improvement (EI) implemented with a small exploration parameter (ξ = 0.01), evaluated a uniform 20 × 20 grid spanning the phosphate and temperature ranges, to rank untested conditions by potential gain; these was a decision criterion to identify which untested conditions are most likely to yield new insights;
• Apply K-means clustering to the top candidate points (ranked by expected improvement), selecting one representative from each cluster so that each experimental cycle explores diverse yet high-potential regions of the parameter space. The number of clusters was set to match the cycle batch size (five experiments), and the algorithm was run with 10 initializations (n_init = 10) to ensure convergence. All implementation details, including complete Python code and example notebooks, are publicly available at https://github.com/benocd/ml-experiment-optimizer (accessed on 15 May 2025).

Our aim was to simulate how such a method would behave based on manual iteration and plotting rather than automated thresholds, beginning with just a handful of experiments and refining predictions as new data becomes available. Importantly, we have elected to constrain the algorithm to just five experiments per cycle, reflecting realistic experimental limitations. After each cycle of 5 experiments, new data are used to retrain the models and update the choice of the next best conditions to test.

In the following sections, we assess how rapidly and accurately this ML-guided procedure converges on reaching a predicted growth rate within 0.01% of the known maximum, and how the number of experimental iterations is affected by the chosen stopping criteria and batch sizes. We also compare its efficiency to the traditional approach taken by the authors of the original research [29], offering insights into the potential of machine learning to streamline empirical research.

3. Results

To test our machine learning–assisted experimental approach, we first reconstructed the phosphate–temperature response surface of Thalassiosira pseudonana using the published model [29]. This model (Equation (1)) describes the organism’s specific growth rate as a function of phosphate concentration and temperature and served as our ground truth for evaluating algorithm performance. By using this validated model, we were able to conduct virtual experiments, that is, to simulate growth outcomes for any chosen combination of phosphate and temperature within the tested range (1–20 µM and 4–36 °C). This approach enabled controlled and reproducible testing of our iterative ML algorithm without requiring new wet-lab experiments, while still being anchored in realistic biological response data. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

$$\mu \left(T,R\right)=b_1\ast \exp \left(b_2\ast T\right)\ast {\displaystyle \frac{R}{e}}-(d_0+d_1\ast \exp \left(d_2\ast T\right))$$

(1)

This equation is reproduced from [29] and describes the specific growth rate (μ) of the diatom Thalassiosira pseudonana as a function of temperature (T, in °C) and phosphate concentration (R, in µM). The fitting parameters resulted from experiments are: b₁ (1.17) maximum birth rate scaling factor, b₂ (0.06) is temperature sensitivity of the birth rate, d₀ (1.12) is baseline death rate, d₁ (0.27) is scaling factor for temperature-dependent death, d₂ (0.01) is temperature sensitivity of the death rate, and K (0.1) is the half-saturation constant for phosphate uptake.

To demonstrate the approach, we used the experimentally derived nutrient–temperature model (Equation (1)) within a simulated feedback loop. Each time the model was queried for a growth rate at a specific phosphate and temperature combination, we treated it as a virtual experiment. In each cycle, the hybrid machine learning algorithm analyzed the results from a strategically selected set of these virtual experiments and then recommended the next best conditions to test. Each cycle comprises the following:

• Initial Data and Model Fitting

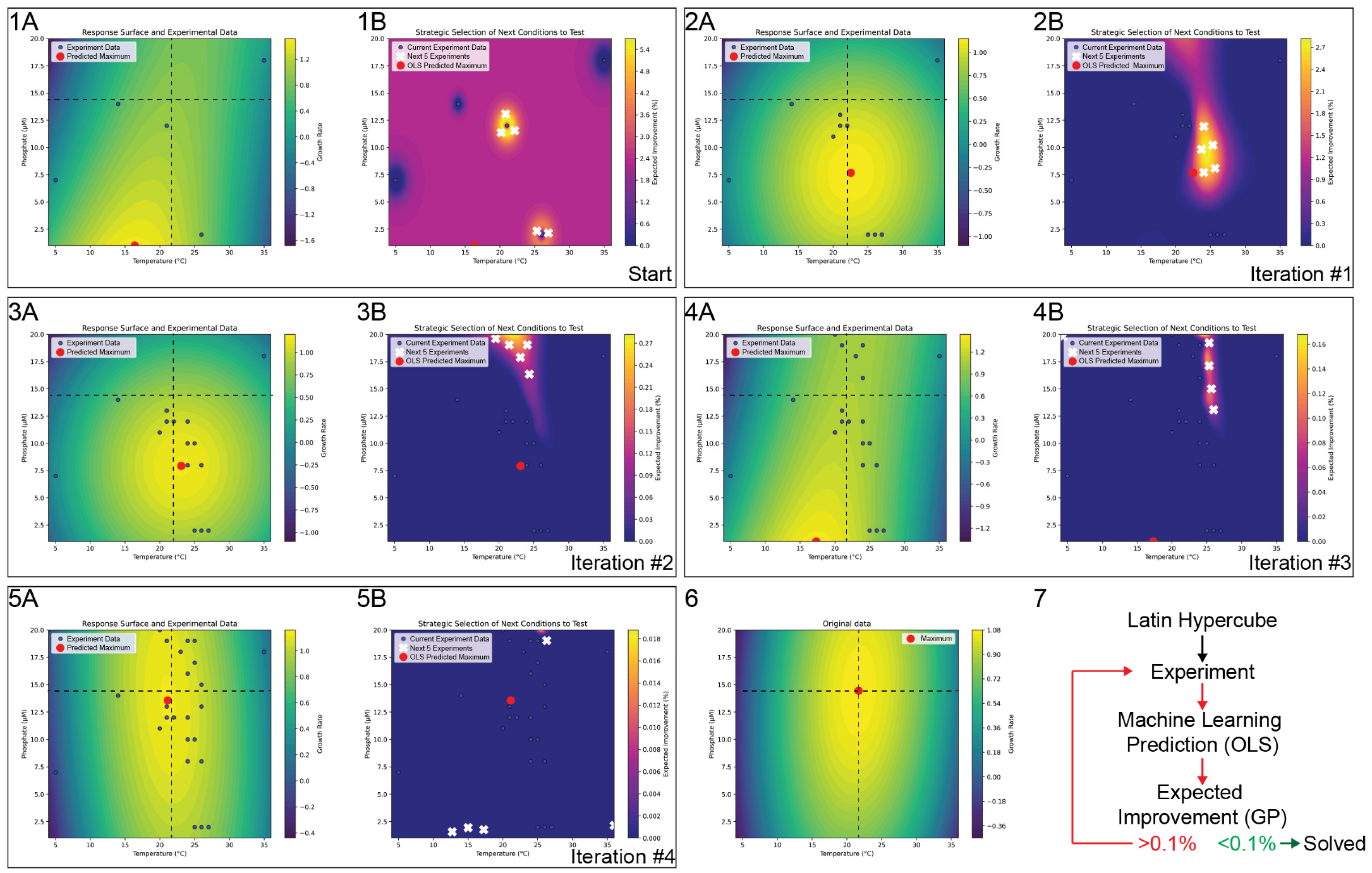
We first use a Latin Hypercube Sampling [30] to suggest the first 5 experiments which will yield the first growth rate data points. Next an Ordinary Least Squares (OLS) quadratic model is fitted to capture the broad shape of the growth-rate surface. In parallel, a Gaussian Process (GP) model is trained on the same dataset to provide an uncertainty estimate at each point in the phosphate–temperature domain (Figure 1(1A,1B)).

2.

Expected Improvement (EI) Computation

Using the GP predictions, we compute expected improvement (EI) over a grid of possible phosphate–temperature pairs. This EI metric indicates how much better than our current best measurement each candidate point might be, thus identifying regions with high potential for improvement.

3.

K-Means Selection of Next Conditions

We then select the top EI points (e.g., the top 300), ensuring we focus only on promising regions. We use K-Means to group the top EI points so they do not all concentrate in the same region of the parameter space. From those groups, we then pick one point per cluster—five in total, matching the number of experiments we can run at once. These conditions are tested in the lab during the next cycle.

4.

Data Update and Refit

After each set of five experiments, we measure the new growth rates, append them to the existing dataset, and refit both the OLS and GP models. This integration of new evidence steadily reduces uncertainty, especially in regions identified as near-optimal.

5.

Stopping Criterion

At the end of each cycle, we check if the maximum EI in the domain is below 0.1%. If so, we deem further exploration unlikely to yield meaningful improvements and stop. Otherwise, the cycle repeats with newly selected conditions.

6.

Results and Convergence

In practice, this machine learning–guided loop quickly narrows in on the maximum growth rate. The OLS model provides a global approximation of how temperature and phosphate interact and influence growth rate, while the GP focuses on local uncertainty to direct experiments toward underexplored but promising areas. By limiting each iterative cycle to five experiments, we reflect a realistic laboratory constraint—one that might stem from the number of available photobioreactors or batch vessels. Nevertheless, the approach efficiently identifies near-optimal conditions in only a few iterations, and a total of 25 experiments. As a result, we found that the hybrid OLS–GP strategy, combined with EI and K-Means clustering for condition selection, converged on a phosphate–temperature growth rate maximum in four cycles (iterations) for our recreated Thalassiosira pseudonana dataset (Figure 1). After these iterations, the EI across the domain remained consistently below the 0.01% threshold, indicating negligible benefit to further experimentation.

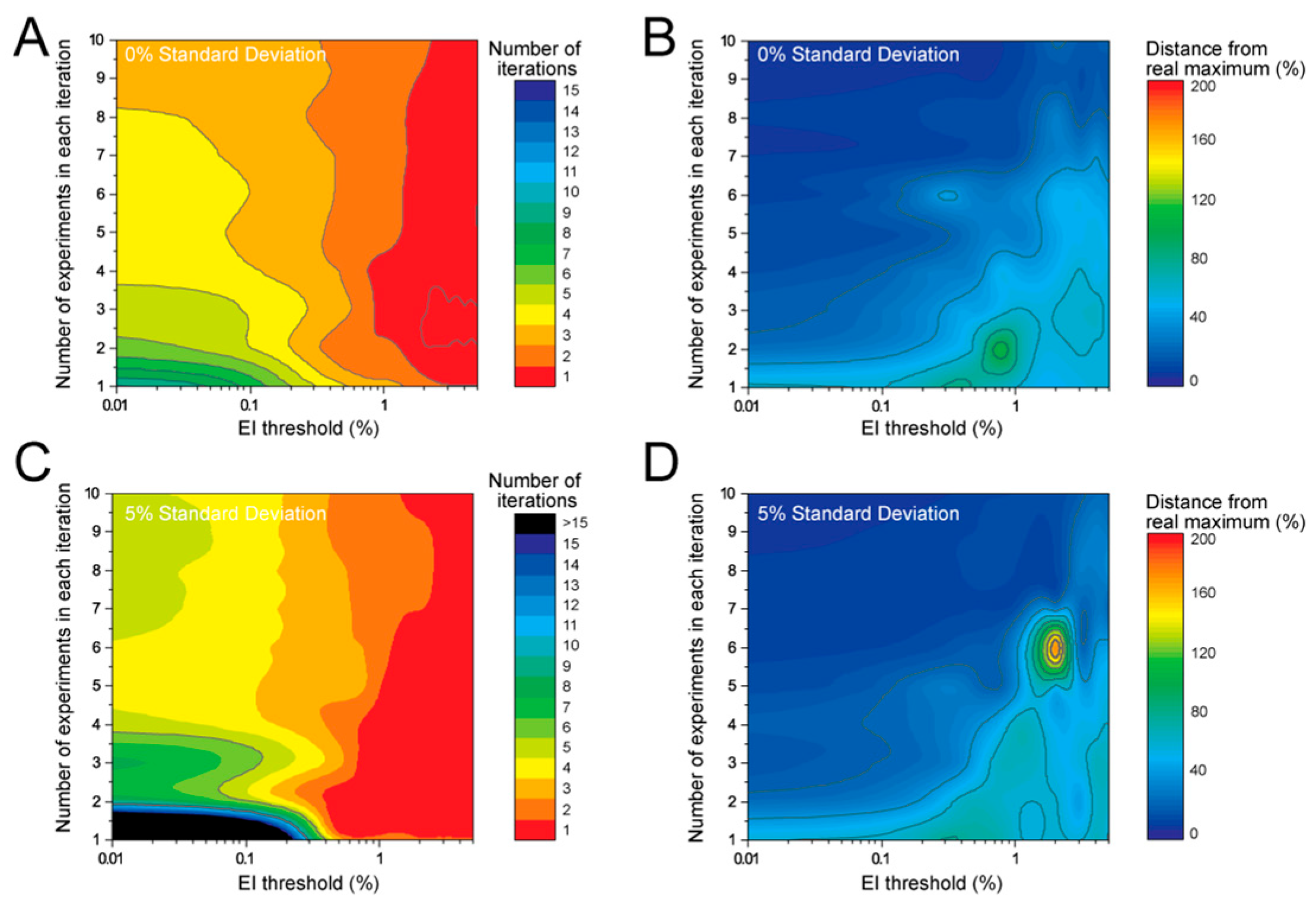
Next, we investigated how the number of required iterations for the results to converge changes as a when we change the number of experiments in each iteration. We performed the same analysis as shown in Figure 1 but changed the number of experiments incrementally from 1 to 10, and tested various stopping criterion by setting the EI threshold to various values between 0.1 and 5% (Figure 2). The results showed that high values for EI threshold, which mean that there are still many potential experiments that can improve the prediction, will lead to the algorithm to stop within 1–2 iterations (red region of Figure 2A,C). That outcome results in a few experiments but also very low accuracy in the predicted outcomes, as shown by the high Euclidian distance between the predictions and the true maxima (Figure 2B,D). The analysis also revealed that placing stricter constraints on the EI (e.g., 0.01%) and performing multiple experiment in each iteration results in an optimal number of iterations with good accuracy., e.g., if five experiments can be performed in each iteration, the ML process will require four iterations (total of 20 experiments) with an EI threshold of 0.01% to find the maxima in the dataset; the discovered maxima is predicted to be ±10% from the real maxima (Figure 2A,B). If the number of experiments is increased to seven in each iteration, with four iterations (total experiments 28) and with an EI threshold of 0.01%, the accuracy improves bringing the discovered maxima to ±5% from the real maxima (Figure 2A,B). The level of variability in the data has significant impact on the model’s behaviour and efficiency with which it can explore the space. When presented with a dataset in which we added randomly 5% standard deviation the model required generally more iterations but also identified a region with no convergence: 1–2 experiments per iteration (Figure 2C, black region of heatmap). Accuracy of the predicted maxima also dropped in low experiments per iteration and high EI thresholds (Figure 2D).

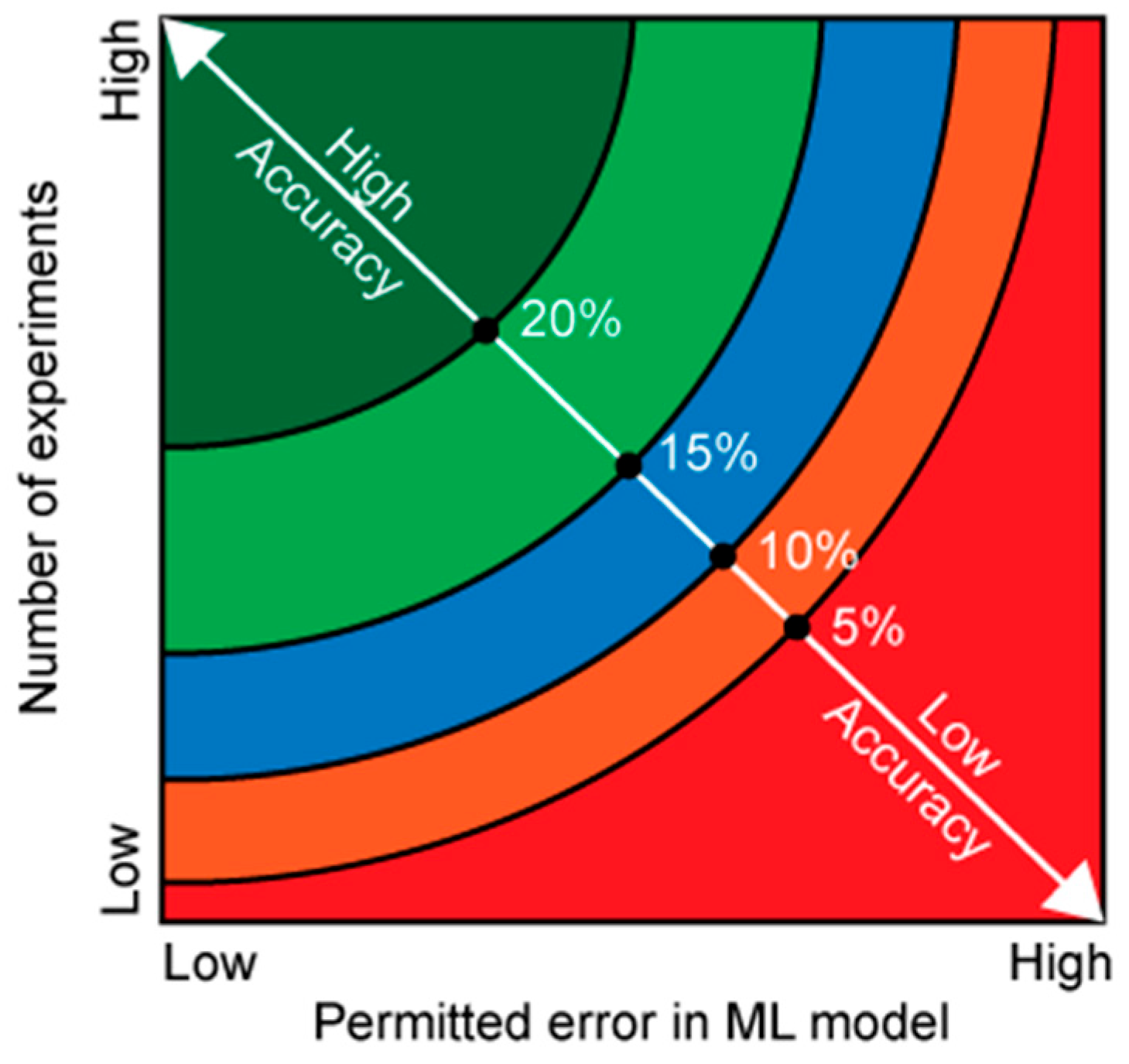
Lastly, we present a simplified model illustrating how (1) the total number of experiments ($experiments\ast \mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s})$, (2) the ML model’s strictness in limiting system variability, and (3) the degree of inherent variability together influences result accuracy (Figure 3). High number of experiments with strict ML parameters will always yield the highest accuracy in the results regardless of the variability in the data (Figure 3 green region). If the data has low variability, then the number of experiments can be reduced while still maintaining accuracy in the outcome.

The original experimental study used a full-factorial design with 75 total measurements to characterize the response surface. In contrast, our ML-guided approach achieved convergence on the same optimum growth region using only 20–25 simulated experiments (4–5 cycles of five experiments each). This corresponds to a ~66% reduction in experimental load while maintaining prediction accuracy within ±10% of the true maximum, under ideal (noise-free) conditions. We also benchmarked our method against a Tree-structured Parzen Estimator (TPE) optimization [31], which, under the same experimental constraints, requires four times more iterations (16.8 ± 4.44 cycles;

Table 1. Benchmark against other ML algorithms. ML developed in this paper (Hybrid) is compared to a simplified Bayesian [25] and Tree-structured Parzen Estimator [31] (TPE) Optimization. The evaluation was performed on sample size of five experiments in each cycle, with a threshold of 0.01% improvement.

Algorithm	Cycles	Growth Rate	Phosphate	Temperature	Accuracy
Hybrid	4.4 ± 0.55	1.09 ± 0.03	15.7 ± 2.8	23.2 ± 0. 9	2.7 ± 2.2
Bayesian Opt.	4.4 ± 0.89	1.15 ± 0.01	16.4 ± 0.6	25.0 ± 0.7	3.9 ± 0.7
TPE	16.8 ± 4.44	1.12 ± 0.04	13.8 ± 5.5	25.8 ± 1.9	5.6 ± 3.6

). Additionally, we performed the same benchmark using a simplified Bayesian optimization (lacking OLS and K-means components). Although it produced results similar to our hybrid approach, it was less accurate, showing a higher relative distance from the true optimum (3.9 ± 0.7).

4. Discussion

Machine learning (ML) is emerging as a highly promising approach and represents the next evolution in data analysis and experimental design, offering powerful tools to uncover complex patterns and optimize protocols with minimal manual intervention [32]. Hybrid ML models, which integrate mechanistic or simulation-based insights with data-driven algorithms, enable iterative testing and rapid convergence on optimal conditions [33]. In this research a new hybrid ML procedure that balances two core modelling approaches is proposed: OLS for broad, global predictions and GP + EI + K-Means for localized, exploratory refinement. OLS, a classic regression technique, underpins the main prediction of where the maximum response (e.g., growth rate) lies. Meanwhile, GP (Gaussian Process) modelling, combined with the expected improvement (EI) metric and K-Means clustering, probes and confirms the reliability of that predicted maximum by systematically sampling the parameter space. This synergy ensures that even if OLS’s polynomial shape is off by some margin, the algorithm can discover unanticipated peaks or validate the predicted optimum through more adaptive, localized exploration.

OLS is often viewed as a baseline ML approach, offering interpretability and computational simplicity. In many biological contexts, we assume that relationships, although nonlinear in raw predictor variables, can be approximated by polynomial expansions in OLS. For instance, including squared or interaction terms for nutrients and temperature effectively captures curved surfaces. By fitting these polynomial terms, OLS provides a single “best guess” for the maximum. It does so by minimizing the sum of squared residuals across the entire dataset, effectively capturing a broad, global shape. This approach is computationally efficient and straightforward to interpret: each coefficient reveals how strongly each (possibly transformed) predictor influences the outcome. However, OLS alone may not fully reflect local uncertainties—especially if data coverage is sparse in certain regions.

Where OLS leaves off in terms of local adaptivity, GP steps in. A Gaussian Process is a nonparametric Bayesian method that provides not only a mean prediction but also an uncertainty estimates at every point in the domain. By computing the expected improvement (EI) relative to the best observed value, the GP identifies parameter combinations where there is both potential for improvement and uncertainty to justify further exploration. From a machine learning vantage, EI is a form of active learning criterion: it seeks to sample next where we stand to gain the most knowledge or improvement. K-Means clustering then ensures that among these high-EI regions, we select a diverse set of points, preventing the algorithm from repeatedly sampling the same narrow hotspot. This strategy ensures robust exploration of the domain, confirming or challenging the OLS optimum.

The synergy arises because OLS yields a stable, polynomial-based global shape, while GP + EI + K-Means refines and tests that shape locally. In practice, the algorithm defers to OLS to generate a preliminary maximum and shape the broad region of interest. Then, each cycle uses GP’s EI to highlight any local pockets that might contradict or refine OLS’s prediction. If the GP consistently finds negligible potential for improvement, the algorithm ceases further experiments, concluding that the OLS-based optimum is indeed accurate. This integration reduces experimental runs, a key consideration in biological research where time, resources, and living material are limited.

From a machine learning perspective, such a hybrid approach, OLS for the main prediction and GP + EI + K-Means for space exploration, leverages the strengths of each method. OLS offers a computationally light, globally interpretable model, while GP + EI adaptively “asks questions” of the domain, ensuring we do not miss unexpected maxima. The result is a biologically pragmatic workflow that both capitalizes on well-established regression principles (OLS) and modern adaptive search (GP + EI + K-Means) to robustly locate near-optimal growth conditions.

Experimentally, this ML-assisted iterative process reduced the number of required experimental cycles dramatically compared to conventional approaches. For instance, with a strict EI threshold of 0.01%, the algorithm required only four iterative cycles (25 total experiments) to achieve a robust approximation of the growth maximum within ±10% accuracy. Increasing the experimental bandwidth per iteration (from 5 to 7 experiments per cycle) further refined accuracy to ±5%, emphasizing the adaptability and scalability of our method. The algorithm’s sensitivity analysis revealed that the method’s efficiency and accuracy were impacted by the inherent variability of the experimental data. Under conditions with higher data variability, the iterative algorithm required additional cycles to converge on the optimum, underscoring the importance of understanding experimental noise when implementing ML-guided strategies. Nonetheless, the combination of OLS, GP, EI, and K-Means consistently demonstrated a robust capability to rapidly and accurately identify optimal experimental conditions.

By comparison, the original full-factorial experiment used 75 measurements, 25 experimental conditions each with 3 biological replicates, to locate the growth optimum. In contrast, our hybrid OLS + GP + EI + K-Means pipeline converged on that same optimum with only 20–25 simulated experiments (4–5 cycles), a ~66% reduction in experimental load while maintaining ± 10% accuracy under ideal, noise-free conditions. The TPE benchmark needed on average 16.8 ± 4.44 cycles (≈ 84 experiments) to reach the same target. These quantitative results are strictly from in silico simulations; implementing this algorithm in a real laboratory—where measurement noise, batch-to-batch variability, and logistical constraints arise—could alter convergence rates and accuracy. Empirical validation and more extensive ablation studies (e.g., testing OLS + EI, GP + EI only, or varying batch sizes) are therefore necessary next steps, but these findings establish a clear proof of concept that combining OLS and K-Means with GP + EI is substantially more efficient than conventional or GP-only strategies.

5. Conclusions

In this case study, we demonstrate that, even without prior knowledge or training data, strategically selected machine learning methods can be employed to explore an unknown experimental space and guide future experiments while maximizing the potential value of each outcome. Remarkably, the presented approach identified the optimal conditions using exactly 25 experiments—the same number performed in the original study by experienced researchers. However, because these results are based on in silico simulations rather than side-by-side wet-lab trials, the assertion that the machine learning–driven procedure can match the decision-making capabilities of expert scientists should be interpreted cautiously. In a real laboratory setting—where noise, measurement variability, and logistical constraints come into play—further validation will be required. Nonetheless, the ability of ML to reach equivalent conclusions under ideal (noise-free) conditions highlights its transformative potential and motivates future work to test and refine this framework in true wet-lab environments.

6. Perspective

Scalability—In this paper, we demonstrated our ML strategy on two-dimensional data (phosphate and temperature). In principle, the same algorithmic pipeline (OLS → GP → EI → K-means) can be extended to higher-dimensional search spaces (e.g., temperature, light intensity, pH, phosphate, nitrogen, macronutrients, micronutrients, CO₂, total nutrients, salinity). However, practical application in 10 or more dimensions will require additional considerations—such as feature selection, kernel scaling, and computational optimizations—to maintain efficiency and interpretability. We therefore consider large-scale, multi-parameter optimization as an important area of future work: verifying performance across diverse biological datasets, assessing computational cost as dimensionality grows, and exploring strategies (e.g., sparse kernels or sequential variable grouping) to keep model inference and decision-making tractable when human intuition alone is insufficient.

Practical Wet-Lab Considerations—Although our simulations assumed ideal (noise-free, or predictable noise) measurements, several challenges arise when deploying this hybrid framework in a real laboratory setting. First, measurement noise—stemming from instrument precision limits (e.g., plate reader fluctuations), pipetting errors, and biological heterogeneity—can obscure true growth-rate signals. Without accounting for heteroscedastic noise, the OLS fit may be biased and the GP’s uncertainty estimates may be overconfident in regions with high variability. Second, data variability between batches (batch-to-batch differences in media preparation, cell inoculum density, or environmental conditions such as ambient temperature or humidity) can introduce systematic shifts that a purely data-driven model might misinterpret as genuine trends. Third, system constraints—such as limited throughput (e.g., only 5–10 assays per day), reagent cost, and turnaround time for readouts—restrict how many conditions can be tested per cycle and how rapidly new data become available for retraining. Fourth, equipment calibration and drift (e.g., changes in light-intensity outputs of incubators or gradual sensor degradation) can violate the assumption of a static response surface, requiring periodic recalibration or the inclusion of time-dependent covariates.

To mitigate these issues, future work should incorporate noise-aware GP kernels (e.g., heteroscedastic or Student-t kernels) and replicate measurements to empirically estimate observation variance. Domain-informed priors in the OLS step (for example, known saturating behaviour at extreme nutrient levels) can help stabilize global fits in the presence of noisy data. Automated experimentation platforms [34] and real-time data pipelines can minimize human-induced variability and accelerate throughput, but they also require validation to ensure that mechanical errors are within acceptable bounds. Finally, adaptive stopping criteria based on confidence intervals—rather than a fixed cycle count—may be necessary when experimental resources are scarce or when early-stage measurements exhibit high uncertainty. Addressing these practical considerations is an important direction for translating our algorithm from in silico validation to robust, reproducible wet-lab workflows.

Agricultural Innovation—In agriculture, this approach could be used to identify optimal growing conditions for different crop varieties, balancing multiple interacting factors such as soil composition, irrigation, fertilization, and climate variables. A purely autonomous system might propose nutrient and water levels without accounting for farmers’ local knowledge or infrastructure constraints. To address this, a human-in-the-loop approach is essential [35]: agronomists and farmers review model suggestions, verify feasibility given resource limitations, and provide feedback (e.g., adjusting target ranges for fertilizer or adjusting for unexpected weather events). This combination of algorithmic exploration and domain expertise can drastically reduce the time and resources needed for crop optimization and precision farming, while ensuring transparency and trust in high-stakes decisions that affect food security and rural livelihoods.

Drug Discovery and Personalized Medicine—In medicine, the methodology could accelerate the optimization of drug combinations, dosages, and treatment schedules tailored to individual patients. By efficiently exploring the multidimensional space of treatment parameters, machine learning can support adaptive clinical trials and personalized therapeutic strategies. However, fully autonomous dose-finding without clinician oversight risks patient safety, especially when complex interactions produce unexpected side effects. Embedding human oversight—as championed in recent debates on trustworthy AI [19]—means that oncologists or clinical pharmacologists examine uncertainty estimates, validate model-driven treatment recommendations, and intervene if the system’s predictions conflict with ethical or physiological considerations. This ensures that model outputs remain interpretable, steerable, and aligned with human values.

AI Assistant for Scientists—These findings point to the realistic potential for developing AI-powered laboratory assistants. Such systems could work alongside human researchers, autonomously suggesting and prioritizing experiments, analyzing interim results, and refining hypotheses. The idea of an AI scientist has been extensively discussed in the literature [36,37]. Yet, as the community increasingly stresses the limits of autonomy and the necessity of human-centred design, we emphasize that such assistants should remain both understandable and steerable. Effective oversight mechanisms allow users to correct, stop, or redirect the AI’s behaviour in uncertain or high-stakes scenarios. In practice, a lab assistant might flag low-confidence suggestions (e.g., “phosphate level at 1.8 mM yields high variance”) for expert review, ensuring that final experimental decisions remain under human supervision.

Sustainable Research Practices—By reducing the number of experiments needed to reach statistically meaningful conclusions, ML-guided strategies promote resource-efficient and environmentally responsible science. This is particularly important in contexts where reagents, time, or biological samples are limiting. Nevertheless, lab workflows must also consider logistical constraints—scheduling of shared instruments, maintenance of sterility, and avoidance of sampling biases. A human-centred AI approach acknowledges these factors by maintaining transparency: researchers can inspect which variables most influenced the surrogate model’s uncertainty estimate, adjust batch sizes to match instrument throughput, and ensure that AI-recommended protocols conform to ethical and safety standards.

Human-Centred AI in High-Stakes Domains—In high-stakes fields such as agriculture, medicine, and environmental biology, decisions can have far-reaching ethical, economic, and social impacts. A human-centred AI philosophy—rooted in participatory design and interpretability—seeks to augment rather than replace human decision-makers. For example, in precision irrigation, an AI model might suggest water volumes that maximize yield, but a farmer can override recommendations based on impending drought forecasts or local water restrictions. Similarly, in yield forecasting, model predictions should be accompanied by confidence intervals and explanations (e.g., “soil nitrogen levels contributed 40% to yield variance”), so that stakeholders understand and trust the system’s suggestions. By explicitly accounting for the needs, goals, and expertise of diverse users—farmers, agronomists, clinicians, and rural communities—these human-centred systems emphasize usability, transparency, and trust, ensuring that AI remains aligned with human values and constraints even as automation increases.