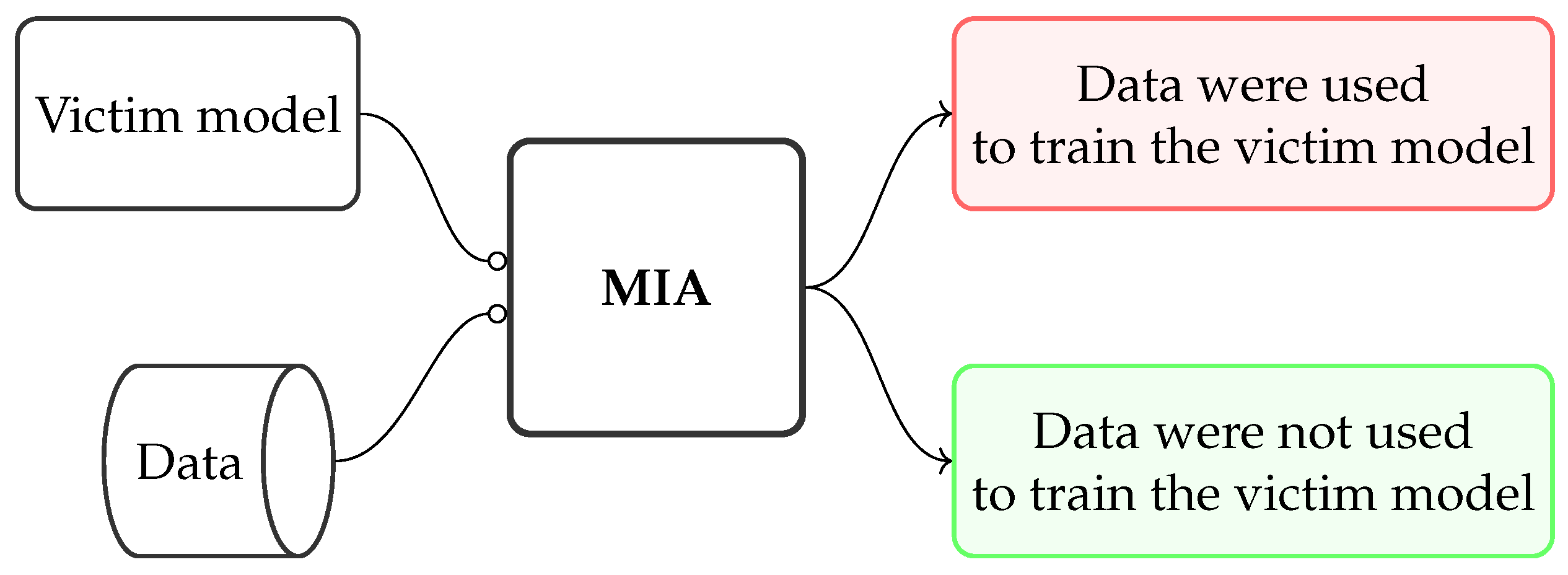
Membership Inference Attacks Fueled by Few-Shot Learning to Detect Privacy Leakage and Address Data Integrity

Abstract

Deep learning models have an intrinsic privacy issue as they memorize parts of their training data, creating a privacy leakage. Membership inference attacks (MIAs) exploit this to obtain confidential information about the data used for training, aiming to steal information. They can be repurposed as a measurement of data integrity by inferring whether the data were used to train a machine learning model. While state-of-the-art attacks achieve significant privacy leakage, their requirements render them infeasible, hindering their use as practical tools to assess the magnitude of the privacy risk. Moreover, the most appropriate evaluation metric of MIA, the true positive rate at a low false positive rate, lacks interpretability. We claim that the incorporation of few-shot learning techniques into the MIA field and a suitable qualitative and quantitative privacy evaluation measure should resolve these issues. In this context, our proposal is twofold. We propose a few-shot learning-based MIA, termed the FeS-MIA model, which eases the evaluation of the privacy breach of a deep learning model by significantly reducing the number of resources required for this purpose. Furthermore, we propose an interpretable quantitative and qualitative measure of privacy, referred to as the Log-MIA measure. Jointly, these proposals provide new tools to assess privacy leakages and to ease the evaluation of the training data integrity of deep learning models, i.e., to analyze the privacy breach of a deep learning model. Experiments carried out with MIA over image classification and language modeling tasks, and a comparison to the state of the art, show that our proposals excel in identifying privacy leakages in a deep learning model with little extra information.

1. Introduction

The increasing rate at which artificial intelligence (AI) systems are being developed and incorporated into our routines not only has increased privacy awareness but also widened the requirements for it. Data privacy is a major concern, as well as data integrity, especially in novel settings such as federated learning [1]. Moreover, the increased extent of surveillance has driven the development of techniques to protect us from the misuse of AI systems and deepen our understanding of them [2].

For a long time, deep learning models were considered black boxes, from which no information apart from what was related to the main task of the model could be extracted. This led to a false sense of security that neglected the issue of the privacy risks to which training data are exposed. In fact, deep learning models are known to be very dependent on their training data. Since a privacy attack can modify these data in order to change the behavior of the model and leak private information, their integrity must be protected.

There is a wide variety of privacy attacks, ranging from the ability to infer whether the training data have a certain property to the ability to reconstruct the training data, through the ability to infer whether some data were used to train the model. These include property inference attacks [3], feature reconstruction attacks [4] and membership inference attacks (MIAs) [5,6]. Such attacks pose a great challenge due to the growing concern about data privacy and the prospective legal regulatory frameworks that will require the safeguarding of data privacy in all stages of any system that relies on AI, as already stated in the currently published recommendations [7]. In this work, we focus on MIAs [8], which pose a significant threat to the privacy of learning models by exploiting differences in how models respond to training and non-training data [9], revealing whether a specific data record was used in training and potentially exposing sensitive information.

In order to defend against privacy attacks and preserve the integrity of the model and its inputs [10], the field of secure, privacy-preserving machine learning was developed. It encourages the creation of defenses based on differential privacy and secure protocols built on top of secure multi-party computation approaches [11].

Fortunately, privacy attacks can be used to evaluate the privacy and integrity of training data, thus addressing the increase in the awareness of data privacy and modifications in international regulations, such as the EU IA Act (https://artificialintelligenceact.eu/ (accessed on 19 May 2020)). This novel viewpoint, for instance, facilitates the auditing of advanced face recognition models for the identification of potential unauthorized data presented in AI models using MIAs [12].

To illustrate the risk of MIAs, we devise the following privacy risk scenario. Let us consider a deep learning classifier with the task of determining the stage of development of a cancer type using cancer tissue collected from patients. Such a model can be attacked by employing an MIA to infer whether a person’s tissue belongs to the training data of the model, concluding on whether she has cancer or not. This is a data integrity challenge, asthis information should remain private given that it was provided privately to support cancer research and not to be used by a third party. A similar privacy leakage scenario is explored in [13].

Furthermore, along this line, in early research related to MIAs, there was no consensus on which metric should be used to evaluate the effectiveness of MIAs, which also poses an issue if we consider MIAs as a tool to evaluate privacy. Recent works [14] have also studied this problem, proposing to report the true positive rate at a low false positive rates (TPR at low FPR), which is a metric that is commonly used in other areas related to computer science and security [15,16,17].

Unfortunately, the TPR at low FPR has an intrinsic issue: it requires fixing a low false positive rate, which depends on the size of the evaluation dataset. It compares the severity of the privacy leakage between different setups, which is not feasible, and this prevents a qualitative understanding of the metric, leading to a lack of interpretability. An incorrect interpretation of a privacy leakage is dangerous as it can be underestimated, leading to the exposure of sensitive data, or overestimated, thus severely impacting the performance of the attacked model [18].

Nonetheless, if we consider MIAs as a tool to evaluate the privacy of a deep learning model, evaluating privacy leakages requires more computing time than when training the attacked model itself. Furthermore, the evaluation demands considerable amounts of private data. These issues are exacerbated by the increasing rate at which the complexity, computing power and data requirements of deep learning architectures are growing nowadays [19,20,21].

These problems raise the question of whether MIAs can perform successfully in real-world environments. The evaluation of the privacy leakage of a model should not be more resource-intensive than the training process of the victim model, nor should it require more data than used when training the victim model. This is particularly relevant in scenarios such as edge computing, regulated environments with restricted data access or rapid auditing pipelines, where both data and computation are limited. Therefore, there is a pressing need for new MIA models with reduced requirements in terms of data availability and time/computing power consumption.

To address these challenges, we hypothesize that few-shot learning techniques can be incorporated into MIAs and the main evaluation metric can be reinterpreted:

(1)

to overcome the computational time and data availability limitations presented in the field of MIAs applied to deep learning models and

(2)

to provide an insightful view of the data integrity of a deep learning model, regardless of the MIA and victim model.

Thus, the contributions of this paper to the literature are twofold.

• The incorporation of a new MIA model based on few-shot learning due to its simplicity and effectiveness, named the FeS-MIA model, to significantly reduce the number of resources required to measure the privacy breach of a deep learning model. This enables the assessment of the integrity of the training data and provides a membership inference scenario with fewer data and a shorter computational time. More specifically, we do not assume access to the training data of the target model, and we limit ourselves to a small support set—reflecting a ‘few-shot’ regime. We argue that membership inference techniques should require no more data, or significantly more computation, than what was needed to train the victim model itself. Therefore, while computational efficiency is not a direct design goal in our approach, it emerges naturally from our low-data assumptions. This distinction is important to highlight, as our aim is not to optimize the runtime but to demonstrate the feasibility of data integrity assessment in scenarios of restricted access. We note that few-shot learning tackles the problem of performing a classification task on unseen classes with as few data as possible. Moreover, we incorporate multiple implementations of FeS-MIA models with the aim of showing the flexibility of this conceptual framework.
• A privacy evaluation measure, the Log-MIA measure, which changes the scale and proportion of the reported metrics to further boost the assessment of the data integrity, leading to a reinterpretation of state-of-the-art MIAs. Log-MIA is a proposal to help identify the extent of a privacy leakage and raises awareness of the data integrity risks present in deep learning models. The proposed measure is not only quantitatively more reasonable but also easier to interpret.
• Jointly, the contributions of this work provide tools to measure the privacy leaks of deep learning models, enabling us to reinterpret and compare the state-of-the-art results and experimentally assess whether it is possible to achieve a significant privacy leakage with as few resources as possible.

To assess the proposed FeS-MIA model, we carry out extensive experiments over image classification and language modeling tasks. By resorting to the proposed Log-MIA measure, we compare the FeS-MIA model with state-of-the-art MIA methods. As a result, we confirm that almost all tools in the MIA literature are capable of achieving significant privacy leakage. Furthermore, we assert that it is possible to achieve a significant privacy leakage with a small number of data and computing resources. Altogether, we confirm with evidence that our contributions constitute a set of tools to enhance and ease the evaluation of the privacy guarantees of a deep learning model.

The rest of this paper is structured as follows. Section 2 builds the context for our contributions. Next, in Section 3, we present our first contribution, the FeS-MIA model for more efficient attacks. This is followed by Section 4, which motivates and defines our second contribution, Log-MIA, an improved privacy measure. Section 5 details our experimental setup and shows the performance of the FeS-MIA model, measured in terms of the Log-MIA measure, in comparison to other state-of-the-art MIAs, whose performance is re-evaluated using our proposed measure. Finally, Section 6 concludes the paper by summarizing our findings and outlining several ways to expand on this work in the future.

2. Background and Related Works

In this section, we introduce some concepts related to the contributions of this paper. Section 2.1 introduces the state of the art in the MIA field and the current metric used to evaluate them. Then, Section 2.2 briefly reviews the foundations of few-shot learning.

2.1. Membership Inference Attacks

MIAs pose a data integrity risk to deep learning models. In what follows, we provide a formal definition of these attacks and comment on the main issues that are insufficiently addressed in the state of the art, focusing on the data and computational resource requirements and the evaluation criteria.

Conceptually, MIAs rely on a meta-classifier that, given a trained machine learning model—which we will refer to as the victim model—and some data, solves the task of detecting whether the data belong to the training dataset of the victim model. A formal definition of an MIA can be stated as follows. Let M be a trained machine learning model, i.e., a victim model, and L a set of data that has a non-empty intersection with $D_M$, the set of data used to train M. An MIA can be defined as a function ${\varphi }_M:L\to \{0,1\}$ given by

$${\varphi }_M\left(x\right):=\left\{\begin{array}{cc}1\hfill & \mathrm{if}x\in D_M,\hfill \\ 0\hfill & \mathrm{if}x\notin D_M.\hfill \end{array}\right.$$

(1)

Therefore, an MIA defined in this way is formulated as a binary classification task. Figure 1 conceptually outlines this definition.

In the following, we summarize the main works in the MIA field and comment on their requirements and evaluation procedures.

The threat that MIAs pose to deep learning models was first introduced in [22], revealing that it is possible to infer the membership of the training dataset of a victim model by training binary classifiers on the output of multiple “shadow models” that imitate the behavior of the victim model. Such models are trained over multiple overlapping splits of similar data used to train the victim model.

An alternative approach to the development of MIAs is introduced in [23]. It exploits the difference between the average training loss and the test loss as a threshold to infer the membership of data. With the assumption that the optimal inference depends entirely on the loss function, ref. [24] derives an MIA strategy using Bayesian techniques. Ref. [25] employs the intuition that a data point used in the training phase of the victim model must be close to a local minimum, so the loss of surrounding data points must be higher. If the data point was not present in the training dataset, similar data points must have a smaller or greater loss in approximately the same proportion. Refs. [26,27] focus on providing good thresholds for individual samples, highlighting that some samples are more vulnerable than others. The improved calibration of the loss threshold according to the difficulty in correctly classifying the target sample is proposed in [28], rendering better performance than previous MIA strategies. By incorporating shadow models to estimate the train and test loss distributions and the likelihood ratio test to find the threshold with the best trade-off between precision and recall in the attack, refs. [14,29] improve on previous works. Both propose quite similar attacks in terms of design and performance, with the main difference being that ref. [29] focuses on a systematic methodology to justify the design of the attacks. Ref. [30] generalizes previous ideas, employing a more sophisticated statistical test, and ref. [14] describes a particular case of their proposal. It also enables them to propose the first MIA with high performance with as little as two shadow models, i.e., they significantly reduce the computational budget required to run the attack. Lastly, ref. [31] proposes a different approach that employs a quantile regression model on a model trained by minimizing the pinball loss to perform the attack; its approach is victim model-agnostic, given that it does not depend on the architecture of the victim model. Although it is less computationally intensive than the strategies proposed in [14,29], it is similar in performance.

2.1.1. Data and Computational Resource Requirements

At the time of writing, the state-of-the-art MIAs are dominated by the attack strategies presented in [14,29,30]. However, their proposals require the training of 256 shadow models for each task in the worst case [14,29] and two shadow models in the best case [30], which is especially intensive for language modeling tasks. For instance, the one under study for WikiText-103 [32] uses a GPT-2 model [33] that contains up to 1.5 billion trainable parameters. Furthermore, it requires the complete availability of the dataset used to train the victim model. The assumptions of the availability of the training procedure and architecture of the victim model and the availability of large amounts of data are common in the literature, but they are far from being feasible in practical settings.

2.1.2. Evaluation

Carlini et al. [14] showed that metrics such as accuracy, precision and recall or the AUC are not suitable for reporting the performance of an MIA, mainly because the binary classification task of an MIA is not a standard one. MIAs solve a binary classification task where members and non-members of the training dataset of the victim model represent the positive class and negative class, respectively. True positives (TP), which are members of the training dataset whose membership is correctly inferred by the attack, are far more valuable than true negatives (TN), which are non-members of the training dataset whose membership is correctly inferred, given that they represent data points whose membership is considered a privacy leakage. These authors showed that most of the current strategies in the field excel in detecting TN but not TP. Moreover, a large proportion of FP can lead to a skewed perception of an MIA’s performance [34]. Thereby, metrics such as accuracy or precision are flawed.

To solve this issue, they proposed the usage of the TPR at low FPR, which is common in other computer science and security areas [15,16], and they re-evaluated the state of the art with it. The main idea behind this metric is to indicate how many members of the training dataset are revealed (TP) when a fixed small number of non-members are misclassified (FP). In addition, they proposed a powerful MIA that trains multiple shadow models and uses them to approximate the distribution of outputs of the loss function for members and non-members of the training dataset of the victim model. Then, they use such distributions to infer the membership of data points according to their loss values.

2.2. Few-Shot Learning

In the few-shot learning field, a typical classification task is normally referred to as N-way K-shot classification, in which N-way stands for N classes and K-shot represents K training samples in each class. A typical N-way K-shot classification task classifies a test example into one out of N unique classes based on $N\times K$ labeled training samples.

We formally define the few-shot classification problem as in [35]. Let $(x,y)$ denote a target sample and its label, respectively. The training and test datasets are $D_s={\left\{(x_i,y_i)\right\}}_{i=1}^{N_s}$ and $D_q={\left\{(x_i,y_i)\right\}}_{i=1}^{N_q}$, respectively, where $y\in C_t$ is a reduced set of classes $C_t$. The training dataset is known as the support set, whereas the test dataset is known as the query set. Jointly, they are referred to as a few-shot episode. The number of classes, or ways, is $N=|C_t|$. The set $\left\{x_i\right|y_i=c,(x_i,y_i)\in D_s\}$ is the support of class c, and its cardinality is K, known as shots. The number K is small in the few-shot setting. The set $\left\{x_i\right|y_i=c,(x_i,y_i)\in D_q\}$ is the query of class c and its cardinality is q, known as query shots. In the related literature, K is usually set equal to 1, 5 or 10, whereas the query set is fixed to 15 samples per class [36].

The goal of few-shot learning is to learn a function F to exploit the training set $D_s$ towards predicting the label of a test datum x, where $(x,y)\in D_q$, by

$$\widehat{y}=F(x;D_s).$$

(2)

In addition to the training set, one can have a meta-training set, $D_m={\left\{(x_i,y_i)\right\}}_{i=1}^{N_m}$, where $y_i\in C_m$, with the set of classes $C_m$ being disjoint from $C_t$. The goal of meta-training is to use $D_m$ towards inferring the parameters of the few-shot learning model F. In such a case, we will denote it as $F_M$.

A few-shot episode is small by definition, and, in practice, when sampled from a larger dataset, the performance of a few-shot model in a single few-shot episode is questionable because of the randomness of the sample. To overcome this issue, few-shot learning techniques are evaluated using the average result of multiple few-shot episodes within a small confidence interval.

A few-shot classification task can be approached from many angles. Based on which aspect is enhanced using prior knowledge, we can categorize the approaches into the following [36].

• Training data: These methods use prior knowledge to augment $D_s$ and significantly increase the number of samples. Standard machine learning models can be used over the augmented data, and a more accurate few-shot model can be obtained [37,38].
• Model: These methods use prior knowledge to constrain the complexity of the space in which model F lies, learning a special model or embedding designed for a specific problem [39,40].
• Algorithm: These methods resort to prior knowledge to improve the best parameters of a meta-trained model, i.e., to refine meta-trained models through an algorithm [35,41,42].

This work focuses on few-shot techniques that enhance the few-shot algorithm by using prior knowledge, given that we deal with meta-trained models.

3. Few-Shot Learning MIA Model

MIAs are useful tools to measure the privacy of a deep learning model. However, MIAs perform poorly and are not feasible in environments outside the research field because

(1)

evaluating the privacy leakage of a model should not be more resource-intensive than training the victim model itself, and

(2)

MIAs should require fewer data than those used to train the victim model.

The application of few-shot techniques to the MIA field can solve these issues. However, not every few-shot method for classification tasks can be applied to create an MIA, because the task that MIAs pose is not a standard binary classification task.

Accordingly, we present the FeS-MIA model and some of its implementations, in order to provide a formal definition of the FeS-MIA model.

Given a few-shot technique F, with certain restrictions that we will specify later, and a victim model M, we define an FeS-MIA applied to M as ${\theta }_M:L\to \{0,1\}$, with ${\theta }_M:=F_M$, where L has a non-empty intersection with $D_M$, the dataset used to train M. The training and test sets of ${\theta }_M$ are $D_s:=\left\{(x_i,y_i)\right|x_i\in L,y_i\in \{0,1\}\}$ and $D_q:=\left\{(x_i,y_i)\right|x_i\in L,y_i\in \{0,1\}\}$, i.e., the support and query sets, respectively, in few-shot learning terminology. We note that classes 1 and 0 are identified as members and non-members of $D_M$, the positive and negative classes, respectively. The sizes of the classes present in the support and query sets are the cardinalities $K=\left|\right\{x_i|y_i=c,(x_i,y_i)\in D_s\}|$ and $q=\left|\right\{x_i|y_i=c,(x_i,y_i)\in D_q\}|$ for class $c\in \{0,1\}$, which are restricted to sets $\{1,5,10\}$ and $\left\{15\right\}$, respectively. In few-shot terminology, the FeS-MIA model is composed of two-way 1-, 5- or 10-shot tasks.

The main restriction in employing a few-shot technique in an FeS-MIA model is the requirement for a meta-trained model, which, in this MIA setting, is the victim model. The FeS-MIA model does not fit the usual classification of MIAs based on the adversarial knowledge of the victim model, i.e., a white-box or black-box MIA [43], given that it does not impose any restrictions on access to the victim model. It can be instantiated as either a white-box or a black-box MIA; in both cases, it is a restriction that is imposed by the few-shot technique in use.

With this setup, an FeS-MIA model reduces significantly the quantity of data required to perform an MIA; however, it still requires a small amount of labeled data, namely members and non-members of the victim model. This requirement might seem impractical; however, poorly anonymized private data [44,45], the prevalence of data reconstruction attacks [4,46,47,48] and social engineering or phishing attacks make it significantly more feasible.

As mentioned, we instantiate our proposed model using the following few-shot techniques due to their simplicity and effectiveness. Moreover, we incorporate multiple implementations of FeS-MIA models with the aim of showing the flexibility of this conceptual framework.

3.1. FeS-MIA Transductive Tuning (FeS-MIA TT)

This employs the transductive tuning technique proposed in [35]. It adds a cross-entropy classifier on top of the outputs of a meta-trained model and fine-tunes the entire model using $D_s$ with a regularization term applied to unlabeled query samples. Specifically, the applied regularization term uses the Shannon entropy over the predictions of the few-shot model on the unlabeled query set. The main idea behind this regularization term is to make the model more confident in its predictions.

3.2. FeS-MIA Simple-Shot (FeS-MIA SS)

This employs the simple-shot technique proposed in [49]. The meta-trained model is used to generate a set of normalized centroids, each representing a class of $D_s$. These centroids are used as class representatives in the logit space to classify the logits of $D_q$ using the class of the nearest centroid.

3.3. FeS-MIA Laplacian-Shot (FeS-MIA LS)

This utilizes the Laplacian-shot (LS) technique proposed in [41] to improve the aforementioned SS approach, incorporating a regularization term that integrates two restrictions: (1) assigning query set samples to the nearest class centroid and (2) pairwise Laplacian potentials, encouraging nearby query set samples to have consistent predictions, i.e., to be assigned the same or similar class labels based on the assumption that spatial proximity in the feature space should reflect semantic similarity.

Given that FeS-MIA TT fine-tunes the entire model, it requires white-box access to the victim model, and it is a white-box MIA. In contrast, FeS-MIA SS and FeS-MIA LS only require access to the outputs of the model, i.e., both are black-box MIAs.

We remark that the above are implementations of the FeS-MIA model that showcase its strengths. However, the FeS-MIA model is not tied to any particular few-shot technique, as long as it fits our model definition.

4. Towards the New Privacy Evaluation Log-MIA Measure

This section is dedicated to describing one of the main problems that we have found in the evaluation scheme usually employed for MIAs. First, we highlight the lack of interpretability of the existing metrics in Section 4.1, which serves as the motivation to reinterpret and refine them in Section 4.2 and Section 4.3. Finally, the last two sections present the definition of the Log-MIA measure (Section 4.4) and the re-evaluation of existing MIAs under this new privacy measure (Section 4.5).

4.1. The Lack of Interpretability of the TPR at Low FPR

The accuracy metric, which is commonly used in classification tasks, is not appropriate for MIAs. It assigns equal weight to being a member or not of the training dataset of the victim. However, correctly inferring a member implies a higher privacy risk than inferring a non-member; moreover, the cardinalities of the classes—member and non-member—differ significantly in size. Thus, it is certainly easier to correctly infer whether a record is a non-member. The state-of-the-art MIA evaluation metric, the TPR at low FPR, is a plausible solution to these problems, but it has an intrinsic issue: the interpretation of a low FPR is bound to the size of the test dataset. It requires fixing the FPR for each dataset, which hinders comparisons among differently sized datasets. Consequently, we are unable to perform a suitable comparison of the FeS-MIA model with the state of the art, particularly in terms of the TPR at low FPR metric.

We emphasize that, while many datasets can contain sensitive and personal information, not every combination of model and training dataset suffers from the same exposure risk. This necessitates the evaluation of MIAs on multiple datasets and, consequently, diverse victim models to properly evaluate the MIA. This can be discussed from the perspective of an adversary that wishes to test the capabilities of an MIA in multiple scenarios. It has been shown in [50] that an attacker can inject poisoned samples into the training dataset of the victim model to enhance the effectiveness of an MIA. Thus, the presence of outliers, either naturally occurring due to the presence of memorization [51] or due to poisoned samples manually crafted in the training dataset, can substantially increase the success of MIAs, showing that their success is related to the training dataset of the victim model.

In

Table 1. Comparison of MIAs under the same settings for well-generalizing deep models on CIFAR-10 (C-10), CIFAR-100 (C-100) and WikiText-103 (WT103) using the true positive rate (TPR) at low false positive rate (FPR) metric. Missing values show that these MIAs cannot be adapted to the natural language processing task of predicting the next word.

	TPR at 0.001% FPR			TPR at 0.1% FPR
Method	C-10	C-100	WT103	C-10	C-100	WT103
Yeom et al. [23]	0%	0%	0%	0%	0%	0%
Shokri et al. [22]	0%	0%	-	0.3%	1.6%	-
Jayaraman et al. [25]	0%	0%	-	0%	0%	-
Song and Mitall [26]	0%	0%	-	0.1%	1.4%	-
Sablayrolles et al. [24]	0.1%	0.8%	0.01%	1.7%	7.4%	1%
Long et al. [27]	0%	0%	-	2.2%	4.7%	-
Watson et al. [28]	0.1%	0.9%	0.02%	1.3%	5.4%	1.10%
Carlini et al. [14]	2.2%	11.2%	0.09%	8.4%	27.6%	1.40%

, we show the TPR at low FPR values of state-of-the-art MIAs on three datasets and in two different tasks: image classification and language modeling. The main problem is that the low FPR values shown in such a table are the same in our definition of the FeS-MIA model, due to the required small test size. We have no clear arguments to justify the use of a different FPR while retaining the ability to perform meaningful comparisons of the performance of our model with the state of the art.

In terms of privacy, we find that the values reported in Table 1 are difficult to interpret, as some values greater than zero are low and do not clarify whether the privacy leakage can be deemed negligible or not. Thus, no qualitative assessment of these results can be performed.

To clearly highlight this issue, we translate some percentages presented in Table 1 into raw numbers. First, with regard to fixing a low FPR, we have the following.

• On the CIFAR datasets, 0.001% and 0.1% are 0 and 25 FP, respectively. The test dataset for the MIA has 50,000 items.
• On the WikiText103 dataset, 0.001% and 0.1% are 0 and 50 FP, respectively. The test dataset for the MIA has 1,000,000 items.
• With the FeS-MIA model, 0.001% and 0.1% are 0 FP because of the small test set; this is an intrinsic limitation when using few-shot techniques. We note that our test dataset has 30 items.

As shown, the significance of low FPR values increases with the size of the tested dataset. However, the size of the test dataset does not necessarily correlate with the difficulty of the task associated with it. For example, the ImageNet dataset has a test size of 150,000 elements, whereas the CIFAR datasets have 10,000 test elements. However, most deep learning models usually achieve higher test accuracy over ImageNet than over the CIFAR datasets [52,53,54]. Hence, the meaning of a low FPR must be calibrated for each dataset, as demonstrated in other fields where this metric is used [15,16,17,55].

Secondly, with regard to reporting the TPR at a fixed low FPR, considering only the last row of Table 1, i.e., the results from Carlini et al. [14], we have the following.

• CIFAR-10: a TPR at 0.001% FPR equal to 2.2% means 550 true positives (TP) and a TPR at 0.1% FPR equal to 8.4% means 2100 TP.
• CIFAR-100: a TRP at 0.001% FPR equal to 11.2% means 2800 TP and a TPR at 0.1% FPR equal to 27.6% means 6900 TP.
• WikiText103: a TPR at 0.001% FPR equal to 0.09% means 450 TP and a TPR at 0.1% FPR equal to 1.40% means 7000 TP.

In conclusion, any TPR > 0 can be regarded as an accountable privacy leakage, i.e., the true membership of at least one item is revealed. However, the reported TPR at low FPR might be so small that it falsely implies that the privacy leakage is negligible.

We highlight two serious issues that appear when using the TPR at low FPR metric:

(1)

the meaning of a low FPR is ambiguous and changes for each dataset, and

(2)

the TPR values can be misleading if the test dataset is too large.

This motivates the rethinking of how MIAs are evaluated and the proposal of a new privacy evaluation measure that addresses these two problems.

4.2. Rethinking the Low FPR

We address the requirement for an improved interpretation of a low FPR, employing the natural logarithm scale. In such a scale, a change of one order of magnitude in a test dataset does not imply a drastic change in the low FPR. For example, we can apply it to the datasets used in Table 1 as follows.

• For the CIFAR datasets, with a test dataset of 50,000 items, log(50,000) ≈ 10.
• For WikiText-103, with a test dataset of 100,000 items, log(100,000) ≈ 11.
• For the FeS-MIA model, with a test dataset of 30 items, $log\left(30\right)\approx 3$.

Therefore, a reasonably small FPR is the one achieved when rounding up to the closest integer of $log\left(\mathit{size}\mathit{of}\mathit{test}\mathit{dataset}\right)$ FP, i.e., $\lceil log\left(\mathit{size}\mathit{of}\mathit{test}\mathit{dataset}\right)\rceil$ FP.

4.3. A More Intuitive Alternative to the TPR

Next, we define our revision of the TPR or recall, also considering the natural logarithm scale. We propose to report the TP log-ratio defined as

$$\mathit{TP} \mathit{log}\text{-}\mathit{ratio}={\displaystyle \frac{log(\mathit{TP}+1)}{log(\mathit{size}\mathit{of}\mathit{positive}\mathit{class}+1)}},$$

(3)

which has the following two interesting properties.

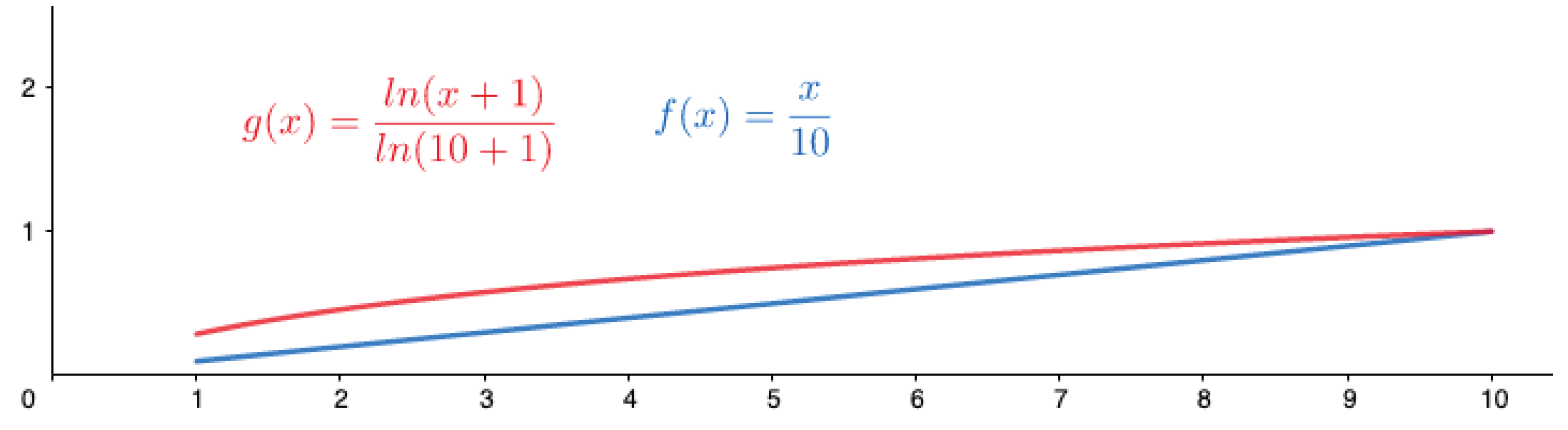
• It grows faster than the TPR, even with small values, representing the idea that there is no negligible privacy leakage. Figure 2 illustrates the effect of this property.
• The non-zero value closest to 0 that the TP log-ratio can report is $\alpha ={\displaystyle \frac{log\left(2\right)}{log(\mathit{size}\mathit{of}\mathit{positive}\mathit{class}+1)}}$. That is, any value smaller than $\alpha$ means that there is no privacy leakage, whereas any value greater than or equal to $\alpha$ indicates a privacy leakage. It is important to note that this value ${\alpha }^{\prime }$ also exists for the TPR metric, i.e., ${\alpha }^{\prime }={\displaystyle \frac{1}{\mathit{size}\mathit{of}\mathit{positive}\mathit{class}}}$. However, ${\alpha }^{\prime }$ can be much smaller than $\alpha$, especially with large test sizes. This fact is supported by the inequality ${\alpha }^{\prime }={\displaystyle \frac{1}{x}}<{\displaystyle \frac{log\left(2\right)}{log(x+1)}}=\alpha ,\forall x\ge 2$, where x is the size of the positive class. Figure 3 shows this behavior.

4.4. Log-MIA: A New Privacy Evaluation Measure

Our interpretation of the low FPR and TPR paves the way for a new privacy evaluation measure, the Log-MIA measure, composed of two regimes.

• Regime A: We report the TP log-ratio at $FP=0$. In this regime, the reported value must be greater than or equal to $\alpha$ to indicate a severe privacy leakage. Otherwise, we can state that the victim model is private.
• Regime B: We report the TP log-ratio at $FP=\lceil log(\mathit{size} \mathit{of} \mathit{test} \mathit{dataset})\rceil$. In this regime, we can establish further severity levels for the privacy leakage.
  • If the reported value is greater than or equal to

    $$\beta ={\displaystyle \frac{log(FP+2)}{log(\mathit{size}\mathit{of}\mathit{positive}\mathit{class}+1)}}$$

    then a severe privacy leakage can be declared. The attacker can flawlessly infer the positive membership of some data used to train the victim model.
  • If the reported value is in the interval $[\alpha ,\beta )$, then there is a moderate privacy leakage. The attacker can reveal the membership of some data. However, at best, it is paired with the same number of FP, i.e., false memberships.
  • Otherwise, there is no privacy leakage. The attacker cannot infer the membership of any data used to train the victim model.

The former is designed to address how many true memberships an MIA can infer without making any mistakes, i.e., its absolute values. The latter indicates whether, by allowing some mistakes in the positive class inferring the true membership, an MIA can still infer more true memberships than false memberships.

4.5. Reevaluating the Privacy Leakage of the State of the Art with the Log-MIA Measure

Once the Log-MIA measure has been defined, it is possible to compare and reinterpret Table 1.

Table 2. Comparison of TPR at 0.001% FPR (left column) versus Regime A (TP log-ratio at 0 FP, right column). Severe privacy leakages are marked with ; otherwise, there is no privacy leakage. For the CIFAR datasets (C-10 and C-100), the smallest non-zero value in the TP log-ratio is $\alpha$ = 0.07, and, for WikiText (WT-103), it is $\alpha$ = 0.06. Note that, in these datasets, 0.001% FPR is the same as 0 FP. Missing values mean that the attack cannot be applied.

	TPR at 0.001% FPR			Regime A
Method	C-10	C-100	WT103	C-10		C-100		WT103
Yeom et al. [23]	0.0%	0.0%	0.00%		0.00		0.00		0.00
Shokri et al. [22]	0.0%	0.0%	-		0.00		0.00		-
Jayaraman et al. [25]	0.0%	0.0%	-		0.00		0.00		-
Song and Mitall [26]	0.0%	0.0%	-		0.00		0.00		-
Sablayrolles et al. [24]	0.1%	0.8%	0.01%		0.32		0.52		0.17
Long et al. [27]	0.0%	0.0%	-		0.00		0.00		-
Watson et al. [28]	0.1%	0.9%	0.02%		0.32		0.54		0.22
Carlini et al. [14]	2.2%	11.2%	0.09%		0.62		0.78		0.35

and

Table 3. Comparison of TPR at 0.1% FPR (left column) versus Regime B (TP log-ratio at FP = $\lceil \log (\mathit{size} \mathit{of} \mathit{test} \mathit{dataset})\rceil$. Severe privacy leakages are marked with , and moderate privacy leakages are marked with ; otherwise, there is no privacy leakage. For the CIFAR datasets (C-10 and C-100), the Regime B interval is [$\alpha$ = 0.068, $\beta$ = 0.245), and, for WikiText (WT-103), it is [$\alpha$ = 0.053, $\beta$ = 0.211). Missing values mean that the attack cannot be applied.

	TPR at 0.1% FPR			Regime B
Method	C-10	C-100	WT103	C-10		C-100		WT103
Yeom et al. [23]	0.0%	0.0%	0.1%		0.000		0.000		0.206
Shokri et al. [22]	0.3%	1.6%	-		0.339		0.502		-
Jayaraman et al. [25]	0.0%	0.0%	-		0.000		0.000		-
Song and Mitall [26]	0.1%	1.5%	-		0.237		0.495		-
Sablayrolles et al. [24]	1.7%	7.4%	1.0%		0.516		0.667		0.400
Long et al. [27]	2.2%	4.7%	-		0.533		0.608		-
Watson et al. [28]	1.3%	5.4%	1.1%		0.492		0.643		0.421
Carlini et al. [14]	8.4%	27.6%	1.4%		0.698		0.829		0.492

report the Log-MIA measure values achieved by state-of-the-art MIAs. The Regime A values (Table 2) are computed by using the values from the TPR at 0.001% FPR column in Table 1. For Regime B (Table 3), we cannot directly use the values provided in Table 1 due to the different FPR values shown therein. Instead, we use the two ROC curve points provided to compute our required values through linear interpolation. Consequently, the values shown in Table 3 are computed using the expected values of the approximate ROC curve [56].

Focusing on Regime A (Table 2), we observe that only the attacks from Sablayrolles et al. [24], Watson et al. [28] and Carlini et al. [14] achieve a severe privacy leakage. Moreover, the MIA from Carlini et al. [14] achieves the most severe privacy leakage.

Similar conclusions can be drawn for Regime B (Table 3), where only the attack from Yeom et al. [23] attains a moderate leakage. From these results, we conclude that the reinterpretation of Table 1 allows us to reason that most attacks described in the literature achieve a severe privacy leakage. Furthermore, the Log-MIA measure is verified to satisfy, by construction, the following properties:

• It adapts the interpretation of a low FPR to the MIA problem;
• It considers that any TPR>0 indicates a non-negligible privacy leakage;
• It allows for the qualitative comparison of privacy leakages when different test sizes are used.

Thereby, we claim that Log-MIA boosts the interpretability of MIAs in terms of privacy.

5. Experimental Analysis of the FeS-MIA Model

In this section, we provide details of the experimental setup chosen to evaluate our proposed FeS-MIA model in Section 5.1. First, we detail the attacks, datasets and victim models that are chosen, as well as under which metrics we evaluate our results. Then, we report the results obtained and comment on them in Section 5.2 and Section 5.3.

5.1. Experimental Setup

Our experiments consider the MIAs from the literature presented in Section 2.1 and reviewed under the Log-MIA measure in Section 4.5 so that we can obtain a clear picture of the performance that the current MIA approaches can achieve versus our proposed FeS-MIA models employing the Log-MIA measure. For the sake of clarity, in the subsequent discussion, we only consider MIAs that attain a non-zero TPR at 0.001% FPR, i.e., they present a severe privacy leakage, namely those of Sablayrolles et al. [24], Watson et al. [28] and Carlini et al. [14] (see Table 2).

5.1.1. Victim Model and Training Datasets

We reproduce the experimental setup shown in Table 1, i.e., the datasets and deep learning models used for the victim models are as follows (the code is available at https://github.com/ari-dasci/S-few-shot-mia (accessed on 19 May 2025)).

• CIFAR-10 and CIFAR-100 [57]. The CIFAR-10 dataset consists of 60,000 32 × 32 color images in 10 classes, with 6000 images per class. There are 50,000 training images and 10,000 test images. CIFAR-100 is an extension of the CIFAR-10 dataset, with 100 classes containing 600 images each. There are 500 training images and 100 testing images per class. Both datasets are approached with a Wide ResNet [54] model, WRN-28-2, with a depth of 28 layers and a widening factor of 2. The model is trained on half of the dataset until 60% accuracy is reached.
• WikiText-103 [32]. The WikiText-103 language modeling dataset is a collection of over 100 million tokens extracted from the set of verified Good and Featured articles on Wikipedia, tackled with the smallest GPT-2 [58] model (124M parameters). The model is trained on half of the dataset for 20 epochs.

We recall that the half used to train each model is labeled as members, and the other half is labeled as non-members. Such labels are considered when building the support and query datasets for the FeS-MIA models.

5.1.2. FeS-MIA Model Experimental Setup

The results of three FeS-MIA models are reported: FeS-MIA TT, FeS-MIA SS and FeS-MIA LS. The Log-MIA measure is computed over 500 runs with its 95% confidence interval for both Regimes A and B. Moreover, we consider 1-shot, 5-shot and 10-shot learning scenarios, with a validation set of the same size as the query set: 15 elements per class, with members and non-members of the training dataset of the victim model. The validation set permits us to discover the best hyperparameter configuration for each few-shot learning technique, where optimality is determined by the maximization of the privacy leakage in Regime A in each run.

We recall that FeS-MIA SS implements the simple-shot technique, a 1-NN classifier, so it outputs discrete probabilities, 0 and 1. Consequently, these outputs are weighted by the inverse of their distance so that the classifier can generate a continuous output in the interval $[0,1]$. We require these probabilities to compute the decision thresholds in the validation set, required for evaluating the TPR at a certain low FPR. Similar considerations are applied for FeS-MIA LS. We also increase the number of neighbors considered, as this provides an important boost in performance. Furthermore, for FeS-MIA SS and FeS-MIA LS, considering all points plus the centroids of each class was found to significantly improve the privacy leakage, as will be exposed in the results. Thus, all values discussed in what follows consider these factors.

5.2. Regime A: Results and Analysis

We begin by analyzing the results obtained in Regime A of the Log-MIA measure, shown in

Table 4. Log-MIA measure, Regime A. Severe privacy leakages are marked with ; otherwise, there is no privacy leakage. For our attacks, the smallest non-zero value in the TP log-ratio is $\alpha$ = 0.25 for all datasets. For other attacks, on the CIFAR datasets (C-10 and C-100), it is $\alpha$ = 0.07, and, on WikiText (WT-103), it is $\alpha$ = 0.06.

	Regime A
Method	C-10		C-100		WT103
Sablayrolles et al. [24]		0.32		0.52		0.17
Watson et al. [28]		0.32		0.54		0.22
Carlini et al. [14]		0.62		0.78		0.35
FeS-MIA TT 1-shot		0.17 ± 0.02		0.16 ± 0.02		0.18 ± 0.02
FeS-MIA TT 5-shots		0.18 ± 0.02		0.17 ± 0.02		0.19 ± 0.02
FeS-MIA TT 10-shots		0.18 ± 0.02		0.18 ± 0.02		0.19 ± 0.02
FeS-MIA SS 1-shot		0.00 ± 0.00		0.00 ± 0.00		0.00 ± 0.00
FeS-MIA SS 5-shots		0.18 ± 0.02		0.17 ± 0.02		0.17 ± 0.02
FeS-MIA SS 10-shots		0.18 ± 0.02		0.18 ± 0.02		0.18 ± 0.02
FeS-MIA LS 1-shot		0.13 ± 0.02		0.12 ± 0.02		0.00 ± 0.00
FeS-MIA LS 5-shots		0.15 ± 0.02		0.14 ± 0.02		0.00 ± 0.00
FeS-MIA LS 10-shots		0.16 ± 0.03		0.14 ± 0.03		0.00 ± 0.00

. This table reveals that none of the proposed MIAs achieve a severe privacy leakage. Furthermore, it is remarkable that our values in every scenario are non-zero, and it is possible to observe that, when more data are available, the scores slightly improve. Still, our values are under $\alpha$, so we cannot report any privacy leakage that is statistically significant. This situation illustrates that MIAs are not easy tasks to handle with scarce data, i.e., our models are not able to achieve a TP with zero FP. Our results are in line with those for other MIAs described in the literature, which, albeit recently published [25,26,27], cannot accomplish a significant privacy leakage in this regime (see Table 2).

We can conclude that, in this regime, with constrained access to labeled data, it is not possible to report a severe privacy leakage using our proposed FeS-MIA models, showing the limitations of our proposal.

5.3. Regime B: Results and Analysis

We now proceed by inspecting the results of the experiments under Regime B of the Log-MIA measure, which are given in

Table 5. Log-MIA measure, Regime B. Severe privacy leakages are marked with , and moderate privacy leakages are marked with ; otherwise, there is no privacy leakage. For our attacks, the Regime B interval is [$\alpha$ = 0.25, $\beta$ = 0.58) for all datasets. For other attacks, the interval on the CIFAR datasets (C-10 and C-100) is [$\alpha$ = 0.068, $\beta$ = 0.245), and, on WikiText (WT-103), it is [$\alpha$ = 0.053, $\beta$ = 0.211).

	Regime B
Method	C-10		C-100		WT103
Sablayrolles et al. [24]		0.516		0.667		0.400
Watson et al. [28]		0.492		0.643		0.421
Carlini et al. [14]		0.698		0.829		0.492
FeS-MIA TT 1-shot		0.59 ± 0.01		0.58 ± 0.02		0.58 ± 0.02
FeS-MIA TT 5-shot		0.60 ± 0.01		0.59 ± 0.02		0.59 ± 0.02
FeS-MIA TT 10-shot		0.59 ± 0.02		0.58 ± 0.02		0.60 ± 0.02
FeS-MIA SS 1-shot		0.00 ± 0.00		0.00 ± 0.00		0.00 ± 0.00
FeS-MIA SS 5-shot		0.59 ± 0.02		0.58 ± 0.02		0.57 ± 0.02
FeS-MIA SS 10-shot		0.60 ± 0.02		0.59 ± 0.02		0.58 ± 0.02
FeS-MIA LS 1-shot		0.44 ± 0.03		0.44 ± 0.03		0.00 ± 0.00
FeS-MIA LS 5-shot		0.52 ± 0.02		0.47 ± 0.02		0.00 ± 0.00
FeS-MIA LS 10-shot		0.54 ± 0.02		0.45 ± 0.03		0.00 ± 0.00

. These results show that FeS-MIA LS achieves a moderate privacy leakage in almost every few-shot scenario, i.e., the number of TP unveiled by the attack does not exceed the number of FP. This situation requires special attention, not because it reveals the complete compromise of the training data but because it highlights a partial privacy leakage that, although limited, may still lead to cumulative risks when combined with auxiliary information or repeated queries. It is especially feasible given the low data requirements of our proposed attacks. Accordingly, we argue that a moderate privacy leakage should not be overlooked, as it can potentially lead to a larger privacy leakage, especially with the FeS-MIA.

While the MIAs from [14,24,28] achieve a consistent privacy leakage in both Regimes A and B, our MIA based on few-shot learning exhibits different behavior in Regime B (see Table 5) compared to Regime A (see Table 4). In Regime B, most of the proposed FeS-MIA models achieve a significant privacy leakage regardless of the dataset. FeS-MIA SS and Few-MIA TT produce a stable and significant privacy leakage, improving the results obtained in every scenario in Regime A (see Table 4). That is, all of the proposed models are only capable of inferring successfully the membership of some data, TP, when a small number of FP is allowed. We note that, in most scenarios, the number of TP is greater than that of FP, achieving a significant privacy leakage. This behavior aligns with that of other attacks described in the literature [22,26] (see Table 3).

Moreover, while LS is a technique presented in the few-shot learning field as an improvement over SS, with regard to MIAs, FeS-MIA LS does not perform better than FeS-MIA SS in both regimes. This is probably because the regularization terms that LS adds on top of SS k-NN do not seem to be conceived for the MIA. Still, both of them fail to achieve a significant privacy leakage in the one-shot scenario, while the same does not hold for TT. This difference can be attributed to the white-box access to the victim model that TT requires, compared to the black-box requirements of the other FeS-MIA models. Thus, less restricted access to the victim model results in a greater privacy leakage.

In light of the previous discussion, we can conclude that, in Regime B and when using the adequate few-shot algorithm, as few as one element per class is required to achieve a significant privacy leakage, with FeS-MIA SS and FeS-MIA TT being the best-performing FeS-MIA models. Therefore, the FeS-MIA model is more efficient in reporting privacy vulnerabilities than the state of the art.

FeS-MIA TT is the best FeS-MIA model overall, since it fine-tunes the entire victim model, as opposed to FeS-MIA SS and FeS-MIA LS, which operate on the outputs of the model itself, i.e., a white-box setup enhances the privacy leakage.

While our proposal does not achieve a severe privacy leakage as described in the work from Carlini et al. [14], it does lead to a severe privacy leakage in a specifically constrained setting where data are scarce and state-of-the-art attacks are infeasible. We highlight that the success of our attack contribution is amplified by the fact that we require minimal amounts of data and computing resources to identify a significant privacy leakage.

6. Conclusions

MIAs pose a significant threat to the privacy of learning models by exploiting differences in how models respond to training and non-training data, revealing whether a specific data record was used in training and thus potentially exposing sensitive information. Detecting privacy leakages is crucial in safeguarding sensitive information from unauthorized access and misuse. Hence, our contributions provide a useful set of tools to interpret the privacy of a deep learning model, in terms of revealing the ownership of its training data. In detail, our contributions are as follows.

• The FeS-MIA model proposes a new set of MIAs based on few-shot learning techniques and significantly reduces the resources required to evaluate the data integrity of a deep learning model. These techniques make the assessment of the training data’s integrity more feasible by requiring fewer data and less computational time, thus facilitating the proposition and evaluation of a wider range of membership inference scenarios. The impact of our model’s contribution is heightened by its ability to demonstrate significant privacy leakages with only minimal data and computational resources. Although efficiency was not a primary design goal, it emerges as a positive consequence of our few-shot approach, reinforcing the applicability of our method in constrained environments.
• The Log-MIA measure further boosts the interpretability of MIA privacy risks, leading to the reinterpretation of state-of-the-art MIA metrics. The proposed metric verifies that almost all MIAs are capable of achieving a significant privacy leakage.

By proactively detecting privacy leakages, the contributions of this work, with the proposal of the FeS-MIA model and Log-MIA measure, could be crucial in enhancing the security of machine learning models, especially in scenarios where data privacy is paramount.