Enhanced Graph Representation Convolution: Effective Inferring Gene Regulatory Network Using Graph Convolution Network with Self-Attention Graph Pooling Layer
Abstract
1. Introduction
2. Materials and Methods
2.1. Benchmark Dataset
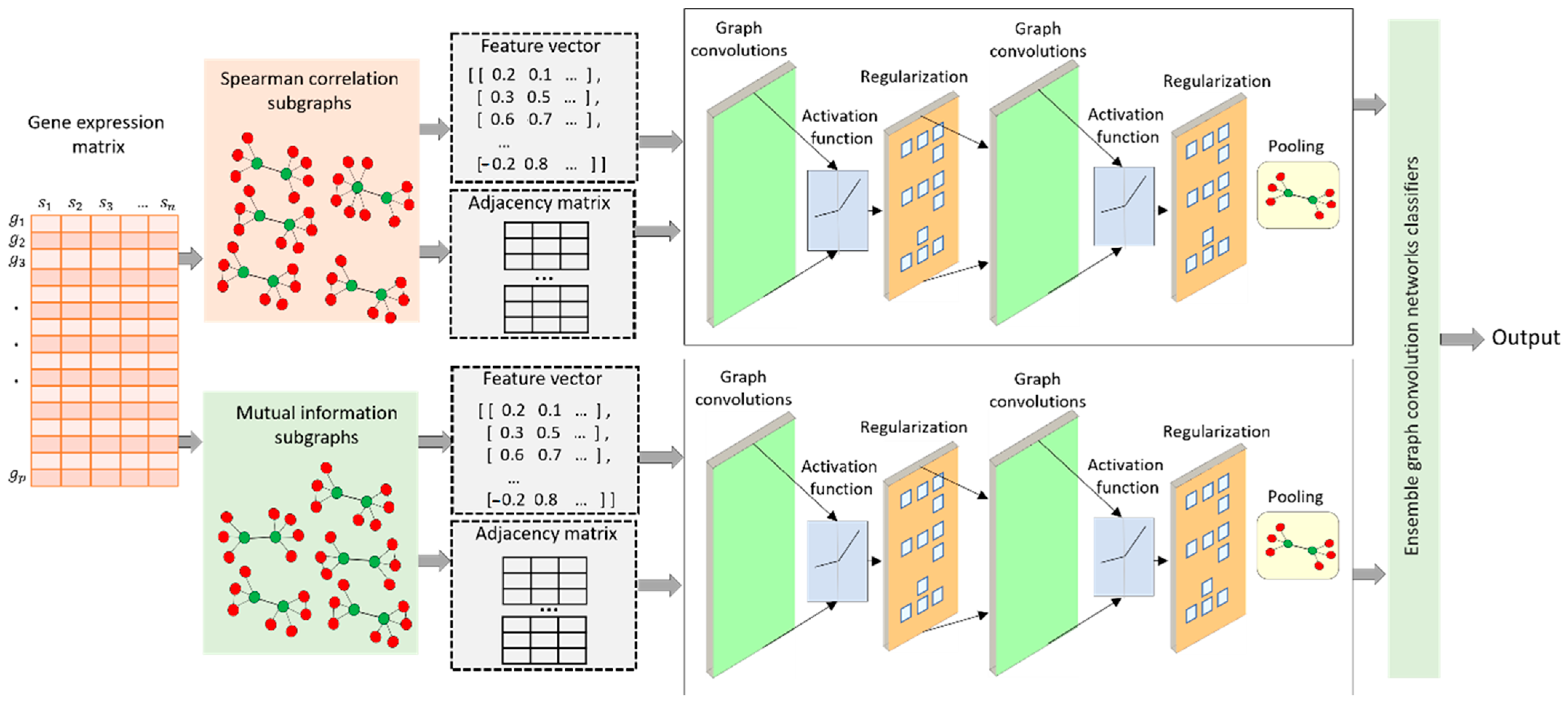
2.2. EGRC Framework
2.2.1. Creating Noisy Initial Skeletons
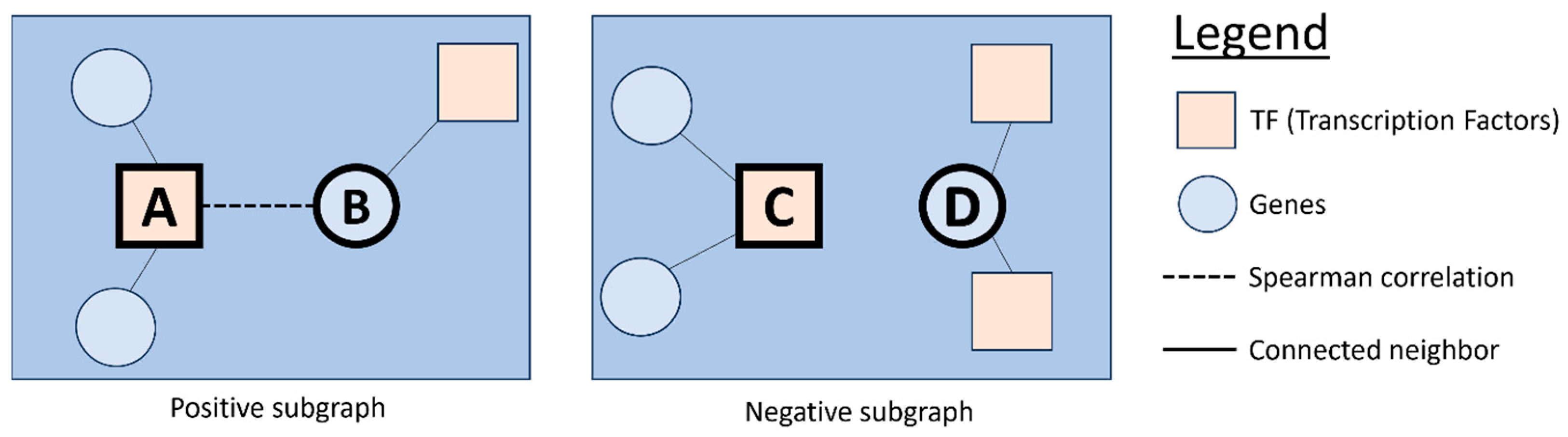
2.2.2. Extracting Enclosed Subgraphs
2.2.3. Constructing Node Features in Each Subgraph
2.2.4. Constructing Ensemble GCN Classifiers
2.3. Performance Evaluation Metrics
3. Results
3.1. Comparing GRN Using Different Pooling Methods
- -
- Selective pooling: SAGPooling employs a self-attention mechanism to selectively pool a subset of nodes pertinent to the graph’s overall properties. This ability can sometimes lead to improved performance by capturing significant structural features of the graph more effectively than other methods.
- -
- Adaptability: SAGPooling demonstrates superior adaptability to various graph structures. In contrast to DiffPool and MinCut Pooling, it does not require clustering the graph into a predetermined number of clusters or partitioning it into non-overlapping clusters, affording it greater flexibility.
- -
- Computational efficiency: SAGPooling is often more computationally efficient than methods like DiffPool or MinCut Pooling, particularly for larger graphs. This efficiency can facilitate the development of more complex or deeper graph convolutional networks (GCNs), potentially enhancing performance.
- -
- Less information loss: SAGPooling retains the most informative nodes and their connections, reducing information loss during the pooling process compared to other methods. This characteristic may lead to improved representation learning, thereby enhancing performance.
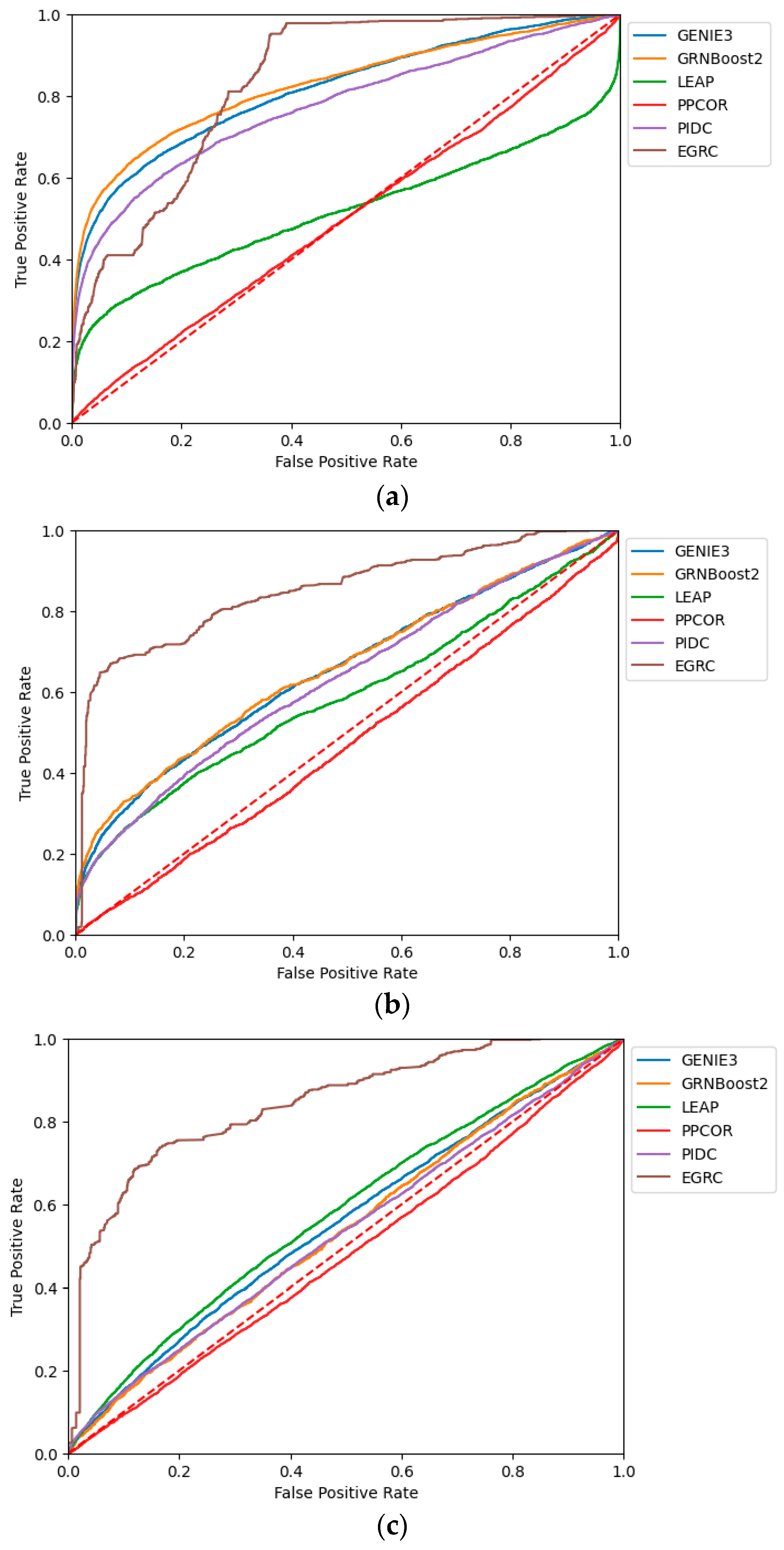
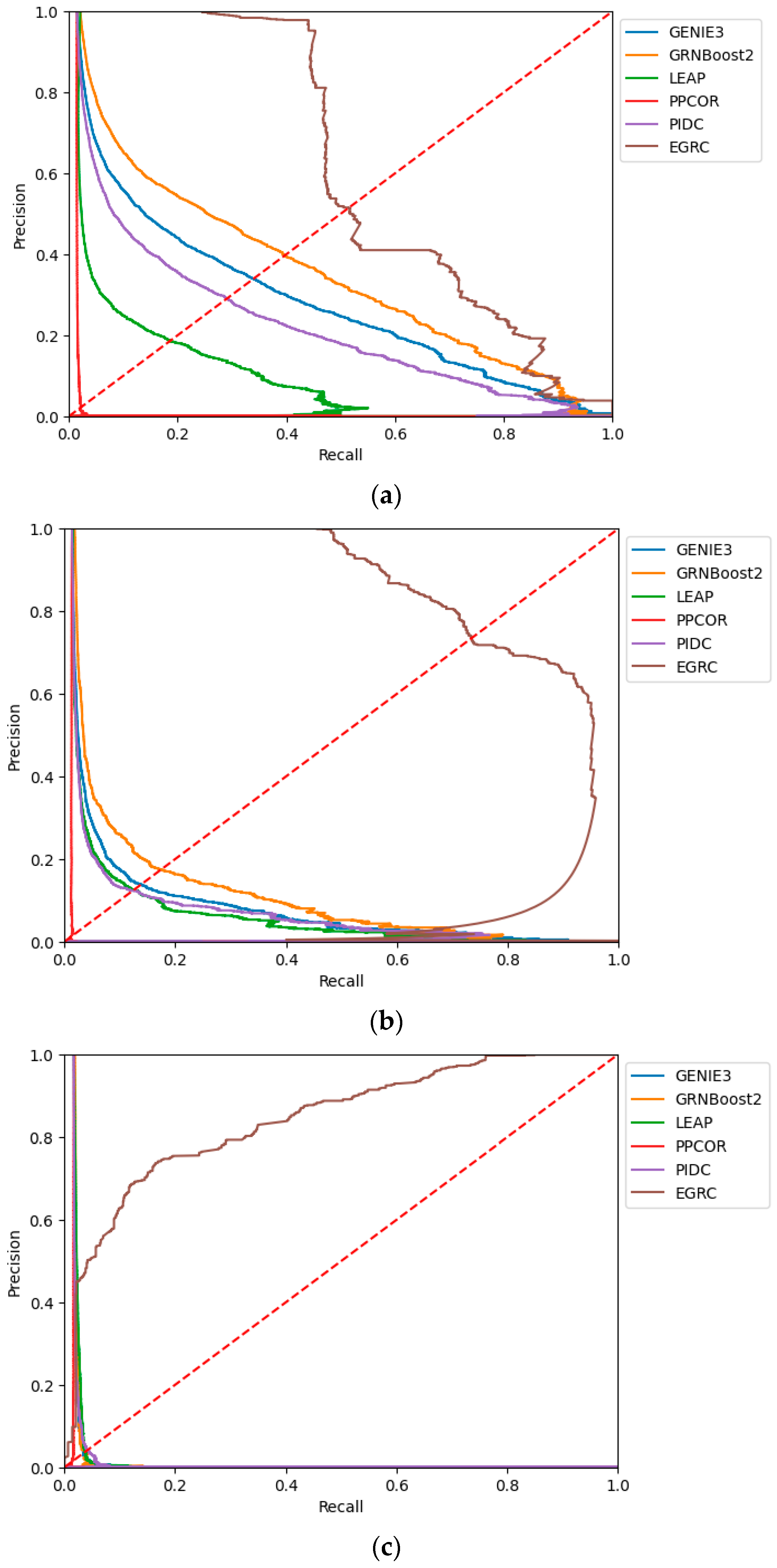
3.2. Analytical Comparison with Existing Approaches
4. Conclusions
5. Expanded Discussion on Particular Biological Implications
- (a)
- Identification of Key Regulatory Genes: An accurate reconstruction of GRNs is crucial for identifying key regulatory genes involved in various biological processes and diseases. For instance, our method can help pinpoint transcription factors (TFs) pivotal in cancer progression, metabolic disorders, or developmental processes. By accurately mapping these regulatory relationships, EGRC aids in uncovering potential targets for therapeutic intervention.
- (b)
- Gene Function Annotation: Understanding gene regulatory interactions enhances gene function annotation. Many genes, especially newly discovered or less studied, have unknown or poorly characterized functions. By identifying regulatory connections, EGRC contributes to predicting the roles of these genes within broader biological pathways, facilitating a deeper understanding of their contributions to cellular functions and organismal development.
- (c)
- Biomarker Discovery: EGRC’s high precision and recall demonstrated in noisy datasets like E. coli suggest its robustness in handling real-world biological data, which often contain variability. This capability is crucial for biomarker discovery, where identifying reliable molecular signatures for disease diagnosis, prognosis, and monitoring is essential. EGRC’s ability to accurately predict regulatory links can lead to identifying novel biomarkers for early disease detection and personalized medicine.
- (d)
- Systems Biology and Pathway Analysis: EGRC enhances the understanding of complex cellular pathways by providing detailed maps of gene regulatory interactions. This is particularly valuable in systems biology, where comprehensive models of cellular networks are constructed to understand how various biological components interact and give rise to phenotypic traits. EGRC’s accurate GRN predictions can be integrated into these models, offering insights into pathway dynamics and cellular responses to stimuli.
- (e)
- Comparative Genomics and Evolutionary Studies: By applying EGRC to datasets from different species, researchers can compare GRNs to explore the evolutionary conservation and divergence of regulatory mechanisms. Understanding these evolutionary aspects can reveal how regulatory networks have adapted to different environmental conditions and evolutionary pressures, shedding light on fundamental biological principles and species-specific adaptations.
- (f)
- Advancements in Personalized Medicine: The precise prediction of GRNs supports personalized medicine by enabling tailored treatment plans based on an individual’s unique regulatory network profile. This approach can improve therapeutic efficacy and reduce adverse effects by targeting specific regulatory pathways involved in a patient’s disease.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Marbach, D.; Costello, J.C.; Küffner, R.; Vega, N.M.; Prill, R.J.; Camacho, D.M.; Allison, K.R.; Kellis, M.; Collins, J.J.; Stolovitzky, G. Wisdom of crowds for robust gene network inference. Nat. Methods 2012, 9, 796–804. [Google Scholar] [CrossRef] [PubMed]
- Mochida, K.; Koda, S.; Inoue, K.; Nishii, R. Statistical and machine learning approaches to predict gene regulatory networks from transcriptome datasets. Front. Plant Sci. 2018, 9, 1770. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ma, A.; Ma, Q.; Xu, D.; Joshi, T. Inductive inference of gene regulatory network using supervised and semi-supervised graph neural networks. Comput. Struct. Biotechnol. J. 2020, 18, 3335–3343. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Ibrahim, F.; Najmulski, E.; Katholos, G.; Altarawy, D.; Heath, L.S.; Tulin, S.L. Developmental gene regulatory network connections predicted by machine learning from gene expression data alone. PLoS ONE 2021, 16, e0261926. [Google Scholar] [CrossRef] [PubMed]
- Lim, N.; Şenbabaoğlu, Y.; Michailidis, G.; d’Alché-Buc, F. OKVAR-Boost: A novel boosting algorithm to infer nonlinear dynamics and interactions in gene regulatory networks. Bioinformatics 2013, 29, 1416–1423. [Google Scholar] [CrossRef]
- Alawad, D.M.; Katebi, A.; Kabir, M.W.U.; Hoque, M.T. AGRN: Accurate gene regulatory network inference using ensemble machine learning methods. Bioinform. Adv. 2023, 3, vbad032. [Google Scholar] [CrossRef] [PubMed]
- Pirgazi, J.; Khanteymoori, A.R. A robust gene regulatory network inference method base on Kalman filter and linear regression. PLoS ONE 2018, 13, e0200094. [Google Scholar] [CrossRef] [PubMed]
- Pirgazi, J.; Khanteymoori, A.R.; Jalilkhani, M. TIGRNCRN: Trustful inference of gene regulatory network using clustering and refining the network. J. Bioinform. Comput. Biol. 2019, 17, 1950018. [Google Scholar] [CrossRef]
- Haury, A.-C.; Mordelet, F.; Vera-Licona, P.; Vert, J.-P. TIGRESS: Trustful inference of gene regulation using stability selection. BMC Syst. Biol. 2012, 6, 145. [Google Scholar] [CrossRef]
- Margolin, A.A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Favera, R.D.; Califano, A. ARACNE: An algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinform. 2006, 7, S7. [Google Scholar] [CrossRef]
- Gillani, Z.; Akash, M.S.H.; Rahaman, M.; Chen, M. CompareSVM: Supervised, Support Vector Machine (SVM) inference of gene regularity networks. BMC Bioinform. 2014, 15, 395. [Google Scholar] [CrossRef] [PubMed]
- Kotera, M.; Yamanishi, Y.; Moriya, Y.; Kanehisa, M.; Goto, S. GENIES: Gene network inference engine based on supervised analysis. Nucleic Acids Res. 2012, 40, W162–W167. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Daoudi, M.; Meshoul, S.; Tahi, F. A Machine Learning Approach for Gene Regulatory Network Inference. Int. J. Biosci. Biochem. Bioinform. 2019, 9, 82–89. [Google Scholar]
- Turki, T.; Wang, J.T.; Rajikhan, I. Inferring gene regulatory networks by combining supervised and unsupervised methods. In Proceedings of the 2016 15th IEEE International Conference on Machine Learning and Applications (ICMLA), Anaheim, CA, USA, 18–20 December 2016; pp. 140–145. [Google Scholar]
- Meyer, P.E.; Kontos, K.; Lafitte, F.; Bontempi, G. Information-theoretic inference of large transcriptional regulatory networks. EURASIP J. Bioinform. Syst. Biol. 2007, 2007, 79879. [Google Scholar] [CrossRef]
- Aliferis, C.F.; Statnikov, A.; Tsamardinos, I.; Mani, S.; Koutsoukos, X.D. Local causal and Markov blanket induction for causal discovery and feature selection for classification part I: Algorithms and empirical evaluation. J. Mach. Learn. Res. 2010, 11, 17–234. [Google Scholar]
- Mao, G.; Liu, J. An unsupervised deep learning framework for gene regulatory network inference from single-cell expression data. In Proceedings of the 2023 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Istanbul, Turkey, 5–8 December 2023; pp. 2663–2670. [Google Scholar]
- Mordelet, F.; Vert, J.-P. SIRENE: Supervised inference of regulatory networks. Bioinformatics 2008, 24, i76–i82. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Jiang, Q.; Chen, L.; Guo, D. Gene regulatory network inference using PLS-based methods. BMC Bioinform. 2016, 17, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Razaghi-Moghadam, Z.; Nikoloski, Z. Supervised learning of gene-regulatory networks based on graph distance profiles of transcriptomics data. NPJ Syst. Biol. Appl. 2020, 6, 21. [Google Scholar] [CrossRef] [PubMed]
- Augustine, J.; Jereesh, A. Gene regulatory network inference: A semi-supervised approach. In Proceedings of the 2017 International conference of Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 20–22 April 2017; pp. 68–72. [Google Scholar]
- Wang, Q.; Guo, M.; Chen, J.; Duan, R. A gene regulatory network inference model based on pseudo-siamese network. BMC Bioinform. 2023, 24, 163. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.; Hu, X.; Zou, G.; Yan, C.; Xu, G. Inferring gene regulatory networks from single-cell transcriptomic data using bidirectional rnn. Front. Oncol. 2022, 12, 899825. [Google Scholar] [CrossRef]
- Zhao, M.; He, W.; Tang, J.; Zou, Q.; Guo, F. A hybrid deep learning framework for gene regulatory network inference from single-cell transcriptomic data. Brief. Bioinform. 2022, 23, bbab568. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Zhu, Y.; Wu, S.; Wang, L.; Tan, T. Hierarchical graph convolutional networks for semi-supervised node classification. arXiv 2019, arXiv:190206667. [Google Scholar]
- Shang, J.; Ma, T.; Xiao, C.; Sun, J. Pre-training of graph augmented transformers for medication recommendation. arXiv 2019, arXiv:190600346. [Google Scholar]
- Palumbo, E.; Rizzo, G.; Troncy, R.; Baralis, E.; Osella, M.; Ferro, E. Knowledge graph embeddings with node2vec for item recommendation. In The Semantic Web: ESWC 2018 Satellite Events: ESWC 2018 Satellite Events, Heraklion, Crete, Greece, June 3–7, 2018, Revised Selected Papers 15; Springer: Berlin/Heidelberg, Germany, 2018; pp. 117–120. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: A comprehensive review. Comput. Soc. Netw. 2019, 6, 11. [Google Scholar] [CrossRef] [PubMed]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Sun, M.; Song, Z.; Jiang, X.; Pan, J.; Pang, Y. Learning pooling for convolutional neural network. Neurocomputing 2017, 224, 96–104. [Google Scholar] [CrossRef]
- Diehl, F. Edge contraction pooling for graph neural networks. arXiv 2019, arXiv:1905.10990. [Google Scholar]
- Mesquita, D.; Souza, A.; Kaski, S. Rethinking pooling in graph neural networks. Adv. Neural Inf. Process. Syst. 2020, 33, 2220–2231. [Google Scholar]
- Ying, Z.; You, J.; Morris, C.; Ren, X.; Hamilton, W.; Leskovec, J. Hierarchical graph representation learning with differentiable pooling. In Proceedings of the Advances in Neural Information Processing Systems 31, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Lee, J.; Lee, I.; Kang, J. Self-attention graph pooling. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 3734–3743. [Google Scholar]
- Ranjan, E.; Sanyal, S.; Talukdar, P. Asap: Adaptive structure aware pooling for learning hierarchical graph representations. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 5470–5477. [Google Scholar]
- Bianchi, F.M.; Grattarola, D.; Alippi, C. Mincut pooling in graph neural networks. In Proceedings of the ICLR 2020 Conference, Addis Ababa, Ethiopia, 27–30 April 2019. [Google Scholar]
- Bianchi, F.M.; Grattarola, D.; Alippi, C. Spectral clustering with graph neural networks for graph pooling. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 12–18 July 2020; pp. 874–883. [Google Scholar]
- Grattarola, D.; Zambon, D.; Bianchi, F.M.; Alippi, C. Understanding pooling in graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 2708–2718. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 233–240. [Google Scholar]
- Shengping, Y.; Gilbert, B. The receiver operating characteristic (ROC) curve. Southwest Respir. Crit. Care Chron. 2017, 5, 34–36. [Google Scholar]
- Pratapa, A.; Jalihal, A.P.; Law, J.N.; Bharadwaj, A.; Murali, T. Benchmarking algorithms for gene regulatory network inference from single-cell transcriptomic data. Nat. Methods 2020, 17, 147–154. [Google Scholar] [CrossRef]
- Specht, A.T.; Li, J. LEAP: Constructing gene co-expression networks for single-cell RNA-sequencing data using pseudotime ordering. Bioinformatics 2017, 33, 764–766. [Google Scholar] [CrossRef]
- Huynh-Thu, V.A.; Irrthum, A.; Wehenkel, L.; Geurts, P. Inferring regulatory networks from expression data using tree-based methods. PLoS ONE 2010, 5, e12776. [Google Scholar] [CrossRef] [PubMed]
- Moerman, T.; Aibar Santos, S.; Bravo González-Blas, C.; Simm, J.; Moreau, Y.; Aerts, J.; Aerts, S. GRNBoost2 and Arboreto: Efficient and scalable inference of gene regulatory networks. Bioinformatics 2019, 35, 2159–2161. [Google Scholar] [CrossRef] [PubMed]
- Chan, T.E.; Stumpf, M.P.; Babtie, A.C. Gene regulatory network inference from single-cell data using multivariate information measures. Cell Syst. 2017, 5, 251–267. [Google Scholar] [CrossRef]
- Kim, S. Ppcor: An R package for a fast calculation to semi-partial correlation coefficients. Commun. Stat. Appl. Methods 2015, 22, 665. [Google Scholar] [CrossRef]
| Species | #Nodes | #TF | #Target Genes | #Links | #Samples |
|---|---|---|---|---|---|
| In silico | 1643 | 195 | 1448 | 4012 | 805 |
| E. coli | 4511 | 334 | 4177 | 2066 | 805 |
| S. cerevisiae | 5950 | 333 | 5617 | 3940 | 536 |
| Method | Skeleton Type | AUROC | AUPR |
|---|---|---|---|
| DiffPool | Spearman correlation (SP) | 0.600 | 0.287 |
| Mutual information (MI) | 0.834 | 0.556 | |
| Ensemble (SP + MI) | 0.807 | 0.500 | |
| MinCutPool | Spearman correlation (SP) | 0.745 | 0.426 |
| Mutual information (MI) | 0.844 | 0.590 | |
| Ensemble (SP + MI) | 0.808 | 0.516 | |
| SAGPool | Spearman correlation (SP) | 0.834 | 0.623 |
| Mutual information (MI) | 0.793 | 0.476 | |
| Ensemble (SP + MI) | 0.835 | 0.612 |
| Method | Skeleton Type | AUROC | AUPR |
|---|---|---|---|
| DiffPool | Spearman correlation (SP) | 0.382 | 0.442 |
| Mutual information (MI) | 0.731 | 0.679 | |
| Ensemble (SP + MI) | 0.635 | 0.606 | |
| MinCutPool | Spearman correlation (SP) | 0.837 | 0.821 |
| Mutual information (MI) | 0.797 | 0.725 | |
| Ensemble (SP + MI) | 0.848 | 0.797 | |
| SAGPool | Spearman correlation (SP) | 0.834 | 0.818 |
| Mutual information (MI) | 0.807 | 0.807 | |
| Ensemble (SP + MI) | 0.854 | 0.807 |
| Method | Skeleton Type | AUROC | AUPR |
|---|---|---|---|
| DiffPool | Spearman correlation (SP) | 0.279 | 0.337 |
| Mutual information (MI) | 0.808 | 0.735 | |
| Ensemble (SP + MI) | 0.715 | 0.655 | |
| MinCutPool | Spearman correlation (SP) | 0.788 | 0.730 |
| Mutual information (MI) | 0.831 | 0.758 | |
| Ensemble (SP + MI) | 0.828 | 0.781 | |
| SAGPool | Spearman correlation (SP) | 0.805 | 0.771 |
| Mutual information (MI) | 0.860 | 0.825 | |
| Ensemble (SP + MI) | 0.858 | 0.842 |
| Dataset | Method | Skeleton Type | AUROC | AUPR |
|---|---|---|---|---|
| In silico | DiffPool | Ensemble (SP + MI) | 0.807 | 0.5 |
| MinCutPool | Ensemble (SP + MI) | 0.808 | 0.516 | |
| SAGPool | Ensemble (SP + MI) | 0.835 | 0.612 | |
| S. cerevisiae | DiffPool | Ensemble (SP + MI) | 0.635 | 0.606 |
| MinCutPool | Ensemble (SP + MI) | 0.848 | 0.797 | |
| SAGPool | Ensemble (SP + MI) | 0.854 | 0.807 | |
| Ecoli | DiffPool | Ensemble (SP + MI) | 0.715 | 0.655 |
| MinCutPool | Ensemble (SP + MI) | 0.828 | 0.781 | |
| SAGPool | Ensemble (SP + MI) | 0.858 | 0.842 |
| Method | Skeleton Type | Time in Minutes |
|---|---|---|
| MincutPool | Spearman’s correlation (SC) | 14.24 |
| Mutual information (MI) | 14.21 | |
| DiffPool | Spearman’s correlation (SC) | 19.50 |
| Mutual information (MI) | 19.14 | |
| SAGPool | Spearman’s correlation (SC) | 3.21 |
| Mutual information (MI) | 3.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alawad, D.M.; Katebi, A.; Hoque, M.T. Enhanced Graph Representation Convolution: Effective Inferring Gene Regulatory Network Using Graph Convolution Network with Self-Attention Graph Pooling Layer. Mach. Learn. Knowl. Extr. 2024, 6, 1818-1839. https://doi.org/10.3390/make6030089
Alawad DM, Katebi A, Hoque MT. Enhanced Graph Representation Convolution: Effective Inferring Gene Regulatory Network Using Graph Convolution Network with Self-Attention Graph Pooling Layer. Machine Learning and Knowledge Extraction. 2024; 6(3):1818-1839. https://doi.org/10.3390/make6030089
Chicago/Turabian StyleAlawad, Duaa Mohammad, Ataur Katebi, and Md Tamjidul Hoque. 2024. "Enhanced Graph Representation Convolution: Effective Inferring Gene Regulatory Network Using Graph Convolution Network with Self-Attention Graph Pooling Layer" Machine Learning and Knowledge Extraction 6, no. 3: 1818-1839. https://doi.org/10.3390/make6030089
APA StyleAlawad, D. M., Katebi, A., & Hoque, M. T. (2024). Enhanced Graph Representation Convolution: Effective Inferring Gene Regulatory Network Using Graph Convolution Network with Self-Attention Graph Pooling Layer. Machine Learning and Knowledge Extraction, 6(3), 1818-1839. https://doi.org/10.3390/make6030089







