Motor PHM on Edge Computing with Anomaly Detection and Fault Severity Estimation through Compressed Data Using PCA and Autoencoder
Abstract
1. Introduction
- 1.
- We introduce an efficient data compression method for motor PHM on edge devices, addressing the limitations of their limited computational resources and memory.
- 2.
- We analyze how different compression levels affect fault detection accuracy and severity classification, highlighting the trade-offs between data compression and diagnostic performance.
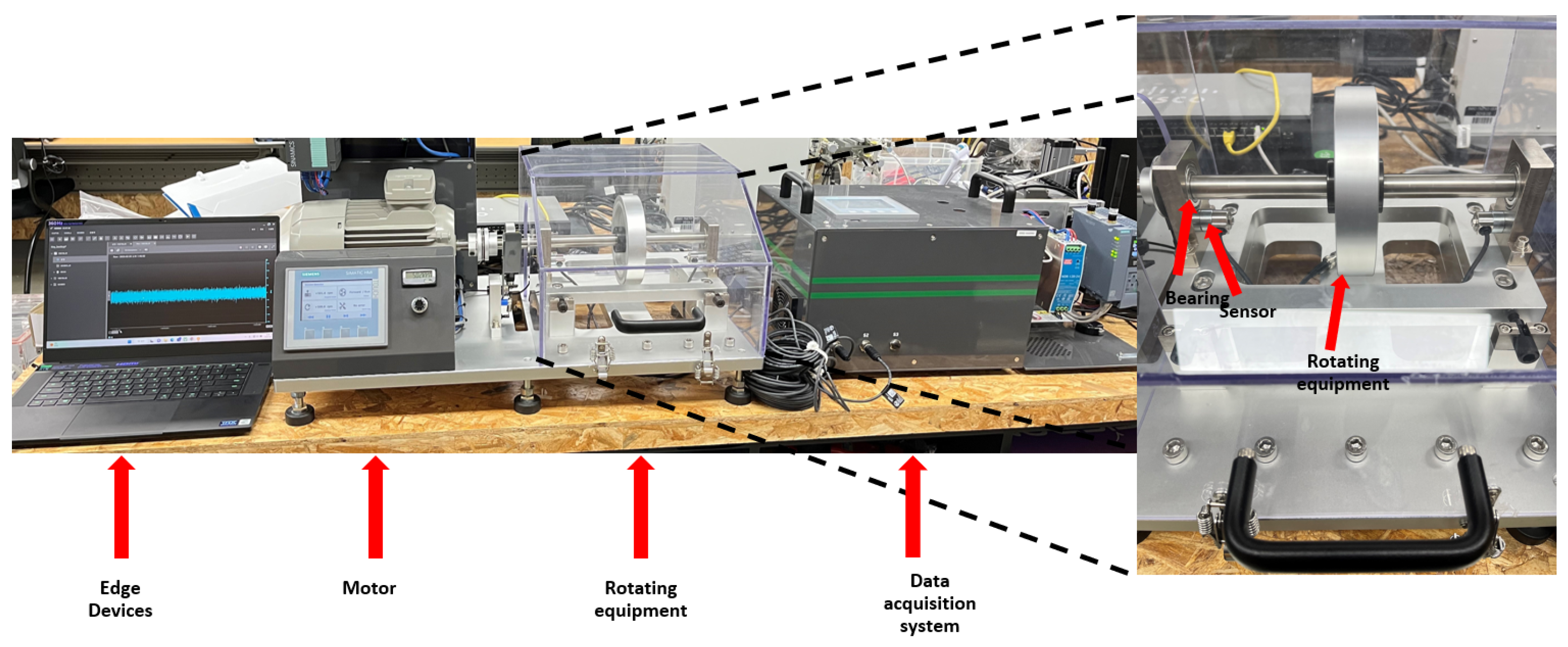
2. Experimental Platform and Data Acquisition
3. Methodology
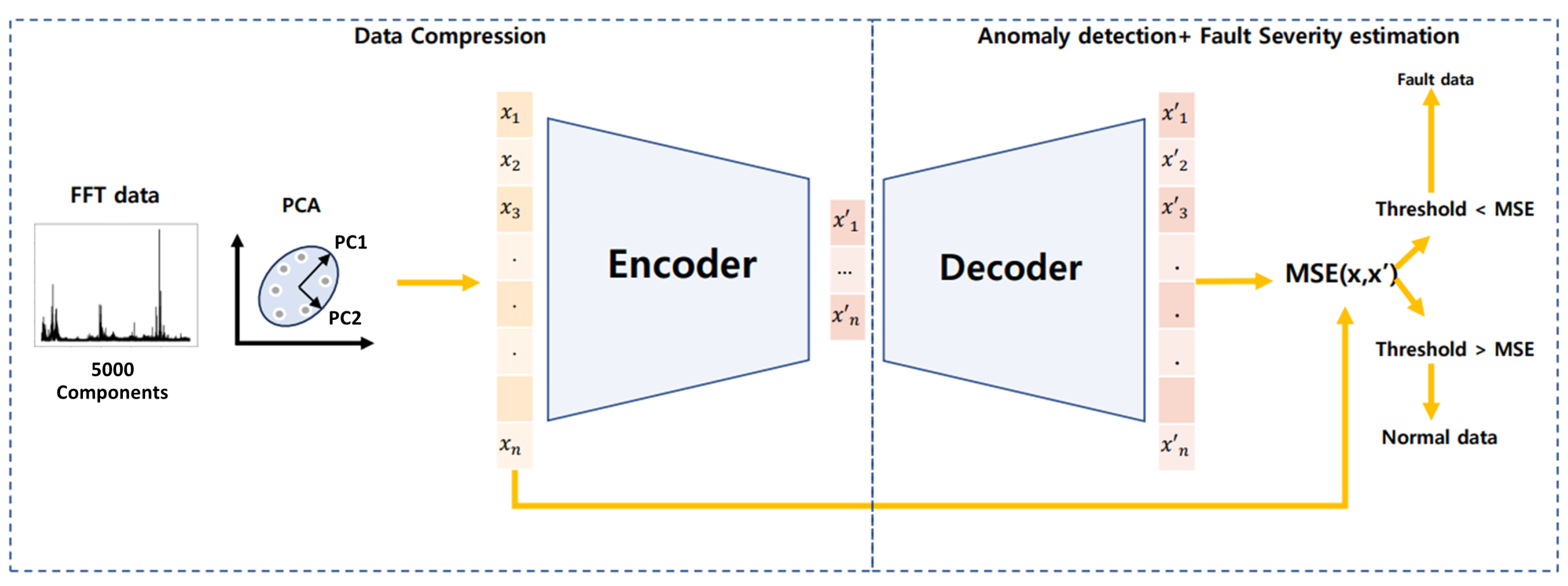
3.1. Principal Component Analysis
3.2. Autoencoder
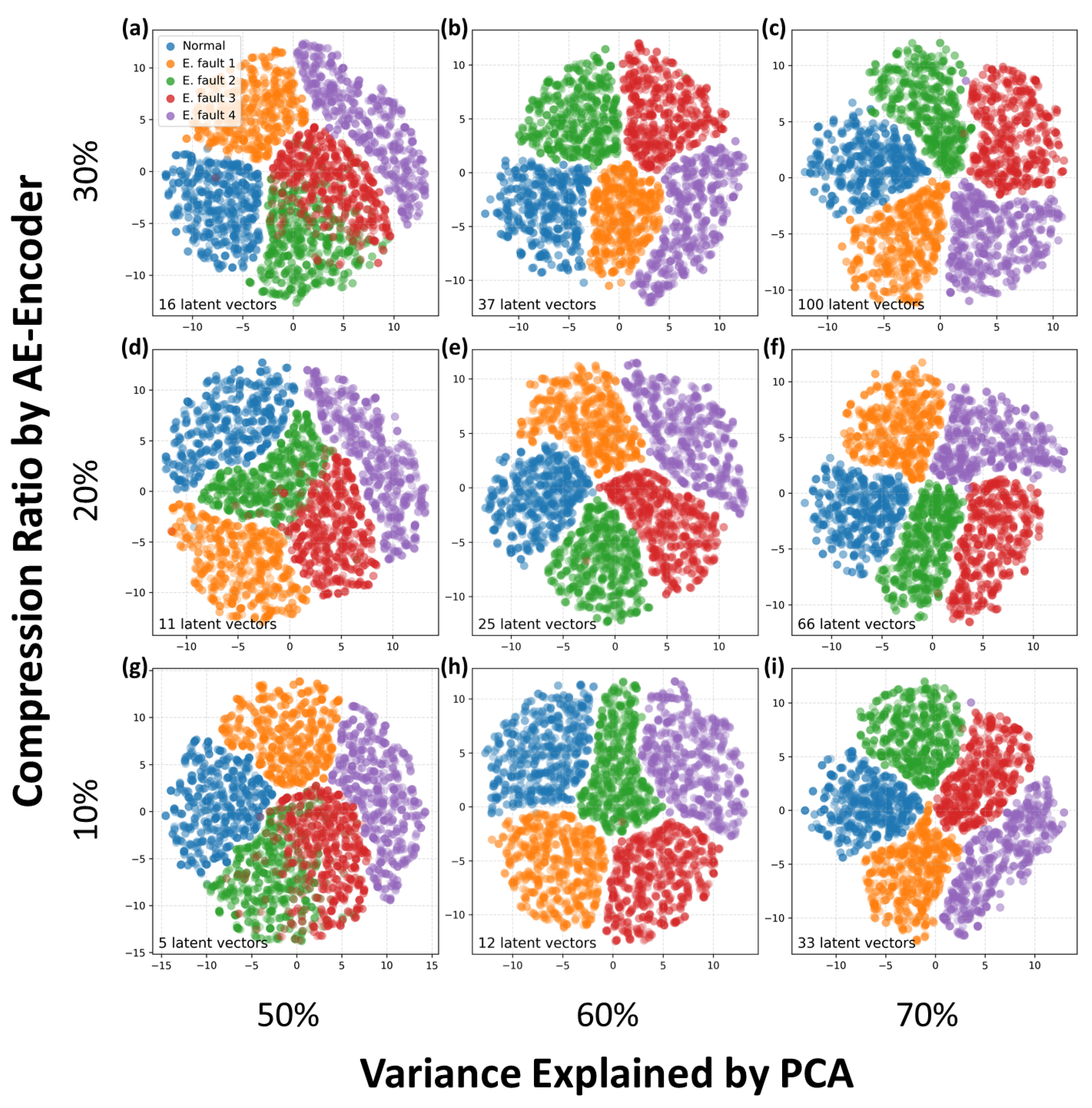
3.3. t-Distributed Stochastic Neighbor Embedding
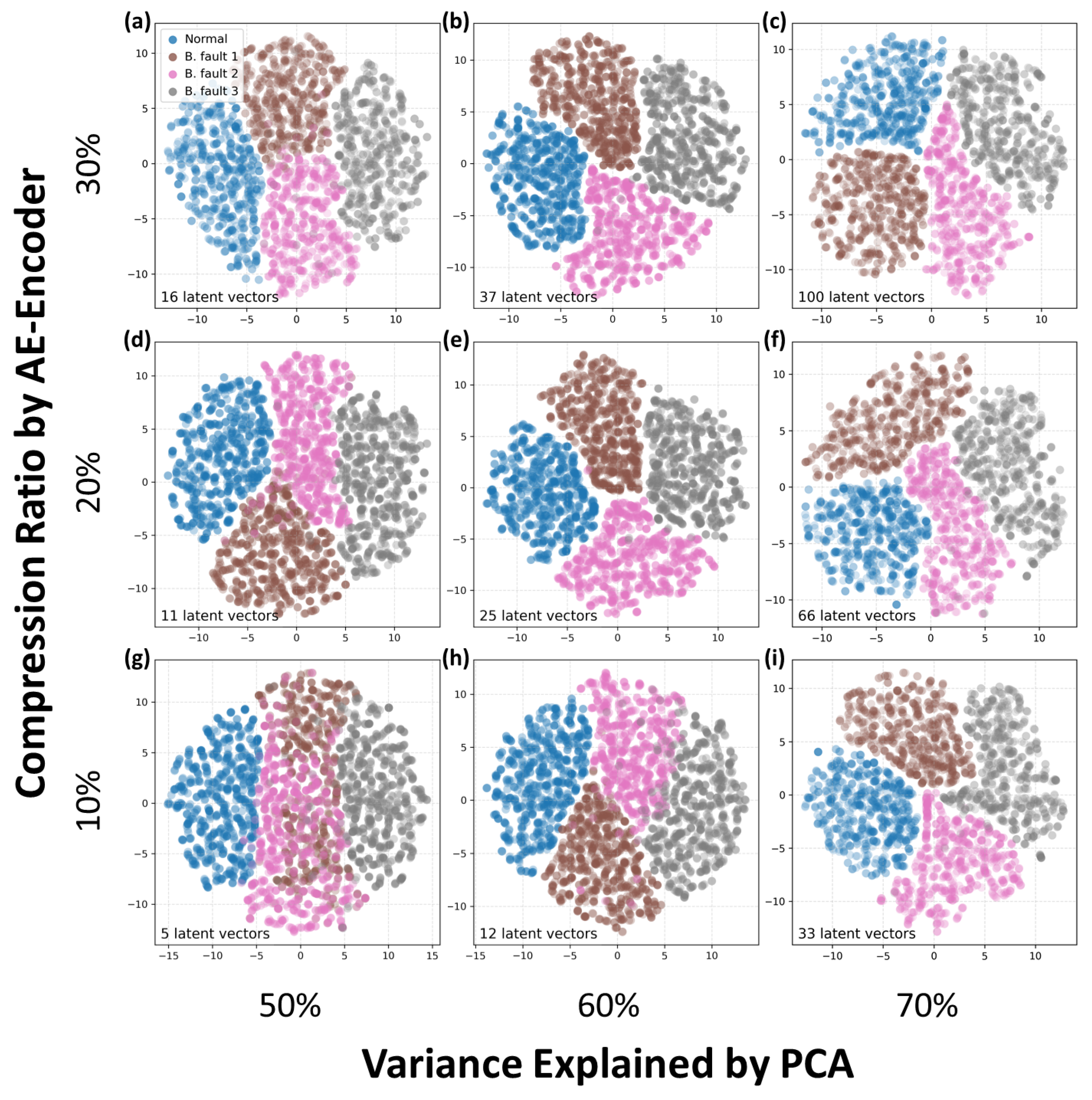
4. Result
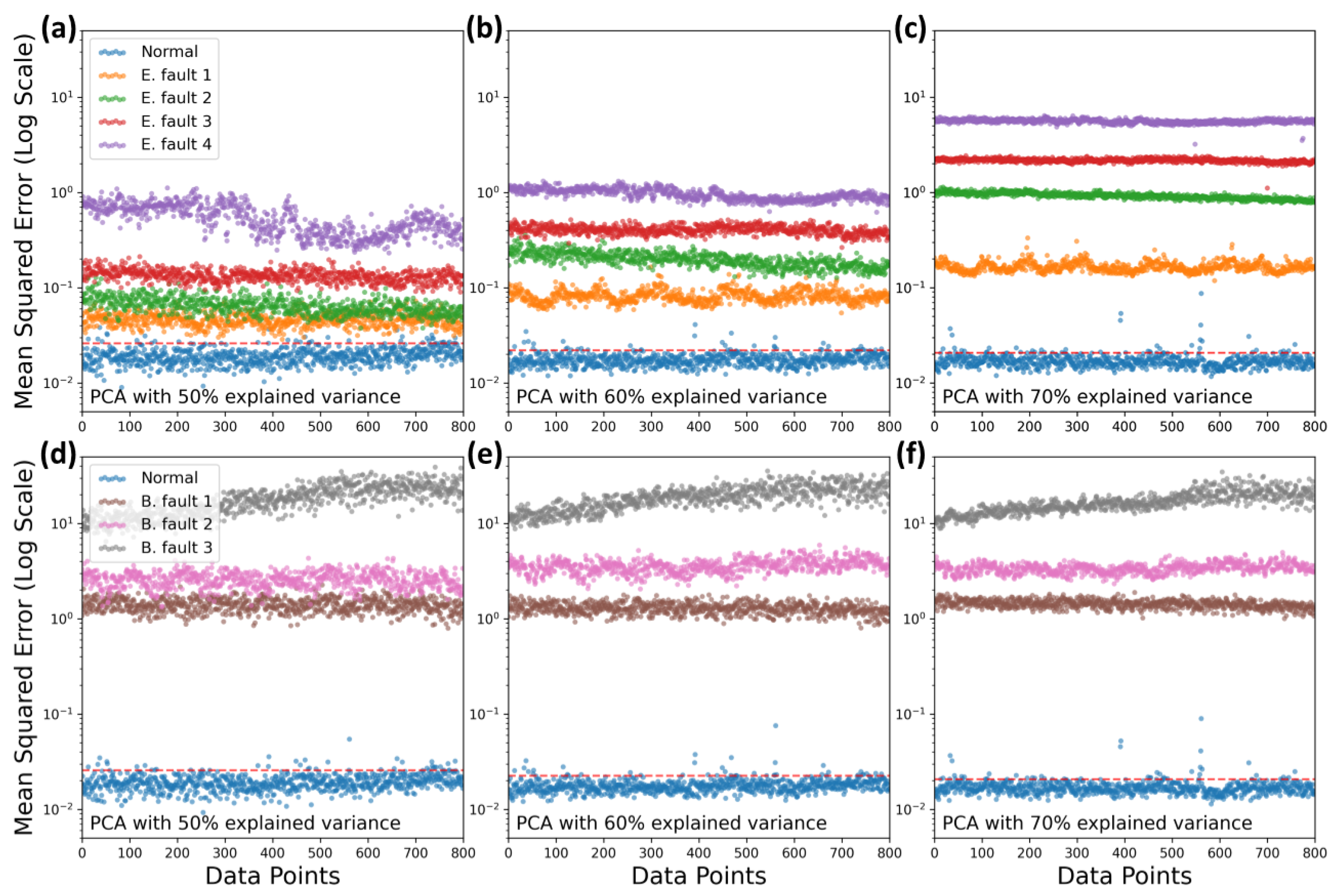
4.1. PCA Fitting with Only Normal Data
4.2. PCA with 1% Anomaly Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and Health Management Design for Rotary Machinery Systems—Reviews, Methodology and Applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Y.; Xu, L. PHM-Oriented Integrated Fusion Prognostics for Aircraft Engines Based on Sensor Data. IEEE Sens. J. 2014, 14, 1124–1132. [Google Scholar] [CrossRef]
- Guan, F.; Cui, W.W.; Li, L.F.; Wu, J. A Comprehensive Evaluation Method of Sensor Selection for PHM Based on Grey Clustering. Sensors 2020, 20, 1710. [Google Scholar] [CrossRef]
- Zhao, J.; Burke, A.F. Electric Vehicle Batteries: Status and Perspectives of Data-Driven Diagnosis and Prognosis. Batteries 2022, 8, 142. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, P.H.; Wu, C.W.; Ding, J.J.; Wang, C.C. Bearing Fault Diagnosis Based on Multiscale Permutation Entropy and Support Vector Machine. Entropy 2012, 14, 1343–1356. [Google Scholar] [CrossRef]
- Xu, G.; Liu, M.; Jiang, Z.; Söffker, D.; Shen, W. Bearing Fault Diagnosis Method Based on Deep Convolutional Neural Network and Random Forest Ensemble Learning. Sensors 2019, 19, 1088. [Google Scholar] [CrossRef]
- Meng, H.; Li, Y.F. A Review on Prognostics and Health Management (PHM) Methods of Lithium-Ion Batteries. Renew. Sustain. Energy Rev. 2019, 116, 109405. [Google Scholar] [CrossRef]
- Zio, E. Prognostics and Health Management (PHM): Where Are We and Where Do We (Need to) Go in Theory and Practice. Reliab. Eng. Syst. Saf. 2022, 218, 108119. [Google Scholar] [CrossRef]
- Cui, L.; Tian, X.; Wei, Q.; Liu, Y. A Self-Attention Based Contrastive Learning Method for Bearing Fault Diagnosis. Expert Syst. Appl. 2024, 238, 121645. [Google Scholar] [CrossRef]
- Ding, Y.; Zhuang, J.; Ding, P.; Jia, M. Self-Supervised Pretraining via Contrast Learning for Intelligent Incipient Fault Detection of Bearings. Reliab. Eng. Syst. Saf. 2022, 218, 108126. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Ge, Y.; Peng, D. Self-Supervised Signal Representation Learning for Machinery Fault Diagnosis under Limited Annotation Data. Knowl.-Based Syst. 2022, 239, 107978. [Google Scholar] [CrossRef]
- Yu, K.; Ma, H.; Lin, T.R.; Li, X. A Consistency Regularization Based Semi-Supervised Learning Approach for Intelligent Fault Diagnosis of Rolling Bearing. Measurement 2020, 165, 107987. [Google Scholar] [CrossRef]
- Chen, C.; Wang, Y.; Ruan, H.; Qin, Y.; Tang, B. A Robust Intelligent Fault Diagnosis Method for Rotating Machinery under Noisy Labels. Meas. Sci. Technol. 2023, 34, 125153. [Google Scholar] [CrossRef]
- Miao, J.; Deng, Z.; Deng, C.; Chen, C. Boosting Efficient Attention Assisted Cyclic Adversarial Auto-Encoder for Rotating Component Fault Diagnosis under Low Label Rates. Eng. Appl. Artif. Intell. 2024, 133, 108499. [Google Scholar] [CrossRef]
- Zhao, B.; Cheng, C.; Zhao, S.; Peng, Z. Hybrid Semi-Supervised Learning for Rotating Machinery Fault Diagnosis Based on Grouped Pseudo Labeling and Consistency Regularization. IEEE Trans. Instrum. Meas. 2023, 72, 3515812. [Google Scholar] [CrossRef]
- Su, H.; Yao, Q.; Xiang, L.; Hu, A. Semi-Supervised Temporal Meta-Learning Framework for Wind Turbine Bearing Fault Diagnosis under Limited Annotation Data. IEEE Trans. Instrum. Meas. 2024, 73, 3512309. [Google Scholar] [CrossRef]
- Yan, S.; Shao, H.; Xiao, Y.; Zhou, J.; Xu, Y.; Wan, J. Semi-Supervised Fault Diagnosis of Machinery Using LPS-DGAT under Speed Fluctuation and Extremely Low Labeled Rates. Adv. Eng. Inform. 2022, 53, 101648. [Google Scholar] [CrossRef]
- Zhao, X.; Jia, M.; Liu, Z. Semisupervised Deep Sparse Auto-Encoder with Local and Nonlocal Information for Intelligent Fault Diagnosis of Rotating Machinery. IEEE Trans. Instrum. Meas. 2021, 70, 3501413. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, J.; Ren, Z.; Ni, Q.; Gu, F.; Feng, K.; Yu, K.; Ge, J.; Lei, Z.; Liu, Z. Digital Twin-Driven Partial Domain Adaptation Network for Intelligent Fault Diagnosis of Rolling Bearing. Reliab. Eng. Syst. Saf. 2023, 234, 109186. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Yan, K.; Shao, H.; (Jing) Lin, J. Intelligent Fault Diagnosis of Bevel Gearboxes Using Semi-Supervised Probability Support Matrix Machine and Infrared Imaging. Reliab. Eng. Syst. Saf. 2023, 230, 108921. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z.; Zhang, Z.; Jia, L.; Qin, Y. A Semi-Supervised Approach to Bearing Fault Diagnosis under Variable Conditions towards Imbalanced Unlabeled Data. Sensors 2018, 18, 2097. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Yang, R.; Zhong, M. Graph-Based Semi-Supervised Random Forest for Rotating Machinery Gearbox Fault Diagnosis. Control Eng. Pract. 2021, 117, 104952. [Google Scholar] [CrossRef]
- Pan, H.; Xu, H.; Zheng, J.; Shao, H.; Tong, J. A Semi-Supervised Matrixized Graph Embedding Machine for Roller Bearing Fault Diagnosis under Few-Labeled Samples. IEEE Trans. Ind. Inform. 2024, 20, 854–863. [Google Scholar] [CrossRef]
- Maestro-Prieto, J.A.; Ramírez-Sanz, J.M.; Bustillo, A.; Rodriguez-Díez, J.J. Semi-Supervised Diagnosis of Wind-Turbine Gearbox Misalignment and Imbalance Faults. Appl. Intell. 2024, 54, 4525–4544. [Google Scholar] [CrossRef]
- Cui, L.; Tian, X.; Shi, X.; Wang, X.; Cui, Y. A Semi-Supervised Fault Diagnosis Method Based on Improved Bidirectional Generative Adversarial Network. Appl. Sci. 2021, 11, 9401. [Google Scholar] [CrossRef]
- Li, X.; Zhang, F.L. Classification of Multi-Type Bearing Fault Features Based on Semi-Supervised Generative Adversarial Network (GAN). Meas. Sci. Technol. 2024, 35, 025107. [Google Scholar] [CrossRef]
- Zhang, T.; Li, C.; Chen, J.; He, S.; Zhou, Z. Feature-Level Consistency Regularized Semi-supervised Scheme with Data Augmentation for Intelligent Fault Diagnosis under Small Samples. Mech. Syst. Signal Process. 2023, 203, 110747. [Google Scholar] [CrossRef]
- Huo, D.; Kang, Y.; Wang, B.; Feng, G.; Zhang, J.; Zhang, H. Gear Fault Diagnosis Method Based on Multi-Sensor Information Fusion and VGG. Entropy 2022, 24, 1618. [Google Scholar] [CrossRef]
- Zhu, J.; Jiang, Q.; Shen, Y.; Xu, F.; Zhu, Q. Res-HSA: Residual Hybrid Network with Self-Attention Mechanism for RUL Prediction of Rotating Machinery. Eng. Appl. Artif. Intell. 2023, 124, 106491. [Google Scholar] [CrossRef]
- Sun, K.; Liu, D.; Cui, L. Rotating Machinery Fault Diagnosis Based on Optimized Hilbert Curve Images and a Novel Bi-Channel CNN with Attention Mechanism. Meas. Sci. Technol. 2023, 34, 125022. [Google Scholar] [CrossRef]
- Wei, Q.; Tian, X.; Cui, L.; Zheng, F.; Liu, L. WSAFormer-DFFN: A Model for Rotating Machinery Fault Diagnosis Using 1D Window-Based Multi-Head Self-Attention and Deep Feature Fusion Network. Eng. Appl. Artif. Intell. 2023, 124, 106633. [Google Scholar] [CrossRef]
- Jin, Y.; Yang, J.; Yang, X.; Liu, Z. Cross-Domain Bearing Fault Diagnosis Method Based on SMOTENC and Deep Transfer Learning under Imbalanced Data. Meas. Sci. Technol. 2024, 35, 015121. [Google Scholar] [CrossRef]
- Fang, H.; Liu, H.; Wang, X.; Deng, J.; An, J. The Method Based on Clustering for Unknown Failure Diagnosis of Rolling Bearings. IEEE Trans. Instrum. Meas. 2023, 72, 3509508. [Google Scholar] [CrossRef]
- Huang, X.; Wen, G.; Dong, S.; Zhou, H.; Lei, Z.; Zhang, Z.; Chen, X. Memory Residual Regression Autoencoder for Bearing Fault Detection. IEEE Trans. Instrum. Meas. 2021, 70, 3515512. [Google Scholar] [CrossRef]
- Li, Z.; Xu, P.; Wang, X.B. Online Anomaly Detection and Remaining Useful Life Prediction of Rotating Machinery Based on Cumulative Summation Features. Meas. Control 2023, 56, 615–629. [Google Scholar] [CrossRef]
- Xiao, D.; Qin, C.; Yu, H.; Huang, Y.; Liu, C.; Zhang, J. Unsupervised Machine Fault Diagnosis for Noisy Domain Adaptation Using Marginal Denoising Autoencoder Based on Acoustic Signals. Measurement 2021, 176, 109186. [Google Scholar] [CrossRef]
- Rezaeianjouybari, B.; Shang, Y. Deep Learning for Prognostics and Health Management: State of the Art, Challenges, and Opportunities. Measurement 2020, 163, 107929. [Google Scholar] [CrossRef]
- Shi, W.; Dustdar, S. The Promise of Edge Computing. Computer 2016, 49, 78–81. [Google Scholar] [CrossRef]
- Çınar, Z.M.; Abdussalam Nuhu, A.; Zeeshan, Q.; Korhan, O.; Asmael, M.; Safaei, B. Machine Learning in Predictive Maintenance towards Sustainable Smart Manufacturing in Industry 4.0. Sustainability 2020, 12, 8211. [Google Scholar] [CrossRef]
- Nain, G.; Pattanaik, K.K.; Sharma, G.K. Towards Edge Computing in Intelligent Manufacturing: Past, Present and Future. J. Manuf. Syst. 2022, 62, 588–611. [Google Scholar] [CrossRef]
- Zhou, Q.; Chen, R.; Huang, B.; Liu, C.; Yu, J.; Yu, X. An Automatic Surface Defect Inspection System for Automobiles Using Machine Vision Methods. Sensors 2019, 19, 644. [Google Scholar] [CrossRef]
- Kristiani, E.; Wang, L.Y.; Liu, J.C.; Huang, C.K.; Wei, S.J.; Yang, C.T. An Intelligent Thermal Compensation System Using Edge Computing for Machine Tools. Sensors 2024, 24, 2531. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, L.; Gao, Y.; Li, S. Vibration Signal Extraction Based on FFT and Least Square Method. IEEE Access 2020, 8, 224092–224107. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal Component Analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Dunteman, G.H. Principal Components Analysis; Sage: Newcastle upon Tyne, UK, 1989. [Google Scholar]
- Sehgal, S.; Singh, H.; Agarwal, M.; Bhasker, V.; Shantanu. Data Analysis Using Principal Component Analysis. In Proceedings of the 2014 International Conference on Medical Imaging, m-Health and Emerging Communication Systems (MedCom), Greater Noida, India, 7–8 November 2014; pp. 45–48. [Google Scholar] [CrossRef]
- Chen, S.; Guo, W. Auto-Encoders in Deep Learning—A Review with New Perspectives. Mathematics 2023, 11, 1777. [Google Scholar] [CrossRef]
- Ng, A. Sparse Autoencoder. CS294A Lect. Notes 2011, 72, 1–19. [Google Scholar]
- Kraljevski, I.; Duckhorn, F.; Tschöpe, C.; Wolff, M. Machine Learning for Anomaly Assessment in Sensor Networks for NDT in Aerospace. IEEE Sens. J. 2021, 21, 11000–11008. [Google Scholar] [CrossRef]
- Wei, Y.; Jang-Jaccard, J.; Xu, W.; Sabrina, F.; Camtepe, S.; Boulic, M. LSTM-Autoencoder-Based Anomaly Detection for Indoor Air Quality Time-Series Data. IEEE Sens. J. 2023, 23, 3787–3800. [Google Scholar] [CrossRef]
- Nizam, H.; Zafar, S.; Lv, Z.; Wang, F.; Hu, X. Real-Time Deep Anomaly Detection Framework for Multivariate Time-Series Data in Industrial IoT. IEEE Sens. J. 2022, 22, 22836–22849. [Google Scholar] [CrossRef]
- van der Maaten, L.; Hinton, G. Visualizing Data Using T-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Anowar, F.; Sadaoui, S.; Selim, B. Conceptual and Empirical Comparison of Dimensionality Reduction Algorithms (PCA, KPCA, LDA, MDS, SVD, LLE, ISOMAP, LE, ICA, t-SNE). Comput. Sci. Rev. 2021, 40, 100378. [Google Scholar] [CrossRef]
- Oliveira, F.H.M.; Machado, A.R.P.; Andrade, A.O. On the Use of T-Distributed Stochastic Neighbor Embedding for Data Visualization and Classification of Individuals with Parkinson’s Disease. Comput. Math. Methods Med. 2018, 2018, 8019232. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, H.; Zhao, S. Auto-Encoder Based Dimensionality Reduction. Neurocomputing 2016, 184, 232–242. [Google Scholar] [CrossRef]
- Hou, X.; Shen, L.; Sun, K.; Qiu, G. Deep Feature Consistent Variational Autoencoder. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 1133–1141. [Google Scholar] [CrossRef]




| Model | Reference | |
|---|---|---|
| Self-Supervised Learning | Self-Attention-Based Signal Transformer | [10] |
| Momentum Contrast Learning (MCL) | [11] | |
| 1D Convolutional Neural Network (1DCNN) | [12] | |
| Semi-Supervised Learning | Convolutional Residual Network (CRN) | [13] |
| Deep Neural Networks (DNNs), Two-Component Gaussian Mixture Model (GMM) | [14] | |
| Cyclic Adversarial Autoencoder (CAAE), Boosting Efficient Attention (BEA) | [15] | |
| Grouped Pseudo-Labeling, Consistency Regularization, Convolutional Neural Network (CNN) | [16] | |
| Label Propagation Strategy and Dynamic Graph Attention Network (LPS-DGAT) | [17] | |
| Relevant Random Subspace Method for Co-Training (Rel-RASCO), Co-Training by Committee (CoBC) | [18] | |
| Semi-Supervised Meta-Learning Framework (SeMeF) with Temporal Convolutional Module | [19] | |
| Partial Domain Adaptation Network Driven by Digital Twin | [20] | |
| Semi-Supervised Probability Support Matrix Machine (SPSMM) | [21] | |
| Visibility Graph Feature (VGF), Graph-Based Semi-Supervised Learning | [22] | |
| Random Forest, Graph-Based Semi-Supervised Learning | [23] | |
| Semi-Supervised Matrixized Graph Embedding Machine (SMGEM) | [24] | |
| Semi-Supervised Deep Sparse Autoencoder | [25] | |
| Bidirectional Wasserstein Generative Adversarial Network with Gradient Penalty (BiWGAN-GP) | [26] | |
| Semi-Supervised Generative Adversarial Network (GAN) | [27] | |
| Generative Adversarial Networks (GAN), Earth Mover’s Distance (EMD), Feature Consistency Regularization (FCR) | [28] | |
| Supervised Learning | Visual Geometry Group Network (VGG), Convolutional Neural Network (CNN) | [29] |
| Convolutional Neural Network (CNN) and Gated Recurrent Units (GRUs) with Self-Attention Mechanism | [30] | |
| Convolutional Neural Network (CNN) with Attention Mechanisms | [31] | |
| 1D Window-Based Self-Attention and Deep Feature Fusion Network (WSAFormer-DFFN) | [32] | |
| Transfer Learning | Synthetic Minority Over-sampling Technique Nominal and Continuous (SMOTENC) and Deep Transfer Learning | [33] |
| Transfer Clustering Calculation Center Points (TCCP) | [34] | |
| Unsupervised Learning | Memory Residual Regression Autoencoder (MRRAE) | [35] |
| Discrete Wavelet Transform (DWT), Regression Analysis | [36] | |
| Noisy Domain Adaptive Marginal Stacking Denoising Autoencoder (NDAmSDA) | [37] |
| Number of Components | Explained Variance Ratio (%) |
|---|---|
| 1 | 12.93 |
| 54 | 50.15 |
| 81 | 55.00 |
| 124 | 60.06 |
| 197 | 65.03 |
| 332 | 70.00 |
| 514 | 75.01 |
| 745 | 80.01 |
| 1043 | 85.00 |
| 1451 | 90.01 |
| 2083 | 95.00 |
| 4800 | 100 |
| Number of Components | Explained Variance Ratio (%) |
|---|---|
| 1 | 14.84 |
| 27 | 50.02 |
| 44 | 55.07 |
| 71 | 60.05 |
| 114 | 65.05 |
| 188 | 70.01 |
| 339 | 75.00 |
| 561 | 80.01 |
| 858 | 85.01 |
| 1272 | 90.01 |
| 1926 | 95.00 |
| 4800 | 100 |
| Number of Components | Explained Variance Ratio (%) |
|---|---|
| 1 | 33.74 |
| 7 | 50.28 |
| 14 | 55.46 |
| 24 | 60.21 |
| 41 | 65.13 |
| 70 | 70.12 |
| 121 | 75.03 |
| 234 | 80.02 |
| 500 | 85.00 |
| 916 | 90.01 |
| 1606 | 95.00 |
| 4800 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.H.; Jang, S.K.; Cho, W.H.; Moon, S.; Kim, H. Motor PHM on Edge Computing with Anomaly Detection and Fault Severity Estimation through Compressed Data Using PCA and Autoencoder. Mach. Learn. Knowl. Extr. 2024, 6, 1466-1483. https://doi.org/10.3390/make6030069
Choi JH, Jang SK, Cho WH, Moon S, Kim H. Motor PHM on Edge Computing with Anomaly Detection and Fault Severity Estimation through Compressed Data Using PCA and Autoencoder. Machine Learning and Knowledge Extraction. 2024; 6(3):1466-1483. https://doi.org/10.3390/make6030069
Chicago/Turabian StyleChoi, Jong Hyun, Sung Kyu Jang, Woon Hyung Cho, Seokbae Moon, and Hyeongkeun Kim. 2024. "Motor PHM on Edge Computing with Anomaly Detection and Fault Severity Estimation through Compressed Data Using PCA and Autoencoder" Machine Learning and Knowledge Extraction 6, no. 3: 1466-1483. https://doi.org/10.3390/make6030069
APA StyleChoi, J. H., Jang, S. K., Cho, W. H., Moon, S., & Kim, H. (2024). Motor PHM on Edge Computing with Anomaly Detection and Fault Severity Estimation through Compressed Data Using PCA and Autoencoder. Machine Learning and Knowledge Extraction, 6(3), 1466-1483. https://doi.org/10.3390/make6030069







