Enhancing Computation-Efficiency of Deep Neural Network Processing on Edge Devices through Serial/Parallel Systolic Computing
Abstract
1. Introduction
- (1)
- We propose a serial/parallel systolic array architecture and data flow;
- (2)
- We introduce a bit-serial processing of activation with zero skipping capability;
- (3)
- Our design exploits activation precision adjustment in a systolic array accelerator;
- (4)
- We improve energy efficiency by replacing complicated multipliers with simpler and low-cost serial circuits.
2. Baseline System
- Specifying fixed precision at design-time;
- Static trade-offs among operational factors like accuracy;
- High latency (cycle-time) due to complicated operations.
3. Related Work
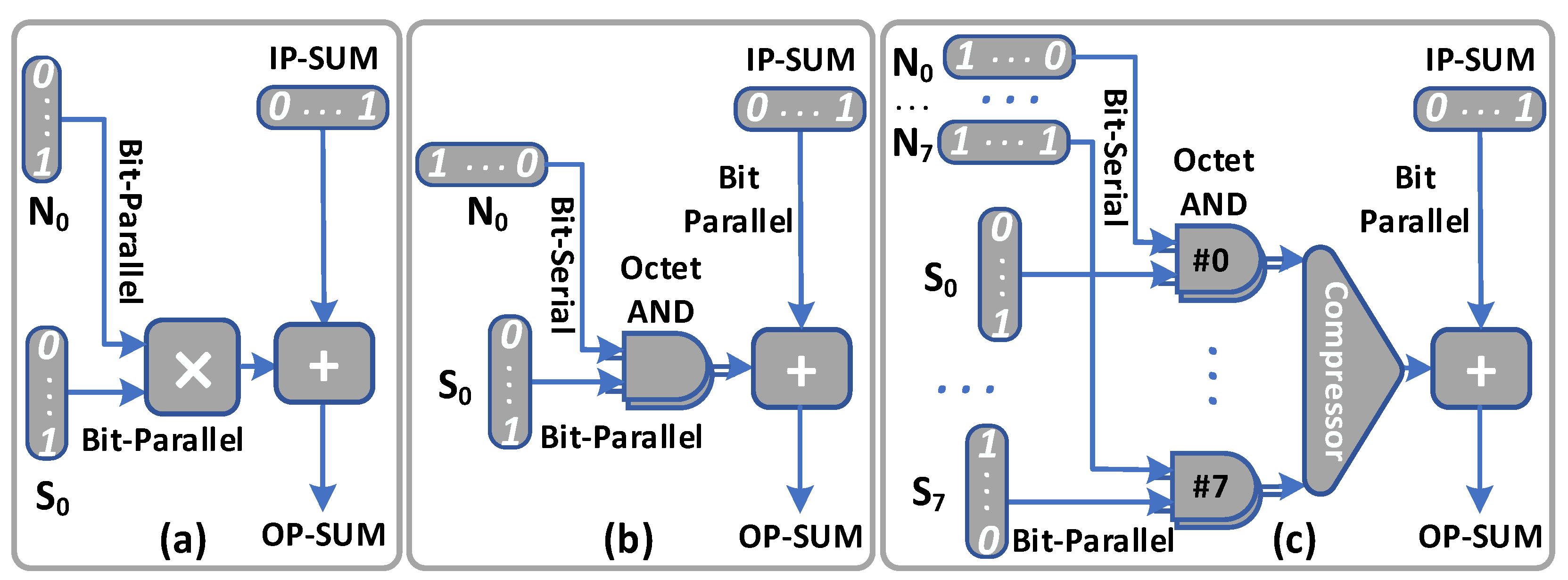
4. Octet Serial Processing Approach
5. SPSA Accelerator Architecture
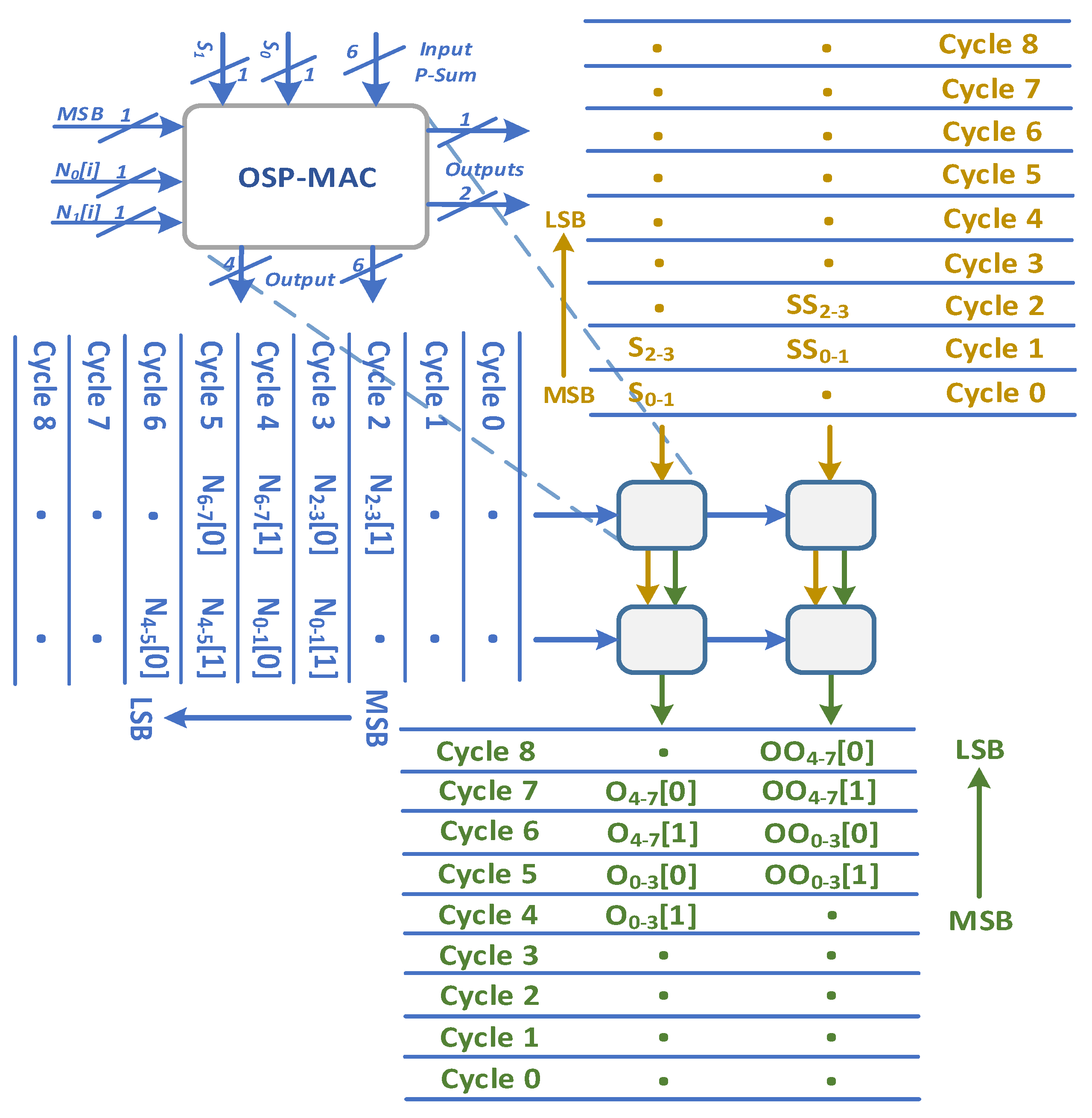
5.1. Overall Accelerator Architecture
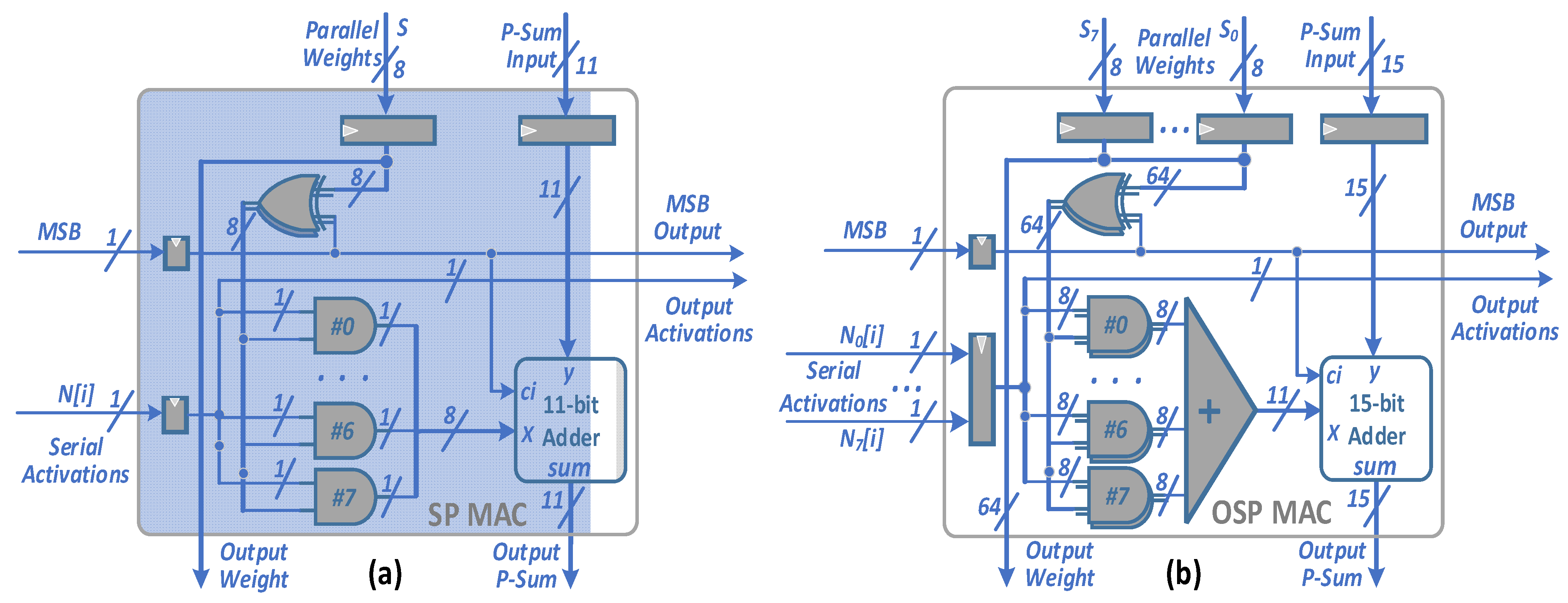
5.2. SPSA-MAC Processing Elements
6. Evaluation and Comparison
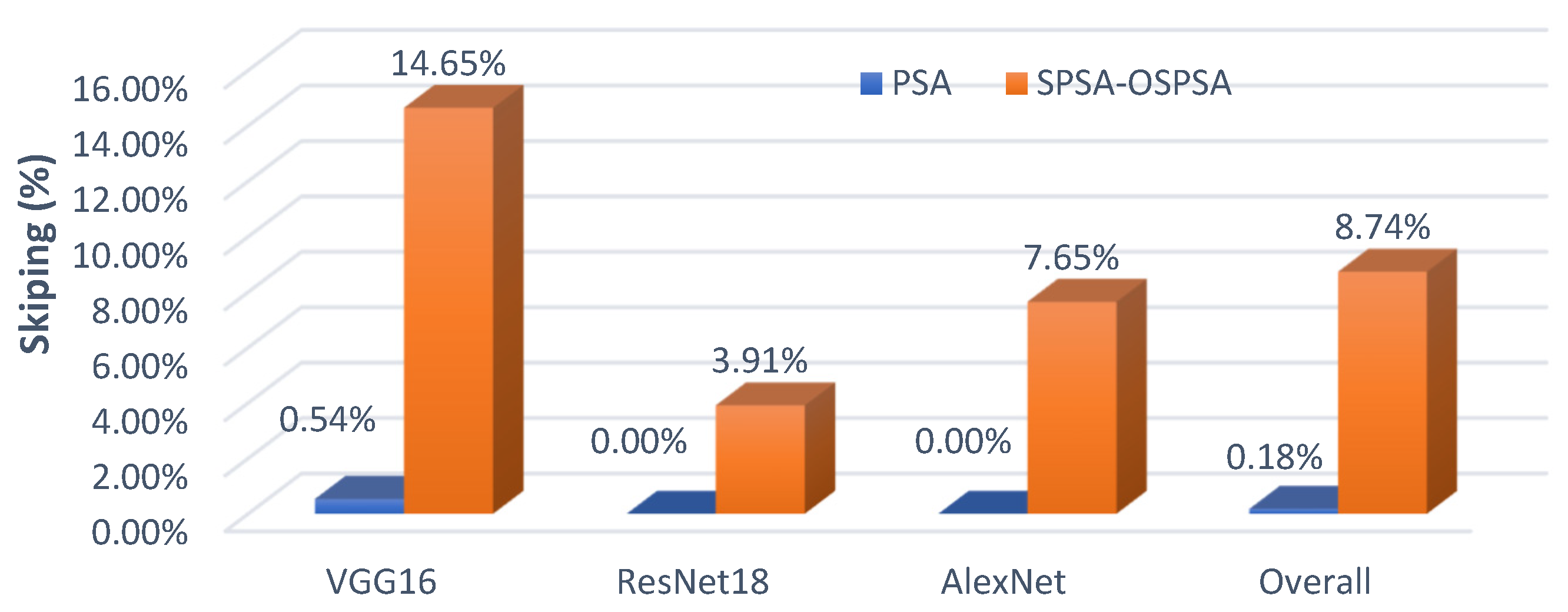
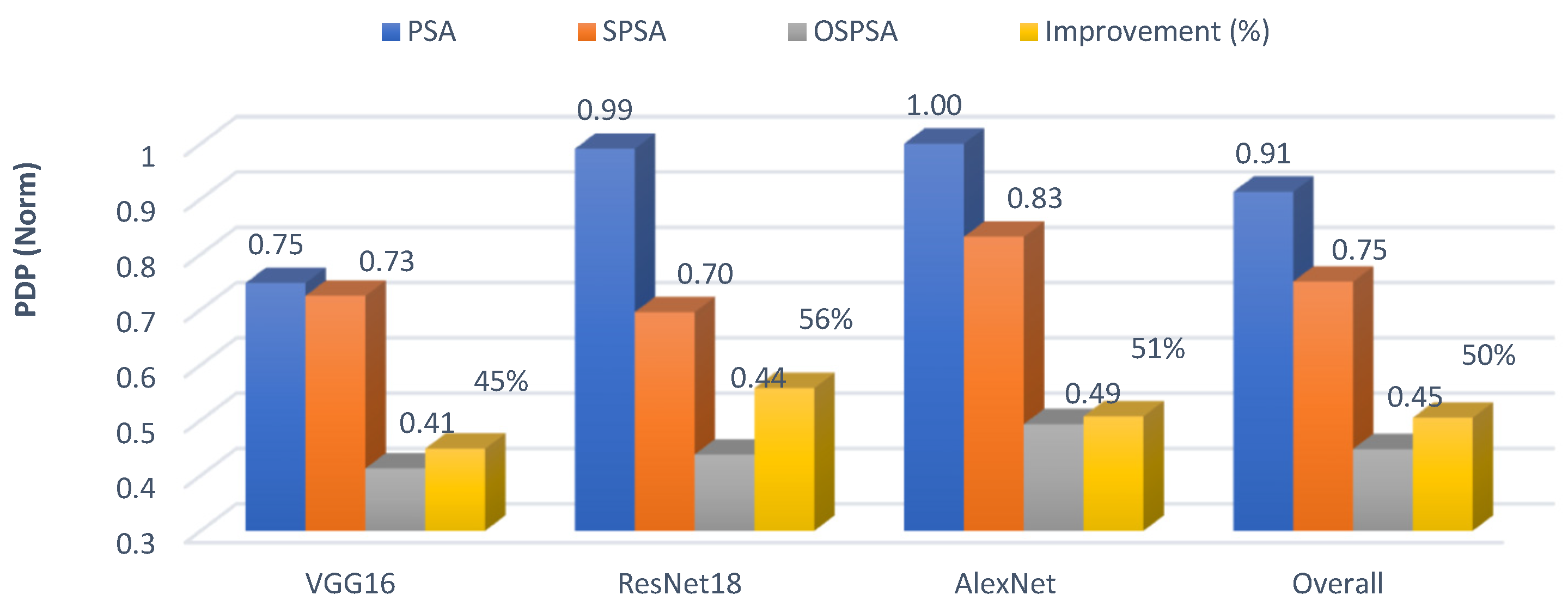
6.1. Computation Pruning by Zero Skipping
6.2. Energy Efficiency Improvement
7. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Chen, Y.-H.; Emer, J.; Sze, V. Eyeriss: A spatial architecture for energy-efficient dataflow for convolutional neural networks. ACM SIGARCH Comput. Archit. News 2016, 44, 367–379. [Google Scholar] [CrossRef]
- Villa, O.; Johnson, D.R.; Oconnor, M.; Bolotin, E.; Nellans, D.; Luitjens, J.; Sakharnykh, N.; Wang, P.; Micikevicius, P.; Scudiero, A.; et al. Scaling the power wall: A path to exascale. In Proceedings of the SC’14: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 16–21 November 2014; pp. 830–841. [Google Scholar]
- Horowitz, M. Computing’s energy problem (and what we can do about it). In Proceedings of the 2014 IEEE International Solid-state Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 9–13 February 2014; pp. 10–14. [Google Scholar]
- Chen, Y.; Xie, Y.; Song, L.; Chen, F.; Tang, T. A Survey of Accelerator Architectures for Deep Neural Networks. Engineering 2020, 6, 264–274. [Google Scholar] [CrossRef]
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Bates, S.; Bhatia, S.; Boden, N.; Borchers, A.; et al. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the 44th Annual International Symposium on Computer Architecture, Toronto, ON, Canada, 24–28 June 2017; pp. 1–12. [Google Scholar]
- Park, J.S.; Jang, J.W.; Lee, H.; Lee, D.; Lee, S.; Jung, H.; Lee, S.; Kwon, S.; Jeong, K.; Song, J.H.; et al. 9.5 A 6K-MAC feature-map-sparsity-aware neural processing unit in 5nm flagship mobile SoC. In Proceedings of the 2021 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 13–22 February 2021; pp. 152–154. [Google Scholar]
- Zervakis, G.; Anagnostopoulos, I.; Salamin, S.; Spantidi, O.; Roman-Ballesteros, I.; Henkel, J.; Amrouch, H. Thermal-aware design for approximate dnn accelerators. IEEE Trans. Comput. 2022, 71, 2687–2697. [Google Scholar] [CrossRef]
- Moghaddasi, I.; Gorgin, S.; Lee, J.-A. Dependable DNN Accelerator for Safety-critical Systems: A Review on the Aging Perspective. IEEE Access 2023, 11, 89803–89834. [Google Scholar] [CrossRef]
- Kim, N.; Park, H.; Lee, D.; Kang, S.; Lee, J.; Choi, K. ComPreEND: Computation pruning through predictive early negative detection for ReLU in a deep neural network accelerator. IEEE Trans. Comput. 2021, 71, 1537–1550. [Google Scholar] [CrossRef]
- Judd, P.; Albericio, J.; Hetherington, T.; Aamodt, T.M.; Moshovos, A. Stripes: Bit-serial deep neural network computing. In Proceedings of the 2016 49th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Taipei, Taiwan, 15–19 October 2016; pp. 1–12. [Google Scholar]
- Lee, J.; Kim, C.; Kang, S.; Shin, D.; Kim, S.; Yoo, H.-J. UNPU: An energy-efficient deep neural network accelerator with fully variable weight bit precision. IEEE J. Solid-State Circuits 2018, 54, 173–185. [Google Scholar] [CrossRef]
- Houshmand, P.; Sarda, G.M.; Jain, V.; Ueyoshi, K.; Papistas, I.A.; Shi, M.; Zheng, Q.; Bhattacharjee, D.; Mallik, A.; Debacker, P.; et al. Diana: An end-to-end hybrid digital and analog neural network soc for the edge. IEEE J. Solid-State Circuits 2022, 58, 203–215. [Google Scholar] [CrossRef]
- Eckert, C.; Wang, X.; Wang, J.; Subramaniyan, A.; Iyer, R.; Sylvester, D.; Blaaauw, D.; Das, R. Neural cache: Bit-serial in-cache acceleration of deep neural networks. In Proceedings of the 2018 ACM/IEEE 45Th Annual International Symposium on Computer Architecture (ISCA), Los Angeles, CA, USA, 1–6 June 2018; pp. 383–396. [Google Scholar]
- Wang, X.; Yu, J.; Augustine, C.; Iyer, R.; Das, R. Bit prudent in-cache acceleration of deep convolutional neural networks. In Proceedings of the 2019 IEEE International Symposium on High Performance Computer Architecture (HPCA), Washington, DC, USA, 16–20 February 2019; pp. 81–93. [Google Scholar]
- Kung, H.-T. Why systolic architectures? Computer 1982, 15, 37–46. [Google Scholar] [CrossRef]
- Wang, Y.E.; Wei, G.-Y.; Brooks, D. Benchmarking TPU, GPU, and CPU platforms for deep learning. arXiv 2019, arXiv:1907.10701. [Google Scholar]
- Xu, R.; Ma, S.; Guo, Y.; Li, D. A Survey of Design and Optimization for Systolic Array-Based DNN Accelerators. ACM Comput. Surv. 2023, 56, 1–37. [Google Scholar] [CrossRef]
- Samajdar, A.; Joseph, J.M.; Zhu, Y.; Whatmough, P.; Mattina, M.; Krishna, T. A systematic methodology for characterizing scalability of dnn accelerators using scale-sim. In Proceedings of the 2020 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), Boston, MA, USA, 23–25 August 2020; pp. 58–68. [Google Scholar]
- Ardakani, A.; Condo, C.; Ahmadi, M.; Gross, W.J. An architecture to accelerate convolution in deep neural networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 65, 1349–1362. [Google Scholar] [CrossRef]
- Lu, L.; Guan, N.; Wang, Y.; Jia, L.; Luo, Z.; Yin, J.; Cong, J.; Liang, Y. Tenet: A framework for modeling tensor dataflow based on relation-centric notation. In Proceedings of the 2021 ACM/IEEE 48th Annual International Symposium on Computer Architecture (ISCA), Valencia, Spain, 14–18 June 2021; pp. 720–733. [Google Scholar]
- Chen, Y.-H. Architecture Design for Highly Flexible and Energy-Efficient Deep Neural Network Accelerators. Doctoral Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 2018. [Google Scholar]
- Albericio, J.; Judd, P.; Hetherington, T.; Aamodt, T.; Jerger, N.E.; Moshovos, A. Cnvlutin: Ineffectual-neuron-free deep neural network computing. ACM SIGARCH Comput. Archit. News 2016, 44, 1–13. [Google Scholar] [CrossRef]
- Ayachi, R.; Said, Y.; Ben Abdelali, A. Optimizing Neural Networks for Efficient FPGA Implementation: A Survey. Arch. Comput. Methods Eng. 2021, 28, 4537–4547. [Google Scholar] [CrossRef]
- Lu, H.; Chang, L.; Li, C.; Zhu, Z.; Lu, S.; Liu, Y.; Zhang, M. Distilling bit-level sparsity parallelism for general purpose deep learning acceleration. In Proceedings of the MICRO-54: 54th Annual IEEE/ACM International Symposium on Microarchitecture, Virtual, 18–22 October 2021; pp. 963–976. [Google Scholar]
- Kim, S.; Lee, J.; Kang, S.; Han, D.; Jo, W.; Yoo, H.-J. Tsunami: Triple sparsity-aware ultra energy-efficient neural network training accelerator with multi-modal iterative pruning. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 1494–1506. [Google Scholar] [CrossRef]
- Mao, W.; Wang, M.; Xie, X.; Wu, X.; Wang, Z. Hardware Accelerator Design for Sparse DNN Inference and Training: A Tutorial. IEEE Trans. Circuits Syst. II Express Briefs 2023, 71, 1708–1714. [Google Scholar] [CrossRef]
- Xu, R.; Ma, S.; Wang, Y.; Guo, Y.; Li, D.; Qiao, Y. Heterogeneous systolic array architecture for compact cnns hardware accelerators. IEEE Trans. Parallel Distrib. Syst. 2021, 33, 2860–2871. [Google Scholar]
- Spantidi, O.; Zervakis, G.; Alsalamin, S.; Roman-Ballesteros, I.; Henkel, J.; Amrouch, H.; Anagnostopoulos, I. Targeting dnn inference via efficient utilization of heterogeneous precision dnn accelerators. IEEE Trans. Emerg. Top. Comput. 2022, 11, 112–125. [Google Scholar] [CrossRef]
- Dai, L.; Cheng, Q.; Wang, Y.; Huang, G.; Zhou, J.; Li, K.; Mao, W.; Yu, H. An energy-efficient bit-split-and-combination systolic accelerator for nas-based multi-precision convolution neural networks. In Proceedings of the 2022 27th Asia and South Pacific Design Automation Conference (ASP-DAC), Taipei, Taiwan, 17–20 January 2022; pp. 448–453. [Google Scholar]
- Sharma, H.; Park, J.; Suda, N.; Lai, L.; Chau, B.; Kim, J.K.; Chandra, V.; Esmaeilzadeh, H. Bit fusion: Bit-level dynamically composable architecture for accelerating deep neural network. In Proceedings of the 2018 ACM/IEEE 45th Annual International Symposium on Computer Architecture (ISCA), Los Angeles, CA, USA, 1–6 June 2018; pp. 764–775. [Google Scholar]
- Sharify, S.; Lascorz, A.D.; Siu, K.; Judd, P.; Moshovos, A. Loom: Exploiting weight and activation precisions to accelerate convolutional neural networks. In Proceedings of the 55th Annual Design Automation Conference, San Francisco, CA, USA, 24–28 June 2018; pp. 1–6. [Google Scholar]
- Chhajed, H.; Raut, G.; Dhakad, N.; Vishwakarma, S.; Vishvakarma, S.K. Bitmac: Bit-serial computation-based efficient multiply-accumulate unit for dnn accelerator. Circuits Syst. Signal Process. 2022, 41, 2045–2060. [Google Scholar] [CrossRef]

| Feature | PSA (16 × 16) | SPSA (16 × 16) | Improvement | OSPSA (2 × 16) | Improvement |
|---|---|---|---|---|---|
| Area | 243,624 | 63,475 | +74% | 37,401 | +84% |
| Leakage Power | 1.456 mW | 0.504 mW | +65% | 0.299 mW | +79% |
| Dynamic Power | 17.88 mW | 4.42 mW | +72% | 2.44 mW | +88% |
| Latency (Cycle Time) | 2.30 ns | 1.00 ns | +56% | 1.38 ns | +40% |
| Max Frequency | 434 MHz | 1000 MHz | +130% | 724 MHz | +67% |
| Max Performance | 111 GMac/s | 32.0 GMac/s | −71% | 23.2 GMac/s | −0.79% |
| Max Perf./Area (PPA) | 456 × 103 | 504 × 103 | +10% | 619 × 103 | +35% |
| Max Perf./Watt (PPW) | 5.74 × 1012 | 6.50 × 1012 | +13% | 8.47 × 1012 | +47% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moghaddasi, I.; Nam, B.-G. Enhancing Computation-Efficiency of Deep Neural Network Processing on Edge Devices through Serial/Parallel Systolic Computing. Mach. Learn. Knowl. Extr. 2024, 6, 1484-1493. https://doi.org/10.3390/make6030070
Moghaddasi I, Nam B-G. Enhancing Computation-Efficiency of Deep Neural Network Processing on Edge Devices through Serial/Parallel Systolic Computing. Machine Learning and Knowledge Extraction. 2024; 6(3):1484-1493. https://doi.org/10.3390/make6030070
Chicago/Turabian StyleMoghaddasi, Iraj, and Byeong-Gyu Nam. 2024. "Enhancing Computation-Efficiency of Deep Neural Network Processing on Edge Devices through Serial/Parallel Systolic Computing" Machine Learning and Knowledge Extraction 6, no. 3: 1484-1493. https://doi.org/10.3390/make6030070
APA StyleMoghaddasi, I., & Nam, B.-G. (2024). Enhancing Computation-Efficiency of Deep Neural Network Processing on Edge Devices through Serial/Parallel Systolic Computing. Machine Learning and Knowledge Extraction, 6(3), 1484-1493. https://doi.org/10.3390/make6030070






