Abstract
Chest X-rays are vital in healthcare for diagnosing various conditions due to their low Radiation exposure, widespread availability, and rapid interpretation. However, their interpretation requires specialized expertise, which can limit scalability and delay diagnoses. This study addresses the multi-label classification challenge of chest X-ray images using the Chest X-ray14 dataset. We propose a novel online ensemble technique that differs from previous penalty-based methods by focusing on combining individual model losses with the overall ensemble loss. This approach enhances interaction and feedback among models during training. Our method integrates multiple pre-trained CNNs using strategies like combining CNNs through an additional fully connected layer and employing a label-weighted average for outputs. This multi-layered approach leverages the strengths of each model component, improving classification accuracy and generalization. By focusing solely on image data, our ensemble model addresses the challenges posed by null vectors and diverse pathologies, advancing computer-aided radiology.
1. Introduction
The essential role that chest X-rays play in healthcare is undeniable, serving as a part of the diagnostic process for a wide range of medical conditions. Their widespread use is supported by several advantages, including the low radiation exposure associated with them and their availability in healthcare settings from small clinics to large hospitals, along with the speed with which results can be obtained and understood [1]. These qualities make chest radiographs a tool for diagnosing various underlying diseases, such as lung infections, pneumonia, heart issues, and certain types of cancer.
Given their importance, it is expected that chest radiographs will continue to be among the most frequently requested diagnostic tests globally in the near future. Their effectiveness in providing information swiftly cannot be emphasized enough making them essential in emergency rooms, intensive care units, and regular health checkups.
Nevertheless, interpreting chest X-rays comes with a set of challenges. It requires a high level of knowledge and expertise typically possessed by trained radiologists. This need presents an obstacle, in healthcare systems, particularly in areas facing a shortage of qualified professionals [2]. Analyzing these images thoroughly for interpretation can limit scalability and can cause delays in diagnosing and treating patients.
The analysis of chest X-ray images is a complex challenge, as they often contain multiple pathologies, leading to a multi-label classification problem. For example, in the Chest X-ray14 dataset [3], each image is annotated with multiple pathologies, mainly involving the lungs and heart.
Several techniques have been developed over the years to help radiologists interpret more X-rays. In the early days of computer aid diagnostics (CAD), the image-processing expert and the radiologist had to collaborate closely. They used hand-coded features with decision trees or some basic machine learning algorithms [4,5,6,7]. Currently, the commonly used techniques are based on convolutional neural networks (CNN) in computer-aided radiology. They can handle image processing problems efficiently using the power of the graphical processing units (GPU). Most algorithms use one CNN architecture with some modifications to make it useable for multi-label classification. Some of them use attention techniques or long short-term memory to improve performance [3,8,9,10,11,12,13]. Some other works used additional data to increase efficiency, Yao et al. [14] used an additional bounding box about the region of interest, to focus on the problematic region. Baltruschat et al. [15] used patient information to achieve a better AUC score, they put patient age and gender next to the X-ray image information. In this research, we focus solely on the image data and do not use any additional external information.
We already have some publications in this field, our first result in this research area was to create a new architecture from scratch [16]. We already published our development that aimed to use transfer learning and modified head for improved performance [17].
These works, including ours, used one CNN model for the labeling of X-rays. However, many other real-world problems show us that the capacity of a single monolithic system may not be sufficient to solve them. Recognizing this, both natural and artificial systems are adopting approaches that rely on the cooperation of multiple, interconnected subsystems to reduce complexity and efficiently address complex challenges. The methodology for creating neural network ensembles varies.
The most commonly used approach is a two-step (offline) process, described by [18,19]. In the first step, individual networks are created and then combined in a particular way. This process is usually conducted by training each network separately and independently of the others. One major drawback of this procedure is that the possibility of interaction between the individual networks is lost during training. There is no possibility of feedback at these stages of ensemble formation, which means that there is no information flow between the formation of each network and its combination. This may result in some independently designed networks contributing less to the performance of the ensemble.
Online ensemble models are advanced machine learning approaches in which the members of each model are trained simultaneously in a single network, allowing interactions and feedback between members to directly influence each other [20,21,22]. This approach helps to exploit synergies between models, as members learn from each other during the learning process, which increases the prediction accuracy and overall model robustness.
Many articles show us that the ensemble model can be used in classification problems [23,24,25]. There are several techniques that exist to concatenate models into an ensemble from the basic arithmetic means, weighted means, voting to an advanced meta-learner [26,27,28,29,30,31]. Some other papers show the medical usage of CNN ensemble techniques [32,33,34]. There are some interesting offline methods, including those from Zhu et al. (2023), who demonstrated improvements using dynamic ensemble learning [35]; Xia et al. (2021), who highlighted the effectiveness of weighted classifier selection and stacked ensembles [36]; Yao et al. (2021), who introduced the MLCE method using label correlations effectively [37] and Nanni et al. (2021), who combined ensemble methods with deep learning techniques, showing significant performance boosts [38].
Providing diversity is critical to optimizing online ensemble models, which can significantly improve the model’s generalization ability. Some techniques can be applied to both online and offline ensemble models, including various pre-processing and data augmentation techniques [20] and using different architectures [39]. One of the most practical and efficient approaches to achieve this is to integrate diversity constraints directly into the loss function. In the literature, this approach first appeared in works that introduced correlation penalty factors into the loss function [40]. They aimed to encourage the gradient reduction algorithm to produce more diverse ensembles. In [21], a specially developed loss function for image metric learning with the goal of generating a diverse and low-correlation embedding was presented. Using cosine similarity as a penalty term also proved to be an effective method to increase the diversity of the model [20]. In our previous research, we have demonstrated the use of Pearson’s correlation for categorical image classification tasks to increase the diversity of ensemble learning [41]. These approaches allow us to exploit the potential of ensemble models better, increasing the efficiency of the learning process and the accuracy of the final model.
A special aspect of multi-label classification tasks is that it is possible to have cases where no label is associated with a given sample, resulting in a null vector. Another special case is when we have multiple ones (including all ones) in the vector referring to the presence of multiple (or all) labels. This situation is particularly challenging when applying penalty techniques to increase model diversity. Pearson correlation or cosine similarity, which are generally effective tools for measuring the relationships between models and their diversity, prove impractical when the complete missing of labels is also an option. In this case, these metrics may produce biased or irrelevant results, as they are not able to handle the special cases indicated by null vectors.
Taking into account the losses of each model allows the final decision mechanism to focus not only on the overall performance of the ensemble but also on assessing the contribution of each member. Therefore, if the ensemble is composed of significantly different architectures, the diversity of the model increases, as the ensemble does not only make an “averaged” decision but also takes into account the individual, potentially different signals of each member, which improves the robustness and adaptability of the model to diverse labeling situations.
In this research, we present a novel online ensemble technique for image classification tasks. The key to our innovation is a specially developed combined loss function, which uniquely computes the loss of the entire ensemble model and calculates the loss of the participating model components. We implemented this idea by merging several models and varying their concatenation to increase classification accuracy by applying a new network architecture. Finally, we created an ensemble of several pre-trained CNNs and applied different combination (fusion) methods (see Figure 1). For using ImageNet weights we have to use backbone-specific preprocessing, which we have implemented as a layer and put above the backbones separately (see Figure 1).
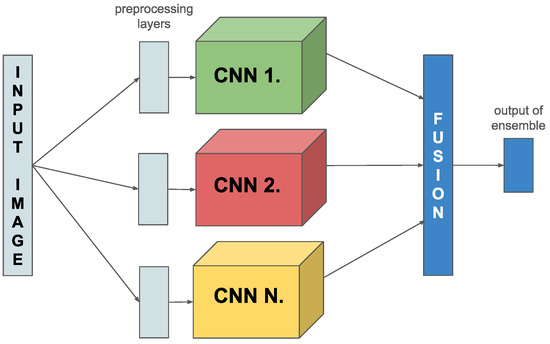
Figure 1.
Flowchart of the proposed algorithm.
One method is to connect the separate CNNs through an additional fully connected (FC) layer inserted after the last FC layer of the original CNNs. In addition, another strategy is used, where the last FC layers of the model components are combined by a label-weighted average, where the parameters of the average calculation can be learned. Finally, we adopt a method in which, although each member model has its own FC layer, these are used exclusively to compute the combined loss function. In contrast, for the linking we combine the feature extraction layers of the member components and place the new fully connected layer on top of them. This multi-layered approach allows us to exploit the strengths of each model component while improving classification performance and increasing the model’s generalization ability.
2. Materials and Methods
In this section, we first thoroughly examine sets of chest X-ray data that cover labels, emphasizing their crucial role in improving deep learning models for automatically labeling X-rays. These datasets, which come with annotations for chest conditions, are essential for training models to identify and label several pathologies precisely on X-ray images.
Next, we discuss the core structures that underpin our models and are vital for extracting features from the images. We talked about the selection of activation functions. The significance of choosing loss functions is also discussed, emphasizing their importance in tasks involving multi-label classification. Finally, we explore techniques that are a crucial aspect of our ensemble methodologies.
2.1. Datasets
In our research, we used two different multi-label X-ray databases. The first dataset, known as the Chest X-ray14 dataset [3] or the NIH Chest X-ray dataset, is a widely used asset in the field of medical imaging specifically for computer-aided diagnosis systems. Provided by the National Institutes of Health (NIH), this dataset contains more than 112,000 X-ray images from more than 30,000 patients. Each image is labeled with up to 14 thoracic pathologies, such as pneumonia, edema, and effusion.
This extensive collection of images and associated labels serves as a cornerstone for the development and benchmarking of machine-learning models, especially those aimed at detecting and classifying thoracic diseases. The Chest X-ray14 dataset has been instrumental in advancing the field of deep learning in medical imaging by providing a vast and varied data source for training models that can accurately identify and predict multiple pathologies from X-ray images. This chest radiograph dataset is widely used, as evidenced by the publications cited [3,8,9,10,11,12,13,14,15,42] in Section 1 are also used this dataset. We choose this set to make our result comparable with other state-of-the-art algorithms.
MIMIC-CXR [43] is another available dataset for chest radiographs. It was created to support and promote research in medical image analysis. This dataset was compiled by the Massachusetts Institute of Technology (MIT) in partnership with the Beth Israel Deaconess Medical Center as part of the Medical Information Mart for Intensive Care (MIMIC) initiative, which seeks to offer medical datasets to facilitate various biomedical studies. Access was obtained through PhysioNet [44]. We used JPG conversion for MIMIC images [45].
Chest X-ray14 and MIMIC-CXR datasets are two major sources of chest X-ray images, both widely used in machine learning, especially in image classification tasks. The Chest X-ray14 dataset contains 14 labels covering a wide range of chest diseases, while the MIMIC-CXR database contains 13. There is a large overlap between the datasets in terms of labels.
MIMIC-CXR contains more than three times as many images as Chest X-ray14, providing an excellent basis for demonstrating the effectiveness of transfer learning for X-ray images. Table 1 contains the common and dissimilar labels of the databases and also shows the number of occurrences of the labels. We put n.a. when the label does not exist in the dataset.

Table 1.
Overview of label counts in the MIMIC-CXR and Chest X-ray14 datasets.
2.2. Medical Background
Atelectasis is the absence of inflation (i.e., collapse) of part of the lung, resulting in reduced volume and increased opacity of the lung tissue on radiographs [46], see on Figure 2a). Cardiomegaly is the enlargement of the heart, whereby the transverse diameter of the cardiac silhouette is greater than or equal to 50% of the transverse diameter of the chest [47] (see Figure 2b,c). Consolation refers to the increased lung opacity on radiographs with various patterns, indicating that the lung tissue is filled with liquid, such as exudate, pus, water, or blood, instead of air [48] (see Figure 2b). Although pneumonia is the most common cause of consolidation, it is not the sole causative factor. Edema is another opacity of the lungs that may appear as ill-defined nodular opacities tending to confluence in alveolar edemas or present as peripheral lines in interstitial edema (see Figure 2c). In the pneumothorax, the radiograph shows a thin, sharply defined opaque (white) line (displaced visceral pleura) outlined by a lucent (dark) air-filled lung [49]. For a special case with no findings see Figure 2d.
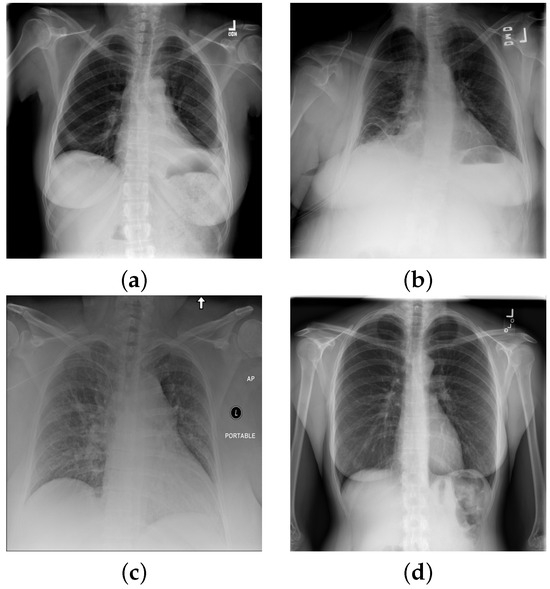
Figure 2.
Chest X-ray images with with distinct conditions: (a) atelectasis; (b) cardiomegaly; (c) cardiomegaly, consolidation, edema; (d) no finding.
2.3. Backbones of CNN
Over the past few years, convolutional neural networks have become the industry-leading technology for pattern recognition tasks in digital image processing, such as object detection, localization, segmentation, and classification. These networks are able to learn the parameters of convolutional filters and extract meaningful and higher-level features that can be used to discriminate between different categories of images. The training phase requires a large scale of computational power and thousands of manually labeled images. The proposed networks are general enough to be applied for different classification tasks with a low error margin. This need has recently led to the development of several new CNN architectures such as InceptionV3 [50], ResNet [51], DenseNet [52], MobileNet [53], RegNet [54] and Xception [55]. These are also available as pre-trained models, originally trained on the ImageNet dataset. These models can be used in the context of transfer learning, where weights and biases are used to fine-tune the models for our own data. If enough annotated images are available to create a model starting from scratch, we can randomly initialize the network parameters.
InceptionV3 [50] developed by Szegedy et al. represents a step in the realm of convolutional neural networks, introducing a refined structure that aims to improve image classification performance while keeping computational efficiency in check.
ResNet50V2 [51] improves the ResNet model by introducing activation residual units and adjusting the design of residual blocks to improve performance and stability.
DenseNet121 [52] is well known for its design which promotes the reuse of features by utilizing connected convolutional networks. This model combines features from layers within a block before passing them to the layers, ensuring smooth information flow.
MobileNetV2 [53], an addition to the MobileNets series, is designed to excel in mobile vision tasks by prioritizing efficiency. This method uses inverted residuals and linear bottlenecks to enhance the flow of information within the network while reducing the burden.
RegNet [54], a set of network structures introduced by Facebook AI, prioritizes simplicity and scalability in its design, presenting models that are fine-tuned for both accuracy and efficiency. As part of the RegNetX series, RegNetX 016 focuses on efficiency by utilizing grouped convolutions to find a harmony between requirements and performance.
The Xception [55] design transforms convolutional neural networks by introducing a new approach. It uses convolutions that separate the handling of cross-channel and spatial correlations. This architecture consists of 36 layers organized into 14 sections focusing on efficiency and performance by utilizing connections to address gradient vanishing issues.
2.4. Multi-Label Classification
In multi-label classification, the model simultaneously predicts multiple independent labels for a given input. This differs from traditional single-label classification, where each input belongs to exactly one class. In the context of the multi-label classification, we represent target labels with an N-dimensional vector , where N denotes the number of labels and denotes
We have to highlight some special cases: indicates that no one of the labels persists in the image; implies that at least one label persists in the image and means that all the labels persist in the image.
Two key components could be used to solve multi-label classification problems: the sigmoid activation function and the binary cross-entropy loss function.
The sigmoid activation function is an ideal choice for multi-label classification because each output neuron has a label associated with it, and the sigmoid allows each neuron output to take a value between 0 and 1 independently. This means that the presence or absence of each label is treated as a separate, independent probability, which fits perfectly with the nature of multi-label classification.
The binary cross-entropy loss function (2) is also a critical component of multilabel classification tasks, as it allows the accuracy of the predictions of each label to be measured. This loss function measures for each label separately how accurate the model’s predictions are relative to the true labels, thus supporting model fine-tuning and improving overall classification performance.
In the Equation (2), symbolizes the true label (0 or 1) of the i-th label on the j-th image, while of i-th probability computed by i-th output neuron regarding the j-th image, N denotes the number of labels, S denotes the number of images.
In summary, combining the sigmoid activation function and the binary cross-entropy loss function enables efficient handling of multi-label classification tasks. This allows each label to be treated as an independent likelihood while optimizing the model performance on a label-by-label basis, thus increasing the accuracy and reliability of multi-label classification schemes.
2.5. Ensemble Networks
As we mentioned in the introduction we focus only on the online ensemble technique. In this paper, we used two different types of ensembles. Both types can consist of M different members. The first type is when all members have their own output layer. Individual predictions of these models are concatenated together, using one fully connected layer (or more) which is inserted to combine these predictions. This type is called class-level (see Figure 3a).
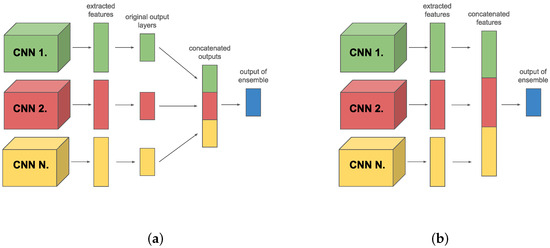
Figure 3.
Different types of ensemble: (a) class-level; (b) feature-level.
The second type is where only the features extracted by the backbones are concatenated, and these members do not have their own output layer. A fully connected layer is applied over the concatenated features, similar to the class-level ensemble. This approach allows directly using the extracted features to integrate and refine the predictions. This type is called a feature-level ensemble (see Figure 3b).
Both types of ensemble aim to exploit the diversity of information provided by different models, thus improving the accuracy of the predictions and the model’s generalization ability. The class-level ensemble exploits the diversity among model-specific decisions. In contrast, the feature-level ensemble focuses on the diversity of extracted features, providing a more robust decision mechanism in the final classification.
For the sake of completeness, we also used the weighted average of the output layers of the members as a reference. In this case, we do not use a FC for a concatenation. We used a custom layer that calculated the average of the output labels with trainable weights:
In (3), symbolizes the weighted averaged prediction and M represents the total number of members within the ensemble. The refers to the prediction output of the k-th model, while is the weight assigned to the k-th member. In the multi-label case, and are vectors containing the probabilities of the labels.
Using these weights allows us to dynamically adjust of each model’s influence on the final prediction, acknowledging that some models may contribute more reliably or relevantly to certain predictions than others. This flexibility is a crucial advantage of the weighted-mean approach over the simple mean, enabling a more targeted exploitation of the strengths of individual models.
Determining the optimal set of weights, is a critical aspect of the effective use of the weighted mean strategy. In our case, the weights are trainable and these weights were trained automatically from the data; however, it is possible to adjust weights manually.
Proposed Ensemble Loss
In multi-label classification, samples may have no labels, resulting in null vectors. Common penalty terms used in categorical classification do not perform well in this context. Currently, we focused on combined loss, this approach considers both the ensemble’s overall performance and each model’s contribution, enhancing adaptability and robustness. This diversity is crucial, especially when using models with different architectures, as it improves classification accuracy by addressing the problem from multiple perspectives.
In this way, our model can integrate the information provided by each component more efficiently, optimizing the classification performance. In particular, we expect our solution to yield significant accuracy improvements in multi-label image classification tasks. Thus, our approach not only improves the efficiency of the learning process but also significantly enhances the generalization capability of our model, ensuring that it is more adaptable to various challenges.
The deep ensemble model presented in this paper has trainable head layers, and is a structure with a high level of complexity and many parameters, making it a particularly challenging structure for effective learning. In the case of the online ensemble method, we could optimize these parameters simultaneously in a coordinated learning step that aims to improve the performance of the ensemble model. Our method combines the losses of the individual members of the model with the loss computed on the output layer of the ensemble. This strategy allows us to fine-tune the contribution of each model component in the ensemble decision-making process, thus increasing learning efficiency and improving classification accuracy. Thus, our approach not only opens up new dimensions in deep learning model learning but also improves the results achievable in multi-label image classification tasks, exploiting the hidden potential of ensemble models. Our proposed composite loss function is calculated as:
where M denotes the number of members networks, denotes the multi-label binary cross-entropy loss function (2), y means the true label of the image, denotes the output of the ensemble, and denotes the output of the k-th member and finally controls the members’ loss. weighting provides a tool to manage the influence of individual saturations of the different model components on the ensemble.
In the class-level case, we used the output of members for calculating members’ loss. However, in the case of the feature-level ensemble, we had to modify the model, and add FC layers as output layers for calculating loss (see Figure 4). In that case, FC layers play a critical role beyond traditional use; they are explicitly employed to calculate the loss, as detailed in Equation (4). This setup allows for deeper integration of member model strengths, optimizing the ensemble’s overall predictive capability by leveraging the specialized loss calculation to enhance learning efficiency and model accuracy.
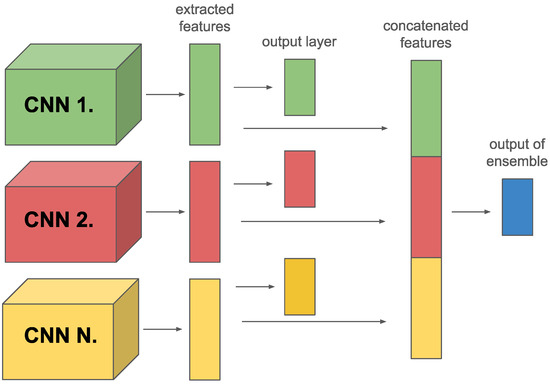
Figure 4.
Feature-level ensemble with extended output layers for calculating loss.
3. Results
In the results section, we discuss the results and our comprehensive data preparation process, which includes extensive image augmentation techniques to enhance model robustness. We provide an in-depth analysis of individual CNN backbone performances, laying the groundwork for understanding the comparative effectiveness of different architectures. Based on this evaluation, we introduce our proposed ensemble configurations, carefully considering memory usage and the number of parameters to optimize computational efficiency. Furthermore, we present the results of the class-level, feature-level and weighted average ensembles that incorporate heads, demonstrating the impact of these configurations on model performance. Lastly, we highlight the significant improvements achieved by applying transfer learning from the MIMIC-CXR dataset, underscoring the value of pre-trained models in enhancing diagnostic accuracy in medical imaging.
3.1. Preparation of the Data
To use the backbone models with ImageNet pre-trained weights, it was necessary to convert the images to a three-channel format with dimensions of . Initially, the grayscale images were expanded to three channels. This was followed by resizing all images to dimensions (we use cropping later), down from for Chest X-ray14 images. During the training phase, we used random cropping to achieve dimensions , while for validation and test sets, center cropping was used. Image augmentation techniques included random flips and rotations within a range of to radians to improve model robustness and generalization. For using ImageNet pre-trained weights, we had to utilize a specific prepocessing task to rescale and normalize with ImageNet means. We reimplemented this model-specific preprocessing as layers and built it into a model.
3.2. Evaluation of the Different Members CNNs
We created a comprehensive overview performance of DenseNet121, InceptionV3, MobileNetV2, RegNetX016, ResNet50V2 and Xception. All evaluation was made in 25% of the Chest X-ray15 dataset, preserving the original distribution of the labels as much as possible. We used a five-fold cross-validation, to show the mean of the values of the AUC on Table 2. These measurements were performed with 32 batch sizes, 30 epochs, and two optimizer configurations. The first optimization configuration is Adam [56] with a learning rate of 0.001 and and , the second is a stochastic gradient descent [57] (hereafter, we refer as SGD) with and a learning rate of 0.01. We saw that all models have stable performance (see Table 2) on SGD, so the two created ensembles employ SGD as its optimizer learning rate at and momentum at 0. Specifically, the standard deviations for SGD range from 0.0023 to 0.0084, whereas for Adam, they range from 0.0143 to 0.0304. Lower standard deviation indicates that the performance of SGD is more stable and less variable across different runs, so we use only SGD further.

Table 2.
Finding members of proposed ensembles.
3.3. Evaluation of the Ensembles
After the comprehensive evaluation, we propose two distinct ensemble architectures, adhering to a critical limitation: the overall memory consumption of the ensemble must not exceed 14 GB, we calculated the memory usage with 32 batch sizes and image size. Table 3 illustrates a comparative overview of these ensembles, showing the total number of parameters and memory footprint for each configuration. In the first ensemble, some models rely on special connections between layers (DenseNet121), or work at different scales simultaneously (InceptionV3), or models that help you build deeper networks without running into problems (ResNet50V2). DenseNet121 is special in that each layer is connected to the ones before, so it makes better use of the data and can run with fewer parameters. InceptionV3 works in multiple sizes, so it can more easily recognize things of different sizes. ResNet50V2 helps to make networks deeper without losing control during learning.

Table 3.
Memory usage and number of trainable parameters of the members and the ensembles.
In the second ensemble, we focused on the systematic design (RegNetX016) worked with small computational power (MobileNetV2), and used new methods of convolutions (Xception). RegNetX016 is a network designed to work efficiently and works well with a variety of tasks. MobileNetV2 also uses special solutions to make it work well on mobile devices, while Xception innovates by handling spatial and channel information separately, improving performance. This split ensures that the memory usage remains below 14 GB.
Thus, these two ensembles use different architectures to solve multi-label classification problems, and we believe that their diversity will improve the performance of ensemble models.
As a baseline evaluation, we have implemented and according to Table 3. In both ensembles, the members are connected alongside a feature-level or class-level or a simple weighted average methodology (described in Section 2.5).
We also used a five-fold cross-validation. The result is shown in Table 4. These configurations are performed on the Chest X-ray14 dataset, using multi-label binary cross-entropy (2).

Table 4.
Results of and without proposed loss.
As a next step, we will investigate how our proposed loss function can improve the performance of these ensembles (see Section “Proposed Ensemble Loss”), particularly by examining the role of the parameter . This parameter affects the weight of the individual losses of each model in the final loss calculation. By increasing the value of , we wanted to test how much the losses contributed by each model dominate the total loss and how this affects the performance of the ensemble model. Our results show in Table 5 that when we moderately increased the value of from to and then to , the performance of the model improved significantly compared to the baseline version without combined loss.

Table 5.
Results of and with different -s.
However, when the value increased to an unrealistically high value of or , we observed a decrease in the model’s performance compared to the conventional one. Careful adjustment of the parameter, emphasizing individual model losses can improve the generalizability and AUC by leveraging each component’s unique characteristics. Interestingly, class-wise ensembles do not perform better with our proposed loss, so our current focus is solely on optimizing outcomes. Fine-tuning allows precise control over each model’s contribution, creating a balanced and efficient classification scheme. This approach highlights the importance of individual model losses in enhancing the overall performance of multi-label ensemble models.
This phenomenon suggests that with excessively high values, the model focuses too much on the individual losses of each model, which may limit the learning process and negatively affect the model’s adaptability.
3.4. Using the Power of the Transfer Learning
In our previous work [17], we focused on training the backbone architectures using the MIMIC-CXR dataset, followed by adjustments to fully connected layers. The current study advances this approach by training each ensemble member independently on the MIMIC-CXR dataset, employing the designated optimizers and ensemble configurations as previously determined. For this training phase, we adopted a batch size of 256 and a total of 50 epochs, utilizing a dataset comprising 250,000 frontal chest X-ray images to develop pre-trained models. We used an SGD optimizer with a learning rate of and momentum of , trained on 50 epochs, chose the best AUC on a valid dataset, and ran it on the official test set. For these ensembles, we used the modified loss function with at and we chose a weighted average head. We used the official Chest X-ray14 split. The results are shown in Table 6, we used bold to mark the better result.

Table 6.
Evaluation the best lamba on Chest X-ray14 using pre-learned weights from MIMIC-CXR.
3.5. Compare Our Result with the State-of-Arts Algorithms
Based on the results of the evaluation and tests carried out in our research (see Table 7), our first ensemble model () outperformed state-of-the-art models. On the contrary, our second ensemble (), although it did not reach the outstanding performance of the first model, performed better than many other systems. These results represent a significant milestone in our approach to multi-label classification tasks, particularly in the area of deep learning and ensemble models.

Table 7.
Comparison of our results with state-of-art results.
The success of highlights that our innovative methodology, in particular by combining different models and using a specially developed loss function, opens new avenues to improve the efficiency of image classification tasks. This encourages us to further explore the potential of ensemble models, especially in the multi-label context. Yao et al. [14] had AUC as the same performance as our but used a bounding box to focus the classifier, Kufel et al. [42] produced a better result () than our ensemble but used a non-official data split, so these results are not comparable with our results.
The results of , while not reaching the outstanding performance of the first group, confirm the view that the use of ensemble models can represent a significant improvement over many current models. This suggests that even less optimal configurations can achieve competitive results, especially when considering the complexity and challenges of multi-label problems.
4. Conclusions
Seeing the results of our ensemble models, we can conclude that significant improvements can be achieved even for multi-label problems. We, therefore, propose further studies, including the investigation of a broader range of models as well as the configuration of even more models up to 4-6-8. Furthermore, we recommend digging deeper into the ensemble methods, including new loss functions and their impact on model performance. By taking an even broader view of model interactions and the diversity that comes from this combined approach, we hypothesize an even greater performance in multi-label image classification. Moreover, integrating additional models offers a richer field for exploring their joint dynamics and optimizing their joint performance. Our research highlights the significant promise of multi-label ensemble models in addressing image classification challenges and presents new avenues for future research. These results reinforce our commitment to devoting more time and resources to this multi-label field due to its immense potential.
Author Contributions
Conceptualization, T.K., G.T., M.P. and B.H.; data curation, T.K.; formal analysis, T.K. and B.H.; methodology, T.K. and B.H.; software, T.K.; supervision, B.H.; validation, G.T., M.P. and B.H.; visualization, T.K.; writing—original draft, T.K., G.T., M.P. and B.H.; writing—review and editing, T.K., G.T., M.P. and B.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the project TKP2021-NKTA-34, implemented with the support provided by the National Research, Development, and Innovation Fund of Hungary under the TKP2021-NKTA funding scheme.
Data Availability Statement
Chest X-ray14: Publicly available dataset was analyzed in this study. This data can be found here: https://nihcc.app.box.com/v/ChestXray-NIHCC/file/220660789610 (accessed on 2 May 2023). MIMIC-CXR-JPG: Restrictions apply to the availability of these data. Data were obtained from PhysioNet and are available https://physionet.org/content/mimic-cxr/2.0.0/ with the permission of PhysioNet (accessed on 15 January 2020).
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Rosenkrantz, A.B.; Hughes, D.R.; Duszak, R., Jr. The U.S. Radiologist Workforce: An Analysis of Temporal and Geographic Variation by Using Large National Datasets. Radiology 2016, 279, 175–184. [Google Scholar] [CrossRef] [PubMed]
- Ali, F.; Harrington, S.; Kennedy, S.; Hussain, S. Diagnostic radiology in Liberia: A country report. J. Glob. Radiol. 2015, 1, 6. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Y.; Lu, L.; Lu, Z.; Bagheri, M.; Summers, R.M. Chestx-ray8: Hospital-scale chest X-ray database and benchmarks on weakly-supervised classification and localization of common thorax diseases. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 3462–3471. [Google Scholar]
- Kruger, R.P.; Townes, J.R.; Hall, D.L.; Dwyer, S.J.; Lodwick, G.S. Automated Radiographic Diagnosis via Feature Extraction and Classification of Cardiac Size and Shape Descriptors. IEEE Trans. Biomed. Eng. 1972, BME-19, 174–186. [Google Scholar] [CrossRef]
- Lodwick, G.S.; Keats, T.E.; Dorst, J.P. The Coding of Roentgen Images for Computer Analysis as Applied to Lung Cancer. Radiology 1963, 81, 185–200. [Google Scholar] [CrossRef] [PubMed]
- Meyers, P.H.; Nice, C.M.; Becker, H.C.; Nettleton, W.J.; Sweeney, J.W.; Meckstroth, G.R. Automated Computer Analysis of Radiographic Images. Radiology 1964, 83, 1029–1034. [Google Scholar] [CrossRef] [PubMed]
- de Bruijne, M. Machine learning approaches in medical image analysis: From detection to diagnosis. Med. Image Anal. 2016, 476, 94–97. [Google Scholar] [CrossRef] [PubMed]
- Irvin, J.; Rajpurkar, P.; Ko, M.; Yu, Y.; Ciurea-Ilcus, S.; Chute, C.; Marklund, H.; Haghgoo, B.; Ball, R.; Shpanskaya, K.; et al. CheXpert: A Large Chest Radiograph Dataset with Uncertainty Labels and Expert Comparison. In Proceedings of the AAAI Conference on Artificial Intelligence 2019, Honolulu, HI, USA, 27 January–1 February 2019; pp. 590–597. [Google Scholar]
- Wang, X.; Peng, Y.; Lu, L.; Lu, Z.; Summers, R.M. TieNet: Text-Image Embedding Network for Common Thorax Disease Classification and Reporting in Chest X-Rays. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2018), Salt Lake City, UT, USA, 18–22 June 2018; pp. 9049–9058. [Google Scholar]
- Tang, Y.; Wang, X.; Harrison, A.P.; Lu, L.; Xiao, J.; Summers, R.M. Attention-guided curriculum learning for weakly supervised classification and localization of thoracic diseases on chest radiographs. In Proceedings of the International Workshop on Machine Learning in Medical Imaging (MLMI 2018), Granada, Spain, 16 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; Volume 1, pp. 249–258. [Google Scholar]
- Yao, L.; Prosky, J.; Poblenz, E.; Covington, B.; Lyman, K. Weakly supervised medical diagnosis and localization from multiple resolutions. arXiv 2018, arXiv:1803.07703. [Google Scholar]
- Guan, Q.; Huang, Y. Multi-label chest X-ray image classification via category-wise residual attention learning. Pattern Recognit. Lett. 2020, 130, 259–266. [Google Scholar] [CrossRef]
- Wang, H.; Wang, S.; Qin, Z.; Zhang, Y.; Li, R.; Xia, Y. Triple attention learning for classification of 14 thoracic diseases using chest radiography. Med. Image Anal. 2021, 67, 101846. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.; Yao, J.; Li, R.; Xu, Z.; Huang, J. Weakly Supervised Deep Learning for Thoracic Disease Classification and Localization on Chest X-rays. In Proceedings of the 2018 ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics, Washington DC, USA, 29 August–1 September 2018; pp. 103–110. [Google Scholar] [CrossRef]
- Baltruschat, I.M.; Nickisch, H.; Grass, M.; Knopp, T.; Saalbach, A. Comparison of Deep Learning Approaches for Multi-Label Chest X-ray Classification. Sci. Rep. 2019, 9, 6381. [Google Scholar] [CrossRef]
- Katona, T.; Antal, B. Automated analysis of radiology images using Convolutional Neural Networks. In Proceedings of the 2019 11th International Symposium on Image and Signal Processing and Analysis (ISPA 2019), Dubrovnik, Croatia, 23–25 September 2019; pp. 89–92. [Google Scholar] [CrossRef]
- Katona, T.; Tóth, G.; Petró, M.; Harangi, B. Developing New Fully Connected Layers for Convolutional Neural Networks with Hyperparameter Optimization for Improved Multi-Label Image Classification. Mathematics 2024, 12, 806. [Google Scholar] [CrossRef]
- Sharkey, A.J.C. On combining artificial neural nets. Connect. Sci. 1996, 8, 299–314. [Google Scholar] [CrossRef]
- Sharkey, A.J.C.; Sharkey, N.E.; Gerecke, U.; Chandroth, G.O. The “Test and Select” Approach to Ensemble Combination. In Proceedings of the Multiple Classifier Systems. Multiple Classifier Systems 2000, Calgiari, Italy, 21–23 June 2000; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2000; Volume 1857. [Google Scholar] [CrossRef]
- Dvornik, N.; Mairal, J.; Schmid, C. Diversity with Cooperation: Ensemble Methods for Few-Shot Classification. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3722–3730. [Google Scholar] [CrossRef]
- Opitz, M.; Waltner, G.; Possegger, H.; Bischof, H. Deep Metric Learning with BIER: Boosting Independent Embeddings Robustly. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 276–290. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Shi, Z.; Cheng, M.M.; Liu, Y.; Bian, J.W.; Zhou, J.T.; Zheng, G.; Zeng, Z. Nonlinear Regression via Deep Negative Correlation Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 982–998. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Qi, S.; Monkam, P.; Li, C.; Yang, F.; Yao, Y.D.; Qian, W. Ensemble Learners of Multiple Deep CNNs for Pulmonary Nodules Classification Using CT Images. IEEE Access 2019, 7, 110358–110371. [Google Scholar] [CrossRef]
- Kuehlkamp, A.; Pinto, A.; Rocha, A.; Bowyer, K.W.; Czajka, A. Ensemble of Multi-View Learning Classifiers for Cross-Domain Iris Presentation Attack Detection. IEEE Trans. Inf. Forensics Secur. 2019, 14, 1419–1431. [Google Scholar] [CrossRef]
- Maarouf, A.A.; Hachouf, F. Transfer Learning-based Ensemble Deep Learning for Road Cracks Detection. In Proceedings of the 2022 International Conference on Advanced Aspects of Software Engineering (ICAASE), Constantine, Algeria, 17–18 September 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Khan, I.A.; Sajeeb, A.; Fattah, S.A. An Automatic Ocular Disease Detection Scheme from Enhanced Fundus Images Based on Ensembling Deep CNN Networks. In Proceedings of the 11th International Conference on Electrical and Computer Engineering, Dhaka, Bangladesh, 17–19 December 2020; pp. 491–494. [Google Scholar] [CrossRef]
- Li, W.; Liu, H.; Wang, Y.; Li, Z.; Jia, Y.; Gui, G. Deep Learning-Based Classification Methods for Remote Sensing Images in Urban Built-Up Areas. IEEE Access 2019, 7, 36274–36284. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Gu, Y.; He, X.; Ghamisi, P.; Jia, X. Deep Learning Ensemble for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1882–1897. [Google Scholar] [CrossRef]
- Minetto, R.; Pamplona Segundo, M.; Sarkar, S. Hydra: An Ensemble of Convolutional Neural Networks for Geospatial Land Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6530–6541. [Google Scholar] [CrossRef]
- Dong, S.; Feng, W.; Quan, Y.; Dauphin, G.; Gao, L.; Xing, M. Deep Ensemble CNN Method Based on Sample Expansion for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Alosaimi, N.; Alhichri, H. Fusion of CNN ensemble for Remote Sensing Scene Classification. In Proceedings of the 2020 3rd International Conference on Computer Applications Information Security (ICCAIS), Riyadh, Saudi Arabia, 19–21 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Elmannai, H.; Saleh, H.; Algarni, A.D.; Mashal, I.; Kwak, K.S.; El-Sappagh, S.; Mostafa, S. Diagnosis Myocardial Infarction Based on Stacking Ensemble of Convolutional Neural Network. Electronics 2022, 11, 3976. [Google Scholar] [CrossRef]
- Mansoor, R.; Shah, M.A.; Khattak, H.A.; Mussadiq, S.; Rauf, H.T.; Ameer, Z. Detection of Diseases in Pandemic: A Predictive Approach Using Stack Ensembling on Multi-Modal Imaging Data. Electronics 2022, 11, 3974. [Google Scholar] [CrossRef]
- Mahanty, C.; Kumar, R.; Asteris, P.G.; Gandomi, A.H. COVID-19 Patient Detection Based on Fusion of Transfer Learning and Fuzzy Ensemble Models Using CXR Images. Appl. Sci. 2021, 11, 11423. [Google Scholar] [CrossRef]
- Zhu, X.; Li, J.; Ren, J.; Wang, J.; Wang, G. Dynamic ensemble learning for multi-label classification. Inf. Sci. 2023, 623, 94–111. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, K.; Yang, Y. Multi-label classification with weighted classifier selection and stacked ensemble. Inf. Sci. 2021, 557, 421–442. [Google Scholar] [CrossRef]
- Yao, Y.; Li, Y.; Ye, Y.; Li, X. MLCE: A Multi-Label Crotch Ensemble Method for Multi-Label Classification. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2151006. [Google Scholar] [CrossRef]
- Nanni, L.; Trambaiollo, L.; Brahnam, S.; Guo, X.; Woolsey, C. Ensemble of Networks for Multilabel Classification. Signals 2022, 3, 911–931. [Google Scholar] [CrossRef]
- Harangi, B. Skin lesion classification with ensembles of deep convolutional neural networks. J. Biomed. Inform. 2018, 86, 25–32. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, X. Ensemble learning via negative correlation. Neural Netw. 1999, 12, 1399–1404. [Google Scholar] [CrossRef] [PubMed]
- Harangi, B.; Baran, A.; Beregi-Kovacs, M.; Hajdu, A. Composing Diverse Ensembles of Convolutional Neural Networks by Penalization. Mathematics 2023, 11, 4730. [Google Scholar] [CrossRef]
- Kufel, J.; Bielówka, M.; Rojek, M.; Mitręga, A.; Lewandowski, P.; Cebula, M.; Krawczyk, D.; Bielówka, M.; Kondoł, D.; Bargieł-Łączek, K.; et al. Multi-Label Classification of Chest X-ray Abnormalities Using Transfer Learning Techniques. J. Pers. Med. 2023, 13, 1426. [Google Scholar] [CrossRef]
- Johnson, A.E.W.; Pollard, T.J.; Berkowitz, S.J.; Greenbaum, N.R.; Lungren, M.P.; Deng, C.Y.; Mark, R.G.; Horng, S. MIMIC-CXR, a de-identified publicly available database of chest radiographs with free-text reports. Sci. Data 2019, 6, 317. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, E215–E220. [Google Scholar] [CrossRef] [PubMed]
- Johnson, A.E.W.; Pollard, T.J.; Greenbaum, N.R.; Lungren, M.P.; Deng, C.-y.; Peng, Y.; Lu, Z.; Mark, R.G.; Berkowitz, S.J.; Horng, S. MIMIC-CXR-JPG, a large publicly available database of labeled chest radiographs. arXiv 2019, arXiv:1901.07042. [Google Scholar]
- Peroni, D.G.; Boner, A.L. Atelectasis: Mechanisms, diagnosis and management. Paediatr. Respir. Rev. 2000, 1, 274–278. [Google Scholar] [CrossRef] [PubMed]
- Dähnert, W. Radiology Review Manual; Wolters Kluwer Health/Lippincott Williams Wilkins: Philadelphia, PA, USA, 2011. [Google Scholar]
- Franquet, T. Imaging of pneumonia: Trends and algorithms. Eur. Respir. J. 2001, 18, 196–208. [Google Scholar] [CrossRef] [PubMed]
- Kattea, M.O.; Lababede, O. Differentiating Pneumothorax from the Common Radiographic Skinfold Artifact. Ann. Am. Thorac. Soc. 2015, 12, 928–931. [Google Scholar] [CrossRef] [PubMed]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. arXiv 2015, arXiv:1512.00567. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. arXiv 2018, arXiv:1801.04381. [Google Scholar]
- Radosavovic, I.; Kosaraju, R.P.; Girshick, R.; He, K.; Dollár, P. Designing Network Design Spaces. arXiv 2020, arXiv:2003.13678. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. arXiv 2017, arXiv:1610.02357. [Google Scholar]
- Diederik, P.K.; Jimmy, B. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).