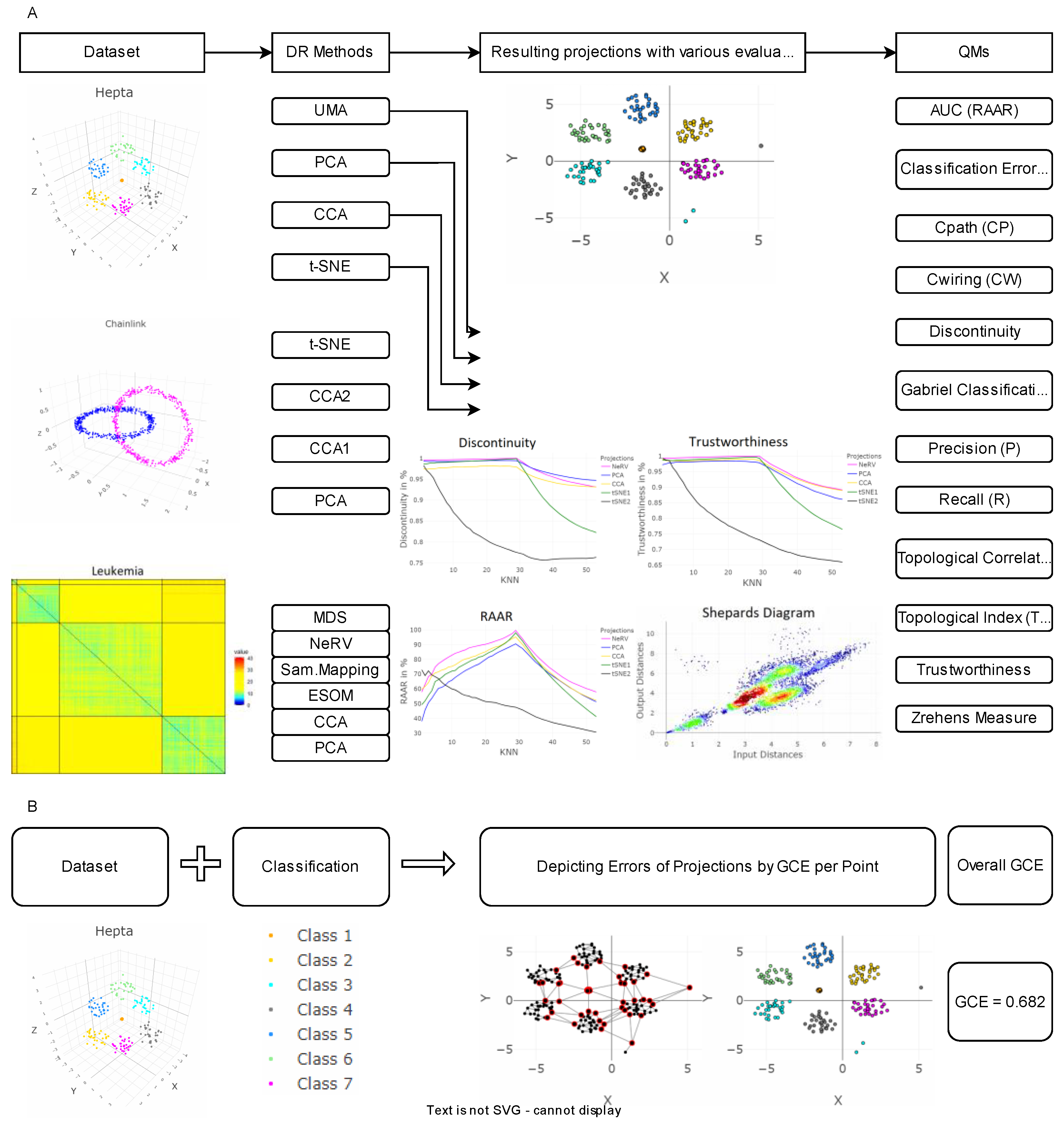
Analyzing Quality Measurements for Dimensionality Reduction
Abstract
:1. Introduction
- Theoretical comparison with prior works about quality measurement of DR methods reveals biases that can be aggregated into semantic classes.
- Hence, a new open-source available quality measure called Gabriel classification error (GCE) is proposed for investigating the quality of DR methods given prior knowledge about a dataset.
- The overall value yielded by GCE ranks projections more intuitively, choosing projections with a higher class-based structure separation above others.
- GCE can be visualized as an error per point, providing the user a focus on the critical areas of the projection of the DR method.
- Using three datasets, GCE is compared to prior works.
2. Generalization of Neighbourhoods
2.1. Graph Metrics
2.2. Structure Preservation
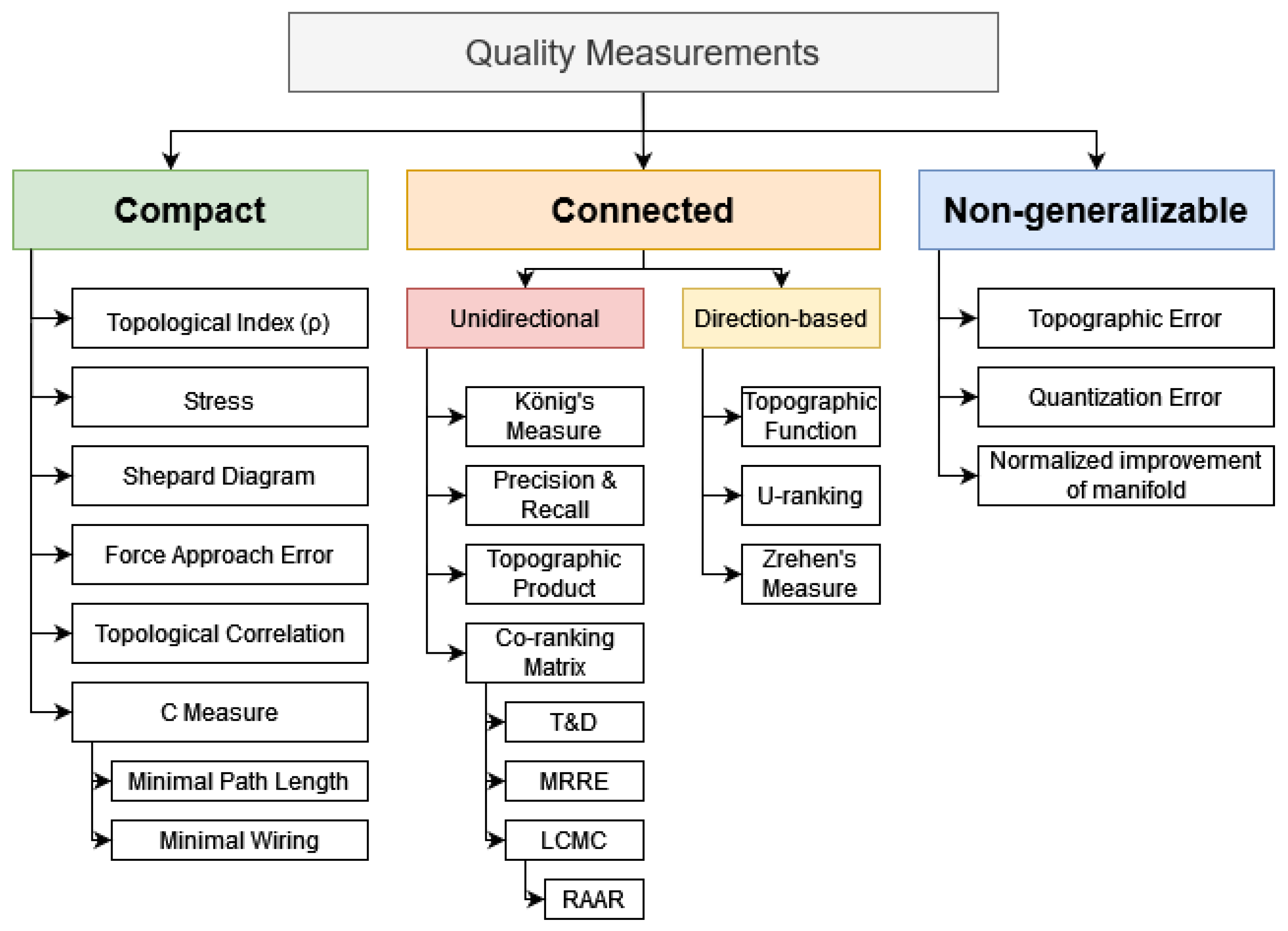
3. Quality Measurements (QMs)
3.1. Common Quality Measurements
3.1.1. Classification Error (CE)
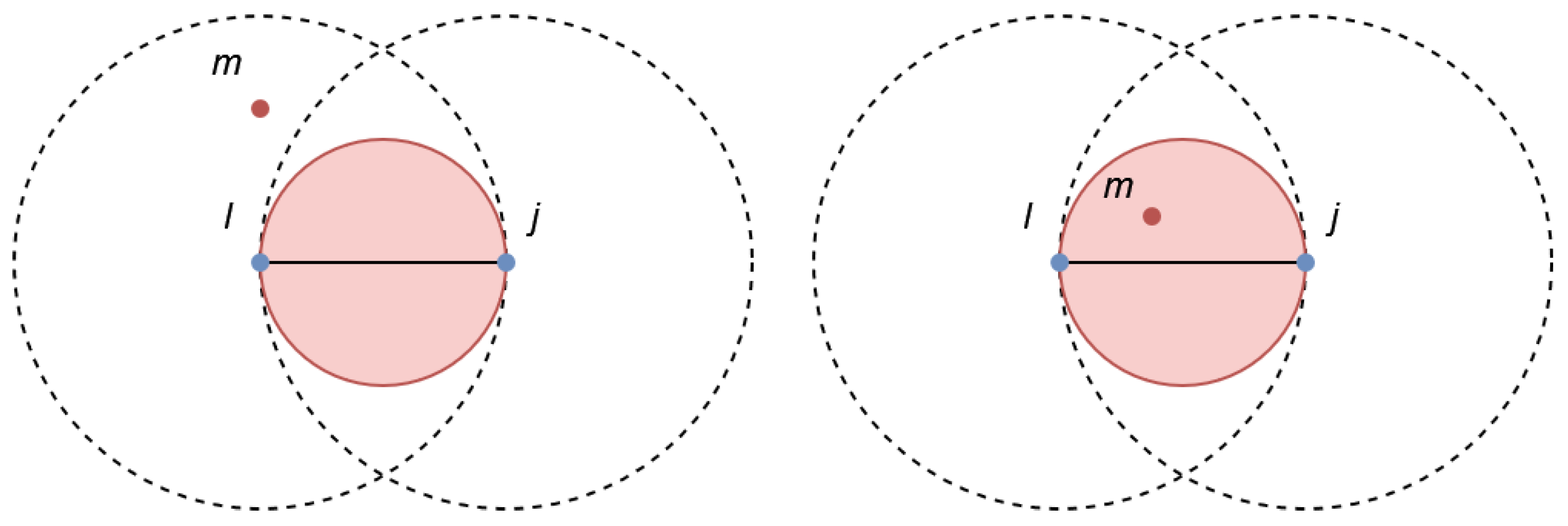
3.1.2. C Measure
3.1.3. Two Variants of the C Measure: Minimal Path Length and Minimal Wiring
3.1.4. Precision and Recall
3.1.5. Rescaled Average Agreement Rate (RAAR)
3.1.6. Stress and the Shepard Diagram
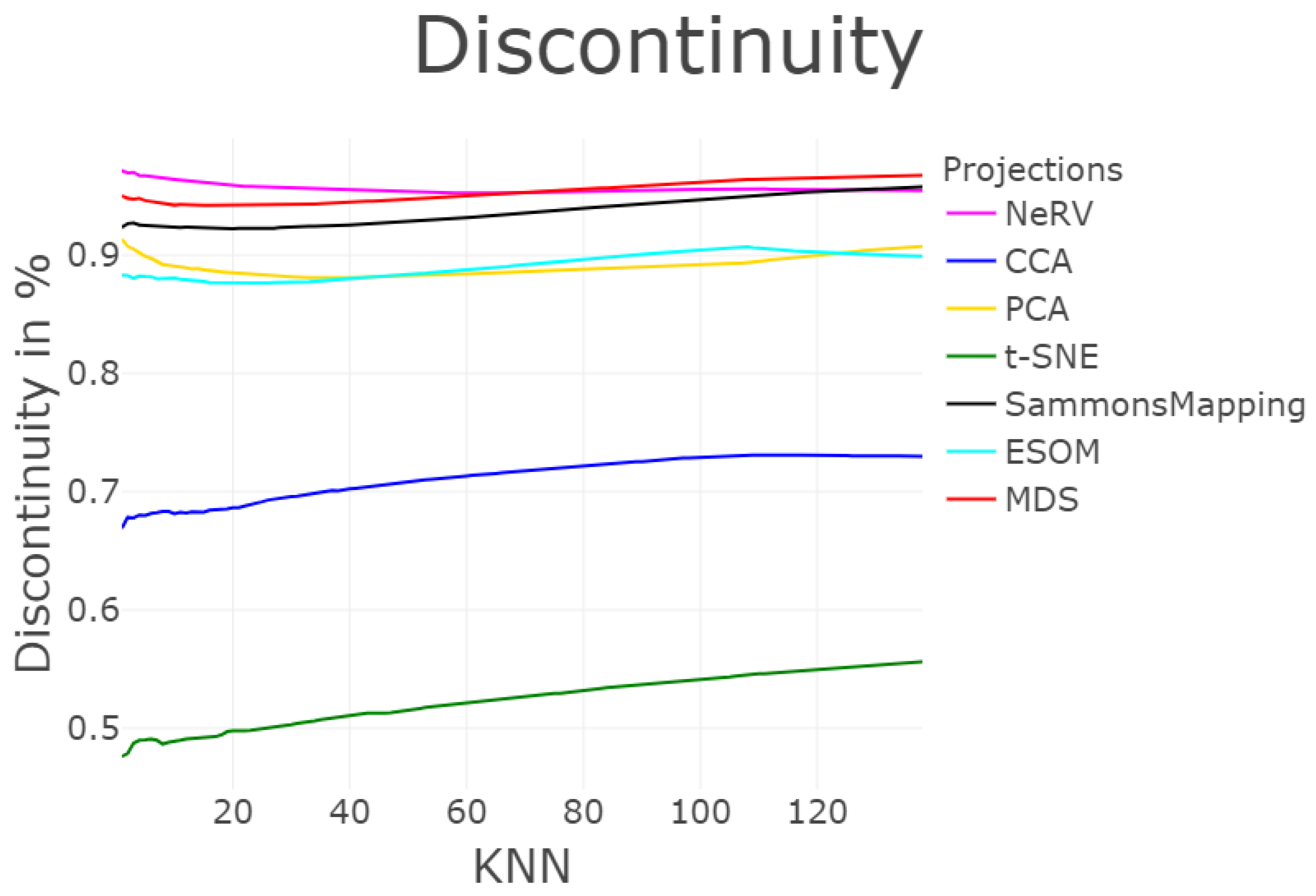
3.1.7. Trustworthiness and Discontinuity (T&D)
3.1.8. Overall Correlations: Topological Index (TI) and Topological Correlation (TC)
3.1.9. Zrehen’s Measure
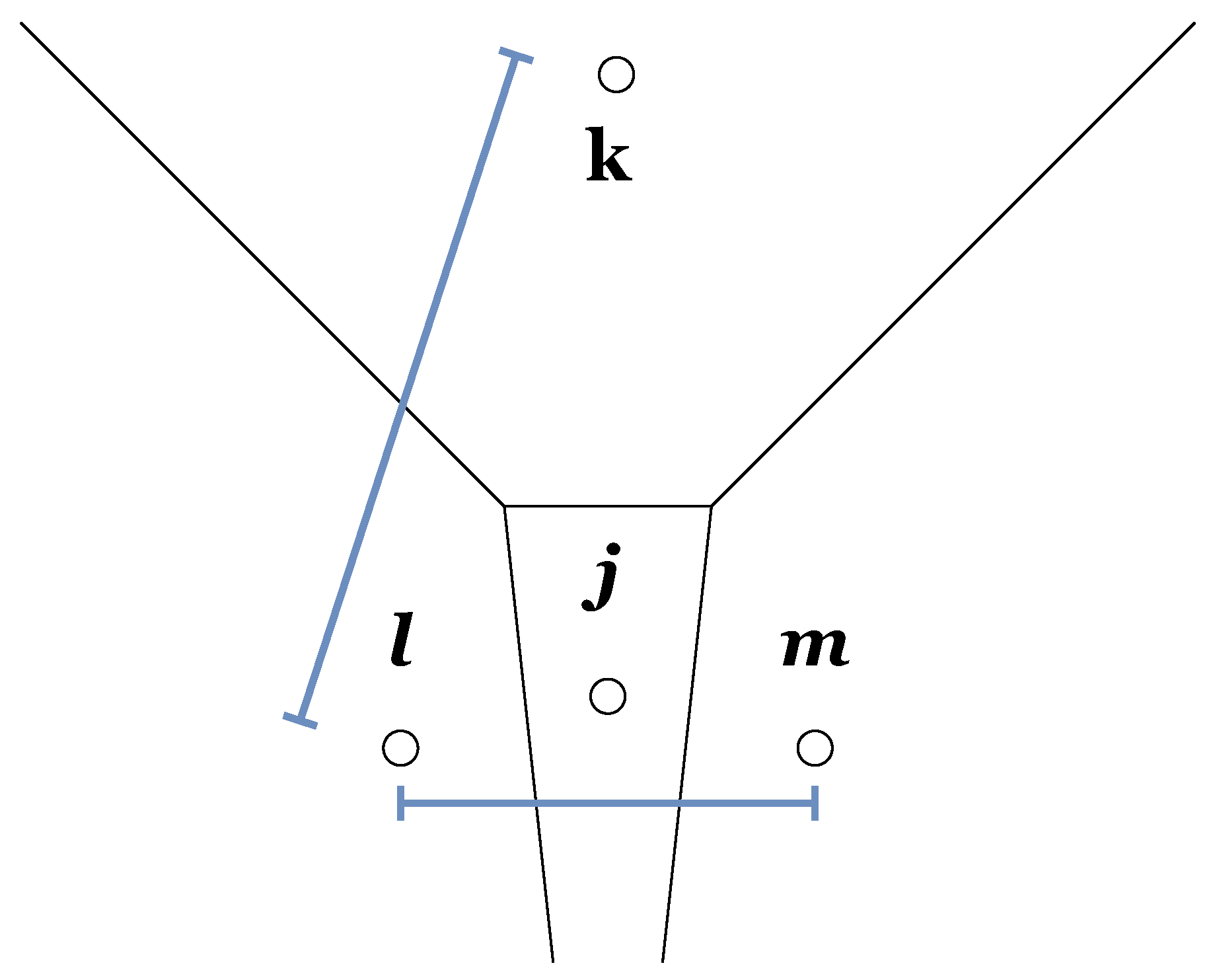
“A pair of neighbor cells A and B is locally organized if the straight line joining their weight vectors W(A) and W(B) contains points which are closer to W(A) or W(B) than they are to any other” [40].
3.2. Types of Quality Measurements (QMs) for Assessing Structure Preservation
4. Introducing the Gabriel Classification Error
5. Results
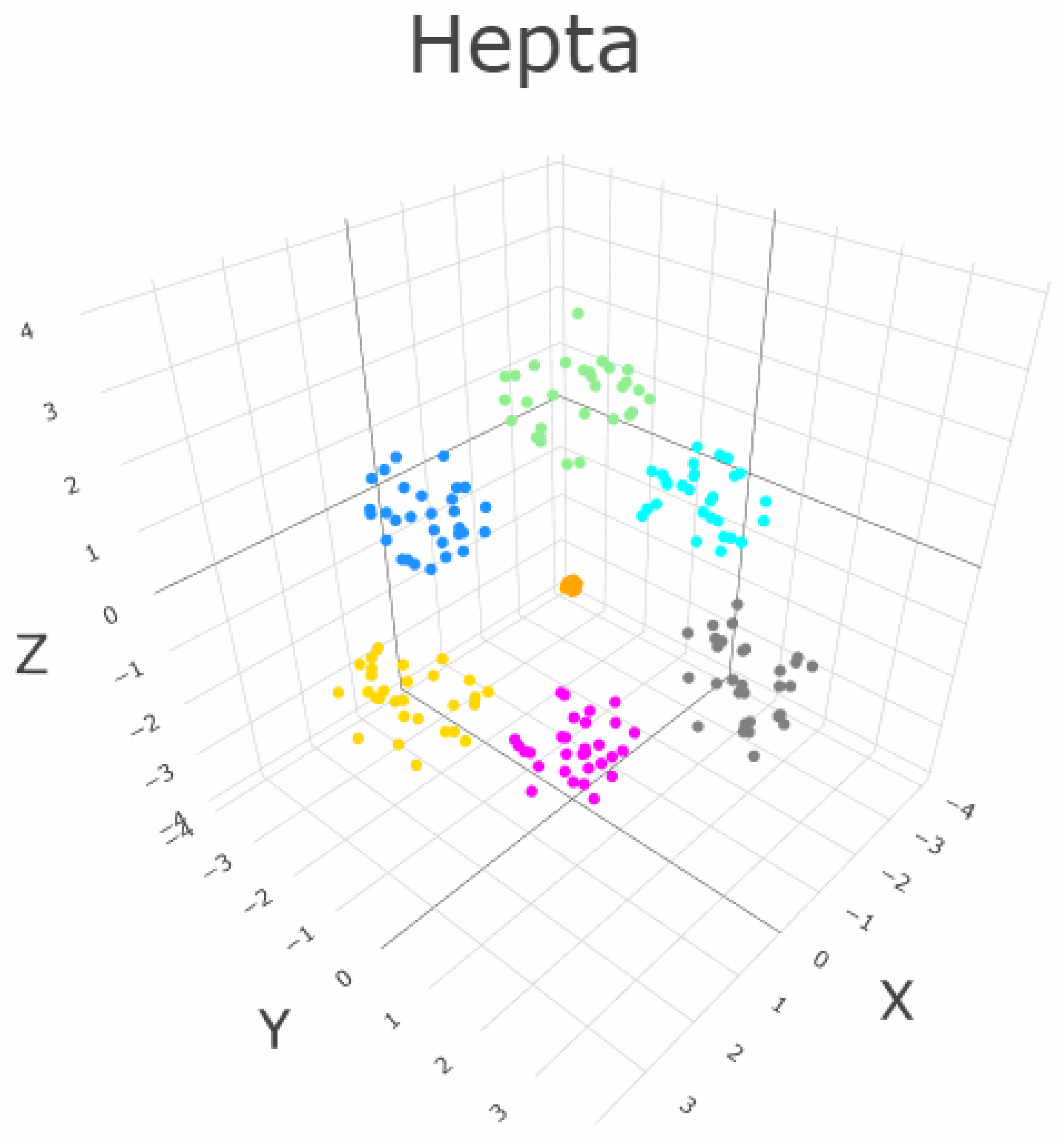
5.1. Linear Separable Structures of Hepta
5.2. Linear Non-Separable Structures of Chainlink
5.3. High-Dimensional Data of Leukemia
6. Discussion
- The result should be easily interpretable and should enable a comparison of different DR methods.
- The result should be deterministic, with no or only simple parameters.
- The result should be statistically stable and calculable for high-dimensional data in .
- The result should measure the preservation of high-dimensional linear and nonlinear structural separability.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. More Quality Measures and Preservation of High-Dimensional Distances in the Two-Dimensional Space
Appendix A.1.1. Force Approach Error
Appendix A.1.2. König’s Measure
Appendix A.1.3. Local Continuity Meta-Criterion (LCMC)
Appendix A.1.4. Mean Relative Rank Error (MRRE) and the Co-Ranking Matrix
Appendix A.1.5. Topographic Product
Appendix A.1.6. Topographic Function (TF)
Appendix A.1.7. U-Ranking
Appendix B. Shepard Diagrams Visualized as Density Plot
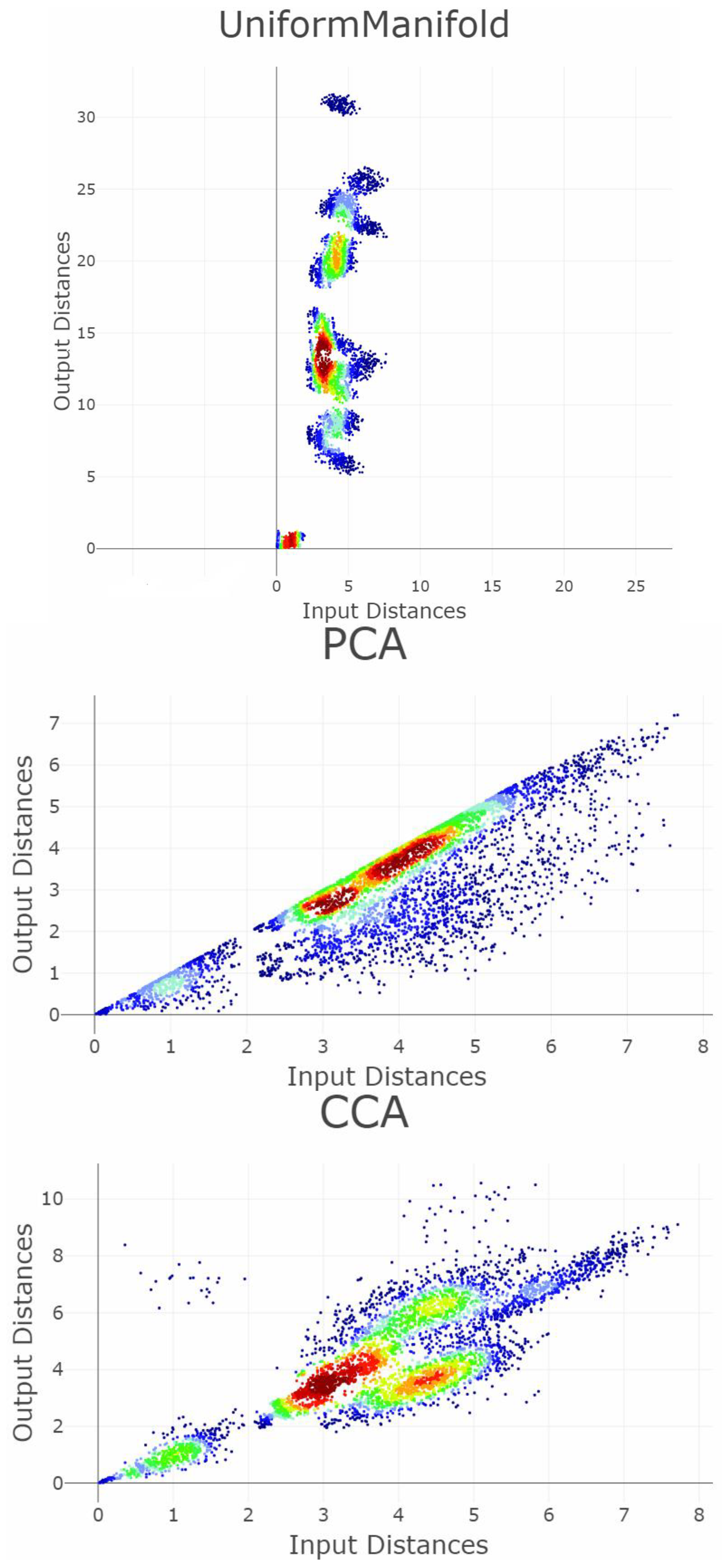
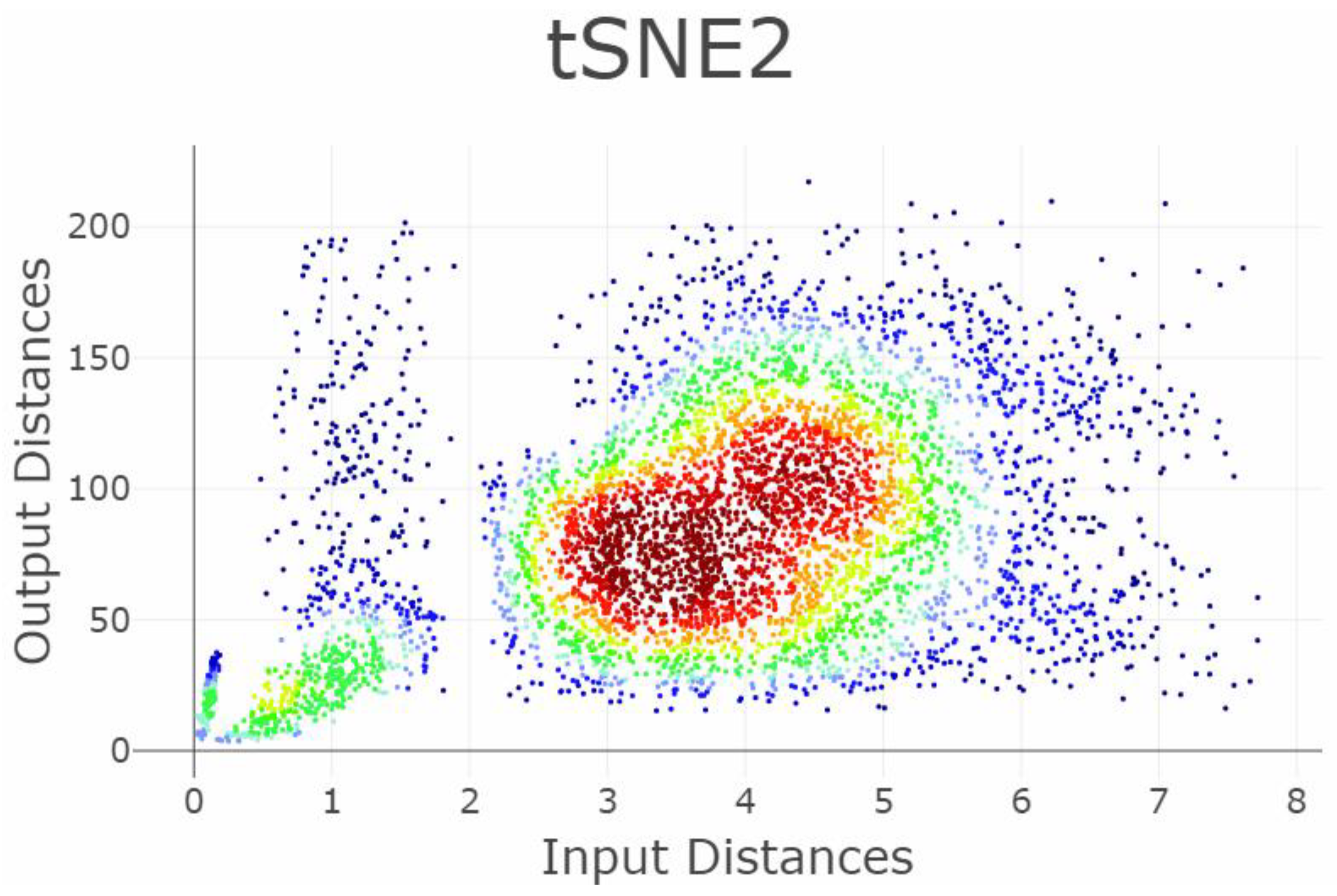
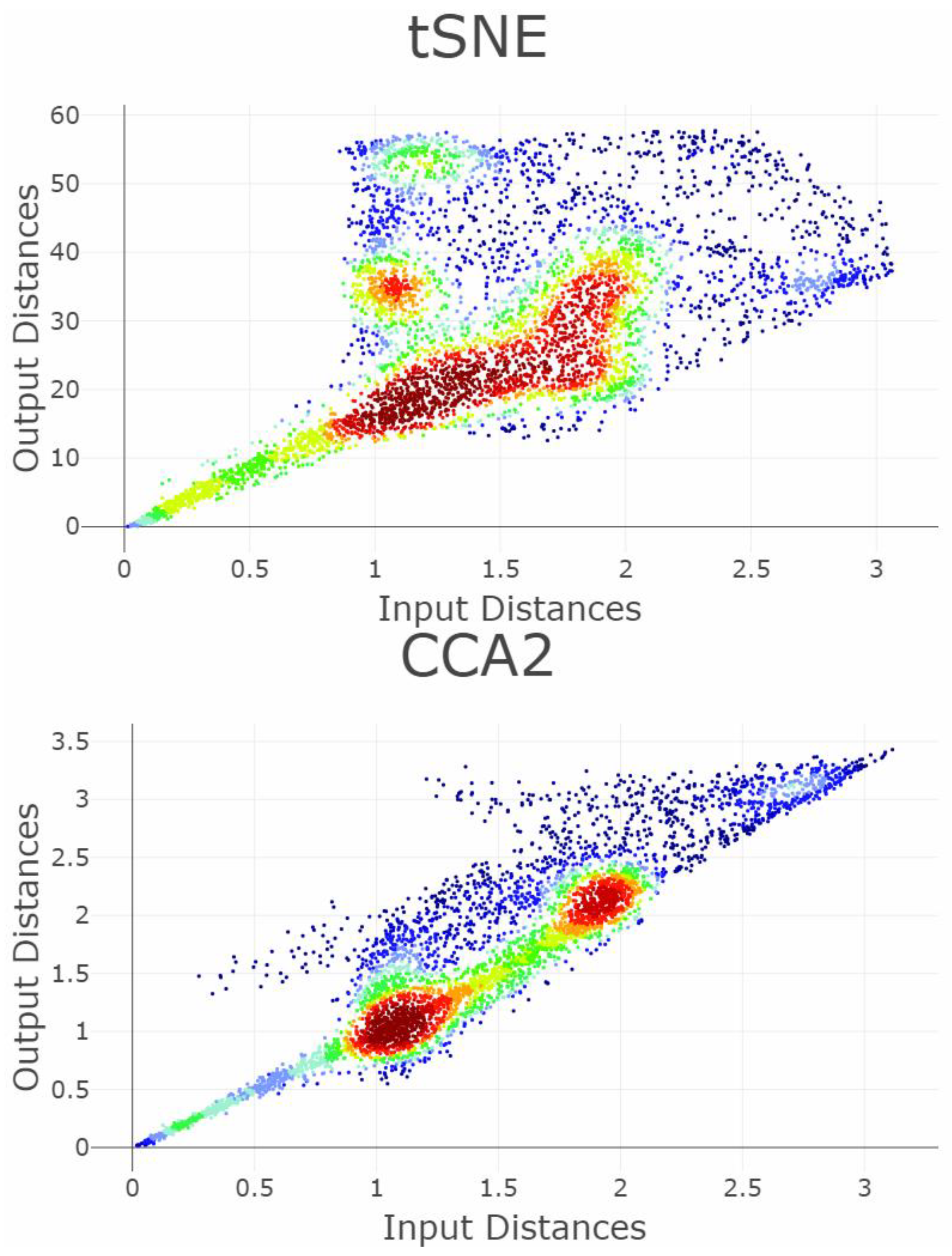
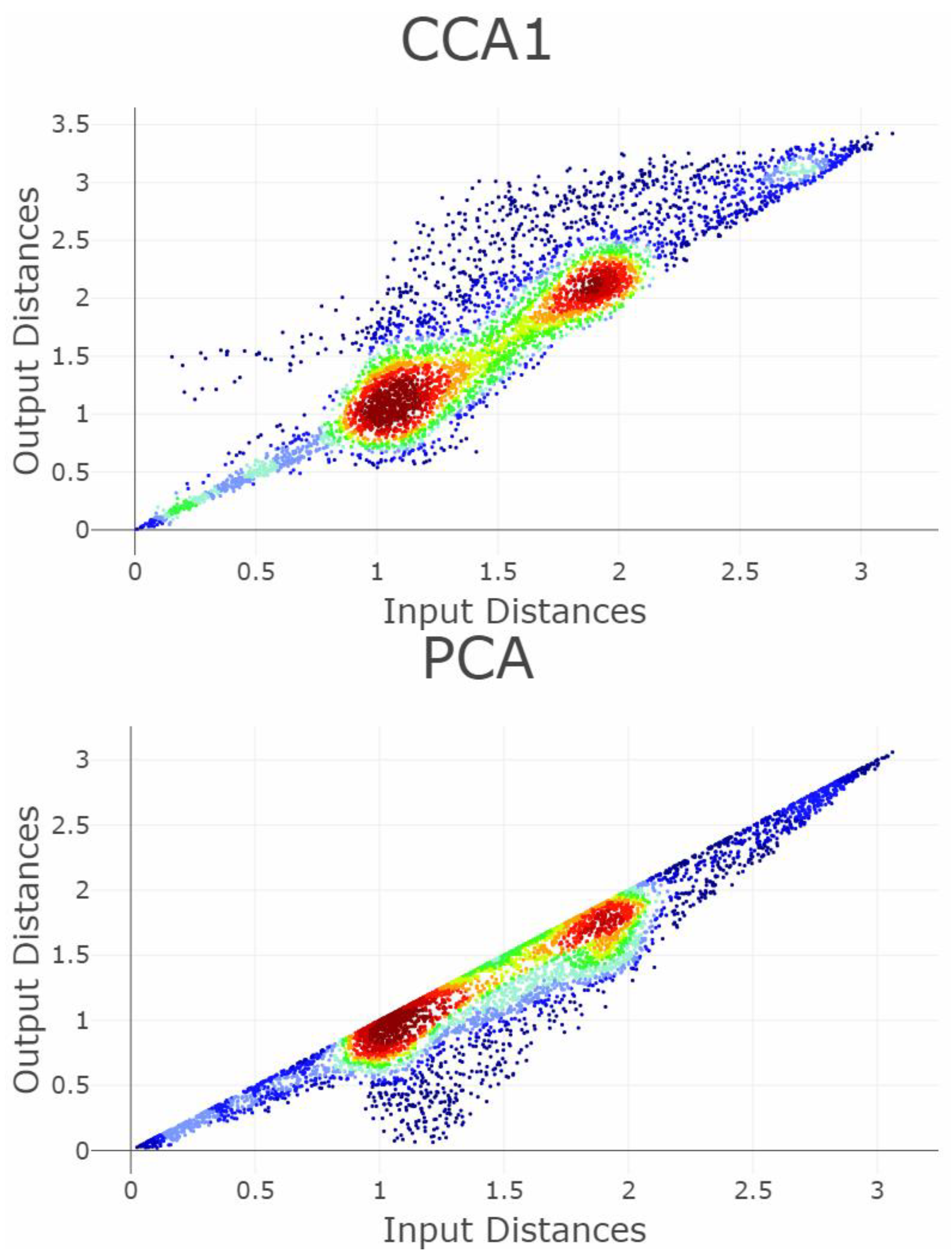
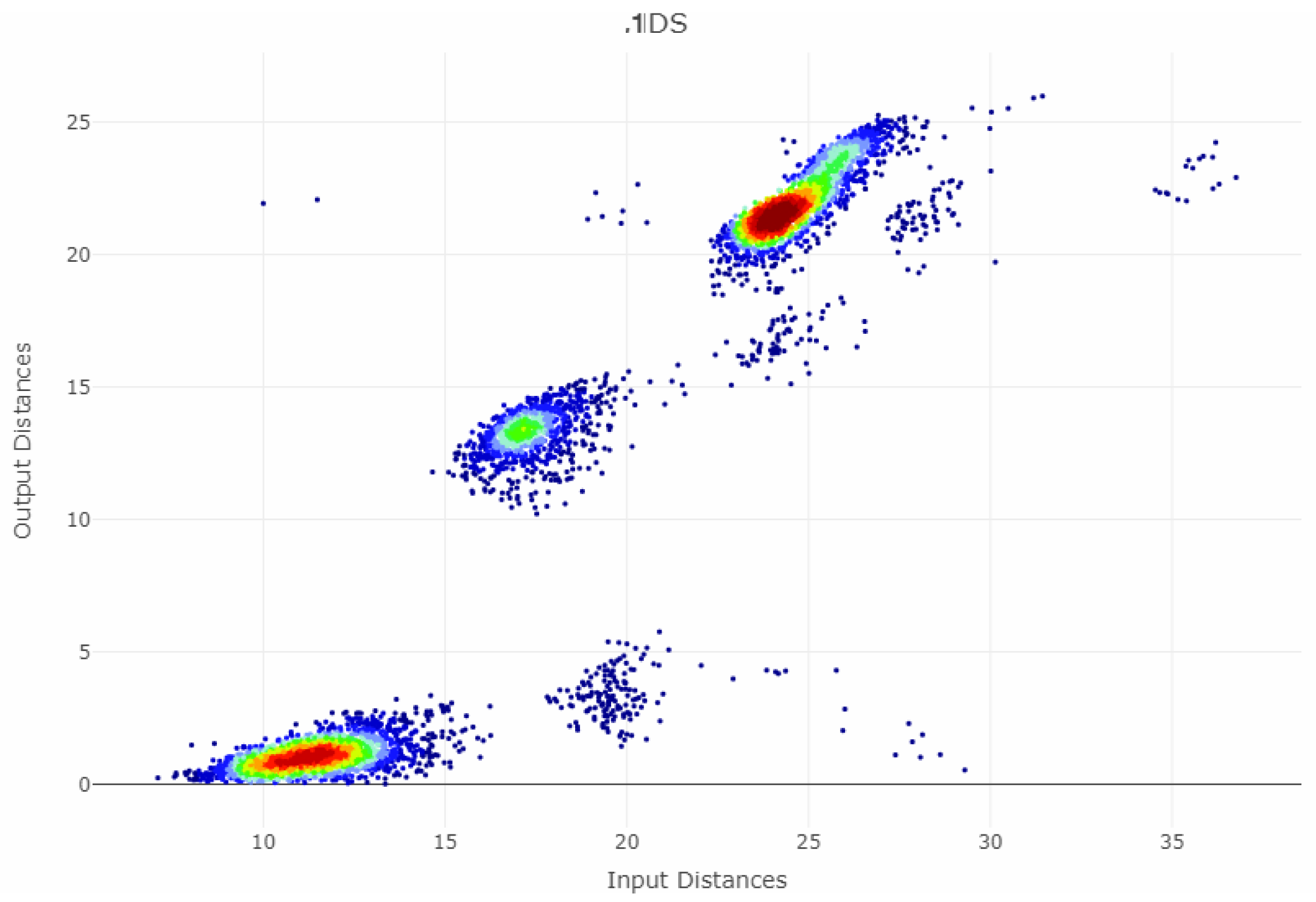
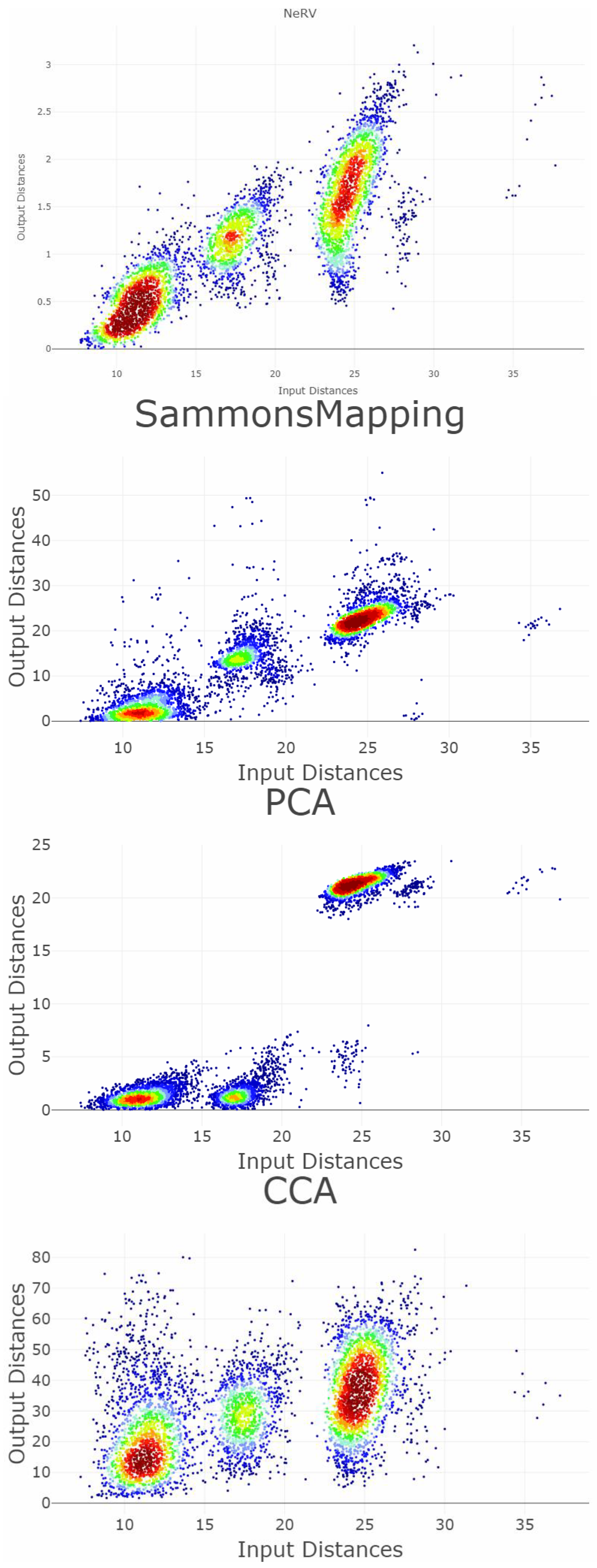
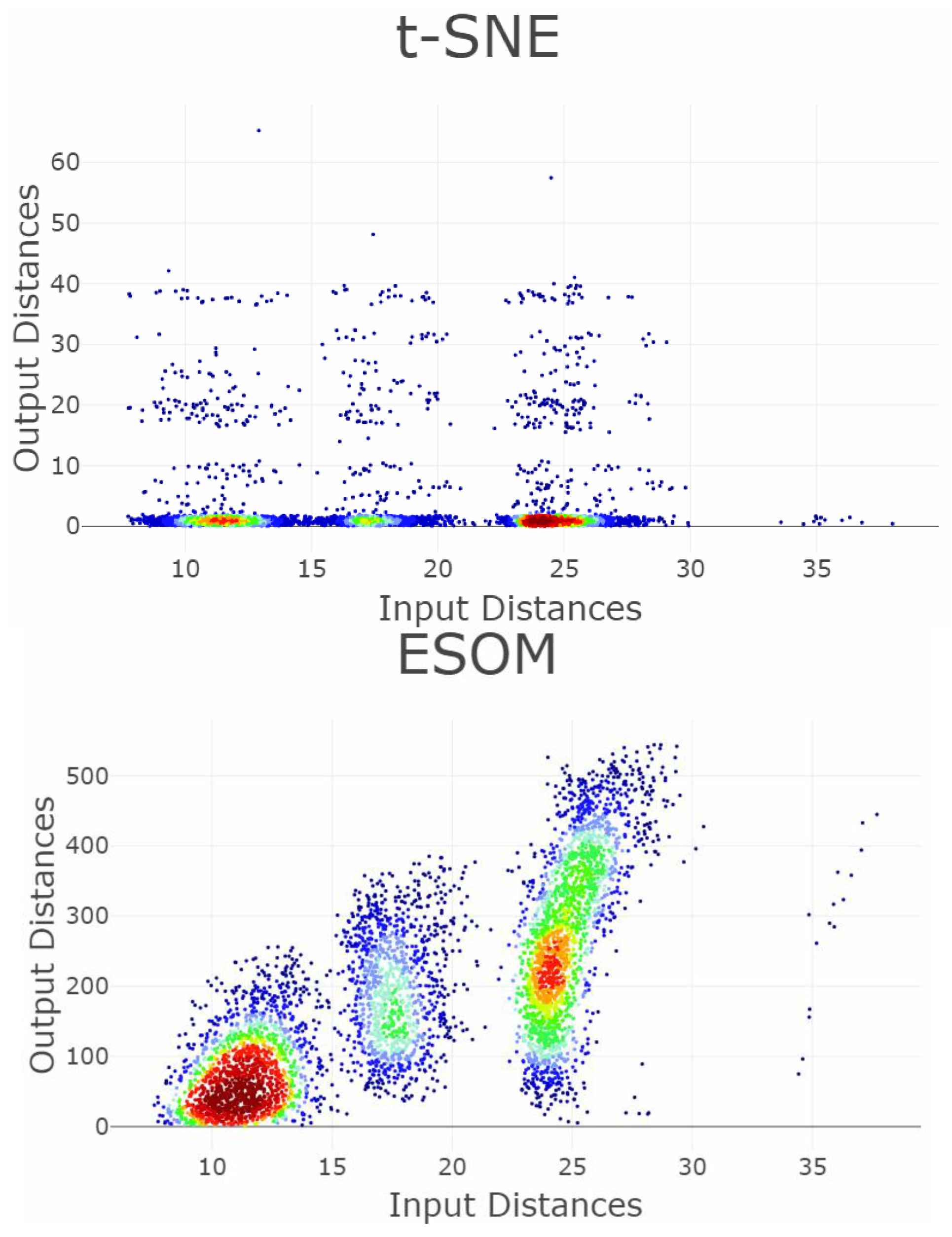
Appendix C
Appendix C.1. Parameter Settings and Source Code Availability
Appendix C.1.1. Quality Measures (QMs)
Appendix C.1.2. Projection Methods
References
- Everitt, B.S.; Landau, S.; Leese, M. Cluster Analysis; Arnold: London, UK, 2001. [Google Scholar]
- Mirkin, B.G. Clustering: A Data Recovery Approach; Chapman & Hall/CRC: Boca Raton, FL, USA, 2005. [Google Scholar]
- Ritter, G. Robust Cluster Analysis and Variable Selection; Chapman & Hall/CRC Press: Passau, Germany, 2014. [Google Scholar]
- Hennig, C.; Meila, M. Handbook of Cluster Analysis; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- van der Maaten, L.J.; Postma, E.O.; van den Herik, H.J. Dimensionality reduction: A comparative review. J. Mach. Learn. Res. 2009, 10, 66–71. [Google Scholar]
- Mokbel, B.; Lueks, W.; Gisbrecht, A.; Hammer, B. Visualizing the quality of dimensionality reduction. Neurocomputing 2013, 112, 109–123. [Google Scholar] [CrossRef]
- Yin, H. Nonlinear dimensionality reduction and data visualization: A review. Int. J. Autom. Comput. 2007, 4, 294–303. [Google Scholar] [CrossRef]
- Venna, J.; Peltonen, J.; Nybo, K.; Aidos, H.; Kaski, S. Information retrieval perspective to nonlinear dimensionality reduction for data visualization. J. Mach. Learn. Res. 2010, 11, 451–490. [Google Scholar]
- Gracia, A.; González, S.; Robles, V.; Menasalvas, E. A methodology to compare Dimensionality Reduction algorithms in terms of loss of quality. Inf. Sci. 2014, 270, 1–27. [Google Scholar] [CrossRef]
- Ray, P.; Reddy, S.S.; Banerjee, T. Various dimension reduction techniques for high dimensional data analysis: A review. Artif. Intell. Rev. 2021, 54, 3473–3515. [Google Scholar] [CrossRef]
- Ayesha, S.; Hanif, M.K.; Talib, R. Overview and comparative study of dimensionality reduction techniques for high dimensional data. Inf. Fusion 2020, 59, 44–58. [Google Scholar] [CrossRef]
- Toussaint, G.T. The relative neighbourhood graph of a finite planar set. Pattern Recognit. 1980, 12, 261–268. [Google Scholar] [CrossRef]
- Delaunay, B. Sur la sphere vide. 1934. Available online: http://galiulin.narod.ru/delaunay_.pdf (accessed on 11 July 2023).
- Gabriel, K.R.; Sokal, R.R. A new statistical approach to geographic variation analysis. Syst. Biol. 1969, 18, 259–278. [Google Scholar] [CrossRef]
- Brito, M.; Chávez, E.; Quiroz, A.; Yukich, J. Connectivity of the mutual k-nearest-neighbor graph in clustering and outlier detection. Stat. Probab. Lett. 1997, 35, 33–42. [Google Scholar] [CrossRef]
- Clark, B.N.; Colbourn, C.J.; Johnson, D.S. Unit disk graphs. Discret. Math. 1990, 86, 165–177. [Google Scholar] [CrossRef]
- Ultsch, A.; Herrmann, L. The architecture of emergent self-organizing maps to reduce projection errors. In Proceedings of the 13th European Symposium on Artificial Neural Networks (ESANN), Bruges, Belgium, 27–29 April 2005; pp. 1–6. [Google Scholar]
- Aupetit, M. Visualizing distortions and recovering topology in continuous projection techniques. Neurocomputing 2007, 70, 1304–1330. [Google Scholar] [CrossRef]
- Mair, F.; Hartmann, F.J.; Mrdjen, D.; Tosevski, V.; Krieg, C.; Becher, B. The end of gating? An introduction to automated analysis of high dimensional cytometry data. Eur. J. Immunol. 2016, 46, 34–43. [Google Scholar] [CrossRef] [PubMed]
- Ultsch, A.; Lötsch, J. Machine-learned cluster identification in high-dimensional data. J. Biomed. Inform. 2017, 66, 95–104. [Google Scholar] [CrossRef] [PubMed]
- Bunte, K.; Biehl, M.; Hammer, B. A general framework for dimensionality-reducing data visualization mapping. Neural Comput. 2012, 24, 771–804. [Google Scholar] [CrossRef]
- Goodhill, G.J.; Finch, S.; Sejnowski, T.J. Quantifying Neighbourhood Preservation in Topographic Mappings; Chapman & Hall/CRC: Boca Raton, FL, USA, 1995. [Google Scholar]
- Durbin, R.; Mitchison, G. A dimension reduction framework for understanding cortical maps. Nature 1990, 343, 644–647. [Google Scholar] [CrossRef] [PubMed]
- Mitchison, G. A type of duality between self-organizing maps and minimal wiring. Neural Comput. 1995, 7, 25–35. [Google Scholar] [CrossRef]
- Hinton, G.E.; Roweis, S.T. Stochastic neighbor embedding. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MSA, USA, 2002; pp. 833–840. [Google Scholar]
- Lee, J.A.; Peluffo-Ordonez, D.H.; Verleysen, M. Multiscale stochastic neighbor embedding: Towards parameter-free dimensionality reduction. In Proceedings of the 22nd European Symposium on Artificial Neural Networks, Computational Intelligence And Machine Learning (ESANN), Bruges, Belgium, 23–25 April 2014. [Google Scholar]
- Lee, J.A.; Verleysen, M. Rank-based quality assessment of nonlinear dimensionality reduction. In Proceedings of the 16th European Symposium on Artificial Neural Networks (ESANN), Bruges, Belgium, 23–15 April 2008; pp. 49–54. [Google Scholar]
- Lee, J.A.; Verleysen, M. Quality assessment of dimensionality reduction: Rank-based criteria. Neurocomputing 2009, 72, 1431–1443. [Google Scholar] [CrossRef]
- Shepard, R.N. Multidimensional scaling, tree-fitting, and clustering. Science 1980, 210, 390–398. [Google Scholar] [CrossRef]
- Kruskal, J.B. Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika 1964, 29, 1–27. [Google Scholar] [CrossRef]
- Kruskal, J.B. Nonmetric multidimensional scaling: A numerical method. Psychometrika 1964, 29, 115–129. [Google Scholar] [CrossRef]
- Venna, J.; Kaski, S. Neighborhood preservation in nonlinear projection methods: An experimental study. In Artificial Neural Networks—ICANN 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 485–491. [Google Scholar]
- Kaski, S.; Nikkilä, J.; Oja, M.; Venna, J.; Törönen, P.; Castrén, E. Trustworthiness and metrics in visualizing similarity of gene expression. BMC Bioinform. 2003, 4, 48. [Google Scholar] [CrossRef] [PubMed]
- Siegel, S.; Castellan, N.J. Nonparametric Statistics for the Behavioural Sciences; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Bezdek, J.C.; Pal, N.R. An index of topological preservation and its application to self-organizing feature maps. In Proceedings of the 1993 International Conference on Neural Networks (IJCNN-93-Nagoya, Japan), Nagoya, Japan, 25–29 October 1993; pp. 2435–2440. [Google Scholar]
- Bezdek, J.C.; Pal, N.R. An index of topological preservation for feature extraction. Pattern Recognit. 1995, 28, 381–391. [Google Scholar] [CrossRef]
- Karbauskaitė, R.; Dzemyda, G. Topology preservation measures in the visualization of manifold-type multidimensional data. Informatica 2009, 20, 235–254. [Google Scholar] [CrossRef]
- Handl, J.; Knowles, J.; Dorigo, M. Ant-based clustering and topographic mapping. Artif. Life 2006, 12, 35–62. [Google Scholar] [CrossRef] [PubMed]
- Doherty, K.; Adams, R.; Davey, N. Topological correlation. In Proceedings of the 14th European Symposium on Artificial Neural Networks (ESANN), Bruges, Belgium, 26–28 April 2006; pp. 125–130. [Google Scholar]
- Zrehen, S. Analyzing Kohonen maps with geometry. In ICANN’93; Springer: Berlin/Heidelberg, Germany, 1993; pp. 609–612. [Google Scholar]
- Bauer, H.-U.; Herrmann, M.; Villmann, T. Neural maps and topographic vector quantization. Neural Netw. 1999, 12, 659–676. [Google Scholar] [CrossRef]
- Uriarte, E.A.; Martín, F.D. Topology preservation in SOM. Int. J. Math. Comput. Sci. 2005, 1, 19–22. [Google Scholar]
- Kiviluoto, K. Topology preservation in self-organizing maps. In Proceedings of the International Conference on Neural Networks, Washington, DC, USA, 3–6 June 1996; pp. 294–299. [Google Scholar] [CrossRef]
- Cunningham, J.P.; Ghahramani, Z. Linear dimensionality reduction: Survey, insights, and generalizations. J. Mach. Learn. Res. 2015, 16, 2859–2900. [Google Scholar]
- Pölzlbauer, G. Survey and comparison of quality measures for self-organizing maps. In Proceedings of the Fifth Workshop on Data Analysis (WDA′04), Vysoké Tatry, Slovakia, 13–15 June 2003; pp. 67–82. [Google Scholar]
- Beaton, D.; Valova, I.; MacLean, D. CQoCO: A measure for comparative quality of coverage and organization for self-organizing maps. Neurocomputing 2010, 73, 2147–2159. [Google Scholar] [CrossRef]
- Thrun, M.C.; Ultsch, A. Swarm Intelligence for Self-Organized Clustering. Artif. Intell. 2021, 290, 103237. [Google Scholar] [CrossRef]
- Thrun, M.C.; Pape, F.; Ultsch, A. Conventional Displays of Structures in Data Compared with Interactive Projection-Based Clustering (IPBC). Int. J. Data Sci. Anal. 2021, 12, 249–271. [Google Scholar] [CrossRef]
- Thrun, M.C. Distance-Based Clustering Challenges for Unbiased Benchmarking Studies. Nat. Sci. Rep. 2021, 11, 18988. [Google Scholar] [CrossRef] [PubMed]
- Thrun, M.C.; Ultsch, A. Clustering Benchmark Datasets Exploiting the Fundamental Clustering Problems. Data Brief 2020, 30, 105501. [Google Scholar] [CrossRef] [PubMed]
- Thrun, M.C.; Ultsch, A. Effects of the payout system of income taxes to municipalities in Germany. In Proceedings of the 12th Professor Aleksander Zelias International Conference on Modelling and Forecasting of Socio-Economic Phenomena, Cracow, Poland, 8–11 May 2018; pp. 533–542. [Google Scholar]
- Ultsch, A. Data mining and knowledge discovery with emergent self-organizing feature maps for multivariate time series. In Kohonen Maps, 1st ed.; Oja, E., Kaski, S., Eds.; Elsevier: Amsterdam, The Netherlands, 1999; pp. 33–46. [Google Scholar]
- Ultsch, A.; Mörchen, F. ESOM-Maps: Tools for Clustering, Visualization, and Classification with EMERGENT SOM; University of Marburg: Marburg, Germany, 2005. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
- Demartines, P.; Hérault, J. CCA: “Curvilinear component analysis”. In Proceedings of the 15° Colloque sur le Traitement du Signal et des Images, Antibes, France, 18–21 September 1995. [Google Scholar]
- Thrun, M.C.; Stier, Q. Fundamental Clustering Algorithms Suite. SoftwareX 2021, 13, 100642. [Google Scholar] [CrossRef]
- Drygas, H. Über multidimensionale Skalierung. Stat. Pap. 1978, 19, 63–66. [Google Scholar] [CrossRef]
- Kirsch, A. Bemerkung zu H. Drygas, “Über multidimensionale Skalierung”. Stat. Pap. 1978, 19, 211–212. [Google Scholar] [CrossRef]
- Schmid, F. Über ein Problem der mehrdimensionalen Skalierung. Stat. Pap. 1980, 21, 140–144. [Google Scholar] [CrossRef]
- König, A. Interactive visualization and analysis of hierarchical neural projections for data mining. IEEE Trans. Neural Netw. 2000, 11, 615–624. [Google Scholar] [CrossRef]
- Lee, J.A.; Verleysen, M. Scale-independent quality criteria for dimensionality reduction. Pattern Recognit. Lett. 2010, 31, 2248–2257. [Google Scholar] [CrossRef]
- Lueks, W.; Mokbel, B.; Biehl, M.; Hammer, B. How to Evaluate Dimensionality Reduction?-Improving the Co-ranking Matrix. arXiv 2011, arXiv:1110.3917. [Google Scholar]
- Chen, L.; Buja, A. Local multidimensional scaling for nonlinear dimension reduction, graph drawing, and proximity analysis. J. Am. Stat. Assoc. 2009, 104, 209–219. [Google Scholar] [CrossRef]
- Aupetit, M. Robust Topology Representing Networks. In Proceedings of the 11th European Symposium on Artificial Neural Networks (ESANN), Bruges, Belgium, 23–25 April 2003; pp. 45–50. [Google Scholar]
- Villmann, T.; Der, R.; Herrmann, M.; Martinetz, T.M. Topology preservation in self-organizing feature maps: Exact definition and measurement. IEEE Trans. Neural Netw. 1997, 8, 256–266. [Google Scholar] [CrossRef] [PubMed]
- Grassberger, P.; Procaccia, I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591–2593. [Google Scholar] [CrossRef]
- De Berg, M.; van Kreveld, M.; Overmars, M.; Schwarzkopf, O. Computational Geometry: Algorithms and Applications; Springer: New York, NY, USA, 2008. [Google Scholar]
- Shamos, M.I.; Hoey, D. Closest-point problems. In Proceedings of the 16th Annual Symposium on Foundations of Computer Science (sfcs 1975), Berkeley, CA, USA, 13–15 October 1975; pp. 151–162. [Google Scholar]
- Bhattacharya, B.; Mukherjee, K.; Toussaint, G. Geometric decision rules for high dimensions. In Proceedings of the 55th Session of the International Statistics Institute, Sydney, Australia, 5–12 April 2005. [Google Scholar]
- Matula, D.W.; Sokal, R.R. Properties of Gabriel graphs relevant to geographic variation research and the clustering of points in the plane. Geogr. Anal. 1980, 12, 205–222. [Google Scholar] [CrossRef]
- Holzinger, A. Interactive machine learning for health informatics: When do we need the human-in-the-loop? Brain Inform. 2016, 3, 119–131. [Google Scholar] [CrossRef]
- van Unen, V.; Höllt, T.; Pezzotti, N.; Li, N.; Reinders, M.J.; Eisemann, E.; Koning, F.; Vilanova, A.; Lelieveldt, B.P. Visual analysis of mass cytometry data by hierarchical stochastic neighbour embedding reveals rare cell types. Nat. Commun. 2017, 8, 1740. [Google Scholar] [CrossRef]
- Hund, M.; Böhm, D.; Sturm, W.; Sedlmair, M.; Schreck, T.; Ullrich, T.; Keim, D.A.; Majnaric, L.; Holzinger, A. Visual analytics for concept exploration in subspaces of patient groups. Brain Inform. 2016, 3, 233–247. [Google Scholar] [CrossRef]
- Tejada, E.; Minghim, R.; Nonato, L.G. On improved projection techniques to support visual exploration of multi-dimensional data sets. Inf. Vis. 2003, 2, 218–231. [Google Scholar] [CrossRef]
- König, A.; Bulmahn, O.; Glesner, M. Systematic Methods for Multivariate Data Visualization and Numerical Assessment of Class Separability and Overlap in Automated Visual Industrial Quality Control. In Proceedings of the British Machine Vision Conference, BMVC 1994, York, UK, 31 August–3 September 1994; pp. 19.1–19.10. [Google Scholar]
- Chen, L.; Buja, A. Local Multidimensional Scaling for Nonlinear Dimensionality Reduction, Graph Layout, and Proximity Analysis; University of Pennsylviana: Philadelphia, PA, USA, 2006. [Google Scholar]
- Akkucuk, U.; Carroll, J.D. PARAMAP vs. Isomap: A comparison of two nonlinear mapping algorithms. J. Classif. 2006, 23, 221–254. [Google Scholar] [CrossRef]
- Lee, J.A.; Verleysen, M. Nonlinear Dimensionality Reduction; Springer: New York, NY, USA, 2007. [Google Scholar]
- Bauer, H.-U.; Pawelzik, K.R. Quantifying the neighborhood preservation of self-organizing feature maps. IEEE Trans. Neural Netw. 1992, 3, 570–579. [Google Scholar] [CrossRef]
- Revuelta, F.F.; Chamizo, J.M.G.; Rodríguez, J.G.; Sáez, A.H. Geodesic topographic product: An improvement to measure topology preservation of self-organizing neural networks. In Advances in Artificial Intelligence–IBERAMIA 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 841–850. [Google Scholar]
- Villmann, T.; Der, R.; Herrmann, M.; Martinetz, T.M. A novel approach to measure the topology preservation of feature maps. In ICANN’94; Springer: Berlin/Heidelberg, Germany, 1994; pp. 298–301. [Google Scholar]
- Herrmann, L. Swarm-Organized Topographic Mapping. Doctoral Dissertation, Philipps-Universität Marburg, Marburg, Germany, 2011. [Google Scholar]
- Lötsch, J.; Ultsch, A. Exploiting the Structures of the U-Matrix. In Proceedings of the Advances in Self-Organizing Maps and Learning Vector Quantization, Mittweida, Germany, 2–4 July 2014; Villmann, T., Schleif, F.-M., Kaden, M., Lange, M., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 249–257. [Google Scholar]
- Brinkmann, L.; Stier, Q.; Thrun, M.C. Computing Sensitive Color Transitions for the Identification of Two-Dimensional Structures. In Proceedings of the Data Science, Statistics & Visualisation (DSSV) and the European Conference on Data Analysis (ECDA), Antwerp, Belgium, 5–7 July 2023; p. 57. [Google Scholar]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing, 3.2.5; R Foundation for Statistical Computing: Vienna, Austria, 2008. [Google Scholar]
- Sammon, J.W. A nonlinear mapping for data structure analysis. IEEE Trans. Comput. 1969, 18, 401–409. [Google Scholar] [CrossRef]
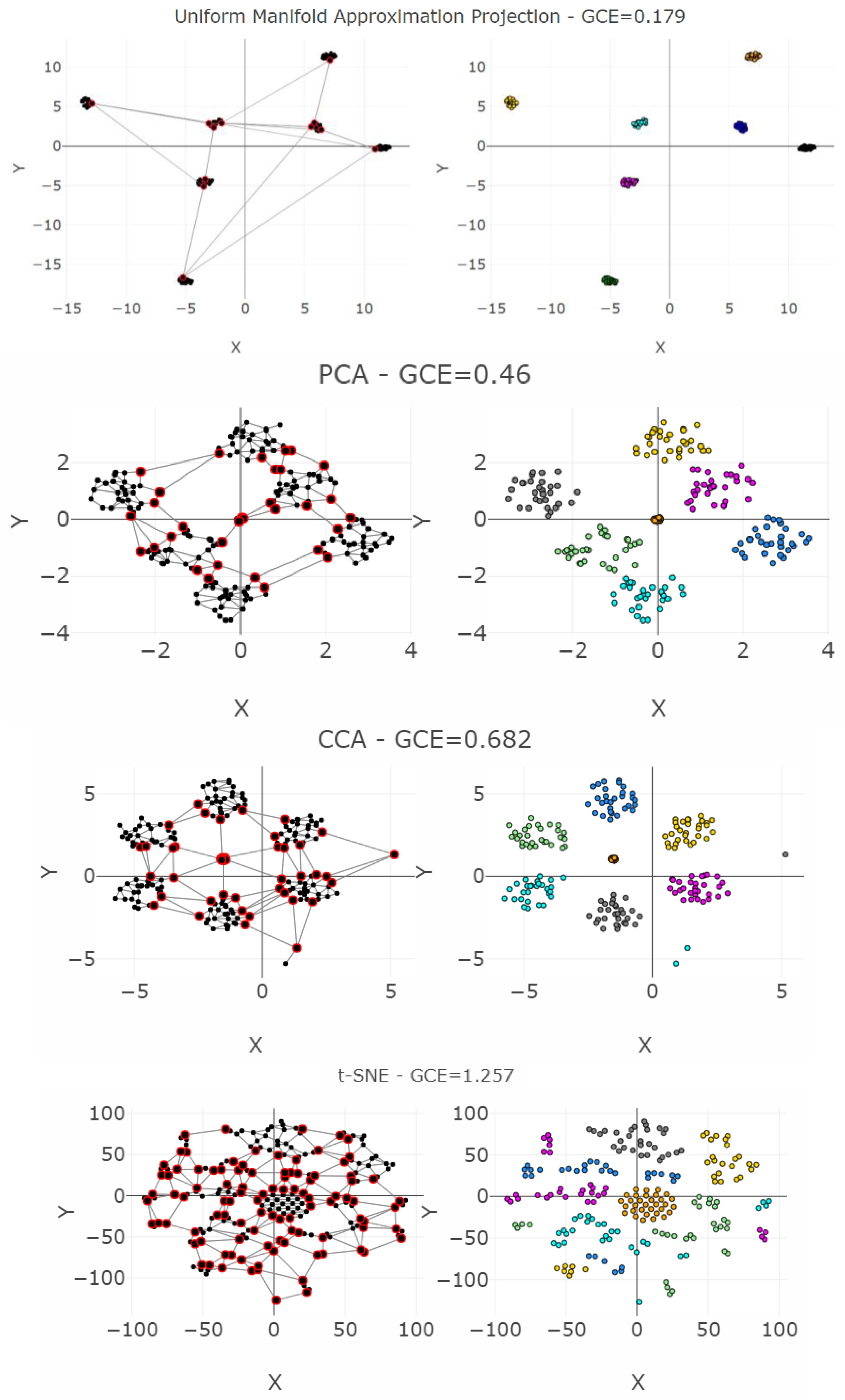
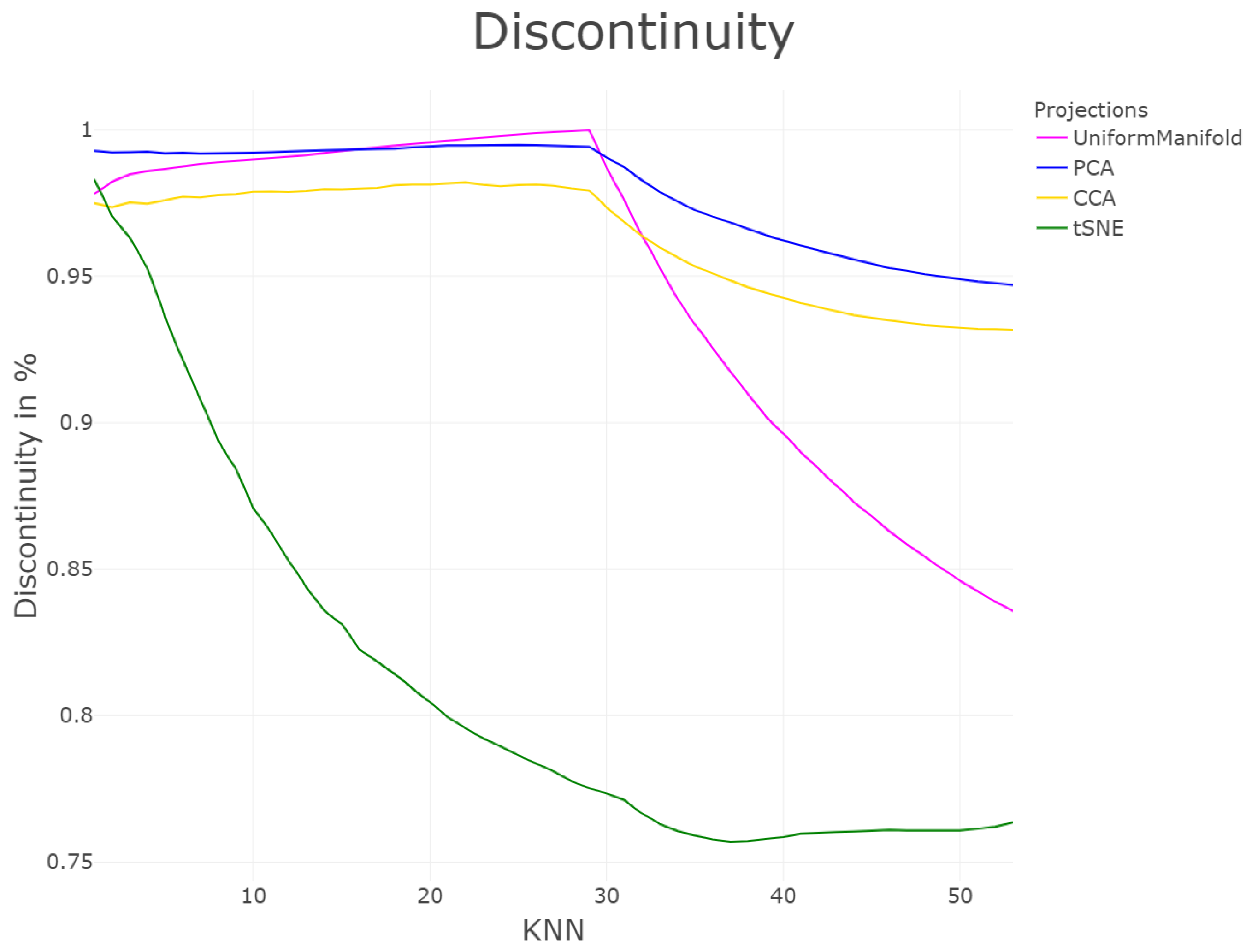
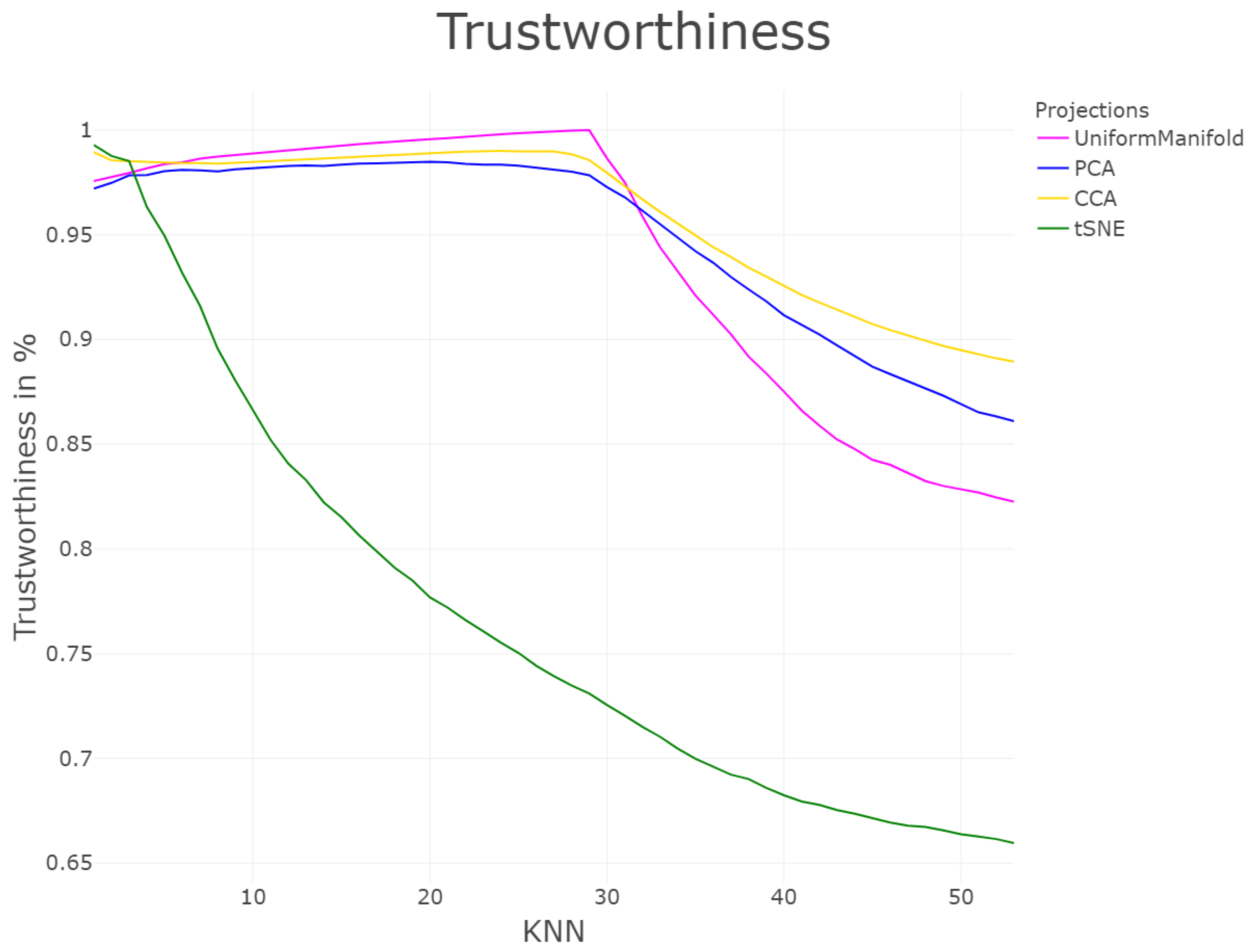
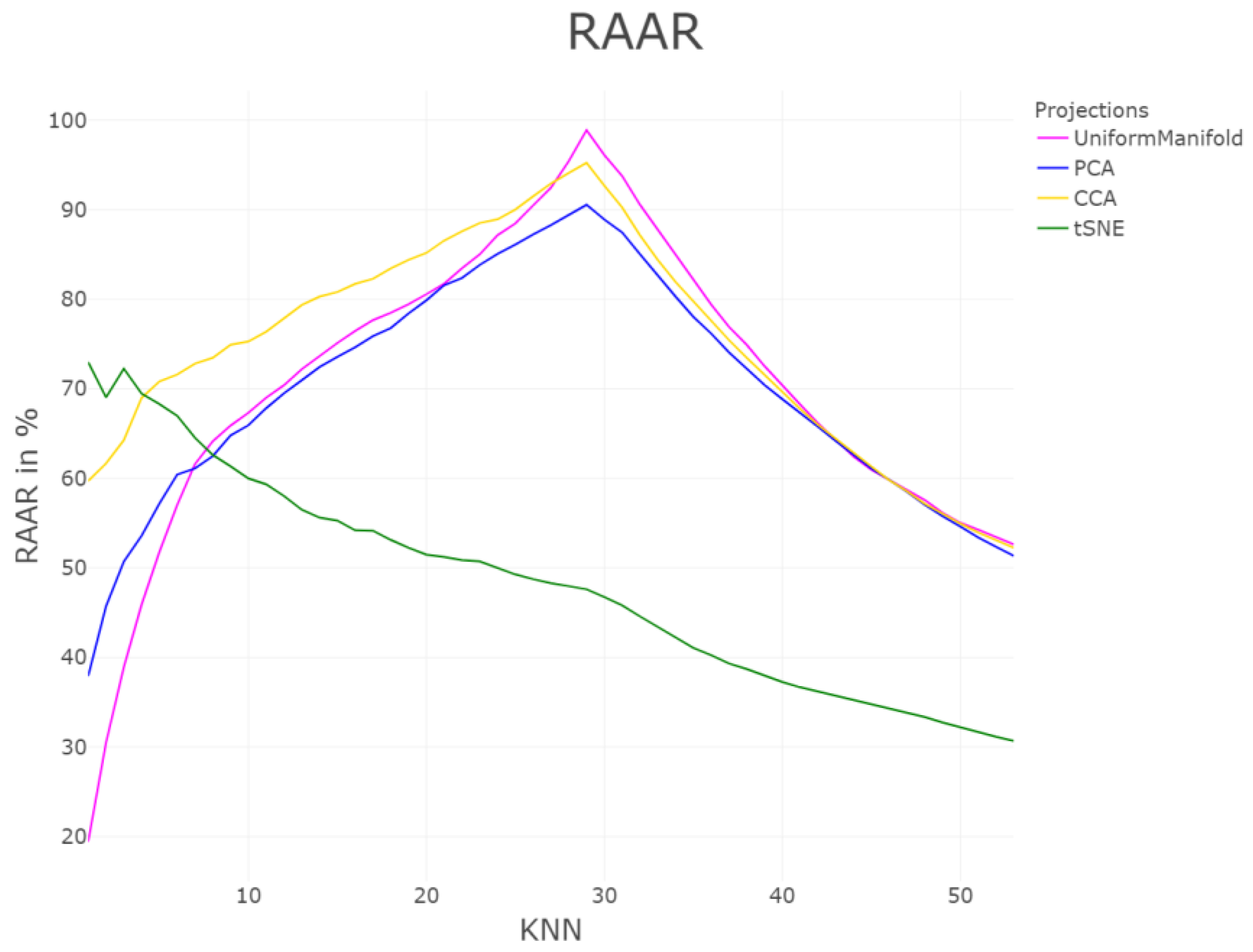
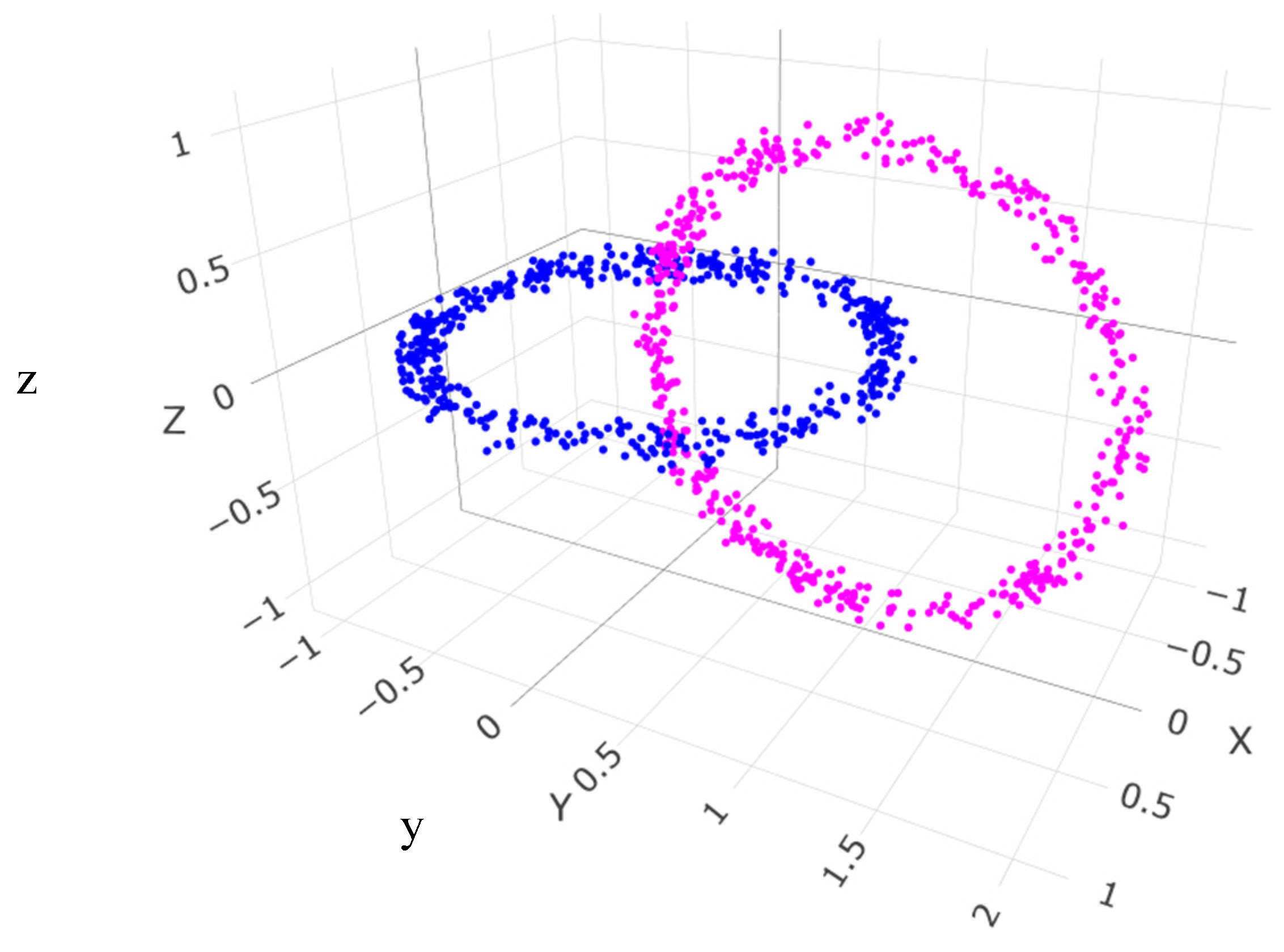

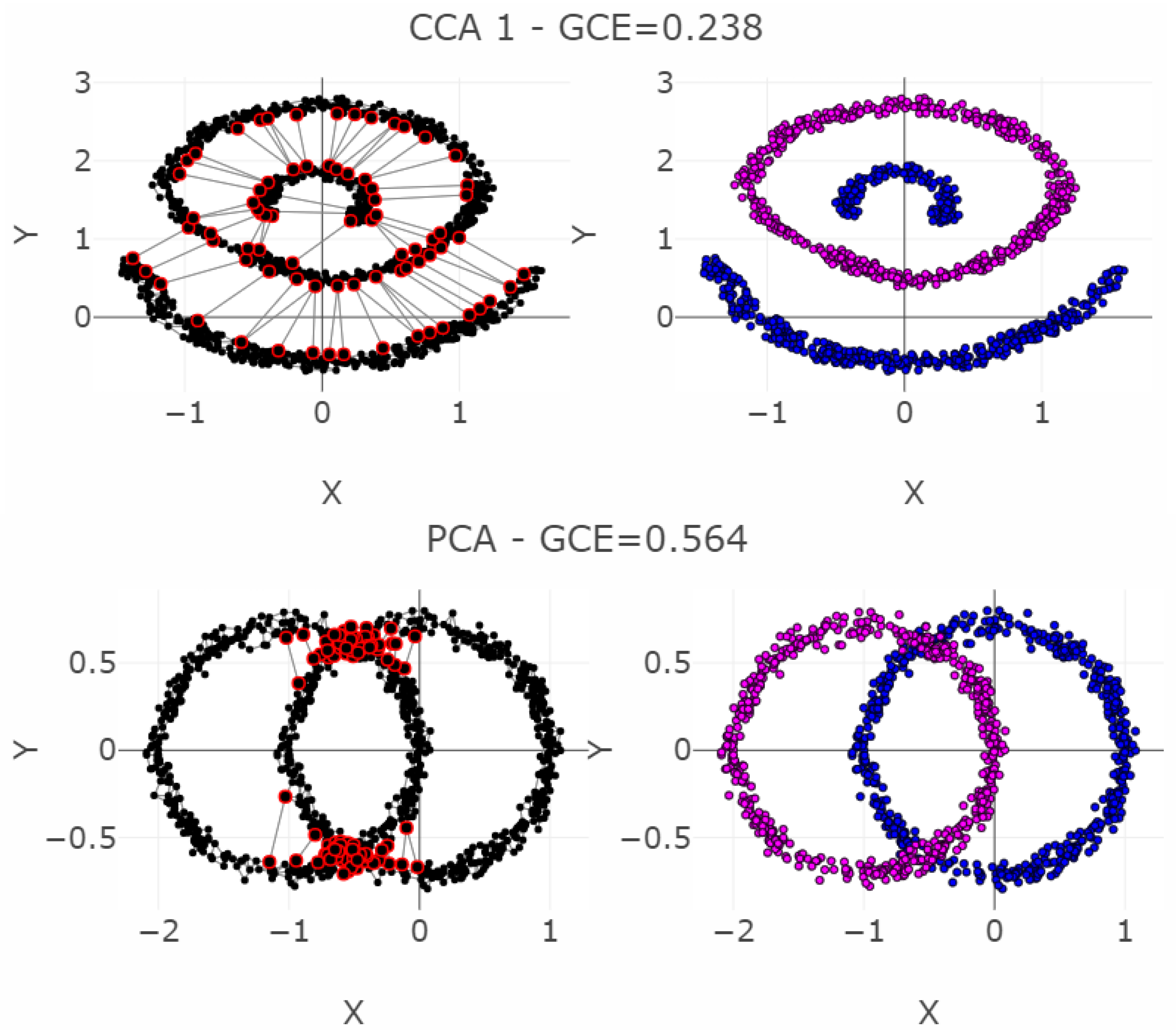
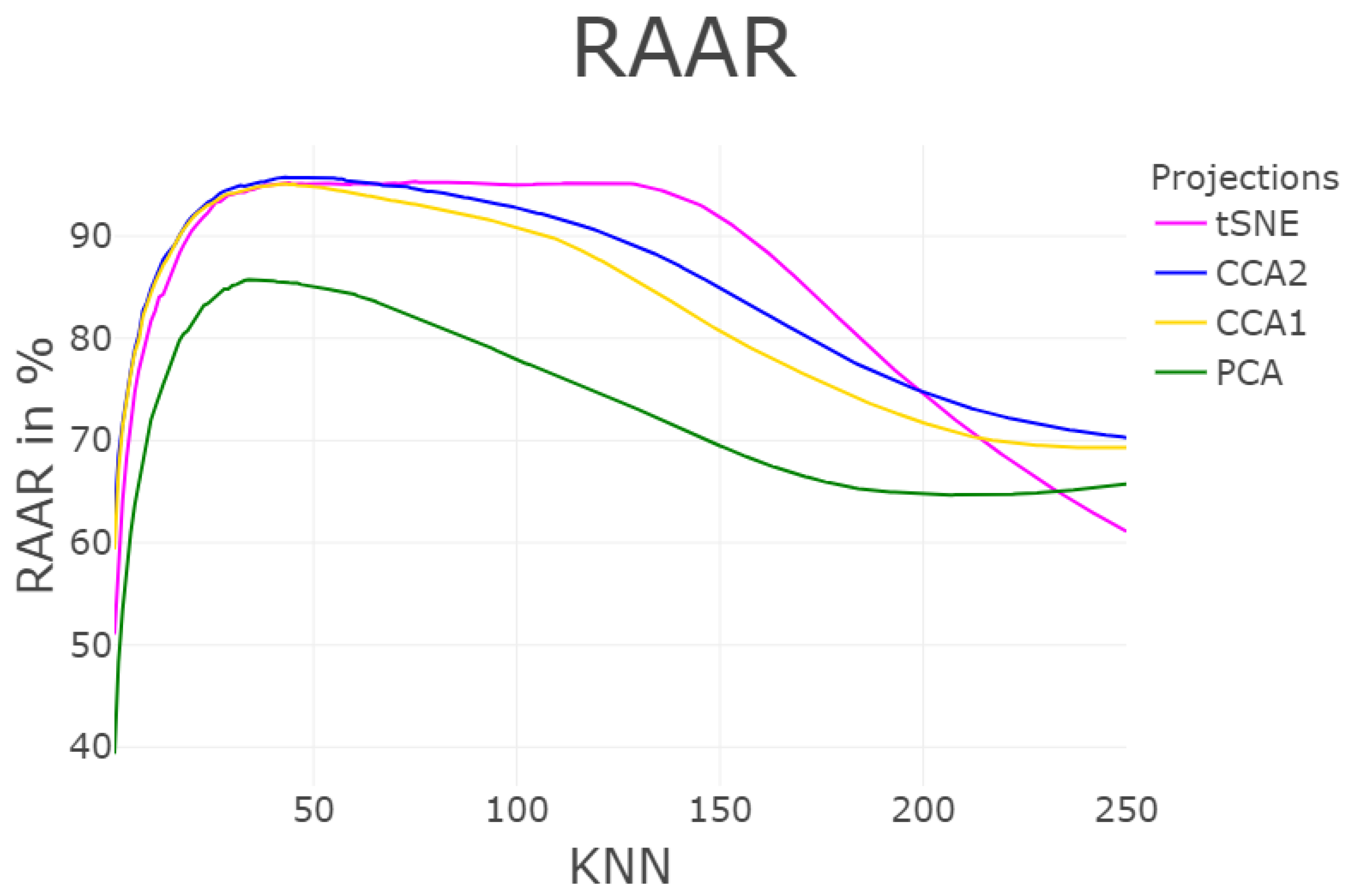
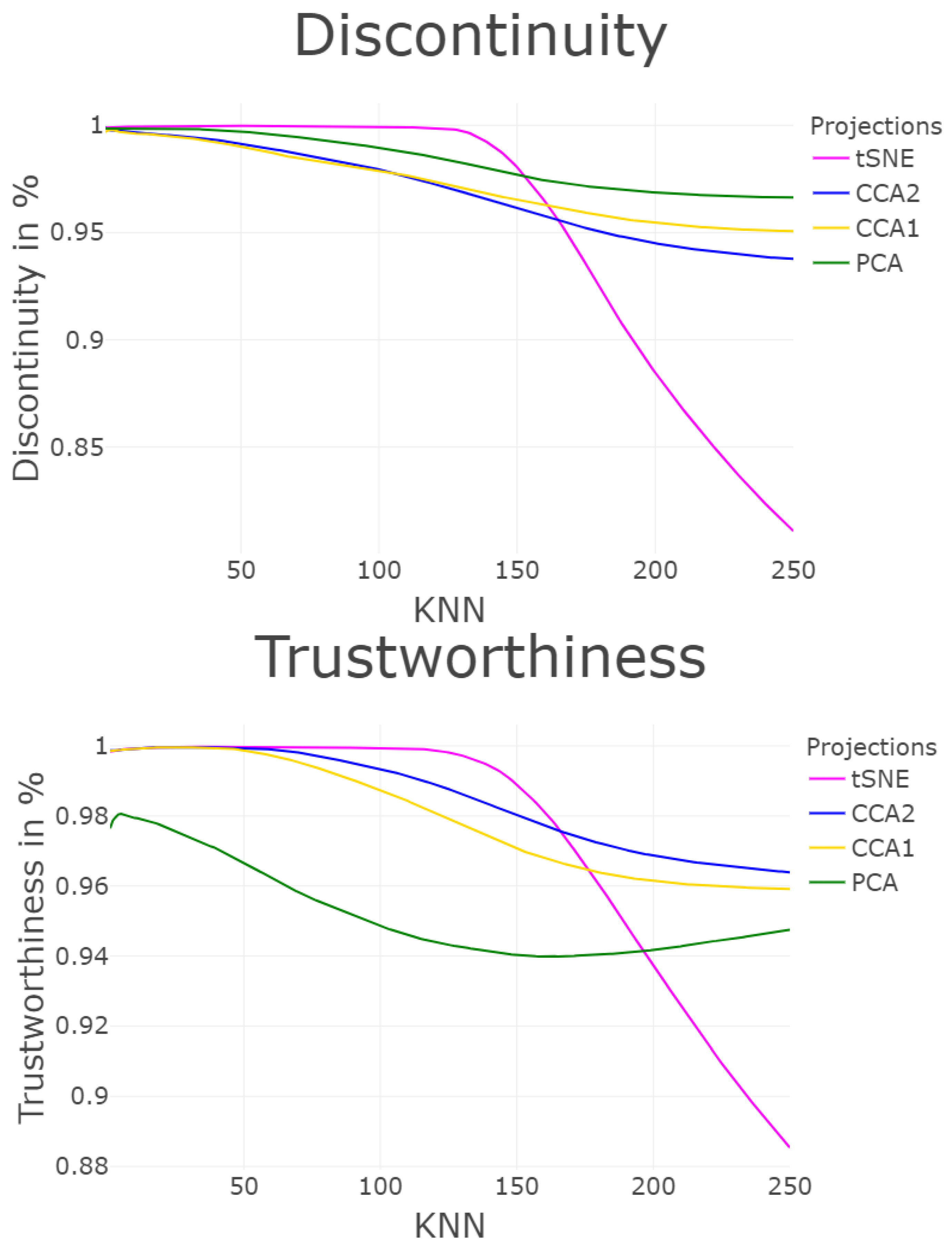
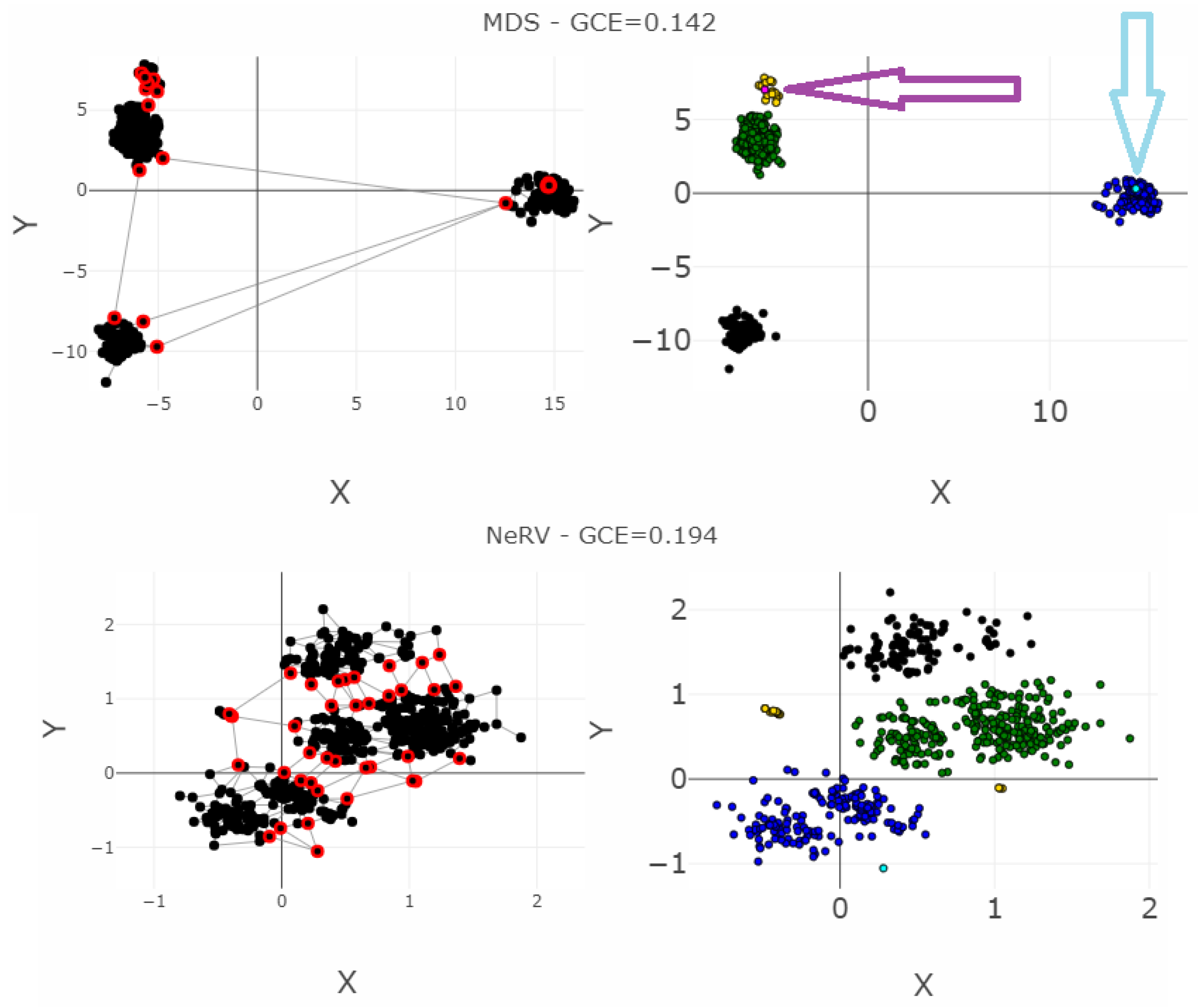
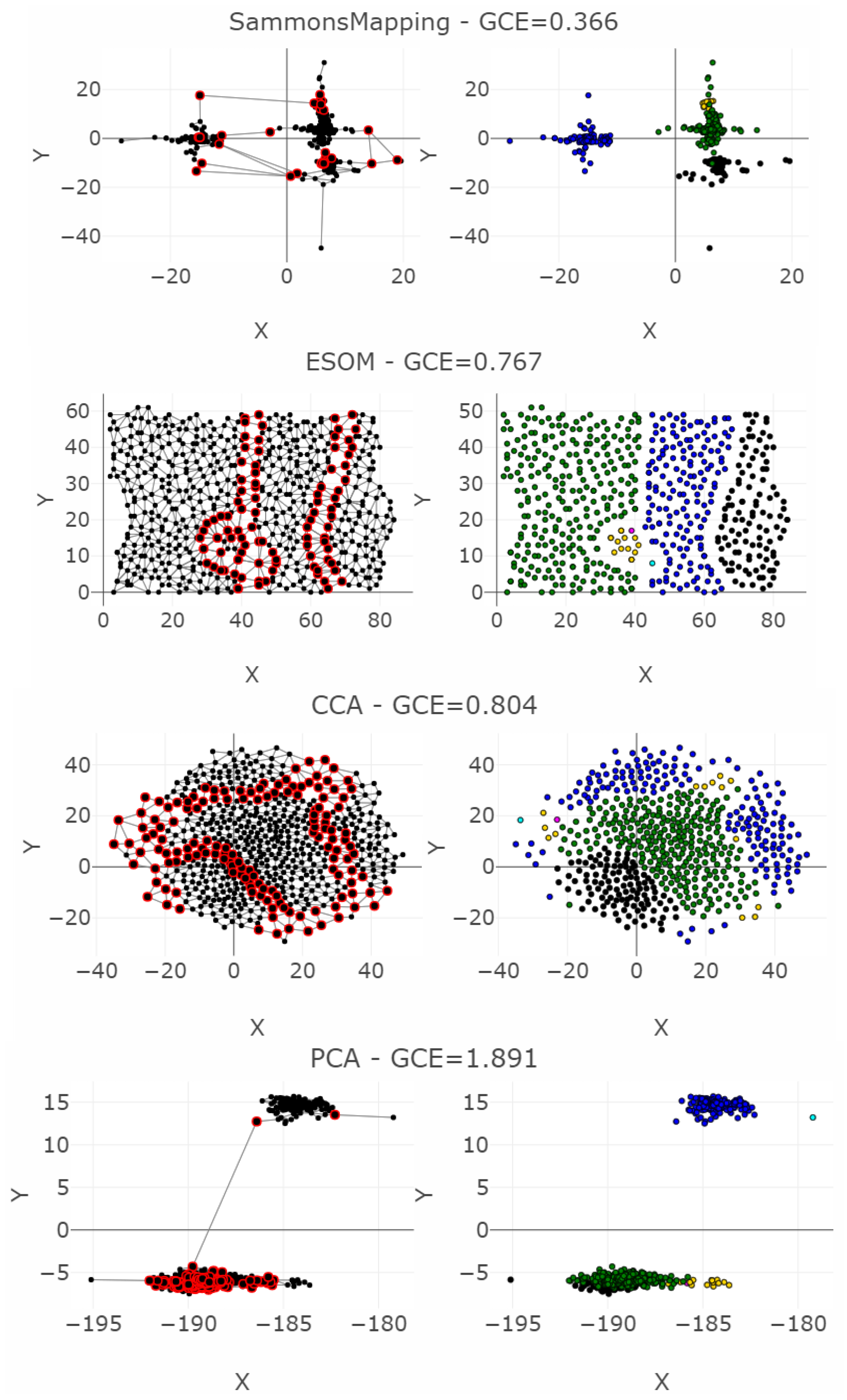
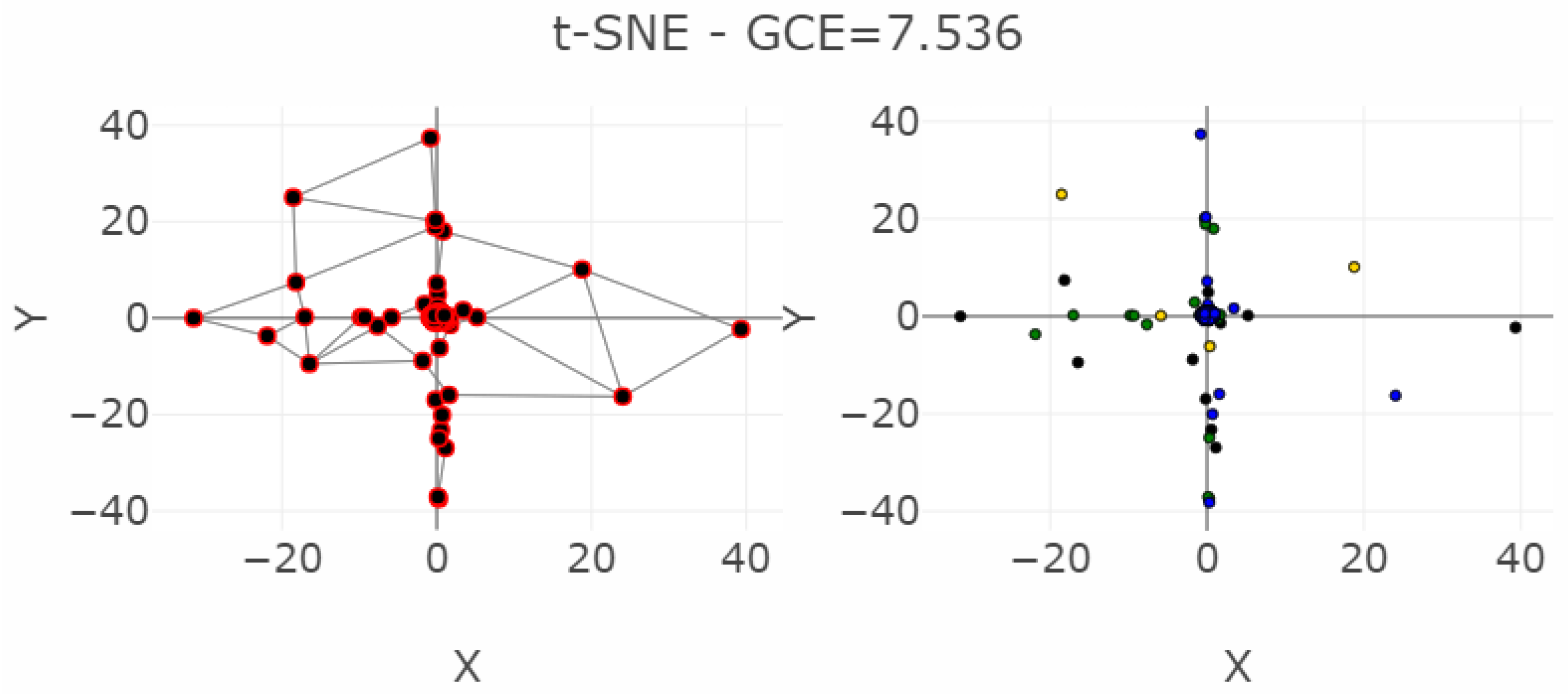
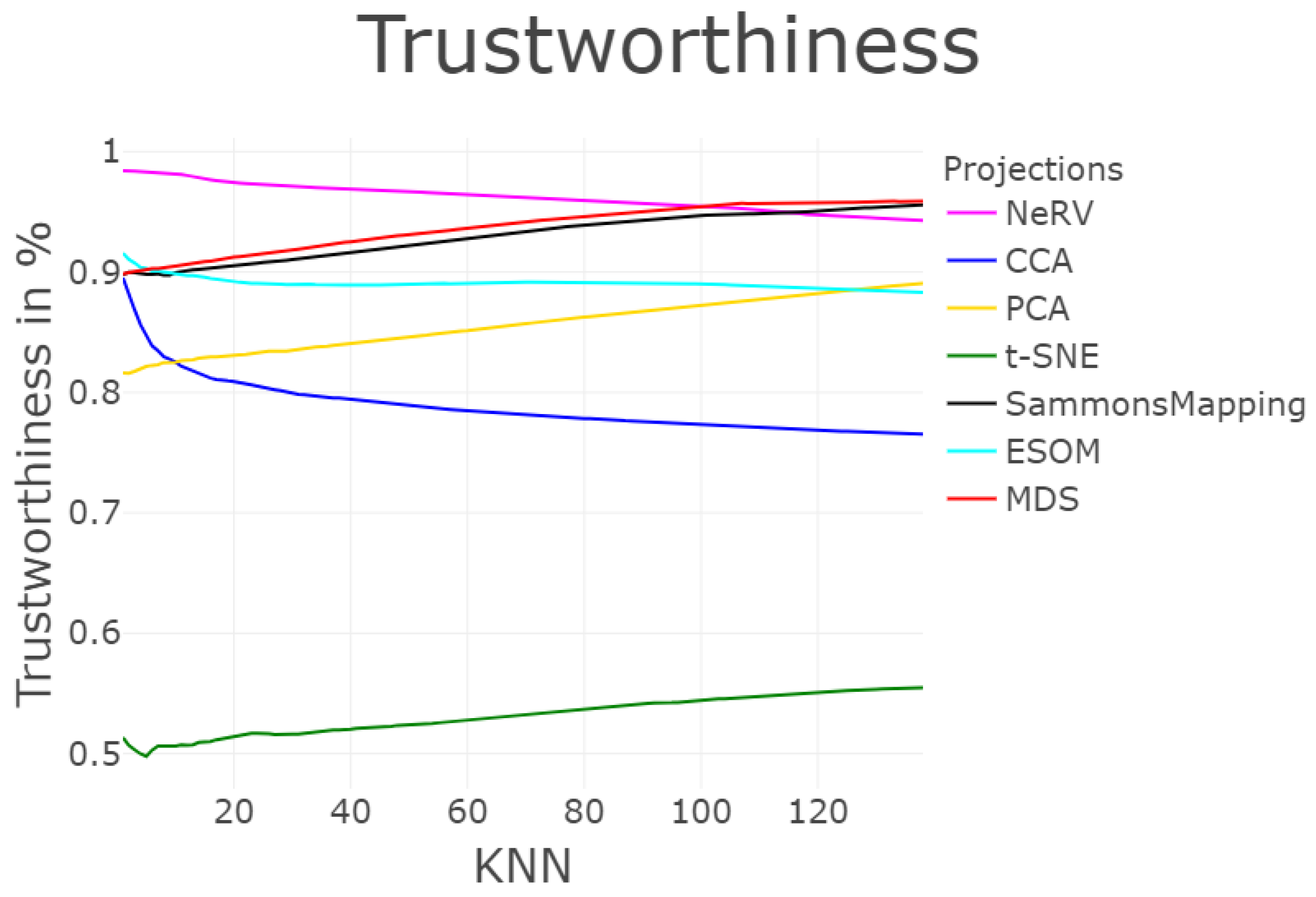
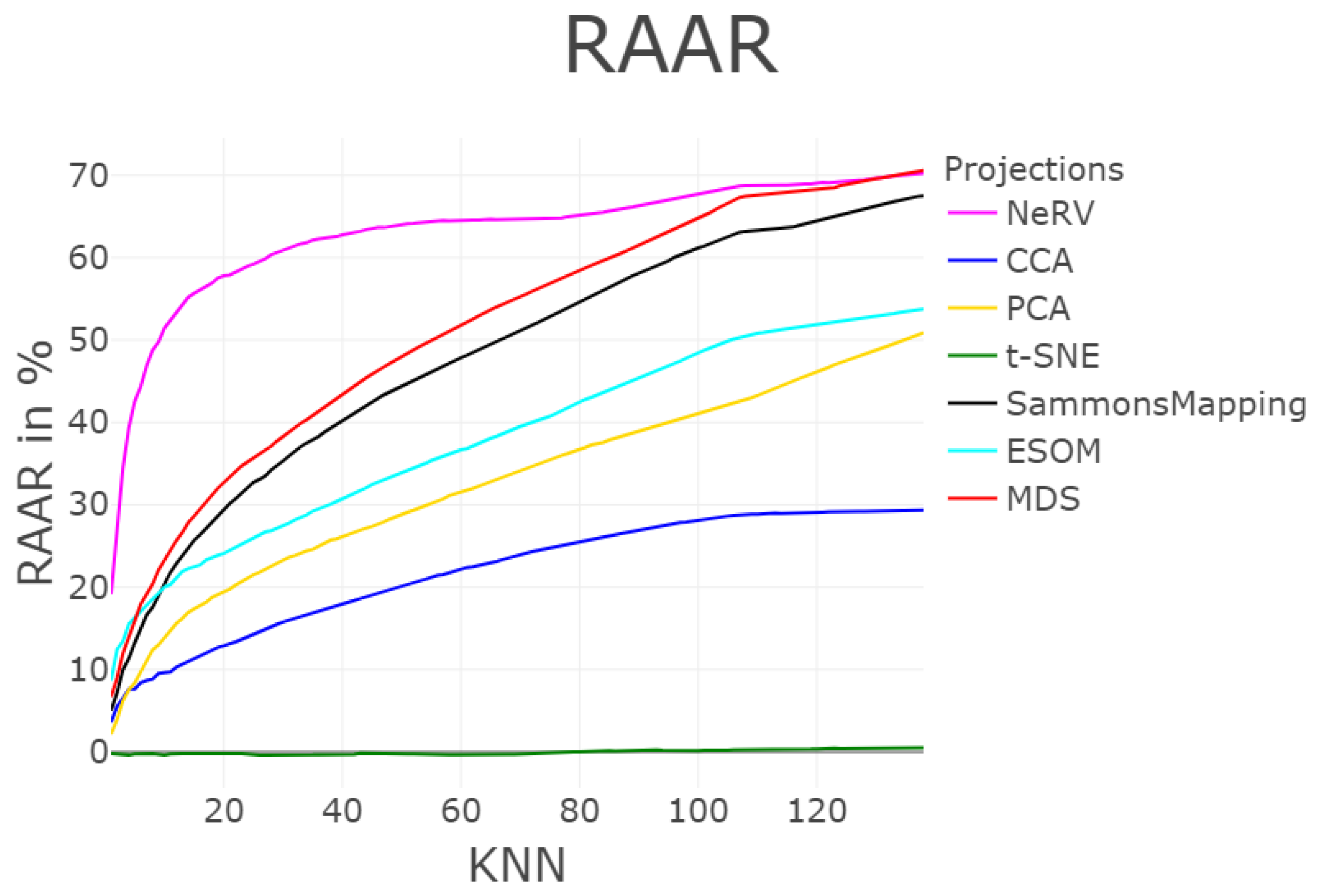
| DR | Cp | Cw | P | R | Zrehen | CE | AUC | TC | GCE | |
|---|---|---|---|---|---|---|---|---|---|---|
| UMA | 73.4 | 31.95 | 127 | 69.0 | 1.45 | 0 | 51.6 | 0.33 | 0.54 | 0.18 |
| PCA | 52.9 | 22.9 | 161 | 48.3 | 1.22 | 0 | 58.1 | 0.67 | 0.81 | 0.46 |
| CCA | 28.6 | 70.5 | 102 | 320 | 1.88 | 0.01 | 70.2 | 0.67 | 0.81 | 0.68 |
| t-SNE | 38.3 | 1170 | 1092 | 2300 | 12.2 | 0.02 | 61.8 | 0.19 | 0.33 | 1.26 |
| DR | Cp | Cw | P | R | Zrehen | CE | AUC | TC | GCE | |
|---|---|---|---|---|---|---|---|---|---|---|
| t-SNE | 29.9 | 168 | 177 | 140 | 2.11 | 0 | 76.7 | 0.26 | 0.50 | 0.07 |
| CCA 2 | 24.3 | 15.0 | 108 | 1298 | 0.52 | 0 | 80.7 | 0.67 | 0.90 | 0.21 |
| CCA 1 | 25.3 | 20.0 | 116 | 1705 | 0.74 | 0 | 79.3 | 0.68 | 0.91 | 0.24 |
| PCA | 76.0 | 14.4 | 9435 | 234 | 2.95 | 0.04 | 65.5 | 0.67 | 0.93 | 0.56 |
| DR | Cp | Cw | P | R | Zrehen | CE | AUC | TC | GCE | |
|---|---|---|---|---|---|---|---|---|---|---|
| MDS | 3547 | 58 | 2194 | 1074 | 0 | 0.004 | 27.69 | 0.95 | / | 0.141 |
| NeRV | 2992 | 18 | 684 | 1041 | 0.023 | 0.009 | 45.85 | 0.87 | / | 0.194 |
| SammonsMapping | 3494 | 305 | 2278 | 2686 | 0 | 0.013 | 24.57 | 0.90 | / | 0.366 |
| ESOM | 4988 | 1199 | 2879 | 7059 | 0.002 | 0.005 | 38.33 | 0.29 | / | 0.767 |
| CCA | 2746 | 3963 | 5289 | 22511 | 0.016 | 0.03 | 11.97 | 0.47 | / | 0.804 |
| PCA | 3959 | 83 | 5560 | 1220 | 0 | 0.173 | 16.15 | 0.86 | / | 1.891 |
| t-SNE | 6216 | 709 | 23629 | 29919 | 0.045 | 0.621 | −0.20 | 0.02 | / | 7.536 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thrun, M.C.; Märte, J.; Stier, Q. Analyzing Quality Measurements for Dimensionality Reduction. Mach. Learn. Knowl. Extr. 2023, 5, 1076-1118. https://doi.org/10.3390/make5030056
Thrun MC, Märte J, Stier Q. Analyzing Quality Measurements for Dimensionality Reduction. Machine Learning and Knowledge Extraction. 2023; 5(3):1076-1118. https://doi.org/10.3390/make5030056
Chicago/Turabian StyleThrun, Michael C., Julian Märte, and Quirin Stier. 2023. "Analyzing Quality Measurements for Dimensionality Reduction" Machine Learning and Knowledge Extraction 5, no. 3: 1076-1118. https://doi.org/10.3390/make5030056
APA StyleThrun, M. C., Märte, J., & Stier, Q. (2023). Analyzing Quality Measurements for Dimensionality Reduction. Machine Learning and Knowledge Extraction, 5(3), 1076-1118. https://doi.org/10.3390/make5030056






