Actionable Explainable AI (AxAI): A Practical Example with Aggregation Functions for Adaptive Classification and Textual Explanations for Interpretable Machine Learning
Abstract
1. Introduction and Motivation
2. Preliminaries of Classification by Rule-Based Systems, Neural Networks and Ordinal Sums
2.1. Classification by Rule-Based Systems
- IF A is LOW and B is LOW, then C is no
- IF A is LOW and B is HIGH, then C is maybe
- IF A is HIGH and B is LOW, then C is maybe
- IF A is HIGH and B is HIGH, then C is yes
- where A and B are atomic or compound attributes.
2.2. Classification by Neural Networks
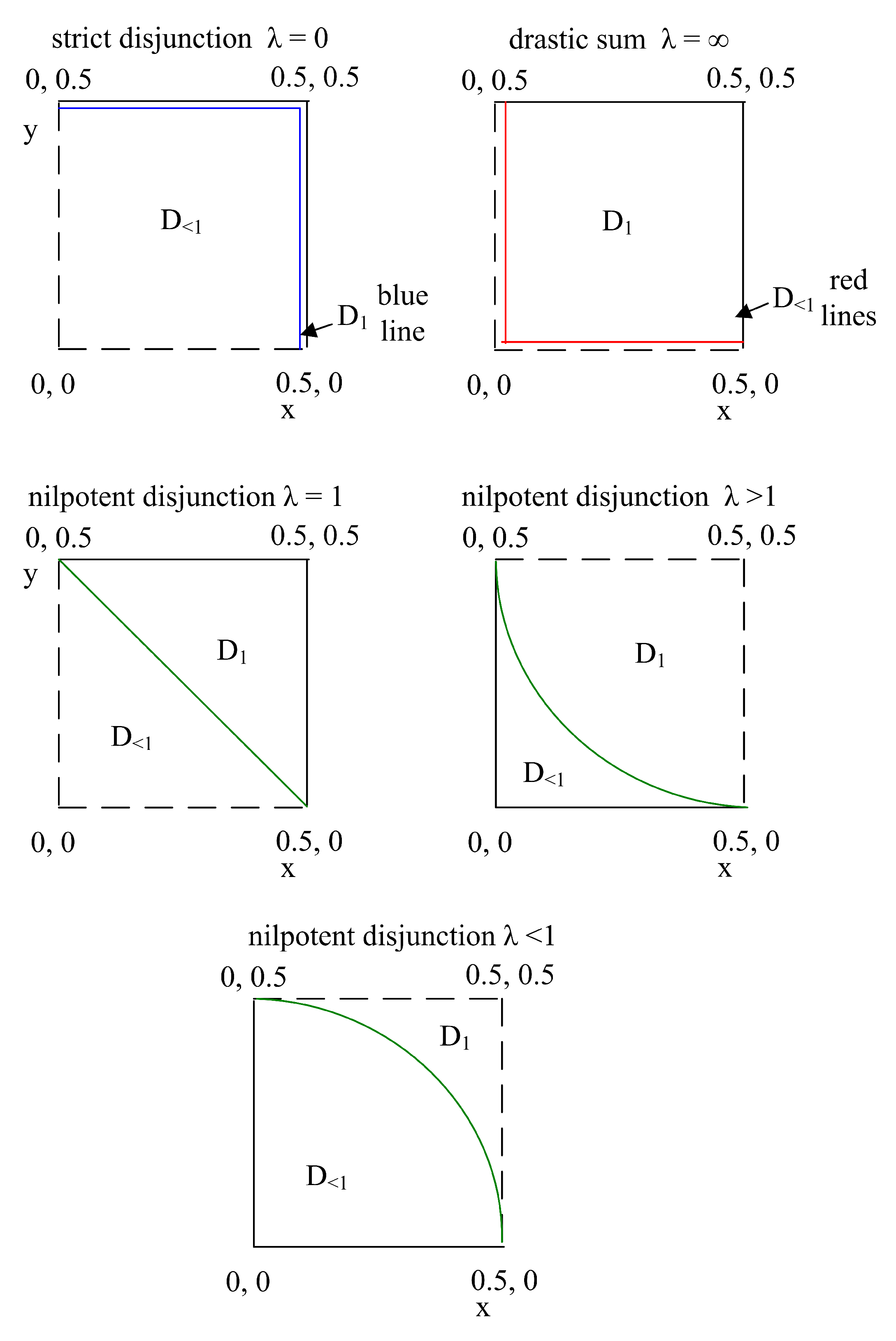
2.3. Classification of Ordinal Sums of Conjunctive and Disjunctive Functions
- 1.
- if , ,
- 2.
- if , ,
- 3.
- if
- 4.
- if
3. Learning Parameters from Data for Classifying by Ordinal Sums of Conjunctive and Disjunctive Functions Expressed by Nilpotent Functions
- For data points in the ML model learns parameters for strict or nilpotent conjunction to classify into class no
- For data points in the ML model learns parameters for strict or nilpotent disjunction to classify into class yes
- For data points in the ML model learns parameters for power means to classify into class maybe
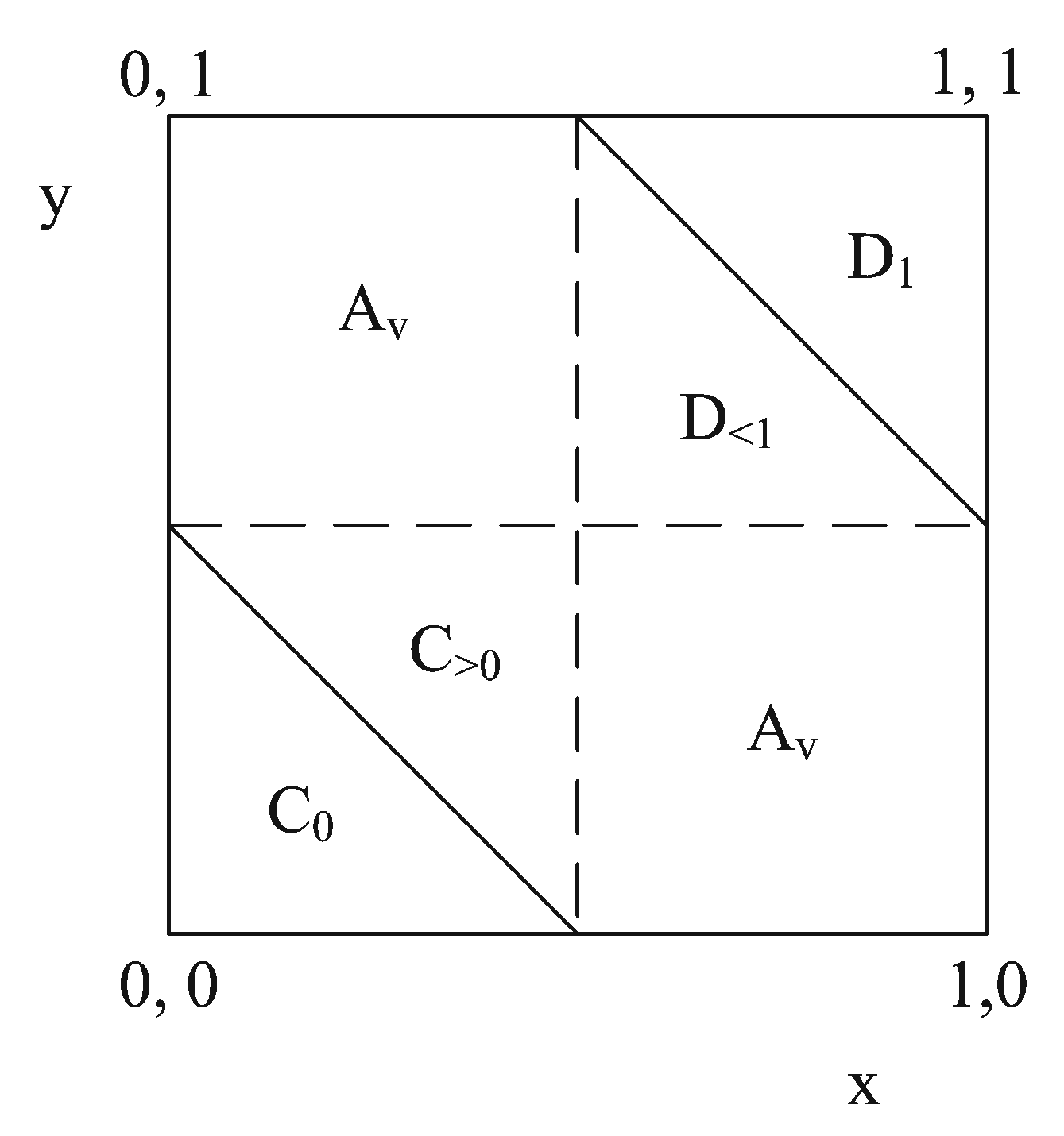
4. A New Dissimilarity Function for Classifying by XOR into Classes Yes, No and Maybe
- (QD1) ;
- (QD2) ;
- (QD3) ;
- (QD4) whenever ;
- (QD5) and whenever .
- , ;
- ;
- .
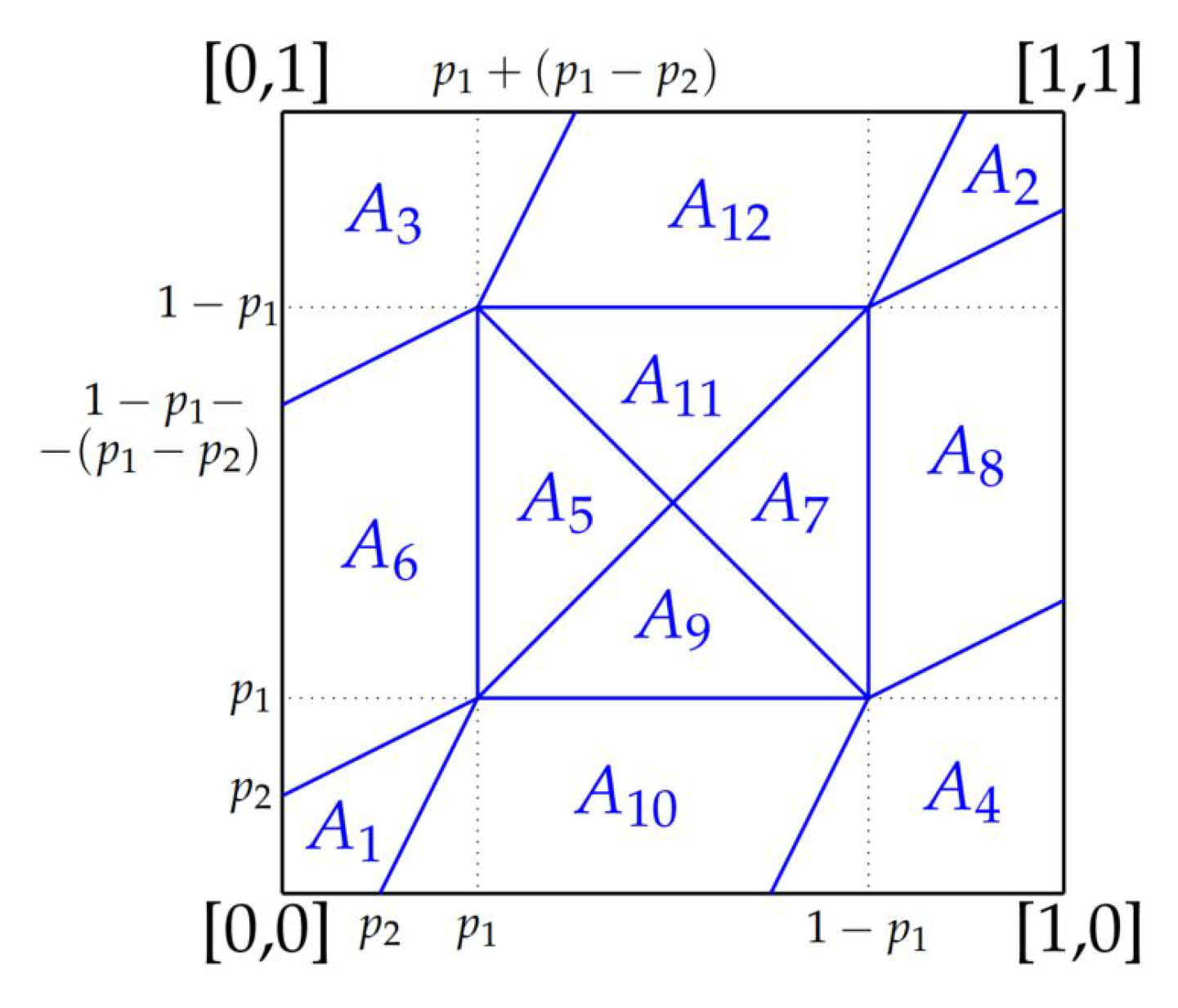

5. Parameter Learning in Classification by Ordinal Sums with Evolutionary Algorithm and Reinforcement Learning
5.1. Parameter Learning for Conjunctive and Averaging Functions
- —Clear no
- —Very significant inclination to no
- Avg—Averaging functions with possible inclination to no or yes
- —Very significant inclination to yes
- —Clear yes
5.1.1. Averaging Behaviour for Class Maybe
- : Neutral
- : Optimistic—A bit inclination to yes
- : Pessimistic—A bit inclination to no
5.1.2. Conjunctive Behaviour for Class No
- For area : and
- For area :
- : Linear case, i.e.,
- : More restrictive, for instance , for
- : Less restrictive, for instance , for
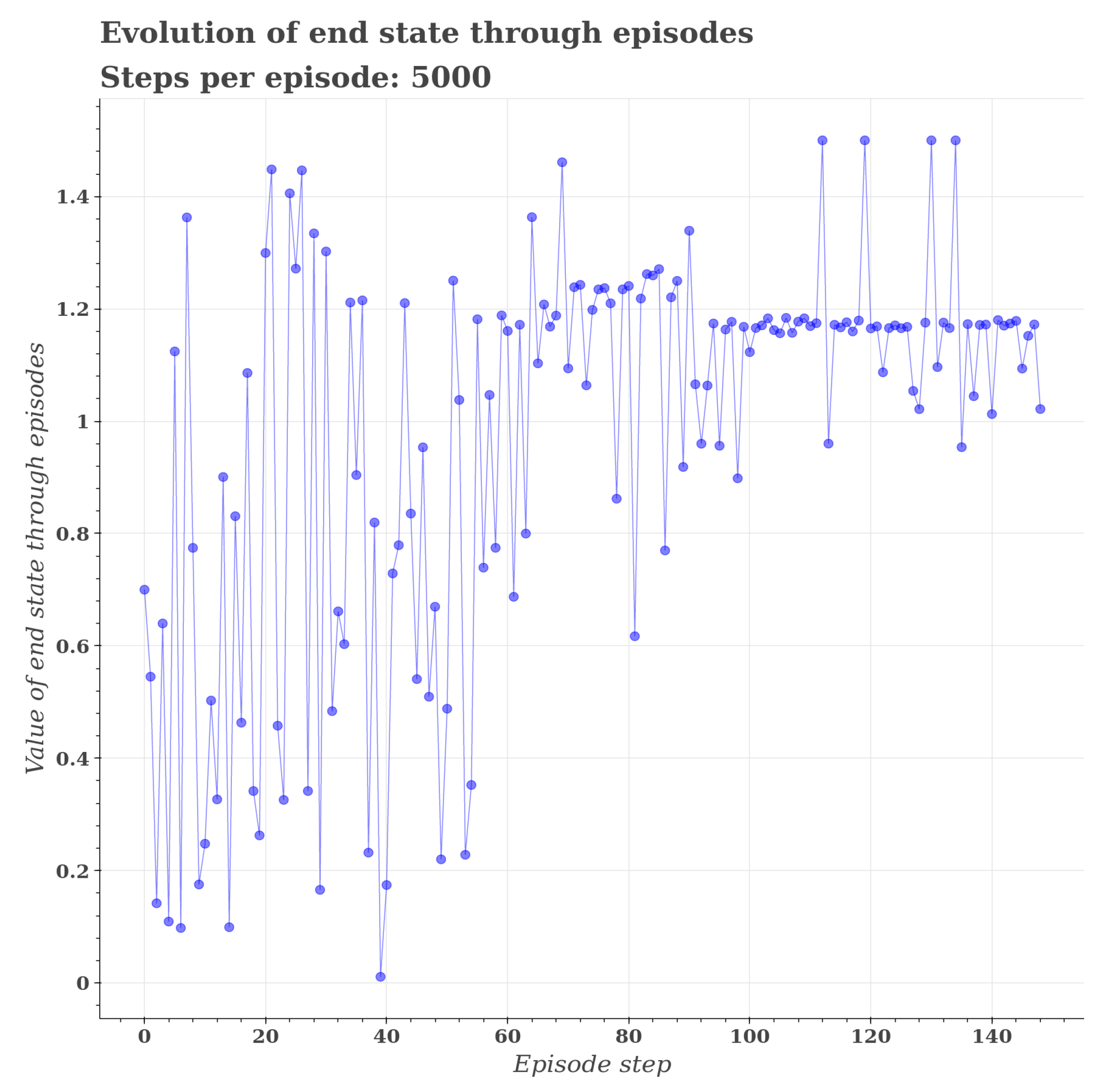
5.1.3. Implementation of Parameter Estimation from Synthetically Generated Noisy Data with an Evolutionary Algorithm
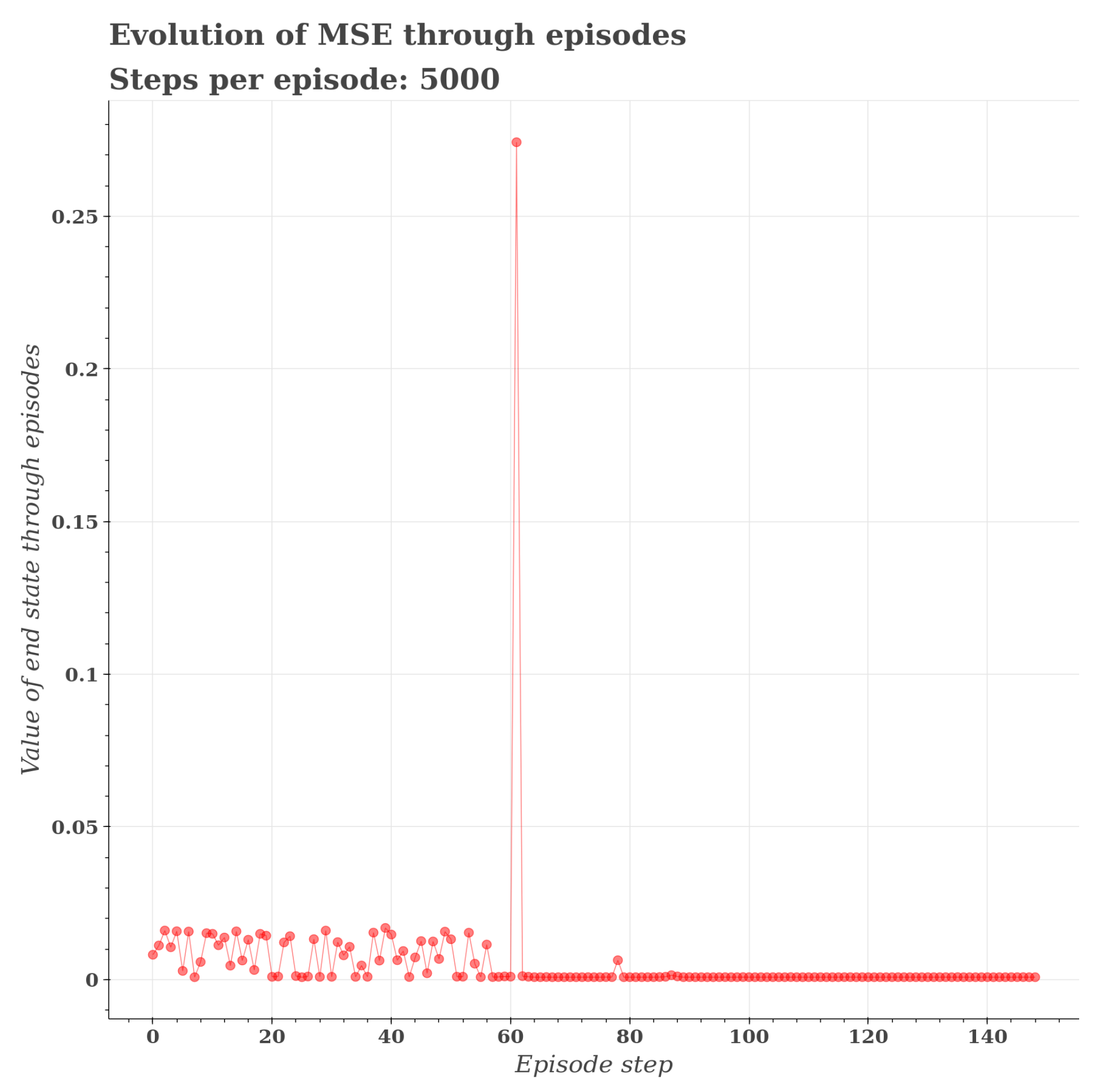
5.1.4. Implementation of Parameter Estimation from Synthetically Generated Noisy Data with Reinforcement Learning
6. Experiment on Medical Data for Classification by Ordinal Sums
6.1. Dataset Information
6.2. Data Preprocessing
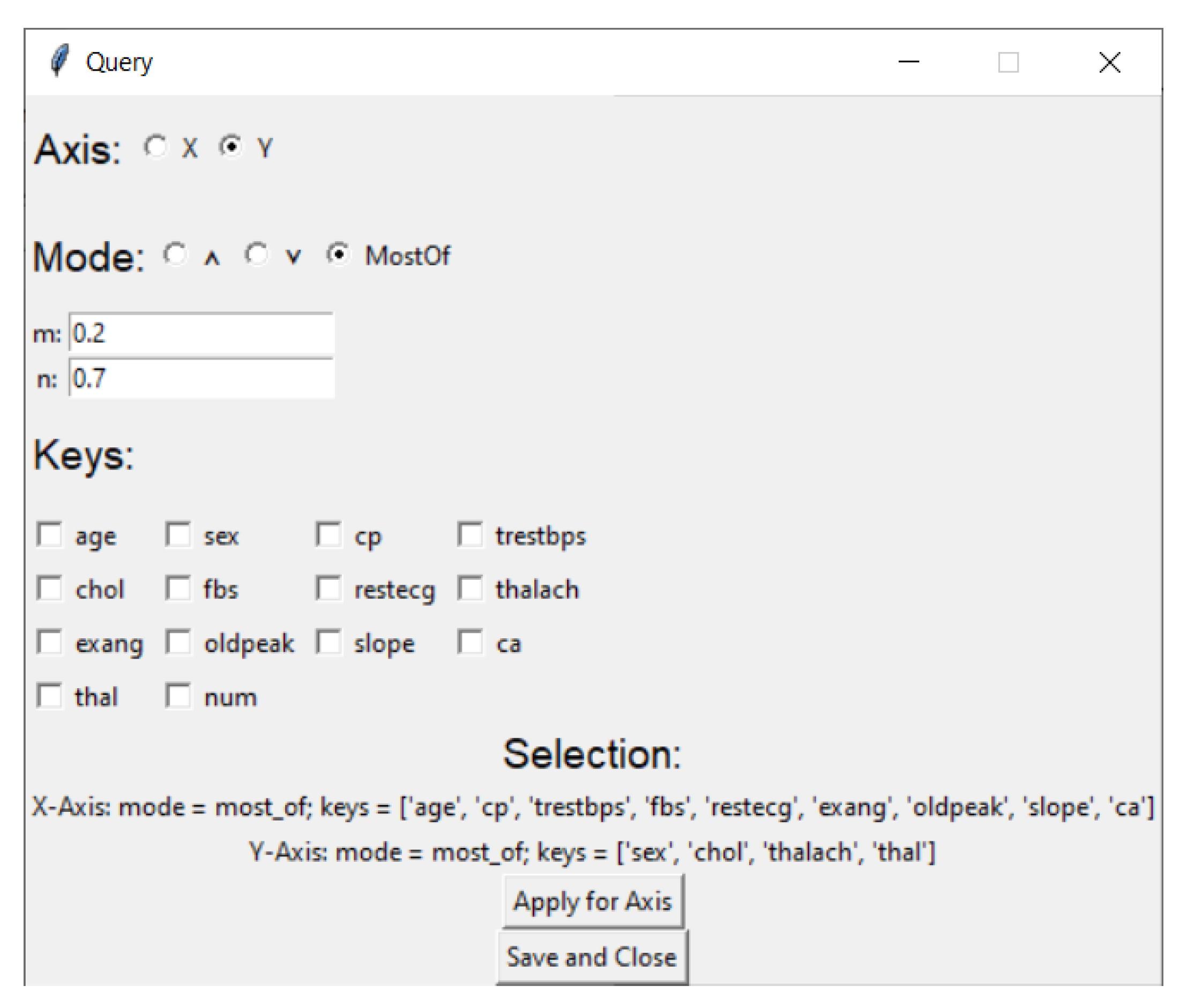
6.3. Tool Navigation
6.4. Fitting Parameters
- m: 0.2
- n: 0.7
- x axis: [age, cp, trestbps, fbs, restecg, exang, oldpeak, slope, ca]
- y axis: [sex, chol, thalach, thal]

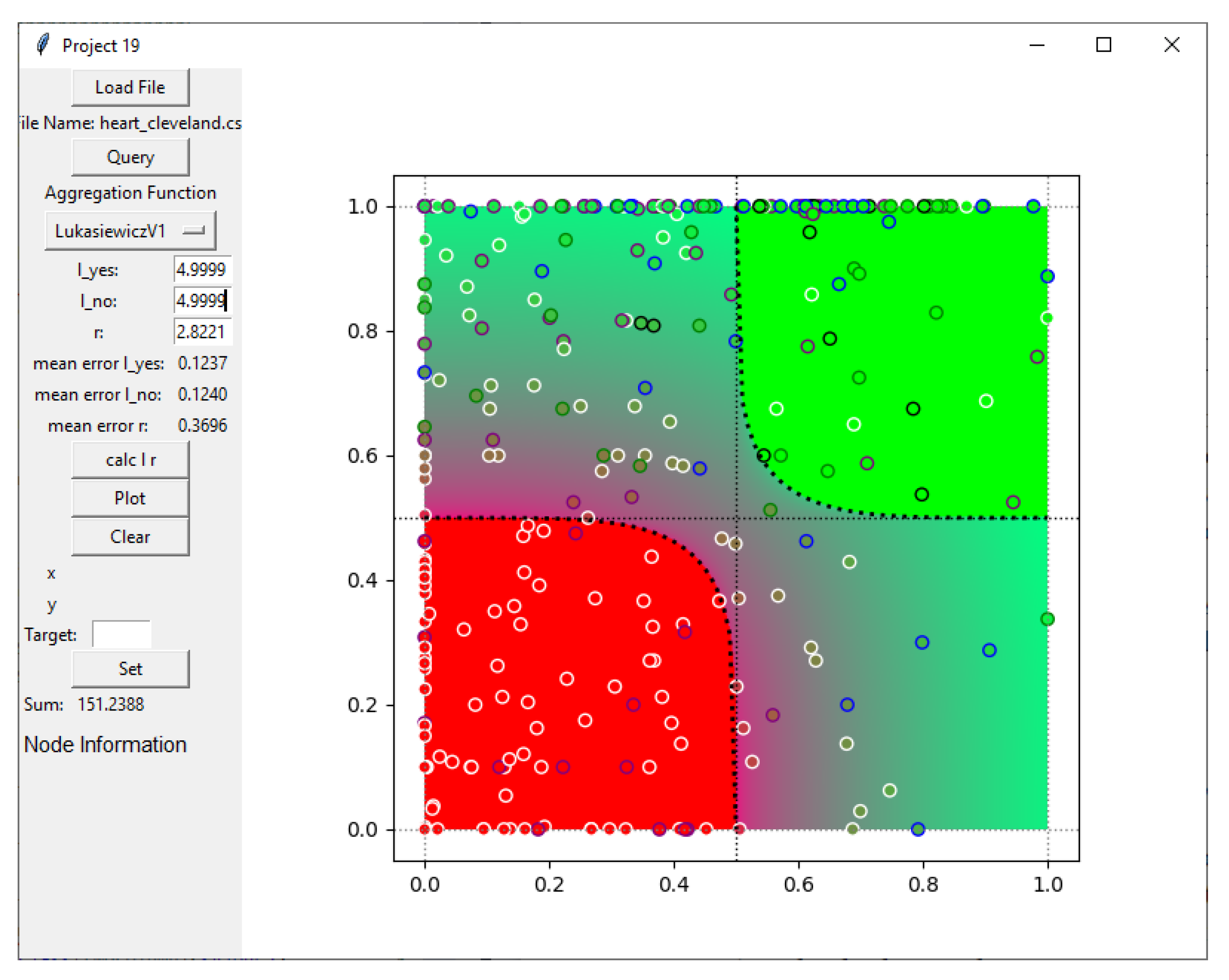
6.5. Adjusting and r
6.6. Interpretation of the Visualisation
7. Discussion and Future Works
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bartoszuk, M.; Gagolewski, M. T-norms or t-conorms? How to aggregate similarity degrees for plagiarism detection. Knowl.-Based Syst. 2021, 231, 107427. [Google Scholar] [CrossRef]
- Patricia, M.; Daniel, S. Optimal design of type-2 fuzzy systems for diabetes classification based on genetic algorithms. Int. J. Hybrid Intell. Syst. 2021, 17, 15–32. [Google Scholar]
- Hudec, M.; Minarikova, E.; Mesiar, R.; Saranti, A.; Holzinger, A. Classification by ordinal sums of conjunctive and disjunctive functions for explainable AI and interpretable machine learning solutions. Knowl. Based Syst. 2021, 220, 106916. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic = computing with words. IEEE Trans. Fuzzy Syst. 1996, 4, 103–111. [Google Scholar] [CrossRef]
- Alonso, J.M.; Castiello, C.; Magdalena, L.; Mencar, C. Explainable Fuzzy Systems; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Wei, Z.; Man, L.; Zeshui, X.; Herrera-Viedma, E. Global fusion of multiple order relations and hesitant fuzzy decision analysis. Appl. Intell. 2021, 52, 6866–6888. [Google Scholar] [CrossRef]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Murray, B.; Anderson, D.T.; Havens, T.C. Actionable XAI for the Fuzzy Integral. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Virtual, 11–14 July 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Zhou, J.; Gandomi, A.H.; Chen, F.; Holzinger, A. Evaluating the Quality of Machine Learning Explanations: A Survey on Methods and Metrics. Electronics 2021, 10, 593. [Google Scholar] [CrossRef]
- Holzinger, A.; Saranti, A.; Molnar, C.; Biececk, P.; Samek, W. Explainable AI Methods - A Brief Overview. In XXAI-Lecture Notes in Artificial Intelligence LNAI 13200; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Shehab, M.; Abualigah, L.; Shambour, Q.; Abu-Hashem, M.A.; Shambour, M.K.Y.; Alsalibi, A.I.; Gandomi, A.H. Machine learning in medical applications: A review of state-of-the-art methods. Comput. Biol. Med. 2022, 145, 105458. [Google Scholar] [CrossRef]
- Holzinger, A.; Saranti, A.; Angerschmid, A.; Retzlaff, C.O.; Gronauer, A.; Pejakovic, V.; Medel, F.; Krexner, T.; Gollob, C.; Stampfer, K. Digital Transformation in Smart Farm and Forest Operations needs Human-Centered AI: Challenges and Future Directions. Sensors 2022, 22, 3043. [Google Scholar] [CrossRef]
- Hoenigsberger, F.; Saranti, A.; Angerschmid, A.; Retzlaff, C.O.; Gollob, C.; Witzmann, S.; Nothdurft, A.; Kieseberg, P.; Holzinger, A.; Stampfer, K. Machine Learning and Knowledge Extraction to Support Work Safety for Smart Forest Operations. In Proceedings of the International Cross-Domain Conference for Machine Learning and Knowledge Extraction, Vienna, Austria, 23–26 August 2022; pp. 362–375. [Google Scholar] [CrossRef]
- Holzinger, A.; Stampfer, K.; Nothdurft, A.; Gollob, C.; Kieseberg, P. Challenges in Artificial Intelligence for Smart Forestry. Eur. Res. Consort. Informatics Math. (ERCIM) News 2022, 130, 40–41. [Google Scholar]
- Holzinger, A. The Next Frontier: AI We Can Really Trust. In Proceedings of the ECML PKDD 2021, CCIS 1524, Bilbao, Spain, 13–17 September 2022; Kamp, M., Ed.; Springer Nature: Berlin/Heidelberg, Germany, 2021; pp. 427–440. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Araújo, T.; Aresta, G.; Castro, E.; Rouco, J.; Aguiar, P.; Eloy, C.; Polónia, A.; Campilho, A. Classification of breast cancer histology images using convolutional neural networks. PLoS ONE 2017, 12, e0177544. [Google Scholar] [CrossRef]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef]
- Burt, J.R.; Torosdagli, N.; Khosravan, N.; RaviPrakash, H.; Mortazi, A.; Tissavirasingham, F.; Hussein, S.; Bagci, U. Deep learning beyond cats and dogs: Recent advances in diagnosing breast cancer with deep neural networks. Br. J. Radiol. 2018, 91, 20170545. [Google Scholar] [CrossRef]
- Stoeger, K.; Schneeberger, D.; Kieseberg, P.; Holzinger, A. Legal aspects of data cleansing in medical AI. Comput. Law Secur. Rev. 2021, 42, 105587. [Google Scholar] [CrossRef]
- French, R.M. Catastrophic forgetting in connectionist networks. Trends Cogn. Sci. 1999, 3, 128–135. [Google Scholar] [CrossRef]
- Novak, R.; Bahri, Y.; Abolafia, D.A.; Pennington, J.; Sohl-Dickstein, J. Sensitivity and generalization in neural networks: An empirical study. In Proceedings of the International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Stoeger, K.; Schneeberger, D.; Holzinger, A. Medical Artificial Intelligence: The European Legal Perspective. Commun. ACM 2021, 64, 34–36. [Google Scholar] [CrossRef]
- Holzinger, A.; Mueller, H. Toward Human-AI Interfaces to Support Explainability and Causability in Medical AI. IEEE Comput. 2021, 54, 78–86. [Google Scholar] [CrossRef]
- Bedregal, B.C.; Reiser, R.H.; Dimuro, G.P. Xor-implications and E-implications: Classes of fuzzy implications based on fuzzy Xor. Electron. Notes Theor. Comput. Sci. 2009, 247, 5–18. [Google Scholar] [CrossRef]
- Mesiar, R.; Kolesarova, A.; Komornikova, M. Aggregation Functions on [0, 1]. In Springer Handbook of Computational Intelligence; Kacprzyk, J., Pedrycz, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 61–74. [Google Scholar]
- Couso, I.; Garrido, L.; Sánchez, L. Similarity and dissimilarity measures between fuzzy sets: A formal relational study. Inf. Sci. 2013, 229, 122–141. [Google Scholar] [CrossRef]
- Bustince, H.; Mesiar, R.; Fernandez, J.; Galar, M.; Paternain, D.; Altalhi, A.; Dimuro, G.; Bedregal, B.; Takáč, Z. d-Choquet integrals: Choquet integrals based on dissimilarities. Fuzzy Sets Syst. 2021, 414, 1–27. [Google Scholar] [CrossRef]
- Kuncheva, L. Fuzzy Classifier Design; Physica-Verlag: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Holzinger, A.; Plass, M.; Kickmeier-Rust, M.; Holzinger, K.; Crişan, G.C.; Pintea, C.M.; Palade, V. Interactive machine learning: Experimental evidence for the human in the algorithmic loop. Appl. Intell. 2019, 49, 2401–2414. [Google Scholar] [CrossRef]
- Lippmann, R.P. Pattern classification using neural networks. IEEE Commun. Mag. 1989, 27, 47–50. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Keller, J.; Deroung, L.; Fogel, D. Fundamentals of Computational Intelligence; IEEE Press Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Aggarwal, C.C. Neural Networks and Deep Learning; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Chollet, F. Deep Learning with Python; Simon and Schuster: New York, NY, USA, 2021. [Google Scholar]
- Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.R.; Samek, W. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS ONE 2015, 10, e0130140. [Google Scholar] [CrossRef]
- Alber, M.; Lapuschkin, S.; Seegerer, P.; Hägele, M.; Schütt, K.T.; Montavon, G.; Samek, W.; Müller, K.R.; Dähne, S.; Kindermans, P.J. iNNvestigate neural networks! J. Mach. Learn. Res. (JMLR) 2019, 20, 1–8. [Google Scholar]
- Yeom, S.K.; Seegerer, P.; Lapuschkin, S.; Binder, A.; Wiedemann, S.; Müller, K.R.; Samek, W. Pruning by explaining: A novel criterion for deep neural network pruning. Pattern Recognit. 2021, 115, 107899. [Google Scholar] [CrossRef]
- De Baets, B.; Mesiar, R. Ordinal sums of aggregation operators. In Technologies for Constructing Intelligent Systems 2; Springer: Berlin/Heidelberg, Germany, 2002; pp. 137–147. [Google Scholar]
- Durante, F.; Sempi, C. Semicopulae. Kybernetika 2005, 41, 315–328. [Google Scholar]
- Dujmovic, J. Soft Computing Evaluation Logic: The LSP Decision Method and Its Applications; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Schweizer, B.; Sklar, A. Statistical metric spaces. Pac. J. Math. 1960, 10, 313–334. [Google Scholar] [CrossRef]
- Beliakov, G.; Pradera, A.; Calvo, T. Aggregation Functions: A Guide for Practitioners; Springer: Berlin/Heidelberg, Germany, 2007; Volume 221. [Google Scholar]
- Liu, X. Entropy, distance measure and similarity measure of fuzzy sets and their relations. Fuzzy Sets Syst. 1992, 52, 305–318. [Google Scholar] [CrossRef]
- Takáč, Z.; Uriz, M.; Galar, M.; Paternain, D.; Bustince, H. Discrete IV dG-Choquet integrals with respect to admissible orders. Fuzzy Sets Syst. 2022, 441, 169–195. [Google Scholar] [CrossRef]
- Minkowski, H. Geometrie der Zahlen; BG Teubner; Springer: Berlin/Heidelberg, Germany, 1910. [Google Scholar]
- Kochenderfer, M.J.; Wheeler, T.A. Algorithms for Optimization; MIT Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Buontempo, F. Genetic Algorithms and Machine Learning for Programmers: Create AI Models and Evolve Solutions; The Pragmatic Bookshelf; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Morales, M. Grokking Deep Reinforcement Learning; Manning Publications: Shelter Island, NY, USA, 2020. [Google Scholar]
- Graesser, L.; Keng, W.L. Foundations of Deep Reinforcement Learning: Theory and Practice in Python; Addison-Wesley Professional: Boston, MA, USA, 2019. [Google Scholar]
- Seijen, H.; Sutton, R. True online TD (lambda). In Proceedings of the International Conference on Machine Learning, PMLR, Reykjavik, Iceland, 22–25 April 2014; pp. 692–700. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Detrano, R. The Cleveland Heart Disease Data Set; VA Medical Center, Long Beach and Cleveland Clinic Foundation: Long Beach, CA, USA, 1988.
- Pouriyeh, S.; Vahid, S.; Sannino, G.; De Pietro, G.; Arabnia, H.; Gutierrez, J. A comprehensive investigation and comparison of machine learning techniques in the domain of heart disease. In Proceedings of the 2017 IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July 2017; pp. 204–207. [Google Scholar]
- Haq, A.U.; Li, J.P.; Memon, M.H.; Nazir, S.; Sun, R. A hybrid intelligent system framework for the prediction of heart disease using machine learning algorithms. Mob. Inf. Syst. 2018, 2018, 3860146. [Google Scholar] [CrossRef]
- Nahar, J.; Imam, T.; Tickle, K.S.; Chen, Y.P.P. Computational intelligence for heart disease diagnosis: A medical knowledge driven approach. Expert Syst. Appl. 2013, 40, 96–104. [Google Scholar] [CrossRef]
- Detrano, R.; Janosi, A.; Steinbrunn, W.; Pfisterer, M.; Schmid, J.J.; Sandhu, S.; Guppy, K.H.; Lee, S.; Froelicher, V. International application of a new probability algorithm for the diagnosis of coronary artery disease. Am. J. Cardiol. 1989, 64, 304–310. [Google Scholar] [CrossRef]
- Kannel, W.B.; Feinleib, M. Natural history of angina pectoris in the Framingham study: Prognosis and survival. Am. J. Cardiol. 1972, 29, 154–163. [Google Scholar] [CrossRef]
- Detrano, R.; Yiannikas, J.; Salcedo, E.E.; Rincon, G.; Go, R.; Williams, G.; Leatherman, J. Bayesian probability analysis: A prospective demonstration of its clinical utility in diagnosing coronary disease. Circulation 1984, 69, 541–547. [Google Scholar] [CrossRef]
- Mesquita, A.; Trabulo, M.; Mendes, M.; Viana, J.; Seabra-Gomes, R. The maximum heart rate in the exercise test: The 220-age formula or Sheffield’s table? Rev. Port. Cardiol. Orgao Of. Soc. Port. Cardiol. Port. J. Cardiol. Off. J. Port. Soc. Cardiol. 1996, 15, 139–144. [Google Scholar]
- Abdar, M. Using decision trees in data mining for predicting factors influencing of heart disease. Carpathian J. Electron. Comput. Eng. 2015, 8, 31. [Google Scholar]
- McKinney, W. Python for Data Analysis: Data Wrangling with Pandas, NumPy, and IPython; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2012. [Google Scholar]
- Sojka, P.; Hudec, M.; Švaňa, M. Linguistic Summaries in Evaluating Elementary Conditions, Summarizing Data and Managing Nested Queries. Informatica 2020, 31, 841–856. [Google Scholar] [CrossRef]
- Kacprzyk, J.; Zadrożny, S. Protoforms of linguistic database summaries as a human consistent tool for using natural language in data mining. Int. J. Softw. Sci. Comput. Intell. 2009, 1, 100–111. [Google Scholar] [CrossRef]
- Jeanquartier, F.; Jean-Quartier, C.; Holzinger, A. Integrated web visualizations for protein-protein interaction databases. BMC Bioinform. 2015, 16, 195. [Google Scholar] [CrossRef] [PubMed]
- Holzinger, A.; Malle, B.; Saranti, A.; Pfeifer, B. Towards Multi-Modal Causability with Graph Neural Networks enabling Information Fusion for explainable AI. Inf. Fusion 2021, 71, 28–37. [Google Scholar] [CrossRef]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019. [Google Scholar]
- MacKay, D.J.; Mac Kay, D.J. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]







| 1.25 | 1.25 | 1.25 | 1.25 | 0.75 | 1.25 | 1.25 | 1.25 | 1.25 | 1.25 | |
| x | 0.01 | 0.25 | 0.26 | 0.23 | 0.25 | 0.27 | 0.05 | 0.49 | 0.22 | 0.48 |
| y | 0.41 | 0.48 | 0.39 | 0.34 | 0.35 | 0.30 | 0.49 | 0.49 | 0.06 | 0 |
| solution | 0 | 0.22 | 0.12 | 0 | 0.12 | 0 | 0.03 | 0.47 | 0 | 0 |
| 1.25 | 1.25 | 1.25 | 0.75 | 1.25 | 1.25 | 1.25 | 1.25 | 1.25 | 1.25 | |
| x | 0.50 | 0.39 | 0.03 | 0.20 | 0.09 | 0.25 | 0.40 | 0.11 | 0.10 | 0.35 |
| y | 0.13 | 0.39 | 0.20 | 0.30 | 0.20 | 0.09 | 0.49 | 0.50 | 0.10 | 0.07 |
| solution | 0.13 | 0.27 | 0 | 0.05 | 0 | 0 | 0.38 | 0.11 | 0 | 0 |
| 1 | 1.25 | 1.25 | 1.25 | 1.25 | 1.25 | 1.25 | 1 | |||
| x | 0.25 | 0.46 | 0.46 | 0.50 | 0.21 | 0.50 | 0.11 | 0.19 | ||
| y | 0.44 | 0 | 0.03 | 0.24 | 0.24 | 0.03 | 0.32 | 0.35 | ||
| solution | 0.19 | 0 | 0 | 0.24 | 0 | 0.03 | 0 | 0.04 |
| r | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 1.25 | 0.75 | 0.75 | 0.75 | 0.75 |
| x | 0.42 | 0.37 | 0.26 | 0.10 | 0.29 | 0.29 | 0.42 | 0.32 | 0.36 | 0.35 |
| y | 0.80 | 0.57 | 0.95 | 0.55 | 0.67 | 0.70 | 0.98 | 0.78 | 0.99 | 0.63 |
| solution | 0.70 | 0.43 | 0.65 | 0.13 | 0.44 | 0.51 | 0.88 | 0.57 | 0.82 | 0.46 |
| r | 1 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 1.25 | 0.75 | 0.75 | 0.75 |
| x | 0.0 | 0.14 | 0.31 | 0.36 | 0.37 | 0.47 | 0.12 | 0.38 | 0.34 | 0.44 |
| y | 1.0 | 0.69 | 0.96 | 0.60 | 0.92 | 0.57 | 0.59 | 0.78 | 0.57 | 0.73 |
| solution | 0.5 | 0.28 | 0.73 | 0.45 | 0.76 | 0.53 | 0.23 | 0.64 | 0.40 | 0.66 |
| r | 0.75 | 0.75 | 0.75 | 1 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | |
| x | 0.46 | 0.50 | 0.36 | 0.20 | 0.01 | 0.17 | 0.45 | 0.47 | 0.02 | |
| y | 0.56 | 0.50 | 0.74 | 0.80 | 0.63 | 0.56 | 0.71 | 0.68 | 0.98 | |
| solution | 0.51 | 0.50 | 0.58 | 0.50 | 0.07 | 0.21 | 0.65 | 0.64 | 0.33 |
| Label | Min Limit | Max Limit | Description |
|---|---|---|---|
| age | 40 | 65 | Age in years |
| sex | 0 | 1 | Sex |
| cp | 2 | 1 | Chest pain type |
| trestbps | 120 | 140 | Resting blood pressure in mm Hg |
| chol | 180 | 300 | Serum cholesterol in mg/dL |
| fbs | 0 | 1 | Fasting blood sugar |
| restecg | 0 | 2 | Resting electrocardiographic results |
| thalach | 160 | 120 | Maximum heart rate during exercise electrocardiogram. |
| exang | 0 | 1 | Exercise-induced angina |
| oldpeak | 0 | 4.4 | ST depression relative to rest (mV) |
| slope | 1 | 3 | The slope of the peak exercise ST segment (1 = upsloping, 2 = flat, 3 = downsloping) |
| ca | 0 | 3 | Number of major vessels coloured by fluoroscopy |
| thal | 3 | 7 | Thallium scintigraphic defects (3 = normal, 6 = fixed defect, 7 = reversible defect) |
| num | Presence of disease |
| Patients without disease in the no section | 97 |
| Patients with disease in the no section | 13 |
| Patients without disease in the yes section | 7 |
| Patients with disease in the yes section | 52 |
| Patients without disease in the maybe section | 56 |
| Patients with disease in the maybe section | 73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saranti, A.; Hudec, M.; Mináriková, E.; Takáč, Z.; Großschedl, U.; Koch, C.; Pfeifer, B.; Angerschmid, A.; Holzinger, A. Actionable Explainable AI (AxAI): A Practical Example with Aggregation Functions for Adaptive Classification and Textual Explanations for Interpretable Machine Learning. Mach. Learn. Knowl. Extr. 2022, 4, 924-953. https://doi.org/10.3390/make4040047
Saranti A, Hudec M, Mináriková E, Takáč Z, Großschedl U, Koch C, Pfeifer B, Angerschmid A, Holzinger A. Actionable Explainable AI (AxAI): A Practical Example with Aggregation Functions for Adaptive Classification and Textual Explanations for Interpretable Machine Learning. Machine Learning and Knowledge Extraction. 2022; 4(4):924-953. https://doi.org/10.3390/make4040047
Chicago/Turabian StyleSaranti, Anna, Miroslav Hudec, Erika Mináriková, Zdenko Takáč, Udo Großschedl, Christoph Koch, Bastian Pfeifer, Alessa Angerschmid, and Andreas Holzinger. 2022. "Actionable Explainable AI (AxAI): A Practical Example with Aggregation Functions for Adaptive Classification and Textual Explanations for Interpretable Machine Learning" Machine Learning and Knowledge Extraction 4, no. 4: 924-953. https://doi.org/10.3390/make4040047
APA StyleSaranti, A., Hudec, M., Mináriková, E., Takáč, Z., Großschedl, U., Koch, C., Pfeifer, B., Angerschmid, A., & Holzinger, A. (2022). Actionable Explainable AI (AxAI): A Practical Example with Aggregation Functions for Adaptive Classification and Textual Explanations for Interpretable Machine Learning. Machine Learning and Knowledge Extraction, 4(4), 924-953. https://doi.org/10.3390/make4040047







