Fully Homomorphically Encrypted Deep Learning as a Service

Abstract

Fully Homomorphic Encryption (FHE) is a relatively recent advancement in the field of privacy-preserving technologies. FHE allows for the arbitrary depth computation of both addition and multiplication, and thus the application of abelian/polynomial equations, like those found in deep learning algorithms. This project investigates how FHE with deep learning can be used at scale toward accurate sequence prediction, with a relatively low time complexity, the problems that such a system incurs, and mitigations/solutions for such problems. In addition, we discuss how this could have an impact on the future of data privacy and how it can enable data sharing across various actors in the agri-food supply chain, hence allowing the development of machine learning-based systems. Finally, we find that although FHE incurs a high spatial complexity cost, the run time is within expected reasonable bounds, while allowing for absolutely private predictions to be made, in our case for milk yield prediction with a Mean Absolute Percentage Error (MAPE) of 12.4% and an accuracy of 87.6% on average.

1. Introduction

Fully Homomorphic Encryption (FHE) is a structure-preserving encryption transformation [1] first appearing in 2009 [2], and having several generational advancements since to improve its efficiency, usability and speed. FHE promises to enable encrypted computation of cyphertexts directly without needing the associated private keys required for decryption. The ability to process cyphertexts directly makes it possible to provide encrypted computations in particular with deep learning what we term Encrypted Deep Learning as a Service (EDLaaS), and will be the subject matter we are interested in progressing along with collaboration in agri-food. Deep learning lends itself particularly to FHE since many neural networks are already formed of polynomials that are innately abelian compatible. Abelian compatibility is important when using FHE as we are limited to only abelian operations such as addition and multiplication, however, there are particular issues with activation functions and loss functions that are frequently incompatible by default. Take for instance the sigmoid activation function ($\frac{1}{1+e^{-x}}$) which is not abelian compatible, we would need to either use a different function or approximate this sigmoid activation. One possible way to enable computation of the sigmoid function is to approximate using a form of the Taylor expansion series. Other approximations have also been found for other activation functions like Rectified Linuar Unit (ReLU), however, we still cannot fully implement every neural network component in FHE compatible form. For further more in-depth commutative algebra and rings related to the ring learning with errors (RLWE) problem of which FHE is based [1], an in-depth breakdown is provided in Section 1.2.

FHE/RLWE has recently been paired with deep learning with success, which we will term the encrypted deep learning field. In the encrypted deep learning field, the overwhelming majority of implementations are primarily for convolutional neural networks (CNNs) on image data [3,4,5,6]. For instance Lee [5] uses a deep set of 2D convolutional neural networks with the batch norm, and ReLU activation functions via a data-packing method (multiple data single cyphertext) on the CIFAR-10 dataset [7] using the Cheon, Kim, Kim and Song (CKKS) scheme over fixed-point numbers [8,9]. In Lee’s work they propose an FHE compatible softmax layer however between the softmax and categorical cross-entropy (CCE) layers in each iteration they still need to resort to plaintext for loss calculation, which at some point all implementations will, due to not all necessary components in a neural network being FHE compatible at this time. This means plaintext loss calculation in each forward pass, and then plaintext backpropagation is the norm. this also helps avoid cyphertext weights and optimisation functions which are also not FHE compatible like the most popular optimisation function adam using decaying first and second-order moments, and parameter updates both in incompatible forms [10]. This is not a problem when considering encrypted inference/prediction, since largely the entire circuit with the exception of argmax can be computed on behalf of a data owner using FHE once the model is trained which could lead to interesting combinations with transfer learning in future works.

Juvekar [6] showed encrypted deep learning applied to both MNIST [11] and CIFAR-10 [7], using the PALISADE library. They use the Brakerski-Fan-Vercauteren (BFV) scheme on integers, unlike the much later work by Lee which uses the CKKS scheme provided by the Microsoft Simple Encrypted Arithmetic Library (MS-SEAL). Juvekar just like the much later work by Lee [5] uses cyphertext packing to feed multiple data into a convolutional neural network and was one of the first to propose this packing to optimise cyphertext compatible CNNs, allowing them to operate between much fewer cyphertexts and thus much less cyphertext overhead. However, both papers show how FHE is not possible in the entire neural network graph due to incompatible operations in particular the softmax and CCE in both classification cases. Both papers also show encrypted deep learning with spacial/image data but not sequence data.

Ali [12] applies encrypted deep learning to both the CIFAR-10 and CIFAR-100 datasets, using an improved ReLU, and min-max approximation. It is not apparent what or indeed if Ali used any existing FHE scheme like CKKS, BFV, etc as they do not elaborate. Similarly to all previous papers the problems they are solving are spatial problems, using 2D CNNs, with partially FHE compatible networks.

From our brief summary, all of these works highlight how encrypted deep learning has scarcely been applied towards sequence models, nor towards real-world problems, or solving real client-server approaches to facilitate its use in practice. This is likely why the Royal Society states that FHE is still a proof of concept technology [13] and why we have seen little of encrypted deep learning providing practical use. All of these papers highlight how there is a further need for approximations of neural network components, to facilitate more and varied encrypted computations. All of these papers appear to compute backpropagation along with loss calculation in plaintext. The levels of inference speed vary drastically from paper to paper, due to both the scheme used, the data, and the neural network complexity.

1.1. Motivation

Current encrypted deep learning as previously mentioned has multiple gaps, in particular of applications. We chose to focus on agri-food as a way to expand the coverage of encrypted deep learning. Neural networks in the context of agri-food have already been used across a number of settings, e.g., yield forecasting [14,15,16], crop and fruit detection [17], pest detection [18], etc. In agri-food, as well as in other industries, there are large concerns over potential data leaks over perceived or real sensitivity latent in their data such as genetics/breeding, or feed composition in the case of the milk industry. In addition, concerns around food traceability and safety, along with how information can be safeguarded against malicious input are very important in the agri-food sector [19]. Moreover, considering that data in such industries is a very valuable intellectual property, stakeholders are hesitant to share their data, even when they are seeing some benefits in doing so. There is too much at stake for them, therefore solutions that could enable data sharing or alternatively sharing encrypted data that can be used to develop machine learning applications would be a game-changer for the sector [20]. To test and evaluate our implementation we were provided with the last 30 years of breeding, feeding, and milk yield data, by the Langhill Dairy herd based at the SRUC Dairy Innovation Centre, Dumfries.

To train (deep) neural networks and exploit their full potential we require more and more data. There are major concerns on behalf of the data owners, specifically on the commercial sensitivity of their data, and its (mis)use if it were to be shared with others. This issue creates a reluctance to share, especially if the collaboration is new, as there is a lack of trust, along with issues around background and foreground IP. If we want to create new collaborations to enable net-zero transition, enhance environmental sustainability and improve productivity, it is necessary to build up this trust or create a system, where they do not need to trust the data processor as it will work with encrypted data. This lends itself to fully homomorphically encrypted data, as they no longer need to trust the data processor, as their data cannot be decrypted, read, or leaked, but they can still be used for computation to produce effective predictions for the data owners.

Stemming from all the above our motivation has been to investigate how FHE can be used to enable the exchange of encrypted data in an agri-food setting and enable the use of ML as part of the pipeline via the use of edge devices and virtual machines (VMs). FHE as part of an ML pipeline is still in its infancy [13], which means that in contrast with ML methods that work with non-encrypted data, no off-the-shelf approaches exist that can be routinely used, making their adoption a hard process; hence still considered an emerging and possibly disruptive technology.

Finally, the aim of this paper is thus:

• To test the feasibility of using FHE on a new application in agri-food, specifically dairy milk data for milk yield forecasting.
• To evaluate the performance of using encrypted deep learning as a service towards solving this agri-food milk yield forecasting problem/application.
• To show how sequence models can be built in an FHE compatible manner which is a void in the current encrypted deep learning field.

1.2. Commutative Rings Formalisation

Commutative rings are sets in which it is possible to add, subtract (via the additive inverse) and multiply, and still result in a member of the set. This includes the sets:

• $\mathbb{Z}$; integers, e.g., $(-1,0,1,2,\dots )$ Formally: An integer is any number that has no fractional part (not a decimal).
• $\mathbb{Q}$; rational numbers, e.g., $(5,1.75,0.001,-0.1,\dots )=(\frac{5}{1},\frac{7}{4},\frac{1}{1000},\frac{-1}{10},\dots )$ Formally; a rational number is a number that can be in the fractional form $\frac{a}{b}$ where a and b are integers and b is non-zero.
• $\mathbb{R}$; real numbers, e.g., $(0,-1.5,3/7,0.32,\pi )$ Formally; a real number is any non-imaginary, non-infinite number.
• $\mathbb{C}$; complex numbers, e.g., $(1+i,32+-2.2i,5,-6i)$ Formally: A number which is a combination of real and imaginary numbers, where either part can be zero.

This does not include the sets:

• $\mathbb{I}$; imaginary numbers, e.g., where: $i=\sqrt{-1},(i,-i,39.8i,\dots )$ Formally: Imaginary numbers are any numbers which are multiplied by the imaginary unit i.

R for (commutative) ring shall henceforth be one of the four sets $\mathbb{Z},\mathbb{Q},\mathbb{R},\mathbb{C}$. In contrast, a field (F) is any commutative ring (R), which may also perform division and still result in elements from that ring. This includes only the sets $\mathbb{Q},\mathbb{R},\mathbb{C}$ as not all elements in the set of integers ($\mathbb{Z}$) can be divided by another integer and still result in an integer [21]. These rings are used through polynomial expressions instead of discrete matrices in the learning with errors (LWE) hence the ring learning with errors (RLWE). For formalization if all of the following axioms are fulfilled then the resulting set is called a field:

• addition axioms;
• given: $(x,y,z\in R)$, then:

$$\begin{array}{c}\hfill \left(unity\right)0\in R\\ \hfill \left(closed\right)x+y\in R\\ \hfill \left(inverse\right)x,-x\in R\\ \hfill \left(commutative\right)x+y=y+x\\ \hfill \left(associative\right)(x+y)+z=x+(y+z)\end{array}$$

(1)

• multiplication axioms;
• given: $(x,y,z\in R)$, then:

$$\begin{array}{c}\hfill \left(unity\right)1\in R\\ \hfill \left(closed\right)x·y\in R\\ \hfill \left(inverse\right)x,x^{-1}\in R\\ \hfill \left(commutative\right)x·y=y·x\\ \hfill \left(associative\right)(x·y)·z=x·(y·z)\end{array}$$

(2)

• multiplicative additive axioms;
• given: $(x,y,z\in R)$, then:

$$\begin{array}{c}\hfill \left(distributivity\right)(x+y)·z=x·z+y·z\end{array}$$

(3)

2. Materials and Methods

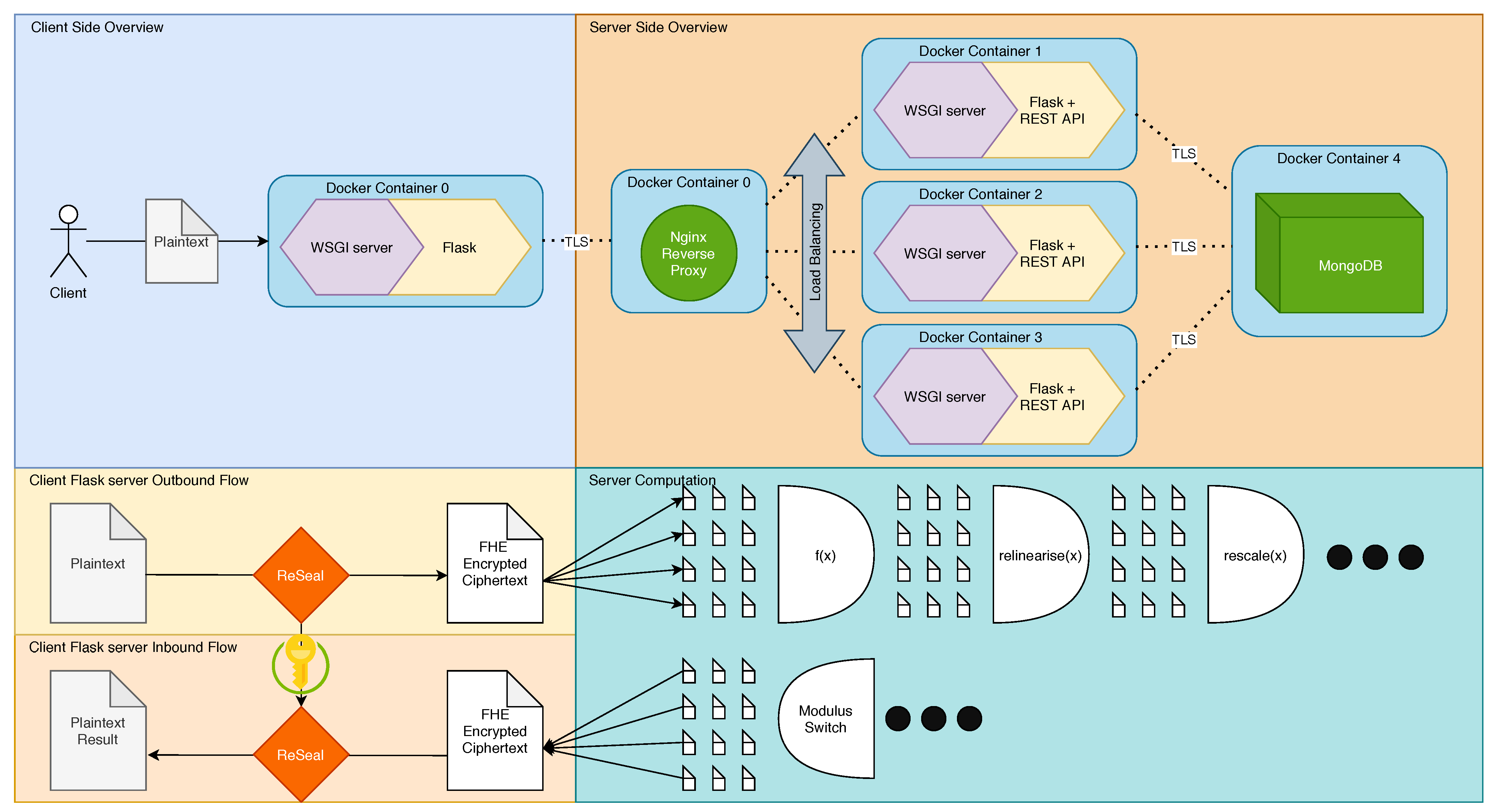
To evaluate FHEs applicability as an EDLaaS we needed to create and mimic as closely as possible what we expect to be a standard industrial use case for third-party data processing, which we can evaluate the effect of FHE on, along with evaluating FHE’s time and spatial performance itself. To this end, we devised a two-part client-server system depicted in Figure 1. It should also be noted that we do still retain the use of HTTPS as opposed to HTTP despite already encrypting our inputs because such a system that relies on HTTP would still be vulnerable to the application level attacks such as man in the middle—also lacking server validation could mean that data could be processed maliciously while also exposing things such as credentials to all parties between the client and the server. An example of possibly malicious data processing would involve purposefully wrong predictions if the still encrypted cyphertexts were sent to an un-validated server because there was no validation through certificates. In the case of milk yield, this could take the form of purposefully over-predicting milk yields such that resources are wasted in preparation for these yield events, or even worse that negotiated supply contracts that expect much greater yields are not met since expectation far exceeded actuality. This could also destroy the data processor’s reputation as a provider of accurate models to name but a few possible malicious data processing possibilities.

Towards the end of creating this pipeline, we had to overcome a few shortfalls we found at the time that prevented FHE to be integrated into an EDLaaS scenario/pipeline.

• Fully Homomorphic encryption itself, specifically CKKS [8,9], and adapting it to be usable at some scale.
• Using FHE towards creating encrypted sequence models, which has only been peripherally explored at this point.

2.1. Data Pipeline

Broadly speaking, our data pipeline can be abstracted into a few different categories, necessary to test and evaluate FHE at some scale, and in a practical manner to garner real results. To this end we have the data source where data is wrangled and encrypted, and also the data sink where the data is processed on much more powerful and fully featured machines.

2.1.1. Data Wrangling

For our study, we used data on dairy herds over the last 30 years provided by the Langhill Dairy herd based at the SRUC Dairy Innovation Centre Dumfries. The data we used was comprised of milking yields, cow consumption/intakes, genetic varieties, which when condensed and parsed became 7 numeric/derived features. These 7 features represent a single time-point, and we used a rolling window comprised of 21 time-points per-cow-per-example we would take the 21st time-point, strip it and use it as our historic ground truth that the previous 20 time-points lead up to. Each cow is milked once a week, rarely once every two weeks, so a sequence of 20 time-points represents roughly 20 weeks of history, leading up to the next (21st) milk yield. These rolling windows stride from the oldest to the newest time-points so the neural network has only seen part of the previous sequence for this cow but not the outcome while training. For the testing set, however, the neural network has neither seen the leading-up-to sequence nor the outcomes. This approach allows us to maximise the amount of data we derive from our 93,283 time-points to give us 57,698 complete sequences between all cows. We split our 57,698 sequences in a 70–30 train-test split (40,389, 17,309) taking the 30% most recent examples so that the testing set was also split temporally, so the network now has not seen the sequences and has no future context with which to make past predictions, making the testing set a representative but separate grouping by time. We further subdivided the training set using another 70–30 split to form the training and validation sets respectively.

We use this data to encrypt and infer on using time series neural networks, in our case a one-dimensional convolutional neural network (1D CNN). We normalised this data between the range of 0–1 following a standard procedure ($z_i=(x_i-\min \left(x\right))/\max \left(x\right)-\min \left(x\right)$) on the client-side, and one hot encoded categorical features. This is fundamentally the same as any other data wrangling where data is prepared for processing by neurons, with the sole exception that the data is then encrypted, meaning this is the final form of the data, and cannot be changed before training/inference, but can, of course, be iteratively adapted if it does not provide the best results by simply feeding more but differently wrangled encrypted data. As there is usually a significant number of empty slots in the encryption vector, it may be possible to optimize further by merging multiple examples into a single encrypted vector [5]. However, this emptiness allows for a lot of variances in wrangling techniques without the need to create whole new neural network architectures.

2.1.2. Client/Data Source

The data that describes the milk yields are provided by the owner as an input to an IoT device, usually, a small embedded device (in our case, NVIDIA jetson nano), which is responsible for data wrangling and encryption, as once encrypted the data can no longer be seen, and cannot be verified; thus the need to be transformed before the encryption stage. The data source must be the encryptor so that they are the only entity with a private key with which to decrypt the data again.

Normally, the data owner cannot be expected to be familiar with FHE, deep learning, and thus the requirements of the data to be properly processable. Some form of interaction/awareness of the data must occur such that appropriate auditable/open-source data processors can be provided. In the ideal scenario, this would not be necessary and the data owner would be capable of wrangling the data according to their needs, but it should be noted this is an unlikely occurrence given there are more data sources than expertise, and the existence of expertise reduces the likelihood in the need for an EDLaaS. However given client expertise or at least proficiency in data cleaning, and the use of open-source helpers and documentation, then no embedded device would be necessary, and the client can instead submit their cyphertext directly for processing with the respective operational keys.

Data from the client is serialised by the embedded device after encryption ready for transmission to the data processor, without the presence of the private key, ensuring the transmitted serialised cyphertext is undecryptable during processing in the later stages. These keys should instead remain indexed on the client machine/embedded device ready to be re-merged for decryption.

2.1.3. Server/Data Processor

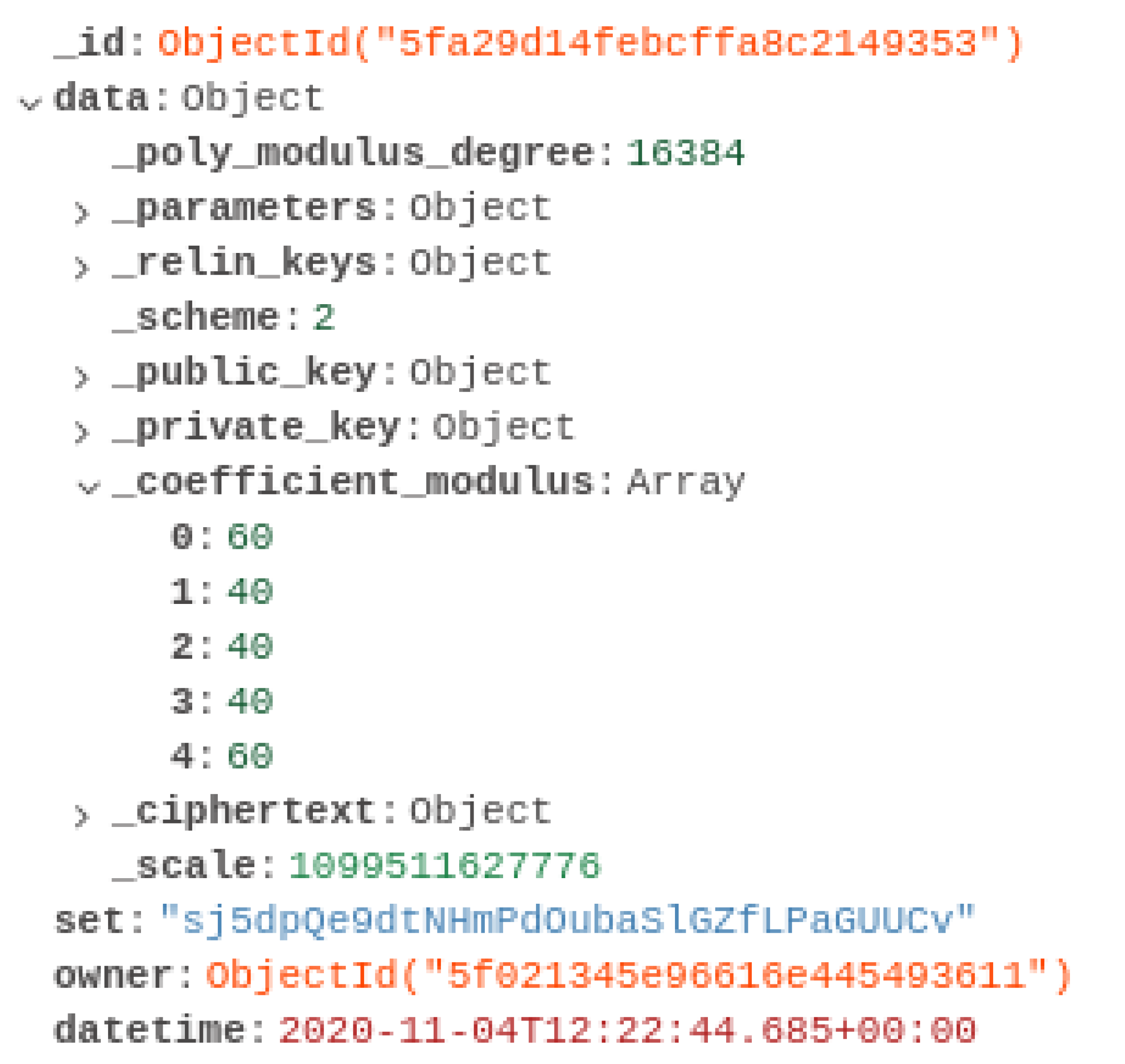
Data from the data source is serialised and transmitted using standard HTTPS requests, to model how it would likely function in such an Internet service. The data sink then proceeds to deserialise and apply the arbitrary computation, in our case a neural network, and then serialises and transmits the still encrypted but now transformed data to the data source for final decryption and use. An example encrypted output can be seen in the following Figure 2 showing cyphertexts, the associated keys, the data set name that it is associated with, who owns this data, and when it was submitted. In practice, we would filter unnecessary information, like the plain parameters, to reduce space and time costs of storing and transmitting this data, hence improving speed, and of course, we would not handle the private key, which is shown here for experimental purposes only.

We can process data as in Figure 2 using our library described in Section 2.3 and with our techniques outlined in Section 2.4. Once processed, to minimise space consumption, we swap all the way down the remaining coefficient chain, to create the smallest possible, and most quickly deciphered cyphertext, thus saving space and time while the data is stored until the data owner decrypts/uses the results.

2.2. Interface

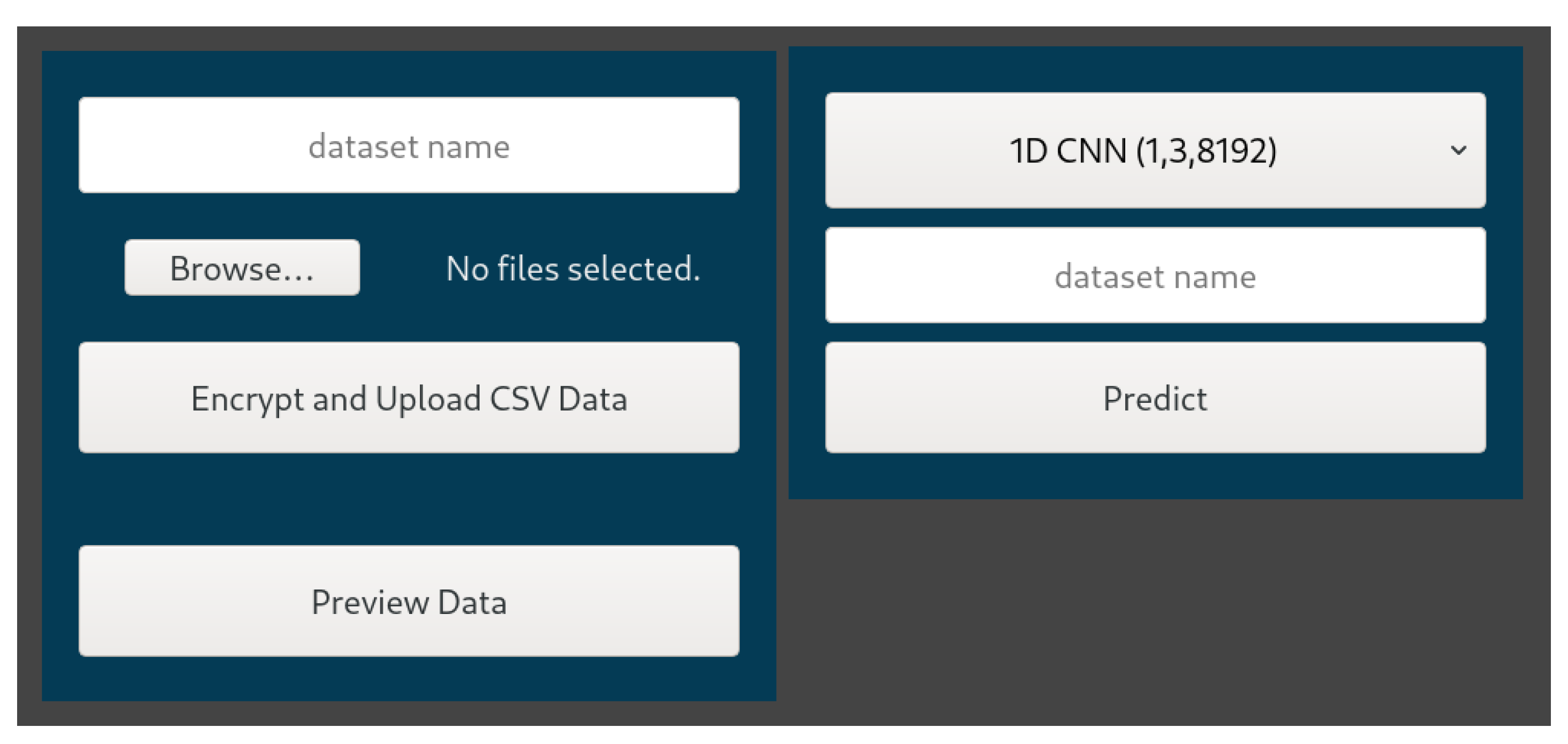
For ease of use and testing we created a simple web interface to be used by the data owner to simplify the process of submitting data to the embedded client device for encryption and transformation, while also serving the purpose of user authentication, as a main dashboard that prompts the user to upload the data to be encrypted (Figure 3), and also an opportunity to view the encrypted data. The training process, given the complexity involved, can run either on the Jetson device or a remote host, e.g., high-performance computing. The user may also select what type of 1D CNN (or other models for good measure) to use to provide them predictions. As far as our techniques are concerned, they can run in both an edge and a non-edge device, depending on the scalability of the problem and other constraints related to the amounts of data, training time, etc.

2.3. Fully Homomorphic Encryption Library

Across the community, there has been little work available to easily use fully homomorphic encryption in conjunction with deep learning, and of what was available they often did not support the more complicated Cheon, Kim, Kim and Song (CKKS) [8,9] FHE scheme, and its serialisation, or harbour some hidden catches. The CKKS scheme can operate on fixed precision numbers which is necessary as normalised neural networks operate on floating point numbers usually, often in the range 0–1. The base library we used after quite some deliberation was the Microsoft Simple Encrypted Arithmetic Library (MS-SEAL) since it supports CKKS and some form of serialisation necessary to broadcast over the internet, and is broadly a very popular FHE library. We chose to use our own Python-Reseal [22] library that binds MS-SEAL directly as a base/low-level FHE library which also implements our own abstraction layers because many other abstraction libraries simply did not suit our needs. We required both FHE and some way to operate deep learning models with this FHE, many of which were too immature/newer than ours, or lacked documentation/examples. Take for instance Microsoft’s own encrypted vector arithmetic (MS-EVA) library that similarly uses a graphing approach to represent computation, and also binds from MS-SEAL itself to python as PyEVA. PyEVA is and was at the time too new (V1 released 23 April 2021) and lacked documentation to make it readily usable. Similarly, other libraries like PySyft were originally created for other privacy-preserving machine learning methods like federated computing, differential privacy, and multi-party computation, and have only very recently begun to implement homomorphic operations, but again this still means they lacked the necessary documentation and thus are yet unusable for FHE deep learning. In contrast, our library started implementing FHE in June 2020, with first-class support for serialisation, FHE deep learning, and rich documentation with examples of encrypted neural networks specifically. It should also be noted that many of these libraries are just higher-level FHE libraries that do not include or naturally form neural networks, whereas we needed specifically encrypted deep learning. MS-SEAL however is neither GPU compatible and does not support bootstrapping yet, meaning there is a limit to the number of computations we can process, but since we were intending to stay within this limit for the sake of noise budgeting this should be relatively equivalent to its bootstrapped counterpart, and can in future be swapped to its bootstrapped variant without having to adapt any of the neural network components.

We chose Python as most deep learning applications and the associated plethora of libraries primarily use the programming language Python. Our existing open-source (OSLv3 Licensed) library Python-ReSeal [22] was well placed to allow us to take full advantage of the high-level features of Python and included all the serialisation logic, and abstractions necessary for use in deep learning.

2.4. Fully Homomorphic Encryption in Deep Learning

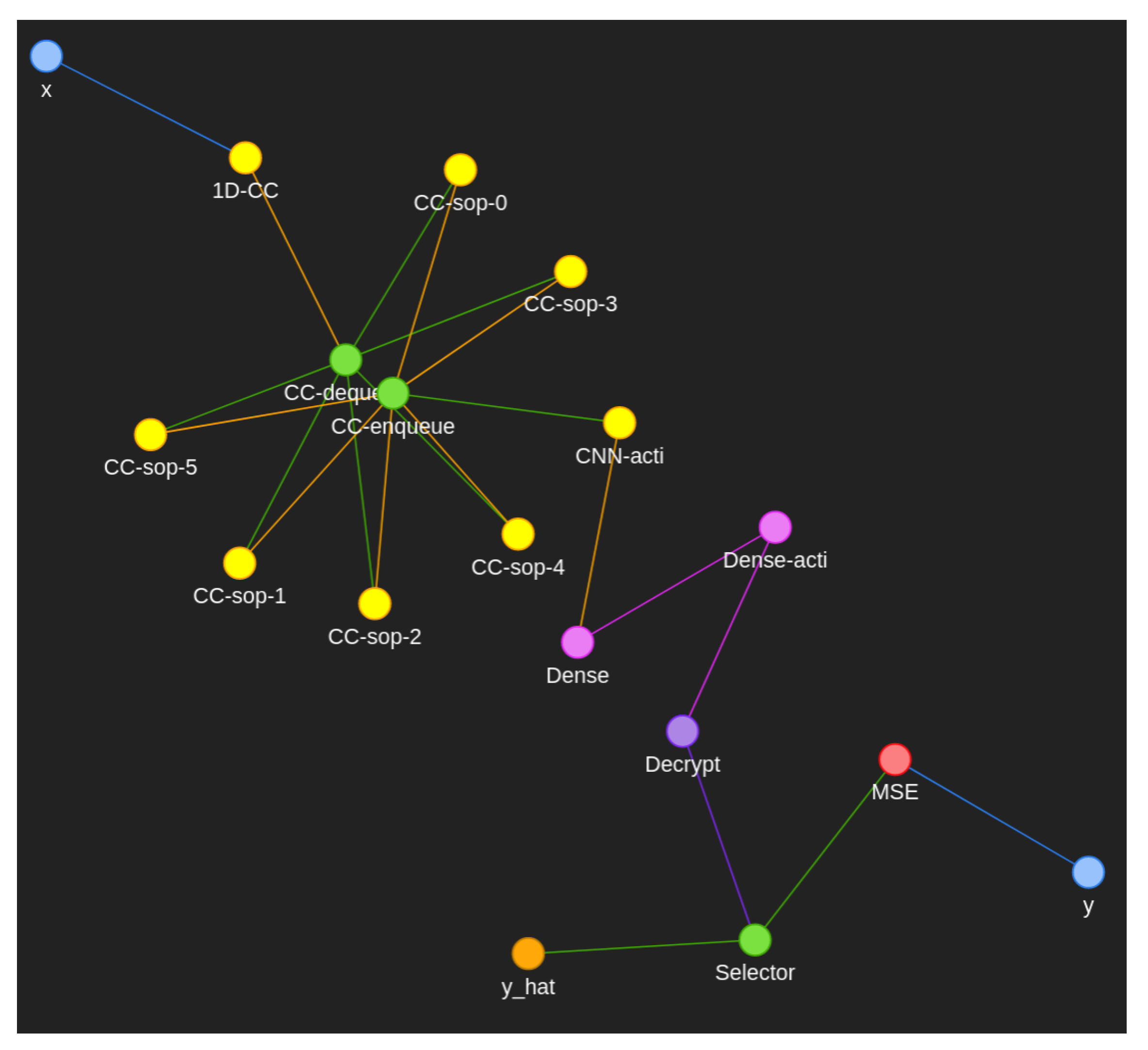
Deep learning can broadly be abstracted into three stages, namely forward pass, backward pass, and the weight update; forward pass propagates some inputs (x, y in Figure 4 and

Table 1. Tabular-summarised neural network architecture, outlining the neural network components and how they are constructed using various constituent nodes, along with the parameters these nodes received such as filter shapes to randomly initialise the weights.

Neural Network Component	Constituent Nodes	Parameters
Inputs	x, y
One Dimensional Convolutional Neural Network (1D CNN)	1D-CC, CC-dequeue, CC-enqueue, CC-sop- *, CNN-acti	filter shape: (5, 1, 7), bias: 0
Fully Connected Artificial Neural Network (ANN/Dense)	Dense, Dense-acti	weight shape: (16), bias: 0
Mean Squared Error (MSE) Loss	MSE
Adaptive moment (Adam) Optimiser	Not a Node *	alpha: 0.001, beta_1: 0.9, beta_2: 0.999
Outputs	y_hat

* Adam is not a node but is instead embedded in the abstraction of nodes as the default optimiser. The default optimiser can be overridden with parameters to use others.

) against the weights and internal activation functions of the whole network to produce some form of prediction ($\widehat{y}$ in Figure 4). Backward pass calculates the effect of all weights and biases on the final result by differentiation and the chain rule. The weight update takes these weights and adjusts them given the loss (a measure of wrongness), and the gradient of the weight in question to approach a lower loss, usually using a flavour of the gradient descent algorithm.

Fully homomorphic encryption requires that certain constraints be maintained, such as the inability to compute division, thus we describe our process as well as how we overcome these obstacles as follows.

2.4.1. Forward Pass

As briefly described previously, the forward pass takes some input x, applies some transformation according to the internal weights of the neural network and outputs some prediction (Figure 4 and Table 1). However, depending on the neural network in question, these transformations are usually not FHE compatible or are not performant under FHE. An example of FHE incompatibility is most activation functions, e.g., ReLU, and sigmoid, which require operations such as max and division that are impossible, requiring context and a non-abelian operation, respectively. To overcome this, we found in literature approximations for—in particular—sigmoid (Equation (4)), which uses polynomials to overcome the barrier of the divisions in the standard sigmoid. For the sake of repetition sigmoid shall hereby refer to the sigmoid approximation unless otherwise stated:

$$\sigma \left(x\right)\approx 0.5+0.197x+-0.004x^3$$

(4)

where:

• $\sigma$ = sigmoid
• x = some input vector x

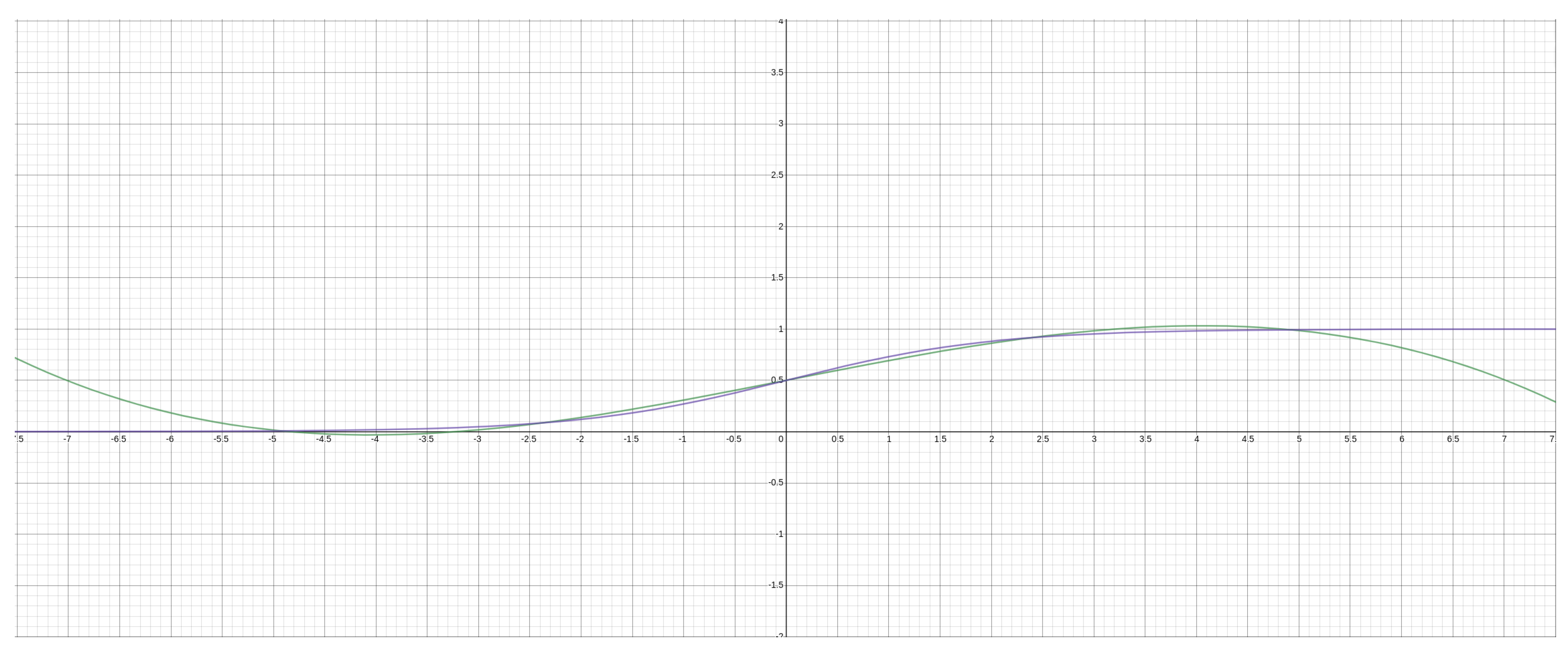
This approximation closely follows the standard sigmoid between the ranges of −5 and 5 (Figure 5), which is more than sufficient for our purposes since, when normalised, most data, weights, and subsequently, activations will likely fall in the range 0–1; however it is still possible throughout training to exceed this boundary and is a good candidate for FHE compatible batch norm.

This approximation in question, proposed by Chen et al. [23] in Equation (4), is used interchangeably with sigmoid in our equations, thus our neural network Equation (5) will stay relatively normal aside from the use of time t as a 1D (time series) CNN.

The specific neural network we used for this forward pass was a 1D convolutional neural network (1D CNN), where we substituted space for time, thus our activation equation becomes what is depicted by Equation (5). We used a 1D CNN over traditional time series neural networks despite having a time series dataset as not only have 1D CNNs been shown to be good time-series predictors that are more parallelisable, but the nature of a CNN means computations are wider rather than deeper. In practice, this means that less expensive operations such as bootstrapping are necessary (and in our case impossible), since after a few computations deep it is necessary to bootstrap and shrink the cyphertext, thus improving the overall time efficiency of the resulting computational graph.

We initialise our 1D CNN, with a filter of shape (5, 1, 7) with random weights between 0–1 divided by the total number of elements in the filter $5\times 1\times 7=35$ so that when summed the sum-of-products (SOP) does not exceed 1 at least initially. We use a batch size of 3 to keep the cyphertext size down since the forward pass requires significant caching in training and a larger batch size would entail more data to cache in an already data-heavy scenario with encrypted cyphertexts taking large amounts of space compared to their plaintext counterparts. The bias for both the 1D-CNN and the dense-net are initialised to 0 since we never assume the input is biased and instead desire to let the neural network find the bias itself. The dense-net similar to the 1D CNN has its weights randomly initialised between 0–1 of shape (16) again such that the sum of products never exceeds 1 initially. The reason we want to ensure we stay within this range where possible is to minimise the chance of exceeding the golden range of our approximations, like the aforementioned sigmoid approximation range of −5 to 5. Both the dense layer and the CNN layer depicted in Figure 4 use Sigmoid as their activation node, although in future we will plug in a ReLU approximation to improve on the polynomials computation time, ReLU being a lower order polynomial.

$$a^{<t>}=\sigma (w_i^{<t>}{x}^{<t>}+b_i^{<t>})$$

(5)

where:

• $\sigma$ = sigmoid/sigmoid approximation
• x = some input vector x
• e = eulers number

2.4.2. Backward Pass

The backward pass, as touched on before, is the process of calculating the gradients of the weights and biases with respect to the output. However, to do this you require some cached input which is used to derive the differentials. An example of this dependency of input could be sigmoid which to calculate the gradient requires x the encrypted input.

To calculate the sigmoids gradient, x is required, and this means that either this gradient becomes encrypted in the process of using the currently encrypted x, or that this can only be calculated in plaintext. For now, we choose to calculate gradients in plaintext, as encrypting the gradients would inevitably mean encrypting the new weights, which would mean every operation would become between two cyphertexts, adding substantial time complexity (an order of magnitude), when unnecessary for our purposes, and would function to limit the neural network to that one specific key from that one specific data owner. While this may be desirable in certain bespoke situations, generally, as a data processor, however, this is largely undesirable since it is necessary to serve multiple data owners/sources simultaneously. It may be instead possible to have generic models that can then be privately tailored to the specific data in question. For these bespoke models, this could potentially be represented somewhat like a graph/digraph for each individual weight with respect to the generic models, such that if in future the data owner allows these weights to be decrypted, that they can be retroactively used to update other pre-existing models stemming from the same generic model/node.

2.4.3. Weight Update

The weight update using gradient descent simply moves the weights in whichever direction approaches a lower/minimum loss. They do this according to some optimisation function. Since we do this in plaintext is it done normally without the need for special considerations. In our FHE neural network, we use Adam [10] by default since it is the most prevalent, and frequently used optimiser. We use Adam with the standard parameterisation as outlined in the original paper; $\alpha =0.001$, ${\beta }_1=0.9$, ${\beta }_2=0.999$$ϵ=1\times {10}^{-8}$.

3. Results and Discussion

In the work presented in this paper, we created a two-part client and server system to facilitate EDLaaS at scale, just like any other platform as a service. We used our own libraries which have consequences on the computational speed of the whole pipeline.

Table 2. Time performance for different operations, both locally and remotely. It should be noted that N/A (not applicable) is used to identify operations which are not implemented atomically as remote API operations as they would not make sense since they are too atomic to warrant the transmission overhead alone. These operations of course still exist on the server side but embedded into much more complex operations such as part of inference in our neural network depicted in Figure 4.

Operation	Locally (Seconds 3 s.f)	Remotely (Seconds 3 s.f)
Encryption	0.0136	0.454
Decryption	0.0330	1.14
Inference	0.966	3.13
Cyphertext + Cyphertext	0.287	N/A
Cyphertext + Plaintext	0.0480	N/A
Cyphertext*Cyphertext	0.277	N/A
Cyphertext*Plaintext	0.0500	N/A

represents the computational times we achieved against milk yield prediction using a 1D convolutional neural network as outlined in Section 2.4. These results are averages of testing set computations (17,309 examples) and the associated time of execution, including in the case of the remote examples the transmission time. For the sake of consistency, all results presented were obtained on the same local area network (LAN) to prevent the effect of otherwise uncontrollable conditions and traffic over the wider area network (WAN). While this is still a fairly small scale relative to production settings, our use of containers can easily be expanded upon such as with Kubernetes, Apache Mesos, or Docker Swarm, allowing for scaling up and down. As can be seen in

Table 3. Output of loss functions for both validation and testing sets, using Mean Squared Error (MSE), and Mean Absolute Error (MAE) when using our neural network from Figure 4.

Data Set	MSE Cyphertext (4 s.f.)	MSE Plaintext (4 s.f.)	MAE Cyphertext (4 s.f.)	MAE Plaintext (4 s.f.)
validation	0.02226	0.02225	0.1240	0.1240
testing	0.02233	0.02233	0.1241	0.1241

, the absolute difference in loss vs. the exact same network in plaintext is minimal, such that it could be mistaken for a rounding error even at 3 significant figures. This means the only significant difference between plaintext and cyphertext processing is the cost of processing it, I.E computational and spacial cost. This table also shows how the network architecture despite being quite shallow is still capable of learning this problem while achieving an MAE of 0.124 no less, which means since the data is normalised between 0–1 that our Mean Absolute Percentage Error (MAPE) is 12.4%, or put another way our neural network can accurately infer the next milk yield while encrypted with an accuracy of 87.6% on average.

It may also be noted in Table 2 that some fields are left blank. These blank fields in the remote column are remote operations left unimplemented as they are too low-level operations to be worth the overhead cost of transmission, also considering that simple operations alone, such as cyphertext + cyphertext, are not in of themselves deep learning as deep learning is comprised of many of these atomic operations combined rather than as singular API calls that need to be transmitted each time, and would not have been worthy candidates to implement, taking time away from more critical research.

It can be seen in Table 2 that local time performance effectively represents the efficiency of our rebinding and abstraction implementation of MS-SEAL, whereas the remote results represent the time taken for the pipeline overall. That is to say remote encryption, remote decryption, and remote inference.

Space taken as shown in

Table 4. Space taken of different length vectors, unencrypted as NumPy arrays and encrypted as ReSeal vectors, including private keys and all meta-data required for operation.

Length	Polynomial Modulus Degree	Numpy Plaintext Size (bytes)	Encrypted Vector Size (bytes)
4096	8192	32,880	4,800,310
8192	16,384	65,648	9,600,592

however shows how much larger an encrypted cyphertext is relative to its unencrypted counterpart. in the case where the polynomial modulus degree is 16,384 and thus the length of the array is half of the poly-mod-degree at 8192, the plaintext NumPy array is only 0.0656 MB, compared to 9.60 MB if it was to be encrypted. However, this is the total size of the cyphertext, including all the other required information necessary to store with it, namely its private key, and at the highest point in the modulus switching chain, which is only necessary before computation begins. Thus there will be some gains once unnecessary information to the data processor is stripped, and the data has been computed thus approaching the end of its modulus switching chain, which produces a smaller cyphertext as a side effect, while also being the result of several other cyphertexts combined into a single prediction. This space taken is likely easily optimised as this size is a result of some difficult serialisation logic necessary when going from MS-SEAL in C++ to ReSeal in Python, and is likely an area where easy gains can be garnered in future.

Lastly a discussion on the privacy of models built with plaintext backpropagation. As repeatedly stated thought that the training of the neural networks or more specifically the backpropagation is done in plaintext which means that the model weights can begin to approximate the distribution of the data. If these were generative models we could likely recreate at least a form of the original data since the weights are still usable without the data owner since they are in plaintext. However we can easily mitigate this through transfer learning (something we do not cover here in-depth) and pre-trained models; If the data privacy is paramount such that the dataset itself cannot be decrypted for the purposes of training, then we can instead use FHE modified pre-trained models for the inference that most closely match the data scenario, of which as depicted in Figure 3 the user would be able to select. It is possible that the data owners data closely matches the scenarios covered by these pre-trained networks (e.g., inceptionv3, resnet, alexnet, etc.) however if not it would be further possible to tune these pre-trained networks locally on (in this instance) the Jetson-Nano since tuning would require far fewer resources, then use the model on the server-side after serialising the now tuned graph. That way the exposure of the data is kept locally only. If even this is too much since the weights are still exposed then encrypted weights could also be deployed for their specific model however this would come at significant computation and conceptual complexity costs. All in all, while FHE is not a panacea to all privacy problems it significantly reduces many concerns, and if used in conjunction further with other forms of privacy-preserving machine learning that it would become private to all but the most sensitive applications. At the very least while the inference that uses transferred models would be inferior to bespoke models specially tailored to those use cases, having more data owners (such as in agri-food) have access to neural network predictions will possibly act as a gateway at least of awareness such that once the data owners experience what sort of performance neural networks can give them, that they may have more reason to share plaintext data to attain more and better predictions, even faster, and more tailored to their needs.

4. Future Work

Our future work will focus on expanding and improving our presented approaches further. More specifically, areas of improvement include:

Neural network components: We are working on improving some of the approximations and components presented here, taking into account recent advancements made on sigmoid approximation and ReLU, as proposed by Ali [12]. There have also been some very recent techniques proposed, which are relevant to our work, such as Lee et al. batch normalisation and kernel implementation [5]. Nevertheless, the purpose of this paper was to consider FHE in conjunction with deep learning and show at least that it can be applied and use in practical client-server settings.

FHE: In this paper, we treat FHE and leveled-FHE (LFHE) as if they are the same, however, FHE includes the use of a bootstrapping function, which is an operation which Microsoft-SEAL does not yet support, however, this is a road-mapped feature which means in due course this initially LFHE implementation can be reused for FHE as it becomes available.

Plaintext Backpropagration: Readers will note that we have in several places mentioned that backpropagation is calculated in plaintext. This is a prevalent limitation in all FHE deep learning implementations that is often overlooked/attention is not drawn to. This is primarily due to both the aforementioned lack of bootstrapping in many implementations which makes such long computations untenable (due to cyphertext size and computation time), the lack of compatibility in loss functions (which we and the broader community are working towards improving), and finally the inoperability of encrypted weights. Here, by inoperability we mean the following:

• Cyphertext + Cyphertext operations take an order of magnitude longer to compute; if we maintained encryption throughout the backward pass and kept the data absolutely secret then we would also have to pay this computational cost.
• Cyphertext + Cyphertext operations can only be computed on identically parameterised and borne of the same secret key, which means we would require all EDLaaS data owners to encrypt their data using the same key, which would mean the point of encryption would be lost since the secret key would then be effectively openly accessible.
• We could decrypt the finalised weights to overcome these previous limitations but then we could still derive at least a generalised representation of the source data in which case there is not much to be gained by computing backpropagation while encrypted.
• There is nothing stopping us from only using the forward pass for data owners while having pre-trained or transferred models to various scenarios of which they can choose. This would lose some accuracy but at this current time, it seems like the optimal scenario if data privacy/sensitivity is of key importance but computation is still required.

5. Conclusions

FHE and deep learning are an interesting pairing, together they allow data to be inferred completely privately, and could also be used for training to improve privacy significantly in client-server scenarios like ours. We have applied encrypted deep learning to a whole new application, how it can be used for accurate (MAPE 12.4%) prediction of milk yield forecasting in the agri-food sector, and have discussed to some length privacy considerations, and the cost of cyphertext processing. We have shown how the relative performance of cyphertext vs plaintext processing on the exact same neural networks is negligible such that it could be mistaken for a rounding error even at 3 significant figures. We have also shown how we can develop sequence models using FHE compatible methods, thanks to the co-similar nature of space and time in 1D CNNs. We have found that while we pay a high penalty for cyphertext processing it is more than reasonable towards encrypted inference or EDLaaS. We have also found that FHE is not a panacea, and it does not solve all of the privacy-preserving considerations that would be required in particular for the training of neural networks, but it does offer a way, albeit a highly complex and expensive way to if we so desired to use encrypted weight bespoke models for individual data owners specific requirements, such as those in the highly competitive agri-food industry. There is still much improvement that can be sought in particular with the efficiency of our MS-SEAL bindings but despite all the difficulties we get timely, accurate predictions, in a reasonably secure client-server model.