Statistical Aspects of High-Dimensional Sparse Artificial Neural Network Models

Abstract

An artificial neural network (ANN) is an automatic way of capturing linear and nonlinear correlations, spatial and other structural dependence among features. This machine performs well in many application areas such as classification and prediction from magnetic resonance imaging, spatial data and computer vision tasks. Most commonly used ANNs assume the availability of large training data compared to the dimension of feature vector. However, in modern applications, as mentioned above, the training sample sizes are often low, and may be even lower than the dimension of feature vector. In this paper, we consider a single layer ANN classification model that is suitable for analyzing high-dimensional low sample-size (HDLSS) data. We investigate the theoretical properties of the sparse group lasso regularized neural network and show that under mild conditions, the classification risk converges to the optimal Bayes classifier’s risk (universal consistency). Moreover, we proposed a variation on the regularization term. A few examples in popular research fields are also provided to illustrate the theory and methods.

1. Introduction

High-dimensional models with correlated predictors are commonly seen in practice. Most statistical models work well either in low-dimensional correlated case, or in high-dimensional independent case. There are few methods that deal with high-dimensional correlated predictors, which usually have limited theoretical and practical capacity. Neural networks have been applied in practice for years, which have a good performance under correlated predictors. The reason is that the non-linearity and interactions are brought in by the activation functions and nodes in the hidden layers. A universal approximation theorem guarantees that a single-layer artificial neural network is able to approximate any continuous function with an arbitrarily small approximation error, provided that there is a large enough number of hidden nodes in the architecture. Thus, the artificial neural network (ANN) handles the correlation and interactions automatically and implicitly. A popular machine learning application that deals with this type of dependency is the spatio-temporal data, where the traditional statistical methods model the spatial covariance matrix of the predictors. However, by artificial neural networks, working with this big covariance matrix can be avoided. Moreover, artificial neural networks also have good performance in computer vision tasks in practice.

A main drawback of neural networks is that it requires a huge number of training sample due to large number of inherent parameters. In some application fields, such as clinical trials, brain imaging data analysis and some computer vision applications, it is usually hard to obtain such a large number of observations in the training sample. Thus, there is a need for developing high-dimensional neural networks with regularization or dimension reduction techniques. It is known that $l_1$ norm regularization [26] shrinks insignificant parameters to zero. Commonly used regularization includes $l_p$ norm regularization, for example, see the keras package [6]. $l_p$ norm regularization with $p\ge 2$ controls the model sensitivity [15]. On the other hand $l_p$ norm regularization with $p<2$, where people usually take $p=1$ for computation efficiency, does not encourage group information. The group lasso regularization [27] yields group-wise sparseness while keeping parameters dense within the groups. A common regularization used in high-dimensional artificial neural network is the sparse group lasso by [21], see for example [11], which is a weighted combination of the lasso regularization and the group lasso regularization. The group lasso regularization part penalizes the input features’ weights group-wisely: A feature is either selected or dropped, and it is connected to all nodes in the hidden layer if selected. The lasso part further shrinks some weights of the selected inputs features to zero: A feature does not need to be connected to all nodes in the hidden layer when selected. This penalization encourages as many zero weights as possible. Another common way to overcome the high-dimensionality is to add dropout layers [23]. Randomly setting parameters in the later layers to zero keeps less non-zero estimations and reduces the variance. Dropout layer is proved to work well in practice, but no theoretical guarantee is available. [17] considers a deep network with the combination of regularization in the first layer and dropout in other layers. With a deep representation, neural networks have more approximation power which works well in practice. They propose a fast and stable algorithm to train the deep network. However, no theoretical guarantee is given for the proposed method other than practical examples.

On the other hand, though widely used, high-dimensional artificial neural networks still do not have a solid theoretical foundation for statistical validation, especially in the case of classification. Typical theory for low-dimensional ANNs traces back to the 1990s, including [1,2,8,25]. The existing results include the universal approximation capabilities of single layer neural networks, the estimation and classification consistency under the Gaussian assumption and 0-1 loss in the low dimensional case. These theory assumes the 0-1 loss which is not used nowadays and are not sufficient for high-dimensional case as considered here. Current works focus more on developing new computing algorithms rather building theoretical foundations or only have limited theoretical foundations. [11] derived a convergence rate of the log-likelihood function in the neural network model, but this does not guarantee the universal classification consistency or the convergence of the classification risk. The convergence of the log-likelihood function is necessary but not sufficient for the classification risk to converge. In this paper, we obtained consistency results of classification risk for high-dimensional artificial neural networks. We derived the convergence rate for the prediction error, and proved that under mild conditions, the classification risk of a high-dimensional artificial neural network classifier actually tends to the optimal Bayes classifier’s risk. This type of property has been established on other classifiers such as KNN [7], which derived the result that the classification risk of KNN tends to the Bayes risk, LDA [28], which derives the classification error rate under Gaussian assumptions, etc. Popular tasks, like analyzing MRI data and computer vision models, were also included in these research papers, and we applied the high-dimensional neural network to these demanding tasks as well.

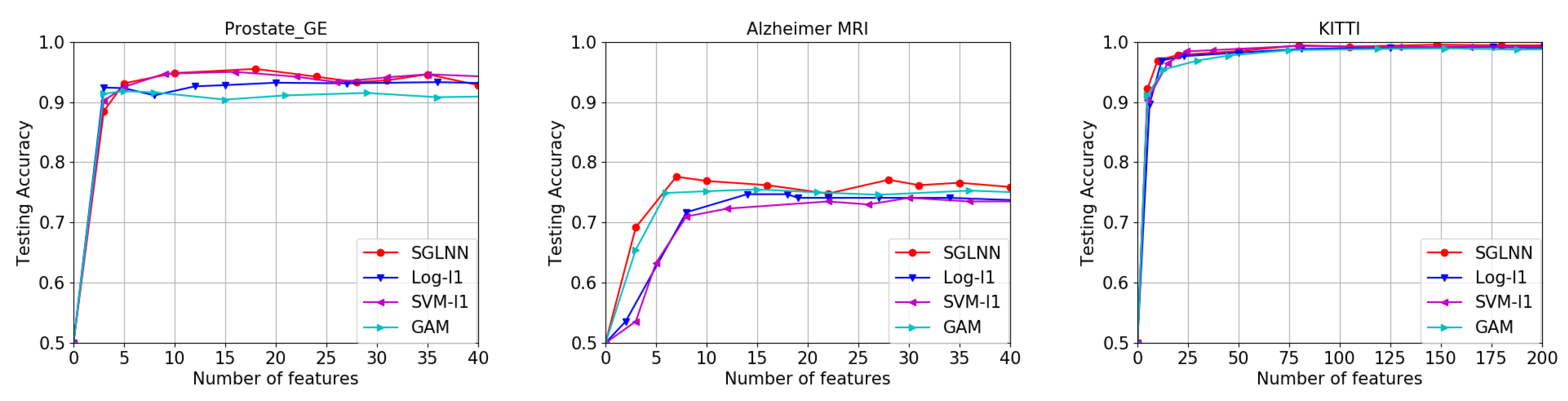
In Section 2, we will formulate the problem and the high-dimensional neural network formally. In Section 3, we state the assumptions and the main consistency result. In Section 5, we apply the high-dimensional neural network in three different aspects of examples: the gene data, the MRI data and the computer vision data. In Section 6, further ideas are discussed.

2. The Binary Classification Problem

Consider the binary classification problem

$$P(Y=1|X=x)=f(\mathit{x}),P(Y=0|X=x)=1-f\left(\mathit{x}\right),$$

where $\mathit{x}\in {\mathbb{R}}^p$ is the feature vector drawn from the feature space according to some distribution $P_{\mathit{X}}$, and $f(·):{\mathbb{R}}^p\to \mathbb{R}$ is some continuous function. Note here that, in the function $f\left(\mathit{x}\right)$, there can be any interactions among the predictors in $\mathit{x}$, which ensures the possibility to handle correlated predictors. Let $P_{\mathit{X},Y}$ be the joint distribution on $(\mathit{X},Y)$, where $\mathit{X}\in {\mathbb{R}}^p$ and $Y\in \{0,1\}$. Here p could be large, and may be even larger than the training sample size n. To study the theory, we assume p has some relationship with n, for example, $p=O\left(\exp \right(n\left)\right)$. Therefore, p should be written as $p_n$, which indicates the dependency. However, for simplicity, we suppress the notation $p_n$ and denote it with p.

For a new observation ${\mathit{x}}_0\in {\mathbb{R}}^p$, the Bayes classifier, denoted $C^{*}\left(\mathit{X}\right)$, predicts 1 if $f\left(\mathit{x}\right)\ge p_s$ and 0 otherwise, where $p_s\in (0,1)$ is a probability threshold, which is usually chosen as $1/2$ in practice. The Bayes classifier is proved to minimize the risk

$$R\left(C\right)={\int }_{{\mathbb{R}}^p\times \{0,1\}}{𝟙}_{\left\{C\right(\mathit{X})\ne Y\}}d{P}_{\mathit{X},Y}.$$

(1)

However, the Bayes classifier is not useful in practice, since $f\left(\mathit{x}\right)$ is unknown. Thus a classifier is to be found based on the observations $\{({\mathit{x}}_1,y_1),\dots ,({\mathit{x}}_n,y_n)\}$, which are drawn from $P_{\mathit{X},Y}$. A good classifier based on the sample should have its risk tend to the Bayes risk as the number of observations tends to infinity, without any requirement for its probability distribution. This is the so-called universal consistency.

Multiple methods have been adopted to estimate $f\left(\mathit{x}\right)$, including the logistic regression (a linear approximation), generalized additive models (GAM, a non-parametric nonlinear approximation which does not take interactions into account), neural networks (a complicated structure which is dense in continuous functions space), etc. 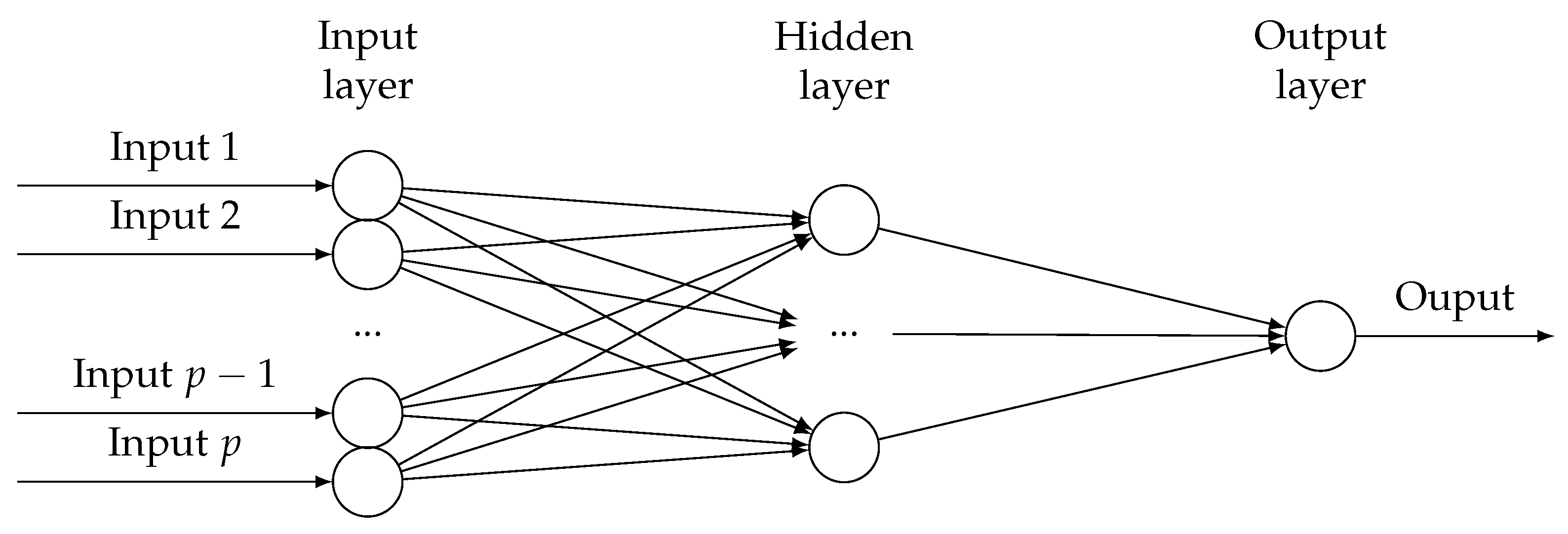The first two methods usually work in practice with a good theoretical foundation, however, they sometimes fail to catch the complicated dependency among the feature vector $\mathit{x}$ in a wide range of applications (brain images, computer visions and spatial data analysis). The neural network structure is proved to be able to capture this dependency implicitly without explicitly specifying the dependency hyper-parameters. Consider a single layer neural network model with p predictor variables. The hidden layer has $m_n$ nodes, where $m_n$ may be a diverging sequence depending on n. Similar to $p_n$, we suppress $m_n$ as m. A diagram is shown in Figure 1.

For an input vector $\mathit{x}\in {\mathbb{R}}^p$, its weight matrix $\mathit{\theta }\in {\mathbb{R}}^{p\times m}$ and its hidden layer intercept vector $\mathit{t}\in {\mathbb{R}}^m$, let the vector $\mathit{\xi }\in {\mathbb{R}}^m$ be the corresponding values in the hidden nodes, which is defined as

$${\xi }_k=t_k+{\mathit{\theta }}_k^T\mathit{x},k=1,\dots ,m.$$

Let $\psi (·)$ be an activation function, then the output for a given set of weight $\mathit{\beta }$ is calculated by

$$b+{\mathit{\beta }}^T\mathit{\psi }\left(\mathit{\xi }\right),$$

where the function $\mathit{\psi }(·)$ is the function $\psi (·)$ being applied element-wisely. We have a wide range of choices for the activation function. [16] proved that as long as the activation is not algebraic polynomials, the single layer neural network is dense in the continuous function space, and can thus be used to approximate any continuous function. This structure can be considered as a model which, for a given activation function $\psi (·)$, maps a $p\times 1$ input vector to an real-valued output

$${\eta }_{(\mathit{\theta },\mathit{t},\mathit{\beta },b)}\left(\mathit{x}\right)={\mathit{\beta }}^T\mathit{\psi }(\mathit{t}+{\mathit{\theta }}^T\mathit{x})+b=\sum _{k=1}^m{\beta }_k\psi (t_k+{\mathit{\theta }}_k^T\mathit{x})+b,$$

where ${\eta }_{(\mathit{\theta },\mathit{t},\mathit{\beta },b)}\left(\mathit{x}\right)\in \mathbb{R}$ is the output of the single hidden layer neural network with parameter $(\mathit{\theta },\mathit{t},\mathit{\beta },b)$. Applying the logistic function $\sigma (·)$, $\sigma \left({\eta }_{(\mathit{\theta },\mathit{t},\mathit{\beta },b)}\left(\mathit{x}\right)\right)\in (0,1)$ as an approximation of $f\left(\mathit{x}\right)$ with parameters $(\mathit{\theta },\mathit{t},\mathit{\beta },b)$

$$P(Y=1|X=x)\approx \sigma \left({\eta }_{(\mathit{\theta },\mathit{t},\mathit{\beta },b)}\left(\mathit{x}\right)\right),P(Y=0|X=x)\approx 1-\sigma \left({\eta }_{(\mathit{\theta },\mathit{t},\mathit{\beta },b)}\left(\mathit{x}\right)\right),$$

where $\sigma (·)=\exp (·)/[1+\exp (·\left)\right]$. According to the universal approximation theorem, see [8], with a big enough m, the single layer neural network is able to approximate any continuous function with a quite small approximation error.

By [2], assuming that there is a Fourier representation of $f\left(\mathit{x}\right)$ of the form $f\left(\mathit{x}\right)={\int }_{{\mathbb{R}}^p}{e}^{i{\mathit{\omega }}^T\mathit{x}}\tilde{F}\left(d\mathit{\omega }\right)$, let ${\Gamma }_{B,C}=\{f(·):{\int }_B{\Vert \mathit{\omega }\Vert }_2|\tilde{f}\left(d\mathit{\omega }\right)<C\}$ for some bounded subset of ${\mathbb{R}}^p$ containing zero and for some constant $C>0$. Then for all functions $f\in {\Gamma }_{B,C}$, there exists a single layer neural network output $\eta \left(\mathit{x}\right)$ such that ${\Vert \eta \left(\mathit{x}\right)-f\left(\mathit{x}\right)\Vert }_2=O(1/\sqrt{m})$ on B. Later [20] generalizes the result by relaxing the assumptions on the activation function and improved the rate of approximation by a logarithmic factor. They showed that on a bounded domain $\Omega \subset {\mathbb{R}}^p$ with Lipschitz boundary, assuming $f\in H^r(\Omega )$ satisfies $\gamma \left(f\right)={\int }_{{\mathbb{R}}^p}{(1+|\omega \left|\right)}^{m+1}\left|{\hat{f}}_e\left(\omega \right)\right|d\omega <\infty$ for some extension $f_e\in H^r\left({\mathbb{R}}^p\right)$ with $f_{e|\Omega }$, if the activation function $\sigma \in W^{r,\infty }\left(\mathbb{R}\right)$ is non-zero and satisfies the polynomial decay condition $|\left(D^k\sigma \left(t\right)\right)|\le C_r{(1+|t\left|\right)}^{-s}$ for some $0\le k\le r$ and some $s>1$, we have

$$\underset{f_m\in NeuNe{t}_m}{inf}{\Vert f-f_m\Vert }_{H^r(\Omega )}\le C(s,r,\Omega ,\sigma )\gamma \left(f\right)m^{-1/2},$$

where the norm is in Sobolev space of order r, and $C(s,r,\Omega ,\sigma )$ is a function of s, r, $\Omega$ and $\sigma$ only. Both results ensure the good approximation property of single layer neural network, and the convergence rate is independent of the dimension of $\mathit{x}$, p, as long as f has a Fourier transform which decays sufficiently fast.

Towards building the high-dimensional ANN, we start by formalizing the model. Let $\mathit{X}$ be a $n\times p$ design or input matrix,

$$\mathit{X}=\left[\begin{array}{ccc}{x}_{11}& \cdots & x_{1p}\\ \cdots & \cdots & \cdots \\ x_{n1}& \cdots & x_{np}\end{array}\right]=\left[\begin{array}{c}{\mathit{x}}_1^T\\ ⋮\\ {\mathit{x}}_n^T\end{array}\right]=\left[\begin{array}{cc}{\mathit{x}}_{\left(1\right)}& \cdots {\mathit{x}}_{\left(p\right)}\end{array}\right],$$

let $\mathit{y}$ be a $n\times 1$ response or outcome vector,

$$\mathit{y}={\left[\begin{array}{ccc}{y}_1& \cdots & y_n\end{array}\right]}^T,$$

let $\mathit{\theta }$ be a $p\times m$ parameter or input weight matrix,

$$\mathit{\theta }=\left[\begin{array}{ccc}{\theta }_{11}& \cdots & {\theta }_{1m}\\ \cdots & \cdots & \cdots \\ {\theta }_{p1}& \cdots & {\theta }_{pm}\end{array}\right]=\left[\begin{array}{c}{\mathit{\theta }}_{\left(1\right)}^T\\ ⋮\\ {\mathit{\theta }}_{\left(p\right)}^T\end{array}\right]=\left[\begin{array}{cc}{\mathit{\theta }}_1& \cdots {\mathit{\theta }}_m\end{array}\right],$$

let $\mathit{t}$ be a $p\times 1$ parameter vector,

$$\mathit{t}={\left[\begin{array}{ccc}{t}_1& \cdots & t_m\end{array}\right]}^T,$$

let $\mathit{\beta }$ be a $m\times 1$ parameter vector representing node weights,

$$\mathit{\beta }={\left[\begin{array}{ccc}{\beta }_1& \cdots & {\beta }_m\end{array}\right]}^T,$$

and let b be a scalar parameter.

When one tries to bring neural network into the high-dimension set up, or equivalently, the small sample size scenario, it usually does not work well. The estimability issue [14] arise from the fact that even a single layer neural network may have too many parameters. This issue might already exist in the low dimensional case ($n<p$), let alone the high dimension case. A single layer neural network usually includes $mp+2m+1$ parameters, which is possible to be much more than the training sample size n. In practice, a neural network may work well with one of the local optimal solutions although this is not guaranteed by theory. Regularization methods can be applied to help obtain a sparse solution. On one hand, proper choice of regularization shrinks partial parameters to zero, which addresses the statistical estimability issue. On the other hand, regularization makes the model more robust.

Assuming sparsity is usually the most efficient way of dealing with the high dimensionality. A lasso type regularization on the parameters has been shown numerically to have poor performance on neural network models. On one hand, lasso does not drop a feature entirely but only disconnect it with some hidden nodes. On the other hand, lasso does not select dependent predictor variables in a good manner [9]. Consider the sparse group lasso proposed by [21], which penalizes the predictors group-wise and individually simultaneously. It is a combination of the group lasso and the lasso, see for example [11]. The group lasso regularization part penalizes the input features’ weights group-wisely: a feature is either selected or dropped, and it is connected to all nodes in the hidden layer if selected. The lasso part further shrinks some weights of the selected inputs features to zero: a feature does not need to be connected to all nodes in the hidden layer when selected.

Define the loss function as the log-likelihood function

$$l(\mathit{\theta },\mathit{t},\mathit{\beta },b)=\sum _{i=1}^n\left[y_i(\sum _{k=1}^m{\beta }_k\psi (t_k+{\mathit{\theta }}_k^T{\mathit{x}}_i)+b)-\log \left(1+\exp \left(\sum _{k=1}^m{\beta }_k\psi (t_k+{\mathit{\theta }}_k^T{\mathit{x}}_i)+b\right)\right)\right].$$

(2)

Besides the sparse group lasso regularization, we consider a $l_2$ regularization on other parameters. Then we have

$$\begin{array}{ll}{\hat{\mathit{\theta }}}_{sgl},{\hat{\mathit{t}}}_{sgl},{\hat{\mathit{\beta }}}_{sgl},{\hat{b}}_{sgl}& =\underset{\mathit{\theta },\mathit{t},\mathit{\beta },b\in {\mathbb{R}}^{pm\times m\times m\times 1}}{\mathrm{arg\; min}}-\frac{1}{n}l(\mathit{\theta },\mathit{t},\mathit{\beta },b)\\ & +\alpha \lambda \sum _{j=1}^p\Vert {\mathit{\theta }}_{\left(j\right)}{\Vert }_2+(1-\alpha )\lambda {\Vert \mathit{\theta }\Vert }_1,\end{array}$$

(3)

such that

$${\Vert \mathit{\beta }\Vert }_2^2+{\Vert \mathit{t}\Vert }_2^2+b^2\le K.$$

The sparse group lasso penalty [11,21] includes a group lasso part and a lasso part, which are balanced using the hyper-parameter $\alpha \in (0,1)$. The group lasso part treats each input as group of m variables, including the weights for the m hidden nodes connected to each input. This regularization will be able to include or drop an input variable’s m hidden nodes group-wisely [27]. The lasso regularization is used to further make the weights sparse within each group, i.e., each input selected by the group lasso regularization does not have to connect to all hidden nodes. This combination of the two regularizations makes the estimation even easier for small sample problems. The $l_2$ norm regularization on the other parameters is more about practical concerns, since it further reduces the risk of overfitting.

Though with slight difference on the regularization, [11] proposed a fast coordinate gradient descent algorithm for the estimation, which cycles the gradient descent for the differentiable part of the loss function, the threshold function for the group lasso part and the threshold function for the lasso part. Three tuning parameters, $\alpha$, $\lambda$ and K can be selected with cross-validations on a grid search.

3. The Consistency of Neural Network Classification Risk

In this section, we conduct the theoretical investigation of classification accuracy of the neural network model. Before stating the theorems, we need a few assumptions. The independence property of neural networks, see [1,25] and [11], states that the first-layer weights in $\mathit{\theta },\mathit{t}$ satisfy

$$({\mathit{\theta }}_i,t_i)\ne \pm ({\mathit{\theta }}_{i^{\prime }},t_{i^{\prime }}),\forall i\ne i^{\prime }=1,\cdots ,m$$

and

$${\mathit{\theta }}_i\ne \mathbf{0},\forall i,$$

the set of dilated and translated functions ${\mathbb{R}}^p\to \mathbb{R}$

$$\{1,\sigma ({\mathit{\theta }}_1^T\mathit{x}+t_1),\dots ,\sigma ({\mathit{\theta }}_m^T\mathit{x}+t_m)\}$$

is linearly independent.

The independence property means that different nodes depend on the input predictor variables through different linear combinations and none of the hidden nodes is a linear combination of the other nodes, which is crucial in the universal approximation capability of neural networks. [20] proved that the above set is linearly independent if ${\mathit{\theta }}_i^{\prime }s$ are pairwise linearly independent, as long as the non-polynomial activation function is an integrable function which satisfies a polynomial growth condition.

According to [11], if the parameters $\mathit{\varphi }=(\mathit{\theta },\mathit{t},\mathit{\beta },b)$ satisfy the independence property, the following equivalence class of parameters

$$EQ\left(\mathit{\varphi }\right)=\{\tilde{\mathit{\varphi }}\in \Theta :{\eta }_{\tilde{\mathit{\varphi }}}\left(\mathit{x}\right)={\eta }_{\mathit{\varphi }}\left(\mathit{x}\right)\forall \mathit{x}\}$$

contains only parameterizations that are sign-flips or rotations and has cardinality exactly $2^{m}m!$.

Let $\mathbb{P}$ be the distribution of Y for fixed $\mathit{X}$ and ${\mathbb{P}}_n$ be the empirical measure. The best approximation in the neural network space is the equivalence class of parameters by minimizing the population loss

$$E{Q}_0=\underset{\mathit{\varphi }\in \Theta }{\mathrm{arg\; min}}{\int }_{{\mathbb{R}}^p\times \{0,1\}}{l}_{\mathit{\varphi }}(y,\mathit{x})d{P}_{\mathit{X},Y},$$

where $l_{\mathit{\varphi }}(y,\mathit{x})d{P}_{\mathit{X},Y}$ is the loss function with parameters $\mathit{\varphi }$. Let Q be the number of equivalent classes in $E{Q}_0$. The Excess loss is defined as

$$\epsilon \left(\mathit{\varphi }\right)={\int }_{{\mathbb{R}}^p\times \{0,1\}}\left(l_{\mathit{\varphi }}(Y,\mathit{X})-l_{{\mathit{\varphi }}^0}(Y,\mathit{X})\right)d{P}_{\mathit{X},Y}$$

(4)

where ${\mathit{\varphi }}^0$ is a set of parameters in $E{Q}_0$. Moreover, when we refer to a set of parameters in $E{Q}_0$ for some parameter $\mathit{\varphi }$, we mean that ${\mathit{\varphi }}^0\in E{Q}_0$ has the minimum distance to $\mathit{\varphi }$. [11] has shown that this excess loss plus the estimation of the irrelevant weights is bounded from above and may tend to zero with proper choices of n, p and the tuning parameters.

Another concern is the estimability of the parameters. A common remedy is to assume sparsity of the predictors. Thus we make the following assumption.

Assumption 1.

(Sparsity) Only s of the predictors are relevant in predicting y (without loss of generality, we assume the first s predictors, denoted S are relevant, and the rest, denoted$S^C$, are irrelevant), all weights in θ associated with$S^C$, denoted${\mathit{\theta }}_{S^C}$, are zero in the optimal neural network$E{Q}_0$.

The next assumption is a standard assumption in generalized models, which controls the variance of the response from below and above. Consider a general exponential family distribution on y with canonical function $b\left(\theta \right)$, common assumptions is to bound $b^{\prime \prime }\left(\theta \right)$ and $b^{\prime \prime \prime }\left(\theta \right)$ from above and below. However, in binary classification problems, these functions are automatically bounded from above by 1, thus we only need to assume the boundedness from below. Some literature assume constant bounds on these quantities, however, we do allow the bounds to change with n and the bounds may tend to zero as n goes to infinity.

Assumption 2.

(Boundedness of variance) The true conditional probability of y for a given$\mathit{x}$is bounded away from 0 and 1 by a quantity$\widetilde{ϵ}$, which might tend to zero.

The following two assumptions are inherited from [11]. The next assumption is a relatively weak assumption on the local convexity of the parameters.

Assumption 3.

(Local convexity) There is a constant$h_{min}>0$that may depend on m, s, f and the distribution$P_{\mathit{X},Y}$, but does not depend on p such that for all$\mathit{\varphi }\in E{Q}_0$, we have

$${\left[{\nabla }_{\mathit{\varphi }}^2\left({\int }_{{\mathbb{R}}^p\times \{0,1\}}{l}_{\mathit{\varphi }}(y,\mathit{x})d{P}_{\mathit{X},Y}\right)\right]}_{\mathit{\varphi }={\mathit{\varphi }}^0}⪰h_{min}\left[\begin{array}{cc}\mathbf{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right]$$

where$A⪰B$means that$A-B$is a positive semi-definite matrix.

The next assumption is made to bound the excess loss from below for the parameters outside $E{Q}_0$, i.e., the true model is identifiable. Let $d_0\left(\mathit{\varphi }\right)$ be the minimum distance from an element in $E{Q}_0$ to $\mathit{\varphi }$, then we assume

Assumption 4.

(Identifiability) For all$ϵ>0$, there is an${\alpha }_{ϵ}$that may depend on m, s, f and the distribution$P_{\mathit{X},Y}$, but does not depend on p such that

$$\begin{array}{l}{\alpha }_{ϵ}\le \underset{\mathit{\varphi }}{\inf }\left\{\epsilon \left(\mathit{\varphi }\right):d_0\left(\mathit{\varphi }\right)\ge ϵand{\Vert {\mathit{\theta }}_{S^C}\Vert }_1\le 3\sum _{j\in S}{\Omega }_{\alpha }({\mathit{\theta }}_{\left(j\right)}\right.\\ \hspace{1em}\hspace{1em} \left.-{\mathit{\theta }}_{\left(j\right)}^{0,\left(\mathit{\varphi }\right)})+{\Vert (\mathit{t},\mathit{\beta },b)-({\mathit{t}}^{0,\left(\mathit{\varphi }\right)},{\mathit{\beta }}^{0,\left(\mathit{\varphi }\right)},b^{0,\left(\mathit{\varphi }\right)})\Vert }_2\right\}.\end{array}$$

Assumption 3 states that though neural network is a non-convex optimization problem globally, the parameters of the best neural network approximation of the true function $f\left(x\right)$ has a locally convex neighborhood. The assumption can be assured in this way. By the continuity of the representation of the neural network and the loss function, the integration in Assumption 3 is infinitely continuously differentiable with respect to the nonzero parameters, therefore the second derivative is a continuous function of the nonzero parameters. By the definition of the parameters of the best neural network approximation, ${\mathit{\varphi }}_0$ minimizes the integration in Assumption 3. If there is not a positive $h_{min}$ that satisfies assumption, it either contradicts with the fact that the second derivative is continuous or the definition of ${\mathit{\varphi }}_0$.

Assumption 4 states that the non-optimal neural networks can be distinguished from the best neural network approximation in terms of the excess loss, if the parameters of the non-optimal neural network is not in the $ϵ$-neighborhood of any of the parameters of the best neural network class $E{Q}_0$. Similar to the compatibility condition in [4], the condition does not have to or even may not hold for the whole space, but is only needed in the subspace $\{\mathit{\varphi }:\Vert {\mathit{\theta }}_{S^C}{\Vert }_1\le 3{\sum }_{j\in S}{\Omega }_{\alpha }({\mathit{\theta }}_{\left(j\right)}-{\mathit{\theta }}_{\left(j\right)}^{0,\left(\mathit{\varphi }\right)})+\Vert (\mathit{t},\mathit{\beta },b)-({\mathit{t}}^{0,\left(\mathit{\varphi }\right)},{\mathit{\beta }}^{0,\left(\mathit{\varphi }\right)},b^{0,\left(\mathit{\varphi }\right)}){\Vert }_2\}$, thus this is a weaker condition than imposing the lower bound on the excess loss. The subspace is derived from the the basic inequality of the definition of $\hat{\mathit{\varphi }}$ with rearranging terms and norm inequalities, see for example [4]. Similar subspace can also been found in the compatible condition in [19]. Since s is unknown, it can not be checked in practice, but it is sufficient to check the inequality for all sets $S\in \{1,\dots ,p\}$ with cardinality $s_0$ if $s_0$ is known, which is a stronger version of Assumption 4.

Now we are ready to state our main result. We have to admit that our theory based on the estimator from (3) is the global optima, which suffers from the biggest problem in optimization research: the gap between the global optima in theory and a local optima in practice. We will leave this computational issue to future research.

Theorem 1.

Under Assumptions 1–4, let our estimation be from Equation (3), choosing tuning parameter$\lambda \ge 2T\tilde{\lambda }$for some constant$T\ge 1$and$\tilde{\lambda }=c\sqrt{m\log n/n}(\sqrt{\log Q}+\sqrt{m\log p}\log \left(nm\right)/(1-\alpha +\alpha /\sqrt{m}))$, if$\log \left(n\right)/\left(n{\widetilde{ϵ}}^2\right)\to 0$,$s^{2}m{\lambda }^2/\left(n{\widetilde{ϵ}}^2\right)\to 0$and$n^{-1}{m}^{9/2}{s}^{5/2}\sqrt{\log \left(p\right)}\to 0$as$n\to \infty$, assume that our prediction is within a constant distance from the best approximation${\eta }^0\left(\mathit{x}\right)$, then we have

$$R\left(\hat{C}\right)-R\left(C^{*}\right)\to 0asn\to \infty$$

A proof of this theorem is given in appendix. This theorem states that with proper choice of tuning parameters and under some mild assumptions and controls of n, p and s, the high-dimensional neural network with sparse group lasso regularization tends to have the optimal classification risk. This is a significant improvement in the theoretical neural network study, since it gives the theoretical guarantee that high dimensional neural network will definitely work in such situations.

4. Simulation

In this section, we will show two examples. The first example is a revisit of the simulation study in [17], where we show numerical results that the sparse group lasso neural network (SGLNN)’s performance is close to the Deep Neural Persuit (DNP)’s performance in their set up. The second example considers a scenario where the sample size is much smaller, where we show numerical results that the SGLNN out-performs the DNP.

4.1. Dnp Simulation: Revisit

In this subsection, we revisit the experiment in [17] and compare those models with the neural network with sparse group lasso regularization. We used exactly the same setup as [17]. The input variable $\mathit{X}$ was drawn from $U(-1,1)$, where the feature dimension p was fixed to be $10,000$. The corresponding labels were obtained by passing $\mathit{X}$ into the feed forward neural network with hidden layer sizes $\{50,30,15,10\}$ and ReLU activation functions. Input weights connecting the first m inputs were randomly sampled from $N(0,0.5)$. The remaining input weights were kept zero. Furthermore, 5% of the labels were randomly chosen and flipped to add noises. For each $m=2,5,10,25$, we generated 800 training samples, 200 validation samples and 7500 test samples. We report the AUC and F1 scores of the models in

Table 1. The AUC and F1 score of the compared models in the simulation study. Standard errors are given in the parentheses.

	True Dim	2	5	10	25
LogR-$l_1$	AUC(std)	0.897(0.015)	0.745(0.035)	0.661(0.029)	0.629(0.015)
HSIC-Lasso	AUC(std)	0.920(0.001)	0.844(0.015)	0.732(0.025)	0.638(0.021)
DNP	AUC(std)	0.925(0.020)	0.879(0.035)	0.784(0.020)	0.669(0.016)
SGLNN	AUC(std)	0.911(0.015)	0.862(0.021)	0.770(0.021)	0.658(0.016)
LogR-$l_1$	F1 score(std)	0.889(0.022)	0.748(0.032)	0.668(0.037)	0.638(0.027)
HSIC-Lasso	F1 score(std)	0.914(0.000)	0.791(0.010)	0.680(0.012)	0.368(0.028)
DNP	F1 score(std)	0.959(0.009)	0.849(0.033)	0.769(0.017)	0.811(0.015)
SGLNN	F1 score(std)	0.940(0.005)	0.839(0.012)	0.747(0.019)	0.754(0.015)

on 5 repetitions of the data generation, which was exactly the same as in [17]. The DNP model was coded according to their algorithm outline in python with pyTorch. The HSICLasso was implemented with the package by the authors followed by the support vector machine (SVM) package in scikit-learn. The LogR-$l_1$ model was implemented with the LogisticRegressionCV package in scikit-learn.

In this simulation study, the assumptions in our theory are all satisfied. First, we have a sparse level of 2, 5, 10 and 25, which are very small portions of the total number of features, 10,000, thus Assumption 1 is satisfied. Second, we have controlled the seed such that the labels are balanced between 0 and 1, and the true probabilities generated from the neural network are bounded away from 0 and 1 by a non-negligible constant, thus assumption 2 is satisfied. Then, we generate x from uniform distribution and y from a neural network structure, which is a continuous distribution plus a continuous map from the original space to the probabilities $[0,1]$. Therefore, the local convexity assumption is justified by continuity. Finally, Assumption 4 is a property of neural networks that has been argued in Section 3. Therefore, this example not only serves as a revisit of the DNP paper, but also serves as a support for our theory.

From the results, we see both the SGLNN model and the DNP model outperform the other two baseline models. The SGLNN’s performance is very close to the performance of DNP with a small gap, which is in accordance to our expectations. Deeper neural networks have much higher representation powers of complicated functions. The stability of the two models are close, with the SGLNN having slightly smaller SE in the $m=2$ and $m=5$ cases. The DNP model does not use dropout in the prediction process, while the SGLNN uses $l_1$ norm penalty along with the group lasso penalty. The SGLNN is expected to show stabler results. The reason that we see no significant difference in SE is that the sample size, 800, is large enough to train the DNP with a full network on the selected variables without overfitting. To further investigate the performance, we study the smaller sample scenario in the next subsection.

4.2. Smaller Sample Size Case

In this subsection, we consider a smaller sample size, which happens in many applications such as clinic trials, genetic expression data analysis and MRI data analysis. With the same set up as the model generation in the last subsection, we generate a training sample of size $n=100,200,300$ and 500. The number of active features is fixed to be $m=5$. The total sample size is set to $10,000$, thus the corresponding testing sample sizes are $9900,9800,9700$ and 9500. We compare the performance between the SGLNN and DNP in this set up. The results are shown in

Table 2. The AUC and F1 score of the compared models in a smaller sample size scenario with $m=5$. Standard errors are given in the parentheses.

	Training Sample Size	100	200	300	500
DNP	AUC(std)	0.606(0.118)	0.701(0.091)	0.727(0.074)	0.828(0.043))
SGLNN	AUC(std)	0.624(0.099)	0.703(0.089)	0.762(0.053)	0.820(0.026)
DNP	F1 score(std)	0.567(0.095)	0.634(0.073))	0.679(0.043)	0.750(0.035)
SGLNN	F1 score(std)	0.602(0.073)	0.641(0.069)	0.690(0.029)	0.746(0.029)

.

From the results, we see the SGLNN model outperforms the DNP in the smaller sample size scenario when $n=100,200,300$. The reason is that DNP overfits the training data due to small sample size, while SGLNN has lower risk of overfitting compared with DNP. In all the four sample sizes, the SGLNN has smaller SE than the DNP model’s SE. SGLNN achieved this by a simpler representation and the extra $l_1$ norm regularization. The results suggest that we need a simpler model to prevent overfitting when the training sample size is very small, which is the case in most biology data. Moreover, an extra $l_1$ regularization makes the model more stable and reliable.

5. Real Data Examples

In this section, we gave real data applications in different research areas: gene expression data, MRI data and computer vision data. These examples indicate that the sparse neural network has good performance and is useful in correlated predictor situations. Through all three examples, the regularized neural network was implemented with fast speed using the algorithm by [11] through their library in python3 on a desktop computer with Ubuntu 18 system on a i7 processor and GTX1660TI graphic cards.

To evaluate the model performance, all accuracy results were measured on the testing sets which were not used for training and averaged on different train test splits. The number of features in the results are medians among all numbers of features that correspond to the best models evaluated from cross-validation.

5.1. Example 1: Prostate Cancer Data

In this example, we considered a prostate cancer gene expression data, which is publicly available in http://featureselection.asu.edu/datasets.php. The data set contains a binary response with 102 observations on 5966 predictor variables. Clearly, the data set is really a high-dimensional data set. The responses have values 1 (50 sample points) and 2 (52 sample points), where 1 indicates normal and 2 indicates tumor. All predictors are continuous predictors, with positive values.

Forty observations from no expression group and forty observations from the expression group were randomly selected to form the training group. The remaining 22 observations form the testing group. We run the sparse ANN model on a replication of 100 different train–test splits. On average, the sparse neural network selects only 18 predictors and uses four hidden nodes. Using a cross-validation technique, the hyper-parameters, and thus the number of features were decided. It has a average training error rate of $0.04$ and a testing error rate of $0.045$. The results compared with other methods are listed in

Table 3. Test accuracy with standard error in parentheses and median of number of features for different classifiers in the Prostate gene data example.

Classifier	Test Accuracy	Number of Features
Regularized neural network	0.955(0.066)	18
Gradient boosting tree	0.922(0.058)	83.5
Logistic Regression with Lasso	0.933(0.058)	36
l1 penalized Linear SVM	0.950(0.052)	16
Generalized additive model with group lasso	0.918(0.061)	5

. The sparse ANN and $l_1$ penalized linear SVM perform the best with 95.5% and 95% accuracy, respectively. The gradient boosting tree classifier [5] is a powerful ensemble classification method but performs worse than regularized methods in the high-dimensional setting with an accuracy of 92.2% using 83.5 features (on average). The logistic regression with $l_1$ regularization uses 36 features and achieves an accuracy of 93.3%. The generalized additive model (GAM) performs the worst with an accuracy of 91.8%, mainly due to the infeasibility of basis expansion in this data set, where the data distribution is highly skewed.

In summary, we showed numerically that the sparse group lasso penalized neural network is able to achieve at least as good as the existing methods along with providing strong theoretical support. The greater standard error mainly comes from additional tuning parameters. In terms of the number of predictor variables, it is not the best. However, as we found in the investigation, since ANN is a non-convex optimization problem, as people continue to train the model and tune the hyper-parameters, they get better accuracy rates with less number of predictor variables.

5.2. Example 2: Mri Data for Alzheimer’S Disease

Data used in this example is from the Alzheimer’s disease Neuroimaging Initiative (ADNI) database (http://www.loni.ucla.edu/ADNI). We used T1-weighted MRI images from the collection of standardized datasets. The description of the standardized MRI imaging from ADNI can be found in http://adni.loni.usc.edu/methods/mri-analysis/adni-standardized-data/. The images were obtained using magnetization prepared rapid gradient echo (MARAGE) or equivalent protocols with varying resolutions (typically $1.0\times 1.0$ mm in plane spatial resolution and 1.2 mm thick sagittal slices with $256\times 256\times 256$ voxels). The images were then pre-processed according to a number of steps detailed at http://adni.loni.usc.edu/methods/mri-analysis/mri-pre-processing/, which corrected gradient non-linearity, intensity inhomogeneity and phantom-based distortion. In addition, the pre-processed imaging were processed by FreeSurfer for cortical reconstruction and volumetric segmentation by Center for Imaging of Neurodegnerative Diseases, UCSF. The skull-stripped volume (brain mask) obtained by FreeSurfer cross-sectional processing were used in this study.

In our example, we used images from ADNI-1 subjects obtained using 1.5 T scanners at screening visits, and we used the first time point if there are multiple images of the same subject acquired at different times. There are totally 414 subjects, among which 187 are diagnosed as Alzheimer’s disease and 227 healthy subjects at the screening visit. An R package ANTsR were applied for imaging registration. Then, the 3dresample commands in AFNI were used to adjust the resolution and reduce the total number of voxels of the imaging to $18\times 22\times 18$. The x axis and y axis for horizontal plane, x axis and z axis for coronal plane and y axis and z axis for sagittal plane. Only the 1100 voxels located in the center of the brain were used as features for classification. After removing the voxels with zero signal for most of the subjects, we have 1971 voxels left in use.

We randomly sampled 100 from the 187 AD subjects and 100 from the 227 healthy subjects as our training set, and the rest 214 subjects as testing set. The sparse ANN model was run on 100 replications of different train–test split. On average, the neural network finally selects seven predictors and used 12 hidden nodes. It has a training error rate of $0.21$ and a testing error rate of $0.224$. The results compared with other methods are listed in

Table 4. Test accuracy with standard error in parentheses and median of the number of features for different classifiers in the MRI Alzheimer’s disease example.

Classifier	Test Accuracy	Number of Features
Regularized neural network	0.776(0.031)	7
MLE-LDA	0.692(0.030)	1971
PREG	0.750(0.029)	3
PMLE-LDA	0.772(0.025)	5
FAIR	0.632(0.033)	7
NB	0.674(0.024)	1971

. The sparse ANN has a competitive performance which is slightly better than the PMLE-LDA with similar standard error. The goal of this experiment is not to show that the sparse group lasso neural network outperforms the other methods significantly, but just demonstrates that the model can be tuned to work as good as the other methods along with statistical theory. With finer tuning of the hyper-parameters, the results can be further improved. We compared the results with a few methods including the MLE-LDA, the PMLE-LDA (penalized MLE-LDA; [28]), the PREG-LDA (penalized regular LDA; [28]), the FAIR (Feature Annealed Independence Rule; [10]) and the NB (Naive Bayes; [3]). Methods without regularization are not presented, since the high dimensionality prevents it from giving stable solutions. The penalized MLE-LDA produces an accuracy rate of 77.2% using only five predictor variables. The PREG-LDA method has the least number of predictors, 3, but has a lower accuracy rate 0.750. The rest of the methods perform worse. Besides the application, this example indicates that the ANN could be an alternative tool for spatial data modeling, at least for classification.

5.3. Example: Karlsruhe Institute of Technology and Toyato Technology Institute (KITTI) Autonomous Driving Data

For the generalization, we also give an example on the computer vision tasks. The data used in this example is from [12], which has different aspect of images or stereos from high-resolution color and gray-scale video cameras or ladar (laser radar). The image and stereo data includes daily traffic data that help developing autonomous driving in different aspects. In our example, we used the 2D object detection data, for example, see Figure 2.

The 2D object data set includes 7481 training images and 7518 testing images, comprising a total of 80,256 labeled objects. All images are colored and saved as a .png file. Since this was an open competition, the labels for testing data are not available. We only used the training data set as our example data. The original data includes 13 different label classes, however, to emphasize the binary classification ability of the regularized ANN model, we took only two classes: pedestrian and car. The sub-images of pedestrians and cars were extracted from the original images using the location information provided by the data set. This gives us 18,000 car images and 7000 pedestrian images of resolution ranging from 40-by-40 to 180-by-150. Since the regularized ANN methods is especially useful when the sample size is small, we randomly sampled 2000 cars and 2000 pedestrians as our data. We shuffled the 4000 images, and divided them into 800 training images and 3200 testing images. Figure 3 show the images after pre-processing. A pre-processing steps are done with python libraries including matplotlib, PIL and pandas.

Since ANN does not handle local feature information as good as convolutional neural networks (CNN), we did a feature extraction using the pre-trained VGG19 CNN model [22], whose weights were trained on 120 million images of over 1000 classes. We adopted the convolutional layers from the model as a feature extractor. To feed the images into the model, a re-sizing (from the original size to 224-by-224-by-3) were performed using bi-linear interpolation methods. The VGG19 feature extractor generates a 4096-by-1 vector from each image. Our ANN model takes this 4096-dimensional input and trains on the 800 images. We compare our results with the regular ANN, the logistic regression with $l_1$ regularization, the SVM with $l_1$ regularization and the GAM with group lasso regularization. The results are shown in

Table 5. Test accuracy with standard error in parentheses and median of the number of features for different classifiers in the KITTI autonomous driving example.

Classifier	Test Accuracy	Number of Features
SGLNN	0.994(0.001)	148
Neural network	0.514(0.102)	4096
Log-$l_1$	0.991(0.002)	176
SVM-$l_1$	0.993(0.001)	144
GAM	0.989(0.002)	152

. The regular neural network totally failed due to the high-dimensionality and hence estimability issue. The logistic regression and the GAM have more nonzero features and slightly greater standard error. The SVM has similar result to the SGLNN, but the SGLNN gains a slightly better performance.

Moreover, we have plotted the accuracy score for all three examples along with the sparsity level. $l_1$ logistic regression, $l_1$ SVM and group lasso penalized generalized additive model (GAM) are used along with the sparse group lasso neural network (SGLNN). These plots give us a hint how sparsity level influences the prediction results. The plots are given in Figure 4. All these examples illustrate the usefulness and the numerical properties of our proposed high dimensional neural network model.

6. Discussion

In this paper, we considered the sparse group lasso regularization on high-dimensional neural networks and proved that under mild assumptions, the classification risk converges to the optimal Bayes classifier’s risk. To the best of our knowledge, this is the first result that the classification risk of high-dimensional sparse neural network converges to the optimal Bayes risk. Neural networks are very good approximations to correlated feature functions, including computer vision tasks, MRI data analysis and spatial data analysis. We expect further investigation is warranted in the future.

An innovative idea that deserves further investigation is to specify a larger number of hidden nodes and use a $l_0+l_1$ norm penalty on the hidden nodes parameters $\mathit{\beta }$. This methods searches a larger solution field and will give a model at least as good as the $l_2$ norm penalty. Moreover, $l_0+l_1$ norm penalty is proved to work well in low signal cases [18]. In detail, the formulation is to minimize (3) plus an extra regularization on $\mathit{\beta }$: ${\lambda }_3{\Vert \mathit{\beta }\Vert }_0+{\lambda }_4{\Vert \mathit{\beta }\Vert }_1$. This formulation does not bring in extra tuning parameters, since we release the penalization on $l_2$ norm of $\mathit{\beta }$ and the number of hidden nodes m. With $l_0+l_1$ norm penalty, the parameters can be trained using coordinate descent algorithm with the $l_0+l_1$ norm penalty being handled by mixed integer second order cone optimization (MISOCO) algorithms via optimization software like Gurobi. This algorithm adds an extra step to the algorithm in [11] to handle the $l_0+l_1$ norm penalty.

The computational issue of finding the global optimal in non-convex optimization problems is still waiting to be solved to eliminate the gap between theory and practice. This will pave way for further theoretical research.