Generalization of Parameter Selection of SVM and LS-SVM for Regression
Abstract
1. Introduction
2. Materials and Methods
2.1. Models
2.2. Software
2.3. Data
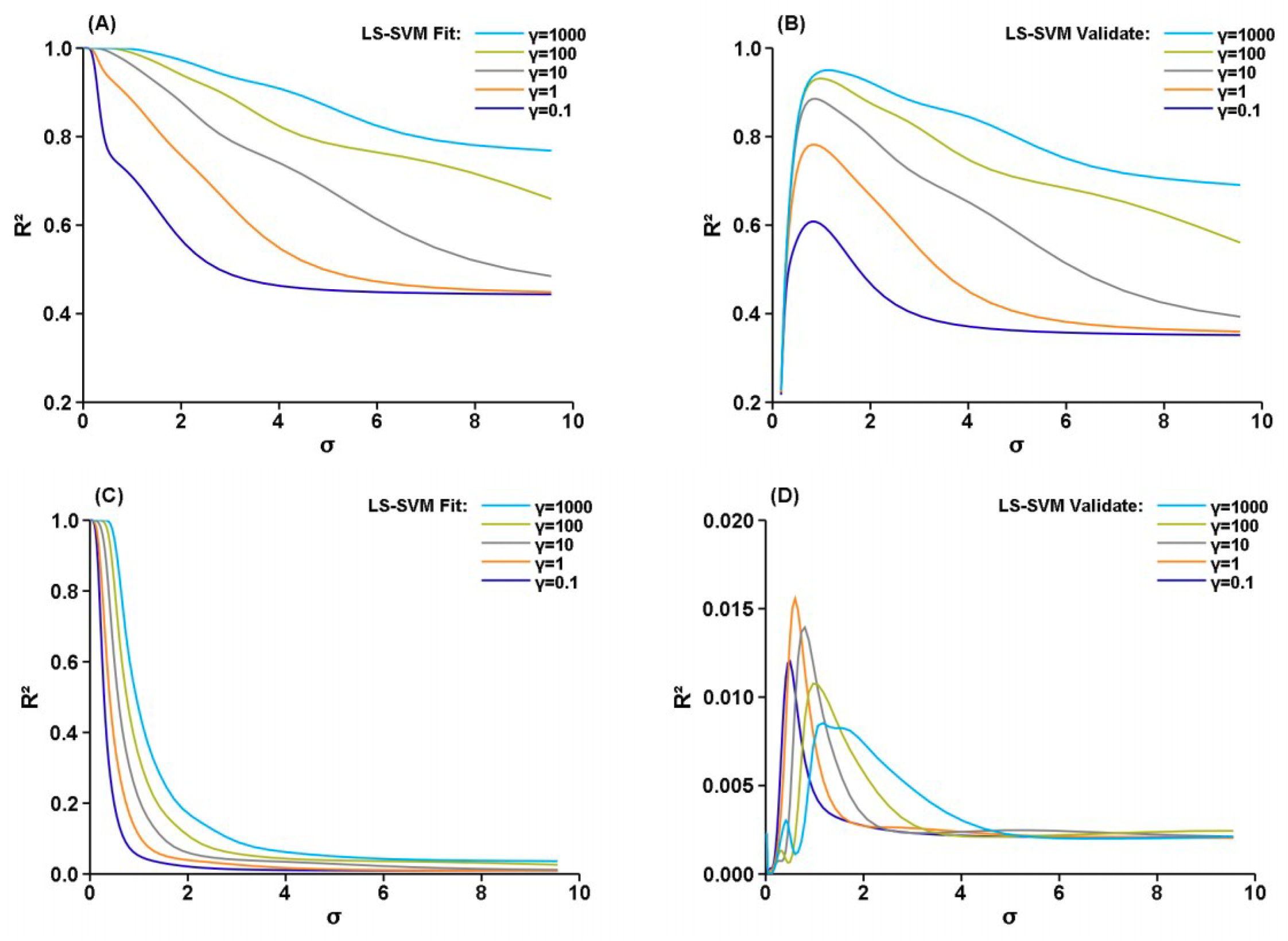
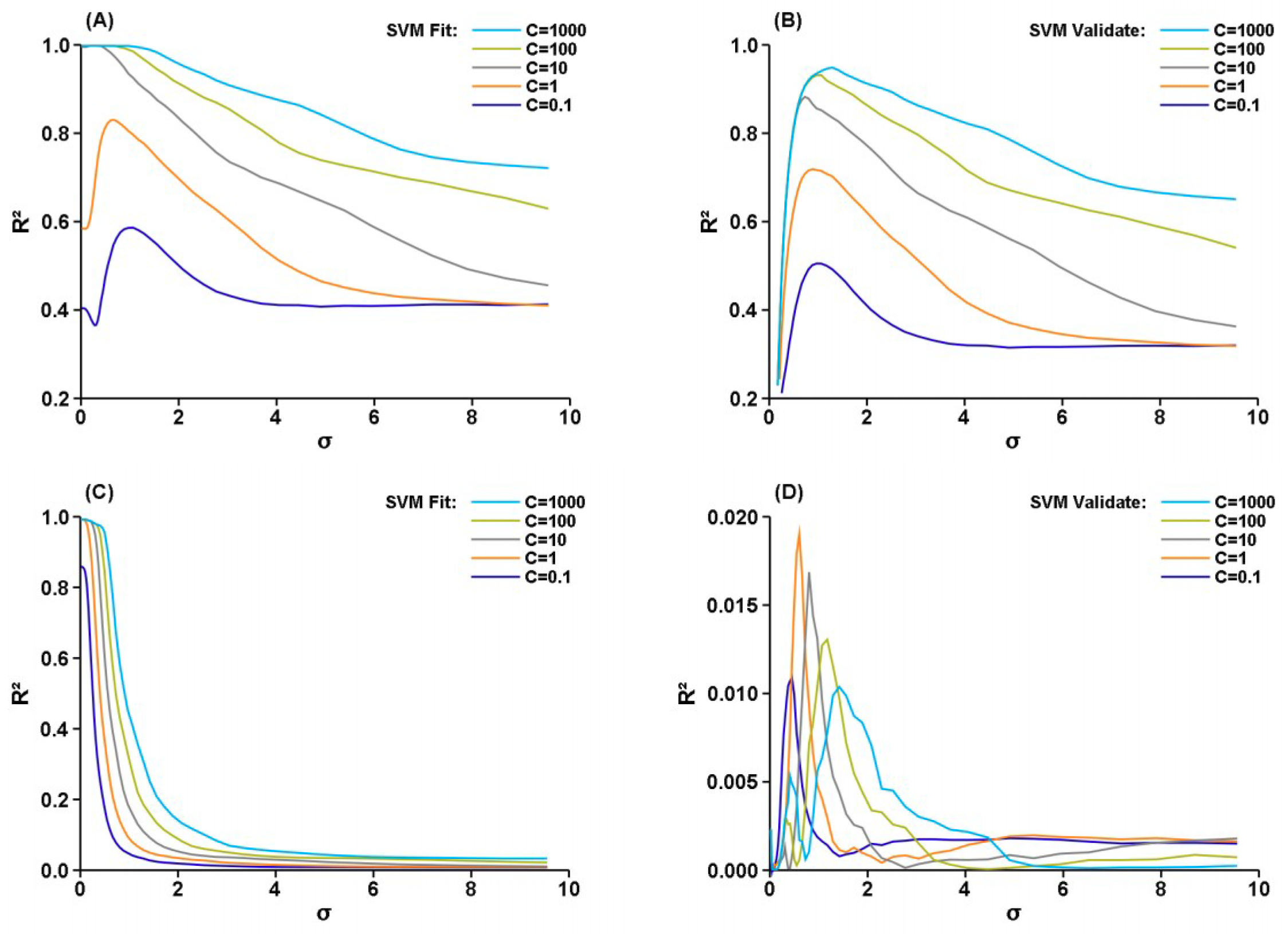
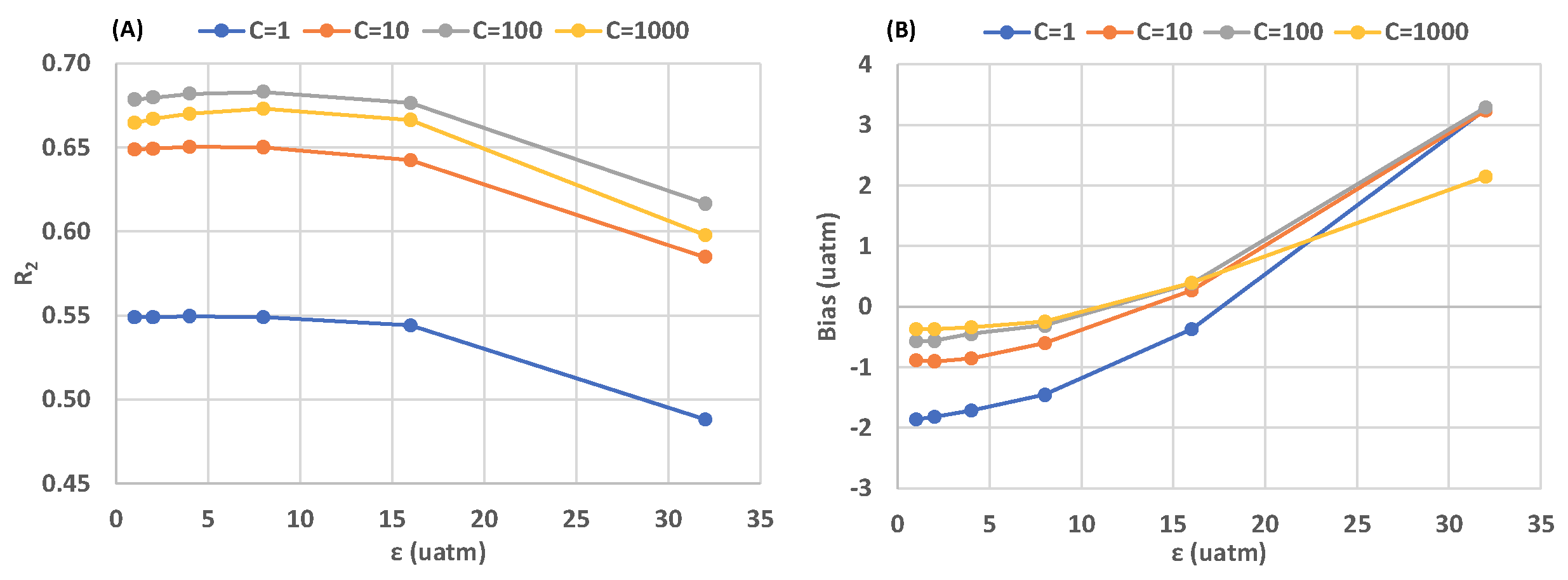
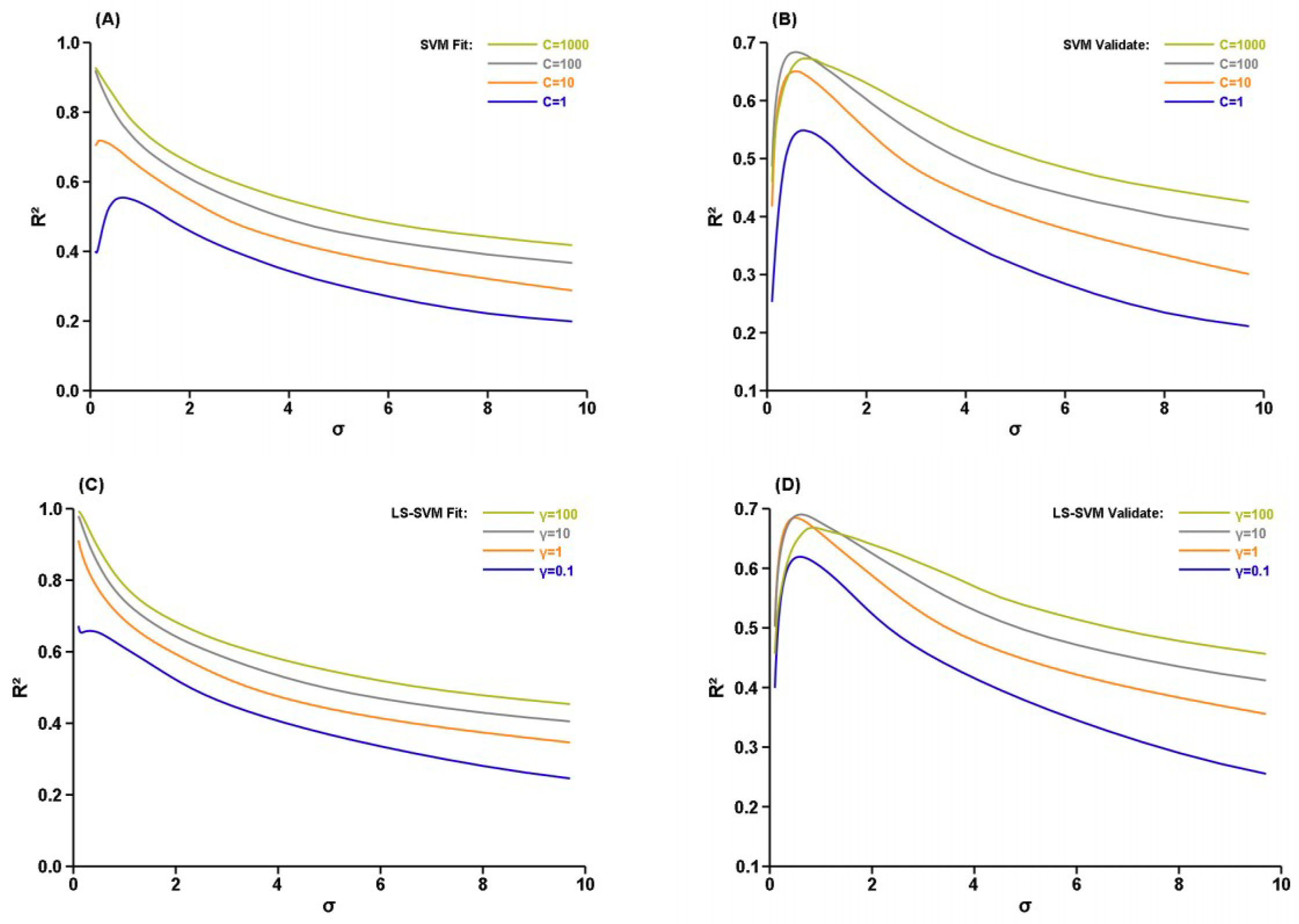
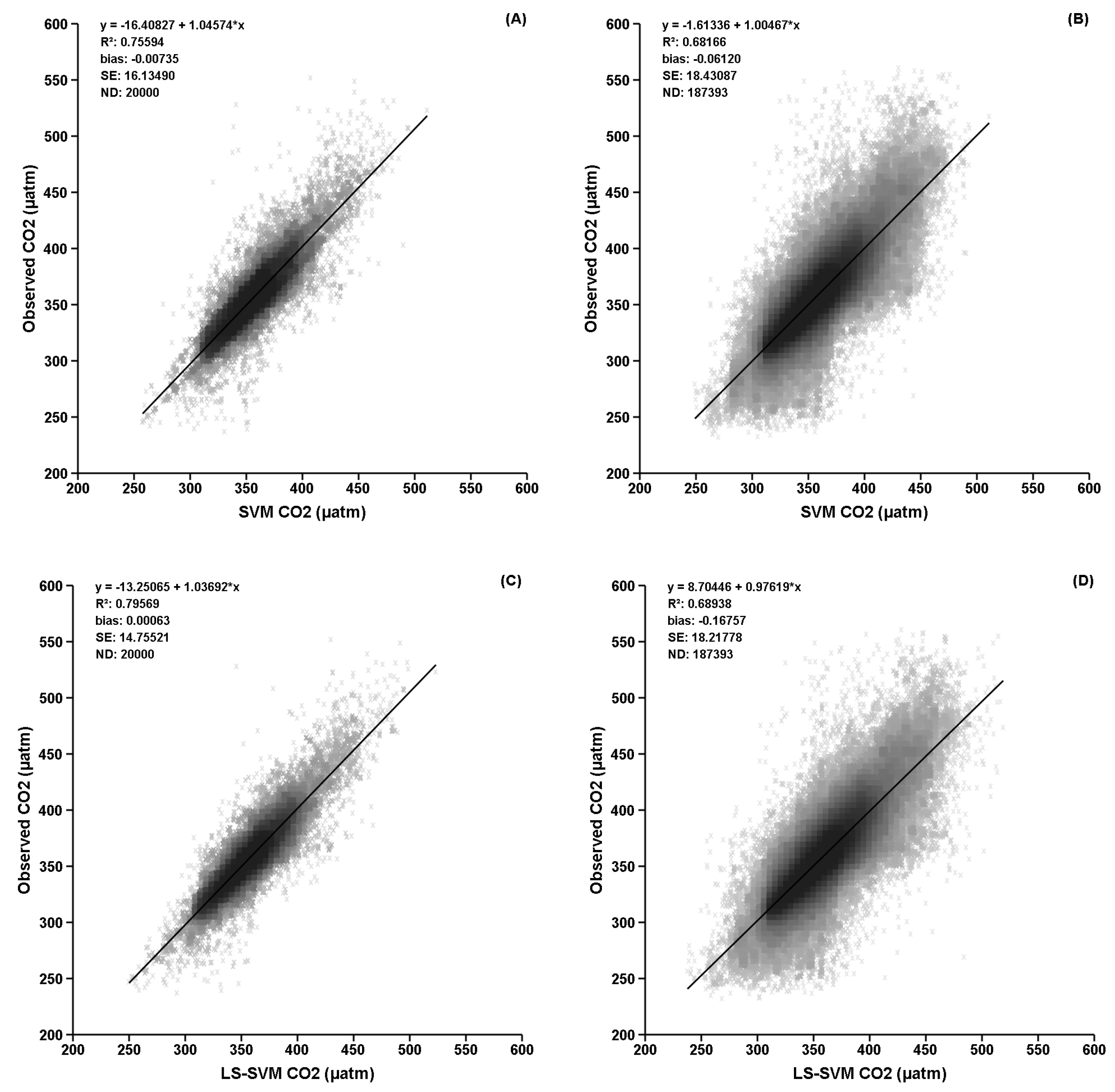
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Ge, J.; Meng, B.; Liang, T.; Feng, Q.; Gao, J.; Yang, S.; Huang, X.; Xie, H. Modeling alpine grassland cover based on MODIS data and support vector machine regression in the headwater region of the Huanghe River, China. Remote Sens. Environ. 2018, 218, 162–173. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Behmanesh, J.; Khalili, K. Comprehensive modeling of monthly mean soil temperature using multivariate adaptive regression splines and support vector machine. Theor. Appl. Climatol. 2018, 133, 911–924. [Google Scholar] [CrossRef]
- Jang, E.; Im, J.; Park, G.H.; Park, Y.G. Estimation of fugacity of carbon dioxide in the east sea using in situ measurements and geostationary ocean color imager satellite data. Remote Sens. 2017, 9, 821. [Google Scholar] [CrossRef]
- Gregor, L.; Kok, S.; Monteiro, P.M.S. Empirical methods for the estimation of Southern Ocean CO2: Support vector and random forest regression. Biogeosciences 2017, 14, 5551–5569. [Google Scholar] [CrossRef]
- Yang, F.; White, M.A.; Michaelis, A.R.; Ichii, K.; Hashimoto, H.; Votava, P.; Zhu, A.-X.; Nemani, R.R. Prediction of Continental-Scale Evapotranspiration by Combining MODIS and AmeriFlux Data Through Support Vector Machine. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3452–3461. [Google Scholar] [CrossRef]
- Sachindra, D.A.; Huang, F.; Barton, A.; Perera, B.J.C. Least square support vector and multi-linear regression for statistically downscaling general circulation model outputs to catchment streamflows. Int. J. Climatol. 2013, 33, 1087–1106. [Google Scholar] [CrossRef]
- Zeng, J.; Matsunaga, T.; Saigusa, N.; Shirai, T.; Nakaoka, S.I.; Tan, Z.H. Technical note: Evaluation of three machine learning models for surface ocean CO2 mapping. Ocean Sci. 2017, 13, 303–313. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Van Gestel, T.; De Brabanter, J.; De Moor, B.; Vandewalle, J. Least Squares Support Vector Machines; World Scientific: Singapore, 2002; ISBN 981-238-151-1. [Google Scholar]
- Meza, A.M.Á.; Santacoloma, G.D.; Medina, C.D.A.; Dominguez, G.C. Parameter selection in least squares-support vector machines regression oriented, using generalized cross-validation. Rev. DYNA 2011, 171, 23–30. [Google Scholar]
- Cherkassky, V.; Ma, Y. Selection of Meta-Parameters for Support Vector Regression. In Proceedings of the International Conference on Artificial Neural Networks 2002, Madrid, Spain, 28–30 August 2002; Dorronsoro, J.R., Ed.; LNCS. Volume 2415, pp. 687–693. [Google Scholar] [CrossRef]
- Chapelle, O.; Vapnik, V.; Bousquet, O.; Mukherjee, S. Choosing multiple parameters for support vector machines. Mach. Learn. 2002, 46, 131–159. [Google Scholar] [CrossRef]
- Frauke, F.; Christian, I. Evolutionary Tuning of Multiple SVM Parameters. In Proceedings of the ESANN’2004 Proceedings—European Symposium on Artificial Neural Networks, Bruges, Belgium, 27–29 April 2004; pp. 519–524, ISBN 2-930307-04-8. [Google Scholar]
- Glasmachers, T.; Igel, C. Gradient-based adaptation of general gaussian kernels. Neural Comput. 2005, 17, 2099–2105. [Google Scholar] [CrossRef] [PubMed]
- Lendasse, A.; Ji, Y.; Reyhani, N.; Verleysen, M. LS-SVM hyperparameter selection with a nonparametric noise estimator. Robotics 2005, 3697, 625–630. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, Y.; Huang, W.; Zhang, H.; Jiang, S.; Zhu, L. Study on Parameter Optimization for Support Vector Regression in Solving the Inverse ECG Problem. Comput. Math. Methods Med. 2013, 2013, 158056. [Google Scholar] [CrossRef] [PubMed]
- Laref, R.; Losson, E.; Sava, A.; Siadat, M. On the optimization of the support vector machine regression hyperparameters setting for gas sensors array applications. Chemom. Intell. Lab. Syst. 2019, 184, 22–27. [Google Scholar] [CrossRef]
- Zhang, L.; Lei, J.; Zhou, Q.; Wang, Y. Using Genetic Algorithm to Optimize Parameters of Support Vector Machine and Its Application in Material Fatigue Life Prediction. Adv. Nat. Sci. 2015, 8, 21–26. [Google Scholar] [CrossRef]
- De Brabanter, K.; Suykens, J.A.K.; De Moor, B. Nonparametric Regression via StatLSSVM. J. Stat. Softw. 2015, 55. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. Libsvm. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Joachims, T. Making Large-Scale SVM Learning Practical. Advances in Kernel Methods—Support Vector Learning; Schölkopf, B., Burges, J.C.C., Smola, A.J., Eds.; MIT Press: Cambridge, MA, USA, 1998; pp. 169–184. [Google Scholar]
- Collobert, R.; Williamson, R.C. SVMTorch: Support Vector Machines for Large-Scale Regression Problems. J. Mach. Learn. Res. 2001, 1, 143–160. [Google Scholar]
- Zeng, J.; Nojiri, Y.; Landschützer, P.; Telszewski, M.; Nakaoka, S. A global surface ocean fCO2 climatology based on a feed-forward neural network. J. Atmos. Ocean. Technol. 2014, 31, 1838–1849. [Google Scholar] [CrossRef]
- Bakker, D.C.E.; Pfeil, B.; Landa, C.S.; Metzl, N.; O’Brien, K.M.; Olsen, A.; Xu, S. A multi-decade record of high-quality fCO2 data in version 3 of the Surface Ocean CO2 Atlas (SOCAT). Earth Syst. Sci. Data 2016, 8, 383–413. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Rayner, N.A.; Smith, T.M.; Stokes, D.C.; Wang, W. An Improved In Situ and Satellite SST Analysis for Climate. J. Clim. 2002, 15, 1609–1625. [Google Scholar] [CrossRef]
- Boyer, T.P.; Antonov, J.I.; Baranova, O.K.; Coleman, C.; Garcia, H.E.; Grodsky, A.; Sullivan, K.D. World Ocean Database 2013, NOAA Atlas NESDIS 72; Levitus, S., Mishonoc, A., Eds.; NOAA Printing Office: Silver Spring, MD, USA, 2013; 209p. [CrossRef]
- O’Reilly, J.E.; Maritorena, S.; Siegel, D.; O’Brien, M.C.; Toole, D.; Mitchell, B.G.; Culver, M. Ocean color chlorophyll a algorithms for SeaWiFS, OC2, and OC4: Version 4. In SeaWiFS Postlaunch Technical Report Series; SeaWiFS Postlaunch Calibration and Validation Analyses, Part 3; NASA Goddard Space Flight Center: Washington, DC, USA, 2000; Volume 11, pp. 9–23. [Google Scholar] [CrossRef]
- Schmidtko, S.; Johnson, G.C.; Lyman, J.M. MIMOC: A global monthly isopycnal upper-ocean climatology with mixed layers. J. Geophys. Res. Ocean. 2013, 118, 1658–1672. [Google Scholar] [CrossRef]
- Xu, Q.S.; Liang, Y.Z. Monte Carlo cross validation. Chemom. Intell. Lab. Syst. 2001, 56, 1–11. [Google Scholar] [CrossRef]
- Zeng, J.; Nojiri, Y.; Nakaoka, S.; Nakajima, H.; Shirai, T. Surface ocean CO2 in 1990–2011 modelled using a feed-forward neural network. Geosci. Data J. 2015, 2, 47–51. [Google Scholar] [CrossRef]
| Sample ID | Training R2 | Training Bias | Validate R2 | Validate Bias |
|---|---|---|---|---|
| 1 | 0.756 | −0.01 | 0.682 | −0.06 |
| 2 | 0.763 | −0.03 | 0.679 | 0.00 |
| 3 | 0.758 | −0.11 | 0.678 | −0.81 |
| 4 | 0.757 | −0.02 | 0.680 | −0.38 |
| 5 | 0.764 | −0.10 | 0.681 | −0.23 |
| 6 | 0.765 | −0.02 | 0.682 | 0.06 |
| 7 | 0.770 | −0.02 | 0.680 | 0.29 |
| 8 | 0.751 | −0.07 | 0.680 | −0.12 |
| 9 | 0.762 | −0.02 | 0.680 | −0.17 |
| 10 | 0.764 | −0.11 | 0.679 | −0.27 |
| Mean | 0.761 | −0.05 | 0.680 | −0.17 |
| STDEV | 0.005 | 0.05 | 0.001 | 0.29 |
| Sample ID | Training R2 | Training Bias | Validate R2 | Validate Bias |
|---|---|---|---|---|
| 1 | 0.796 | 0.00 | 0.689 | −0.17 |
| 2 | 0.802 | 0.00 | 0.693 | −0.11 |
| 3 | 0.798 | 0.00 | 0.691 | −0.42 |
| 4 | 0.795 | 0.00 | 0.689 | −0.21 |
| 5 | 0.804 | −0.00 | 0.693 | −0.16 |
| 6 | 0.804 | 0.00 | 0.692 | 0.02 |
| 7 | 0.807 | 0.00 | 0.691 | 0.09 |
| 8 | 0.793 | 0.00 | 0.688 | −0.09 |
| 9 | 0.803 | 0.00 | 0.689 | −0.14 |
| 10 | 0.804 | 0.00 | 0.691 | −0.16 |
| Mean | 0.801 | 0.00 | 0.691 | −0.14 |
| STDEV | 0.005 | 0.00 | 0.002 | 0.14 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, J.; Tan, Z.-H.; Matsunaga, T.; Shirai, T. Generalization of Parameter Selection of SVM and LS-SVM for Regression. Mach. Learn. Knowl. Extr. 2019, 1, 745-755. https://doi.org/10.3390/make1020043
Zeng J, Tan Z-H, Matsunaga T, Shirai T. Generalization of Parameter Selection of SVM and LS-SVM for Regression. Machine Learning and Knowledge Extraction. 2019; 1(2):745-755. https://doi.org/10.3390/make1020043
Chicago/Turabian StyleZeng, Jiye, Zheng-Hong Tan, Tsuneo Matsunaga, and Tomoko Shirai. 2019. "Generalization of Parameter Selection of SVM and LS-SVM for Regression" Machine Learning and Knowledge Extraction 1, no. 2: 745-755. https://doi.org/10.3390/make1020043
APA StyleZeng, J., Tan, Z.-H., Matsunaga, T., & Shirai, T. (2019). Generalization of Parameter Selection of SVM and LS-SVM for Regression. Machine Learning and Knowledge Extraction, 1(2), 745-755. https://doi.org/10.3390/make1020043





