1. Introduction
This manuscript specifically targets the problem of reducing the cardinality of high-dimensional solutions that are encountered in heuristic many-objective optimization problems. The holy grail in the heuristic search optimization domain is to essentially minimize the subjective areas (mainly tied to visualization), of reducing the cardinality of solutions and the deployment of the time-consuming Multi-Criteria Decision Making (MCDM) to determine the unique solution from the shortlist. Near-real time applications that are the domain of Industrial Internet of Things (IoT)IoT applications drive the quest. This work goes as far as finding the unique shortlist in a high-dimensional data set but determining the unique data point in that shortlist is ongoing and beyond the scope of this manuscript. However, the techniques that are employed will apply to any exploratory data analytics and, as such, the introduction is written in a generic sense and the results and discussion are certainly invaluable to general data science. In other words, this is a case where data science meets the heuristic search optimization.
The ability to make sense of multi-dimensional data has proven to be of high value in exploratory analysis, i.e., presenting the data in an interactive, graphical form, opening new insights, encouraging the formation and validation of new hypotheses, and ultimately better problem-solving abilities [
1,
2]. Exploratory analysis will most invariably seek to reduce the dimensionality of datasets in order to make analysis computationally tractable and to facilitate visualization [
3], which is a worthwhile contribution to science and humanity, given the benefits and successes that have been reported in literature [
4]. Making sense of multi-dimensional data is a cognitive activity that graphical external representations facilitate, from which the observer or explorer may construct an internal mental representation of the world from the data.
Although computers are used to facilitate the visualization process, ultimately it is the understanding that is conjured in the mind of the explorer that is of paramount importance. Despite the benefits of visualization, it introduces subjectivity, and the more that we can “mathematize” the processes that reduce dimensionality of hyperspaces and faithfully produce lower dimensional spaces that preserve geometric relationships among the variables of the data, the greater the likelihood of reducing the dependency on subjectivity in interpreting the data. Humans are indeed wired to think and view objects in lower dimensions and higher dimensional data (beyond three dimensions) offer no clues. The perception of high-dimensional data has seen applications far and wide, which have included: discovery of reasons for bank failures; discovery of hidden pricing mechanisms for commercial products, such as cereals; discovery of physical structure of pi meson-proton collisions, creation of detection schemes for chemical and biological warfare agents; the ability to detect buried landmines; and, so on [
4].
Historically, the analysis of high-dimensional data has been the fantasy for the revered mathematicians who could visualize objects in high-dimensional spaces [
4]. Therefore, many of the implementations for making sense of multivariate data are not that accessible to the casual user and, in most cases, do not readily encourage experimentation [
5]. Accordingly, it is fair to say that this is technically difficult to do and it may be computationally intensive [
6]. Multivariate and high-dimensional data are interchangeably used in this manuscript, and for our intent and purposes, these terms are used to describe a representation of a high-dimensional data space, which has a dimension for each variable (i.e., the columns of the dataset) and an instance for each case (i.e., the rows of the dataset).
It is notable that linear models are used far too often as a default tool for multivariate data analyses, because visualization techniques are not yet fully standardized for use to gain insight into the structural and functional relationships among many variables [
7]. With the advent of massive data collection via sensor networks, it is becoming increasingly prevalent to use visualization techniques and it is certainly an exciting time for developing and/or packaging the appropriate tools and strategies for exploratory visualization. The use of computer-based interactive visual representations that are designed to amplify human cognition have now become the domain of visual data exploration. The more accessible techniques that are proposed for multivariate data representation and exploration include [
8]:
- (a)
axes reconfiguration techniques (such as Parallel Coordinates Plots [
9] and glyphs [
10];
- (b)
dimensional embedding techniques (such as dimensional stacking and worlds within worlds);
- (c)
dimensional sub-setting (such as scatterplots) limited to relatively small and low-dimensional datasets [
1]; and,
- (d)
dimensional reduction techniques (such as multi-dimensional scaling (MDS), self-organizing maps [
11], and principal component analysis [
12].
However, it seems too often that the conventional and easy way is to reduce high dimensions into lower dimensions for Cartesian coordinate representation in two-dimensional (2D) plotting using scatterplots, which elicits the ease of comprehension, but without fully addressing the consequences of dimension reduction. Although such an approach makes for easy 2D graphical scatterplots, it is rendered inadequate because of the over-plotting of points, which results in incomprehensible data clouds. There is always the dreaded side effect of burying important information by collapsing the high dimensions into lower ones.
We propose a suite of tools that combine a projection and clustering methods, and three-dimensional (3D) visualization for making sense of multivariate datasets. The projection method that we present is a well-known technique, but it is the clustering process that includes a not so familiar algorithm for determining a near-optimal/optimal number of clusters, called the elbow rule [
13]. The second phase of the clustering process uses this optimal number of clusters to initialize the K-means++ algorithm [
14] to determine the clusters for the high-dimensional data. Anyone that has ever used the K-means or K-means++ appreciates the importance of having a good idea of the number of clusters in the high-dimensional data. We are able to visualize the high-dimensional data in 3D, where color is used to distinguish the different clusters by employing a projection technique, the Sammon’s nonlinear mapping [
15], or classic MDS. We demonstrate that the ability to determine the near-optimal/optimal clusters in a dimensional data is critical to such a process. Care has been taken to combine the tools, such that the visual representations or outcomes preserve consistency, rationality, “informativeness”, reproducibility, and richness in perceptual uniformity.
In this manuscript we describe the datasets used, the description of the suite of tools and method, and a discussion of the results, with a conclusion on our thoughts regarding where this proposed suite of tools might be of use, or possibly another good alternative in unsupervised learning or making sense of high-dimensional data.
2. Data Representation and Problem Formulation
The data used for developing the suite tools was a sample from a real world, many-objective optimization for a farming problem in New Zealand and a detailed description of the farm and data are found in [
16].
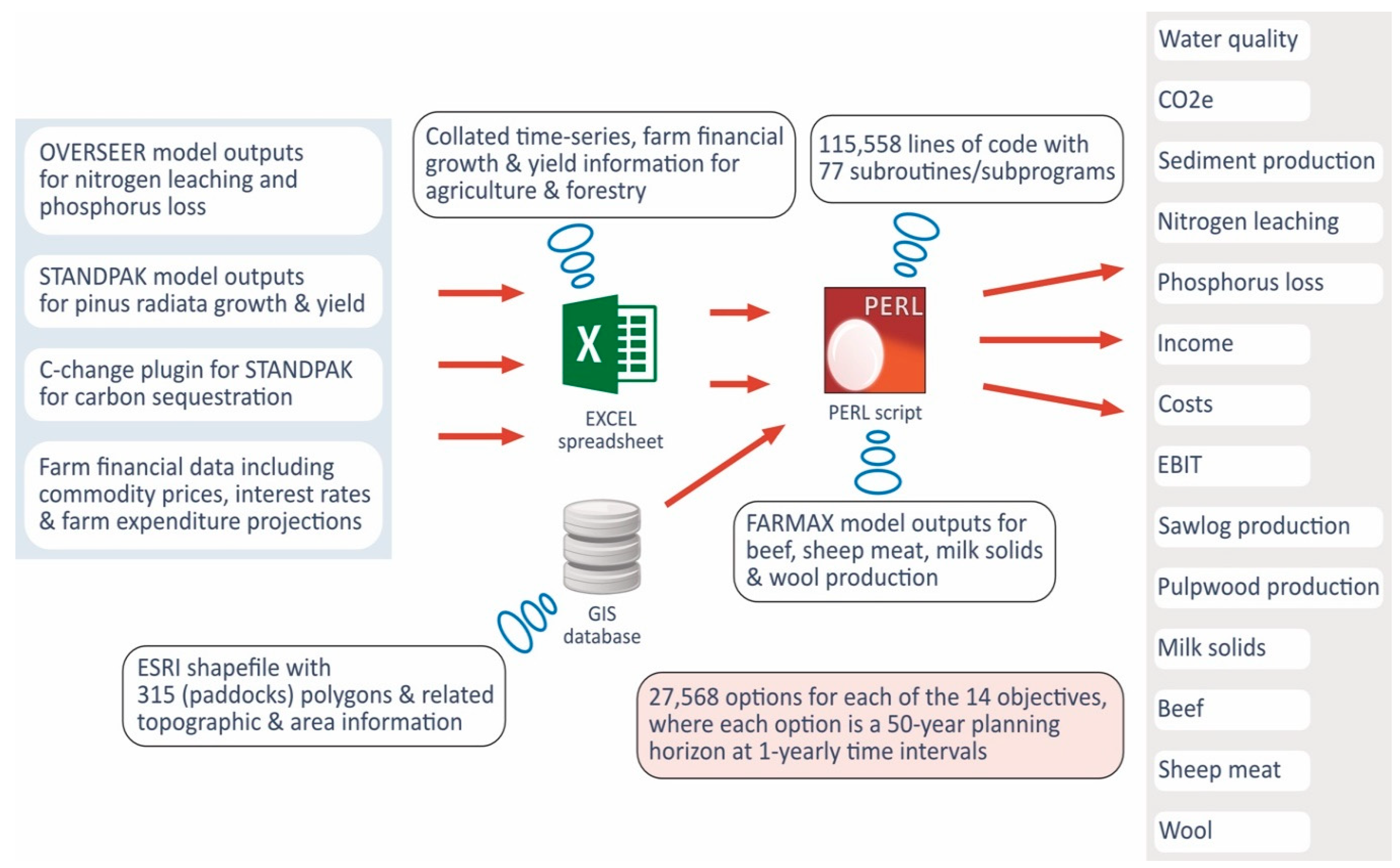
The farm property was 1500 hectares in size, consisting of 315 paddocks, each with a different land use, which included dairy, beef-cattle, and sheep/lamb farming, plantation forestry, and other land uses that could not be changed. Under each potential land use were different management options with unique environmental impacts and economic outputs, and the collation of the data via a large Perl script is shown in
Figure 1, with:
- (a)
spatial data of the topographic, edaphic, tenure and topology of paddocks (i.e., Geographic Information System’s ESRI shapefile);
- (b)
financial data records including commodity prices with their related genetic programming projection models, interest rates and their related genetic programming projection models, and farm expenditure projections; and,
- (c)
related specialist simulation models for forestry growth and yield (i.e., STANDPAK) [
17] and C-change for estimating carbon sequestration [
18], nutrient management (i.e., Overseer) [
19] and animal farming (i.e., Farmax) [
20].
The land use changes could only be carried out once at any one time during the initial decade of the 50-year planning period. Land use changes were carried out beyond the first ten years of the planning period in only a few cases, particularly the conversions from forestry to dairy farming. For example, a paddock with a forestry stand that is five years of age at the start of the planning period and harvested at the age of 30 years means that a change of land use only shows up in the 26th year of the planning horizon, which is way past the first decade in the planning period. The constraints were spatial and based on the first order neighborhood of paddocks, so as to encourage economies of scale by aggregating paddocks as much as possible into contiguous blocks with the same land use, hence adjacency constraints.
Following the determination of the solution, the objectives were integrated into meaningful multi-super-variables that were scaled to lower dimensions via appropriate MDS, making visualization in 3D possible without the loss of context. This process is elaborated under the Method and Discussion section. The optimization problem determined an optimal or near-optimal tradeoff mix of land uses and their related management options that would simultaneously satisfy 14 objectives together with the spatial constraints. Each of the objectives was a 50-year time-series at a one-year time interval. The desired strategic goal of the farm was to reduce the environmental footprint whilst maintaining a viable farming business. The 14 objectives that were listed under the super-objectives included:
- (a)
maximization of productivity: i.e., sawlog production, pulpwood production, milksolids, beef, sheep meat, wool, carbon sequestration, and water production;
- (b)
maximization of profitability: i.e., income, costs (minimized), and Earnings Before Interest and Tax (EBIT); and,
- (c)
minimization of the environmental footprint: i.e., nitrate leaching, phosphorus loss, and sedimentation.
It is important to note that the vast number of optimization search problems were characterized with features including nonlinearity, high-dimensionality, difficulty in modeling and finding derivatives, and so on [
21]; traditional techniques, such as linear, nonlinear, dynamic, or integer programming, etc., no longer apply. The conventional wisdom in computer science is to use search heuristics with the goal of finding approximate solutions to the problems or converging faster towards some desired solutions [
22]. The heuristic of choice for exploring the New Zealand farm search space was a highly-specialized nature-inspired genetic algorithm (GA), because, in general, GAs have been demonstrated to outperform application-independent heuristics while using random and systematic searches for exploring very large search spaces [
22]. This is because GAs make it possible to explore a far greater range of potential solutions to a problem than other conventional search algorithms [
23].
The large many-objective optimization problem formulation had a chromosomal data structure of up to 111 alleles or management options for each of its 240 genes (representing the paddocks); 66 options for each of the nine paddocks; 11 options for each of the 26 paddocks; nine options for one paddock; and, one option for each of the remaining 39 paddocks. Having 111 alleles on a gene is not unusual in the biological world. For instance, the human blood group system consists of 38 genes with 643 alleles [
24], and the cystic fibrosis related gene has over 1500 known allelic variants [
25]. However, it is nontrivial to search a space of 1.9 * 10
535 (i.e., 111
240 * 66
9 * 11
26 * 9
1 * 1
39) possible combinations of management options for this land use management problem with a generic many-objective evolutionary algorithm. It would take thousands of years to exhaustively search all of the possible combinations by calculating their fitness values, even on a super computer. The generic many-objective evolutionary algorithm would take a horrendously long period of time to search the space, as mutation alone would regulate the gradual accumulation of advantageous changes at a glacial pace over innumerable generations.
Therefore, the modifications of the many-objective evolutionary algorithm were based on cues that were taken from nature with a mathematical foundation, as described in the 2013 Wiley Practical Prize Award winning paper [
26], which used to take 10 hours to solve on a Mac pro with a 6-core processor, but still without successfully resolving the spatial constraints. The current modifications satisfy the spatial constraints and convergence is tracked while using an average Minkowski’s distance [
27] for each generation based on parallel coordinate plots of the 14 fitness functions. A clearly exponential decay trend of the average Minkowski’s distance is observed, something that could not be achieved by [
26], and it is now taking under two hours to solve on the same 6-core processor Mac pro. We avoid a full description here and also the improvements, because this is outside the scope of this manuscript and it would be in breach of Living PlanIT trade secrets. Note that evolutionary processes in the real world inextricably occur with epigenetics and epistasis, two critical phenomena that, respectively, make gene-to-environment and gene-to-gene interactions possible. Current biological research is showing that these processes form an effective coalition, particularly for the paradoxical and yet quintessential co-existence of robustness and responsiveness to environmental changes. The upshot of this paradox is shorter evolutionary times for evolving innovative phenotypic patterns that are suited to the prevailing environment.
In general, most Evolutionary Algorithms (EAs) are based on the Modern Synthesis and, to their credit, have been remarkably successful in solving difficult optimization problems, albeit when coupled with knowledge-enhanced procedures that require a deeper understanding of the problem.
A dynamic epigenetic and reprogramming resistance region (RRR) metaphor is combined with an Evolutionary Many-Objective Optimization Algorithm (EMOA), in a bid to replicate the benefits of knowledge-enhanced procedures, as in rapid convergence and the ability to find “interesting” areas in the search space for this heavily modified GA. A theoretical epigenetic and RRR model is deciphered from current biological research and is applied as a coupling algorithm to an EMOA to solve a constrained land use management problem with 14 objectives. The RRR model includes compositional epistasis, where the genes are essentially team players and other genes regulate their activities. The inclusion of epigenetics operators introduces the ability of the algorithm to learn, and forming memory that is managed via its persistence and transience (to reduce the influence of outdated information), hence the observed hot spot mutations. This makes it possible to approximate the Pareto-optimal front of a high dimensional problem, overcoming the many challenges that are faced by other variants of genetic algorithms, thus achieving the following:
- (a)
uniformly well-spaced approximation points for the Pareto front rather than producing disjointed clusters of approximation points;
- (b)
proportionately enriched Pareto front with higher quality approximation points in the region of interest (as directed by the placement of “preference points”); and,
- (c)
diverse approximation points representative of the broad spectrum of efficient solutions, without estimating the entire Pareto optimal set. The Pareto front of a high-dimensional problem is an overwhelmingly large subspace and to cover it sufficiently, a small representative set of Pareto-optimal solutions is estimated; and,
- (d)
a robust convergence whilst maintaining a good diversity between the solution estimates—a difficult feat to achieve with a higher number of objectives. The trending of historical fitness values (using the average Minkowski’s distance as a proxy), for all of the generations provided a basis for monitoring the convergence.
However, to stay on message for the clustering problem, it is important to note that, when objectives are many, sometimes conflicting and incommensurable, there is no unique solution that satisfies all of the objectives, rather it is a suite of elite solutions, known as non-dominated solutions or the Pareto front, with a diversity of trade-offs between the objectives for each solution. The Pareto front for the New Zealand farm problem had 100 solutions, each with 14 objectives. The heuristic was run over 100 generations and the Pareto fronts from the last 10 generations, i.e., generations 91–100, were used to determine the suite of tools for making sense of multivariate data. The converged Pareto fronts achieve uniformly well-spaced, distributed approximation points and clustering them is nontrivial, which happens to be the initial treatment in our method, as outlined in the next section, for understanding these multivariate data. Other methods, such as t-Distributed Stochastic Neighbor Embedding (t-SNE), Diffusion maps, Principal Component Analysis (PCA), and Isomaps, for identifying clusters in Pareto fronts are showing mixed results, although this work is still ongoing.
4. Results and Discussion
For all the 10 Pareto fronts, the highest Calinski-Harabasz criterion consistently indicated an optimal number of two clusters. The elbow rule estimated higher optimal numbers in all cases, as summarized in
Table 1. The elbow rule would always estimate higher numbers of clusters than the highest Calinski–Harabasz criterion method, even when
K-means or the Gaussian mixture models were used to estimate the criterion. It is important to remember that the datasets were high-dimensional and tightly distributed, making it difficult to delineate the boundaries of the clusters based on interpoint distances. Given that the iterative clustering algorithms rely on some random initialization or probabilistic search process, the key may just be the ability to locate these “no-man’s-land regions” at the boundaries of these clusters, where there is no exact border delineation on which points belong to which cluster. The unique solution we seek may just be laying at these no-man’s-land regions.
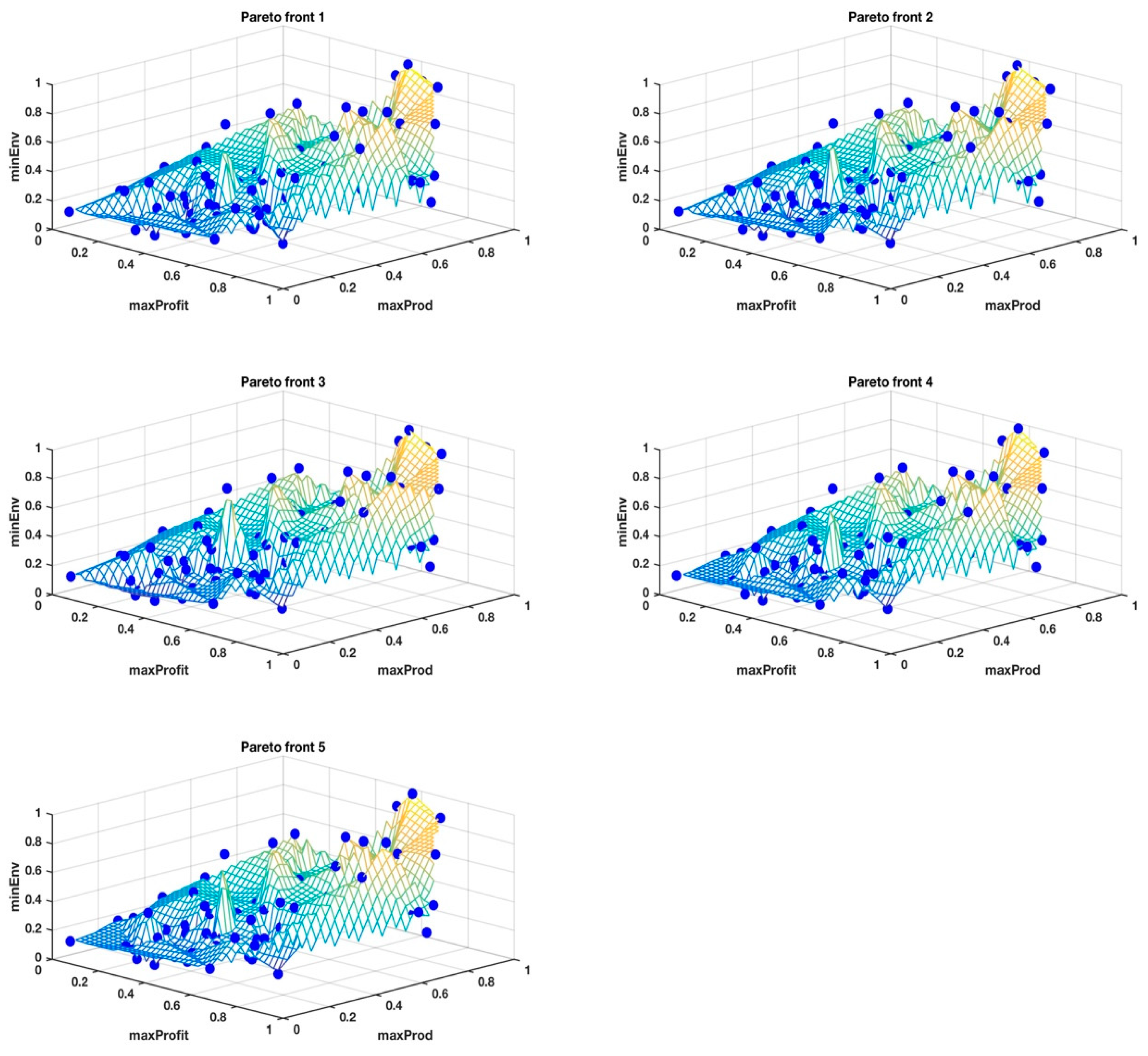
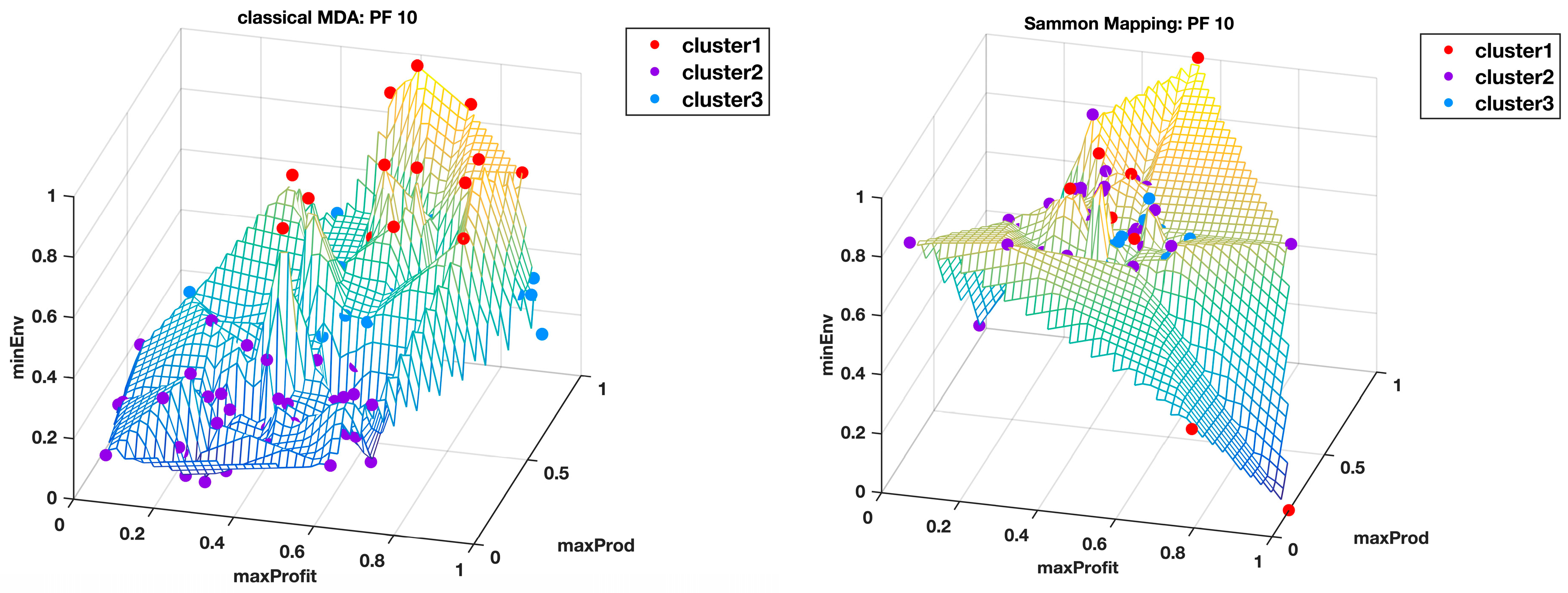
The classical MDS was used to visualize the 14-dimensional Pareto fronts in 3D, where integration of the data into three super objectives made it possible to view the data points in their unique cluster groups identified by different colors and superimposed on the wireframe mesh plots to help us have a better comprehension of what the results in
Table 1 mean. The wireframe mesh gave the 3D plots a landscape impression with peaks, valleys, and saddle points that enhanced the perception of the data point locations.
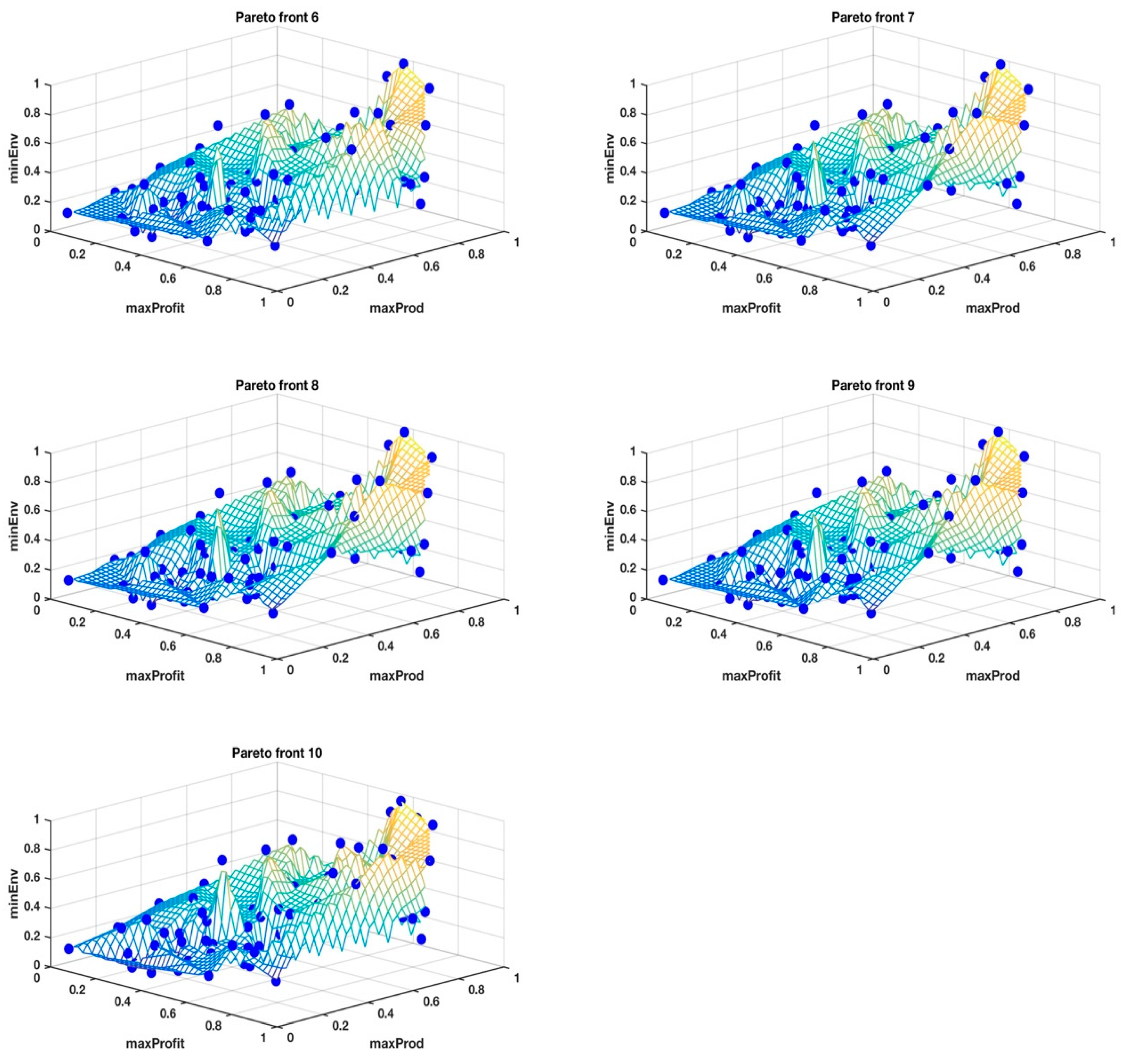
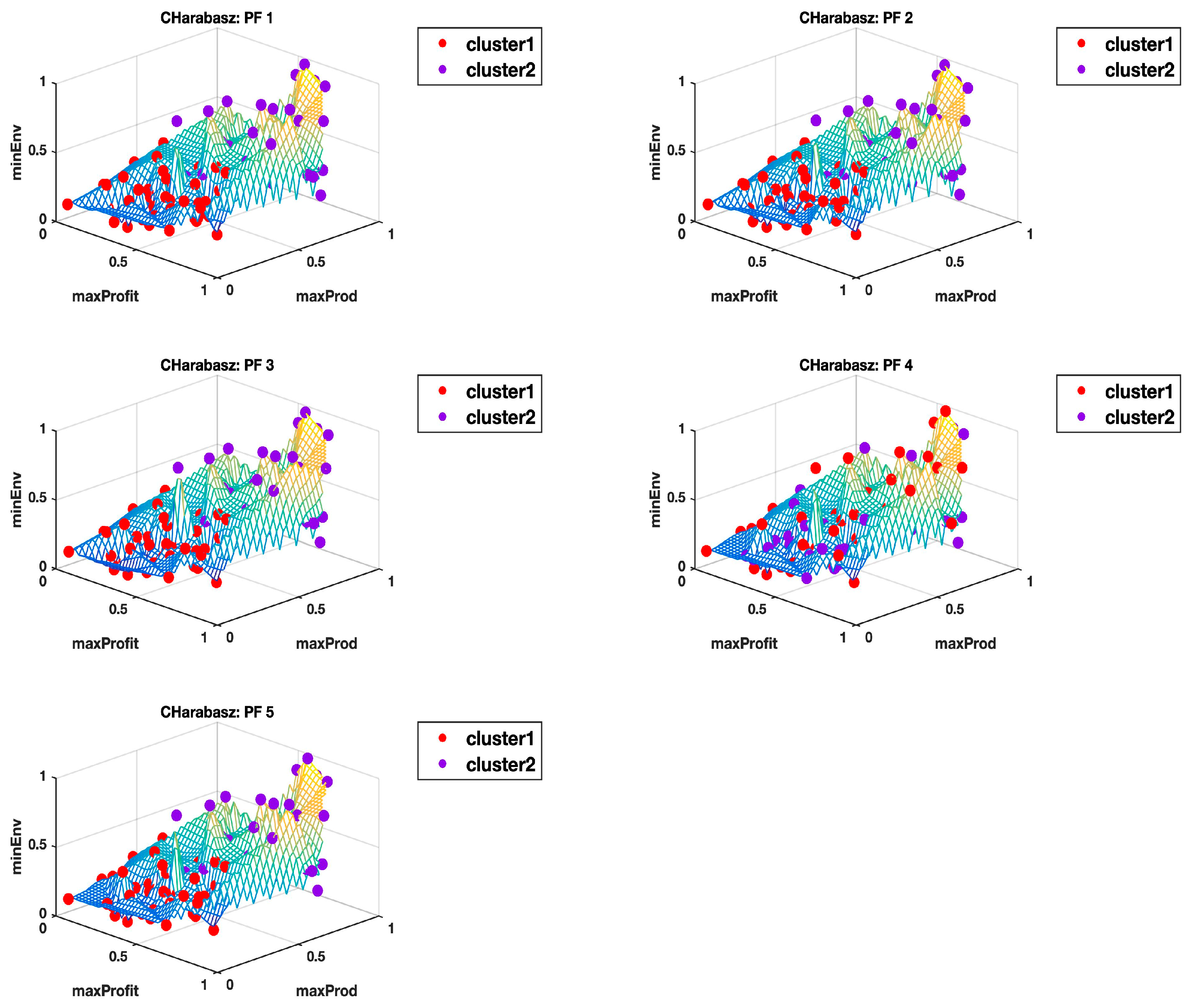
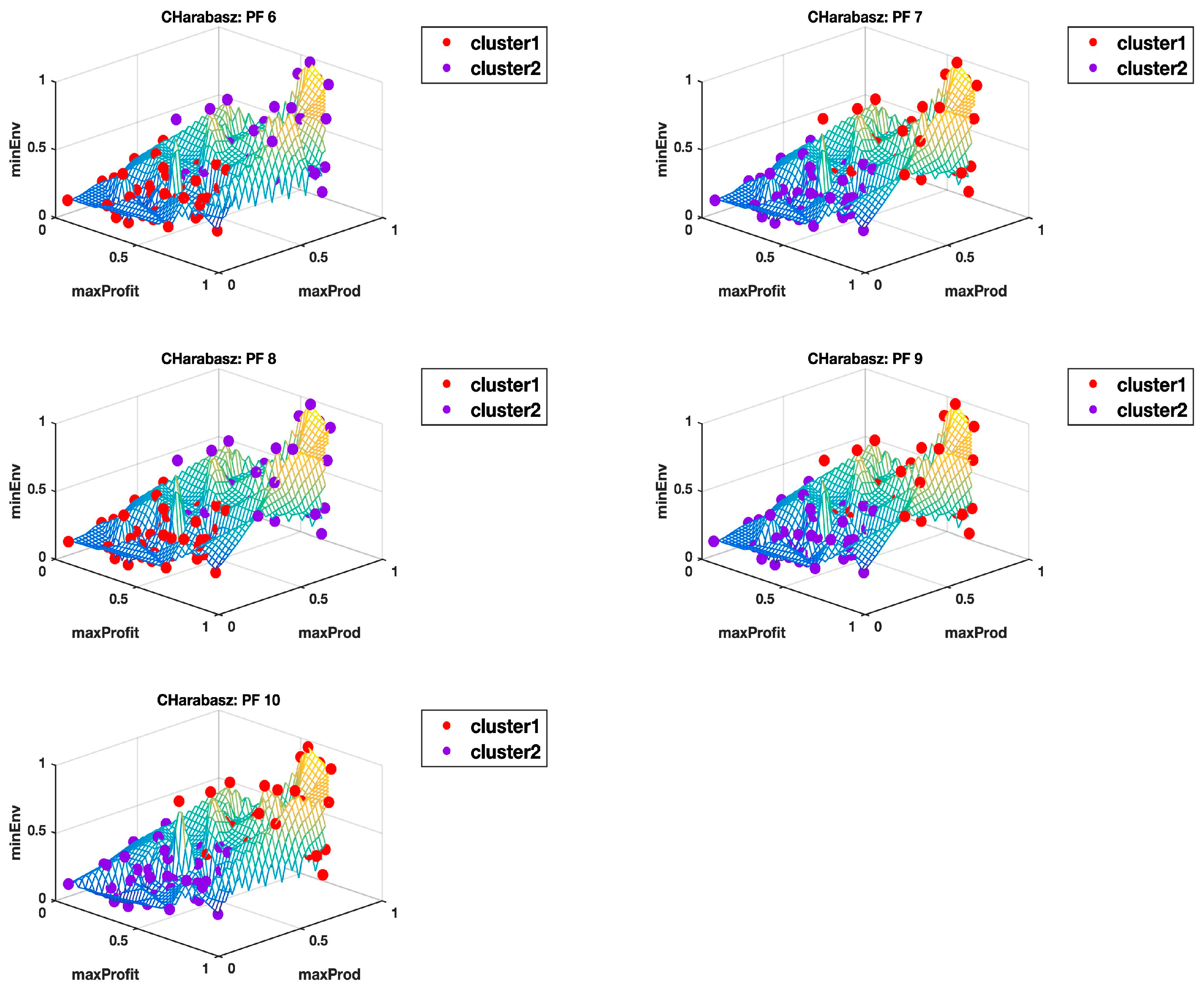
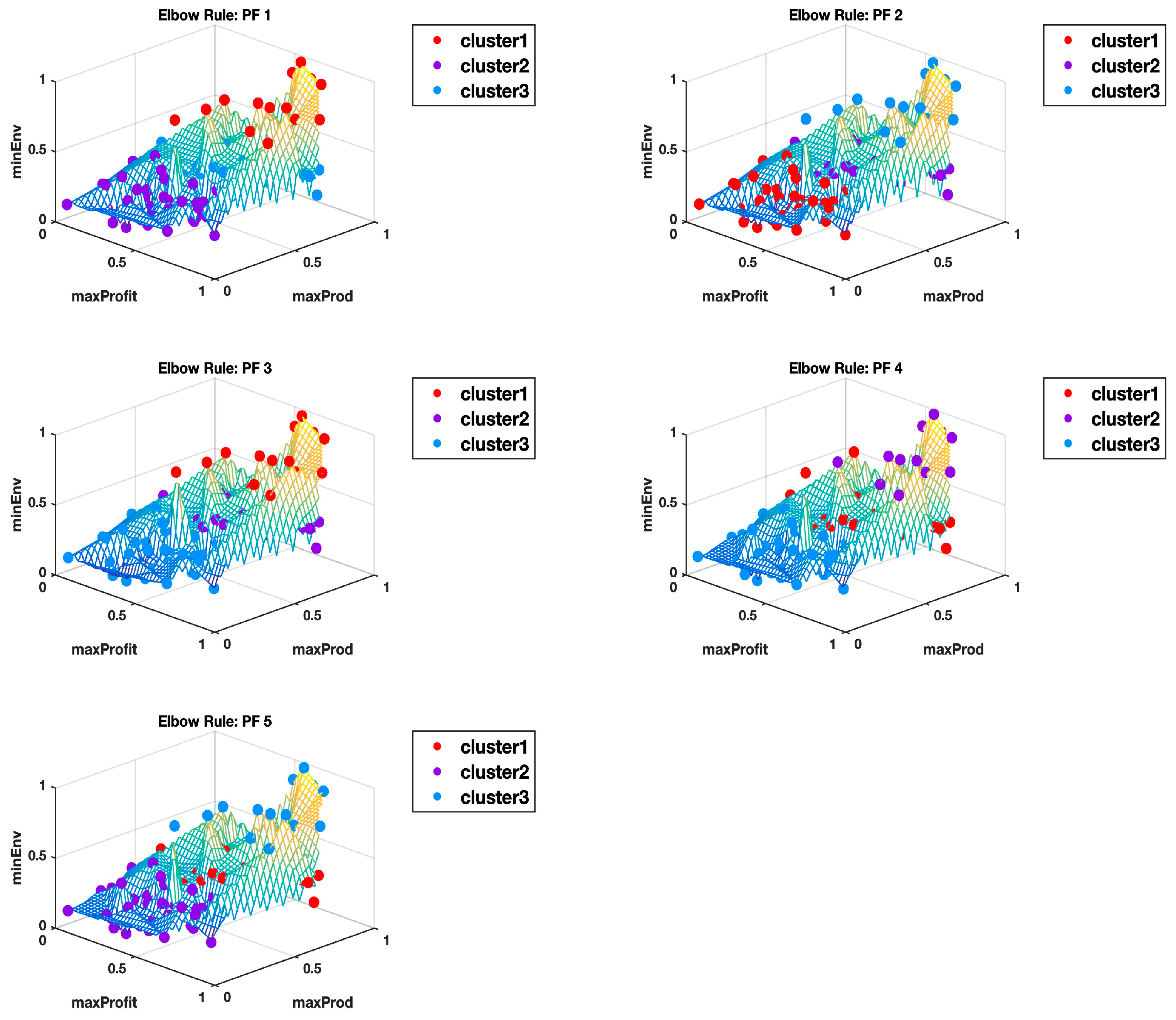
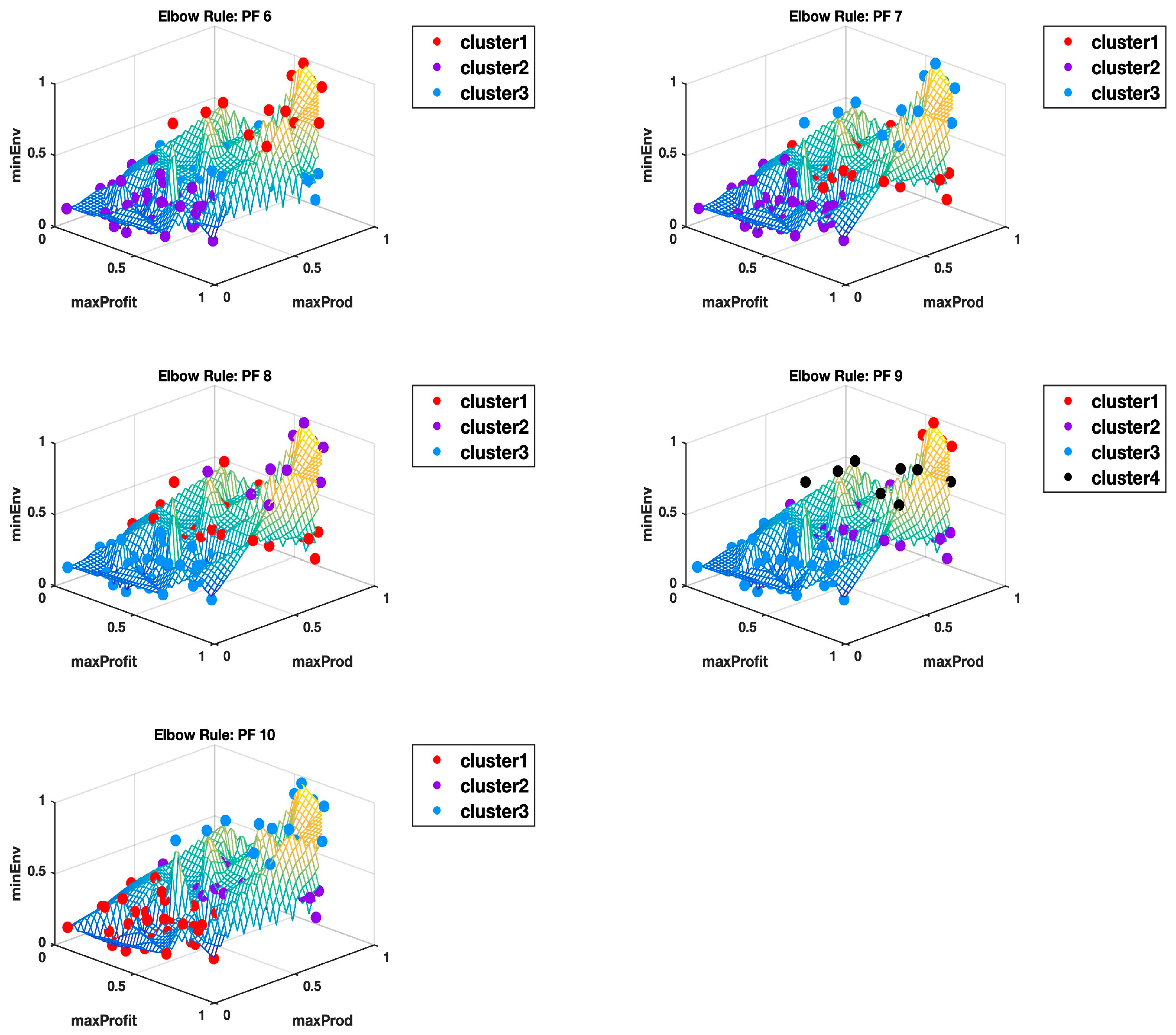
Appendix B and
Appendix C show the plots of all the 10 Pareto fronts with the cluster delineation being determined using the highest Calinski–Harabasz criterion method and the elbow rule, respectively. Just from the observations of these plots, it is clear to see how, in most cases, three clusters could easily be justified, but then again this may come down to subjectivity, hence why we use the hyper radial distance summary statistics for clarity.
Table 2 and
Table 3 show a summary of the means and standard deviations of the hyper radial distances for each cluster in each Pareto front based on the identified optimal number of clusters displayed in
Table 1.
There is a clear distinction of the clusters for every Pareto front in
Table 2 for the highest Calinski–Harabasz criterion, except for the Pareto front PF4 dataset where the means of the clusters are very close, albeit with comparatively higher standard deviations than observed for the rest of the other datasets. The 3D plot in
Appendix B (CHarabasz: PF4) is also very difficult to make sense of, as there does not seem to be a clear delineation of the clusters. However, the equivalent 3D plot with three clusters identified using the elbow rule (see
Appendix C—Elbow Rule: PF4) visually shows some clarity that is aesthetically pleasing. This is not implying in any way that visually believable boundaries disannul border disputes at the no-man’s-land regions. That is an issue that can only be verified by many runs of the
K-means++ to see if it will consistently yield the same points at the boundary dispute of the same clusters. From
Table 3, the cluster means of the hyper radial distances for the Pareto front PF4 dataset show a clear separation of the three clusters. In fact, there is a clear differentiation of the average hyper radial distances of all clusters across all of the 10 Pareto fronts in
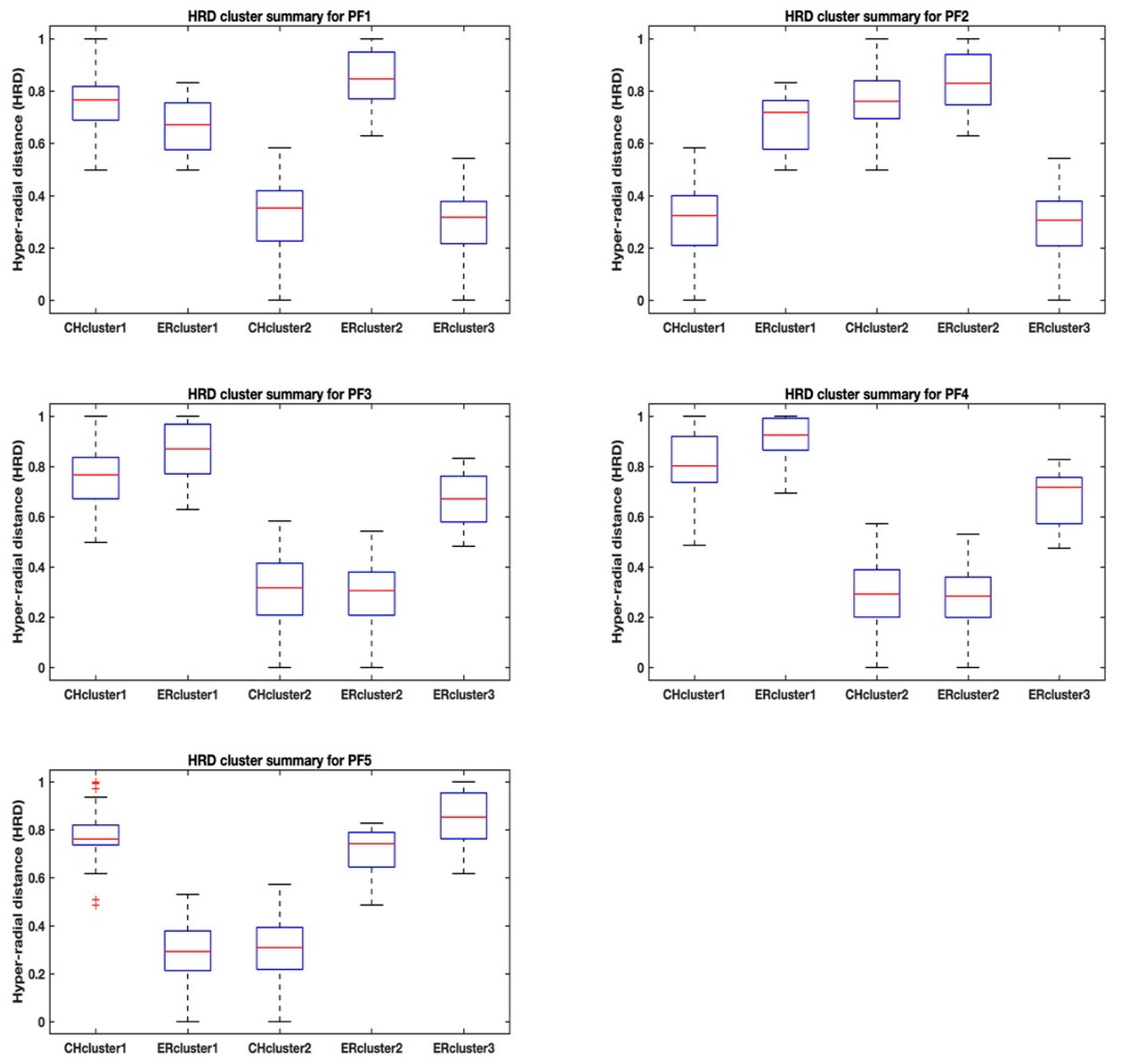
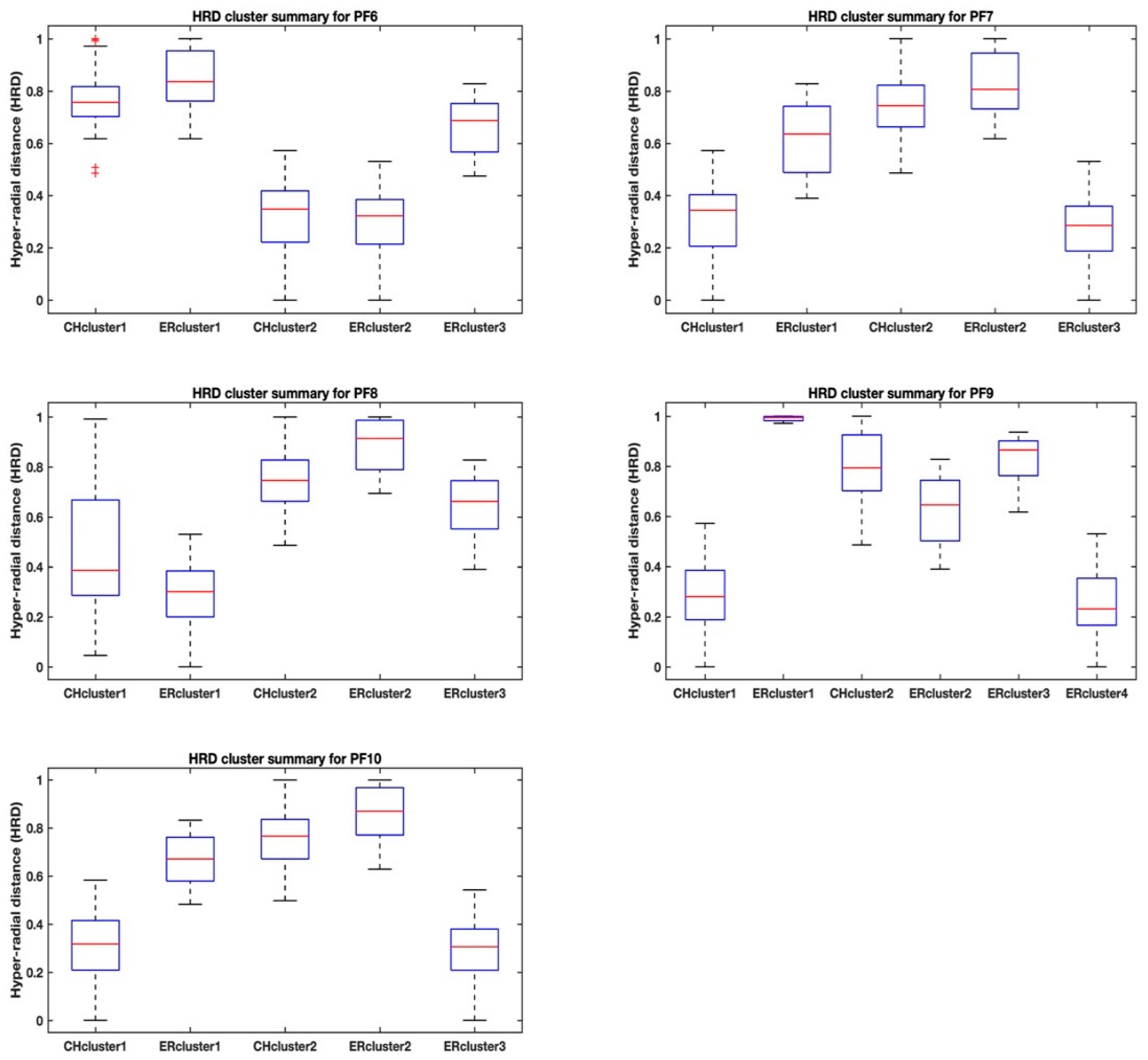
Table 3. More revealing trends are observed by looking at the ranges of the hyper radial distances using boxplots that show max-min values, 25th and 75th percentiles and the medians. The boxplots as shown in
Figure 3 and
Figure 4 help us to visualize the separation of the clusters for each Pareto front dataset and between the two methods, the highest Calinski–Harabasz criterion (i.e., CHcluster#) and the elbow rule (i.e., ERcluster#). The cluster groups from the highest Calinski–Harabasz criterion are identified with an alphanumeric, CHcluster#, where the hash represents the numeric identity of the cluster, and similarly the cluster groups from the elbow rule are identified with the alphanumeric, ERcluster#.
We could generalize that for the most part the boxplots for the CHcluster groups show separation across all the Pareto front datasets, including the Pareto front PF4 dataset in
Figure 3, which, by the way, showed almost similar means and standard deviations, a classic case of things not being the way they seem, or data are the same and not the same. At least we have some idea of how the
K-means++ may have succeeded in splitting the Pareto front PF4 dataset into two cluster groups, despite having similar means.
There is also a curious observation of “outliers” for the CHcluster1 group of PF5 in
Figure 3, although we know that there are no outliers in this Pareto set of solutions in the sense of bad data-points, as all the points are optimal or near-optimal. Note also that, on the basis of means and standard deviations, the Pareto front PF5 dataset is similar to Pareto fronts PF2 and PF3 (see
Table 2). It seems that, although the highest Calinski–Harabasz criterion has identified two clusters for the Pareto front PF5 in
Figure 3, the CHcluster1 has a few points that may be allocated a different cluster group, if there was a sufficient between-cluster separation distance and/or a small enough within-cluster separation distance to justify the creation of a third cluster group. Our opinion is based on how the elbow rule is able to cluster the Pareto front PF5 dataset into three cluster groups without similar outliers, resulting in a comparatively lower standard deviation for the ERcluster1 group in comparison to the CHcluster1 group.
A similar situation is also observed for the CHcluster1 group of the Pareto front PF6 dataset in
Figure 4, where the “outliers” are identified. Again, the elbow rule, in contrast, discriminates the Pareto front PF6 dataset into three cluster groups without any outliers by its ability to confine the separation of the cluster groups in agreement with the cluster group means and standard deviations. This seems to suggest the different ways that the two clustering methods work in discriminating data into different clustering groups. In fact, all of the ERcluster groups of all the Pareto front datasets based on the elbow rule in both
Figure 3 and
Figure 4 seem to be in agreement with the means and standard deviations in
Table 3. Accordingly, what does this mean and is the elbow rule identifying the true optimal number of clusters and what would be the implications in terms of reducing the cardinality of solutions using either the highest Calinski–Harabasz criterion method or the elbow rule?
Although visualization is not part of the solution that we are seeking, but rather a systematic way of finding this short list of the very best solutions from a Pareto front with less subjectivity and in near real-time, we use it here to try to answer parts of our inquiry. Therefore, when it comes to visualization, one cannot help but notice that there is more inconsistency on the cluster that has the least average hyper radial distance, as observed in both
Table 3 and
Appendix C, where the elbow rule has been used to estimate the optimal number of clusters. There is better visualization consistency with fewer clusters being estimated using the highest Calinski–Harabasz criterion method. This is not saying much in terms of understanding which of the two optimal clustering approaches is yielding the true optimal number of clusters, rather that the estimation for the cluster groups may not yield an exact solution, especially if the clusters have too much overlap, as do some of the Pareto front clusters (see the boxplots in
Figure 3 and
Figure 4). Hence, now it is no longer just subjectivity that we have to try to minimize, but we see how visualizations can still expose disputes of “point belongingness” among different clusters, (which is a result of solving nontrivial multi-dimensional scaling problems). We need to figure out a way of taking advantage of this dispute, rather than covering it up.
It will take results from both clustering approaches to identify the no-man’s-land regions or boundaries, due to the overlaps of the clusters that are revealed by the summary statistics of the hyper radial distances, where algorithms, such as the
K-means++, used in this exercise have problems delineating clusters. Therefore, we switch our focus to the 100th generation Pareto front, PF10, which was the final Pareto front solution to the New Zealand farming problem. The reason for this switch is because this Pareto front has been thoroughly investigated using a bevy of visualization techniques, such as Parallel Coordinates Plots, Andrew plots, 3D Andrews plots, Permutation Tours, Grand Tours, and DMS [
26], a visualization virtual-reality or desktop based visual-steering technique derived from the concepts of Design by Shopping [
39], and Hyper Radial Visualization [
37], as described earlier. Therefore, we do have an idea of what the very best solutions are.
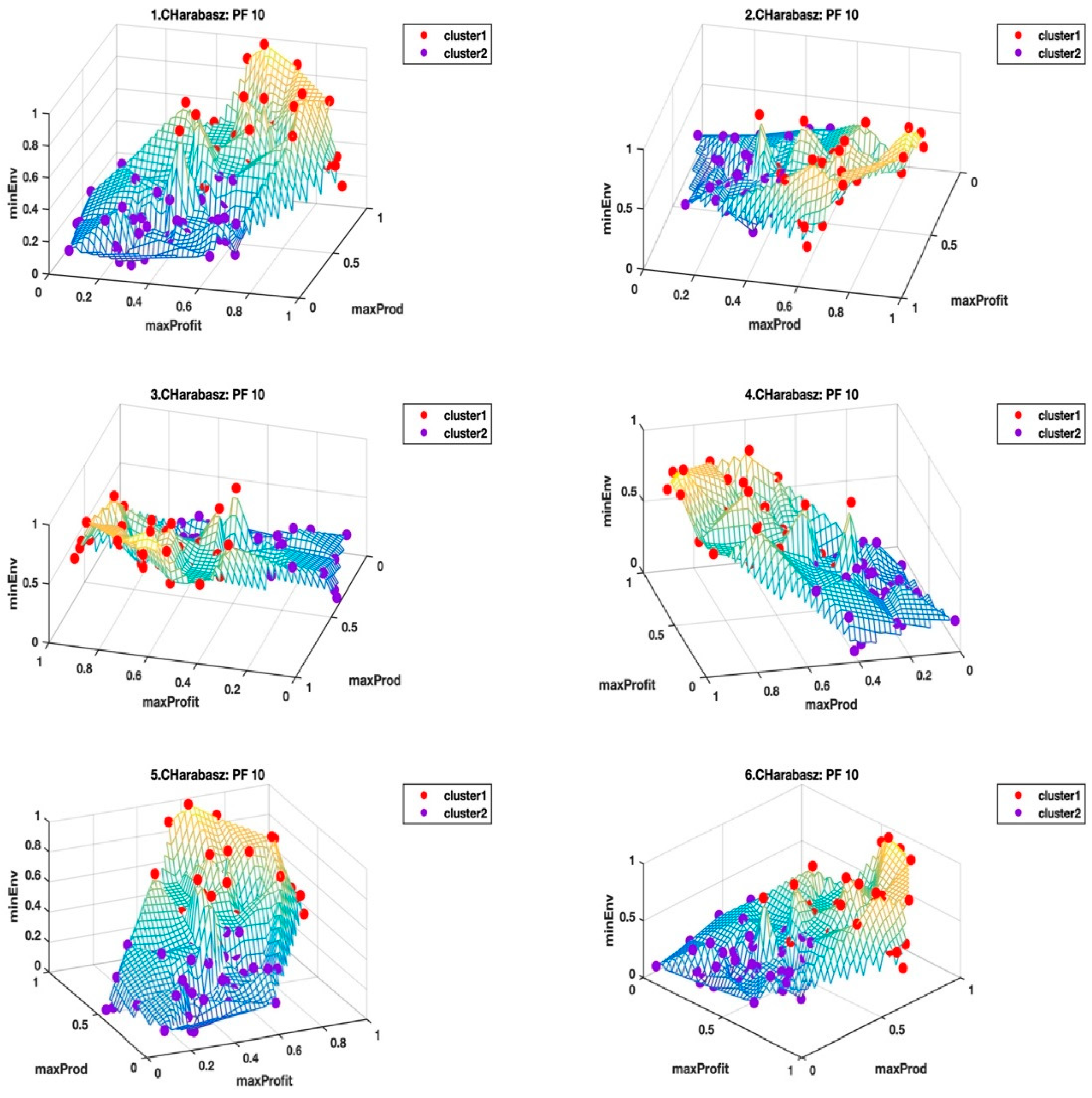
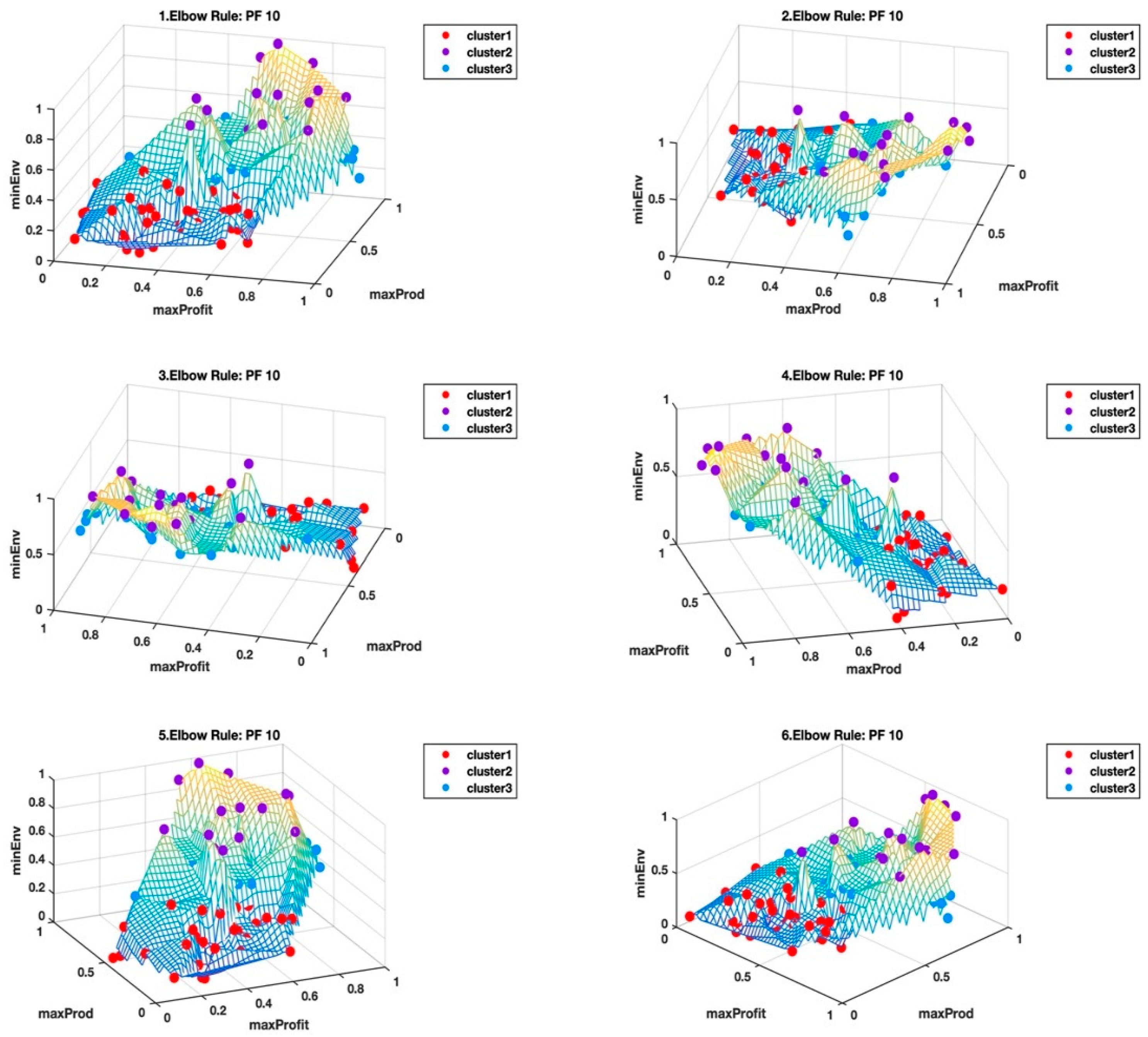
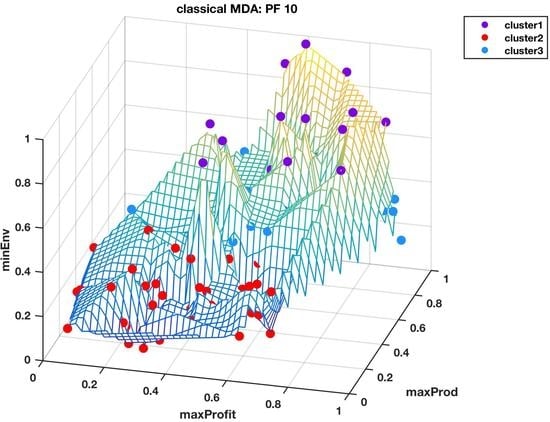
Figure 5 and
Figure 6 shows the Pareto front PF10 dataset with six images each in different orientations for a better visual perception of the clustering, based on the highest Calinski–Harabasz criterion method and elbow rule, respectively. The solutions for each cluster are also shown in the captions.
Cluster 1: [1, 2, 4, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 20, 22, 24, 27, 29, 31, 32, 34, 36, 37, 41, 44, 46, 47, 49, 51, 56, 57, 59, 60, 62, 63, 65, 66, 68, 69, 70, 71, 72, 73, 74, 76, 77, 79, 80, 81, 83, 84, 85, 86, 88, 91, 92, 93, 94, 95, 97, 98, 99, 100]; and
Cluster 2: [3, 5, 6, 12, 18, 19, 21, 23, 25, 26, 28, 30, 33, 35, 38, 39, 40, 42, 43, 45, 48, 50, 52, 53, 54, 55, 58, 61, 64, 67, 75, 78, 82, 87, 89, 90, 96].
Cluster 1: [3, 5, 6, 12, 15, 33, 35, 38, 39, 40, 42, 43, 48, 54, 55, 57, 58, 59, 61, 64, 66, 67, 79, 87, 89, 90, 96, 99];
Cluster 2: [18, 19, 21, 23, 25, 26, 28, 30, 45, 50, 52, 53, 75, 78, 82]; and
Cluster 3: [1, 2, 4, 7, 8, 9, 10, 11, 13, 14, 16, 17, 20, 22, 24, 27, 29, 31, 32, 34, 36, 37, 41, 44, 46, 47, 49, 51, 56, 60, 62, 63, 65, 68, 69, 70, 71, 72, 73, 74, 76, 77, 80, 81, 83, 84, 85, 86, 88, 91, 92, 93, 94, 95, 97, 98, 100].
From
Table 2 and
Table 3, we selected the clusters (i.e., CHcluster1 from the Calinski-Harabasz criterion method and ERcluster3 from the elbow rule), with the least average hyper radial distance for Pareto front PF10 dataset. In
Figure 5 and
Figure 6, CHcluster1 group and ERcluster3 group had many points in common, as they all came from more or less a similar part of the data landscape, i.e., where the environmental impact was low and with moderate profitability and productivity. The total number of solutions in the CHcluster1 group and the ERcluster3 group were 63 and 57, respectively, with a set difference of the following solutions: {15,57,59,66,79,99}. In other words, the set difference defines the set of solutions that was not included in the smaller ERcluster3 group, but included in the larger CHcluster1 group. Another way of getting the same result was to go to the next level up in the average hyper radial distances, i.e., ERcluster1 group from the elbow rule and the CHcluster2 group from the Calinski-Harabasz criterion method. We first find the intersection of the two cluster groups, which we will call cluster
n, and then find the set difference between cluster
n and ERcluster1 group, which yields the same set: {15,57,59,66,79,99}.
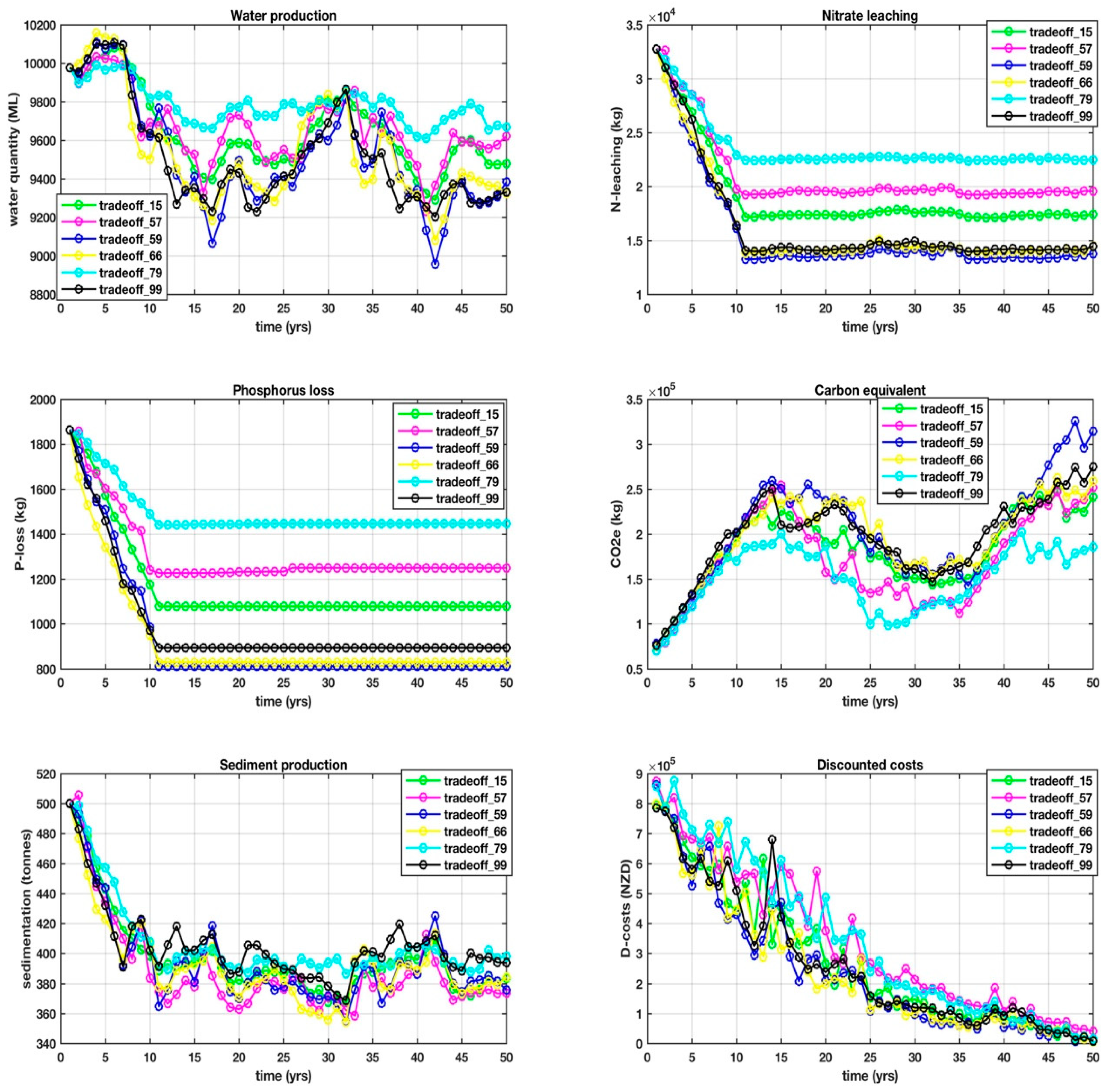
This is where things get interesting, because it is this set difference that defined some of the points that were identified while using other visualization techniques, in particular, DMS that consistently identified 59 and 66. The 14 objectives over a 50 year, one-yearly interval planning horizon for the set difference are shown in
Appendix D, with trade-offs between the objectives, making it difficult from which to select a unique solution. Our goal is to arrive at a shortlist of the very best solutions that will form the basis for the next stage of research, which is to identify yet another mathematical process to find the unique solution in near-real-time.
Going back to the set difference list, we are left wondering whether, for the Pareto front datasets, the no-man’s-land region or border may just serve as a way of identifying sweet spots where the short list of the very best solutions resides. We also start to wonder that for difficult datasets with no clear delineation between clusters, the optimal number of clusters might not necessarily be an integer, but may actually be a fractional number. That means for the Pareto front PF10, the optimal number of clusters is between 2 and 3, where the Calinski–Harabasz criterion method finds the minimum of the optimal number of clusters and the elbow rule finds the maximum. Even if this is proven to be the case, the importance might just be the ability of finding the points in the no-man’s-land region, which in this case is verified to carry some of the very best solutions. Out of the set difference list, solutions 57 and 79 were the hardest to find while using the other visual techniques.
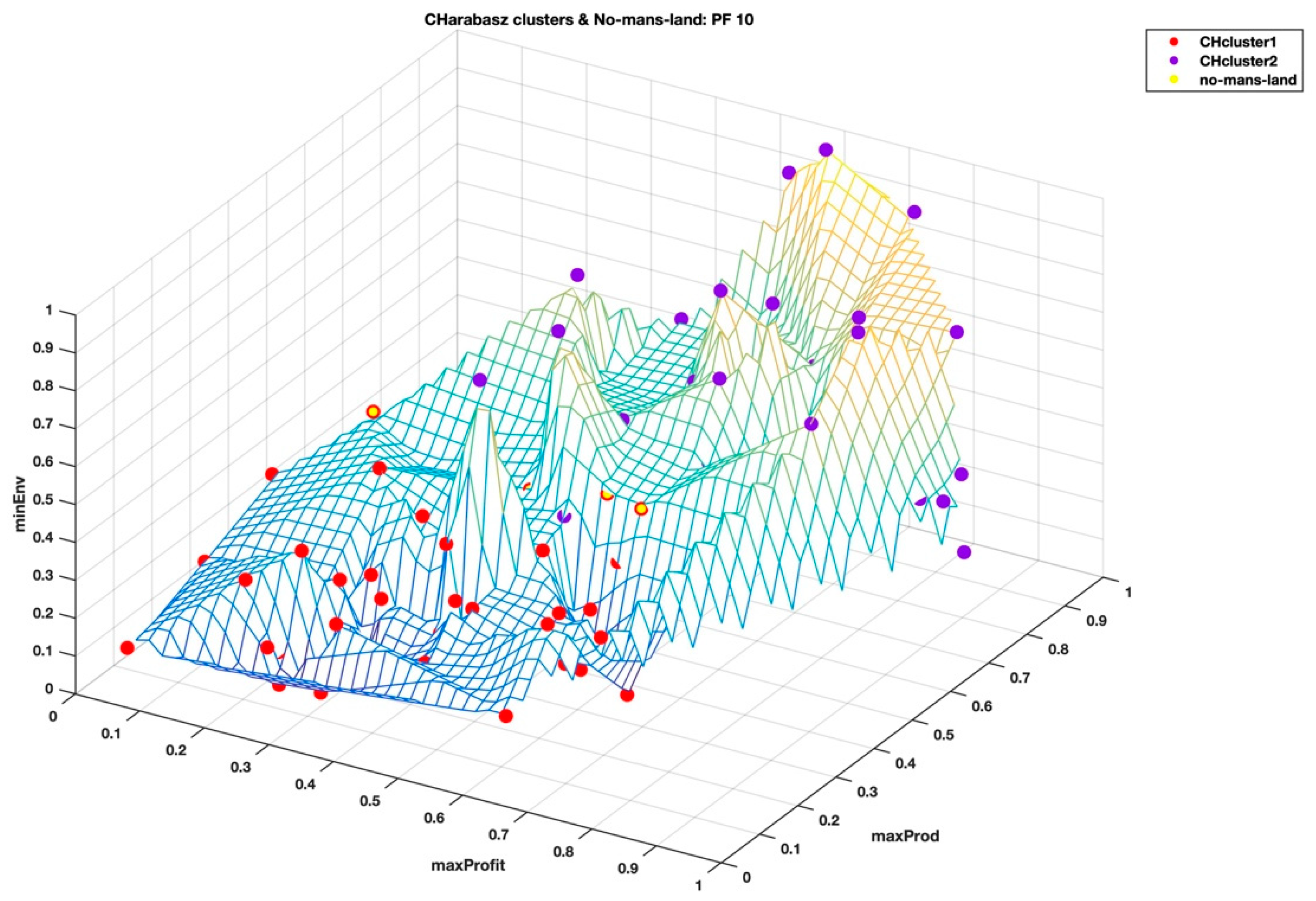
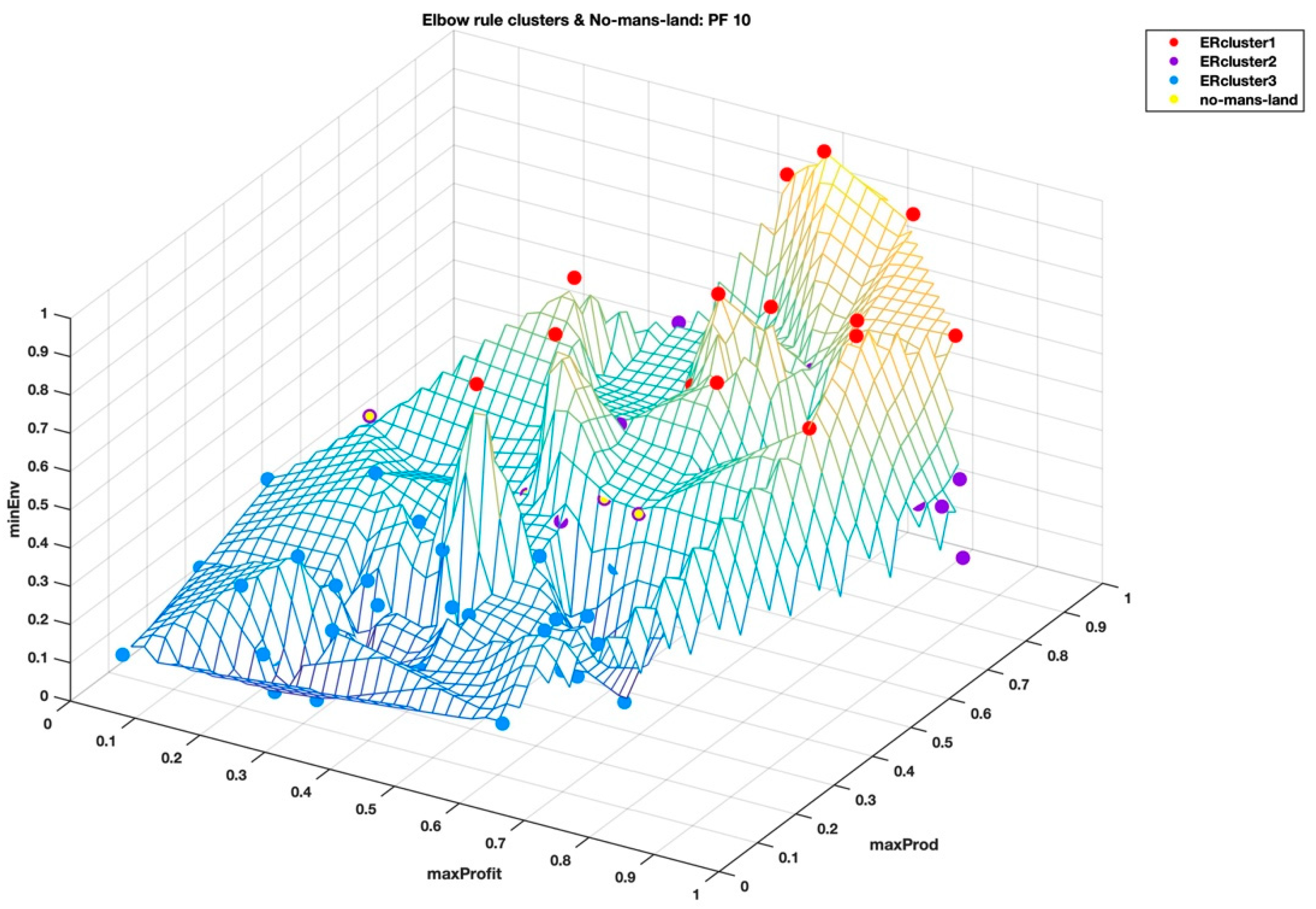
When we visualize the points in the no-man’s-land region in
Figure 7 and
Figure 8, from the highest Calinski–Harabasz criterion method and the elbow rule, respectively, these points look like they form a “fault line” across the middle of the wireframe mesh plot; seemingly, like the two clustering methods have different ways of dealing with these border disputes. As shown in the
Table 1 and
Table 2 and also the box plots in
Figure 3 and
Figure 4, it is easy to see the separation of the clusters that is determined by the two clustering methods based on the summary statistics of the hyper radial distances. We can only speculate at this stage that this hyperspace Pareto front has inherent complexity that is not so easy to find, as both the highest Calinski–Harabasz criterion method and the elbow rule have graceful ways of dealing with border disputes. The former method settles the dispute by assigning fewer numbers of clusters and the latter by an increased number of clusters. Only by looking at the clustering results of both methods are we able to realize that there is a border dispute of point belongingness. On the other hand, the interactive visualization, DMS, reveals that the no-man’s-land region is the sweet spot for the shortlist of the very best solutions, which seems to be the balance among the three super objectives, i.e. minimal environmental impact, maximum profitability, and maximum productivity.
We have obviously raised more questions than answers for this exercise and are left with an inconclusive result as to which method would give us an optimal number of clusters for the high dimensional dataset with tightly distributed points. So far, it seems both of the clustering methods are critical and extracting meaning out of the estimated number of clusters from these algorithms, require other information and techniques to make sense of the high-dimensional data. However, we see a way forward by removing subjectivity and bypassing visualization to obtain to a reduced list of the very best solutions. More tests would need to be done to verify the consistency of this procedure that we have presented. In the interim, research to develop the next level of capability that will choose the unique solution in near real-time from the short list will continue.
It is also an interesting observation that is just based on the hyper-radial distance summary statistics, it is inconclusive whether lower profitability and productivity and minimal environmental impact are more preferable than high profitability and productivity, and high environmental impact. Obviously, the data picks the middle ground as the best. This may spark heated debates regarding which extreme is the lesser evil, and we are not inferring anything by it, rather emphasizing the program’s objective choice of middle of the ground, as the data shows.