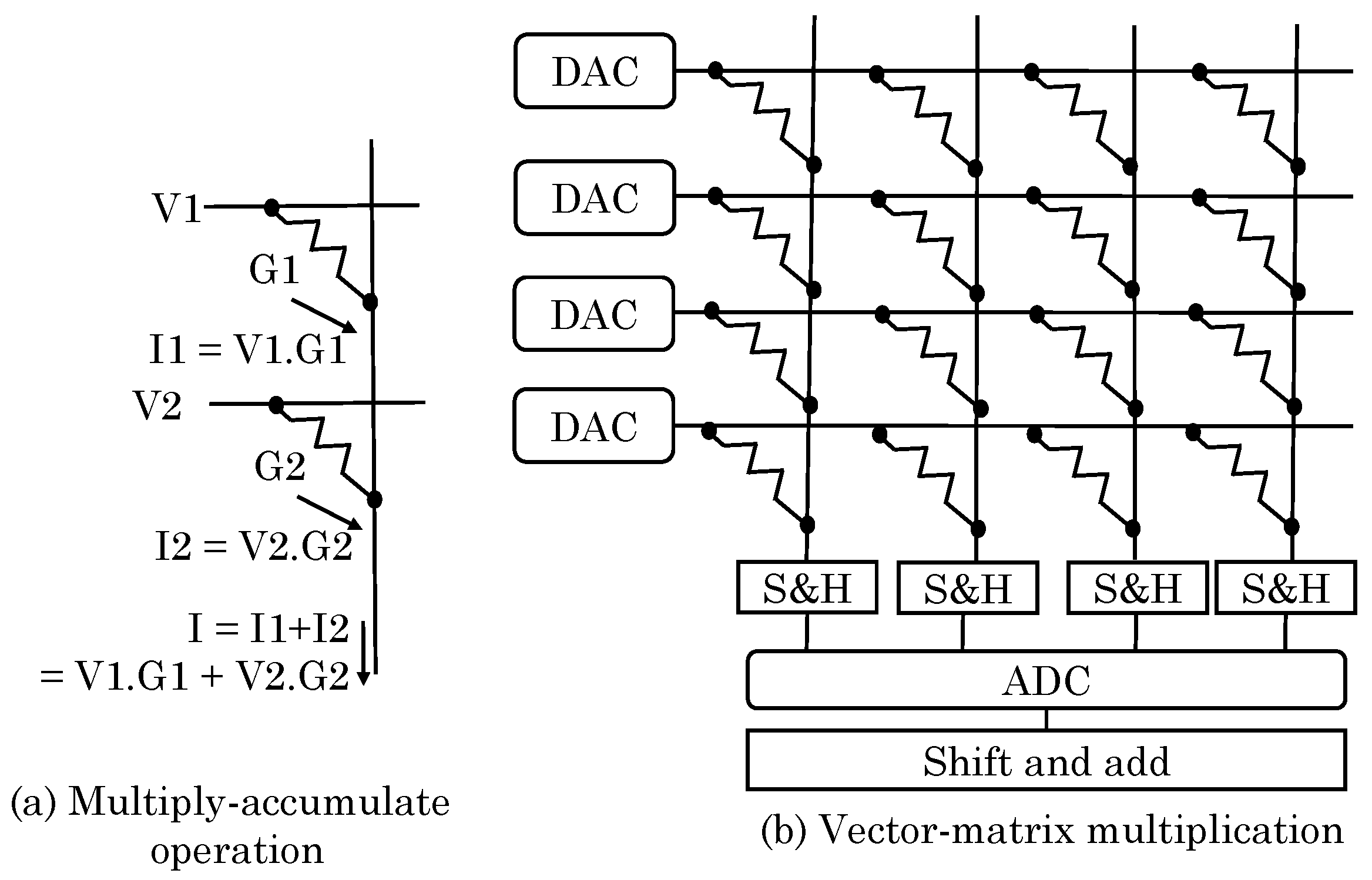
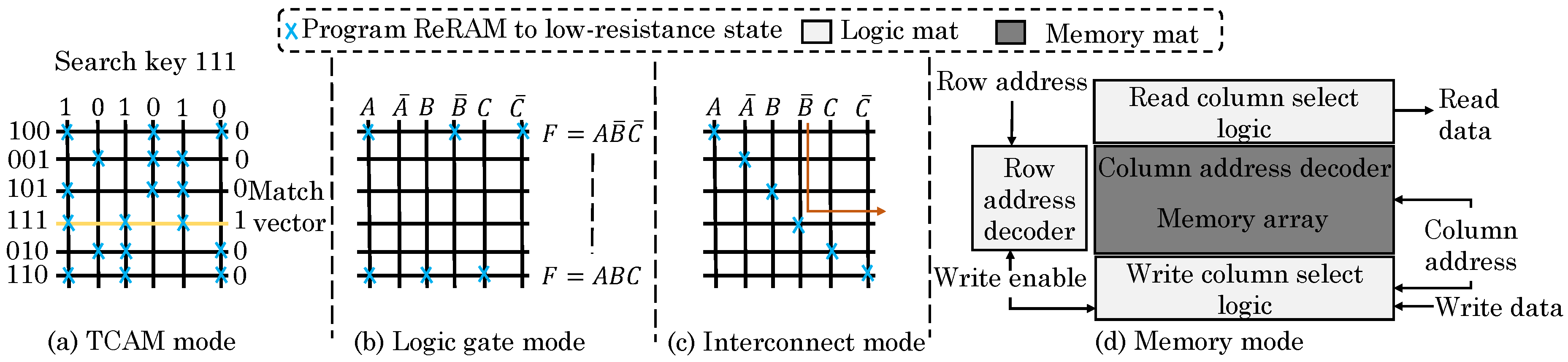
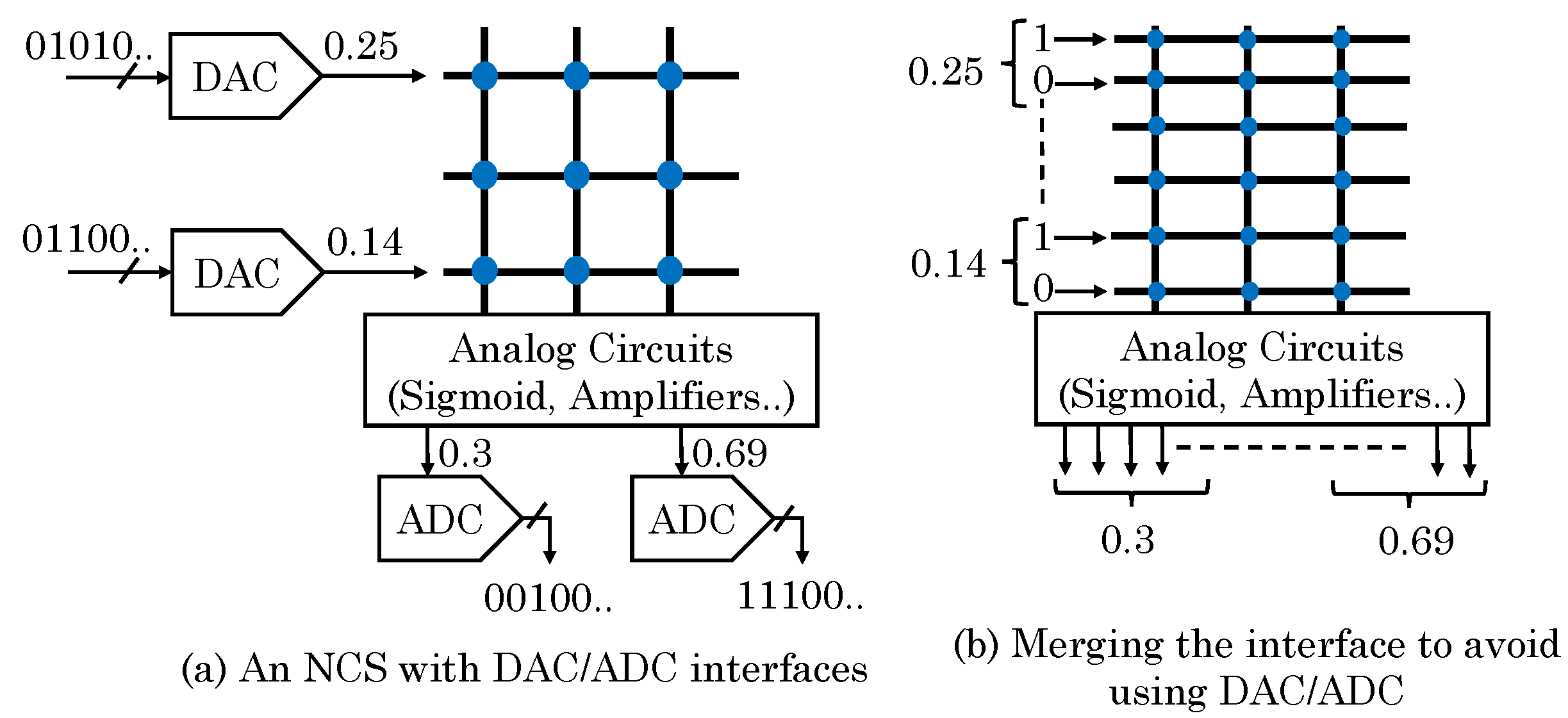
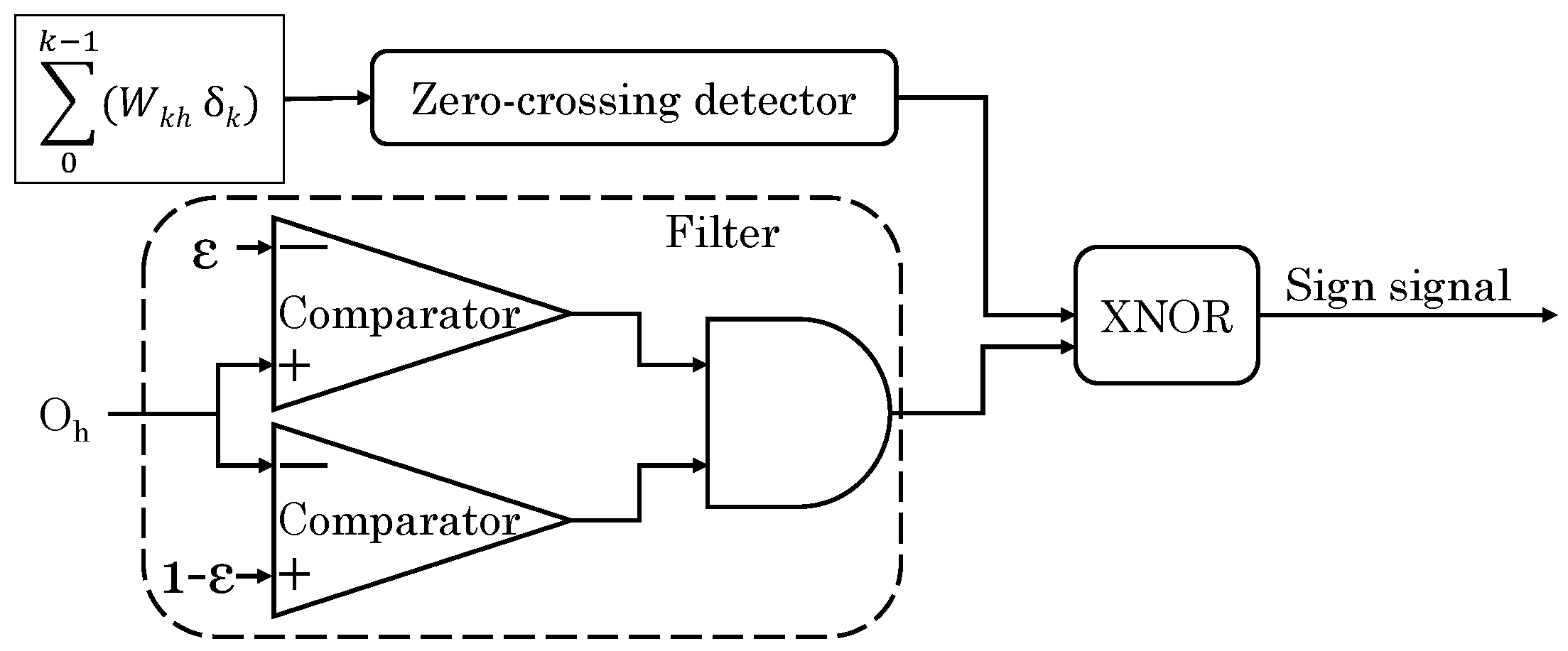
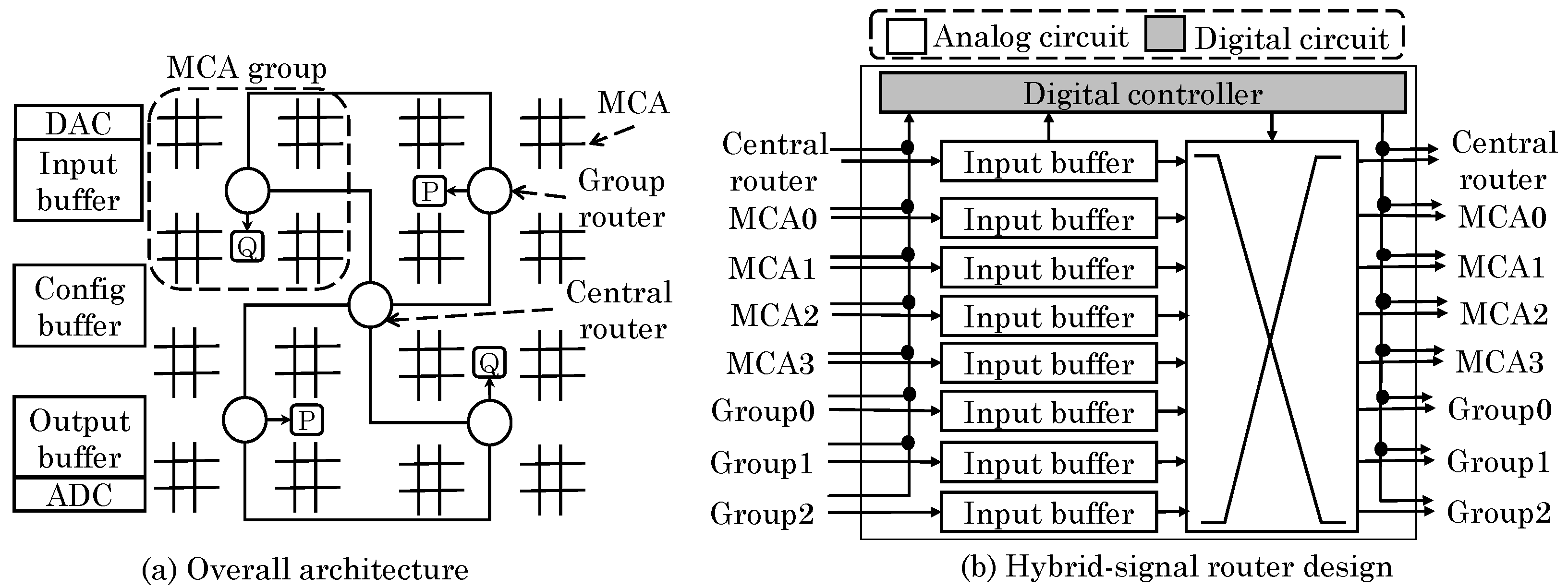
5.1. Arithmetic and Logical Operations
Li et al. [
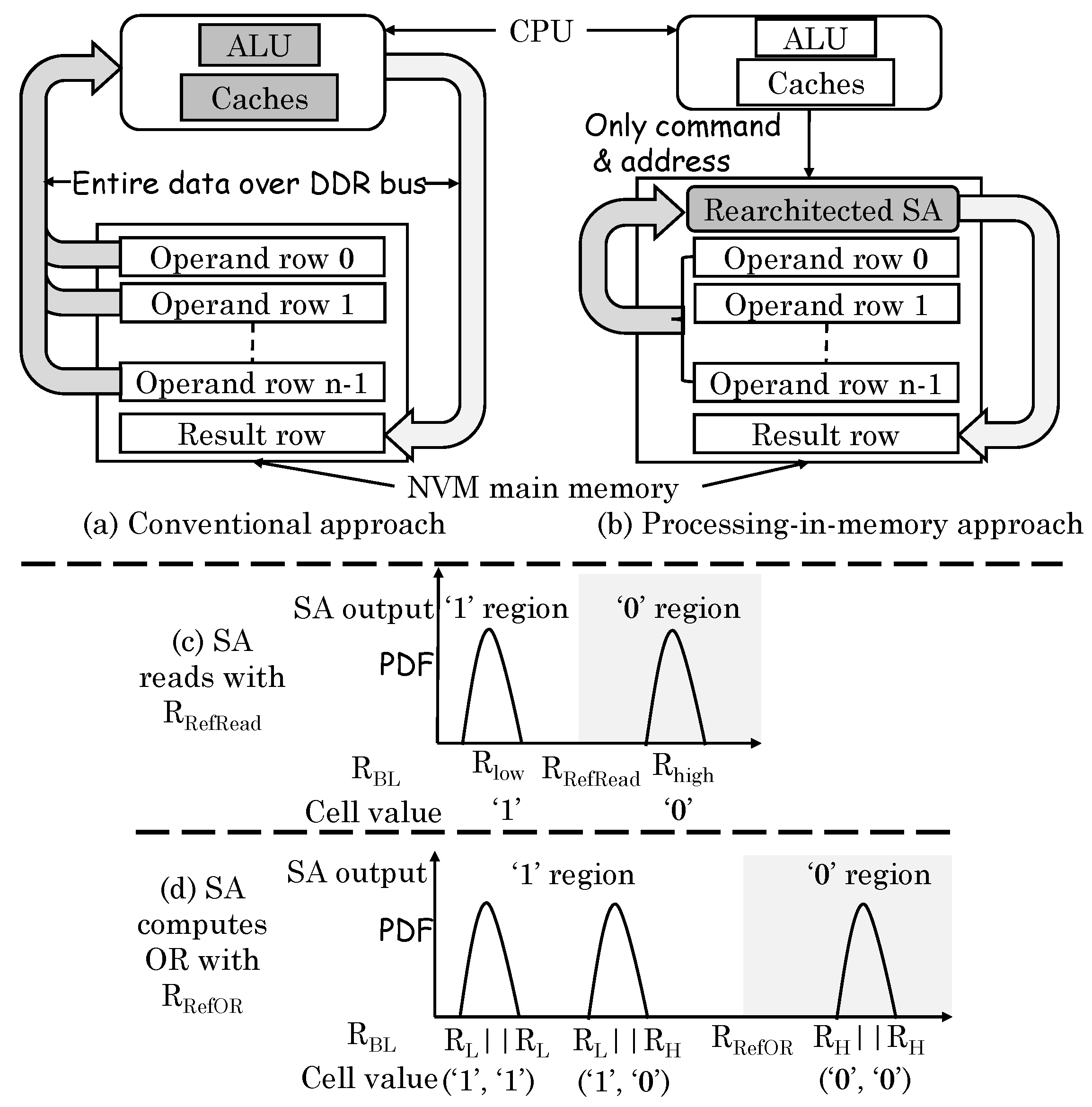
54] noted that the compute-centric architecture (
Figure 24a) leads to large data transfer between core and memory, whereas the PIM approach (
Figure 24b) can reduce the data movement significantly. They presented a technique for performing bulk bitwise operations (OR, AND, XOR, and NOT) in ReRAM. Conventionally, for reading a cell, the resistance of a cell is compared against a reference resistance value to ascertain the stored value as 0 or 1, as shown in
Figure 24c. Their technique activates two rows simultaneously and thus, the resistance on the bitline becomes the parallel connection of those cells. For computing AND/OR operations, only the reference resistance needs to be changed, for example, for computing OR operation, the reference resistance should be changed to R
, as shown in
Figure 24d. For XOR operation, one operand is read in a capacitor and another operand is read in the latch. The output of two add-on transistors provides XOR outcome. For inversion (NOT) operation, the differential value from the latch itself can be taken as the result. By using a multiplexor, a normal read or AND/OR/XOR/NOT operation can be selected. The circuit can be extended to compute OR operation on multiple rows, but AND operation on multiple rows are not supported. By comparison, DRAM-based PIM techniques support two-row operations only.
Their technique requires changes to sense amplifier, e.g., local wordlines and device driver. Thus, by merely changing the read-circuit, their technique computes bitwise operations on multiple memory rows. The output can be written to the I/O bus or another memory row. Since their technique performs row-level operations only, the software need to allocate data in PIM-aware manner. Their technique can perform operations at intra-subarray, inter-subarray or inter-bank levels. Their technique achieves higher energy efficiency and performance compared to general-purpose processor and DRAM-based PIM techniques.
Lebdeh et al. [
76] presented a design for implementing stateful XNOR/XOR gate in MCA. Their design uses two “bipolar memristors (BMs)” for storing input and one “unipolar memristor (UM)” for storing the output. For cascading the gates, the value of UM is buffered in a BM. They use “threshold switching memristors” and leverage the ability of memristors to provide different values of reset (OFF) and set (ON) threshold voltages. The ratio of OFF to ON resistance should be high. Both OFF and ON resistance values of unipolar and bipolar memristors need to be equivalent. Their design needs only two steps which allows using XNOR as the basic logic gate. In the first step, output UM and BM are initialized to
and
, respectively. In the second step, the input memristors are supplied with the execution voltages, whose magnitude is given by
. The output of XNOR for different input combinations is shown in
Table 8, which confirms the functionality of their XNOR gate. While the XNOR is computed in only two steps, using an additional step and a computing memristor, their design also allows logic cascading of gates. Their design reduces area (number of memristors), latency (number of steps) and energy consumption. Their PIM-based design provides higher performance than voltage input/output memristive circuits. The limitation of their design is that it needs both bipolar and unipolar memristors and uses multiple voltage levels.
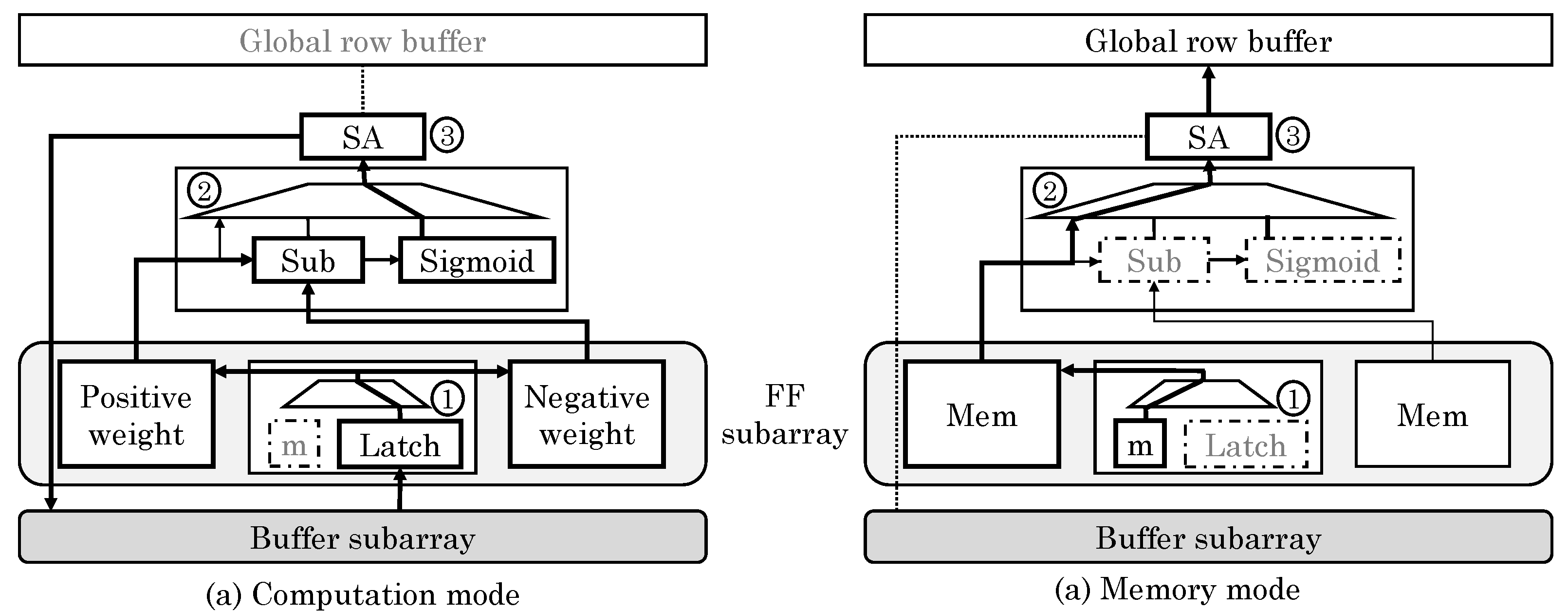
Chi et al. [
43] proposed a PIM architecture for ReRAM-based main memory for accelerating NN computations. They divided a ReRAM bank into three types of subarrays: memory (Mem), buffer and full function (FF). Mem subarrays only store data whereas FF subarrays can either store data or perform NN computations, as shown in
Figure 25. Buffer subarrays buffer the data for FF subarrays without requiring involvement of CPU. FF subarrays benefit from high bandwidth of in-memory data movement and ability to work in parallel to CPU. They noted that an SA performs similar function as an ADC and same is also true for write drivers and DACs. Hence, with only small modifications, they reused write drivers and SAs to perform the function of DAC and ADC, respectively. This sharing of periphery between computation and memory lowers the area overhead.
To switch the FF subarrays from memory to compute mode, data stored in them are moved to memory subarrays. Then, weights of the mapped NNs are written to the FF subarrays and the periphery is reconfigured. Opposite process happens on change from compute to memory mode. Since NN applications can tolerate low precision of inputs and weights, they assumed 3-bit and 4-bit precision of input voltage and synaptic weights, respectively, which implies 8 voltage and 16 resistance levels, respectively. The output precision required is 6-bit and dynamic fixed point format is used. They used a composing scheme whereby two 3-bit inputs are composed into one 6-bit input and two 4-bit cells are used for representing one 8-bit weight. To implement FC layers, they separate synaptic weight matrix in two matrices for storing positive and negative weights and store them in two MCAs. MVM is implemented in ReRAM arrays. They also discussed implementation of convolution and max/mean pooling layers. Depending on the size of NN (e.g., small, medium or large), the mapping of NN to ReRAM is optimized during compilation. Their design can support large-sized CNNs and MLPs and provides large improvement in performance and energy efficiency on ML workloads.
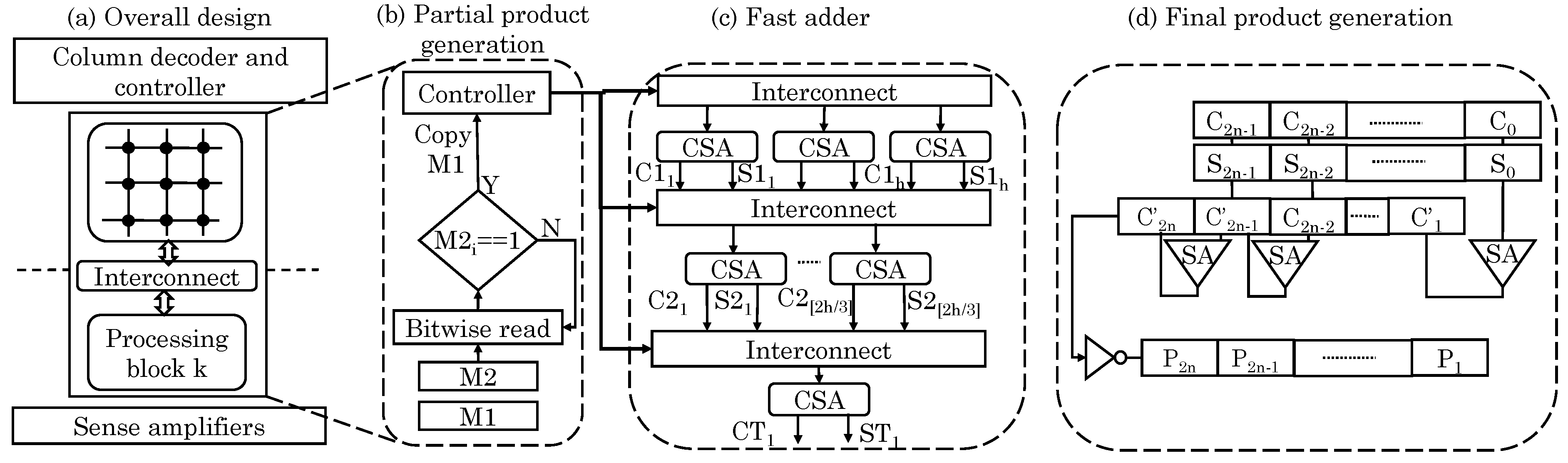
Imani et al. [
63] implemented exact/inexact addition/multiplication operation using PIM capability of MCAs. They used a crossbar memory which is logically partitioned into memory and compute blocks, as shown in
Figure 26a. These blocks connect with each other using reconfigurable interconnects that inherently support shift operations. Thus, data shifting can be done while copying it from one block to another without any additional delay. In addition, unlike bit-wise shifting, entire data can be shifted at once. Their adder is based on the 3:2 CSA (carry save adder) design, as shown in
Figure 26c. It uses
N 1-bit adders that produce two outputs each. The adders do not propagate any carry bit and, hence, can execute in parallel. Using their memory unit which supports shifts, they achieve CSA-like behavior. Finally, the two numbers are serially added. To add multiple numbers, they used a Wallace-tree-like design [
77], which reduces delay by propagating the carry only at the last stage, although this design increases energy consumption and memory writes. The latency of their reduction adder is independent of the size of operands, e.g.,
multiplication takes same time irrespective of the value of
N.
The multiplication involves three steps. First, partial-product of
multiplication is generated, as shown in
Figure 26b. Second, these
N partial products are added to get two numbers. Third, these two numbers are added to obtain the final product, as shown in
Figure 26d. The partial-product is generated by ANDing each bit of multiplier (M1) with the multiplicand (M2). To achieve this, M2 is read bit-wise using sense-amplifier and if it is 1, M1 is copied, but if it is 0, no action is taken which avoids write operation and saves energy. Their blocked architecture allows performing shifting of partial products (for add operation) along with copy operation which avoids their latency overhead. two consecutive NOT operations are equal to the copy operation.
They further noted that the third stage of multiplication above has high latency which becomes a bottleneck. Hence, for approximable applications, they proposed an inexact multiplier design based on the fact that, in 1-bit addition of (
A,
B,
), the sum (
S) is the complement of the generated carry (
) except for two out of eight combinations of inputs, which are (0,0,0) and (1,1,1) when shown as a (
A,
B,
) combination (refer
Table 9). Based on this, they evaluate
precisely and then approximate
S. This scheme reduces latency of
bit addition from
to
cycles. To further exercise tradeoff, parts of the product can be computed in exact/inexact manner. Their design improves performance and energy efficiency with acceptable quality loss.
5.2. Data Search Operations
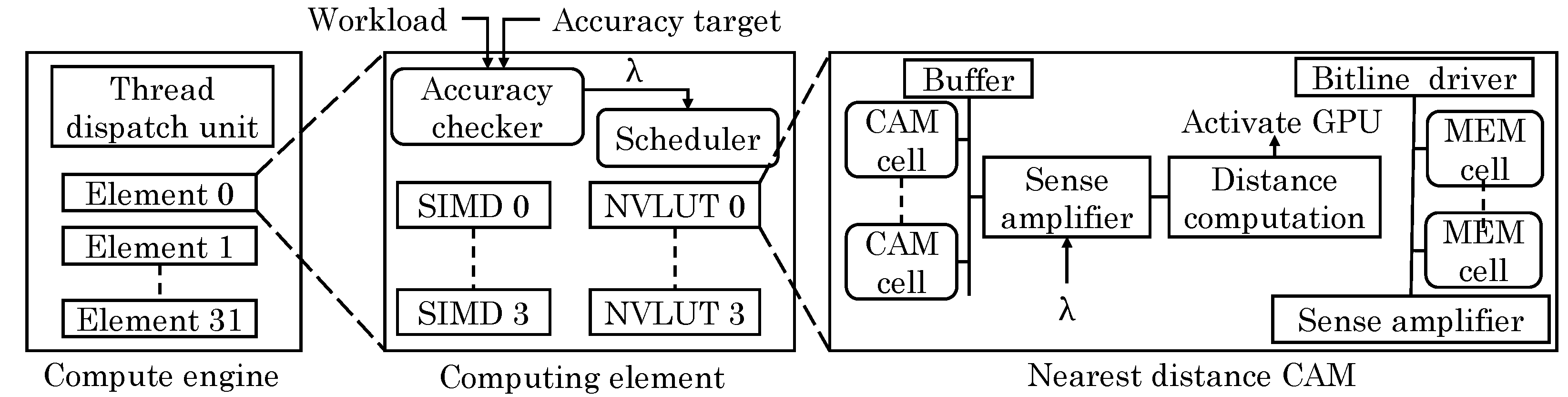
Imani et al. [
64] proposed a resistive CAM (content addressable memory) design which leverages analog features of non-volatile lookup-table (NVLUT) for implementing nearest-element search in GPU applications. They note that GPU applications show high amount of data similarity and locality. For example, fast Fourier transform and multimedia applications have repeated building blocks. Based on this, most basic operations can be performed using an approximate look-up table. Through offline profiling, their technique identifies frequently occurring inputs and stores them, along with their outputs in the NVLUT, as shown in
Figure 27. At runtime, the stored value which is most similar to the input value is searched and the corresponding output is returned which avoids the need of actual evaluation on the GPU core.
NVLUT uses inverse CAMs which can search for the row whose value is nearest to the input. They noted that use of Hamming distance as the similarity metric does not provide high accuracy since it does not account for the contribution of each bit-index. A CAM for searching the exact nearest value incurs high overhead. Instead, their technique changes the weight of every bit-index in the CAM and accounts for these weights during the search operation. For different bit index values, access transistors of different size are used. This allows assigning weight to each bit index during the search operation for finding the row with nearest value. The limitation of their technique is that it works only for approximable applications which have small number of inputs/outputs such that they can fit inside the table.
By increasing the size of NVLUT, output accuracy can be improved at the cost of higher energy overhead. However, increasing NVLUT size beyond a threshold does not improve the efficiency and, hence, they proposed an adaptive approach. If the distance between the input value and stored value exceeds a threshold (shown as
in
Figure 27), the input is assigned to the GPU core for accurate execution, otherwise, it is assigned to NVLUT. By changing this threshold, a tradeoff between performance and accuracy can be exercised. Compared to GPU-only execution, their technique improves performance and saves energy with small loss in quality. A limitation of their technique is the requirement of offline profiling.
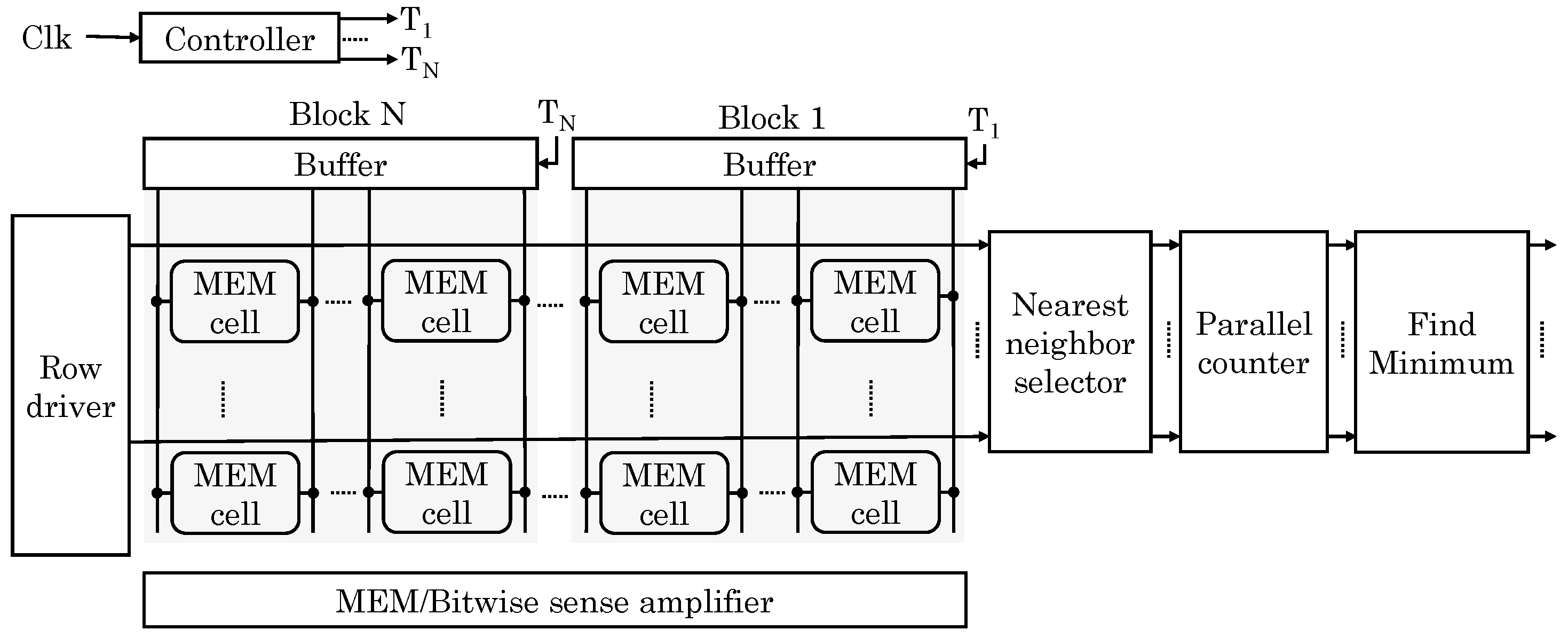
Imani et al. [
59] proposed a memory design which provides capabilities for normal storage, data searching for nearest neighbor and AND/OR/XOR bitwise operations. The proposed memristor-based memory is integrated on top of DRAM using 3D-stacking. Write- and read-intensive data are kept in DRAM and ReRAM memory, respectively, which alleviates limited write-endurance issue of ReRAM. In addition, read-intensive data are generally used for in-memory processing and example of this include reference data for ML workloads, synaptic weights in NN, etc. Each bank of proposed memory has multiple crossbar memories which can be used in CAM or memory mode for search operation or bit-wise operation, respectively.
To search for a given target data, the most similar data points in all banks are simultaneously examined. For this, Hamming distance is computed using analog properties of memristor. A CAM has
N blocks each with
M-bit data and each row corresponds to the matchline, as shown in
Figure 28. Any mismatch on the CAM cells begins to discharge the matchline. With increasing mismatches, discharge-rate increases, e.g., a CAM with 2-bit mismatch discharges faster than a CAM with 1-bit mismatch. The SA detects this by measuring the discharge current in each cycle. A challenge in this approach is that the discharge-rate saturates after a point, e.g., 5-bit and 6-bit mismatch lead to similar discharge-rate. To address this issue, they divide the bitlines into multiple blocks. For each row, a parallel counter accumulates distance values for each row. Finally,
M rows with the smallest distance are selected by a priority checker block. Their design searches in “block-serial, row-parallel” manner which takes constant time. Each CAM requires only one SA, counter and comparator, which reduces area overhead compared to a digital implementation.
For bitwise operations, extra bitwise SAs are used. If both bits are “1” or “0” due to high/low resistance (respectively), bitline discharge current is very small () and large () respectively. If only one of the bits is “0”, bitline offers a middle range of current (). Based on these current differences, a voltage-based SA identifies the result of a bitwise operation. For this, three sense resistance values are used: RMEM, ROR and RAND. For normal read operation, RMEM with low resistance is used for detecting any discharge current upon a row-activation. To perform AND operation, RAND with large sense resistance is used for detecting discharge current of . For OR operation, ROR is used for finding when the discharge current exceeds . XOR is performed based on the results of OR and AND. AND/OR operations can also be performed on multiple rows, whereas the XOR operation is performed for two rows in the same crossbar memory. Their design achieves orders of magnitude improvement in performance and energy efficiency for search and bitwise operations.
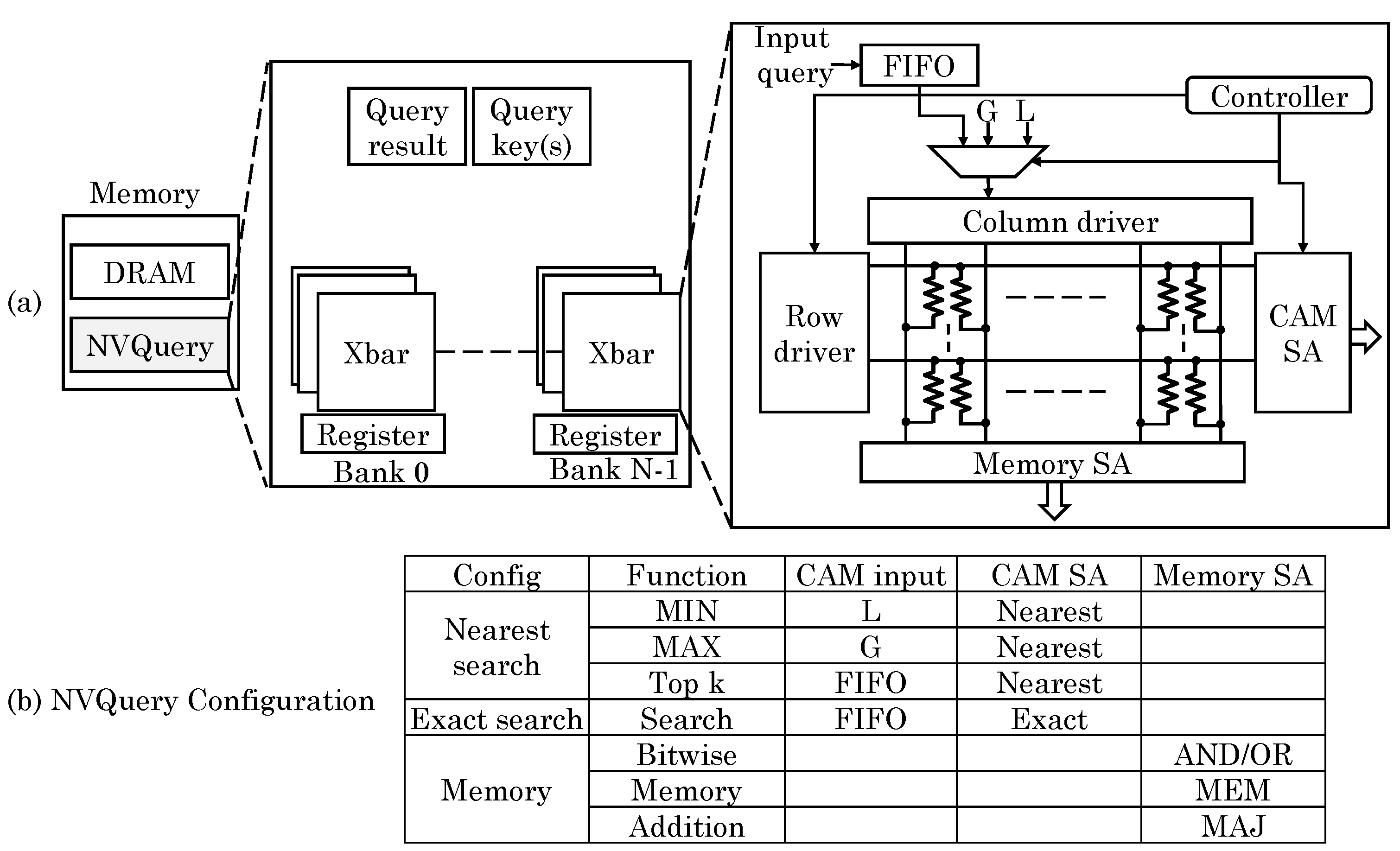
Imani et al. [
72] presented an NVM-based query accelerator, termed “NVQuery” which can perform many query functions in memory such as aggregation (
MIN, MAX, Average, Count), prediction (
Exist,
Search condition,
Top), bit-wise operations and exact and nearest-distance search queries. As shown in
Figure 29, the crossbar memory is designed as a CAM which works based on analog features of NVM. In their design, the crossbar memory can work as memory, LUT (for allowing exact search) and nearest distance search. The memory has
N banks each consisting of
k memory blocks. Each block provides result of the query and the results of all the blocks are finally processed to get the result from the entire dataset. Based on the exact search, the total count of hits can also be computed. To perform nearest distance search, the bit-by-bit search is performed to scan a bit with same index in multiple words. The data-item that remains selected for the highest number of iterations is chosen as the nearest data. Using this functionality, aggregation functions can also be implemented. For example, to compute
MIN function, the number having smallest distance from least possible value (e.g., zero for unsigned number) is searched. This is shown as
L in
Figure 29 and for unsigned numbers,
. For performing
TOP k (i.e., searching
k values closest to the input data), nearest distance search is performed for
k iterations. After every iteration, the selected word is deactivated and the nearest distance search is repeated on the remaining words. This provides
k nearest values ordered by proximity to the input. Thus,
MIN/MAX and
TOP k can be computed in single and
k cycles, respectively.
Further, by searching for the exact and closest values, bit/value-wise comparison can also be performed. To perform bit-wise operations such as AND/OR/XOR and addition/average, the crossbar is set in memory mode and the output is read from the sense amplifiers. They also discussed the hardware extensions required for implementing their technique, e.g., to facilitate nearest-distance search, a bitline driving scheme is used to give weights to the indices of the bits. Compared to CPUs and query accelerators, their design provides large improvements in performance and energy efficiency.
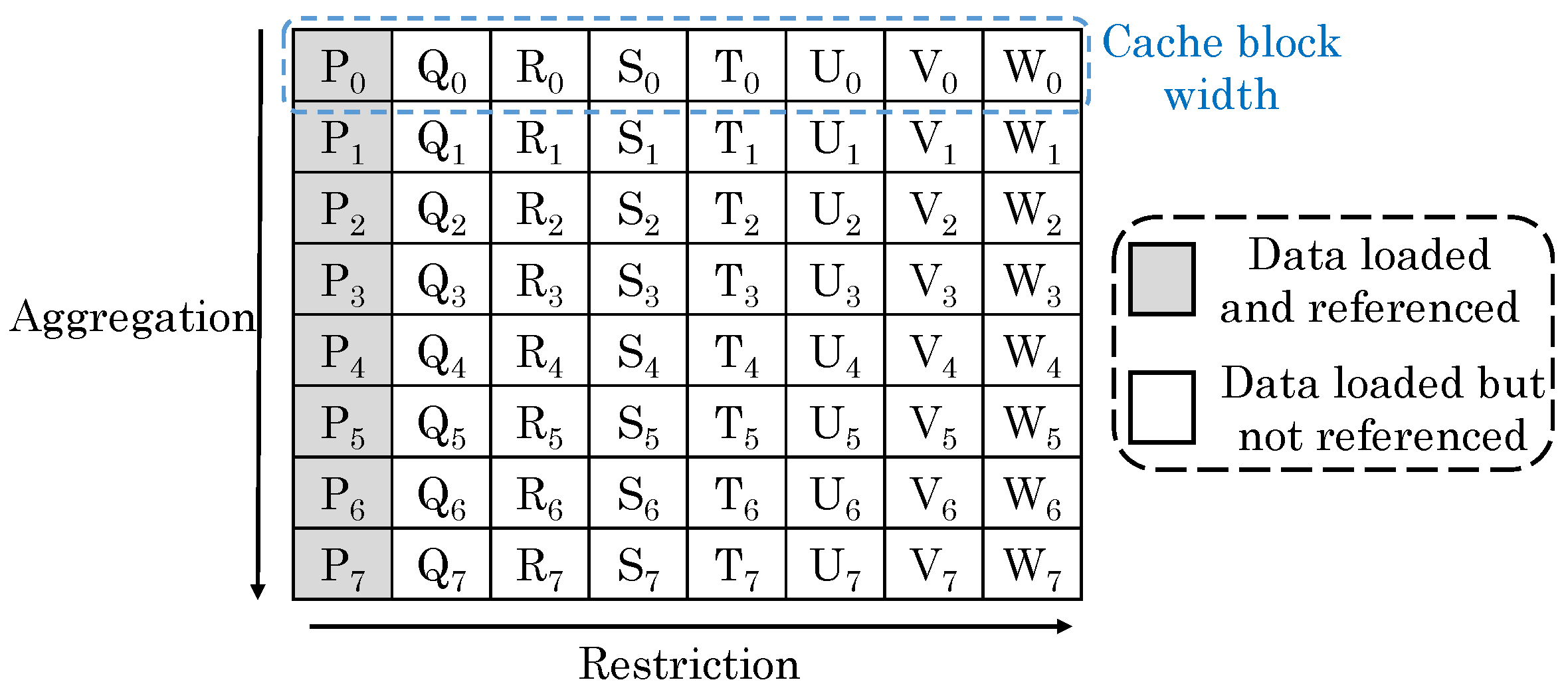
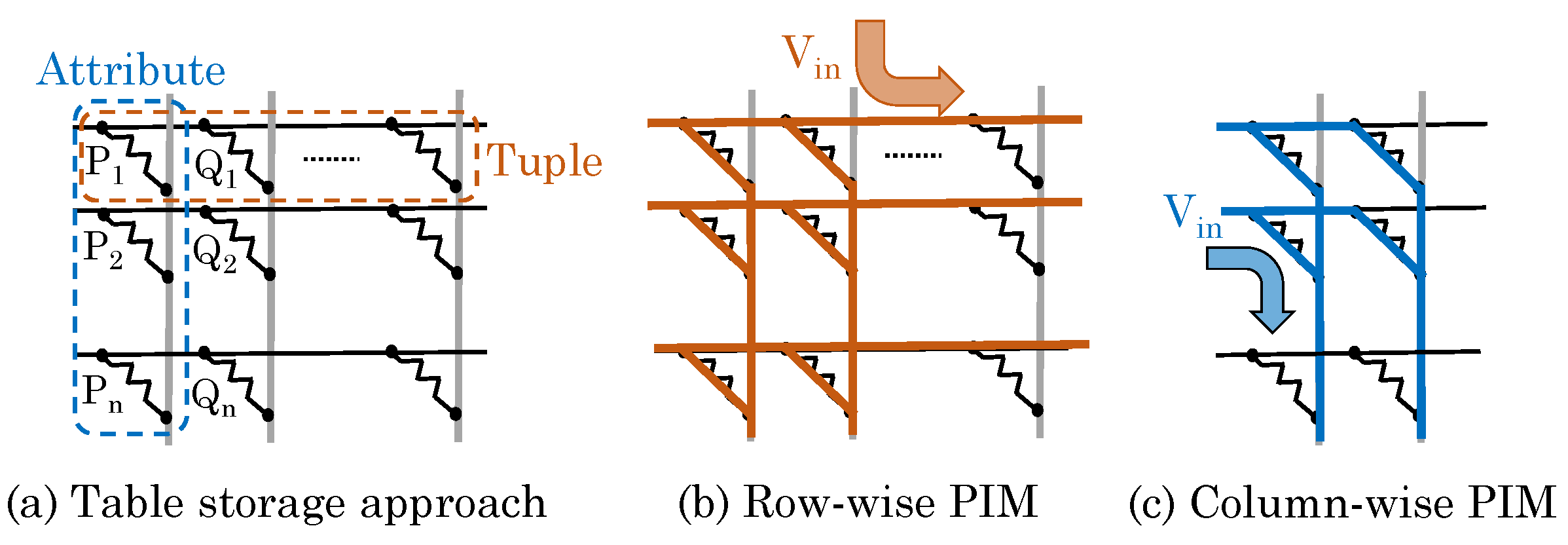
Sun et al. [
71] noted that in a 2D database, each row stores a tuple (e.g., record) of attributes and each of the attribute is stored in a column, as shown in
Figure 30. For simple queries, the row-oriented and column-oriented organizations can fetch right amount of data to reduce cache misses. However, these organizations are ineffective for queries seeking data from a particular column in a particular row. For example, in a row-based organization, multiple rows are consecutively stored, e.g., Tuple
= {P
, Q
, R
, S
, T
, U
, V
, W
} is stored in Row 1 and so on. A query such as “select P from Table where P < 20” inquires for attribute P. As shown in
Figure 30, P
and P
are in different cache blocks, and hence, they do not get loaded together which leads to a cache miss.
Sun et al. [
71] remarked that the bi-polar nature of ReRAM cell and the crossbar design of ReRAM array allow reading data using both row-oriented and column-oriented approaches. Hence, a ReRAM crossbar-based memory can be highly effective in database applications for reducing cache misses. Since computations of SQL (structured query language) queries can be also be considered as matrix operations, a ReRAM-based PIM approach can allow efficiently processing SQL queries. They presented a ReRAM-based PIM architecture for implementing SQL queries. Their technique supports dot-products of ReRAM cells storing identical attribute in different tuples and different attributes in the same tuple. They mapped data to ReRAM such that a tuple is stored in a ReRAM row and attributes of a tuple are stored in columns of a row, as shown in
Figure 31.
Their technique supports three query operations: restriction (selecting rows that fulfill a criterion), projection (selecting specific columns in a row) and aggregation (summarizing specific properties of multiple columns in a group of rows, e.g., adding the values). As for restrictions, their technique supports: +, -, *, >, <, = ,≤, ≥, AND, OR, NOT, XOR, NAND and NOR. The addition/subtraction/multiplication with constants are performed as row-wise dot-product computation as shown in
Figure 32a. To multiply two attributes, they are transferred to CPU to perform the multiplication. To perform comparison operations, an analog comparator is used at the row-output port to avoid ADCs. To process the output by equality or Boolean functions, an ADC is used at row-output for converting the result to digital domain. The digital signal can be buffered and, then, subsequent operations can be performed using digital circuitry.
To perform projection operation, row-wise dot-product computation is performed when specific columns are to be selected, as shown in
Figure 32b. The column to be read is supplied with an input signal of 1 and the remaining columns are supplied with 0 signal. For aggregation, only “sum” operation is supported using column-wise computation, as illustrated in
Figure 32c. Of the tuples selected in restriction step, certain attributes of these tuples are accumulated for performing sum operation. The output of every column shows the result of sum operation for those attributes. At a time, only row-wise or column-wise computations can be performed and, hence, the same ADC can be used for row-ports and column-ports. By virtue of reducing data-transfer, their technique improves energy efficiency over conventional CPU-based approach by orders of magnitude.
5.3. Graph-Processing Operations
Song et al. [
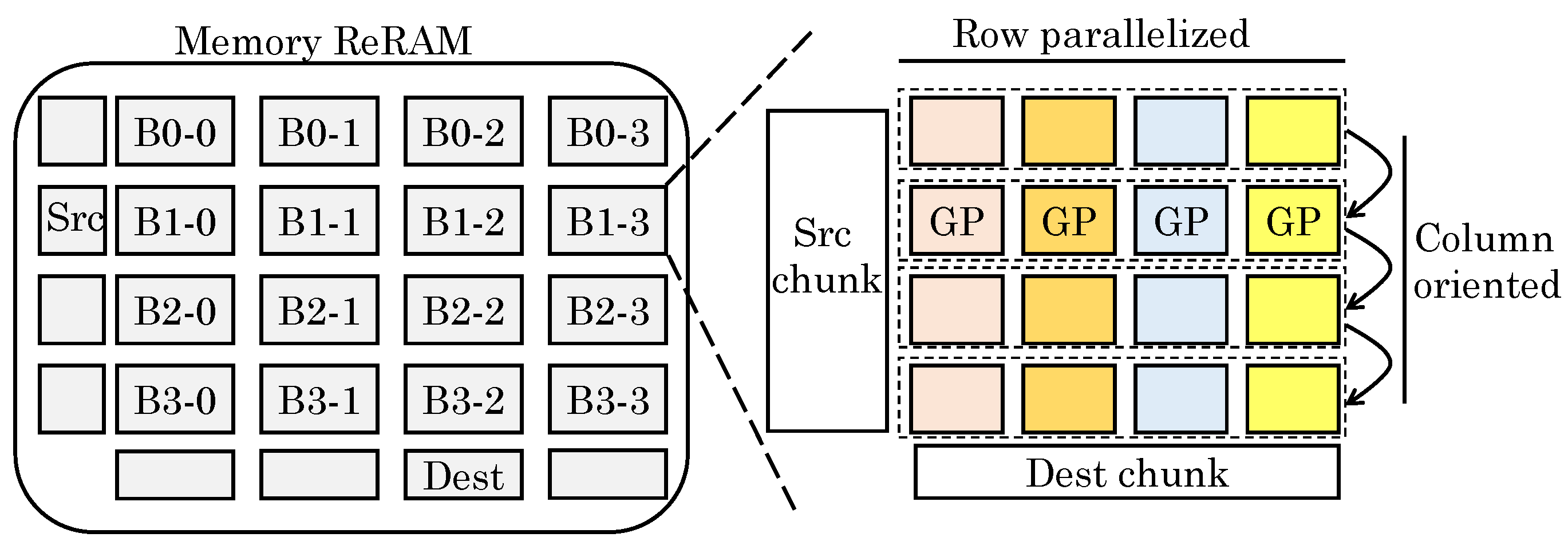
53] noted that graph processing workloads are bottlenecked by memory-bandwidth since they access memory randomly during neighborhood traversal. Since adjacent vertices are not stored in nearby locations, the spatial locality is small and, hence, a cache block is not fully utilized. This increases the data movements and wastage of energy. Even though all graph algorithms perform MVMs, the sparsity of the graph leads to inefficient MVM. Hence, most works do not store graphs in matrix form, but in compressed sparse matrix form. However, due to this, the memory access latency far-exceeds the computation latency. They note that iterative algorithms in graph-computations can tolerate errors. In addition, algorithms working on integers and probability computations such as PageRank are also tolerant to errors. Hence, they propose ReRAM-based analog operation for performing MVMs in graph-computations. The energy efficiency and PIM capability of ReRAM saves energy despite sparsity of computations.
However, use of ReRAM presents challenges of properly representing the data, mapping graph algorithms and minimizing data movements. To address these, their design uses ReRAM as both memory and graph processor. The graph data are stored in compressed form in memory ReRAM. The graph processor (ReRAM crossbar) performs MVMs on the sparse matrix. For enabling processing of an entire large graph and coordinating the data block, they proposed a “streaming-apply execution model”, which is shown in
Figure 33. In the beginning, all data are loaded into memory ReRAM. The graph data processed together in all GPs (graph processing engines) constitute a subgraph. The subgraphs are originally stored in memory ReRAM in sparse format. The vertices and edges are stored as vector and coordinate-list, respectively. The old vertex value for vertex read and new vertex value for vertex update (write) are stored in two different vectors, termed Source and Destination, respectively. After processing of the sub-graphs in an iteration, the Destination is copied to the Source to allow reading new vertices in the next iteration. The subgraphs are processed in the GPs.
Their execution model allows deciding the order of processing of subgraphs and subgraph-regions processed by any GP. Their design requires preprocessing of sparse graph data in coordinate list format for facilitating loading of edge data in GPs. In a subgraph, data in a set of rows are loaded and operated sequentially by all the GPs. The number of rows processed consecutively is decided by the size of crossbars. By controlling the crossbar size, a tradeoff between utilization and parallelism/performance/overhead can be achieved.
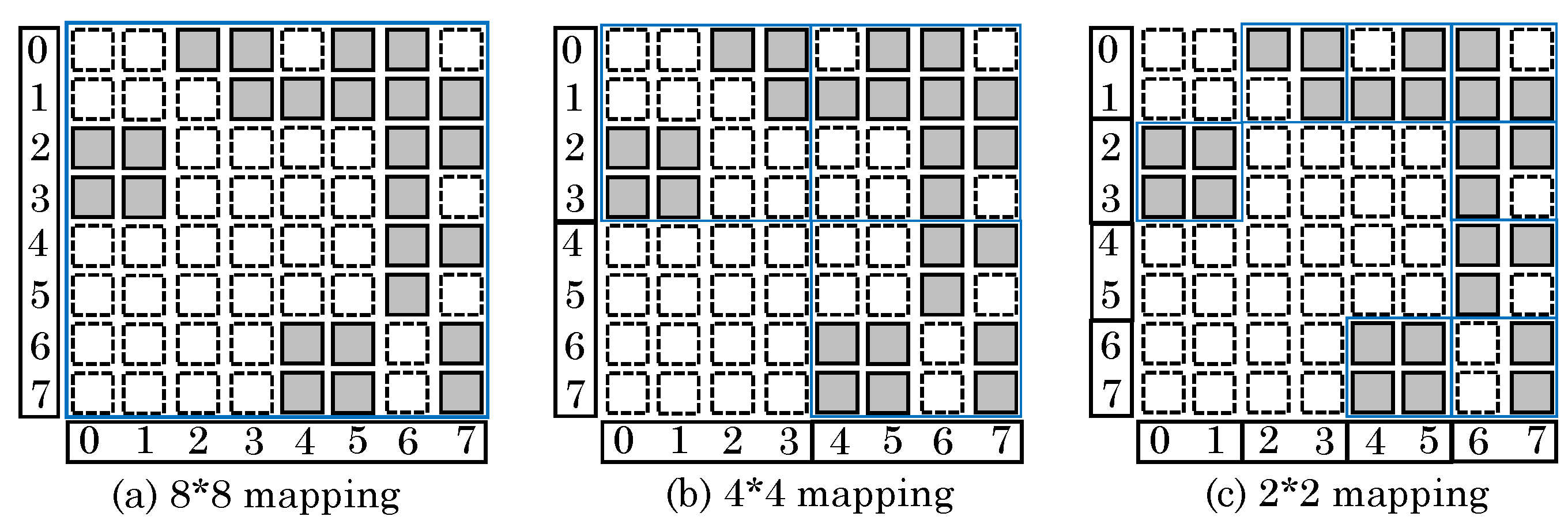
Figure 34a shows an 8 × 8 adjacency matrix, where the shaded/blank squares indicate presence/absence of an edge between two vertices, respectively. Here, although the entire graph could be concurrently processed, only
39% cells are utilized and remaining cells get wasted. On reducing the crossbar dimension to 4 × 4 or 2 × 2 (
Figure 34b,c), the utilization increases to
52% and
78%, respectively. This is because unused squares need not be mapped to ReRAM.
The auxiliary operations are handled by the peripheral logic for supporting data movement. They also proposed techniques for mapping different graph algorithms to the crossbar architecture. Their design provides higher performance than a CPU-based graph processing tool and achieves similar performance as a GPU-based tool on excluding the data transfer overhead.
5.4. Approximate Computing Approaches
Table 10 summarizes several approximate-computing based techniques. We now review them.
An associative processor is an in-memory computing engine for parallel processing. A “memristive associative processor (MAP)” uses a resistive CAM to perform any function by applying its truth table to the resistive CAM. Yantir et al. [
65] proposed two approximate-computing techniques [
78] for improving the efficiency of MAPs: bit-trimming and memristance-scaling. In associative computing, an arithmetic operation is done by processing the bits starting from LSB to MSB. Hence, the overhead of an operation depends on the number of bits, instead of the vector size. Based on this, by skipping lower
K bits, the number of cycles can be reduced for only minor loss in accuracy. Reduction in cycles leads to reduction in write/compare operations which also saves energy. In addition, by changing the value of
K, a balance between accuracy loss and efficiency gain can be achieved.
They further noted that, in memristors, the logic-0 and logic-1 values are represented by the maximum (R = 100 K) and minimum (R = 100 ) memresistance values. However, tuning the memristor precisely to these values incurs large latency and energy overhead. For example, as memresistance approaches R, the energy consumed increases sharply, whereas the rate of change in memresistance is reduced. Hence, a large amount of energy is spent in this region. To reduce this overhead, the memresistance scaling scheme tunes the memristor in a sub-range of the maximum and minimum memresistance values. This is achieved by scaling both write latency and write voltage, which also reduces write energy.
Although the associative processor operates on digital data, the compare operation happens in analog manner and the SAs convert the analog output into digital value. Hence, memresistance scaling makes comparison operations into approximate operations. However, in presence of PV, the error rate can become high, especially when the errors happen in MSBs. To mitigate this issue, the aggressiveness of scaling is kept higher in LSBs than in MSBs. Their memristive associative processor architecture offers higher performance and energy efficiency than CPU, GPU and ASIC implementations with acceptable quality loss.