An Algorithm for Generating Invisible Data Poisoning Using Adversarial Noise That Breaks Image Classification Deep Learning
Abstract
:1. Introduction
2. Related Work
2.1. Why Such Robustness Faults?
2.2. Formal Presentation
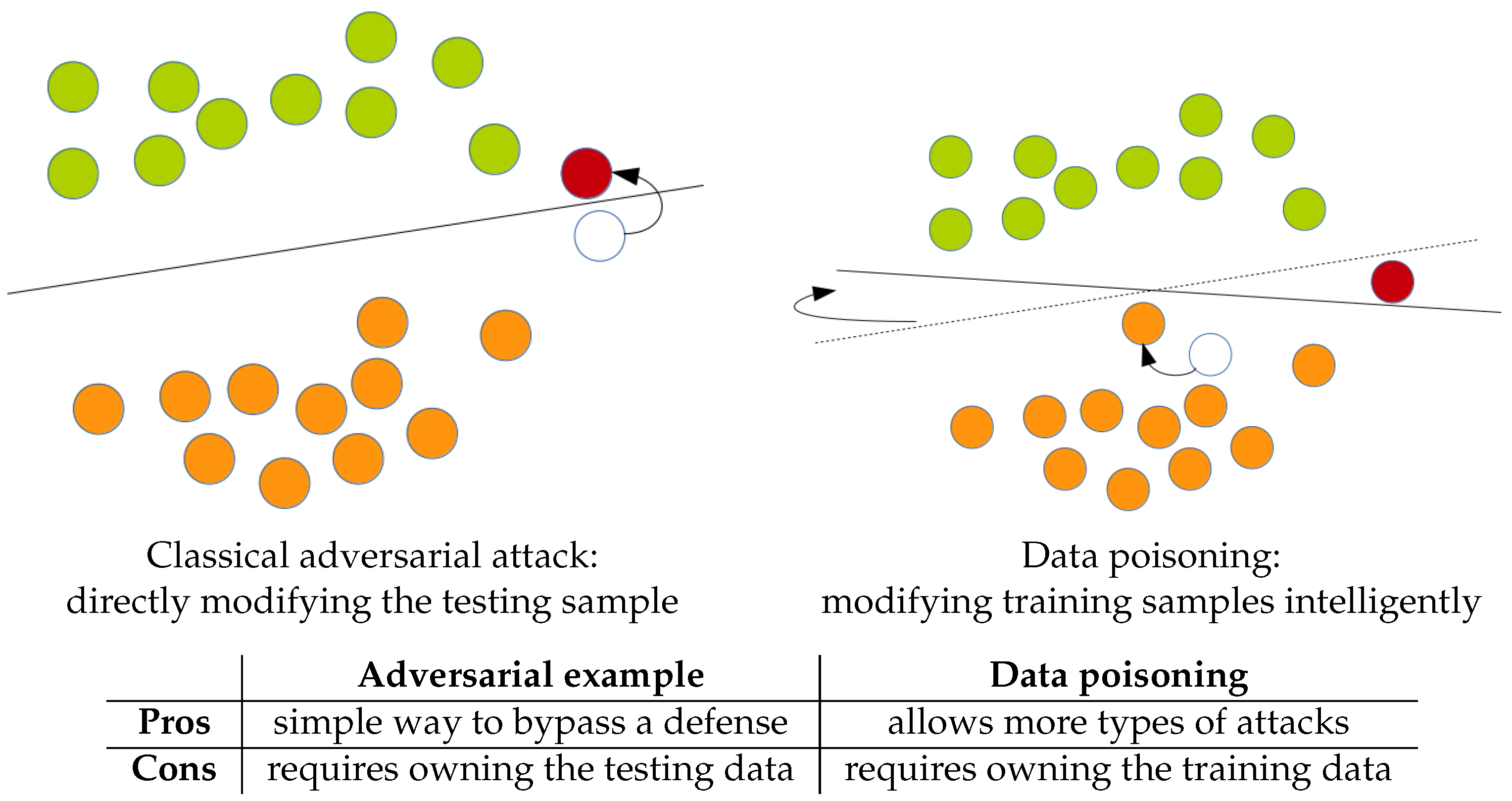
2.2.1. Data Poisoning
2.2.2. Adversarial Examples
| Algorithm 1: A simple baseline to generate adversarial examples |
| adversarialGeneratorBaseline: let be the loss function while not meeting a stopping criterion compute compute derivatives on update to increase the loss |
3. Adversarial-Based Invisible Data Poisoning
3.1. Invisible Data Poisoning
3.2. Using Adversarial-Like Noise
3.3. The Return Favor Algorithm
3.3.1. Requirements
- works in binary or multi-class contexts
- works on both integer and real data
- is not restricted to a specific data poisoning context: no constraint on k, no constraint on the loss (i.e., generic accuracy minimization or specific class accuracy minimization), etc.
- needs some desired weights as input
- works with a deep network plus SVM pipeline [24]
3.3.2. Pseudo-Code
| Algorithm 2: Pseudo-code of a fair training of the last layer of a network. |
| fairLastLayerTraining(CNN,X,Y) theta = randomVect() pipeline = CNN::theta for epoch in nbEpoch: shuffle(X,Y) for x,y in X,Y: gradient = forwardBackward(pipeline,x,y,crossentropy) theta -= lr*gradient[w] return theta |
| Algorithm 3: Pseudo-code of the return favor algorithm. |
| //Here, X corresponds to the subset of the dataset //which is over the control of the hacker. //Output is X’ a modified dataset. //Applying a fair training process on the dataset X’,Y //leads to a model biased toward thetaPoison. returnFavorAlgorithm(CNN,thetaPoison,X,Y) auxiliaryCNN = CNN::thetaPoison X’ = [] for x,y in X,Y: gradient = forwardBackward(auxiliaryCNN,x,y,crossentropy) if data type is integer x’ = x + sign(gradient[x]) else x’ = x + gradient[x]/norm(gradient[x]) X’.append(x’) return X’ |
3.3.3. Key Points of the Algorithm
- desired weights allow for capturing of testing accuracy behavior (approximating in the general equation in Section 3.2)
- scoring the training samples with the auxiliary network allows for capturing the training behavior (approximating in the general equation in Section 3.2)
4. Experiments
4.1. Datasets
4.2. Experimental Setting
4.3. With the Entire Dataset
4.4. On a Subset of the Dataset
4.5. Comparison with Classical Adversarial Attack
- An adversarial attack is a small modification of the testing samples to break the testing accuracy
- Adversarial-based data poisoning is a small modification of the training samples that breaks the testing accuracy after training on the poisoned training data
4.6. Inverse Poisoning
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. An Invisible Data Poisoning with Better Theoretical Properties
- classification problem to be binary
- that hacker could add an adversarial noise in all training samples (i.e., )
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems; 2012; pp. 1097–1105. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Taigman, Y.; Yang, M.; Ranzato, M.; Wolf, L. Deepface: Closing the Gap to Human-Level Performance in Face Verification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 1701–1708. [Google Scholar]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The Cityscapes Dataset for Semantic Urban Scene Understanding. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3213–3223. [Google Scholar]
- Greenspan, H.; van Ginneken, B.; Summers, R.M. Guest Editorial Deep Learning in Medical Imaging: Overview and Future Promise of an Exciting New Technique. IEEE Trans. Med. Imagingg 2016, 35, 1153–1159. [Google Scholar] [CrossRef] [Green Version]
- Alsulami, B.; Dauber, E.; Harang, R.; Mancoridis, S.; Greenstadt, R. Source Code Authorship Attribution Using Long Short-Term Memory Based Networks. In European Symposium on Research in Computer Security; Springer: Cham, Germany, 2017; pp. 65–82. [Google Scholar]
- Javaid, A.; Niyaz, Q.; Sun, W.; Alam, M. A Deep Learning Approach for Network Intrusion Detection System. In Proceedings of the 9th EAI International Conference on Bio-inspired Information and Communications Technologies (formerly BIONETICS); 2016; pp. 21–26. [Google Scholar]
- Moosavi Dezfooli, S.M.; Fawzi, A.; Fawzi, O.; Frossard, P. Universal Adversarial Perturbations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Xie, C.; Wang, J.; Zhang, Z.; Zhou, Y.; Xie, L.; Yuille, A. Adversarial Examples for Semantic Segmentation and Object Detection. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Papernot, N.; McDaniel, P.; Jha, S.; Fredrikson, M.; Celik, Z.B.; Swami, A. The Limitations of Deep Learning in Adversarial Settings. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbrucken, Germany, 21–24 March 2016; pp. 372–387. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.J.; Fergus, R. Intriguing Properties of Neural Networks. arXiv, 2013; arXiv:1312.6199. [Google Scholar]
- Grosse, K.; Papernot, N.; Manoharan, P.; Backes, M.; McDaniel, P. Adversarial Examples for Malware Detection. In European Symposium on Research in Computer Security; Springer: Cham, Germany, 2017; pp. 62–79. [Google Scholar]
- Cisse, M.M.; Adi, Y.; Neverova, N.; Keshet, J. Houdini: Fooling Deep Structured Visual and Speech Recognition Models with Adversarial Examples. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; pp. 6977–6987. [Google Scholar]
- Narodytska, N.; Kasiviswanathan, S. Simple Black-Box Adversarial Attacks on Deep Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 6–14. [Google Scholar]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding Deep Learning Requires Rethinking Generalization. arXiv, 2016; arXiv:1611.03530. [Google Scholar]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial Examples in the Physical World. arXiv, 2016; arXiv:1607.02533. [Google Scholar]
- Liu, L.; De Vel, O.; Han, Q.L.; Zhang, J.; Xiang, Y. Detecting and Preventing Cyber Insider Threats: A Survey. IEEE Commun. Surv. Tutor. 2018, 20, 1397–1417. [Google Scholar] [CrossRef]
- Muñoz-González, L.; Biggio, B.; Demontis, A.; Paudice, A.; Wongrassamee, V.; Lupu, E.C.; Roli, F. Towards Poisoning of Deep Learning Algorithms with Back-Gradient Optimization. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security; ACM: New York, NY, USA, 2017; pp. 27–38. [Google Scholar]
- Krizhevsky, A.; Hinton, G.E. Using very Deep Autoencoders for Content-Based Image Retrieval. In Proceedings of the 19th European Symposium on Artificial Neural Networks, Bruges, Belgium, 27–29 April 2011. [Google Scholar]
- Vapnik, V.N.; Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998; Volume 1. [Google Scholar]
- LeCun, Y.; Boser, B.E.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.E.; Jackel, L.D. Handwritten Digit Recognition with a Back-Propagation Network. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1990; pp. 396–404. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. In Readings in Computer Vision; Elsevier: Amsterdam, The Netherlands, 1987; pp. 726–740. [Google Scholar]
- Liu, S.; Zhang, J.; Wang, Y.; Zhou, W.; Xiang, Y.; Vel., O.D. A Data-driven Attack Against Support Vectors of SVM. In Proceedings of the 2018 on Asia Conference on Computer and Communications Security; ASIACCS ’18; ACM: New York, NY, USA, 2018; pp. 723–734. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 24–27 June 2014; pp. 580–587. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2009), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Fan, R.E.; Chang, K.W.; Hsieh, C.J.; Wang, X.R.; Lin, C.J. LIBLINEAR: A Library for Large Linear Classification. J. Mach. Learn. Res. 2008, 9, 1871–1874. [Google Scholar]

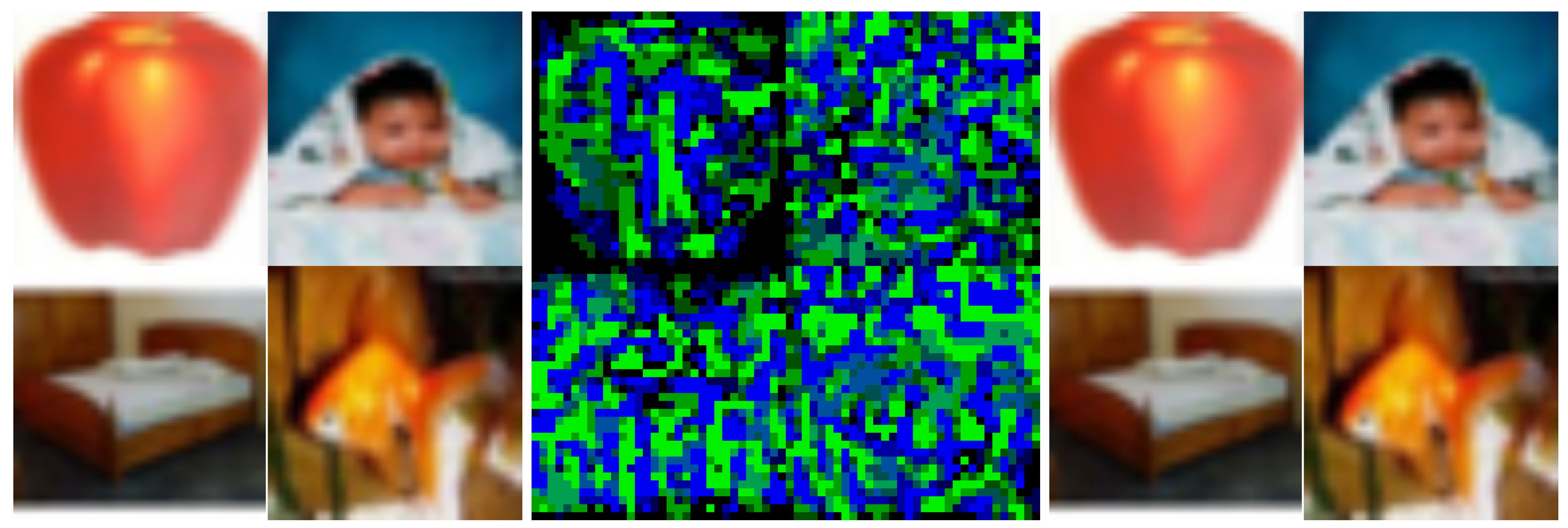
| Accuracy Loss | Data Poisoning | Classical Adversarial | Adversarial Training |
|---|---|---|---|
| vs Dataset | (Hacking Train) | (Hacking Test) | (Updated Training) |
| CIFAR10 | −12% | −18% | 0% |
| CIFAR100 | −13% | −15% | −2% |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
CHAN-HON-TONG, A. An Algorithm for Generating Invisible Data Poisoning Using Adversarial Noise That Breaks Image Classification Deep Learning. Mach. Learn. Knowl. Extr. 2019, 1, 192-204. https://doi.org/10.3390/make1010011
CHAN-HON-TONG A. An Algorithm for Generating Invisible Data Poisoning Using Adversarial Noise That Breaks Image Classification Deep Learning. Machine Learning and Knowledge Extraction. 2019; 1(1):192-204. https://doi.org/10.3390/make1010011
Chicago/Turabian StyleCHAN-HON-TONG, Adrien. 2019. "An Algorithm for Generating Invisible Data Poisoning Using Adversarial Noise That Breaks Image Classification Deep Learning" Machine Learning and Knowledge Extraction 1, no. 1: 192-204. https://doi.org/10.3390/make1010011
APA StyleCHAN-HON-TONG, A. (2019). An Algorithm for Generating Invisible Data Poisoning Using Adversarial Noise That Breaks Image Classification Deep Learning. Machine Learning and Knowledge Extraction, 1(1), 192-204. https://doi.org/10.3390/make1010011





