Next Article in Journal
Statistical Analysis of Tensile Damage of Basalt Fiber Foam Concrete Based on DBSCAN Clustering Method
Previous Article in Journal
Assessing the Eco-Efficiency of High Recycled Content Pavement Solutions: An Evaluation of the Mechanical, Durability, and Environmental Impacts
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
J. Compos. Sci.
Volume 9
Issue 12
10.3390/jcs9120693
jcs-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Influence of FeSiB Layer Thickness on Magnetoelectric Response of Asymmetric and Symmetric Structures of Magnetostrictive/Piezoelectric Composites

by
Lei Chen
*,
Yingjie Cheng
and
Fujian Qin
Multi-Dimensional Data Perception and Intelligent Recognition Chongqing Engineering Research Center, Chongqing University of Arts and Sciences, Chongqing 402160, China
*
Author to whom correspondence should be addressed.
J. Compos. Sci. 2025, 9(12), 693; https://doi.org/10.3390/jcs9120693
Submission received: 30 October 2025 / Revised: 6 December 2025 / Accepted: 7 December 2025 / Published: 12 December 2025
(This article belongs to the Section Composites Applications)
Browse Figures
Versions Notes

Abstract

Asymmetric and symmetric magnetoelectric (ME)-laminated composites with magnetostrictive layer FeNi and piezoelectric layer PZT are prepared. The longitudinal resonance ME voltage coefficient in the symmetric composite is approximately 1.57 times that in the asymmetric composite with same constituents due to the flexural deformation and asymmetric stress distribution in the asymmetric structure. By bonding an additional high-permeability FeSiB, combining FeSiB with FeNi forms magnetization-graded ferromagnetic materials. A stronger maximum ME voltage coefficient, a dual-peak phenomenon, and a self-bias ME effect are observed. The maximum ME voltage coefficients for asymmetric and symmetric composites reach 3.10 V/Oe and 5.67 V/Oe by adjusting the thickness of the FeCuNbSiB layer. The maximum zero-bias ME voltage coefficients for asymmetrical and symmetrical composite materials reach 2.19 V/Oe at 25 µm thickness of FeSiB and 2.87 V/Oe at 75 µm thickness of FeSiB. Such high performances enable the ME composites to possess ideal sensing and make them promising for self-bias current sensor applications.

1. Introduction

The magnetoelectric (ME)-laminated composite consisting of piezoelectric and magnetostrictive materials not only exhibits a much stronger ME effect at room temperature but also has easier fabrication processes compared with particulate ME composites and single-phase ME materials [1,2,3,4,5]. When an ac magnetic field is applied to an ME composite, the magnetostrictive material deforms due to the magnetostrictive effect, and this generates a stronger elastic strain in the magnetostrictive material. Then, the strain is transferred to the piezoelectric material owing to stress-mediated mechanical coupling, resulting in a larger induced voltage output due to the piezoelectric effect. Such a strong ME effect facilitates the conversion between the energies stored in the magnetic and electric fields [6]. One characteristic that the large ME effect can achieve is magnetic field control of polarization or electric field control of magnetization, which provides a new direction for the development of low-power and small-size multifunctional devices [7]. As a result, the ME composites have great potential applications in various electronic devices. The composite materials can be used as magnetic sensors for detecting AC and DC magnetic fields [8,9,10]. They are also useful as ME antennas, which utilize the ac strain produced by the electrically excited piezoelectric layer to alternate the magnetization of the magnetostrictive layer to radiate magnetic field in the transmission process [11,12,13]. The ME composites can effectively achieve energy conversion between the magnetic and electrical energy. As such, they are considered potential energy harvesters that can capture the magnetic energy and provide electric power for an autonomous wireless sensor network [14,15,16]. Other applications include magnetic memory devices [17], current sensors [18], gyrators [19], transformers [20], microwaves [21], filters [16], and resonators [22].
To enable practical application and achieve a large ME voltage coefficient, ME composites have been optimized in various aspects, such as the structural geometry, preparation methods, materials selection, and work modes [23,24,25,26,27,28,29]. Liu et al. have proposed a laminated ME composite consisting of a 80Bi0.5Na0.5TiO3-20Bi0.5K0.5TiO3 (BNKT) layer, a particulate ME transition layer (BNKT-NZFO), and a magnetostrictive Ni0.8Zn0.2Fe2O4 (NZFO) layer. The introduction of a transition layer can effectively connect the two-phase interface and strengthened interface coupling. An optimal ME voltage coefficient of 144 mV/(cm·Oe) at 1 kHz and 1.05 V/(cm·Oe) at the resonant frequency in the composite was achieved [30]. Saengow et al. have investigated the geometry-dependent ME and exchange bias effects of the trilayer sensor consisting of the bilayer multiferroic composites and anti-ferromagnetic material [31]. Sun et al. have studied the resonant ME effect of FeSiB/PZT composites with a surface-modified Fe78Si9B13 amorphous alloy. Heat treatment on Fe-based amorphous ribbons at the proper temperature can effectively improve this efficiency factor. Correspondingly, Fe-based amorphous ribbons with surface crystallization can effectively improve the ME coefficients in magnetostrictive piezoelectric heterostructures [32]. In previous work, we have reported that combining traditional magnetostrictive/piezoelectric laminated composites with magnetization-graded ferromagnetic materials can obtain a highly self-biased ME response, and the preparation method is simple and feasible [33]. Furthermore, our research has found that the magnetostrictive performances of two different magnetostrictive materials are critical to the enhancement of the zero-biased ME response [34]. The design of the self-biased ME composite has prompted a great number of research activities and made progress. However, in previous reports, few articles have analyzed and compared the ME characteristics for the asymmetric and symmetric structures of self-biased ME composites. In fact, the asymmetric and symmetric structures of self-biased ME composites have some discrepancies on the ME effect due to different vibration modes. The asymmetric self-biased ME composite can not only operate in the longitudinal vibration mode but also in the bending vibration mode. In an asymmetric structure, both longitudinal and bending vibrations have an impact on the ME effect, and their contributions to the ME effect are dependent on the layer thickness. The optimum layer structure of self-biased ME composite is critical to the enhancement of the ME response, which is both technologically important and physically interesting to investigate in terms of ME properties of self-biased ME composites.
In this paper, asymmetric and symmetric FeNi/PZT8 composites are prepared through identical preparation techniques, and detailed comparisons of their ME behaviors are carried out. Furthermore, by incorporating a high-permeability FeSiB layer into asymmetric and symmetric laminate composites, we combine FeSiB with FeNi forms of magnetization-graded ferromagnetic materials. The stronger ME voltage coefficient, the self-bias, and the dual-peak ME effect can be explored. The attention is focused on the influence of the thickness of FeSiB layers for asymmetric and symmetric composites on the maximum ME voltage coefficient, the zero-bias ME voltage coefficient, the optimal bias magnetic field, and the coercive field. This study should be beneficial for ME composite design in real applications.

2. Materials and Methods

2.1. Materials

For the fabrication of ME laminated composites, the following materials are used: FeNi alloy (Nispanc902, Chongqing Instrument Materials Research Institute, Chongqing, China), PZT (PZT8, commercially purchased from the Electronics Technology Group Corporation 26th Research Institute, Chongqing, China), FeSiB Metglas ribbons (International standard trademark 1K101, commercially purchased from Foshan Huaxin Microlite Metal Co., Ltd., Foshan, China), and epoxy resin (West System 105/206 resin/hardener, Gougeon Brothers, Inc., Bay City, MI, USA). Here, West System 105/206 resin/hardener epoxy with good mechanical properties and low viscosity is utilized to provide strong bonding among layers. West System 105 epoxy resin is mixed with slow hardener 206 using the recommended ratio of 5:1. And, the thickness of the epoxy layers is controlled to be less than 5 μm through vacuum bagging techniques. The sizes of the FeNi alloy and PZT are 12 × 6 × 0.6 mm3 and 12 × 6 × 0.8 mm3, respectively. And, the dimensions of the FeSiB Metglas ribbon are 12 mm in length, 6 mm in width, and 25 μm in thickness. Table 1 summarizes the material characteristics of FeNi alloy, PZT8, and FeSiB. The key parameters of the West System 105/206 resin/hardener are shown in Table 2.

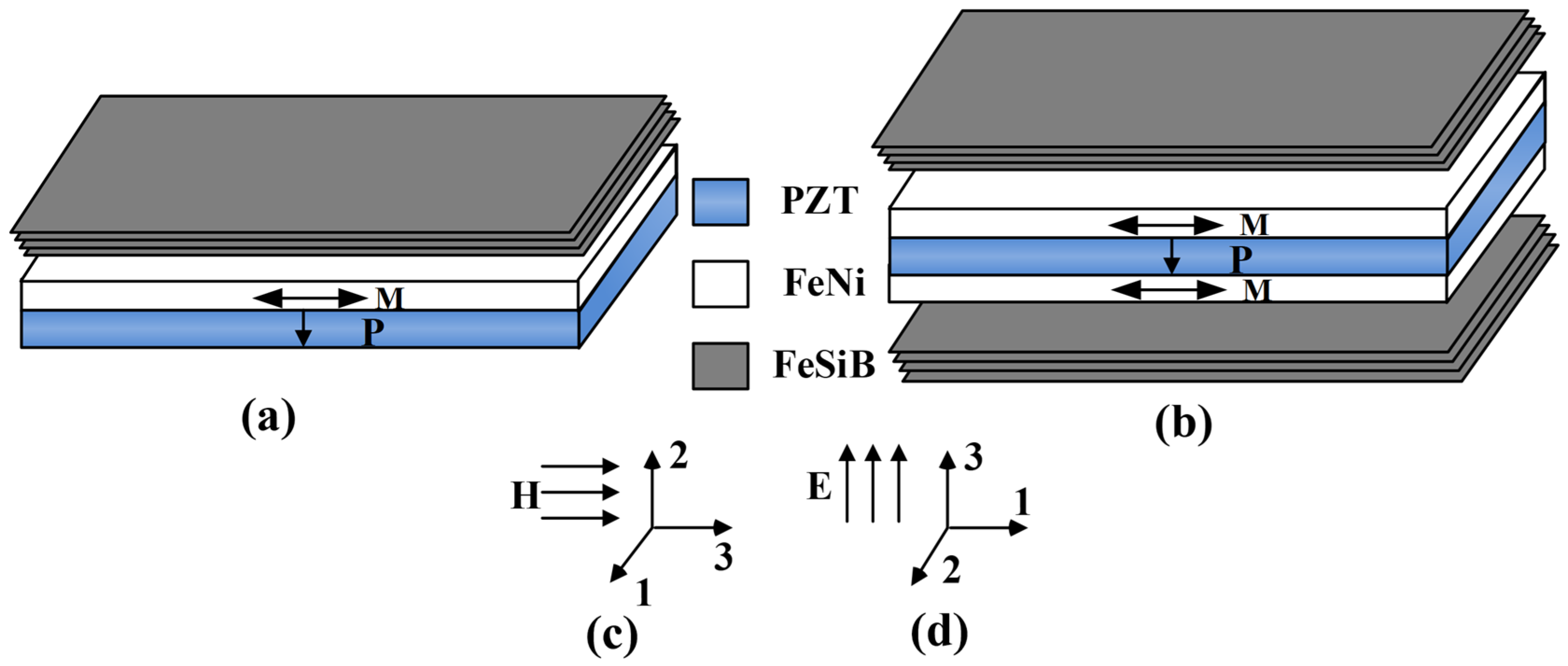
2.2. Composite Structure

Figure 1a,b illustrate the configuration of the asymmetric and symmetric self-biased ME laminated composites, respectively. Figure 1c,d show the definition of local coordinates in magnetostrictive layers and the piezoelectric layer, respectively. Magnetic fields are parallel to each other and lie in the plane of the structure, and the electric field is perpendicular to the plane of the structure. The magnetostrictive layers (FeNi and FeSiB) are magnetized along the longitudinal direction (direction 3). The piezoelectric layer (PZT) is polarized in the vertical direction (direction 3).
The asymmetric and symmetric structure self-biased ME laminated composites are prepared by bonding the multilayer FeSiB ribbons to the top side of the asymmetric structure FeNi/PZT8 (MP) composite and the top/bottom sides of the symmetric structure FeNi/PZT8/FeNi (MPM) composite using epoxy resin, respectively. Then, the ME laminated composites are compacted in a vacuum bag and cured for 12 h at room temperature to further guarantee strong bonding among layers. The thickness of the FeSiB layer is varied from 0 mm to 100 μm in the experiment.
A total of 15 samples with consistent layer interface bonding quality are fabricated, with 3 samples per FeSIB layer thickness (i.e., 0, 25, 50, 75, and 100 μm) to ensure statistical reliability. For each sample, the ME voltage coefficient is measured 4 times under a dynamic frequency-sweeping alternating magnetic field. The frequency range is set to 1–100 kHz, the frequency step size is fixed at 0.1 kHz, and the alternating magnetic field amplitude is maintained at 1 Oe. The repetition process includes demagnetization treatment (300 Oe DC magnetic field) before each measurement to avoid magnetic hysteresis influence. After 4 rounds of testing, the maximum relative deviation of the 4 measured ME voltage coefficient values is controlled within 3%, and the average value is used for subsequent analysis.
In our experiment, a long-straight solenoid driven by a signal generator (Tektronix AFG3021B, Tektronix, Inc., Beaverton, OR, USA) is used to generate a small alternating current (AC) magnetic field signal Hac. A pair of annular neodymium permanent magnets (NdFeB) is used to produce the dc bias magnetic field Hdc, and it is measured with a Gauss meter. The dc bias magnetic field changes in the range of −700 to 700 Oe. The ME composites are placed at the center of the long-straight solenoid. A small alternating current magnetic sine signal (Hac = 1 Oe) superimposed on Hdc is applied to laminate composites along the longitudinal direction. The induced ME voltage output across the two electrodes of the PZT is measured using a lock-in amplifier (7280-DSP lock-in amplifier, AMETEK, Inc., Berwyn, IL, USA) and are then acquired by the data acquisition card (National Instruments Model PCI-6115, National Instruments Corporation, Austin, TX, USA). The acquired data are stored in the computer with the Labview Virtual Instrument Program. Correspondingly, it is measured as the output voltage proportional to the ac magnetic field Hac. Furthermore, magnetization hysteresis (M–H) for FeSiB and FeNi alloy is measured with the vibrating sample magnetometer (VSM).
To investigate the piezomagnetic coefficient of magnetostrive material, the measured magnetostrive material samples are placed at the center of the solenoid. An AC magnetic field superimposed with various DC bias magnetic fields is applied to samples along the longitudinal direction. It causes it to vibrate around the λ/2 longitudinal resonance by Hac superimposed Hdc. The vibration velocity v at the end faces of the samples is measured using a Laser Doppler vibrometer (Polytec Model OFV-5000, Polytec, Inc., Karlsruhe, Germany) [35]. The piezomagnetic coefficients of the samples are calculated using the equation q33 = dλ/dH = v/(πflHac), where v is the vibration velocity of the sample induced by the magnetic field, f is the exciting frequency, l is the length of sample, and Hac is the magnitude of the external AC magnetic field.

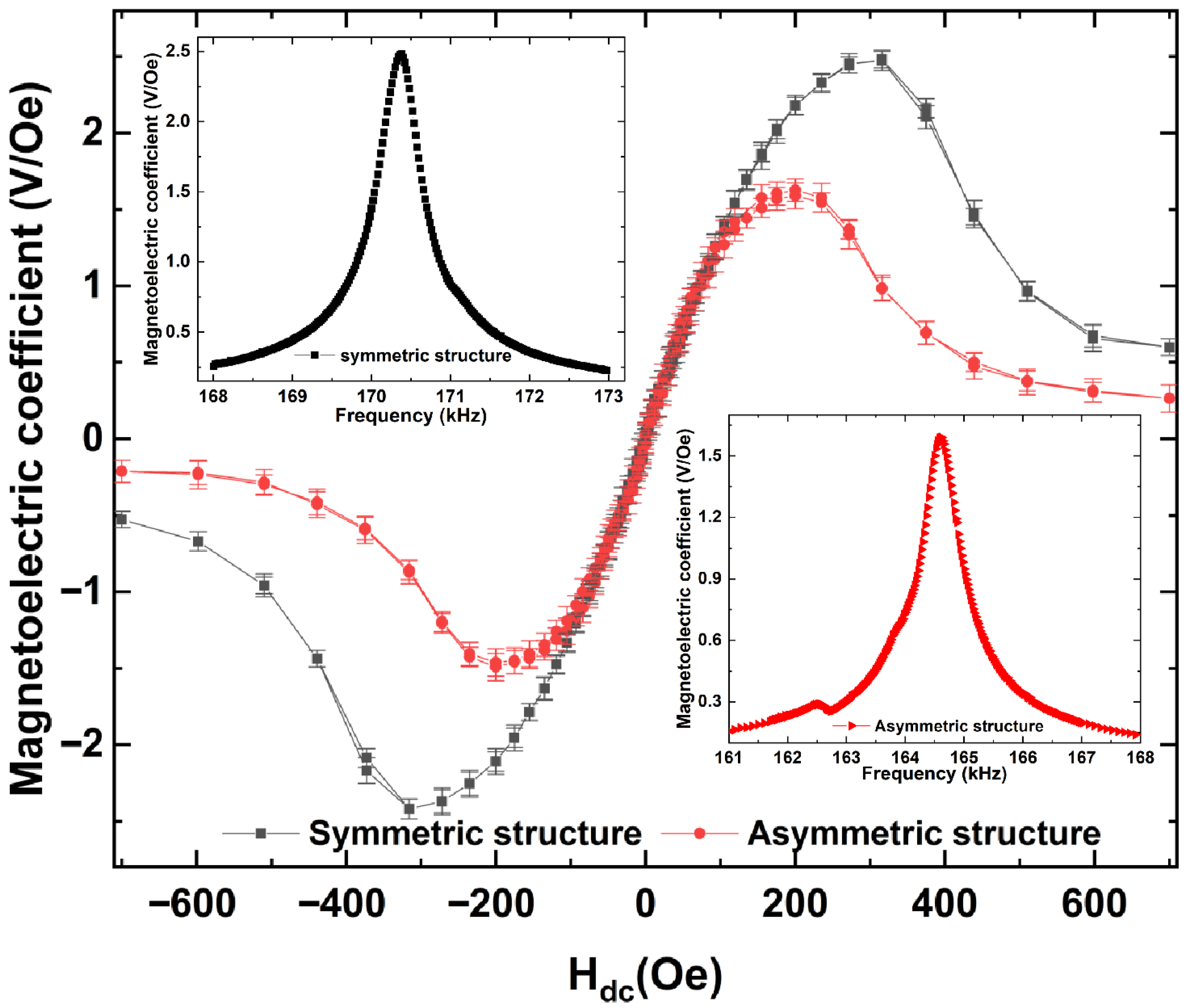
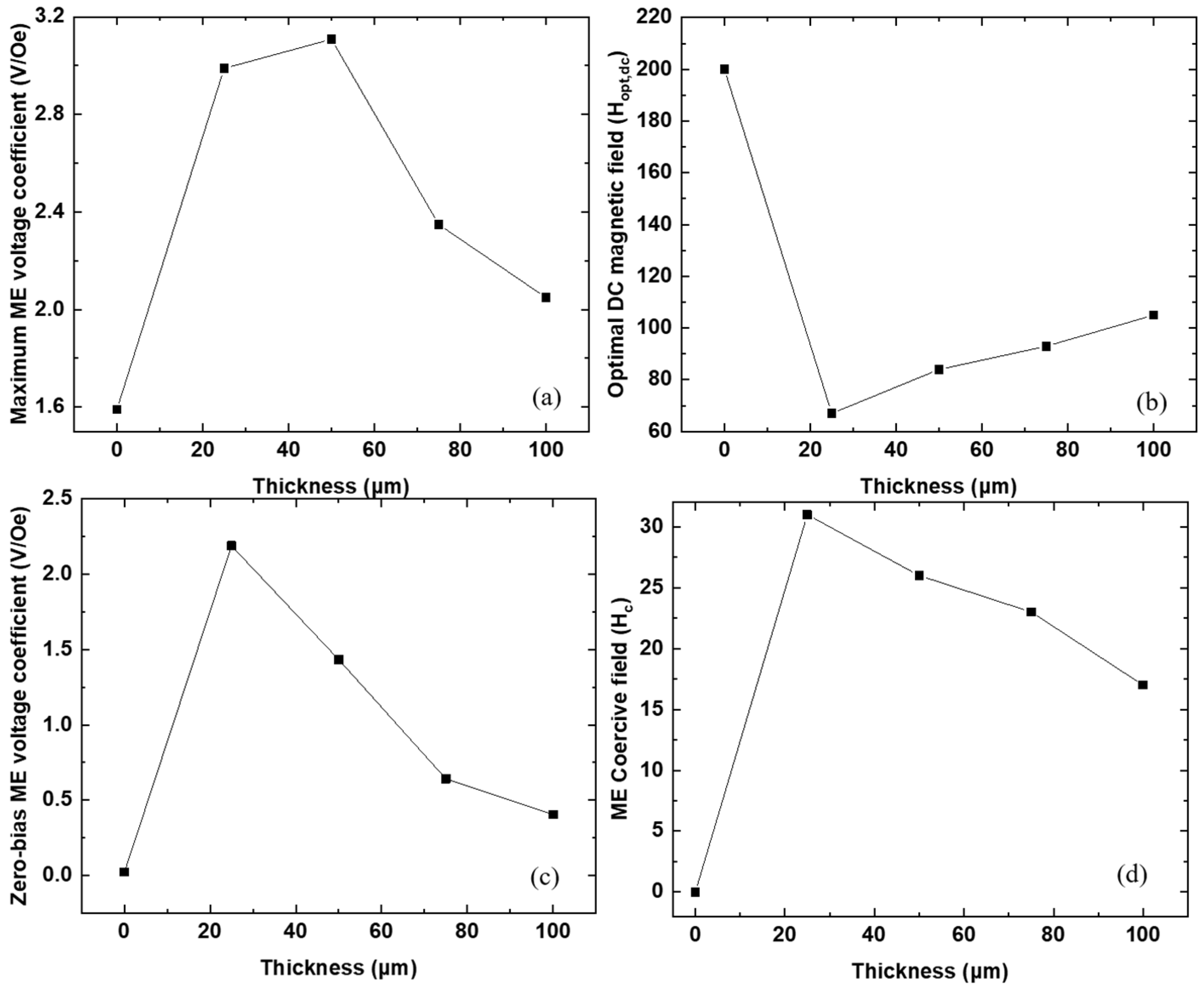
3. Results and Discussion

To investigate the properties of the two magnetostrictive materials, the magnetization curves and the piezomagnetic coefficient for FeSiB and FeNi are measured. Magnetostrictive material FeSiB (Fe78B13Si9) possesses a good mechanical quality factor (Q > 1000) and high flexibility. FeNi (Nispanc902, Chongqing Instrument Materials Research Institute, Chongqing, China) presents very low thermal coefficients of Young’s modulus and expansion, a high mechanical quality factor (Q > 9000), and low relative permeability (μr < 30). Here, the dc magnetic field is applied along the longitudinal direction of the sample when the normalized magnetization curves (Figure 2) are measured with the vibration sample magnetometer (VSM). There is a large difference in magnetization curves for FeNi and FeSiB. This originates from the different structures of magnetic domains for FeNi and FeSiB. Nanosized striped domains in FeSiB can be easily aligned along the direction of the applied dc magnetic field due to its small coercive field and high reversibility. However, FeNi exhibits a larger coercive field relative to FeSiB; it requires the larger dc magnetic field to reach the new equilibrium state once the magnetic domains are reoriented. Furthermore, it is found that FeSiB has a high initial magnetic permeability (μr = 40,000), which shows the good soft magnetic property. For comparison, FeNi has much smaller magnetic permeability (μr = 30) because the larger magnetocrystalline and magnetoelastic anisotropies deteriorate the soft magnetic property. Here, the magnetic permeability of FeSiB is about 1000 times larger than that of FeNi, which produces a significantly lower saturation field and results in higher magnetostrictive strain at a lower dc magnetic field for FeSiB. As shown in Figure 3, with increasing Hdc the piezomagnetic coefficient of FeSiB presents a rapid rise to a maximum value of Hdc = 67 Oe, followed by a sharp drop down to 0 as Hdc is further increased. For FeNi, the piezomagnetic coefficient increases initially with increasing Hdc and reaches a peak value of Hdc = 175 Oe. A further increase in the dc magnetic field leads to a gradual decrease in the magnitude of the piezomagnetic coefficient, and it is equal to zero. Figure 3 shows that FeSiB has a higher piezomagnetic coefficient compared with FeNi. As mentioned above, this results from its extremely high magnetic permeability. The piezomagnetic coefficient is directly proportional to the square of the magnetic permeability. Additionally, the large magnetic permeability for FeSiB concentrates external flux and dramatically drops the saturation field; correspondingly, a high piezomagnetic field can be obtained. For FeNi, its low magnetic permeability results in serious magnetic flux leakage and a smaller piezomagnetic coefficient, as shown in Figure 3.
The ME voltage coefficients for the asymmetric structure MP composite and the symmetric structure MPM composite without FeSiB are investigated. The corresponding measured ME voltage coefficients vs. Hdc at the near longitudinal resonance frequency are shown in Figure 4. ME voltage coefficients for both the asymmetric structure MP composite and the symmetric structure MPM composite strongly depend on Hdc due to the dependence of the piezomagnetic coefficient on Hdc. Furthermore, they vary with similar trends. ME voltage coefficients increase with the biased magnetic field to a maximum value and then gradually decrease with a further increase in the field. However, the maximum value of ME voltage coefficient for the MP composite is 1.58 V/Oe at an optimal bias magnetic field Hdc,opt = 200 Oe and fr = 164.5 kHz, whereas ME voltage coefficients for the MPM composite reach 2.48 V/Oe at Hdc,opt = 316 Oe and fr = 174.6 kHz. Such a discrepancy essentially tracks the ME effects related to the thickness ratio of magnetostrictive layers in the ME composite. According to Refs. [36,37,38,39], the resonant ME voltage coefficient for asymmetric and symmetric structure ME composites depends on the thickness ratio of the magnetostrictive material   n m and the effective mechanical quality factor of the ME composite Q m . An increase in the thickness ratio of the magnetostrictive phase leads to an enhancement in the strain due to magnetostriction and an increase in the ME voltage coefficient. In addition, the effective mechanical quality factor of the ME composites Q m can be derived as [40]
1 Q m =   n m Q m a g + 1 −   n m Q p i e z
where Q m a g and Q p i e z are the mechanical quality factor of the magnetostrictive material and the piezoelectric material, respectively.   n m = t m / ( t m + t p ) is the thickness ratio of the magnetostrictive material FeNi in the ME composite. t m is the thickness of the FeNi layer. t p is the thickness of the PZT layer. From the above formula, Equation (1), Q m is influenced by Q m a g ,     Q p i e z , and n m . The mechanical quality factor of FeNi is significantly higher than that of PZT. Compared to the asymmetric structure MP composite, the higher thickness ratio   n m of the symmetric structure MPM composite results in the higher effective mechanical quality factor Q m . Correspondingly, it leads to the larger ME voltage coefficient. Furthermore, there are some differences in elastic stress between the asymmetric and symmetric structures. The asymmetric stress distribution and flexural deformation in the asymmetric structure MP composite occur due to the difference in the rigidity and Young’s modulus between PZT and FeNi, resulting in nonlinear elastic coupling. Considering the tensor properties of the piezoelectric coefficient, the nonlinear distortion of the PZT layer greatly reduces the ME effect, while the mechanical stress in the symmetric structure MPM composite is symmetric around the central PZT layer. It produces linear elastic coupling, which is responsible for the significantly enhanced ME response in the symmetric structure.
In order to investigate the influence of the FeSiB layer on the ME response of asymmetric and symmetric structure composites, the ME voltage coefficient as a function of the dc magnetic field Hdc at resonance with Hac = 1 Oe for FeNi/PZT and FeNi/PZT/FeNi with different thicknesses of FeSiB ranging from 0 to 100 μm is measured, as shown in Figure 5 and Figure 6. The dual-peak ME effects are observed by incorporating a high-permeability FeSiB layer into FeNi/PZT and FeNi/PZT/FeNi laminate. For FeNi/PZT/FeNi without FeSiB, the single-peak behavior for the ME effect appears around the optimum bias, which is limited in a narrow operating range. For FeNi/PZT with a layer of FeSiB, the first peak appears at the optimum bias Hdc,opti = 60 Oe, and the second peak occurs at a higher dc bias magnetic field Hdc = 200 Oe. For FeNi/PZT/FeNi with a layer of FeSiB, the first peak appears at the optimum bias Hdc,opti = 60 Oe, and the second peak occurs at a higher dc bias magnetic field Hdc = 316 Oe. The dual-peak phenomenon results from the superimposition and interaction of the magnetostrictive strains for FeNi and FeSiB due to the different trends of piezomagnetic coefficients as the function of the dc bias magnetic field for FeNi and FeSiB, as shown in Figure 3. The ME voltage coefficient is proportional to the piezomagnetic coefficient. The ME effect of the symmetric structure FeNi/PZT/FeNi with FeSiB is determined by both magnetostrictions of magnetic materials FeNi and FeSiB. At the lower magnetic field, the magnetostrictions of FeSiB and FeNi do not reach saturation, and the ME voltage coefficient is affected by both FeSiB and FeNi layers. However, according to Figure 3, FeSiB exhibits a high piezomagnetic coefficient due to its much larger permeability relative to FeNi, which induces compressive stress on the FeNi due to the stress–strain coupling of the interlayer and correspondingly results in the first peak of the ME voltage coefficient in a low magnetic field. With the increase in the dc bias magnetic field, the magnetostriction of FeSiB gradually attains saturation in the high dc magnetic field, and FeNi layer is crucial for determining the ME voltage coefficient, which leads to the second peak of the ME voltage coefficient in the high magnetic field. In this case, the ME voltage coefficient for asymmetric structure PZT/FeNi with FeSiB also exhibits a dual-peak effect. However, there are some discrepancies between asymmetric and symmetric structures. The second peak for the asymmetric structure MF composite with FeSiB occurs at dc bias magnetic field Hdc = 200 Oe, whereas the second peak for the symmetric structure appears at Hdc = 316 Oe. Such results can be attributed to the optimum bias magnetics for asymmetric FeNi/PZT and symmetric FeNi/PZT/FeNi laminate. Figure 5 and Figure 6 show that the maximum ME voltage coefficients for asymmetric FeNi/PZT and symmetric FeNi/PZT/FeNi laminates without FeSiB occur at Hdc,opt = 200 Oe and Hdc,opt = 316 Oe due to the optimum bias magnetics related to the demagnetization factor and the shapes of the laminate materials. Correspondingly, when the magnetostriction of FeSiB is saturated in a high magnetic field, the second peak in the high magnetic field appears at the optimum magnetic bias for asymmetric and symmetric laminates with FeSiB. Furthermore, the ME response curve for symmetric structures exhibits a larger hysteresis in the forward and reverse sweep relative to the asymmetric structure.
Additionally, a self-biasing effect characterized by a non-zero ME response at zero bias is observed, as shown in Figure 5 and Figure 6. The zero-bias ME voltage coefficients for FeNi/PZT/FeNi and PZT/FeNi with FeSiB are 2.78 V/Oe and 2.16 V/Oe, respectively. The ME voltage coefficients for FeNi/PZT/FeNi and PZT/FeNi are 0 mV/Oe at zero bias. As the piezomagnetic coefficient of the magnetostrictive material FeNi strongly depends on the dc magnetic bias field (Figure 3), FeNi/PZT/FeNi and PZT/FeNi need to provide an external dc magnetic bias field to generate a strong ME response. Under a zero-bias magnetic field, the magnetostriction coefficient of FeNi approaches zero; correspondingly, the magneto electric voltage coefficient is also zero. By bonding an additional high-permeability FeSiB, combining FeSiB with FeNi forms magnetization-graded ferromagnetic materials. Strong magnetization gradients are achieved due to the great differences in the magnetic permeability and coercivity between FeNi and FeSiB [41]. Consequently, it breaks the spatial symmetry of these ferromagnetic materials and produces a comparatively large internal potential. The spatially varying magnetization in a magnetization-graded ferromagnetic layer induces a large internal magnetic bias Hint. For the ME composites, the total dc magnetic bias (Htotal,dc) consists of the external dc magnetic field (Hdc) and Hint. Due to the dependence of the piezomagnetic coefficient on Htotal,dc, the induced built-in magnetic field Hint results in a high piezomagnetic coefficient of the magnetostrictive material at zero bias, correspondingly resulting in a larger non-zero ME voltage coefficient at zero bias owing to the dependence of the ME voltage coefficient on the piezomagnetic coefficient.
One observes that the ME voltage coefficient of the laminated composite depends strongly on the thickness of the FeSiB ribbon. In order to optimize the ME composite for multifunctional device applications, the influence of the FeSiB ribbon’s thickness for asymmetric and symmetric structure laminate composites on ME performance is investigated. Several important conclusions can be drawn from Figure 7 and Figure 8. (i) As the thickness of the FeSiB ribbon increases, the maximum ME voltage coefficients for asymmetric and symmetric structure laminate composites first increase and reach the maximum value and then decrease (see Figure 7a and Figure 8a). The maximum value for the symmetric structure MPM composite reaches 5.67 V/Oe at the 75 μm thickness of FeSiB, while the maximum value for the asymmetric structure MP composite reaches 3.10 V/Oe at the 50 μm thickness of FeSiB. Such results can be attributed to the ME effects related to the additional stress produced by FeSiB and the adhesive layer. With the increase in FeSiB’s thickness, the greater the additional stress produced by the FeSiB layer becomes, and the higher the ME voltage coefficient that can be achieved. However, strain in the laminated composite is transferred by the adhesive interlayer. As the thickness of the FeSiB layers increases, the thickness of the epoxy layers between the FeSiB and the laminated composite increases. The adhesive layers have a strong effect on mechanical coupling at the interfaces, which causes the great loss of stress–strain coupling and correspondingly reduces the ME coupling. (ii) The Hdc,opti required for the maximum ME voltage coefficient decreases with the increasing thickness of FeSiB, ranging from 0 to 100 μm, and then increases, as shown in Figure 7b and Figure 8b. As mentioned previously, for symmetrical and asymmetrical composite materials without FeSiB, the ME voltage coefficient has only one peak at the optimal bias. However, by binding FeSiB to symmetric and asymmetric composite materials, FeSiB produces a large magnetostrictive strain at a lower magnetic field owing to high magnetic permeability and a good mechanical quality factor, which induces additional stress on the FeNi due to the stress–strain coupling of the interlayer. Such additional stress produces mechanical strain in FeNi and results in a new peak in the ME voltage coefficient at low-bias magnetic fields. Hence, the highest ME voltage coefficient at optimal bias is influenced by the additional stress. Furthermore, the additional stress varies with the thickness of the FeSiB ribbon. (iii) When the thickness of the FeSiB ribbon increases, the zero-bias ME voltage coefficients for asymmetrical and symmetrical composite materials first increase and reach a maximum value of 2.19 V/Oe (27.38 V/cm Oe) at the 25 µm thickness of FeSiB and 2.87 V/Oe (35.88 V/cm Oe) at the 75 µm thickness of FeSiB, which is higher than that of the previously reported NKNLS-NZF/Ni/NKNLS-NZF trilayer composite (147.3 mV/cm Oe) [42]. Then, the zero-bias ME voltage coefficients decrease with the further increase in the thickness of the FeSiB ribbon, as shown in Figure 7c and Figure 8c. This phenomenon can be explained as follows: the magnetic interaction between FeNi and FeSiB produces an internal magnetic field, leading to the change in the total dc magnetic bias. The zero-bias ME voltage coefficient for composite materials is mainly determined by the total dc bias magnetic field and the additional stress. Furthermore, the internal bias magnetic field and the additional stress for two different structure composite materials both change with the thickness of the FeSiB ribbon. Such factors appear to be optimal at different thicknesses of the FeSiB ribbon. (iv) Hc first increases and then decreases when the thickness of the FeSiB ribbon is increased from 0 to 100 µm (see Figure 7d and Figure 8d). Such results can be attributed to an internal magnetic field induced by spatially varying magnetization, leading to the change in the total dc bias magnetic field with the thickness of the FeSiB ribbon.

4. Conclusions

This paper presents a comparison of the longitudinal resonant ME voltage coefficients for asymmetrical and symmetrical composites. With flexural deformation and asymmetric stress distribution in the asymmetric structure, it leads to the nonlinear distortion of the PZT layer, resulting in a decrease in the ME voltage coefficient of the asymmetrical composite. In addition, as the magnetic interaction between FeNi and FeSiB leads to an internal magnetic field, it produces variations in the total dc magnetic bias. By incorporating a high-permeability FeSiB, the maximum value of zero-bias ME voltage coefficients for asymmetrical and symmetrical composite materials reach 2.19 V/Oe at the 25 µm thickness of the FeSiB layer and 2.87 V/Oe at the 75 µm thickness of the FeSiB layer. Meanwhile, the additional stress produced by the FeSiB layer produces a mechanical strain in FeNi and results in a new peak in the ME voltage coefficient in low-bias magnetic fields. In this case, a stronger ME response, self-bias, and a dual-peak phenomenon are observed for asymmetrical and symmetrical composites with the FeSiB layer. By optimizing the thickness of the FeSiB layer, the maximum ME voltage coefficient of the symmetrical composite reaches 5.67 V/Oe at the 75 μm thickness of FeSiB. This study provides the possibility of implementing self-bias ME devices in practical applications. ME composites’ unique advantages (low power consumption, dual-sensing energy harvesting capability) make them ideal for industrial IoT and smart manufacturing, but system-level integration remains underdeveloped. Future research should focus on self-powered sensor nodes, ME-composite-based condition monitoring systems, and ME-composite-based tunable RF components (e.g., filters, antennas) for 5G/6G base stations.

Author Contributions

Conceptualization, F.Q.; Methodology, F.Q.; Formal analysis, Y.C. and F.Q.; Investigation, L.C., Y.C. and F.Q.; Data curation, Y.C.; Writing—original draft, L.C. and Y.C.; Writing—review & editing, L.C. and F.Q.; Supervision, L.C.; Funding acquisition, L.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research is supported by the National Natural Science Foundation of China (Grant No. 61304255) and the Natural Science Foundation of Chongqing (No. CSTB2024NSCQ-MSX1049).

Data Availability Statement

All data generated or analyzed during this study are included in this published article. The data used/analyzed are available from the corresponding author on request.

Acknowledgments

The authors sincerely thank the editors and reviewers for their kind attention and valuable comments dedicated to this paper.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Ryu, J.; Carazo, A.V.; Uchino, K.; Kim, H.E. Magnetoelectric properties in piezoelectric and magnetostrictive laminate composites. Jpn. J. Appl. Phys. 2001, 40, 4948–4951. [Google Scholar] [CrossRef]
  2. Li, M.; Matyushov, A.; Dong, C.; Chen, H.; Lin, H.; Nan, T.; Qian, Z.; Rinaldi, M.; Lin, Y.; Sun, N.X. Ultra-sensitive NEMS magnetoelectric sensor for picotesla DC magnetic field detection. Appl. Phys. Lett. 2017, 110, 143510. [Google Scholar] [CrossRef]
  3. Spaldin, N.A.; Ramesh, R. Advances in magnetoelectric multiferroics. Nat. Mater. 2019, 18, 203–212. [Google Scholar] [CrossRef] [PubMed]
  4. Tu, C.; Chu, Z.-Q.; Spetzler, B.; Hayes, P.; Dong, C.-Z.; Liang, X.-F.; Chen, H.-H.; He, Y.-F.; Wei, Y.-Y.; Lisenkov, I.; et al. Mechanical-Resonance-Enhanced Thin-Film Magnetoelectric Heterostructures for Magnetometers, Mechanical Antennas, Tunable RF Inductors, and Filters. Materials 2019, 12, 2259. [Google Scholar] [CrossRef]
  5. Nan, C.W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
  6. Chu, Z.; Pourhosseiniasl, M.J.; Dong, S. Review of multi-layered magnetoelectric composite materials and devices applications. J. Phys. D Appl. Phys. 2018, 51, 243001. [Google Scholar] [CrossRef]
  7. Liang, X.; Chen, H.; Sun, N.X. Magnetoelectric materials and devices. APL Mater. 2021, 9, 41114. [Google Scholar] [CrossRef]
  8. Wang, Y.; Xiao, N.; Xiao, R.; Wen, Y.; Li, P.; Chen, L.; Ji, X.; Han, T. Enhanced dc Magnetic Field Sensitivity for Coupled ac Magnetic Field and Stress Driven Soft Magnetic Laminate Heterostructure. IEEE Sens. J. 2020, 20, 14756–14763. [Google Scholar] [CrossRef]
  9. Chu, Z.; Shi, H.; Pourhosseiniasl, M.J.; Wu, J.; Shi, W.; Gao, X.; Yuan, X.; Dong, S. A magnetoelectric flux gate: New approach for weak DC magnetic field detection. Sci. Rep. 2017, 7, 8592. [Google Scholar] [CrossRef]
  10. Dong, X.W.; Wang, B.; Wang, K.F.; Wan, J.G.; Liu, J.M. Ultra-sensitive detection of magnetic field and its direction using bilayer PVDF/Metglas laminate. Sens. Actuators A Phys. 2009, 153, 64–68. [Google Scholar] [CrossRef]
  11. Dong, C.; Wang, X.; Lin, H.; Gao, Y.; Zaeimbashi, M. A portable very low frequency (VLF) communication system based on acoustically actuated magnetoelectric antennas. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 398–402. [Google Scholar] [CrossRef]
  12. Zhang, Y.; Jing, L.; Shi, P.; Hou, J.; Yang, X.; Peng, Y.; Chen, S. Research on a miniaturized VLF antenna array based on a magnetoelectric heterojunction. J. Mater. Sci. Mater. Electron. 2022, 33, 11–24. [Google Scholar] [CrossRef]
  13. Mukherjee, D.; Mallick, D. A self-biased, low-frequency, miniaturized magnetoelectric antenna for implantable medical device applications. Appl. Phys. Lett. 2023, 122, 014102. [Google Scholar] [CrossRef]
  14. Mastouri, H.; Ennawaoui, A.; Remaidi, M.; Sabani, E.; Derraz, M.; El Hadraoui, H.; Ennawaoui, C. Design, Modeling, and Experimental Validation of a Hybrid Piezoelectric–Magnetoelectric Energy-Harvesting System for Vehicle Suspensions. World Electr. Veh. J. 2025, 16, 237. [Google Scholar] [CrossRef]
  15. Leung, C.M.; Li, J.; Viehland, D.; Zhuang, X. A review on applications of magnetoelectric composites: From heterostructural uncooled magnetic sensors, energy harvesters to highly efficient power converters. J. Phys. D Appl. Phys. 2018, 51, 263002. [Google Scholar] [CrossRef]
  16. Kozielski, L.; Bochenek, D.; Clemens, F.; Sebastian, T. Magnetoelectric Composites: Engineering for Tunable Filters and Energy Harvesting Applications. Appl. Sci. 2023, 13, 8854. [Google Scholar] [CrossRef]
  17. Wang, J.; Chen, A.; Li, P.; Zhang, S. Magnetoelectric Memory Based on Ferromagnetic/Ferroelectric Multiferroic Heterostructure. Materials 2021, 14, 4623. [Google Scholar] [CrossRef]
  18. Li, F.; Wu, J.; Liu, S.; Gao, J.; Lin, B.; Mo, J.; Qiao, J.; Xu, Y.; Du, Y.; He, X.; et al. Magnetoelectric Sensor Operating in d15 Thickness-Shear Mode for High-Frequency Current Detection. Sensors 2024, 24, 2396. [Google Scholar] [CrossRef] [PubMed]
  19. Leung, C.M.; Zhuang, X.; Friedrichs, D.; Li, J.; Erickson, R.W.; Laletin, V.; Popov, M.; Srinivasan, G.; Viehland, D. Highly efficient solid state magnetoelectric gyrators. Appl. Phys. Lett. 2017, 111, 122904. [Google Scholar] [CrossRef]
  20. Saveliev, D.; Chashin, D.; Fetisov, L.; Shamonin, M.; Fetisov, Y. Ceramic-heterostructure based magnetoelectric voltage transformer with an adjustable transformation ratio. Materials 2020, 13, 3981. [Google Scholar] [CrossRef] [PubMed]
  21. Bichurin, M.; Sokolov, O.; Ivanov, S.; Ivasheva, E.; Leontiev, V.; Lobekin, V.; Semenov, G. Modeling the Composites for Magnetoelectric Microwave Devices. Sensors 2023, 23, 1780. [Google Scholar] [CrossRef]
  22. Costa, C.M.; Cardoso, V.F.; Martins, P.; Correia, D.M.; Gonçalves, R.; Costa, P.; Correia, V.; Ribeiro, C.; Fernandes, M.M.; Martins, P.M.; et al. Smart and multifunctional materials based on electroactive poly (vinylidene fluoride): Recent advances and opportunities in sensors, actuators, energy, environmental, and biomedical applications. Chem. Rev. 2023, 123, 11392–11487. [Google Scholar] [CrossRef] [PubMed]
  23. Pan, D.A.; Zhang, S.G.; Volinsky, A.A.; Qiao, L.J. Shape and size effects on layered Ni/PZT/Ni composites magnetoelectric performance. J. Phys. D Appl. Phys. 2008, 41, 172003. [Google Scholar] [CrossRef]
  24. Chen, L.; Wang, Y. The effects of the soft magnetic alloys’ material characteristics on resonant magnetoelectric coupling for magnetostrictive/piezoelectric composites. Smart Mater. Struct. 2019, 28, 045003. [Google Scholar] [CrossRef]
  25. Wang, Y.J.; Gray, D.; Berry, D.; Li, M.H.; Gao, J.Q.; Li, J.F.; Viehland, D. Influence of interfacial bonding condition on magnetoelectric properties in piezofiber/Metglas heterostructures. J. Alloys Compd. 2012, 513, 242–244. [Google Scholar] [CrossRef]
  26. Dong, S.X.; Li, J.F.; Viehland, D. Longitudinal and transverse magnetoelectric voltage coefficients of magnetostrictive/piezoelectric laminate composite: Theory. IEEE Trans. Ultrason. Ferroelectr. 2003, 50, 1253–1261. [Google Scholar] [CrossRef]
  27. Loyau, V.; Morin, V.; Chaplier, G.; Lobue, M.; Mazaleyrat, F. Magnetoelectric effect in layered ferrite/PZT composites. Study of the demagnetizing effect on the magnetoelectric behaviour. J. Appl. Phys. 2015, 117, 184102. [Google Scholar] [CrossRef]
  28. Ivasheva, E.E.; Leontiev, V.S.; Bichurin, M.I.; Koledov, V.V. Application of Heat Treatment to Optimize the Magnetostrictive Component of a Magnetoelectric Composite. J. Commun. Technol. Electron. 2022, 68, 451–453. [Google Scholar] [CrossRef]
  29. Silva, M.P.; Martins, P.; Lasheras, A.; Gutiérrez, J.; Barandiarán, J.M.; Lanceros-Mendez, S. Size effects on the magnetoelectric response on PVDF/Vitrovac 4040 laminate composites. J. Magn. Magn. Mater. 2015, 377, 29–33. [Google Scholar] [CrossRef]
  30. Liu, S.; Liao, S.; Zou, H.; Qin, B.; Deng, L. Transition-Layer Implantation for Improving Magnetoelectric Response in Co-fired Laminated Composite. Magnetochemistry 2023, 9, 50. [Google Scholar] [CrossRef]
  31. Saengow, T.; Silapunt, R. Geometry–Dependent Magnetoelectric and Exchange Bias Effects of the Nano L–T Mode Bar Structure Magnetoelectric Sensor. Micromachines 2023, 14, 360. [Google Scholar] [CrossRef]
  32. Sun, Y.; Zhang, X.; Wu, S.; Jiang, N.; Zhuang, X.; Yan, B.; Zhang, F.; Dolabdjian, C.; Fang, G. Resonant Magnetoelectric Coupling of Fe-Si-B/Pb(Zr,Ti)O3 Laminated Composites with Surface Crystalline Layers. Sensors 2023, 23, 9622. [Google Scholar] [CrossRef] [PubMed]
  33. Chen, L.; Li, P.; Wen, Y.M.; Zhu, Y. Note: High sensitivity self-bias magnetoelectric sensor with two different magnetostrictive materials. Rev. Sci. Instrum. 2013, 84, 066101. [Google Scholar] [CrossRef] [PubMed]
  34. Chen, L.; Li, P.; Wen, Y.M.; Zhu, Y. Large self-biased effect and dual-peak magnetoelectric effect in different three-phase magnetostrictive/piezoelectric composites. J. Alloys Compd. 2014, 606, 15–20. [Google Scholar] [CrossRef]
  35. Chen, L.; Wang, Y. Dynamic Magneto-mechanical Behavior of Magnetization-graded Ferromagnetic Materials. J. Magn. 2014, 19, 215–220. [Google Scholar] [CrossRef]
  36. Dong, S.; Zhai, J.Y. Equivalent circuit method for static and dynamic analysis of magnetoelectric laminated composites. Chin. Sci. Bull. 2008, 53, 2113–2123. [Google Scholar] [CrossRef]
  37. Guo, M.; Dong, S. A Resonance-Bending Mode Magnetoelectric Coupling Equivalent Circuit. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2009, 56, 2578–2586. [Google Scholar]
  38. Bichurin, M.; Sokolov, O.; Ivanov, S.; Ivasheva, E.; Leontiev, V.; Lobekin, V.; Semenov, G. Modeling the Magnetoelectric Composites in a Wide Frequency Range. Materials 2023, 16, 5813. [Google Scholar] [CrossRef]
  39. Burdin, D.A.; Chashin, D.V.; Ekonomov, N.A.; Fetisov, L.Y.; Preobrazhensky, V.L.; Fetisov, Y.K. Low-Frequency Resonant Magnetoelectric Effects in Layered Heterostructures Antiferromagnet-Piezoelectric. Sensors 2023, 23, 5901. [Google Scholar] [CrossRef]
  40. Yang, F.; Wen, Y.M.; Li, P.; Zheng, M.; Bian, L.X. Resonant magnetoelectric response of magnetostrictive/piezoelectric laminate composite in consideration of losses. Sens. Actuators A Phys. 2008, 141, 129–135. [Google Scholar] [CrossRef]
  41. Sudakar, C.; Naik, R.; Lawes, G.; Mantese, J.V.; Micheli, A.L.; Srinivasan, G.; Alpay, S.P. Internal magnetostatic potentials of magnetization-graded ferromagnetic materials. Appl. Phys. Lett. 2007, 90, 062502. [Google Scholar] [CrossRef]
  42. Yang, S.C.; Park, C.S.; Cho, K.H.; Priya, S. Self-biased magnetoelectric response in three-phase laminates. J. Appl. Phys. 2010, 108, 093706. [Google Scholar] [CrossRef]
Jcs 09 00693 g001
Figure 1. Schematic illustration of (a) the asymmetric structure MP composite with FeSiB, (b) the symmetric structure MPM composite with FeSiB. The definition relates to local coordinates in (c) magnetostrictive layers and (d) the piezoelectric layer, respectively.
Figure 1. Schematic illustration of (a) the asymmetric structure MP composite with FeSiB, (b) the symmetric structure MPM composite with FeSiB. The definition relates to local coordinates in (c) magnetostrictive layers and (d) the piezoelectric layer, respectively.
Jcs 09 00693 g001
Jcs 09 00693 g002
Figure 2. The measured magnetic hysteresis loops of FeSiB and FeNi.
Figure 2. The measured magnetic hysteresis loops of FeSiB and FeNi.
Jcs 09 00693 g002
Jcs 09 00693 g003
Figure 3. The piezomagnetic coefficients q33 as functions of the dc magnetic field Hdc for FeSiB and FeNi.
Figure 3. The piezomagnetic coefficients q33 as functions of the dc magnetic field Hdc for FeSiB and FeNi.
Jcs 09 00693 g003
Jcs 09 00693 g004
Figure 4. ME voltage coefficients for asymmetric and symmetric structure laminate composites without FeSiB versus Hdc ranging from −700 Oe to 700 Oe. The insets show ME voltage coefficients around the resonance frequency for asymmetric and symmetric structure composites.
Figure 4. ME voltage coefficients for asymmetric and symmetric structure laminate composites without FeSiB versus Hdc ranging from −700 Oe to 700 Oe. The insets show ME voltage coefficients around the resonance frequency for asymmetric and symmetric structure composites.
Jcs 09 00693 g004
Jcs 09 00693 g005
Figure 5. The ME voltage coefficients as a function of the dc bias magnetic field for the asymmetric structure MP composite, with the thickness of FeSiB ranging from 0 to 100 μm.
Figure 5. The ME voltage coefficients as a function of the dc bias magnetic field for the asymmetric structure MP composite, with the thickness of FeSiB ranging from 0 to 100 μm.
Jcs 09 00693 g005
Jcs 09 00693 g006
Figure 6. The ME voltage coefficients as a function of the dc bias magnetic field for the symmetric structure MPM composite, with the thickness of FeSiB ranging from 0 to 100 μm.
Figure 6. The ME voltage coefficients as a function of the dc bias magnetic field for the symmetric structure MPM composite, with the thickness of FeSiB ranging from 0 to 100 μm.
Jcs 09 00693 g006
Jcs 09 00693 g007
Figure 7. (a) Maximum ME voltage coefficient. (b) Optimal DC magnetic field. (c) Zero-bias ME voltage coefficient. (d) ME coercive field as a function of FeSiB ribbon thickness for asymmetric structure MP laminate composite.
Figure 7. (a) Maximum ME voltage coefficient. (b) Optimal DC magnetic field. (c) Zero-bias ME voltage coefficient. (d) ME coercive field as a function of FeSiB ribbon thickness for asymmetric structure MP laminate composite.
Jcs 09 00693 g007
Jcs 09 00693 g008
Figure 8. (a) Maximum ME voltage coefficient. (b) Optimal DC magnetic field. (c) Zero-bias ME voltage coefficient. (d) ME coercive field as a function of FeSiB ribbon thickness for symmetric structure MPM laminate composite.
Figure 8. (a) Maximum ME voltage coefficient. (b) Optimal DC magnetic field. (c) Zero-bias ME voltage coefficient. (d) ME coercive field as a function of FeSiB ribbon thickness for symmetric structure MPM laminate composite.
Jcs 09 00693 g008
Table 1. The material characteristics of FeNi alloy, PZT8, and FeSiB.
Table 1. The material characteristics of FeNi alloy, PZT8, and FeSiB.
Material s 33 H or s 11 E (×10−12 m2/N)ρp, ρm, ρf (kg/m3)λs (ppm)μrQm
PZT8 a11.17700 1000
FeNi alloy b40800011309000
FeSiB c9.0972502740,0001000
a Cited from Electronics Technology Group Corporation No. 26 Research Institute, Chongqing, China. b Cited from Chongqing Instrument Materials Research Institute, Chongqing, China. c Cited from Foshan Huaxin Microlite Metal Co., Ltd., Foshan, China.
Table 2. West System 105/206 resin/hardener key parameters d.
Table 2. West System 105/206 resin/hardener key parameters d.
Mix RatioCure TimeViscosityApplications
5:124 h full cure,
7 d max strength at 25 °C		Low-viscosity liquid,
cures to high-strength solid		Structural bonding,
fiberglass reinforcement
d Cited from Gougeon Brothers, Inc., Bay City, MI, USA.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Chen, L.; Cheng, Y.; Qin, F. Influence of FeSiB Layer Thickness on Magnetoelectric Response of Asymmetric and Symmetric Structures of Magnetostrictive/Piezoelectric Composites. J. Compos. Sci. 2025, 9, 693. https://doi.org/10.3390/jcs9120693

AMA Style

Chen L, Cheng Y, Qin F. Influence of FeSiB Layer Thickness on Magnetoelectric Response of Asymmetric and Symmetric Structures of Magnetostrictive/Piezoelectric Composites. Journal of Composites Science. 2025; 9(12):693. https://doi.org/10.3390/jcs9120693

Chicago/Turabian Style

Chen, Lei, Yingjie Cheng, and Fujian Qin. 2025. "Influence of FeSiB Layer Thickness on Magnetoelectric Response of Asymmetric and Symmetric Structures of Magnetostrictive/Piezoelectric Composites" Journal of Composites Science 9, no. 12: 693. https://doi.org/10.3390/jcs9120693

APA Style

Chen, L., Cheng, Y., & Qin, F. (2025). Influence of FeSiB Layer Thickness on Magnetoelectric Response of Asymmetric and Symmetric Structures of Magnetostrictive/Piezoelectric Composites. Journal of Composites Science, 9(12), 693. https://doi.org/10.3390/jcs9120693

Article Metrics

Back to TopTop