Previous Article in Journal
Study of the Stress–Strain State of the Structure of the GP-50 Support Bushing Manufactured by 3D Printing from PLA Plastic
Previous Article in Special Issue
Influential Microstructural Descriptors for Predicting Mechanical Properties of Fiber-Reinforced Composites
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
J. Compos. Sci.
Volume 9
Issue 8
10.3390/jcs9080409
jcs-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Study of Mechanical and Wear Properties of Fabricated Tri-Axial Glass Composites

by
Raghu Somanna
1,
Rudresh Bekkalale Madegowda
2,
Rakesh Mahesh Bilwa
3,
Prashanth Malligere Vishveshwaraiah
4,
Prema Nisana Siddegowda
4,
Sandeep Bagrae
5,
Madhukar Beejaganahalli Sangameshwara
6,
Girish Hunaganahalli Nagaraju
7 and
Madhusudan Puttaswamy
8,*
1
Maharaja Institute of Technology, Thandavapura, Mysuru 571302, India
2
Department of Mechanical Engineering, Government Engineering College, Krishnarajpet, Mandya 571426, India
3
Department of Robotics & Artificial Intelligence, Dayananda Sagar College of Engineering, Bangalore 560111, India
4
Department of Information Science and Engineering, Vidyavardhaka College of Engineering, Mysuru 570002, India
5
Department of Mechanical Engineering, Vidya Vikas Institute of Engineering and Technology, Mysuru 570028, India
6
Department of Chemistry, JSS Science and Technology University, Mysuru 570006, India
7
Department of Studies in Earth Science, University of Mysore, Mysuru 570006, India
8
Department of Civil and Environmental Engineering, Environmental Materials Laboratory, Hanyang University, 222 Wangsimni-ro, Seongdong-gu, Seoul 04763, Republic of Korea
*
Author to whom correspondence should be addressed.
J. Compos. Sci. 2025, 9(8), 409; https://doi.org/10.3390/jcs9080409 (registering DOI)
Submission received: 10 July 2025 / Revised: 29 July 2025 / Accepted: 30 July 2025 / Published: 1 August 2025
(This article belongs to the Special Issue Editorial Board Members' Collection Series: Mechanical Analysis of Composite Materials)
Browse Figures
Versions Notes

Abstract

This study investigates the mechanical, morphological, and wear properties of SiO2-filled tri-axial warp-knitted (TWK) glass fiber-reinforced vinyl ester matrix composites, with a focus on void fraction, tensile, flexural, hardness, and wear behavior. Adding SiO2 fillers reduced void fractions, enhancing composite strength, with values ranging from 1.63% to 5.31%. Tensile tests revealed that composites with 5 wt% SiO2 (GV1) exhibited superior tensile strength, Young’s modulus, and elongation due to enhanced fiber–matrix interaction. Conversely, composites with 10 wt% SiO2 (GV2) showed decreased tensile performance, indicating increased brittleness. Flexural tests demonstrated that GV1 outperformed GV2, showcasing higher flexural strength, elastic modulus, and deflection, reflecting improved load-bearing capacity at optimal filler content. Shore D hardness tests confirmed that GV1 had the highest hardness among the specimens. SEM analysis revealed wear behavior under various loads and sliding distances. GV1 exhibited minimal wear loss at lower loads and distances, while higher loads caused significant matrix detachment and fiber damage. These findings highlight the importance of optimizing SiO2 filler content to enhance epoxy composites’ mechanical and tribological performance.

1. Introduction

The tri–axial warp-knitted E-glass fabric-reinforced vinyl ester composites are advanced materials engineered to deliver higher performance by combining strength, durability, and lightweight properties [1,2,3,4]. Consequently, their applications are expanding across various sectors, including construction, transportation, and aerospace [5,6,7]. Among textile structures, weft-knitted fabrics [8,9,10] exhibit the highest deformability, making them particularly suitable for manufacturing complex composite structures [11,12,13,14]. Furthermore, studies on weft-knitted reinforced composites have demonstrated their notable energy absorption capabilities [15,16] and post-damage performance [17,18], which render them a promising alternative for energy-absorbing structures, especially in the automotive industry [19,20]. In this regard, Ramakrishna et al. [19,21,22] investigated the mechanical performance of weft-knitted reinforced composites under varied loading conditions.
Biaxial and tri–axial fabrics show enhanced mechanical properties such as tensile and flexural strength, with their unique structural configurations. These composites find extensive applications in critical sectors, including medical devices, aerospace systems, rocket propulsion, and transportation industries [23,24,25]. Tri–axial fabrics are specialized textiles with three threads arranged in an equilateral triangular pattern, resulting in a geometrically stable structure. Unlike rectangular weaves, the triangular arrangement enhances stability, uniformity, and strength. The locked intersections within the weave ensure uniform load distribution and balanced strength in all directions, making these fabrics ideal for applications requiring high dimensional stability and multi-directional strength [26]. In the basic tri–axial fabric, two sets of wasp yarns are interwoven at a 45° angle with the weft with each other. The warp yarns move from selvedge to selvedge at a 45° angle to the vertical direction, and at the selvedge, a wasp yarn rotates 90° before continuing to the opposite side, ensuring a firm edge [27]. Compared to conventional fabric designs, tri–axial structures are unmatched in their fundamental stability, featuring higher porosity and open area. These fabrics are often referred to as quasi-isotropic because the yarns interlace at angles of 0°, 45°, and −45°, providing a modulus of elasticity and strength that are nearly uniform in all directions [28,29,30,31]. Triaxial fabrics offer several advantages over biaxial fabrics, including isotropy, shear resistance, and low density. Their primary advantages, however, lie in their efficient use of material, which requires significantly less fiber to achieve comparable performance [32,33,34].
Due to their excellent mechanical properties—such as a modulus of elasticity and strength, superior integral performance and dimensional stability, low thermal expansion, and strong corrosion resistance—woven fabric materials have garnered significant attention in recent years [35,36]. The mechanical behavior of woven structures is largely influenced by the arrangement and development of the yarns.
The tensile properties of textiles are influenced by the number of strands per centimeter [37,38], as well as the interlacing angle, which significantly affects a fabric’s mechanical characteristics [39,40,41]. Woven fabric composites are engineered materials consisting of one or more fabric layers embedded in a resin system [42,43]. Textile preforms may feature knitted, braided, or woven structures [44,45,46,47], and the mechanical properties of textile composites are determined by factors such as fiber type, matrix characteristics, and fabric architecture [45,46,47,48,49,50,51,52,53,54]. Fabricating woven composites is a straightforward method for producing complex components, offering significant labor savings compared to metal matrix composites. Additionally, the process enhances the beneficial mechanical properties of woven fabrics, such as a modulus of elasticity, strength, and fracture resistance [55,56,57]. Key factors influencing the mechanical properties of composites include yarn size, orientation, volume fraction, and interlacing pattern [58]. The mechanical behavior of composites can be categorized into linear and non-linear features [59,60,61]. Fabric composites have a wide range of applications in energy absorption (e.g., helmets), aerospace and defense (e.g., engine inlet cowlings, fuselage sections, rotor blade spars, and fuel pods), and automotive and structural applications (e.g., battery trays, seat structures, front-end modulus, and load floors) [62,63]. The primary objective of this research is to investigate the mechanical properties and behavior of tri–axial glass fabrics, with a focus on the fabrication of composite materials using tri–axial wasp-knit E-glass fabric, particularly triaxial Type I fabrics (−45°, 90°, and +45°).

2. Materials and Methods

Tri-axial warp-knit E-glass fabric (ETLX 1169) is a reinforcing material known for its excellent mechanical properties and stability. The Tri-axial fabric with fabric width of 1.27 m is widely used in industries such as automotive and mire industry. The yarn roving is distributed as follows: 0° directions (567 g/m2), +45° direction (301 g/m2), and −45° direction (301 g/m2). Alongside this reinforcing component, the silicon dioxide (SiO2) as a filler (Loba Chemie Pvt. Ltd., Mumbai, India) with a particle size range of 40 to 150 mesh was first dried at 100 °C for 1 h to eliminate moisture. It was then gradually added to the vinyl ester resin (Polyflex GR 200-60) under continuous mechanical stirring using a high-shear overhead stirrer. The mixture was stirred at 500 rpm for 10 min to achieve uniform particle dispersion. The shear rate and mixing time were selected based on literature-recommended protocols for achieving homogeneity in particulate-filled thermosetting matrices without inducing excessive air entrapment or resin degradation [64,65]. No sedimentation or agglomeration was observed during or after mixing. The filled resin was immediately used for hand lay-up application to prevent settling. The mechanical and physical properties of E-glass and matrix are illustrated in Supporting Information Table S1.
The hand lay-up fabrication process began by cutting the glass fabric into the desired dimensions, using three layers per composite plate. The fabric weight was used to determine the required resin quantity. Granite slabs were cleaned with acetone, and a release film, along with a releasing agent, was applied to the bottom slab. The resin was mixed with curing additives (2 mL of curing agent per 100 mL of vinyl ester) and stirred thoroughly. The first resin coat was applied over the release film, followed by placement and compacting of the first fabric layer to eliminate air bubbles. Subsequent layers of resin and fabric were alternately applied, with the process concluding with a release film on the topmost layer. The assembly was cured under a top slab for 24 h, removed from the mold, and post-cured at 80 °C for one hour. This process was repeated for GV composites with SiO2 filler additions of 0%, 5%, and 10%. The resulting composite consisted of 40% resin and 60% reinforcement in the GV sample, 35% resin and 60% reinforcement in the GV1 sample, and 30% resin and 60% reinforcement in the GV2 sample. A summary of the varying compositions of vinyl ester resin, E-glass fiber, and SiO2 filler in the prepared composites is outlined in Table 1 for quick comparison. A clear tabular representation supports reproducibility, facilitates direct comparison among formulations, and aids in statistical analysis and performance correlation [66].
Further, a schematic flow diagram illustrating the step-by-step process of composite fabrication and subsequent mechanical and wear testing is illustrated in Figure 1.
Figure 2a illustrates the tensile setup, and Figure 2b shows the bending test setup used for evaluating the composite specimens. The additional schematic diagram of hand layup steps and specimen photos are presented in the Supporting Information (Supporting Information Figures S1 and S2).
The characterization of composites was conducted to evaluate density and void fraction, tensile properties (ASTM D-638), flexural properties (ASTM-D7264), and hardness (ASTM D-2240) using a Shore D hardness tester. Mechanical testing was conducted using a J. J. Lloyd universal testing machine. Additionally, the Taguchi experimental design method was employed, and surface morphology was analyzed.

3. Results

3.1. Surface Morphology

The worn surface of the composites was observed using SEM to evaluate the effect of the increase in filler, applied load, and abrading distance on the worn surface morphology, as shown in Figure 3. Images Figure 3a–c display the worn surfaces of GV, GV1, and GV2 composites under a 25 N load and 300 m abrading distance. At this load and distance, only partial matrix removal is observed, with minimal fiber damage. Most fibers remain embedded within the matrix and filler material. The 5% SiO2-filled composite (GV1) exhibits the least wear loss, as SiO2 reduces matrix wear and protects the fibers (Figure 3b). In contrast, Figure 3c–e for the GV1 sample illustrates the composite’s surface under a 45 N load and a 900 m abrading distance. Under these severe testing conditions, significant fiber damage and matrix detachment are evident. The intensified abrasive action results in matrix plowing and cutting by abrasive particles, which leads to microcracking, fiber breaking, and material pulverization. The presence of pulverized debris further indicates a high degree of wear severity. Under these conditions, continuous abrasive action further damages fibers and removes matrix material, resulting in increased wear volume and debris generation.

3.2. Density and Void Fraction of Composite

The theoretical density of composite materials, expressed in terms of weight fraction, can be calculated using Equation (1), as proposed by Agarwal and Broutman [64].
ρ c t = 1 W f ρ f + W m ρ m + W p ρ p
where Wf = weight fraction of fabric, Wm = weight fraction of matrix, Wp = weight fraction of filler material, ρf = density of fabric, ρm = density of matrix, and ρp = density of filler material.
The actual density (ρce) of the composite can be determined experimentally using the Archimedean principle. The volume fraction of voids (Vct) in the composites is calculated using Equation (2):
V c t =   ρ c t −   ρ c e ρ c t
Table 2 and Figure 4 present the theoretical and measured densities alongside the corresponding void volume fractions. The results show that both the theoretical and experimental density values increase as SiO2 content rises, while the void fraction percentage decreases. This suggests that higher SiO2 content enhances material compaction and reduces the number of voids in the composite. According to Thomason et al. [64] and Lee and Jang [65], the physical and mechanical properties of composites deteriorate when the fiber or filler content exceeds the optimal level. Higher void content negatively impacts composite performance, reducing fatigue resistance, increasing water penetration, and affecting weathering resistance. Void content serves as a key indicator of composite quality, with fewer void fractions being desirable. However, voids are difficult to eliminate entirely, particularly in composites fabricated using the hand-lay-up process.

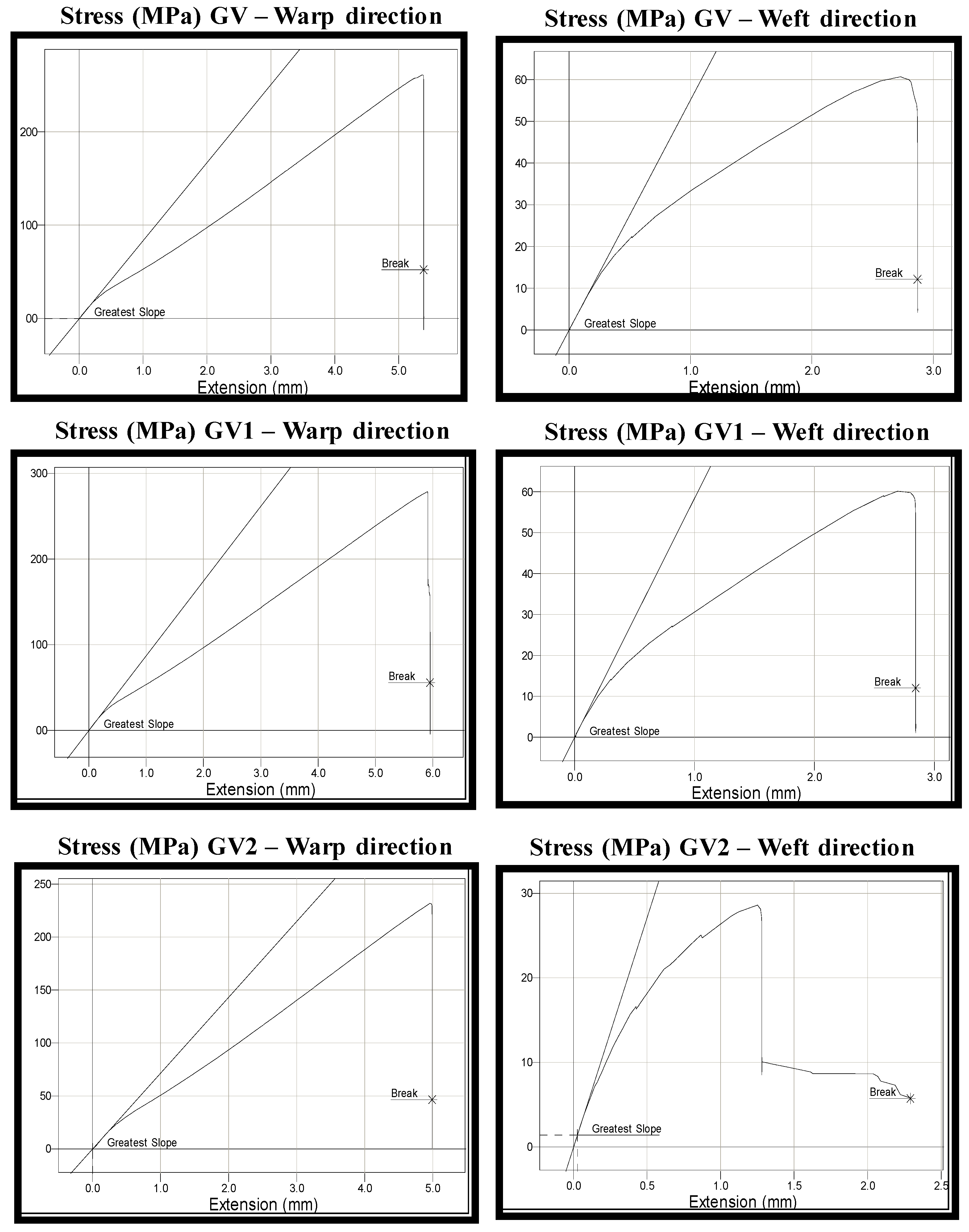
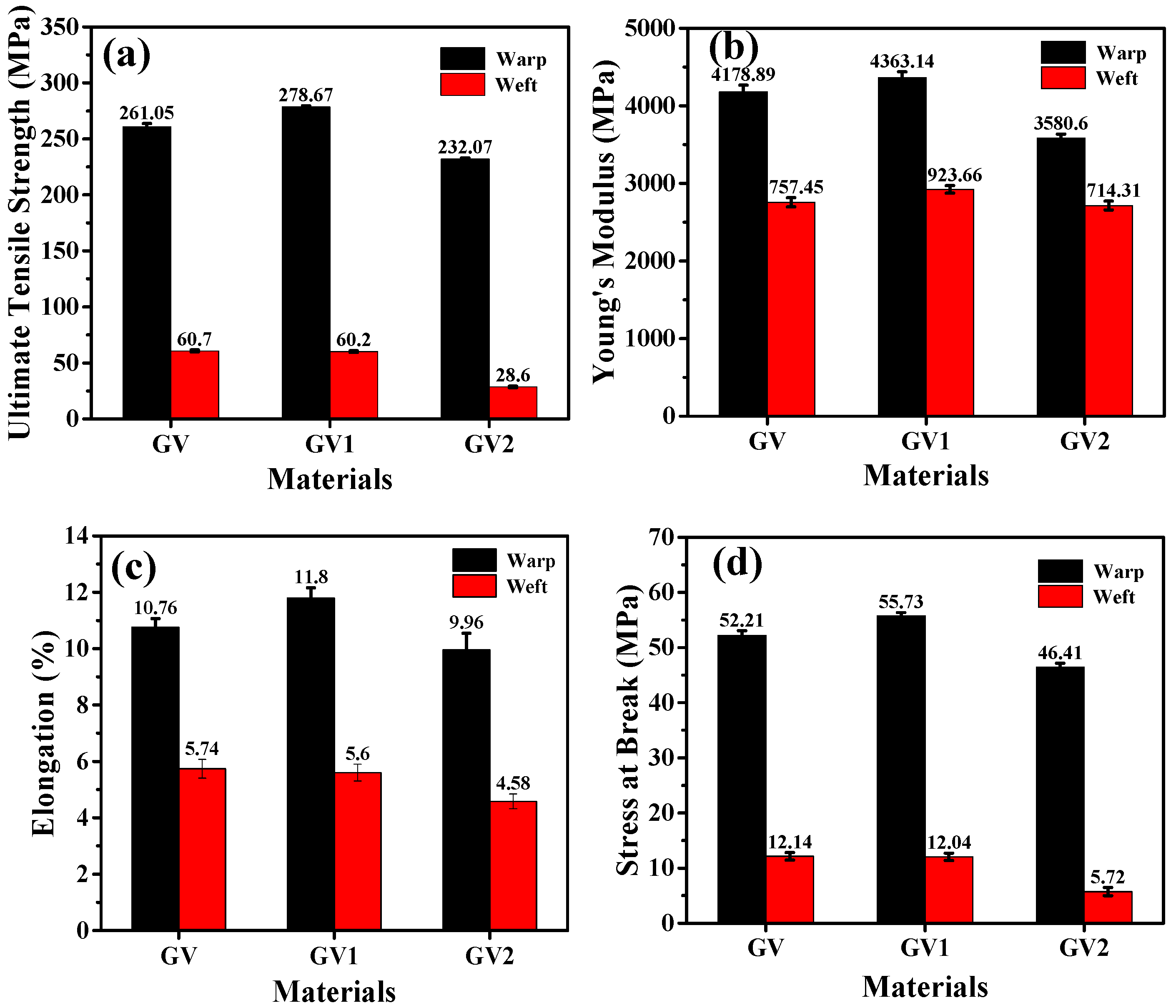
3.3. Tensile Test

Tensile testing is a critical method for evaluating the mechanical properties of composites, such as strength, modulus of elasticity, and elongation, which are essential for structural applications in aerospace and automotive industries. The tensile tests were performed according to ASTM D638 using Type I dog-bone specimens with dimensions of 165 × 19 mm × 3 mm and a gauge length of 50 mm. Each composite group (GV, GV1, and GV2) specimen is tested with three replicates (n = 3). The mean values of tensile strength, modulus of elasticity, and elongation at break were calculated and are reported. The tests were conducted on a J.J. Lloyd universal testing machine at a crosshead speed of 5 mm/min using engineering stress–strain data. The mechanical properties, including tensile strength, Young’s modulus, and elongation, are detailed in Table 3, which highlights the performance of composites with various fabric layer combinations.
The stress versus extension graph for the GV, GV1, and GV2 composites reveals their anisotropic tensile properties (Figure 5 and Figure 6a). In the warp direction of sample GV, the composite achieves a peak tensile strength of 261.05 MPa, attributed to the effective alignment of fibers capable of withstanding higher loads. Conversely, the weft direction of GV exhibits significantly lower tensile strength at 60.70 MPa, reflecting weaker load-bearing capacity due to weaker fiber alignment. After reaching the peak load in both directions, the stress drops sharply by 20%, indicating material failure. Similarly, in the warp direction of sample GV1, the composite demonstrates a peak tensile strength of 278.67 MPa, reflecting the efficient alignment of fibers. In contrast, the weft direction shows a lower tensile strength of 60.20 MPa due to weaker fiber alignment. Both directions exhibit a sharp 20% drop in load following the peak, signifying material failure. For example, in GV2, the composite reaches a peak tensile strength of 232.07 MPa in the warp direction, indicating effective fiber alignment and load-bearing capacity. However, the weft direction records a much lower tensile strength of 28.60 MPa, attributed to weaker fiber orientation. As with the other samples, a sharp drop to 20% of the peak load occurs in both directions after reaching the maximum stress, indicating material failure. Overall, the composites exhibit superior tensile strength in the warp direction compared to the weft direction, highlighting their anisotropic behavior.
The Young’s modulus vs. materials graph (Figure 6b) compares the modulus of elasticity of three composite samples: GV, GV1, and GV2 in both warp and weft directions. For GV, the warp direction shows a Young’s modulus of 4178.89 MPa, and the weft direction has a modulus of 757.45 MPa, indicating a higher modulus of elasticity in the warp direction. GV1 exhibits a slight improvement in warp modulus of elasticity of 4363.14 MPa, with a weft modulus of 2923.66 MPa. GV2 shows a decrease in modulus of elasticity with 3580.6 MPa, and the weft modulus is 2714.31 MPa. This data highlights the directional dependency of the Young’s modulus, with warp direction consistently exhibiting greater modulus of elasticity in all samples.
The elongation vs. materials graph (Figure 6c) compares the strain (elongation at the break) in both warp and weft directions. For GV, the warp direction shows an elongation of 10.76%, while the weft direction exhibits 5.74%, indicating a greater strain capacity in the warp direction. GV1 demonstrates an elongation of 11.8% in the warp direction and 5.6% in the weft, demonstrating improved flexibility compared to GV. GV2, however, exhibits the lowest elongation values, with 9.96% in the warp and 4.58% in the weft, indicating reduced flexibility and higher brittleness relative to the other samples.
The stress at break vs. materials graph (Figure 6d) compares the stress at failure for three composite samples in both warp and weft directions. For GV, the warp direction shows stress at a break of 52.21 MPa, while the weft direction is much lower at 12.14 MPa, indicating greater strength in the warp direction. GV1 has a slightly higher stress at a break with 55.73 MPa in the warp and 12.04 MPa in the weft. GV2 exhibits the lowest stress at break, with 46.41 MPa in the warp and 5.72 MPa in the weft, suggesting reduced strength.
Tensile test results in warp and weft directions for unfilled and silicon dioxide-filled E-glass–vinyl ester composites are summarized in Table 3, with behavior curves in Figure 5 and tensile parameter plots in Figure 6. The mechanical properties of these composites depend on the fiber–matrix interface, where stronger interfaces yield higher strength and modulus of elasticity. GV1 (5 wt% silica–filled composites) exhibited the highest tensile strength, Young’s modulus, and elongation in the warp direction, confirming that SiO2 improves the fiber–matrix interface. In contrast, GV2 composites (higher filler content) showed the lowest tensile strength, elongation, and stress at the break due to poor fiber–matrix interaction and increased brittleness.

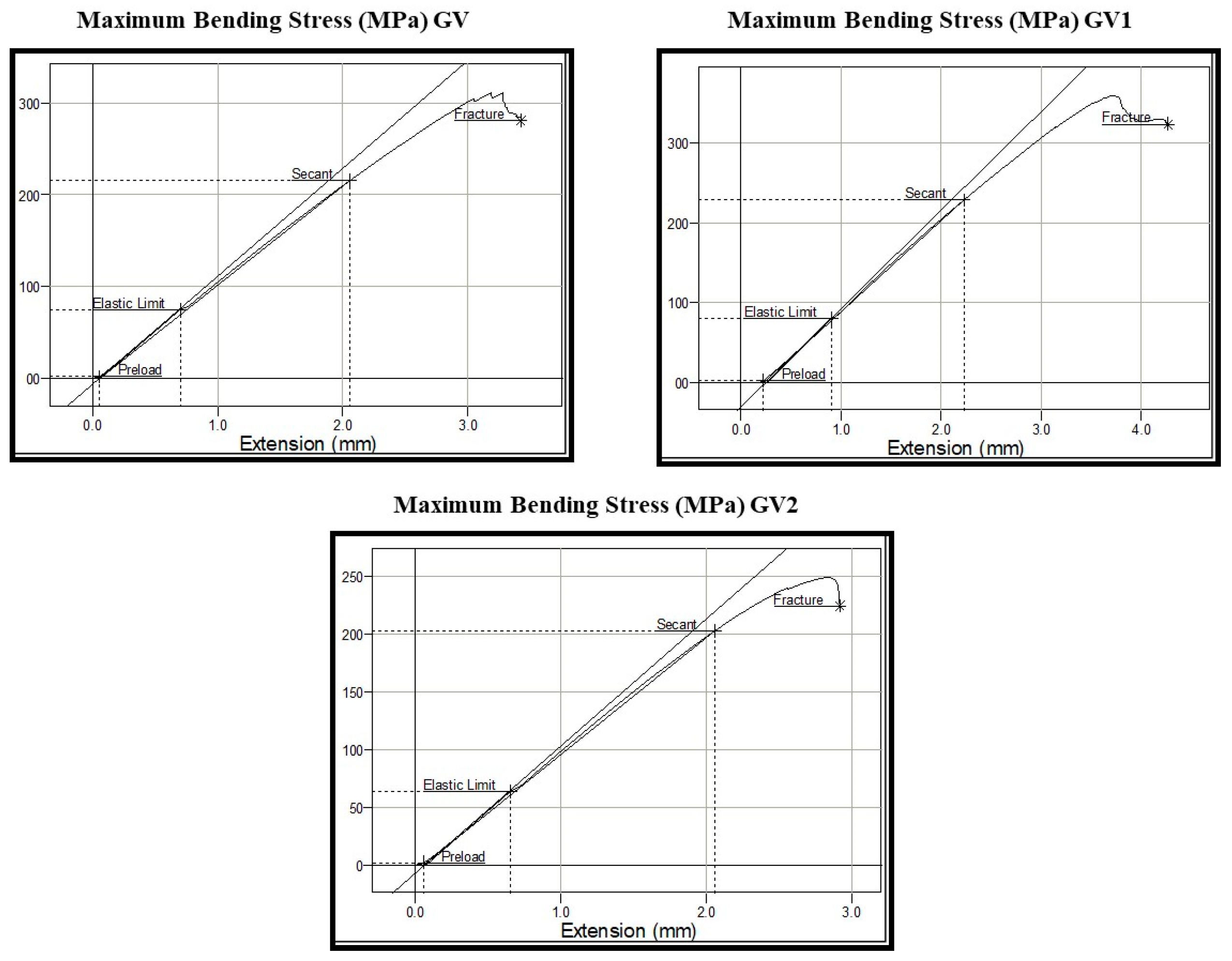
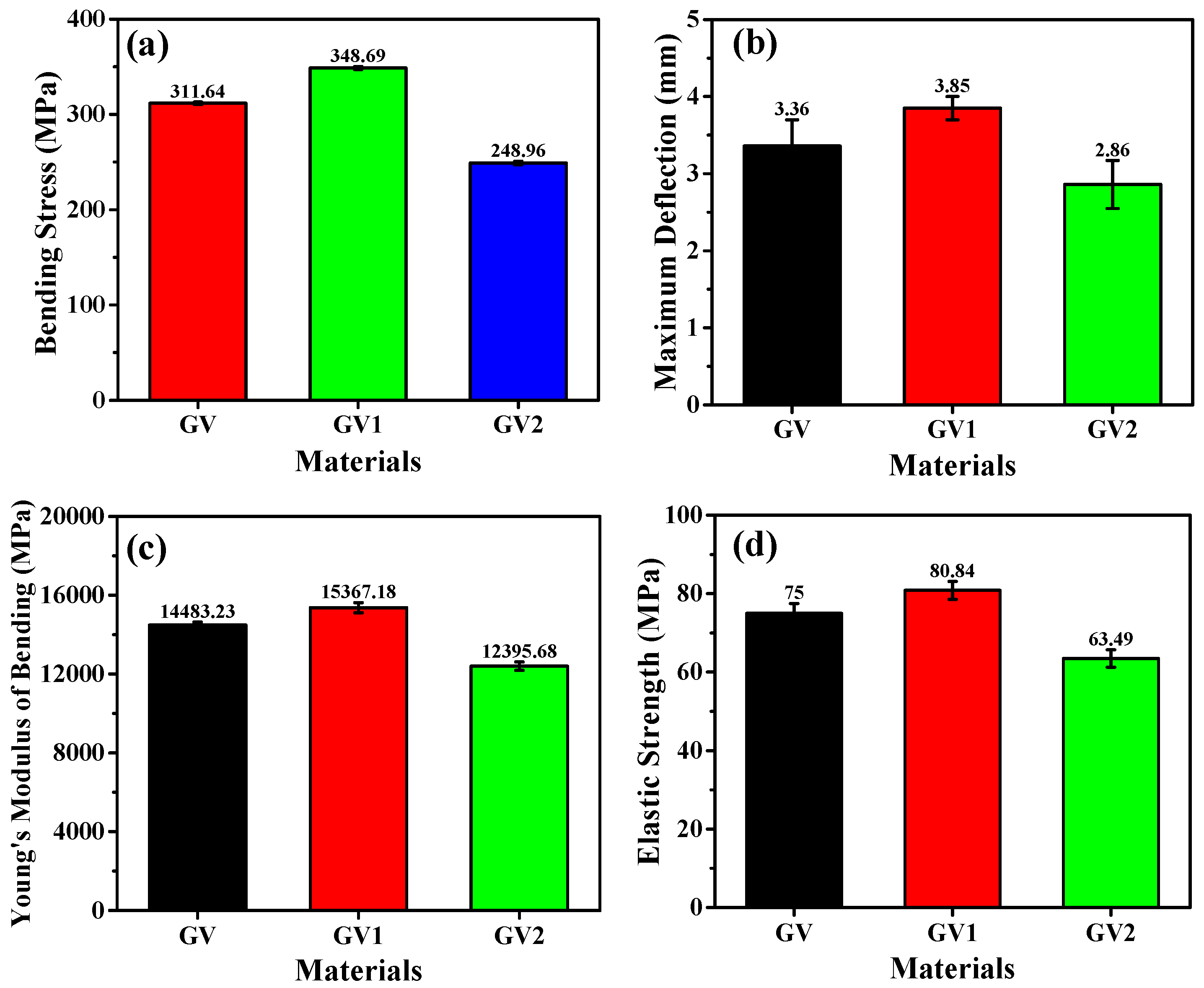
3.4. Flexural Test

In this section, the peak load-bearing capacity of each composite formulation is presented and analyzed first, concerning the reinforcement–matrix bonding and filler dispersion effect. Later, the modulus of elasticity was calculated from the initial slope of the stress–strain curve. Which links to modulus of elasticity changes to interfacial interactions and filler-induced modulus of elasticity embrittlement. Finally, the ductility of each sample is addressed about filler content and matrix plasticity, with an emphasis on how increasing filler content reduces matrix mobility and elongation. The flexural properties were evaluated using the three–point bending method following ASTM D7264. Test specimens measured were 127 mm × 12.7 mm × 3 mm, with a support span of 100 mm. A total of three specimens (n = 3) per group were tested, and the mean values of maximum flexural stress, flexural modulus, elastic strength, and deflection were reported. Testing was carried out on the same universal testing machine at a crosshead speed of 2 mm/min. The outcome of the test results is tabulated in Table 4.
The performance graph of flexurally tested materials highlights maximum bending stress versus extension, showcasing key points like preload, elastic limit, and fracture. This graph provides insights into the modulus of elasticity, deformation behavior, and ultimate flexural strength. These parameters are critical for evaluating the composite’s bending resistance and structural reliability under real-world load conditions.
The flexural strength testing graph (Figure 7 and Figure 8a) illustrates the relationship between maximum bending stress for composite samples, highlighting key phases like preload, elastic limit, secant, and fracture. The GV sample shows a maximum bending stress of 311.64 MPa, indicating good flexural resistance. GV1 demonstrates the highest performance with a maximum bending stress of 348.69 MPa, attributed to better matrix–reinforcement interaction or optimized filler content. In contrast, GV2 exhibits the lowest bending stress of 248.96 MPa, suggesting compromised structural integrity, possibly due to factors like higher void content or weaker fiber–matrix bonding.
The maximum deflection observed during the flexural testing indicates a composite’s bending ability, which depends on factors such as fiber orientation, matrix properties, and filler content. The maximum deflection v/s composite materials graph is shown in Figure 8b, highlighting the bending behavior of samples GV, GV1, and GV2. Sample GV exhibits a maximum deflection of 3.6 mm, while GV1 shows the highest deflection at 3.85 mm, indicating superior flexibility and load absorption capacity. Conversely, GV2 demonstrates the lowest deflection at 2.86 mm, reflecting a higher modulus of elasticity and reduced flexibility compared to the other samples. These variations in deflection are influenced by differences in fiber alignment, matrix composition, and filler content within the composites. Understanding the maximum deflection provides insights into the mechanical behavior and suitability of composites for structural applications.
The Young’s modulus of bending v/s composite materials graph, presented in Figure 8c, reveals variations in modulus of elasticity among samples based on the flexural test results. Sample GV1 has the highest modulus at 15,367.18 MPa, indicating superior rigidity and resistance to bending. This is followed by GV, with a modulus of 14,483.23 MPa, while GV2 demonstrates the lowest value of 12,395.68 MPa, reflecting greater flexibility. These differences arise from variations in fiber alignment, matrix composition, and filler content, highlighting the influence of material properties on bending performance.
The elastic strength v/s composite materials graph from the flexural test, shown in Figure 8d, highlights differences in stress tolerance within the elastic range. Sample GV1 exhibits the highest elastic strength at 80.84 MPa, indicating superior load-bearing capacity before permanent deformation. GV follows with an elastic strength of 75.00 MPa, while GV2 has the lowest value at 63.49 MPa, reflecting reduced elasticity. These variations are influenced by material composition, including fiber–matrix interaction and filler content, emphasizing their role in mechanical performance.
The flexure test results for unfilled and silicon dioxide-filled E-glass–vinyl ester composites are presented in Table 4. Flexural behavior curves of the composites are shown in Figure 7, while plots of various flexural parameters based on silicon dioxide content are presented in Figure 8. The results reveal that the GV1 composite (with 5wt% SiO2) exhibits a higher Young’s modulus of bending, higher elastic strength, greater flexural strength, and maximum deflection compared to other composites. This demonstrates that the addition of SiO2 improves the load-bearing capacity and bending resistance of the composite. On the other hand, the GV2 composite (with higher filler content) shows the lowest flexural strength, possibly due to a poor fiber–matrix interface. This suggests that increasing the filler content reduces flexural strength. Additionally, GV2 exhibits the lowest deflection, indicating that a higher SiO2 filler content leads to more brittle properties, thereby reducing flexibility and overall performance. These findings confirm that excess filler content negatively impacts the composite’s mechanical properties.

3.5. Shore–D Hardness Test

Hardness was measured using a Shore D durometer according to ASTM D2240, and the hardness test instrument is shown in Figure 9a. Measurements were taken at five different locations on each of the three specimens per group, and the average value was reported. The results of the Shore D hardness test for composite materials, presented in Table 5 and Figure 9b, reveal slight variations in surface hardness among the samples. Sample GV1 exhibits the highest hardness value at 74, indicating superior resistance to surface indentation. This is followed by GV, with a hardness of 71, while GV2 has a slightly higher hardness value of 72. These differences reflect the influence of material composition, particularly the matrix and filler content, on surface hardness. Higher hardness values typically correlate with improved wear resistance and durability in composite materials. The Shore D hardness test results for unfilled and silicon dioxide-filled E-glass–vinyl ester composites are presented in Table 5.

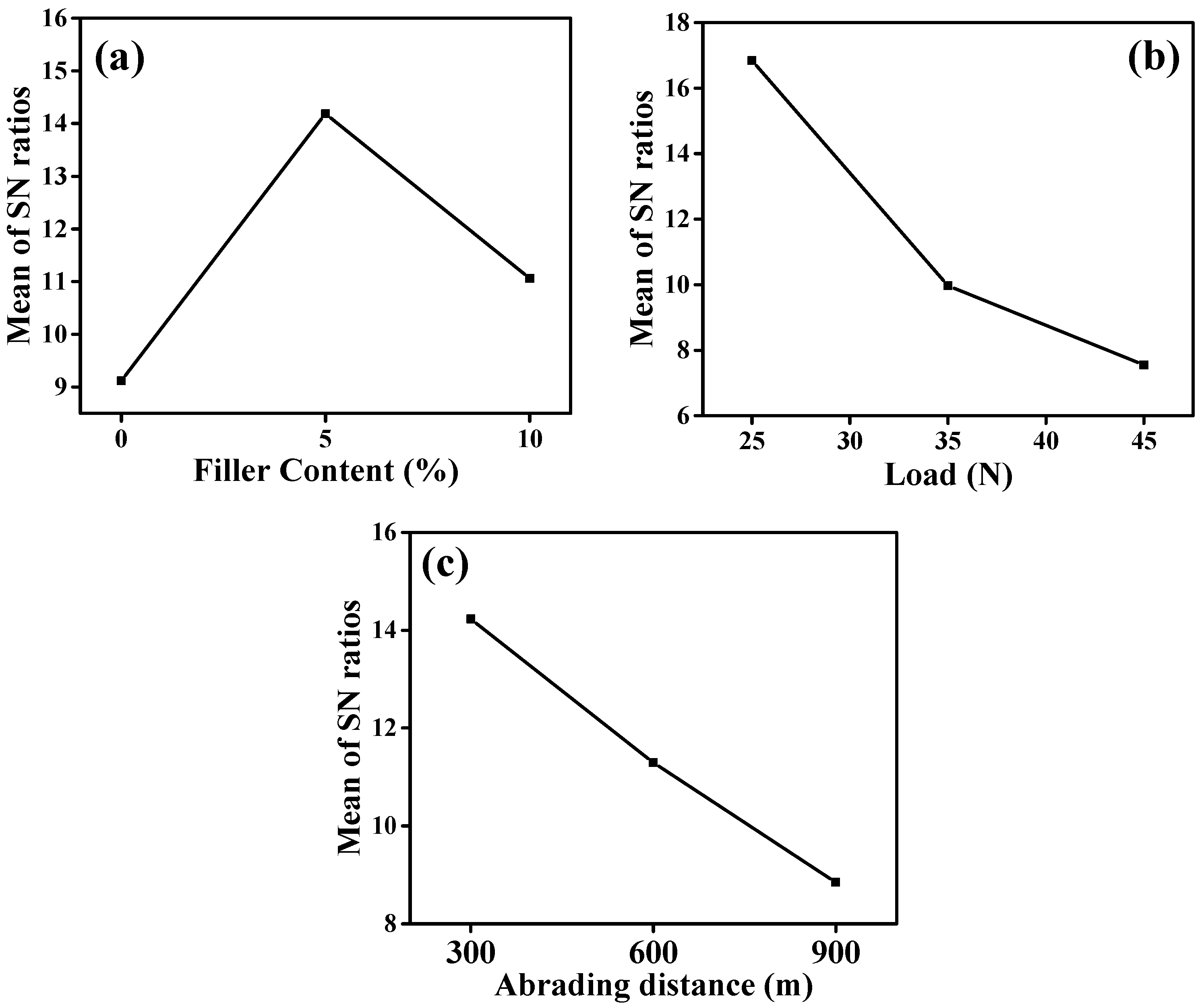
3.6. Analysis of Experimental Results by Taguchi Experimental Design

Taguchi’s experimental approach was applied to determine the dominant factors contributing to an overall reduction in the specific wear rate of silicon dioxide-filled glass fiber-reinforced epoxy composites. The wear testing followed a Taguchi L27 orthogonal array with single-run trials per condition. Each condition was uniquely defined by combinations of SiO2 filler content, applied load, and abrading distance. Weight loss and wear volume were measured for each run. Taguchi’s experimental design is summarized in Table 6.
The overall mean value for the signal-to-noise (S/N) ratio for 27 different iterations is calculated, with the minimum and maximum values of the S/N ratio being 3.9907 dB and 24.182 dB, respectively. The analysis was conducted using MINITAB 15, a widely used software for the design of experimental applications.
The minimum specific wear rate, as observed in Figure 10, shows the S/N ratio for three factors, i.e., filler content, fiber loading, and abrading distance. Table 7 represents the response table for S/N ratios under the “smaller–is–better” criterion. The data confirm that abrasive particle size has a more significant effect on the specific wear rate of SiO2-filled glass fiber-reinforced epoxy composites, followed by filler content, fiber loading, and abrading distance.
Figure 11a illustrates the interaction between filler content and load on wear volume loss. Wear volume increases with load due to matrix damage and fiber exposure, with minimum wear observed at 5% filler content. This indicates optimal mechanical properties and effective fiber–matrix–filler interaction at this filler level.
Figure 11b shows the effect of filler content and abrading distance on wear volume. As abrading distance increases, wear volume also rises, attributed to prolonged exposure to abrasive particles. Maximum wear occurs at an abrading distance of 900 m. Figure 11c depicts the combined effects of load and abrading distance on wear volume. The results show that wear volume increases with both factors, as higher loads exacerbate matrix damage and fiber exposure, leading to higher wear volume loss.

3.7. ANOVA and the Effect of Factors

Based on S/N ratio analysis and other tests the 5 wt% SiO2 filler (GV1) showed the best mechanical and wear performance. Hence, to determine the statistical significance of factors like filler content (A), load (B), and abrading distance (C) on wear volume, an analysis of variance (ANOVA) was conducted at a 5% significance level. The results are summarized in Table 8, where p-values <0.05 indicate significant contributions. The analysis reveals that load has the highest influence on wear volume loss, accounting for 57.1%, followed by abrading distance (23.8%) and filler content (14.7%). Among interaction effects, the combination of load and abrading distance (3.32%) has the most notable effect, whereas the interactions between the filler content and load, as well as filler content and abrading distance, show minimal significance. The pooled error in the ANOVA table is approximately 0.29%. These findings confirm that the applied load is the most critical factor affecting wear volume loss.

4. Conclusions

Experimental observations were conducted on SiO2-filled chopped glass fiber-reinforced vinyl ester matrix composites to examine the effects of void fraction, tensile, flexural, hardness, wear test, and surface morphology. The following outcome was observed from our research work:
  • The introduction of SiO2 filler reduced the void fraction to some extent, thereby enhancing the composite’s strength. Void fractions ranging from 1.63% to 5.31% with a minimum at 0 wt. % SiO2 filler content and a maximum at 10 wt. % SiO2 filler content.
  • Tensile test results on unfilled and silicon dioxide-filled E-glass–vinyl ester composites revealed that GV1 (5 wt% SiO2) exhibited higher tensile strength, Young’s modulus, and elongation in the warp direction, indicating improved fiber–matrix interaction.
  • Conversely, GV2 (10 wt% SiO2) displayed lower tensile strength and elongation, suggesting increased brittleness and weaker bonding.
  • Flexure test results demonstrated that GV1 had superior performance, with a higher Young’s modulus of bending, elastic strength, flexural strength, and maximum deflection, indicating improved load-bearing capacity. In contrast, GV2 exhibited reduced flexural strength and deflection, indicative of increased brittleness due to poor fiber–matrix bonding at higher filler content.
  • Shore D hardness test results showed that GV1 (5 wt% SiO2) exhibits higher hardness than other specimens.
  • SEM analysis of composites further highlighted wear behavior. At 25 N load and 300 m distance, only partial matrix removal and minimal fiber damage were observed, with GV1 showing the least wear loss due to improved fiber–matrix–filler interaction. At higher loads (45 N) and distances (900 m), significant matrix detachment, fiber damage, and increased wear volume were evident, attributed to abrasive particle ploughing and cutting.
  • Further, studies are essential to evaluate the suitability of prepared composites for structural applications.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/jcs9080409/s1.

Author Contributions

R.S., conceptualization, data curation, formal analysis, investigation, methodology, and writing—original draft; R.B.M., project administration, resources, supervision, visualization, and validation; R.M.B., resources and formal analysis; P.M.V., data curation and, software; P.N.S., data curation, software, and validation; S.B., methodology, software, and validation; M.B.S., formal analysis, data curation, and validation; G.H.N., writing—review and editing; M.P. validation and, writing—review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author.

Acknowledgments

The authors would like to thank the Maharaja Institute of Technology, Thandavapura, Mysuru, India and Government Engineering College, K R Pete, Mandya, India for providing the instrumentation. This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Conflicts of Interest

The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Rasin, N.; Kueh, A.B.; Mahat, M.N.; Mohd Yassin, A.Y. Stability of triaxially woven fabric composites employing geometrically nonlinear plate model with volume segmentation ABD constitution. J. Compos. Mater. 2016, 50, 2719–2735. [Google Scholar] [CrossRef]
  2. Shen, Y.; Branscomb, D.J. A general approach to fast prototype the topology of braided structures. Int. J. Eng. Sci. 2018, 131, 40–60. [Google Scholar] [CrossRef]
  3. Hou, J.; Wu, X.; Li, Z.; Li, X.; Liao, Y.; Li, L.; Luo, S.; Wu, Y.; Qing, Y. Aligned bamboo fiber-induced crystallinity mitigation of lightweight polymer composite enables ultrahigh strength and unprecedented toughness. Adv. Funct. Mater. 2024, 34, 2314559. [Google Scholar] [CrossRef]
  4. Chen, X.-w.; Fu, K.-k.; Li, Y. A theoretical modelling of strengthening mechanism in graphene-metal nanolayered composites. Int. J. Eng. Sci. 2024, 195, 103988. [Google Scholar] [CrossRef]
  5. Choi, J.-S.; Lee, H.-J.; Shin, H.-O.; Lee, J.-H.; Yoon, Y.-S. Horizontal shear behavior of self-compacting lightweight concrete composite beams with dry joints and unbonded reinforcements. Cem. Concr. Compos. 2024, 152, 105687. [Google Scholar] [CrossRef]
  6. Karaboğa, F.; Göleç, F.; Yunus, D.E.; Toros, S.; Öz, Y. Mechanical response of carbon fiber reinforced epoxy composite parts joined with varying bonding techniques for aerospace applications. Compos. Struct. 2024, 331, 117920. [Google Scholar] [CrossRef]
  7. Orlik, J.; Neusius, D.; Chakrabortty, A.; Backes, S.; Gries, T.; Steiner, K. Modelling of flat pre-strain driven structures, folding to desired surface and application to 3D-printing on textiles. Int. J. Eng. Sci. 2025, 208, 104201. [Google Scholar] [CrossRef]
  8. Leong, K.H.; Ramakrishna, S.; Huang, Z.; Bibo, G. The potential of knitting for engineering composites—A review. Compos.—A Appl. Sci. Manuf. 2000, 31, 197–220. [Google Scholar] [CrossRef]
  9. Islam, S.; Seyed Bolouri, S.E.; Kim, C.-I. Mechanics of hyperelastic composites reinforced with nonlinear elastic fibrous materials in finite plane elastostatics. Int. J. Eng. Sci. 2021, 165, 103491. [Google Scholar] [CrossRef]
  10. Yang, T.-B.; Zong, J.-Y.; Jia, D.-Z.; Xu, L.; Wang, Y.-Y.; Jia, L.-C.; Yan, D.-X.; Lei, J.; Li, Z.-M. Superhydrophobic stretchable conductive composite textile with weft-knitted structure for excellent electromagnetic interference shielding and Joule heating performance. Chem. Eng. J. 2024, 489, 151360. [Google Scholar] [CrossRef]
  11. Du, W.; Ren, H.; Xu, W.; Liu, Y. Reversible shape memory behavior of knitting-fabric reinforced polymer matrix composites. Compos. Commun. 2024, 48, 101962. [Google Scholar] [CrossRef]
  12. Zhou, M.; Jiang, G. Analysis of loading modes and rates on the mechanical responses of glass fiber weft-knitted biaxial tubular fabric reinforced composites. J. Ind. Text. 2024, 54, 15280837241294068. [Google Scholar] [CrossRef]
  13. Raji, A.; Hasani, H.; Hassanzadeh, S. Multi-cellular 3D flat-knitted composite panels strengthened by PU-foam: Manufacturing, testing and simulating. Appl. Compos. Mater. 2024, 31, 1109–1130. [Google Scholar] [CrossRef]
  14. Izadi, R.; Das, R.; Fantuzzi, N.; Trovalusci, P. Fracture properties of green nano fibrous network with random and aligned fiber distribution: A hierarchical molecular dynamics and peridynamics approach. Int. J. Eng. Sci. 2024, 204, 104136. [Google Scholar] [CrossRef]
  15. Karaoglu, İ.; Alpyildiz, T. Impact performances of monoaxial knitted fabric composites. J. Compos. Mater. 2021, 55, 2275–2287. [Google Scholar] [CrossRef]
  16. Zeidi, M.; Islam, S.; Park, C.B.; Kim, C.I. A pseudoelastic response of hyperelastic composites reinforced with nonlinear elastic fibrous materials: Continuum modeling and analysis. Int. J. Eng. Sci. 2024, 201, 104092. [Google Scholar] [CrossRef]
  17. Leong, K.; Falzon, P.; Bannister, M.; Herszberg, I. An investigation of the mechanical performance of weft-knit milano-rib glass/epoxy composites. Compos. Sci. Technol. 1998, 58, 239–251. [Google Scholar] [CrossRef]
  18. Ramakrishna, S. Energy absorption characteristics of knitted fabric reinforced epoxy composite tubes. J. Reinf. Plast. Compos. 1995, 14, 1121–1141. [Google Scholar] [CrossRef]
  19. Zhu, C.; Shi, J.; Hayashi, K.; Morikawa, H.; Sakaguchi, A.; Ni, Q. Effect of design parameters on the cushioning property of cellular fabric composites. Tex. Res. J. 2019, 89, 3692–3699. [Google Scholar] [CrossRef]
  20. Ramakrishna, S.; Hull, D. Energy absorption capability of epoxy composite tubes with knitted carbon fibre fabric reinforcement. Compos. Sci. Technol. 1993, 49, 349–356. [Google Scholar] [CrossRef]
  21. Ramakrishna, S.; Hamada, H.; Rydin, R.W.; Chou, T. Impact damage resistance of knitted glass fiber fabric reinforced polypropylene composites. Sci. Eng. Compos. Mater. 1995, 4, 61–72. [Google Scholar] [CrossRef]
  22. Fujita, A.; Hamada, H.; Maekawa, Z. Tensile properties of carbon fiber triaxial woven fabric composites. J. Compos. Mater. 1993, 27, 1428–1442. [Google Scholar] [CrossRef]
  23. Bilisik, K. Multiaxis three-dimensional weaving for composites: A review. Text. Res. J. 2012, 82, 725–743. [Google Scholar] [CrossRef]
  24. Ghazimoradi, M.; Carvelli, V.; Marchesi, M.C.; Frassine, R. Mechanical characterization of tetraxial textiles. J. Ind. Text. 2018, 48, 3–24. [Google Scholar] [CrossRef]
  25. Hu, J.; Chen, W.; Li, Y.; Gao, C.; Shi, T.; Yang, D. A triaxial tensile machine for three-dimensional membrane components: Experimental investigations and numerical simulations. Poly. Test. 2018, 65, 206–216. [Google Scholar] [CrossRef]
  26. Gao, Z.; Jiang, G.; Ma, P.; Zhang, Q.; Wan, A. Tear properties and meso-scale mechanism of multi-axial warp-knitted fabric from various architectures: Studied by photography. Fibers Polym. 2013, 14, 1953–1963. [Google Scholar] [CrossRef]
  27. Zhu, B.; Yu, T.; Tao, X. Large deformation and slippage mechanism of plain woven composite in bias extension. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1821–1828. [Google Scholar] [CrossRef]
  28. Aiman, D.; Yahya, M.; Salleh, J. Impact properties of 2D and 3D Woven Composites: A Review. In Proceedings of the AIP Conference, Brisbane, Australia, 19–21 September 2016; AIP Publishing: Melville, NY, USA; Volume 1774. [Google Scholar]
  29. Zhou, X.; Ma, X.; Fan, Y.; Li, H. Tensile and bending behavior of thin-walled triaxial weave fabric composites. J. Eng. Fibers Fabr. 2019, 14, 1558925019893566. [Google Scholar] [CrossRef]
  30. Wu, Z.; Wang, K.; Shi, L.; Cheng, X.; Yuan, Y. Low-velocity impact response and damage tolerance of hybrid biaxial/triaxial braided composite laminates. Poly. Compos. 2023, 44, 3068–3083. [Google Scholar] [CrossRef]
  31. Cao, J.; Akkerman, R.; Boisse, P.; Chen, J.; Cheng, H.; de Graaf, E.; Gorczyca, J.; Harrison, P.; Hivet, G.; Launay, J.; et al. Characterization of mechanical behavior of woven fabrics: Experimental methods and benchmark results. Compos.—A Appl. Sci. Manuf. 2008, 39, 1037–1053. [Google Scholar] [CrossRef]
  32. Samal, S.; Thanh, N.P.; Petríková, I.; Marvalová, B.; Vallons, K.A.; Lomov, S.V. Correlation of microstructure and mechanical properties of various fabric reinforced geo-polymer composites after exposure to elevated temperature. Ceram. Int. 2015, 41, 12115–12129. [Google Scholar] [CrossRef]
  33. Zhang, H.; Zhou, Y.; Li, W. Behaviors of triaxial woven fabric composites reinforced concrete cylinders under eccentric compression. Text. Res. J. 2024, 94, 1959–1970. [Google Scholar] [CrossRef]
  34. Li, Z.; Li, W. Effect of triaxial woven fabric on bending properties of unidirectional composites. Poly. Compos. 2023, 44, 5346–5356. [Google Scholar] [CrossRef]
  35. Wei, Q.; Chen, J.; Liu, Y.; Zhang, H. Numerical analysis of ballistic performance in hybrid structures of triaxial and plain fabrics. J. Mater. Sci. 2024, 59, 21069–21086. [Google Scholar] [CrossRef]
  36. Frontczak-Wasiak, I.; Snycerski, M. Assessment of transversal deformations of multi-axial woven fabrics stretched one-directionally. Fibres Text. East. Eur. 2006, 14, 29. [Google Scholar]
  37. Balcerzak, M. Influence of the construction of a four-axial fabric on its properties. Fibres Text. East. Eur. 2011, 19, 88. [Google Scholar]
  38. Kashani, M.H.; Rashidi, A.; Crawford, B.; Milani, A. Analysis of a two-way tension-shear coupling in woven fabrics under combined loading tests: Global to local transformation of non-orthogonal normalized forces and displacements. Compos. A Appl. Sci. Manuf. 2016, 88, 272–285. [Google Scholar] [CrossRef]
  39. Al-Gaadi, B.; Halász, M. Deformation analysis of composite reinforcing fabrics through yarn pull-out, drape and shear tests. Fibers Polym. 2013, 14, 804–814. [Google Scholar] [CrossRef]
  40. El Mourid, A. Mechanical Behavior of a Triaxially Braided Textile Composite at High Temperature; Ecole Polytechnique de Montreal: Montreal, QC, Canada, 2014. [Google Scholar]
  41. Aruchamy, K.; Mylsamy, B.; Palaniappan, S.K.; Subramani, S.P.; Velayutham, T.; Rangappa, S.M.; Siengchin, S. Influence of weave arrangements on mechanical characteristics of cotton and bamboo woven fabric reinforced composite laminates. J. Reinf. Plast. Comp. 2023, 42, 776–789. [Google Scholar] [CrossRef]
  42. Islam, M.A. 3D woven structures and methods of manufacture. In Woven Textiles; Woodhead Publishing: Amsterdam, The Netherland, 2012; pp. 264–313. [Google Scholar]
  43. Risteska, S.; Srebrenkoska, V.; Zhezhova, S.; Srebrenkoska, S.; Risteski, S.; Jordeva, S.; Golomeova Longurova, S. The effect of textile structure reinforcement on polymer composite material mechanical behavior. Polymers 2024, 16, 3478. [Google Scholar] [CrossRef]
  44. Banerjee, P.K.; Mishra, S.; Ramkumar, T. Effect of sett and construction on uniaxial tensile properties of woven fabrics. J. Eng. Fibers Fabr. 2010, 5, 155892501000500202. [Google Scholar] [CrossRef]
  45. Behera, B.; Dash, B. An experimental investigation into structure and properties of 3D-woven aramid and PBO fabrics. J. Text. Inst. 2013, 104, 1337–1344. [Google Scholar] [CrossRef]
  46. Vanleeuw, B.; Carvelli, V.; Barburski, M.; Lomov, S.; van Vuure, A.W. Quasi-unidirectional flax composite reinforcement: Deformability and complex shape forming. Compos. Sci. Technol. 2015, 110, 76–86. [Google Scholar] [CrossRef]
  47. Aisyah, H.A.; Paridah, M.T.; Sapuan, S.M.; Ilyas, R.A.; Khalina, A.; Nurazzi, N.M.; Lee, S.H.; Lee, C.H. A Comprehensive review on advanced sustainable woven natural fibre polymer composites. Polymers 2021, 13, 471. [Google Scholar] [CrossRef] [PubMed]
  48. Bilisik, K.; Mohamed, M.H. Multiaxis three-dimensional flat woven preform (tube rapier weaving) and circular woven preform (radial crossing weaving). Text. Res. J. 2009, 79, 1067–1084. [Google Scholar] [CrossRef]
  49. Kumaran, P.; Mohanamurugan, S.; Madhu, S.; Vijay, R.; Lenin Singaravelu, D.; Vinod, A.; Sanjay, M.; Siengchin, S. Investigation on thermo-mechanical characteristics of treated/untreated portunus sanguinolentus shell powder-based jute fabrics reinforced epoxy composites. J. Ind. Text. 2020, 50, 427–459. [Google Scholar] [CrossRef]
  50. Praveenkumara, J.; Madhu, P.; Yashas Gowda, T.G.; Sanjay, M.R.; Siengchin, S. A comprehensive review on the effect of synthetic filler materials on fiber-reinforced hybrid polymer composites. J. Text. Inst. 2022, 113, 1231–1239. [Google Scholar] [CrossRef]
  51. Prabhu, L.; Krishnaraj, V.; Gokulkumar, S.; Sathish, S.; Sanjay, M.; Siengchin, S. Mechanical, chemical and sound absorption properties of glass/kenaf/waste tea leaf fiber-reinforced hybrid epoxy composites. J. Ind. Text. 2022, 51, 1674–1700. [Google Scholar] [CrossRef]
  52. Xie, J.; Guo, Z.; Shao, M.; Zhu, W.; Jiao, W.; Yang, Z.; Chen, L. Mechanics of textiles used as composite preforms: A review. Compos. Struct. 2023, 304, 116401. [Google Scholar] [CrossRef]
  53. Aravind, D.; Senthilkumar, K.; Rajini, N.; Siengchin, S.; Yorseng, K.; Kumar, T.S.M.; Chandrasekar, M.; Mohammad, F.; Al-Lohedan, H.A. Flexural, impact, and dynamic mechanical analysis of glass fiber/ABS and glass fiber/carbon fiber/ABS composites. J. Appl. Poly. Sci. 2023, 140, e54007. [Google Scholar] [CrossRef]
  54. Reddy, P.C.G.M.S.; Rajendrachari, S.; Mahale, R.S.; Mahesh, V.; Pandith, A. The behavior of banyan (B)/banana (Ba) fibers reinforced hybrid composites influenced by chemical treatment on tensile, bending and water absorption behavior: An experimental and FEA investigation. J. Comp. Sci. 2024, 8, 31. [Google Scholar] [CrossRef]
  55. Bilisik, K.; Karaduman, N.S.; Bilisik, N.E. Fiber Architectures for Composite Applications, Fibrous and Textile Materials for Composite Applications; Springer: Berlin/Heidelberg, Germany, 2016; pp. 75–134. [Google Scholar] [CrossRef]
  56. Zhao, Z.; Li, B.; Ma, P. Advances in mechanical properties of flexible textile composites. Compos. Struct. 2023, 303, 116350. [Google Scholar] [CrossRef]
  57. Chowdhury, I.R.; Summerscales, J. Woven fabrics for composite reinforcement: A review. J. Compos. Sci. 2024, 8, 280. [Google Scholar] [CrossRef]
  58. El-Messiry, M.; Youssef, S. Analysis of stress–strain of architect woven fabric strength under biaxial extensions. Alex. Eng. J. 2011, 50, 297–303. [Google Scholar] [CrossRef]
  59. Fallahi, H.; Taheri-Behrooz, F.; Asadi, A. Nonlinear mechanical response of polymer matrix composites: A review. Poly. Rev. 2019, 60, 42–85. [Google Scholar] [CrossRef]
  60. Liu, Y.; Straumit, I.; Vasiukov, D.; Lomov, S.V.; Panier, S. Prediction of linear and non-linear behavior of 3D woven composite using mesoscopic voxel models reconstructed from X-ray micro-tomography. Compos. Struct. 2017, 179, 568–579. [Google Scholar] [CrossRef]
  61. Mulenga, T.K.; Ude, A.U.; Vivekanandhan, C. Techniques for modelling and optimizing the mechanical properties of natural fiber composites: A review. Fibers 2021, 9, 6. [Google Scholar] [CrossRef]
  62. Barburski, M.; Masajtis, J. Modelling of the change in structure of woven fabric under mechanical loading. Fibres Text. East. Eur. 2009, 17, 72. [Google Scholar]
  63. Hahn, L.; Zierold, K.; Golla, A.; Friese, D.; Rittner, S. 3D Textiles Based on Warp Knitted Fabrics: A Review. Materials 2023, 16, 3680. [Google Scholar] [CrossRef] [PubMed]
  64. Thomason, J.; Vlug, M.; Schipper, G.; Krikor, H. Influence of fibre length and concentration on the properties of glass fibre-reinforced polypropylene: Part 3. Strength and strain at failure. Compos.—A Appl. Sci. Manuf. 1996, 27, 1075–1084. [Google Scholar] [CrossRef]
  65. Lee, N.-J.; Jang, J. The effect of fibre content on the mechanical properties of glass fibre mat/polypropylene composites. Compos.—A Appl. Sci. Manuf. 1999, 30, 815–822. [Google Scholar] [CrossRef]
  66. Agarwal, B.; Broutman, L. Analysis and Performance of Fiber Composites, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
Jcs 09 00409 g001
Figure 1. Shows SEM images of GV, GV1, and GV2 composites.
Figure 1. Shows SEM images of GV, GV1, and GV2 composites.
Jcs 09 00409 g001
Jcs 09 00409 g002
Figure 2. (a) Shows tensile setup and (b) shows the bending test using Kalpak instrument (100 kN computerized UTM).
Figure 2. (a) Shows tensile setup and (b) shows the bending test using Kalpak instrument (100 kN computerized UTM).
Jcs 09 00409 g002
Jcs 09 00409 g003
Figure 3. Shows SEM images of GV (a), GV1 (b), and GV2 (c) composites and GV1 composite under 45 N load and 900 m abrading distance (c–e) (magnifications of ×500 and ×1000).
Figure 3. Shows SEM images of GV (a), GV1 (b), and GV2 (c) composites and GV1 composite under 45 N load and 900 m abrading distance (c–e) (magnifications of ×500 and ×1000).
Jcs 09 00409 g003
Jcs 09 00409 g004
Figure 4. Measured and theoretical density of composite materials.
Figure 4. Measured and theoretical density of composite materials.
Jcs 09 00409 g004
Jcs 09 00409 g005
Figure 5. Tensile behavior of samples GV, GV1, and GV2.
Figure 5. Tensile behavior of samples GV, GV1, and GV2.
Jcs 09 00409 g005
Jcs 09 00409 g006
Figure 6. (a) Ultimate tensile strength v/s materials composition, (b) Young’s modulus v/s material composition, (c) elongation v/s material composition, and (d) stress at break v/s material composition.
Figure 6. (a) Ultimate tensile strength v/s materials composition, (b) Young’s modulus v/s material composition, (c) elongation v/s material composition, and (d) stress at break v/s material composition.
Jcs 09 00409 g006
Jcs 09 00409 g007
Figure 7. Bending stress material of GV, GV1, and GV2 samples.
Figure 7. Bending stress material of GV, GV1, and GV2 samples.
Jcs 09 00409 g007
Jcs 09 00409 g008
Figure 8. (a) Bending stress material in the bar graph, (b) maximum deflection, (c) Young’s modulus, and (d) elastic strength of materials in a flexural test of GV, GV1, and GV2 samples.
Figure 8. (a) Bending stress material in the bar graph, (b) maximum deflection, (c) Young’s modulus, and (d) elastic strength of materials in a flexural test of GV, GV1, and GV2 samples.
Jcs 09 00409 g008
Jcs 09 00409 g009
Figure 9. (a) Shore D durometer used hardness test and (b) Shore D hardness of the composite of samples GV, GV1, and GV2.
Figure 9. (a) Shore D durometer used hardness test and (b) Shore D hardness of the composite of samples GV, GV1, and GV2.
Jcs 09 00409 g009
Jcs 09 00409 g010
Figure 10. (a) Signal-to-noise ratio for filler content in percentage, (b) fiber loading in Newton, and (c) abrading distance in meters.
Figure 10. (a) Signal-to-noise ratio for filler content in percentage, (b) fiber loading in Newton, and (c) abrading distance in meters.
Jcs 09 00409 g010
Jcs 09 00409 g011
Figure 11. Surface plot of (a) wear volume (mm3) vs. load (N) and filler contents (%), (b) wear volume (mm3) vs. abrading distance (m), filler content (%), and (c) wear volume (mm3) vs. abrading distance (m), load (N).
Figure 11. Surface plot of (a) wear volume (mm3) vs. load (N) and filler contents (%), (b) wear volume (mm3) vs. abrading distance (m), filler content (%), and (c) wear volume (mm3) vs. abrading distance (m), load (N).
Jcs 09 00409 g011
Table 1. Summary of composite formulation (by weight %).
Table 1. Summary of composite formulation (by weight %).
Sample CodeVinyl Ester Resin (wt. %)E-Glass Fiber
(wt. %)		SiO2 Filler
(wt. %)
GV40600
GV135605
GV2303010
Table 2. Composite materials of density and volume fraction of voids.
Table 2. Composite materials of density and volume fraction of voids.
MaterialsMeasured Density (g/cm3)Theoretical Density (g/cm3)Void Fraction (%)
GV1.60701.63371.63
GV11.63341.71064.51
GV21.68121.77555.31
Table 3. Tensile test results.
Table 3. Tensile test results.
Material Tensile Strength (MPa)Young’s Modulus
(MPa)		Elongation
(%)		Stress at Break
(MPa)
Warp*SDWeft*SDWarp*SDWeft*SDWarp*SDWeft*SDWarp*SDWeft*SD
GV261.052.7760.700.924178.8986.672757.4558.8110.760.315.740.3452.210.8512.140.69
GV1278.670.9060.200.824363.1473.542923.6647.6611.80.365.60.355.730.6112.040.67
GV2232.071.0428.600.723580.655.332714.3157.429.960.584.580.2646.410.735.720.73
*SD = standard deviation.
Table 4. Elastic strength test results.
Table 4. Elastic strength test results.
MaterialsMaximum Deflection (mm)*SDMaximum Bending Stress at Maximum Load (MPa)*SDYoung’s Modulus of Bending (MPa)*SDElastic Strength (MPa)*SD
GV3.360.24311.641.314,483.23149.6975.002.52
GV13.850.15348.691.515,367.18258.9180.842.26
GV22.860.21248.961.812,395.68209.3263.492.21
*SD = standard deviation.
Table 5. Shore–D hardness test results.
Table 5. Shore–D hardness test results.
Materials.Shore–D HardnessStandard Deviation
GV713.511
GV1744.042
GV2722.517
Table 6. Results of Taguchi design.
Table 6. Results of Taguchi design.
Si
no		MaterialLoad
(N)		Abrading Distance (m)Initial Weight
(W1) (g)		Final Weight
(W2) (g)		Wear Loss (g)Wear VolumeS/N Ratio
(dB)
1GV2530011.451311.18200.26930.167415.7184
2GV2560011.851511.51060.34090.211913.5087
3GV2590011.243710.79450.44920.279210.8569
4GV3530011.298410.80350.49490.307610.3014
5GV3560010.948410.27700.67140.41737.3677
6GV3590011.059410.23430.82510.51285.9632
7GV4530011.437710.86860.56910.35378.7726
8GV4560011.271210.40540.86580.53815.5748
9GV4590011.340710.31701.02370.63623.9907
10GV12530011.193011.08480.10820.065524.182
11GV12560011.739811.60370.13610.082421.348
12GV12590011.460411.25650.20390.123418.0003
13GV13530011.428811.16810.26070.157815.5598
14GV13560011.262210.82460.43760.264812.0018
15GV13590011.251910.72230.52960.32059.9013
16GV14530010.12219.71810.40400.244512.2056
17GV14560011.375510.75520.62030.37548.3835
18GV14590011.384910.55170.83320.50426.1034
19GV22530010.559210.38190.17730.108618.583
20GV22560011.145810.89380.25200.154316.5349
21GV22590011.083610.69560.38800.237612.8813
22GV23530010.985010.56460.42040.257412.2047
23GV23560010.750010.21350.53650.32859.4325
24GV23590010.974010.26160.71240.43627.0262
25GV24530010.953610.45090.50270.307810.5182
26GV24560010.856310.17130.68500.41947.482
27GV24590010.88909.98250.90650.55504.896
Table 7. Response table for signal–to–noise ratio—smaller the better.
Table 7. Response table for signal–to–noise ratio—smaller the better.
LevelFiller (%)
A		Load(N)
B		Abrading Distance (m)
C
19.11716.84614.227
214.1879.97311.293
311.0627.5478.847
DELTA5.0709.2995.381
RANK312
Table 8. Analysis of variance for wear volume loss (mm3).
Table 8. Analysis of variance for wear volume loss (mm3).
SourceDF *Seq SS **Adj SS #Adj MS @FPP(%)Rank
Filler20.0918750.0918750.045938203.140.00014.73
Load20.3559480.3559480.177974787.020.00057.11
Abrading distance20.1484780.1484780.074239328.290.00023.82
Filler × Load40.0020050.0020050.0005012.220.1570.326
Filler × Abrading distance40.0021270.0021270.0005322.350.1410.345
Load × Abrading distance40.0207380.0207380.00518522.930.0003.324
Error80.0018090.0018090.000226 0.29
Total260.622980 100
* DF—degree of freedom, ** Seq SS—sequential sum of the square, # Adj SS—adjacent sum of the square, @ Adj MS—adjacent sum of the mean square, F—variance, P—test statistics (percentage contribution of each factor in overall performance to find out optimum specific wear rate).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Somanna, R.; Madegowda, R.B.; Mahesh Bilwa, R.; Vishveshwaraiah, P.M.; Siddegowda, P.N.; Bagrae, S.; Sangameshwara, M.B.; Nagaraju, G.H.; Puttaswamy, M. Study of Mechanical and Wear Properties of Fabricated Tri-Axial Glass Composites. J. Compos. Sci. 2025, 9, 409. https://doi.org/10.3390/jcs9080409

AMA Style

Somanna R, Madegowda RB, Mahesh Bilwa R, Vishveshwaraiah PM, Siddegowda PN, Bagrae S, Sangameshwara MB, Nagaraju GH, Puttaswamy M. Study of Mechanical and Wear Properties of Fabricated Tri-Axial Glass Composites. Journal of Composites Science. 2025; 9(8):409. https://doi.org/10.3390/jcs9080409

Chicago/Turabian Style

Somanna, Raghu, Rudresh Bekkalale Madegowda, Rakesh Mahesh Bilwa, Prashanth Malligere Vishveshwaraiah, Prema Nisana Siddegowda, Sandeep Bagrae, Madhukar Beejaganahalli Sangameshwara, Girish Hunaganahalli Nagaraju, and Madhusudan Puttaswamy. 2025. "Study of Mechanical and Wear Properties of Fabricated Tri-Axial Glass Composites" Journal of Composites Science 9, no. 8: 409. https://doi.org/10.3390/jcs9080409

APA Style

Somanna, R., Madegowda, R. B., Mahesh Bilwa, R., Vishveshwaraiah, P. M., Siddegowda, P. N., Bagrae, S., Sangameshwara, M. B., Nagaraju, G. H., & Puttaswamy, M. (2025). Study of Mechanical and Wear Properties of Fabricated Tri-Axial Glass Composites. Journal of Composites Science, 9(8), 409. https://doi.org/10.3390/jcs9080409

Article Metrics

Back to TopTop