Review: Sensing Technologies for the Optimisation and Improving Manufacturing of Fibre-Reinforced Polymeric Structures
Abstract
1. Introduction
2. Sensors and Mechanisms
2.1. Optical Sensors
2.1.1. Quasi-Distributed Optical Sensors
Fibre Bragg Grating
Fibre Bragg Sensors Mechanism for Strain and Temperature
Tilted Fibre Bragg Sensors
Tilted Fibre Bragg Sensors Mechanism for Strain, Temperature, and Refractive Index (Chemical)
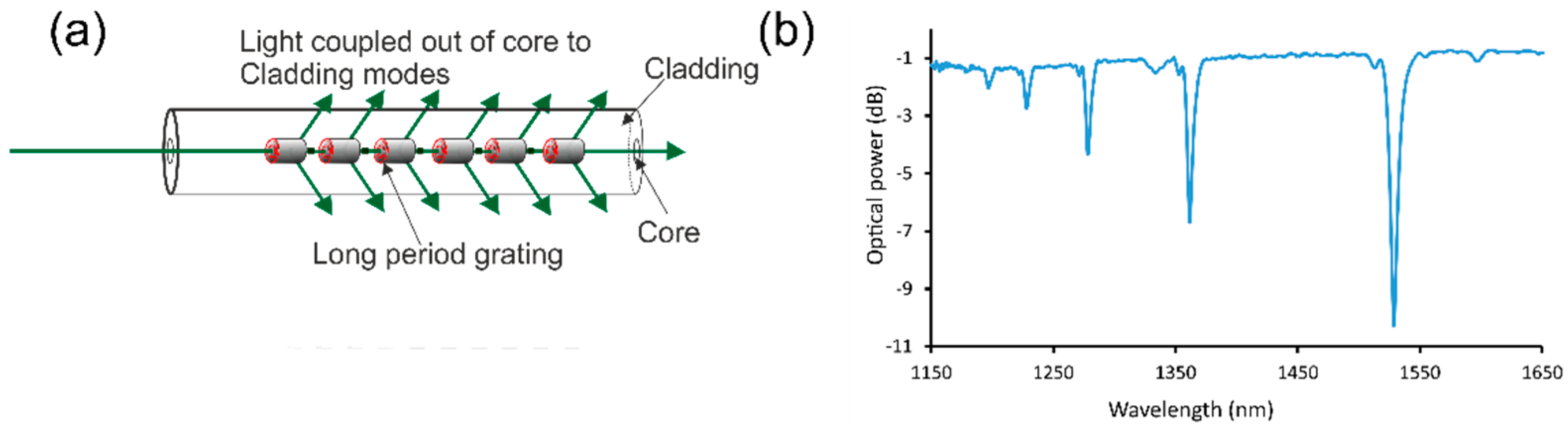
Long-Period Grating Sensors
Fibre Long-Period Sensors Mechanism for Strain, Temperature, and Refractive Index Chemical
2.1.2. Distributed Optical Sensors
Rayleigh Backscattering Sensing Mechanism for Strain and Temperature
Brillouin Scattering
Brillouin Scattering Sensing Mechanism for Strain and Temperature
Raman Scattering
Raman Scattering Sensing Mechanism for Temperature
2.1.3. Piezoelectric Sensors
Piezoelectric Sensing Mechanism for Strain and Temperature
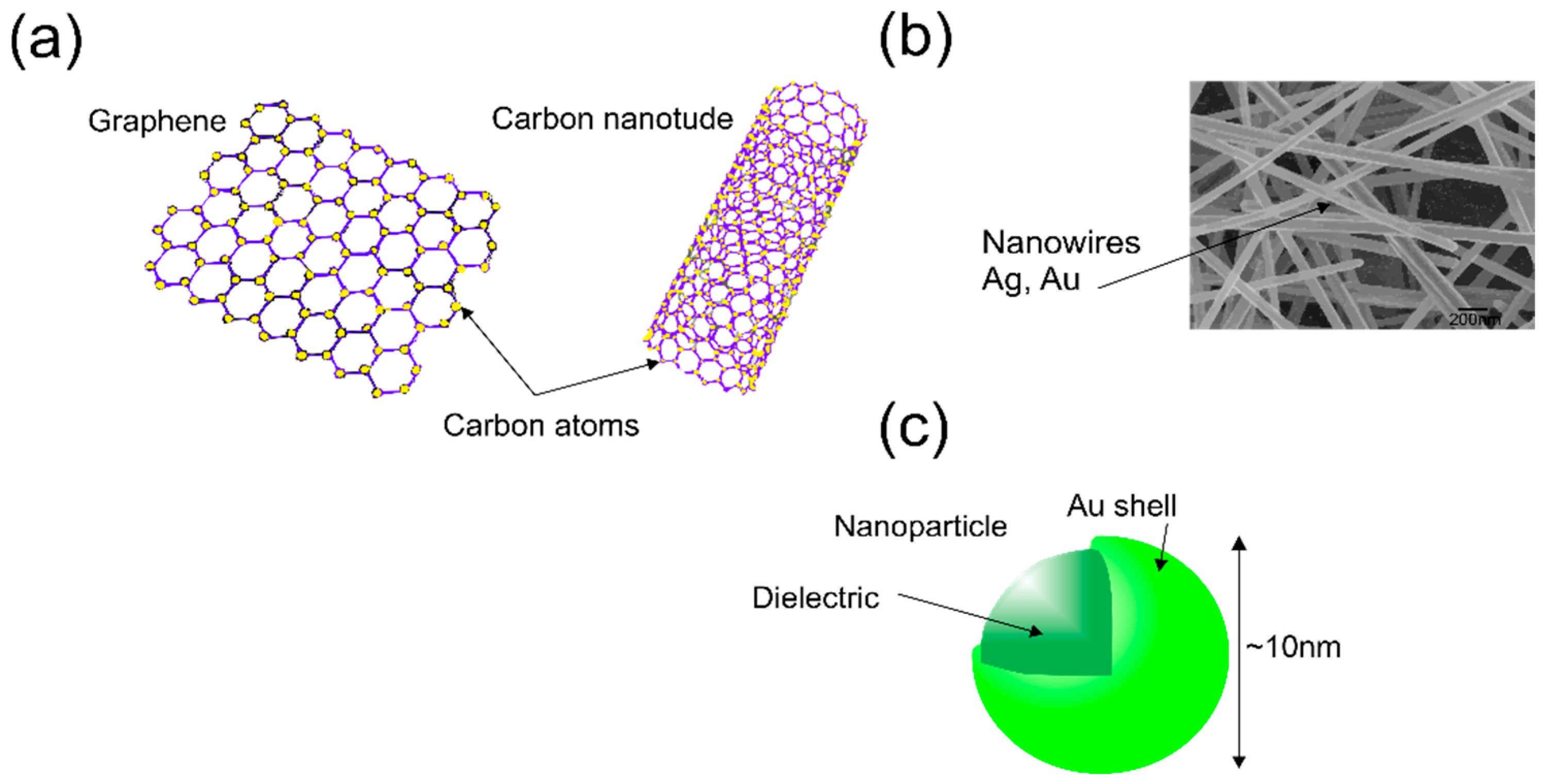
2.2. Nanomaterial-Based Sensors
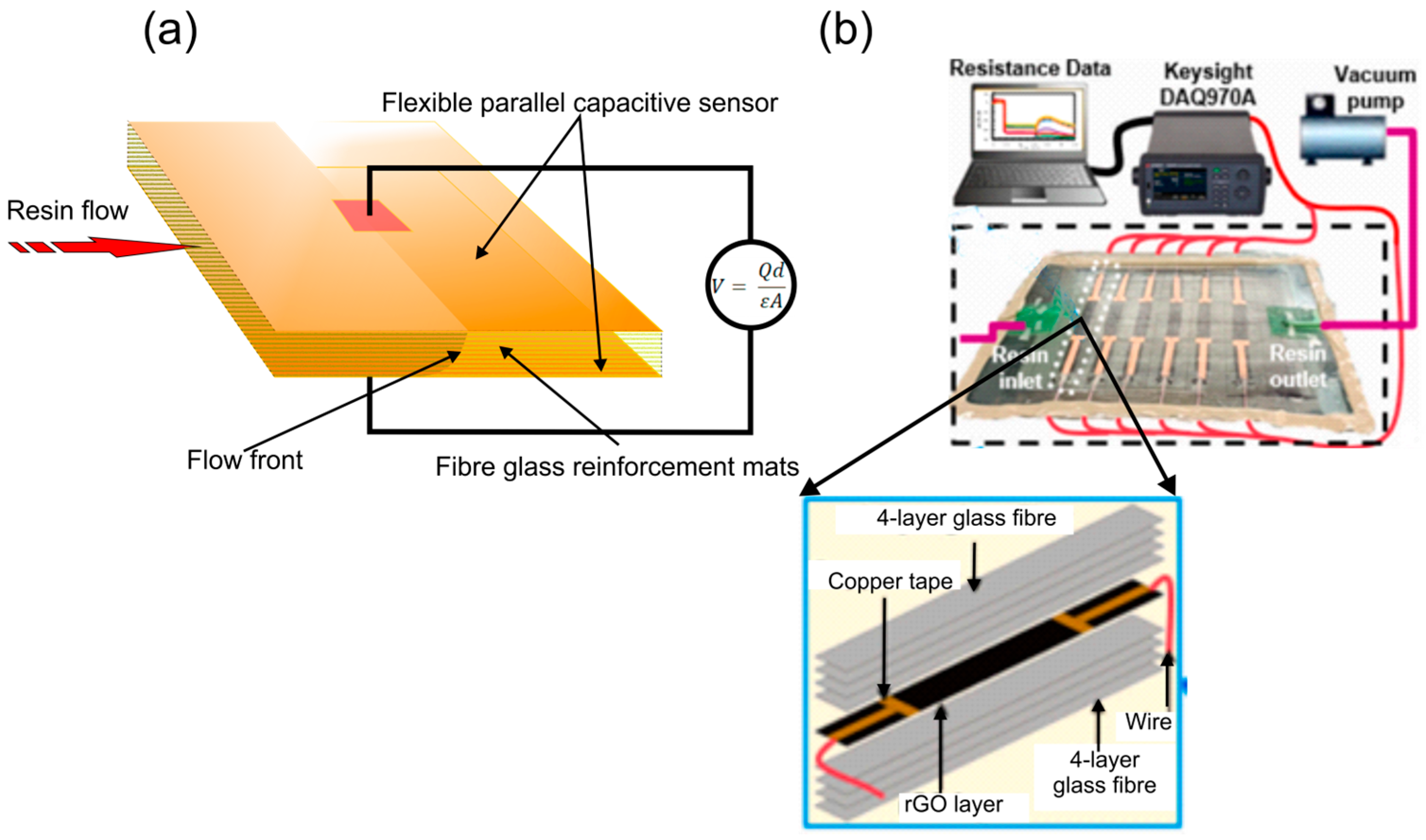
Capacitive Sensors
3. Implementation of Sensors: Arrays and Multiplexing
- (i)
- The capability of multiplexing of sensors: This is important with regard to the spatial resolution of a measurement for a specific parameter. An example is the monitoring of the flow front of the resin within the mould, to ensure complete impregnation of glass fibre reinforcement mats to avoid dry spots that can act as induced cracks within the structure and may prove to be catastrophic for a structure [124,125]:
- (ii)
- The ease of interrogation of sensors/sensor array: This can be a limiting factor in using a specific sensing scheme and can relate to the response time of scheme to obtain a measurement. A quicker response may be desirable to react to a given set of measurements. Also, the interrogation scheme itself may have limitations on the number of sensors it can monitor in total in a reasonable or required time interval. Furthermore, the interrogation scheme itself can have a limit on the spatial resolution, such as SBS or OTDR, which ha a spatial limit on the order of ~0.5 m [126]. Also, interrogation can be complicated because of cross-sensitivity [127] between various parameters, like temperature and the presence of resin/epoxy (changing the permittivity), which leads to misinterpretation. Another overriding factor may be the cost of the interrogation scheme (financial restrictions; too expensive to implement).
- (iii)
- The survivability and reliability of the sensing array; These two attributes refer to practical solutions if there is damage to the sensing array and its abilities to perform the sensing activities to the desired specifications after damage has occurred [128]. Here, “practical solutions” refer to the following: firstly, reasonable costs in hardware as well as other aspects including installation and maintenance and also reliability/durability of the sensing to perform over the required time span. Secondly, to accidental damage of the sensing array, meaning to individual sensors or number of sensors within the array and its ability still to be used as a sensing array yielding meaningful measurements and data [129]. In order to guarantee steady and reliable sensing service, large-scale sensor networks require high “robustness”, which is the ability to maintain system functionality against external and internal interference. Extensive research on the reliability and survivability/robustness of sensing networks with unconventional array architecture, such as a fishnet approach, is given in Refs. [130,131].
- (iv)
- Interpretation of the response of the sensing array design: This topic has created different approaches from machine learning algorithms (pipes) to direct measurement with optimum sensors and location. This is very much dependent upon the environment in which the sensing array/network is operating and varying the number of parameters that affect the sensor’s performance and measurements [131,132,133,134].
- (v)
- The practical implementation (lay-up) of sensing schemes in a workplace: In practical implementation, the lay-up of a sensing scheme within a mould during the liquid composite moulding process requires careful planning to ensure effective integration without disrupting the flow of resin or the structural integrity of the final composite. Sensors—such as fibre optic or piezoelectric types—are typically positioned either on the surface of the mould or embedded within the reinforcement layers, depending on the monitoring objective. Their placement must accommodate resin flow paths, curing behaviour, and fibre architecture, while ensuring reliable data acquisition. Secure fixation and appropriate protection of the sensors are essential to prevent displacement or damage during infusion and curing stages. Due to the nature of the process, the sensor fibres have to remain in the structure. If the sensor fibres are significant in number (a network of fibres), it is vital to consider the adhesion of the resin with the sensor fibres. In general, the fibres used as reinforcement are processed with sizing to achieve good adhesion with fibre interface and the resin [135]. For the sensor fibres, such sizing may not be available, which may result in poor adhesion at the interface of sensor fibres and resin; these sites can act as induced cracks in the structure. The size of the sensor fibre can play a significant role in the practical implementation as its diameter is often considerably larger than that of the reinforcement fibres. This mismatch can lead to local disruptions in the fibre architecture, potentially affecting resin flow, wet-out, and even creating resin-rich zones or voids. Careful consideration must, therefore, be given to sensor selection and placement to minimise such disturbances and ensure reliable integration.
3.1. Comparison of Sensor Performance
Data Management, Processing, and Interpretation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Punera, D.; Mukherjee, P. Recent developments in manufacturing, mechanics, and design optimization of variable stiffness composites. J. Reinf. Plast. Compos. 2022, 41, 917–945. [Google Scholar] [CrossRef]
- Prashanth, S.; Subbaya, K.M.; Nithin, K.; Sachidana, S. Fiber reinforced composites-a review. J. Mater. Sci. Eng. 2017, 6, 2–6. [Google Scholar]
- Prasad, V.V.; Talupula, S. A review on reinforcement of basalt and aramid (Kevlar 129) fibers. Mater. Today Proc. 2018, 5, 5993–5998. [Google Scholar] [CrossRef]
- Ben Brahim, S.; Ben Cheikh, R. Influence of fibre orientation and volume fraction on the tensile properties of unidirectional Alfa-polyester composite. Compos. Sci. Technol. 2007, 67, 140–147. [Google Scholar] [CrossRef]
- Beukers, A.; Bersee, H.; Koussios, S. Future Aircraft Structures: From Metal to Composite Structures. In Composite Materials: A Vision for the Future; Springer: London, UK, 2011; pp. 1–50. [Google Scholar]
- Rajak, D.K.; Wagh, P.H.; Kumar, A.; Behera, A.; Pruncu, C.I. Advanced Polymers in Aircraft Structures. In Materials, Structures and Manufacturing for Aircraft. Sustainable Aviation; Kuşhan, M.C., Gürgen, S., Sofuoğlu, M.A., Eds.; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Pogosyan, M.; Nazarov, E.; Bolshikh, A.; Koroliskii, V.; Turbin, N.; Shramko, K. Aircraft composite structures integrated approach: A review. J. Phys. Conf. Ser. 2021, 1925, 012005. [Google Scholar] [CrossRef]
- Okuma, S.O.; Obaseki, M.; Ofuyekpone, D.O.; Ashibudike, O.E. A review assessment of fiber-reinforced polymers for maritime applications. J. Adv. Ind. Technol. Appl. 2023, 4, 17–28. [Google Scholar] [CrossRef]
- Panagiotis, C.J. The Science Behind the Wind: Materials Driving Wind Energy’s Future-Overview. Int. J. Adv. Eng. Res. Sci. 2024, 11, 11. [Google Scholar] [CrossRef]
- Rubino, F.; Nisticò, A.; Tucci, F.; Carlone, P. Marine application of fiber reinforced composites: A review. J. Mar. Sci. Eng. 2020, 8, 26. [Google Scholar] [CrossRef]
- Sonnenschein, R.; Gajdosova, K.; Holly, I. FRP Composites and their Using in the Construction of Bridges. Procedia Eng. 2016, 161, 477–482. [Google Scholar] [CrossRef]
- Chang, S.; Wang, X.; Ding, L.; Wu, Z.; Ma, X. Durability of seawater sea sand concrete beams reinforced with carbon nanotube-modified BFRP bars in a marine environment. Compos. Struct. 2022, 292, 115642. [Google Scholar]
- Tafsirojjaman, T.; Dogar, A.U.R.; Liu, Y.; Manalo, A.; Thambiratnam, D.P. Thambiratnam. Performance and design of steel structures reinforced with FRP composites: A state-of-the-art review. Eng. Fail. Anal. 2022, 138, 106371. [Google Scholar] [CrossRef]
- Li, J.; Bin, N.; Guo, F.; Gao, X.; Chen, R.; Yao, H.; Zhou, C. Analysis on the influence of sports equipment of fiber reinforced composite material on social sports development. Adv. Nano Res. 2023, 15, 49–57. [Google Scholar]
- Jaradat, M.; Duran, J.L.; Murcia, D.H.; Buechley, L.; Shen, Y.-L.; Christodoulou, C.; Taha, M.R. Cognizant Fiber-Reinforced Polymer Composites Incorporating Seamlessly Integrated Sensing and Computing Circuitry. Polymers 2023, 15, 4401. [Google Scholar] [CrossRef]
- Sayam, A.; Rahman, A.N.M.M.; Rahman, M.S.; Smriti, S.A.; Ahmed, F.; Rabbi, M.F.; Hossain, M.; Faruque, M.O. A review on carbon fiber-reinforced hierarchical composites: Mechanical performance, manufacturing process, structural applications and allied challenges. Carbon Lett. 2022, 32, 1173–1205. [Google Scholar] [CrossRef]
- Rajak, D.K.; Wagh, P.H.; Linul, E. Manufacturing technologies of carbon/glass fiber-reinforced polymer composites and their properties: A review. Polymers 2021, 13, 3721. [Google Scholar] [CrossRef]
- Atalie, D.; Gideon, R.K. 21 Challenges and future prospects of coated fiber–reinforced polymer composites. In Surface Modification and Coating of Fibers, Polymers, and Composites, Techniques, Properties, and Applications, Elsevier Series on Tribology and Surface Engineering; Elsevier: Amsterdam, The Netherlands, 2025; pp. 477–502. [Google Scholar]
- Bhatt, A.T.; Gohil, P.P.; Chaudhary, V. Primary manufacturing processes for fiber reinforced composites: History, development & future research trends. IOP Conf. Ser. Mater. Sci. Eng. 2018, 330, 012107. [Google Scholar]
- Karim, M.A.; Abdullah, M.Z.; Ahmed, T. AN overview: The processing methods of fiber-reinforced polymers (FRPS). J. Mech. Eng. Technol 2021, 12, 10–24. [Google Scholar] [CrossRef]
- Furuta, T.; Kanakubo, T.; Nemoto, T.; Takahashi, K.; Fukuyama, H. Sprayed-up FRP strengthening for concrete structures. Proc. Int. Conf. FRP Compos. Civ. Eng. 2001, 2, 1109–1116. [Google Scholar]
- Torres, M. Parameters’ monitoring and in-situ instrumentation for resin transfer moulding: A review. Compos. Part A Appl. Sci. Manuf. 2019, 124, 105500. [Google Scholar] [CrossRef]
- Khalilabad, E.H.; Emparanza, A.R.; De Caso, F.; Roghani, H.; Khodadadi, N.; Nanni, A. Characterization Specifications for FRP Pultruded Materials: From Constituents to Pultruded Profiles. Fibers 2023, 11, 93. [Google Scholar] [CrossRef]
- Quanjin, M.; Rejab, M.R.M.; Kaige, J.; Idris, M.S.; Harith, M.N. Filament winding technique, experiment and simulation analysis on tubular structure. IOP Conf. Ser. Mater. Sci. Eng. 2018, 342, 012029. [Google Scholar] [CrossRef]
- Fu, H.; Xu, H.; Liu, Y.; Yang, Z.; Kormakov, S.; Wu, D.; Sun, J. Overview of injection molding technology for processing polymers and their composites. ES Mater. Manuf. 2020, 8, 3–23. [Google Scholar] [CrossRef]
- Hammami, A.; Gebart, B.R. Analysis of the vacuum infusion molding process. Polym. Compos. 2000, 21, 28–40. [Google Scholar] [CrossRef]
- Collinson, M.G.; Bower, M.P.; Swait, T.J.; Atkins, C.P.; Hayes, S.A.; Nuhiji, B. Novel composite curing methods for sustainable manufacture: A review. Compos. Part C Open Access 2022, 9, 100293. [Google Scholar] [CrossRef]
- del Bosque, A.; Vergara, D.; Fernández-Arias, P. An overview of smart composites for the aerospace sector. Appl. Sci. 2025, 15, 2986. [Google Scholar] [CrossRef]
- Tahir, M.W.; Khan, U.; Schümann, J.-P. Incorporating Non-Linear Epoxy Resin Development in Infusion Simulations: A Dual-Exponent Viscosity Model Approach. Polymers 2025, 17, 657. [Google Scholar] [CrossRef] [PubMed]
- Thor, M.; Sause, M.G.R.; Hinterhölzl, R.M. Mechanisms of origin and classification of out-of-plane fiber waviness in composite materials—A review. J. Compos. Sci. 2020, 4, 130. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Zhao, X.; Noori, M. State-of-the-art review of FRP composites for major construction with high performance and longevity. Int. J. Sustain. Mater. Struct. Syst. 2014, 1, 201–231. [Google Scholar] [CrossRef]
- Carani, L.B.; Humphrey, J.; Rahman, M.; Okoli, O.I. Advances in Embedded Sensor Technologies for Impact Monitoring in Composite Structures. J. Compos. Sci. 2024, 8, 201. [Google Scholar] [CrossRef]
- Mowla, M.N.; Najmul, M.; Asadi, D.; Durhasan, T.; Jafari, J.R.; Amoozgar, M. Recent advancements in morphing applications: Architecture, artificial intelligence integration, challenges, and future trends-a comprehensive survey. Aerosp. Sci. Technol. 2025, 161, 110102. [Google Scholar] [CrossRef]
- Azad, M.M.; Kim, S.; Cheon, Y.B.; Kim, H.S. Intelligent structural health monitoring of composite structures using machine learning, deep learning, and transfer learning: A review. Adv. Compos. Mater. 2024, 33, 162–188. [Google Scholar] [CrossRef]
- Kosova, F.; Altay, Ö.; Ünver, H.Ö. Structural health monitoring in aviation: A comprehensive review and future directions for machine learning. Nondestruct. Test. Eval. 2025, 40, 1–60. [Google Scholar] [CrossRef]
- Ogunleye, R.O.; Rusnáková, S.; Javořík, J.; Žaludek, M.; Kotlánová, B. Advanced Sensors and Sensing Systems for Structural Health Monitoring in Aerospace Composites. Adv. Eng. Mater. 2024, 26, 2401745. [Google Scholar] [CrossRef]
- Hassani, S.; Mousavi, M.; Gandomi, A.H. Structural health monitoring in composite structures: A comprehensive review. Sensors 2021, 22, 153. [Google Scholar] [CrossRef] [PubMed]
- Konstantopoulos, S.; Fauster, E.; Schledjewski, R. Monitoring the production of FRP composites: A review of in-line sensing methods. Express Polym. Lett. 2014, 8, 9. [Google Scholar] [CrossRef]
- Caglar, B.; Esposito, W.; Nguyen-Dang, T.; Laperrousaz, S.; Michaud, V.; Sorin, F. Functionalized fiber reinforced composites via thermally drawn multifunctional fiber sensors. Adv. Mater. Technol. 2021, 6, 2000957. [Google Scholar] [CrossRef]
- Van Steenkiste, R.J. Strain and Temperature Measurement with Fiber Optic Sensors; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Okamoto, K. Fundamentals of Optical Waveguides; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Allen, C. An Introduction to Optical Fibers; McGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- Udd, E.; Spillman, W.B., Jr. Fiber Optic Sensors: An Introduction for Engineers and Scientists; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Ashry, I.; Mao, Y.; Wang, B.; Hveding, F.; Bukhamsin, A.Y.; Ng, T.K.; Ooi, B.S. A review of distributed fiber–optic sensing in the oil and gas industry. J. Light. Technol. 2022, 40, 1407–1431. [Google Scholar] [CrossRef]
- Grattan, K.T.V.; Meggitt, B.T. Optical Fiber Sensor Technology: Advanced Applications-Bragg Gratings and Distributed Sensors; Springer Science & Business Media: Berlin, Germany, 2000; Volume 5. [Google Scholar]
- Hartog, A. Distributed fiber-optic sensors: Principles and applications. In Optical Fiber Sensor Technology: Advanced Applications—Bragg Gratings and Distributed Sensors; Springer: Boston, MA, USA, 2000; pp. 241–301. [Google Scholar]
- Kashyap, R. Fiber Bragg Gratings; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Othonos, A. Fiber bragg gratings. Rev. Sci. Instrum. 1997, 68, 4309–4341. [Google Scholar] [CrossRef]
- Butov, O.V.; Tomyshev, K.; Nechepurenko, I.; Dorofeenko, A.V.; Nikitov, S.A. Tilted fiber Bragg gratings and their sensing applications. Uspekhi Fiz. Nauk 2022, 192, 1385–1398. [Google Scholar] [CrossRef]
- James, S.W.; Tatam, R.P. Optical fibre long-period grating sensors: Characteristics and application. Meas. Sci. Technol. 2003, 14, R49. [Google Scholar] [CrossRef]
- Avino, S.; Giorgini, A.; Gagliardi, G. Fiber-optic cavities for physical and chemical sensing. Open Opt. J. 2013, 7, 128–140. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Butt, M.A. Optical fibre-based sensors—An assessment of current innovations. Biosensors 2023, 13, 835. [Google Scholar] [CrossRef]
- Sahota, J.K.; Gupta, N.; Dhawan, D. Fiber Bragg grating sensors for monitoring of physical parameters: A comprehensive review. Opt. Eng. 2020, 59, 060901. [Google Scholar] [CrossRef]
- Berghmans, F.; Geernaert, T.; Baghdasaryan, T.; Thienpont, H. Challenges in the fabrication of fibre Bragg gratings in silica and polymer microstructured optical fibres. Laser Photonics Rev. 2014, 8, 27–52. [Google Scholar] [CrossRef]
- He, J.; Xu, B.; Xu, X.; Liao, C.; Wang, Y. Review of femtosecond-laser-inscribed fiber Bragg gratings: Fabrication technologies and sensing applications. Photonic Sens. 2021, 11, 203–226. [Google Scholar] [CrossRef]
- Rego, G. Fibre optic devices produced by arc discharges. J. Opt. 2010, 12, 113002. [Google Scholar] [CrossRef]
- Ivanov, O.V.; Nikitov, S.A.; Gulyaev, Y.V. Cladding modes of optical fibers: Properties and applications. Phys. Uspekhi 2006, 49, 167. [Google Scholar] [CrossRef]
- Tsao, C. Optical Fibre Waveguide Analysis; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Bennion, I.; Williams, J.A.R.; Zhang, L.; Sugden, K.; Doran, N.J. UV-written in-fibre Bragg gratings. Opt. Quantum Electron. 1996, 28, 93–135. [Google Scholar] [CrossRef]
- Luyckx, G.; Voet, E.; Lammens, N.; Degrieck, J. Strain measurements of composite laminates with embedded fibre Bragg gratings: Criticism and opportunities for research. Sensors 2010, 11, 384–408. [Google Scholar] [CrossRef]
- Matveenko, V.; Kosheleva, N.; Serovaev, G.; Fedorov, A. Measurement of gradient strain fields with fiber-optic sensors. Sensors 2022, 23, 410. [Google Scholar] [CrossRef]
- Cusano, A.; Capoluongo, P.; Campopiano, S.; Cutolo, A.; Giordano, M.; Felli, F.; Paolozzi, A.; Caponero, M. Experimental modal analysis of an aircraft model wing by embedded fiber Bragg grating sensors. IEEE Sens. J. 2006, 6, 67–77. [Google Scholar] [CrossRef]
- Capoluongo, P.; Ambrosino, C.; Campopiano, S.; Cutolo, A.; Giordano, M.; Bovio, I.; Lecce, L.; Cusano, A. Modal analysis and damage detection by Fiber Bragg grating sensors. Sens. Actuators A Phys. 2007, 133, 415–424. [Google Scholar] [CrossRef]
- Erdogan, T. Cladding-mode resonances in short-and long-period fiber grating filters. J. Opt. Soc. Am. A 1997, 14, 1760–1773. [Google Scholar] [CrossRef]
- Muanenda, Y.; Oton, C.J.; Di Pasquale, F. Application of Raman and Brillouin scattering phenomena in distributed optical fiber sensing. Front. Phys. 2019, 7, 155. [Google Scholar] [CrossRef]
- Miles, R.B.; Lempert, W.R.; Forkey, J.N. Laser rayleigh scattering. Meas. Sci. Technol. 2001, 12, R33. [Google Scholar] [CrossRef]
- Palmieri, L.; Schenato, L.; Santagiustina, M.; Galtarossa, A. Rayleigh-based distributed optical fiber sensing. Sensors 2022, 22, 6811. [Google Scholar] [CrossRef]
- Elsherif, M.; Salih, A.E.; Muñoz, M.G.; Alam, F.; AlQattan, B.; Antonysamy, D.S.; Zaki, M.F.; Yetisen, A.K.; Park, S.; Wilkinson, T.D.; et al. Optical fiber sensors: Working principle, applications, and limitations. Adv. Photonics Res. 2022, 3, 2100371. [Google Scholar] [CrossRef]
- Breit, G. Topics in scattering theory. Rev. Mod. Phys. 1951, 23, 238. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent progress in Brillouin scattering based fiber sensors. Sensors 2011, 11, 4152–4187. [Google Scholar] [CrossRef]
- Buck, J.A. Fundamentals of Optical Fibers, 2nd ed.; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Murray, M.J.; Murray, J.B.; Redding, B. Temperature-Strain Discrimination Using the Brillouin Frequency and Linewidth; NRL/5670/MR; NRL: Washington, DC, USA, 2022. [Google Scholar]
- Li, J.; Zhang, M. Physics and applications of Raman distributed optical fiber sensing. Light Sci. Appl. 2022, 11, 128. [Google Scholar] [CrossRef]
- Bolognini, G.; Hartog, A. Raman-based fibre sensors: Trends and applications. Opt. Fiber Technol. 2013, 19, 678–688. [Google Scholar] [CrossRef]
- Silva, L.C.; Segatto, M.E.; Castellani, C.E. Raman scattering-based distributed temperature sensors: A comprehensive literature review over the past 37 years and towards new avenues. Opt. Fiber Technol. 2022, 74, 103091. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.; Bowen, C. Piezoelectric effects and electromechanical theories at the nanoscale. Nanoscale 2014, 6, 13314–13327. [Google Scholar] [CrossRef] [PubMed]
- Sekhar, M.C.; Veena, E.; Kumar, N.S.; Naidu, K.C.B.; Mallikarjuna, A.; Basha, D.B. A review on piezoelectric materials and their applications. Cryst. Res. Technol. 2023, 58, 2200130. [Google Scholar] [CrossRef]
- Habib, M.; Lantgios, I.; Hornbostel, K. A review of ceramic, polymer and composite piezoelectric materials. J. Phys. D Appl. Phys. 2022, 55, 423002. [Google Scholar] [CrossRef]
- Duan, S.; Wu, J.; Xia, J.; Lei, W. Innovation strategy selection facilitates high-performance flexible piezoelectric sensors. Sensors 2020, 20, 2820. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, Y.; Zheng, H.; Ramakrishna, S. Piezoelectric materials for flexible and wearable electronics: A review. Mater. Des. 2021, 211, 110164. [Google Scholar] [CrossRef]
- Sim, H.J.; Choi, C.; Lee, C.J.; Kim, Y.T.; Spinks, G.M.; Lima, M.D.; Baughman, R.H.; Kim, S.J. Flexible, stretchable and weavable piezoelectric fiber. Adv. Eng. Mater. 2015, 17, 1270–1275. [Google Scholar] [CrossRef]
- Varga, M.; Morvan, J.; Diorio, N.; Buyuktanir, E.; Harden, J.; West, J.L.; Jakli, A. Direct piezoelectric responses of soft composite fiber mats. Appl. Phys. Lett. 2013, 102, 15. [Google Scholar] [CrossRef]
- Jenkins, K.; Nguyen, V.; Zhu, R.; Yang, R. Piezotronic effect: An emerging mechanism for sensing applications. Sensors 2015, 15, 22914–22940. [Google Scholar] [CrossRef]
- Sirohi, J.; Inderjit, C. Fundamental understanding of piezoelectric strain sensors. J. Intell. Mater. Syst. Struct. 2000, 11, 246–257. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U. A systematic review of advanced sensor technologies for non-destructive testing and structural health monitoring. Sensors 2023, 23, 2204. [Google Scholar] [CrossRef]
- Abdulaziz, A.H.; Hedaya, M.; Elsabbagh, A.; Holford, K.; McCrory, J. Acoustic emission wave propagation in honeycomb sandwich panel structures. Compos. Struct. 2021, 277, 114580. [Google Scholar] [CrossRef]
- James, B.J. A new measurement of the basic elastic and dielectric constants of quartz. In Proceedings of the 42nd Annual Frequency Control Symposium, Baltimore, MD, USA, 1–3 June 1988; IEEE: Piscataway, NJ, USA; pp. 146–154. [Google Scholar]
- Jaffe, B.; Roth, R.; Marzullo, S. Properties of piezoelectric ceramics in the solid-solution series lead titanate-lead zirconate-lead oxide: Tin oxide and lead titanate-lead hafnate. J. Res. Natl. Bur. Stand. 1955, 55, 239–254. [Google Scholar] [CrossRef]
- Saxena, P.; Shukla, P. A comprehensive review on fundamental properties and applications of poly (vinylidene fluoride) (PVDF). Adv. Compos. Hybrid Mater. 2021, 4, 8–26. [Google Scholar] [CrossRef]
- Berlincourt, D.; Jaffe, H. Elastic and piezoelectric coefficients of single-crystal barium titanate. Phys. Rev. 1958, 111, 143. [Google Scholar] [CrossRef]
- Patil, S.P.; Burungale, V.V. Physical and Chemical Properties of Nanomaterials. In Nanomedicines for Breast Cancer Theranostics; Elsevier: Amsterdam, The Netherlands, 2020; pp. 17–31. [Google Scholar]
- Baig, N.; Kammakakam, I.; Falath, W. Nanomaterials: A review of synthesis methods, properties, recent progress, and challenges. Mater. Adv. 2021, 2, 1821–1871. [Google Scholar] [CrossRef]
- Justino, C.I.L.; Rocha-Santos, T.A.P.; Cardoso, S.; Duarte, A.C.; Cardosa, S. Duarte. Strategies for enhancing the analytical performance of nanomaterial-based sensors. TrAC Trends Anal. Chem. 2013, 47, 27–36. [Google Scholar] [CrossRef]
- Barsan, M.M.; Ghica, M.E.; Brett, C.M.A. Electrochemical sensors and biosensors based on redox polymer/carbon nanotube modified electrodes: A review. Anal. Chim. Acta 2015, 881, 1–23. [Google Scholar] [CrossRef]
- Meyyappan, M. Carbon nanotube-based chemical sensors. Small 2016, 12, 2118–2129. [Google Scholar] [CrossRef]
- Chen, L.F.; Lu, Y.; Yu, L.; Lou, X.W. Designed formation of hollow particle-based nitrogen-doped carbon nanofibers for high-performance supercapacitors. Energy Environ. Sci. 2017, 10, 1777–1783. [Google Scholar] [CrossRef]
- Ning, P.G.; Duan, X.C.; Ju, X.K.; Lin, X.P.; Tong, X.B.; Pan, X.; Wang, T.H.; Li, Q.H. Facile synthesis of carbon nanofibers/MnO2 nanosheets as high-performance electrodes for asymmetric supercapacitors. Electrochim. Acta 2016, 210, 754–761. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, S.; Wang, J.; Yu, A.; Wei, G. Carbon nanofiber-based functional nanomaterials for sensor applications. Nanomaterials 2019, 9, 1045. [Google Scholar] [CrossRef]
- Arduini, F.; Cinti, S.; Scognamiglio, V.; Moscone, D. Nanomaterial-Based Sensors. In Handbook of Nanomaterials in Analytical Chemistry; Elsevier: Amsterdam, The Netherlands, 2020; pp. 329–359. [Google Scholar]
- Yan, T.; Wang, Z.; Pan, Z.-J. Flexible strain sensors fabricated using carbon-based nanomaterials: A review. Curr. Opin. Solid State Mater. Sci. 2018, 22, 213–228. [Google Scholar] [CrossRef]
- Nakagawa, K.; Satoh, K.; Murakami, S.; Takei, K.; Akita, S.; Arie, T. Controlling the thermal conductivity of multilayer graphene by strain. Sci. Rep. 2021, 11, 19533. [Google Scholar] [CrossRef]
- Lee, J.E.; Ahn, G.; Shim, J.; Lee, Y.S.; Ryu, S. Optical separation of mechanical strain from charge doping in graphene. Nat. Commun. 2012, 3, 1024. [Google Scholar] [CrossRef]
- Caffrey, E.; Garcia, J.R.; O’sUilleabhain, D.; Gabbett, C.; Carey, T.; Coleman, J.N. Quantifying the piezoresistive mechanism in high-performance printed graphene strain sensors. ACS Appl. Mater. Interfaces 2022, 14, 7141–7151. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, G.-Y.; Shi, D.-X. Review of graphene-based strain sensors. Chin. Phys. B 2013, 22, 057701. [Google Scholar] [CrossRef]
- Ge, P.; Xiao, C.; Hu, D.; Xiong, X.; Liu, Y.; Sun, J.; Zhuo, Q.; Qin, C.; Wang, J.; Dai, L. Facile fabrication of Ag-doped graphene fiber with improved strength and conductivity for wearable sensor via the ion diffusion during fiber coagulation. Synth. Met. 2021, 275, 116741. [Google Scholar] [CrossRef]
- McInnes, M.; Gomes, R.; Mohseni, E.; Pierce, S.G.; Dobie, G.; Zhang, D.; MacLeod, C.N.; Munro, G.; O’Brien-O’Reilly, J.; O’Hare, T. Resin transfer monitoring using capacitive sensors. In Proceedings of the 50th Annual Review of Progress in Quantitative Nondestructive Evaluation, Austin, TX, USA, 24–27 July 2023. [Google Scholar]
- Heerens, W.-C. Application of capacitance techniques in sensor design. J. Phys. E: Sci. Instrum. 1986, 19, 897. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, P.; Jin, K. Design of an HP-RTM Flow Monitoring System Based on Embedded Capacitive Sensors. In Proceedings of the 2025 5th International Conference on Sensors and Information Technology, Nanjing, China, 21–23 March 2025; IEEE: New York, NY, USA, 2025; pp. 91–95. [Google Scholar]
- Dei Sommi, A.; Lionetto, F.; Maffezzoli, A. An overview of the measurement of permeability of composite reinforcements. Polymers 2023, 15, 728. [Google Scholar] [CrossRef] [PubMed]
- Kyriazis, A.; Pommer, C.; Lohuis, D.; Rager, K.; Dietzel, A.; Sinapius, M. Comparison of different cure monitoring techniques. Sensors 2022, 22, 7301. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Guo, H.; Lin, H.; Peng, X.; Zhou, H.; Chen, C.; Huang, Z.; Tao, G.; Zhou, H. Designed multifunctional sensor to monitor resin permeation and thickness variation in liquid composite molding process. NDT E Int. 2024, 142, 103023. [Google Scholar] [CrossRef]
- Bathusha, M.S.S.; Din, I.U.; Umer, R.; Khan, K.A. In-situ monitoring of crack growth and fracture behavior in composite laminates using embedded sensors of rGO coated fabrics and GnP paper. Sens. Actuators A: Phys. 2024, 365, 114850. [Google Scholar] [CrossRef]
- Niklasson, G.A.; Granqvist, C.G.; Hunderi, O. Effective medium models for the optical properties of inhomogeneous materials. Appl. Opt. 1981, 20, 26–30. [Google Scholar] [CrossRef]
- Khardani, M.; Bouaïcha, M.; Bessaïs, B. Bruggeman effective medium approach for modelling optical properties of porous silicon: Comparison with experiment. Phys. Status Solidi C 2007, 4, 1986–1990. [Google Scholar] [CrossRef]
- Markel, V.A. Maxwell Garnett approximation in random media: Tutorial. JOSA A 2022, 39, 535–544. [Google Scholar] [CrossRef]
- Chung, D.D.L. First review of capacitance-based self-sensing in structural materials. Sensors Actuators A Phys. 2023, 354, 114270. [Google Scholar] [CrossRef]
- Neitzel, B.; Puch, F. Application of capacitive sensors and controlled injection pressure to minimize void formation in resin transfer molding. Polym. Compos. 2023, 44, 1658–1671. [Google Scholar] [CrossRef]
- Yenilmez, B.; Sozer, E.M. A grid of dielectric sensors to monitor mold filling and resin cure in resin transfer molding. Compos. Part A: Appl. Sci. Manuf. 2009, 40, 476–489. [Google Scholar] [CrossRef]
- Fisch, W.; Hofmann, W.; Koskikallio, J. The curing mechanism of epoxy resins. J. Appl. Chem. 1956, 6, 429–441. [Google Scholar]
- Mdarhri, A.; Khissi, M.; Achour, M.E.; Carmona, F. Temperature effect on dielectric properties of carbon black filled epoxy polymer composites. Eur. Phys. J.-Appl. Phys. 2008, 41, 215–220. [Google Scholar] [CrossRef]
- Li, W.; Palardy, G. Damage monitoring methods for fiber-reinforced polymer joints: A review. Compos. Struct. 2022, 299, 116043. [Google Scholar] [CrossRef]
- Sarr, C.A.; Chataigner, S.; Gaillet, L.; Godin, N. Nondestructive evaluation of FRP-reinforced structures bonded joints using acousto-ultrasonic: Towards diagnostic of damage state. Constr. Build. Mater. 2021, 313, 125499. [Google Scholar] [CrossRef]
- Soman, R.; Wee, J.; Peters, K. Optical fiber sensors for ultrasonic structural health monitoring: A review. Sensors 2021, 21, 7345. [Google Scholar] [CrossRef] [PubMed]
- Floris, I.; Adam, J.M.; Calderon, P.A.; Sales, S. Fiber optic shape sensors: A comprehensive review. Opt. Lasers Eng. 2021, 139, 106508. [Google Scholar] [CrossRef]
- Antonucci, V.; Giordano, M.L.; Nicolais, A.; Calabro, A.; Cusano, A.; Cutolo, A.; Inserra, S. Resin flow monitoring in resin film infusion process. J. Mater. Process. Technol. 2003, 143, 687–692. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent progress in distributed fiber optic sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef]
- Lu, P.; Lalam, N.; Badar, M.; Liu, B.; Chorpening, B.T.; Buric, M.P.; Ohodnicki, P.R. Distributed optical fiber sensing: Review and perspective. Appl. Phys. Rev. 2019, 6, 041302. [Google Scholar] [CrossRef]
- Zhang, Y.; Xin, J. Survivable deployments of optical sensor networks against multiple failures and disasters: A survey. Sensors 2019, 19, 4790. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, S.; Gong, Y.; Liu, T.; Xu, T.; Jia, D.; Zhang, Y. A quantitative robustness evaluation model for optical fiber sensor networks. J. Light. Technol. 2013, 31, 1240–1246. [Google Scholar] [CrossRef]
- Gillooly, A.M.; Zhang, L.; Bennion, I. High Survivability Fiber Sensor Network for Smart Structures. In Photonics North 2004: Photonic Applications in Telecommunications, Sensors, Software, and Lasers; SPIE: Bellingham, WA, USA, 2004; Volume 5579, pp. 99–106. [Google Scholar]
- Bucsics, T. Metaheuristic Approaches for Designing Survivable Fiber-Optic Networks. Ph.D. Thesis, University of Tehnology, Vienna, Austria, 2007. [Google Scholar]
- Yang, C.; Zheng, W.; Zhang, X. Optimal sensor placement for spatial lattice structure based on three-dimensional redundancy elimination model. Appl. Math. Model. 2019, 66, 576–591. [Google Scholar] [CrossRef]
- Venketeswaran, A.; Lalam, N.; Wuenschell, J.; Ohodnicki, P.R., Jr.; Badar, M.; Chen, K.P.; Lu, P.; Duan, Y.; Chorpening, B.; Buric, M. Recent advances in machine learning for fiber optic sensor applications. Adv. Intell. Syst. 2022, 4, 2100067. [Google Scholar] [CrossRef]
- Naku, W.; Alsalman, O.; Zhu, C. High-sensitivity and large-range displacement sensor based on a balloon-shaped optical fiber and machine learning analysis. J. Light. Technol. 2024, 42, 5399–5406. [Google Scholar] [CrossRef]
- Thomason, J.L. Glass fibre sizing: A review. Compos. Part A 2019, 127, 105619. [Google Scholar] [CrossRef]
- Trochez, A.; Jamora, V.C.; Larson, R.; Wu, K.C.; Ghosh, D.; Kravchenko, O.G. Effects of automated fiber placement defects on high strain rate compressive response in advanced thermosetting composites. J. Compos. Mater. 2021, 55, 4549–4562. [Google Scholar] [CrossRef]
- Gupta, N.; Sundaram, R. Fiber optic sensors for monitoring flow in vacuum enhanced resin infusion technology (VERITy) process. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1065–1070. [Google Scholar] [CrossRef]
- Dong, H.; Liu, H.; Nishimura, A.; Wu, Z.; Zhang, H.; Han, Y.; Wang, T.; Wang, Y.; Huang, C.; Li, L. Monitoring strain response of epoxy resin during curing and cooling using an embedded strain gauge. Sensors 2020, 21, 172. [Google Scholar] [CrossRef]
- Pendão, C.; Silva, I. Optical fiber sensors and sensing networks: Overview of the main principles and applications. Sensors 2022, 22, 7554. [Google Scholar] [CrossRef]
- Gan, J.; Yang, A.; Guo, Q.; Yang, Z. Flexible optical fiber sensing: Materials, methodologies, and applications. Adv. Devices Instrum. 2024, 5, 0046. [Google Scholar] [CrossRef]
- Chiesura, G.; Lamberti, A.; Yang, Y.; Luyckx, G.; Van Paepegem, W.; Vanlanduit, S.; Vanfleteren, J.; Degrieck, J. RTM production monitoring of the A380 hinge arm droop nose mechanism: A multi-sensor approach. Sensors 2016, 16, 866. [Google Scholar] [CrossRef] [PubMed]
- Khan, T.; Ali, M.A.; Irfan, M.S.; Khan, K.A.; Liao, K.; Umer, R. Resin infusion process monitoring using graphene coated glass fabric sensors and infusible thermoplastic and thermoset matrices. Polym. Compos. 2022, 43, 2924–2940. [Google Scholar] [CrossRef]
- Zheng, W.; Huanjia, H.; Zheng, Z.; Weilong, D.; Ricky Lee, S.W.; Furong, G. An Integrated Capacitance-Pressure-Temperature Sensing Probe for Injection Molding Monitoring. IEEE Trans. Instrum. Meas. 2025, 74, 6000810. [Google Scholar] [CrossRef]
- Matsuzaki, R.; Kobayashi, S.; Todoroki, A.; Mizutani, Y. Cross-sectional monitoring of resin impregnation using an area-sensor array in an RTM process. Compos. Part A Appl. Sci. Manuf. 2012, 43, 695–702. [Google Scholar] [CrossRef]
- Yuan, L.; Wang, Q.; Zhao, Y. A wavelength-time division multiplexing sensor network with failure detection using fiber Bragg grating. Opt. Fiber Technol. 2024, 88, 103818. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, X.; Cui, X.; Wang, Y.; Qing, X. In-situ cure monitoring of thick CFRP using multifunctional piezoelectric-fiber hybrid sensor network. Compos. Sci. Technol. 2023, 240, 110079. [Google Scholar] [CrossRef]
- Yu, Y.; Cui, X.; Liang, Z.; Qing, X.; Yan, W. Monitoring of three-dimensional resin flow front using hybrid piezoelectric-fiber sensor network in a liquid composite molding process. Compos. Sci. Technol. 2022, 229, 109712. [Google Scholar] [CrossRef]
- Jeong, J.-M.; Soohyun, E.; Seung, Y.O.; Kazuro, K.; Hideaki, M.; Kiyoshi, U.; Seong, S.K. In-situ resin flow monitoring in VaRTM process by using optical frequency domain reflectometry and long-gauge FBG sensors. Compos. Struct. 2022, 282, 115034. [Google Scholar] [CrossRef]
- Liu, X.; Tang, Z.; Gui, X.; Yin, W.; Cao, J.; Fang, Z.; Li, Z. Weak Fiber Bragg Grating Array-Based In Situ Flow and Defects Monitoring During the Vacuum-Assisted Resin Infusion Process. Sensors 2024, 24, 7637. [Google Scholar] [CrossRef]
- Chehura, E.; James, S.W.; Staines, S.; Groenendijk, C.; Cartie, D.; Portet, S.; Hugon, M.; Tatam, R.P. Production process monitoring and post-production strain measurement on a full-size carbon-fibre composite aircraft tail cone assembly using embedded optical fibre sensors. Meas. Sci. Technol. 2020, 31, 105204. [Google Scholar] [CrossRef]
- Hirota, I.; Takeda, S.-I.; Ogasawara, T. Evaluation of thermosetting resin curing using a tilted fiber Bragg grating. Compos. Part A Appl. Sci. Manuf. 2022, 158, 106956. [Google Scholar] [CrossRef]
- Nair, A.K.; Machavaram, V.R.; Mahendran, R.S.; Pandita, S.D.; Paget, C.; Barrow, C.; Fernando, G.F. Fernando. Process monitoring of fibre reinforced composites using a multi-measurand fibre-optic sensor. Sens. Actuators B Chem. 2015, 212, 93–106. [Google Scholar] [CrossRef]
- Qing, X.; Liu, X.; Zhu, J.; Wang, Y. In-situ monitoring of liquid composite molding process using piezoelectric sensor network. Proc. Struct. Health Monitoring. 2022, 20, 2840–2852. [Google Scholar] [CrossRef]
- Qing, X.; Liu, X.; Wamg, Y. Life-cycle monitoring of CFRP using piezoelectric sensors network. Mater. Res. Proc. 2021, 18, 121–130. [Google Scholar]
- Langat, R.K.; De Luycker, E.; Cantarel, A.; Rakotondrabe, M. Toward the development of a new smart composite structure based on piezoelectric polymer and flax fiber materials: Manufacturing and experimental characterization. Mech. Adv. Mater. Struct. 2024, 31, 9345–9359. [Google Scholar] [CrossRef]
- Moghaddam, M.K.; Salas, M.; Ersöz, I.; Michels, I.; Lang, W. Study of resin flow in carbon fiber reinforced polymer composites by means of pressure sensors. J. Compos. Mater. 2017, 51, 3585–3594. [Google Scholar] [CrossRef]
- Liu, X.; Yu, Y.; Li, J.; Zhu, J.; Wang, Y.; Qing, X. Leaky Lamb wave–based resin impregnation monitoring with noninvasive and integrated piezoelectric sensor network. Measurement 2022, 189, 110480. [Google Scholar] [CrossRef]
- Cui, X.; Yu, Y.; Liu, Q.; Liu, X.; Qing, X. Full-field monitoring of the resin flow front and dry spot with noninvasive and embedded piezoelectric sensor networks. Smart Mater. Struct. 2023, 32, 085021. [Google Scholar] [CrossRef]
- Chilles, J.S.; Koutsomitopoulou, A.F.; Croxford, A.J.; Bond, I.P. Monitoring cure and detecting damage in composites with inductively coupled embedded sensors. Compos. Sci. Technol. 2016, 134, 81–88. [Google Scholar] [CrossRef]
- Mazumder, R.H.; Govindaraj, P.; Salim, N.; Antiohos, D.; Fuss, F.K.; Hameed, N. Digitalization of composite manufacturing using nanomaterials based piezoresistive sensors. Compos. Part A Appl. Sci. Manuf. 2024, 188, 108578. [Google Scholar] [CrossRef]
- del Río, J.S.; Pascual-González, C.; Martínez, V.; Jiménez, J.L.; González, C. 3D-printed resistive carbon-fiber-reinforced sensors for monitoring the resin frontal flow during composite manufacturing. Sens. Actuators A Phys. 2021, 317, 112422. [Google Scholar] [CrossRef]
- del Río, J.S.; Pascual-González, C.; Martínez, V.; Jiménez, J.L.; González, C. CNTs monitoring sensors for resin infusion optimization. Sens. Actuators A Phys. 2023, 364, 114852. [Google Scholar] [CrossRef]
- Mazumder, R.H.; Govindaraj, P.; Hasan, M.M.; Antiohos, D.; Salim, N.; Fuss, F.K.; Hameed, N. Intelligent process monitoring of smart polymer composites using large area graphene coated fabric sensor. ChemPhysChem 2025, 26, e202400189. [Google Scholar] [CrossRef]
- Wan, Y.; Hu, W.; Yang, L.; Wang, Z.; Tan, J.; Liu, Y.; Wang, F.; Yang, B. In-situ monitoring of glass fiber/epoxy composites by the embedded multi-walled carbon nanotube coated glass fiber sensor: From fabrication to application. Polym. Compos. 2022, 43, 4210–4222. [Google Scholar] [CrossRef]
- Irfan, M.S.; Khan, T.; Hussain, T.; Liao, K.; Umer, R. Carbon coated piezoresistive fiber sensors: From process monitoring to structural health monitoring of composites–A review. Compos. Part A Appl. Sci. Manuf. 2021, 141, 106236. [Google Scholar] [CrossRef]
- Su, Y.; Xu, L.; Zhou, P.; Yang, J.; Wang, K.; Zhou, L.-M.; Su, Z. In situ cure monitoring and In-service impact localization of FRPs using Pre-implanted nanocomposite sensors. Compos. Part A Appl. Sci. Manuf. 2022, 154, 106799. [Google Scholar] [CrossRef]
- Kim, J.-H.; Wang, Z.-J.; Kwon, K.-E.; Shim, W.-S.; Yang, S.-B.; Kwon, D.-J. Evaluation of resin impregnation using self-sensing of carbon fibers. Polym. Test. 2024, 131, 108331. [Google Scholar] [CrossRef]
- Jeong, C.; Lee, T.H.; Noh, S.M.; Park, Y.-B. Real-time in situ monitoring of manufacturing process and CFRP quality by relative resistance change measurement. Polym. Test. 2020, 85, 106416. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, B.; Du, K.; Liu, Y.; Kang, R.; Wang, S.; Zhang, J.; Gu, Y.; Li, M. Process Monitoring for Vacuum-Assisted Resin Infusion by Using Carbon Nanotube-Based Sensors. Polymers 2025, 17, 459. [Google Scholar] [CrossRef]
- Mirabedini, A.; Ang, A.; Nikzad, M.; Fox, B.; Lau, K.; Hameed, N. Evolving strategies for producing multiscale graphene-enhanced fiber-reinforced polymer composites for smart structural applications. Adv. Sci. 2020, 7, 1903501. [Google Scholar] [CrossRef]
- Islam, M.H.; Shaila, A.; Mohammad, A.U.; Andreeva, D.V.; Novoselov, K.S.; Nazmul, K. Graphene and CNT-based smart fiber-reinforced composites: A review. Adv. Funct. Mater. 2022, 32, 2205723. [Google Scholar] [CrossRef]
- Tsai, J.-T.; Dustin, J.S.; Mansson, J.-A. Dustin, and Jan-Anders Mansson. Cure strain monitoring in composite laminates with distributed optical sensor. Compos. Part A: Appl. Sci. Manuf. 2019, 125, 105503. [Google Scholar] [CrossRef]
- Qu, X.; Li, J.; Shan, Y.; Yang, Z.; Yang, L.; Xu, H.; Liu, M.; Wu, Z.; Zhao, S. Various static loading condition monitoring of carbon fiber composite cylinder with integrated optical fiber sensors. Opt. Fiber Technol. 2024, 83, 103685. [Google Scholar] [CrossRef]
- Jothibasu, S.; Du, Y.; Anandan, S.; Dhaliwal, G.S.; Kaur, A.; Watkins, S.E.; Chandrashekhara, K.; Huang, J. Chandrashekhara, and Jie Huang. Spatially continuous strain monitoring using distributed fiber optic sensors embedded in carbon fiber composites. Opt. Eng. 2019, 58, 072004. [Google Scholar] [CrossRef]
- Buchinger, V.; Khodaei, Z.S. Vacuum assisted resin transfer moulding process monitoring by means of distributed fibre-optic sensors: A numerical and experimental study. Adv. Compos. Mater. 2022, 31, 467–484. [Google Scholar] [CrossRef]
- Lalam, N.; Ng, W.P.; Dai, X.; Wu, Q.; Fu, Y.Q. Performance improvement of Brillouin ring laser based BOTDR system employing a wavelength diversity technique. J. Light. Technol. 2018, 36, 1084–1090. [Google Scholar] [CrossRef]
- Song, M.; Xia, Q.; Feng, K.; Lu, Y.; Yin, C. 100 km Brillouin optical time-domain reflectometer based on unidirectionally pumped Raman amplification. Opt. Quantum Electron. 2016, 48, 1–10. [Google Scholar] [CrossRef]
- Ruiz-Lombera, R.; Laarossi, I.; Rodriguez-Cobo, L.; Quintela, M.Á.; López-Higuera, J.M.; Mirapeix, J. Distributed high-temperature optical fiber sensor based on a Brillouin optical time domain analyzer and multimode gold-coated fiber. IEEE Sens. J. 2017, 17, 2393–2397. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, L.; Yang, C.; Tong, W.; He, Z. Long-range Raman distributed temperature sensor with high spatial and temperature resolution using graded-index few-mode fiber. Opt. Express 2018, 26, 20562–20571. [Google Scholar] [CrossRef]
- Xu, Y.; Li, J.; Huang, X.; Fan, B.; Feng, K.; Zhang, M. High-Spatial Resolution Raman-Distributed Optical Fiber Sensing Using Differential Pulse-Width Pair Detection. IEEE Sens. J. 2025, 25, 2761–2768. [Google Scholar] [CrossRef]
- Allsop, T.D.; Tahir, M.W.; Bhavsar, K.; Zhang, L.; Webb, D.J.; Gilbert, J.M. Fibre Bragg Gratings: Monitoring of Infusion Process in Liquid Composite Molding Manufacturing. In Optical Sensing and Detection VII; SPIE: Bellingham, WA, USA, 2022; Volume 12139, pp. 298–304. [Google Scholar]
- Froggatt, M.E.; Gifford, D.K.; Kreger, S.; Wolfe, M.; Soller, B.J. Characterization of polarization-maintaining fiber using high-sensitivity optical-frequency-domain reflectometry. J. Light. Technol. 2006, 24, 4149–4154. [Google Scholar] [CrossRef]
- Ali, M.A.; Umer, R.; Khan, K.A.; Samad, Y.A.; Liao, K.; Cantwell, W. Graphene coated piezo-resistive fabrics for liquid composite molding process monitoring. Compos. Sci. Technol. 2017, 148, 106–114. [Google Scholar] [CrossRef]
- Luo, S.; Wang, G.; Wang, Y.; Xu, Y.; Luo, Y. Carbon nanomaterials enabled fiber sensors: A structure-oriented strategy for highly sensitive and versatile in situ monitoring of composite curing process. Compos. Part B Eng. 2019, 166, 645–652. [Google Scholar] [CrossRef]
- Alahmed, N.; Din, I.U.; Cantwell, W.J.; Umer, R.; Khan, K.A. Khan. Multi-scale characterization of self-sensing fiber reinforced composites. Sens. Actuators A Phys. 2024, 379, 115857. [Google Scholar] [CrossRef]
- Lima, R.; Costa, P.; Nunes-Pereira, J.; Silva, A.; Tubio, C.; Lanceros-Mendez, S. Additive manufacturing of multifunctional epoxy adhesives with self-sensing piezoresistive and thermoresistive capabilities. Compos. Part B Eng. 2025, 293, 112130. [Google Scholar] [CrossRef]
- Shahbaz, S.R.; Berkalp Ö, B.; Hassan, S.Z.U.; Siddiqui, M.S.; Bangash, M.K. Fabrication and analysis of integrated multifunctional MWCNTS sensors in glass fiber reinforced polymer composites. Compos. Struct. 2021, 260, 113527. [Google Scholar] [CrossRef]
- Dimassi, A.; Gleason, M.G.V.; Hübner, M.; Herrmann, A.S.; Lang, W. Using piezoresistive pressure sensors for resin flow monitoring in wind turbine blades. Mater. Today Proc. 2021, 34, 140–148. [Google Scholar] [CrossRef]
- Lopes, C.; Araújo, A.; Silva, F.; Pappas, P.-N.; Termine, S.; Trompeta, A.-F.A.; Charitidis, C.A.; Martins, C.; Mould, S.T.; Santos, R.M. Smart carbon fiber-reinforced polymer composites for damage sensing and on-line structural health monitoring applications. Polymers 2024, 16, 2698. [Google Scholar] [CrossRef]
- Gupta, R.; Mitchell, D.; Blanche, J.; Harper, S.; Tang, W.; Pancholi, K.; Baines, L.; Bucknall, D.G.; Flynn, D. A review of sensing technologies for non-destructive evaluation of structural composite materials. J. Compos. Sci. 2021, 5, 319. [Google Scholar] [CrossRef]
- Lekakou, C.; Cook, S.; Deng, Y.; Ang, T.W.; Reed, G.T. Optical fibre sensor for monitoring flow and resin curing in composites manufacturing. Compos. Part A Appl. Sci. Manuf. 2006, 37, 934–938. [Google Scholar] [CrossRef]
- Denkena, B.; Schmidt, C.; Timmermann, M.; Friedel, A. An optical-flow-based monitoring method for measuring translational motion in infrared-thermographic images of AFP processes. Prod. Eng. 2022, 16, 569–578. [Google Scholar] [CrossRef]
- Dorbath, B.; Schür, J.; Ziegmann, G.; Vossiek, M. Passive, Wireless in Situ Millimeterwave Sensor With Mounted Dielectric Channels for Cure Monitoring of Carbon Fiber-Reinforced Polymers. IEEE Sens. J. 2023, 23, 24438–24451. [Google Scholar] [CrossRef]
- Littner, L.; Protz, R.; Kunze, E.; Bernhardt, Y.; Kreutzbruck, M.; Gude, M. Flow front monitoring in high-pressure resin transfer molding using phased array ultrasonic testing to optimize mold filling simulations. Materials 2023, 17, 207. [Google Scholar] [CrossRef] [PubMed]
- Veigt, M.; Hardi, E.; Koerdt, M.; Herrmann, A.S.; Freitag, M. Herrmann, and Michael Freitag. Investigation of using RFID for cure monitoring of glass fiber-reinforced plastics. Prod. Eng. 2020, 14, 499–507. [Google Scholar] [CrossRef]
- Hardi, E.; Veigt, M.; Koerdt, M.; Herrmann, A.S.; Freitag, M. Herrmann, and Michael Freitag. Monitoring of the vacuum infusion process by integrated RFID transponder. Procedia Manuf. 2020, 52, 20–25. [Google Scholar] [CrossRef]
- Le Bot, P.; Lebreton, G.; Siddig, N.; Couarraze, P.; Fouché, O.; Sébastien, C.; De Fongalland, A.; Cara, F.; Gérard, P. Anomaly detection during thermoplastic composite infusion: Monitoring strategy through thermal sensors. Key Eng. Mater. 2022, 926, 1423–1436. [Google Scholar] [CrossRef]
- Allsop, T.; Tahir, M.W.; Bhavasar, K.; Zhang, L.; Webb, D.J.; Bhavsar, K. Long-period gratings for monitoring the resin transfer molding of fiber-reinforced polymer composites. Opt. Lett. 2023, 48, 3503–3506. [Google Scholar] [CrossRef]
- Savastru, D.; Baschir, L.; Miclos, S.; Savastru, R.; Lancranjan, I. Smart composite using fibre optic sensors for fluid flow characterization and temperature measurement. Compos. Struct. 2023, 304, 116382. [Google Scholar] [CrossRef]
- Bertram, L.; Brink, M.; Lang, W. Wireless, Material-Integrated Sensors for Strain and Temperature Measurement in Glass Fibre Reinforced Composites. Sensors 2023, 23, 6375. [Google Scholar] [CrossRef]
- Allsop, T.; Webb, D.; Bennion, I. A comparison of the sensing characteristics of long period gratings written in three different types of fiber. Opt. Fiber Technol. 2003, 9, 210–223. [Google Scholar] [CrossRef]
- Chai, B.X.; Gunaratne, M.; Ravandi, M.; Wang, J.; Dharmawickrema, T.; Di Pietro, A.; Jin, J.; Georgakopoulos, D. Smart industrial internet of things framework for composites manufacturing. Sensors 2024, 24, 4852. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.A.; Irfan, M.S.; Khan, T.; Khalid, M.Y.; Umer, R. Graphene nanoparticles as data generating digital materials in industry 4.0. Sci. Rep. 2023, 13, 4945. [Google Scholar] [CrossRef] [PubMed]
- Priyadharshini, M.; Balaji, D.; Bhuvaneswari, V.; Rajeshkumar, L.; Sanjay, M.R.; Siengchin, S. Fiber reinforced composite manufacturing with the aid of artificial intelligence–a state-of-the-art review. Arch. Comput. Methods Eng. 2022, 29, 5511–5524. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, K.; Zhang, C. Applications of artificial intelligence/machine learning to high-performance composites. Compos. Part B Eng. 2024, 285, 111740. [Google Scholar] [CrossRef]
- Elenchezhian, M.R.P.; Vadlamudi, V.; Raihan, R.; Reifsnider, K.; Reifsnider, E. Artificial intelligence in real-time diagnostics and prognostics of composite materials and its uncertainties—A review. Smart Mater. Struct. 2021, 30, 083001. [Google Scholar] [CrossRef]
- Baran, I.; Cinar, K.; Ersoy, N.; Akkerman, R.; Hattel, J.H. A review on the mechanical modeling of composite manufacturing processes. Arch. Comput. Methods Eng. 2017, 24, 365–395. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.; Mou, S.; Hunt, J.H.; Shi, J. Finite element analysis model-based cautious automatic optimal shape control for fuselage assembly. J. Manuf. Sci. Eng. 2022, 44, 081009. [Google Scholar] [CrossRef]
- Liu, M.; Li, H.; Zhou, H.; Zhang, H.; Huang, G. Development of machine learning methods for mechanical problems associated with fibre composite materials: A review. Compos. Commun. 2024, 49, 101988. [Google Scholar] [CrossRef]
- Uray, M.; Giunti, B.; Kerber, M.; Huber, S. Topological Data Analysis in smart manufacturing: State of the art and future directions. J. Manuf. Syst. 2024, 76, 75–91. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform manifold approximation and projection for dimension reduction. arXiv 2020, arXiv:1802.03426. [Google Scholar]
- Tunukovic, V.; McKnight, S.; Hifi, A.; Mohseni, E.; Pierce, S.G.; Vithanage, R.K.; Gordon, D.; MacLeod, C.N.; Cochran, S.; O’Hare, T. Multi model machine learning approach for automated data analysis of carbon fiber reinforced polymer composites. NDT E Int. 2025, 154, 103392. [Google Scholar] [CrossRef]
- Cao, Z.; Zhang, Y.; Wang, X.; Liu, C. Optimisation of large-Scale composite blade layup using coupled finite element method and machine learning. Compos. Struct. 2025, 364, 119150. [Google Scholar] [CrossRef]
- Babuška, I.; Strouboulis, T. The Finite Element Method and Its Reliability; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Campbell, F.C. Manufacturing Processes for Advanced Composites; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Mallick, P.K. Fiber-Reinforced Composites: Materials, Manufacturing, and Design; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Nijssen, R.P.L. Composite Materials an Introduction, 1st ed.; Based on 3rd Dutch edition; Arnhem and Nijmegen University of Applied Sciences: Arnhem, The Netherlands, 2015; A VKCN Publication; ISBN 978-90-77812-51-8. [Google Scholar]
- Majumder, M.; Gangopadhyay, T.K.; Chakraborty, A.K.; Dasgupta, K.; Bhattacharya, D. Fibre Bragg gratings in structural health monitoring—Present status and applications. Sens. Actuators A Phys. 2008, 147, 150–164. [Google Scholar] [CrossRef]
- Takeda, N.; Okabe, Y.; Kuwahara, J.; Kojima, S.; Ogisu, T. Development of smart composite structures with small-diameter fiber Bragg grating sensors for damage detection: Quantitative evaluation of delamination length in CFRP laminates using Lamb wave sensing. Compos. Sci. Technol. 2005, 65, 2575–2587. [Google Scholar] [CrossRef]
- Marković, M.Z.; Bajić, J.S.; Batilović, M.; Sušić, Z.; Joža, A.; Stojanović, G.M. Comparative Analysis of Deformation Determination by Applying Fiber-optic 2D Deflection Sensors and Geodetic Measurements. Sensors 2019, 19, 844. [Google Scholar] [CrossRef] [PubMed]
- Rocha, H.; Semprimoschnig, C.; Nunes, J.P. Sensors for process and structural health monitoring of aerospace composites: A review. Eng. Struct. 2021, 237, 112231. [Google Scholar] [CrossRef]
- Rodriguez-Cobo, L.; Cobo, A.; Lopez-Higuera, J.-M. Embedded compaction pressure sensor based on Fiber Bragg Gratings. Measurement 2015, 68, 257–261. [Google Scholar] [CrossRef]
- Correia, R.; Chehura, E.; James, S.W.; Tatam, R.P. A pressure sensor based upon the transverse loading of a sub-section of an optical fibre Bragg grating. Meas. Sci. Technol. 2007, 18, 3103. [Google Scholar] [CrossRef]
- Barino, F.; Delgado, F.; Juca, M.A.; Coelho, T.V.; dos Santos, A.B. Comparison of regression methods for transverse load sensor based on optical fiber long-period grating. Measurement 2019, 146, 728–735. [Google Scholar] [CrossRef]
- Allsop, T.; Tahir, M.W.; Bhavsar, K.; Zhang, L. Monitoring of the resin flow front within a resin transfer moulding during fabrication using fibre Bragg gratings. Sens. Actuators A Phys. 2025, 391, 116681. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Z.; Liu, H.; Pang, F.; Chen, Z.; Wang, T. Tensile strength and failure behavior of bare single mode fibers. Opt. Fiber Technol. 2019, 52, 101966. [Google Scholar] [CrossRef]
- Eggleton, B.J.; Poulton, C.G.; Pant, R. Inducing and harnessing stimulated Brillouin scattering in photonic integrated circuits. Adv. Opt. Photonics 2013, 5, 536–587. [Google Scholar] [CrossRef]
- Primerov, N.; Thévenaz, L. Generation and Application of Dynamic Gratings in Optical Fibers Using Stimulated Brillouin Scattering. Ph.D. Thesis, EPFL, Swiss Federal Technology Institute of Lausanne, Lausanne, Switzerland, 2013. [Google Scholar]
- Wolff, C.; Smith, M.J.A.; Stiller, B.; Poulton, C.G. Brillouin scattering—Theory and experiment: Tutorial. J. Opt. Soc. Am. B 2021, 38, 1243–1269. [Google Scholar] [CrossRef]




| Sensors | Reference | Spatial Resolution (m) | Error % | Sensitivity Type Parameter | Multiplexed Sensor Number | Response Time | Sensing Range (m) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Temperature | Strain | Curvature | Other | (s) | ||||||
| Capacitive | [116] | ~0.04 | ~2 | ✓ | ✓ | ✓ | ? | _ | Distributed | ~4 | ~1 |
| Capacitive | [117] | ~0.02 | ~7 | ✓ | ✓ | ✓ | × | Pressure | Distributed | ~1 | _ |
| Capacitive | [140] | ~0.01 | ~2 | ✓ | ✓ | ✓ | × | Quasi Distributed | ~5 | _ | |
| Capacitive + FBG | [141] | ~0.1 | ~0.2 | ✓ | ✓ | ✓ | × | Pressure | 5 section and 1 Distributed | ~16 | Few |
| Capacitive +Graphene | [142] | ~0.02 | _ | ✓ | ✓ | × | × | Distributed | ~20 | _ | |
| Capacitive | [143] | _ | ~3 | ✓ | ✓ | ✓ | × | Pressure | Distributed | ~1 | Few |
| Capacitive | [144] | ~0.01 | ~3 | ✓ | ✓ | × | × | Distributed with 10 points | ~4 | Few | |
| Sensors | Reference | Implementation | Survivability Routes | Reliability Issues | Flow-Front | Curing | Defects |
|---|---|---|---|---|---|---|---|
| Capacitive | [115] | Plate intergation | 1 | Bending, Coupling | ✓ | ✓ | ✓ |
| Capacitive | [116] | Electrodes | 1 | Interpretation | ✓ | ✓ | ✓ |
| Capacitive | [140] | Electrodes | 1 | Intergated response | ✓ | ✓ | ✓ |
| Capacitive + FBG | [141] | Complicated arrangement | 1 | Cross -talk | × | ✓ | ✓ |
| Capacitive + Graphene | [142] | Complicated arrangement | 1 | Cross -talk, Interpretation | × | × | × |
| Capacitive | [143] | Mould design | 1 | Cross -talk, Interpretation | ✓ | ✓ | × |
| Capacitive | [144] | Plate intergation | 1 | Interpretation | ✓ | ✓ | ✓ |
| Sensors | Reference | Spatial Resolution (m) | Error % | Sensitivity Type Parameter | Multiplexed Sensor Number | Response Time | Sensing Range | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Temperature | Strain | Curvature | Other | (s) | (m) | |||||
| FBG | [145] | ~0.04 | ~3 | ✓ | ✓ | ✓ | ✓ | _ | 24 FBG | ~60 | ~5000 |
| FBG +PZT | [146] | ~0.07 | ~5 | ✓ | ✓ | ✓ | × | _ | Distributed + 9 FBG | ~1 | Few |
| FBG +PZT | [147] | ~0.01 | ~2 | ✓ | ✓ | ✓ | × | _ | 9 PZTs + 14 FBG | ~1 | Few |
| FBG+OFDR | [148] | ~0.03 | ~10 | × | ✓ | ✓ | × | _ | Distributed | ~1 | ~1 |
| FBG | [149] | ~003 | ~5 | × | ✓ | ✓ | × | _ | 10 FBG | ~1 | ~1 |
| FBG+Fresnel | [150] | ~0.05 | ~2 | ✓ | ✓ | ✓ | × | Polarisation | 10 Fresnel + 5 FBG | 1 | 3 |
| TFBG +Fresnel | [151] | ~0.001 | ~10 | ✓ | ✓ | ✓ | × | Polarisation | 1TFBG + 1 Fresnel | ~1 | ~0.5 |
| EFPI sensor +FBG | [152] | ~0.001 | ~5 | ✓ | ✓ | ✓ | × | _ | 1 EFPI + 1 FBG | ~10 | ~0.5 |
| Sensors | Reference | Implementation | Survivability routes | Reliability Issues | Flow-Front | Curing | Defects |
|---|---|---|---|---|---|---|---|
| FBG | [145] | WDM | 2 | Losses, Coupling | ✓ | ✓ | ✓ |
| FBG +PZT | [146] | Complex. Wires layout | 1 | Cross-talk | ✓ | ✓ | × |
| FBG +PZT | [147] | Complex. Wires layout | 1 | Fragile connectors | ✓ | ✓ | × |
| FBG+OFDR | [148] | Simple | 1 | Cross -talk | ✓ | × | ✓ |
| FBG | [149] | Sensor in tows, Breakage | 1 | Cross -talk, Interpretation | ✓ | × | ✓ |
| FBG+Fresnel | [150] | Couplers | 4 | Cross -talk, Polarisation | ✓ | ✓ | × |
| TFBG +Fresnel | [151] | Couplers | 4 | Cross -talk, Polarisation | × | ✓ | × |
| EFPI sensor +FBG | [152] | Coupler, Fragile | 1 | Cross -talk, Polarisation | ✓ | ✓ | × |
| Sensors | Reference | Spatial Resolution (m) | Error % | Sensitivity Type Parameter | Multiplexed Sensor Number | Response Time | Sensing Range (m) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Temperature | Strain | Curvature | Other | (s) | ||||||
| PZT | [153] | ~0.05 | ~5 | × | × | ✓ | × | Sound, Lamb wave | 9 PZT | ~10 | ~0.5 |
| PZT | [154] | ~0.1 | ~8 | ✓ | × | ✓ | × | Sound, Lamb wave | 10 PZT | ~10 | ~0.5 |
| PZT+PVDF | [155] | ~0.05 | ~5 | ✓ | ✓ | ✓ | × | _ | 4 PZT | ~1 | ~0.5 |
| PZT | [156] | ~0.12 | ~5 | × | ✓ | ✓ | × | Pressure | 5 PZT | ~20 | ~0.6 |
| PZT | [157] | ~0.05 | ~10 | ✓ | × | ✓ | × | Sound, Lamb wave | 9PZT | ~0.001 | ~0.6 |
| PZT | [158] | ~0.06 | ~7 | ✓ | × | ✓ | × | Sound, Lamb wave | 18 PZT | ~0.001 | ~0.6 |
| PZT | [159] | ~0.001 | ~3 | × | ✓ | ✓ | × | Lamb wave | 1 PZT | ~0.1 | ~3.0 |
| PZT+ Carbon nanomaterial | [160] | ~0.014 | ~5 | ✓ | ✓ | ✓ | × | Resistance | 36 Sensors | ~5 | ~0.3 |
| Sensors | Reference | Implementation | Survivability Routes | Reliability Issues | Flow-Front | Curing | Defects |
|---|---|---|---|---|---|---|---|
| PZT | [153] | Contact wires | 9 | Contacts, Cross-talk | ✓ | ✓ | × |
| PZT | [154] | Contact wires, Complex wiring | 10 | Cross-talk | ✓ | ✓ | ✓ |
| PZT+PVDF | [155] | Complex layup procedure, Breakage | 4 | _ | ✓ | ✓ | × |
| PZT | [156] | Complex layup procedure | 5 | Contacts, Interpretation | ✓ | × | ✓ |
| PZT | [157] | Complex layup procedure | 5 | Cross-talk | ✓ | ✓ | x |
| PZT | [158] | Wire breakages | 9 | Cross-talk | ✓ | ✓ | ✓ |
| PZT | [159] | Complex layup procedure | 1 | _ | × | ✓ | ✓ |
| PZT carbon nanomaterials | [160] | Contacts fragile, Complex layup procedure | 18 | _ | ✓ | ✓ | × |
| Sensors Nanomaterials | Reference | Spatial Resolution (m) | Error % | Sensitivity Type Parameter | Multiplexed Sensor Number | Response Time | Sensing Range (m) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Temperature | Strain | Curvature | Other | (s) | ||||||
| Nano carbon-reinforced sensors | [161] | ~0.01 | ~3 | × | × | ✓ | × | Pressure /Resistance | 9 sensors | ~1 | ~0.5 |
| CNT | [162] | ~0.015 | ~1 | ✓ | ✓ | × | × | Pressure /Resistance | 5 sensors | ~1 | ~0.1 |
| Graphene | [163] | ~0.02 | ~2 | ✓ | ✓ | × | × | Resistance | 20 sensor | ~1 | ~0.4 |
| MWCNT | [164] | ~0.01 | ~3 | ✓ | ✓ | × | × | Resistance | 7 sensors | ~1 | ~0.2 |
| Graphene | [165] | ~0.01 | ~1 | ✓ | ✓ | × | × | Resistance | 8 sensors | ~2 | ~0.2 |
| Fibre-reinforced polymer | [166] | ~0.04 | 15 | ✓ | ✓ | × | × | Guided ultrasonic wave | 8 sensors | ~0.00001 | ~0.5 |
| Carbon fibres | [167] | ~0.02 | ~5 | ✓ | × | × | × | Resistance | 8 sensors | ~1 | ~0.2 |
| Carbon fibres/Teflon | [168] | ~0.05 | ✓ | × | × | × | Resistance | 16 sensors | ~1 | ~0.2 | |
| CNT | [169] | ~0.03 | ~3 | ✓ | ✓ | × | × | Resistance | 7 sensors | ~1 | ~0.3 |
| Sensors Nanomaterials | Reference | Implementation | Survivability Routes | Reliability Issues | Flow-Front | Curing | Defects |
|---|---|---|---|---|---|---|---|
| Nano carbon-reinforced sensors | [161] | Complex layup procedure, Fragile | 4 | Contacts, Cross-talk | ✓ | × | × |
| CNT | [162] | Contact wires | 3 | Cross-talk | ✓ | ✓ | × |
| Graphene | [163] | Complex layup procedure | 10 | Cross-talk | × | ✓ | ✓ |
| MWCNT | [164] | Complex layup procedure | 4 | Contacts, Cross-talk | ✓ | ✓ | ✓ |
| Graphene | [165] | Complex layup procedure | 4 | Cross-talk | ✓ | ✓ | ✓ |
| Fibre-reinforced polymer | [166] | Wire breakages | 4 | Cross-talk | ✓ | ✓ | ✓ |
| Carbon fibres | [167] | Wires complex layup procedure | 3 | _ | ✓ | × | ✓ |
| Carbon fibres/Teflon | [168] | Contacts, complex layup procedure | 8 | Cross-talk | ✓ | ✓ | × |
| CNT | [169] | Contacts, complex layup procedure | 4 | _ | ✓ | ✓ | × |
| Distributed Sensors | Reference | Spatial Resolution (m) | Error % | Sensitivity Type Parameter | Multiplexed Sensor Number | Response Time | Sensing Range (m) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Temperature | Strain | Curvature | Other | (s) | ||||||
| Rayleigh scattering +OFDR | [172] | ~0.005 | ~8 | ✓ | ✓ | ✓ | × | Polarisation | 4 | ~1 | ~1 |
| Rayleigh scattering | [173] | ~0.005 | ~6 | × | ✓ | ✓ | × | Polarisation | 1 | ~0.1 | ~4 |
| Rayleigh scattering +OFDR | [174] | ~0.01 | ~10 | × | ✓ | ✓ | ✓ | Polarisation | 1 | ~0.1 | ~0.3 |
| Rayleigh scattering + OFDR | [175] | ~0.01 | ~3 | ✓ | ✓ | × | × | Polarisation | 5 | ~0.1 | ~0.5 |
| BOTDR +WDM | [176] | ~0.05 | ~5 | × | ✓ | × | × | Polarisation | 1 | ~1 | ~50,000 |
| BOTDR + Raman | [177] | ~0.1 | ~5 | ✓ | ✓ | × | × | _ | 1 | ~1 | ~100,000 |
| BOTDA +Au coating | [178] | ~0.01 | ~5 | ✓ | ✓ | × | × | Polarisation | 1 | ~1 | 80 |
| Raman + OTDR | [179] | ~0.01 | ~5 | × | ✓ | × | × | _ | 1 | ~1 | ~25,000 |
| Raman + Differential pulsewidth pair detection | [180] | ~0.004 | ~3 | ✓ | ✓ | × | × | _ | 1 | ~1 | 6000 |
| Distributed Sensors | Reference | Implementation | Survivability Routes | Reliability Issues | Flow-Front | Curing | Defects |
|---|---|---|---|---|---|---|---|
| Rayleigh scattering +OFDR | [172] | Expensive equipment | 2 | Cross-talk, Polarisation | × | ✓ | × |
| Rayleigh scattering | [173] | Expensive equipment | 1 | Cross-talk, Polarisation | × | ✓ | × |
| Rayleigh scattering +OFDR | [174] | Complex layup procedure | 1 | Cross-talk, Polarisation, Temperature | × | ✓ | × |
| Rayleigh scattering + OFDR | [175] | Expensive equipment | 2 | Contacts, Cross-talk | × | ✓ | × |
| BOTDR +WDM | [176] | Complex layup procedure | 1 | Cross-talk | × | ✓ | × |
| BOTDR + Raman | [177] | Complex layup procedure | 1 | _ | ✓ | ✓ | × |
| BOTDA +Au coating | [178] | Complex layup procedure, Expensive equipment | 1 | _ | ✓ | ✓ | × |
| Raman + OTDR | [179] | Complex layup procedure | 1 | Cross-talk | ✓ | ✓ | × |
| Raman + Differential pulsewidth pair detection | [180] | Complex equiment | 1 | _ | × | ✓ | × |
| Sensors Piezoresistive | Reference | Spatial Resolution (m) | Error % | Sensitivity Type Parameter | Multiplexed Sensor Number | Response Time | Sensing Range (m) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Temperature | Strain | Curvature | Other | (s) | ||||||
| Graphene | [183] | ~0.04 | ~6 | ✓ | ✓ | ✓ | ✓ | Resistance | 6 sensors | ~5 | Semi-intergated response |
| CNT | [184] | ~0.04 | ~8 | ✓ | ✓ | ✓ | ✓ | Resistance | 5 sensors | ~2 | Semi-intergated response |
| Reduce Graphene oxide | [185] | _ | ~4 | ✓ | × | ✓ | ✓ | Resistance | 1 sensor | ~1 | Intergated response |
| CNT | [186] | ~0.03 | ~5 | ✓ | ✓ | ✓ | × | Resistance | 1 sensors | ~1 | Intergated response |
| MWCNT | [187] | ~0.02 | ~5 | ✓ | ✓ | ✓ | × | Resistance | 1 sensors | ~1 | Semi-intergated response |
| Graphene | [188] | ~0.03 | ~3 | ✓ | ✓ | ✓ | ✓ | Resistance | 3 sensors | ~2 | Semi-intergated response |
| Reduce Graphene oxide | [189] | _ | ~1 | ✓ | ✓ | ✓ | ✓ | Resistance | 3 sensors | ~1 | Semi-intergated response |
| Sensors Piezoresistive | Reference | Implementation | Survivability Routes | Reliability Issues | Flow-Front | Curing | Defects |
|---|---|---|---|---|---|---|---|
| Graphene | [183] | Dip/Electrodes | Robust/ whole mould | Response change | ✓ | ✓ | × |
| CNT | [184] | Dip/Electrodes | Robust/ whole mould | Response change | ✓ | ✓ | ✓ |
| Reduce Graphene oxide | [185] | Dip/Electrodes | Robust/ whole mould | Response change | ✓ | ✓ | × |
| CNT | [186] | Dip/Electrodes | Robust/ whole mould | Response change | ✓ | ✓ | × |
| MWCNT | [187] | Dip/Electrodes | Robust/ whole mould | Response change | ✓ | ✓ | × |
| Graphene | [188] | Dip/Electrodes | Robust/ whole mould | Response change | ✓ | ✓ | × |
| Reduce Graphene oxide | [189] | Dip/Electrodes | Robust/ whole mould | Response change | ✓ | ✓ | ✓ |
| Sensors | Reference | Spatial Resolution (m) | Error % | Sensitivity Type Parameter | Multiplexed Sensor Number | Response Time (s) | Sensing Range (m) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Temperature | Strain | Curvature | Other | |||||||
| Ultrasonics | [190] | ~0.001 | ~5 | × | × | × | × | _ | 1 | ~1 | ~0.05 |
| optical fibre losses | [191] | ~0.1 | ~2 | ✓ | x | ✓ | × | Pressure | 5 | ~7 | ~1 |
| infrared-thermal imaging | [192] | ~0.001 | ~1 | × | ✓ | × | × | _ | 1 | ~1 | ~10 |
| Wireless sensor | [193] | ~0.01 | ~2 | ✓ | ✓ | × | × | Resistance | 2 | ~1 | ~0.02 |
| Ultrasonics | [194] | ~0.001 | ~2 | ✓ | × | ✓ | × | _ | 8 | ~1 | ~0.05 |
| RFID | [195] | ~0.01 | ~10 | ✓ | ✓ | × | × | _ | 1 | ~5 | ~1 |
| RFID | [196] | ~0.02 | ~5 | ✓ | x | ✓ | × | 7 | ~10 | ~2 | |
| Thermocouples | [197] | ~0.05 | ~3 | ✓ | ✓ | × | × | Resistance | 7 | ~1 | ~0.5 |
| Long period gratings | [198] | ~0.001 | ~5 | ✓ | ✓ | ✓ | ✓ | Pressure | 1 | ~1 | ~0.02 |
| Long period gratings | [199] | ~0.002 | ~5 | ✓ | ✓ | ✓ | ✓ | _ | 1 | ~1 | ~0.02 |
| Sensors | Reference | Implementation | Survivability Routes | Reliability Issues | Flow-Front | Curing | Defects |
|---|---|---|---|---|---|---|---|
| Ultrasonics | [190] | manual | 1 | large errors, | × | × | ✓ |
| optical fibre losses | [191] | layup breakages | 3 | cross-talk | × | ✓ | × |
| infrared-thermal imaging | [192] | complex equipment | 1 | _ | ✓ | ✓ | ✓ |
| Wireless sensor | [193] | complex sensor | 1 | contacts, cross-talk | × | ✓ | × |
| Ultrasonics | [194] | complex layup | 4 | cross-talk | ✓ | ✓ | × |
| RFID | [195] | Fragile | 1 | _ | × | ✓ | ✓ |
| RFID | [196] | complex layup | 7 | _ | × | ✓ | × |
| Thermocouples | [197] | contacts, complex layup | 7 | _ | ✓ | ✓ | × |
| Long period gratings | [198] | complex interrogation scheme | 1 | cross-talk, | ✓ | ✓ | × |
| Long period gratings | [199] | complex interrogation scheme | 1 | cross-talk, | ✓ | ✓ | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allsop, T.; Tahir, M.W. Review: Sensing Technologies for the Optimisation and Improving Manufacturing of Fibre-Reinforced Polymeric Structures. J. Compos. Sci. 2025, 9, 343. https://doi.org/10.3390/jcs9070343
Allsop T, Tahir MW. Review: Sensing Technologies for the Optimisation and Improving Manufacturing of Fibre-Reinforced Polymeric Structures. Journal of Composites Science. 2025; 9(7):343. https://doi.org/10.3390/jcs9070343
Chicago/Turabian StyleAllsop, Thomas, and Mohammad W. Tahir. 2025. "Review: Sensing Technologies for the Optimisation and Improving Manufacturing of Fibre-Reinforced Polymeric Structures" Journal of Composites Science 9, no. 7: 343. https://doi.org/10.3390/jcs9070343
APA StyleAllsop, T., & Tahir, M. W. (2025). Review: Sensing Technologies for the Optimisation and Improving Manufacturing of Fibre-Reinforced Polymeric Structures. Journal of Composites Science, 9(7), 343. https://doi.org/10.3390/jcs9070343






