Feasibility of the Maturity Concept for Strength Prediction in Geopolymer Based Materials
Abstract
1. Introduction
2. Materials and Methods
2.1. Raw Materials
2.1.1. Fly Ash
2.1.2. GGBFS
2.1.3. Alkali Solution
2.1.4. Aggregate
2.2. Mix Design and Testing Methods
3. Results
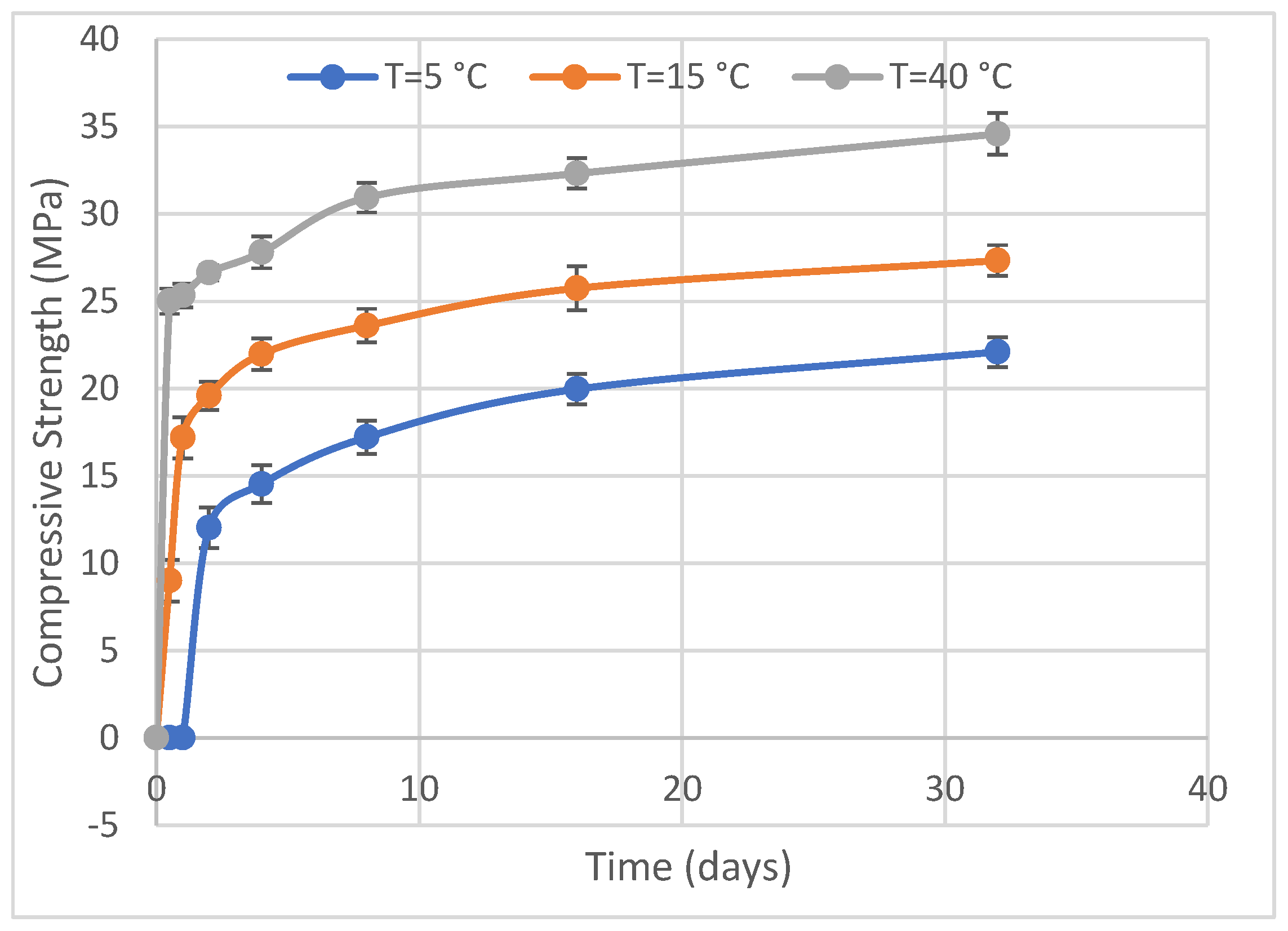
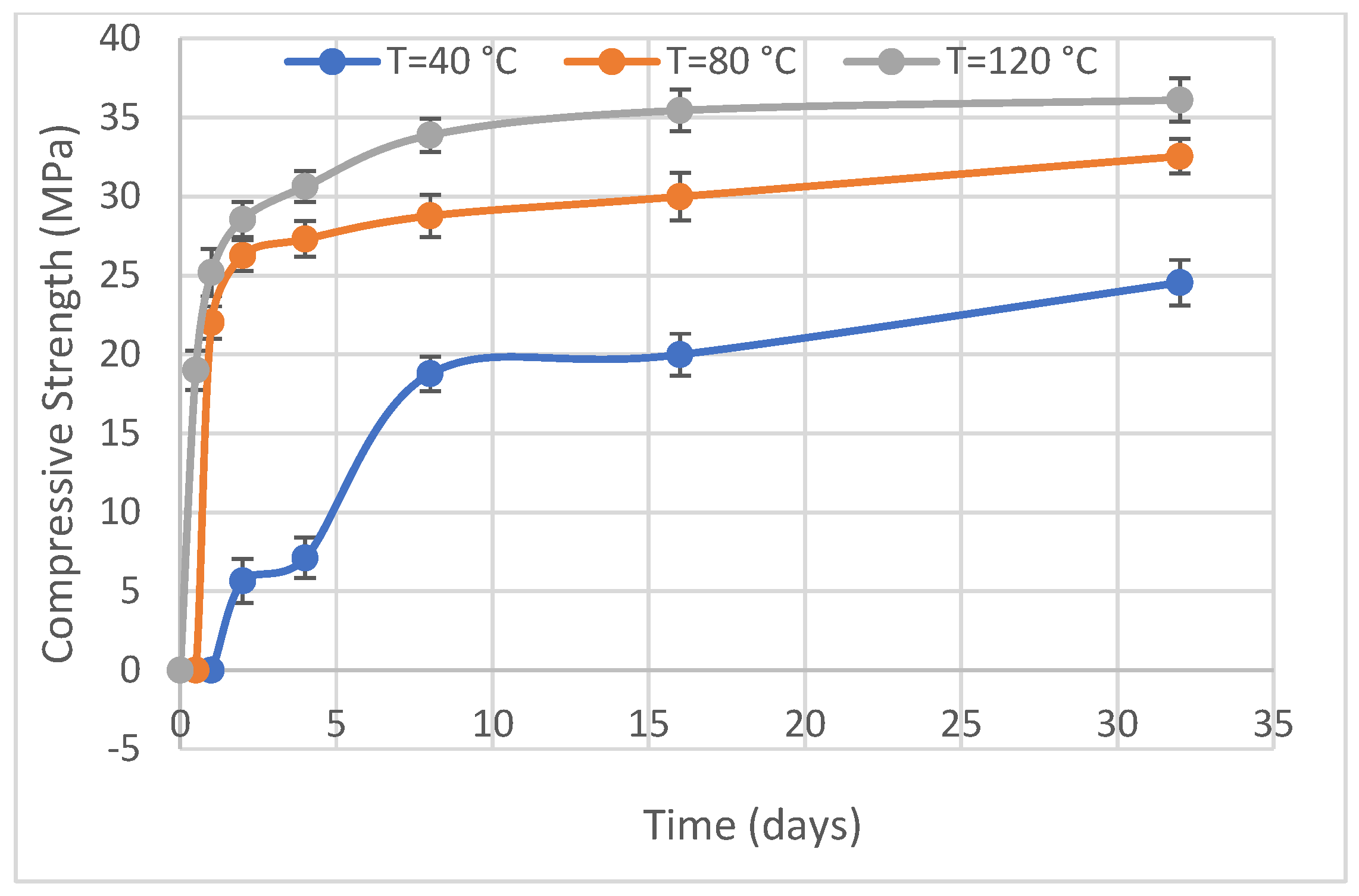
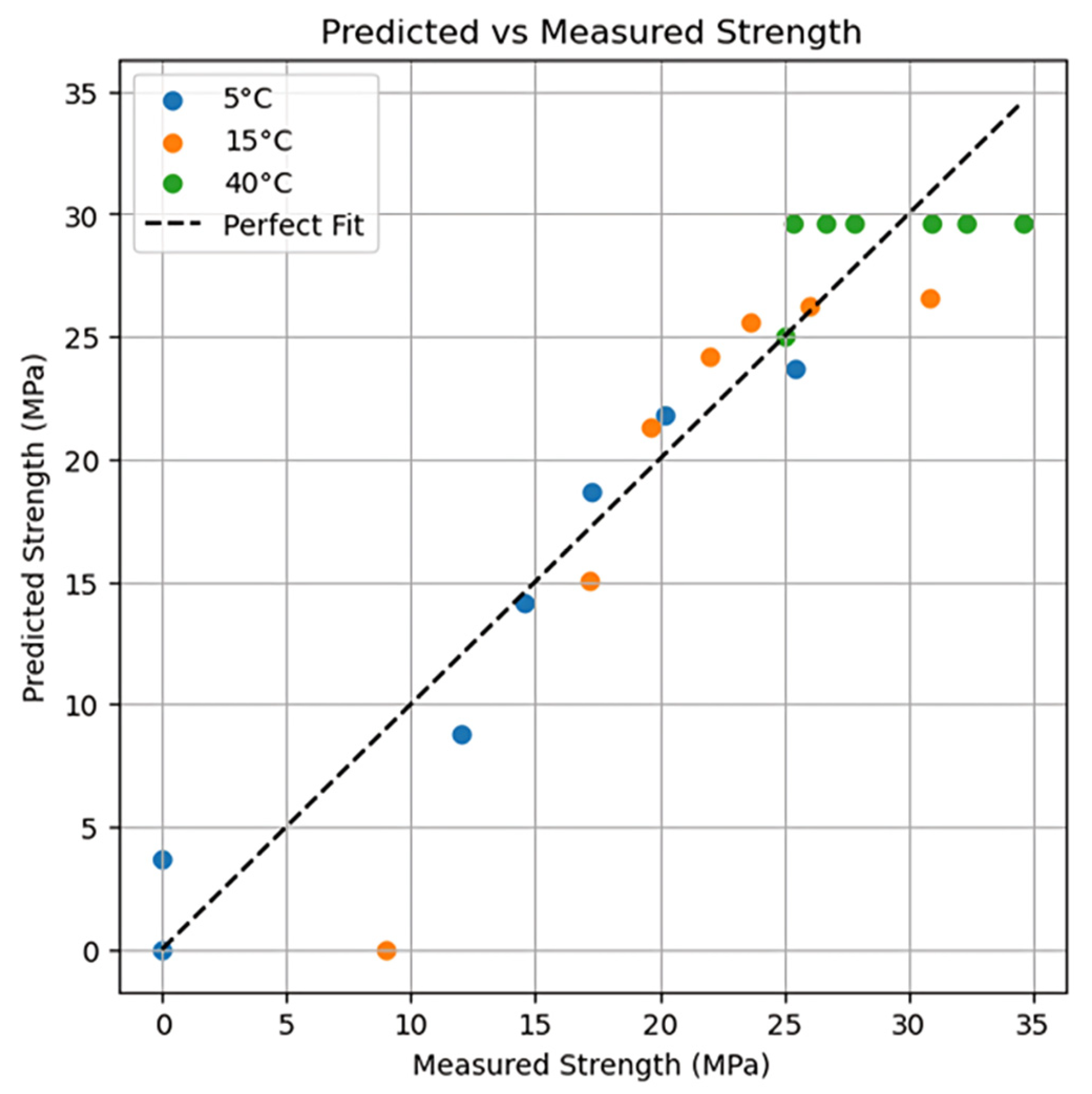
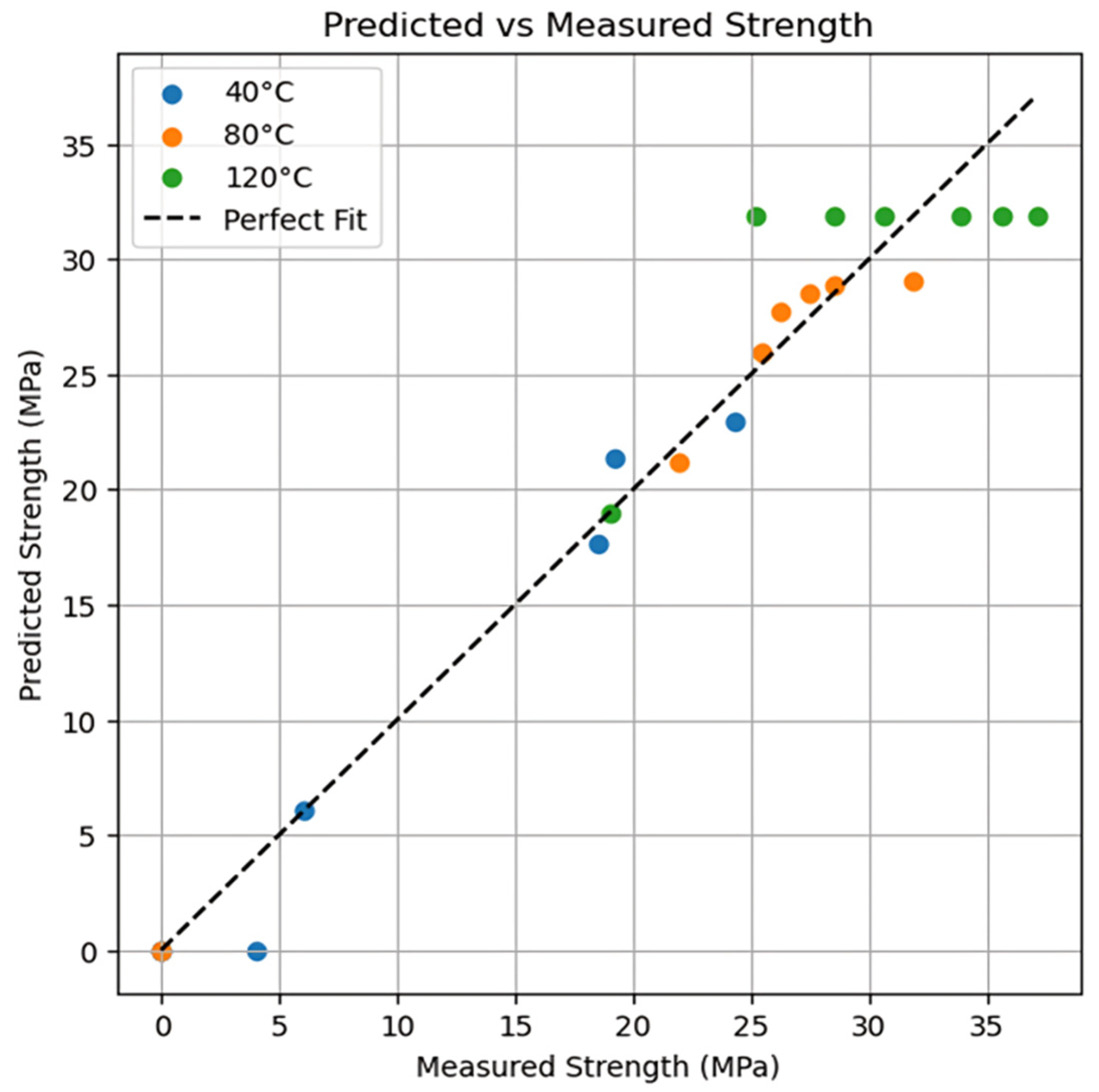
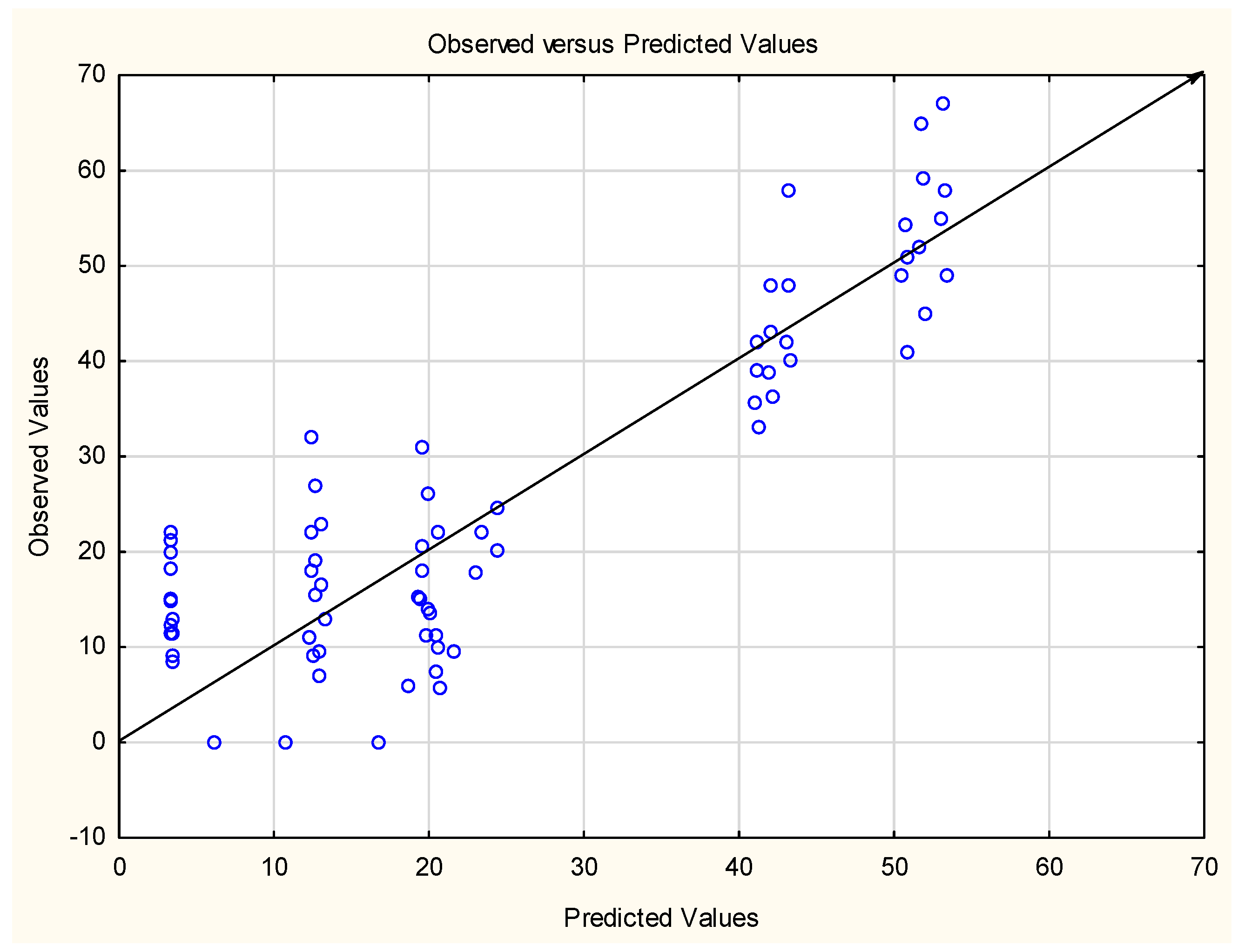
3.1. Compressive Strength of Geopolymer Mortars
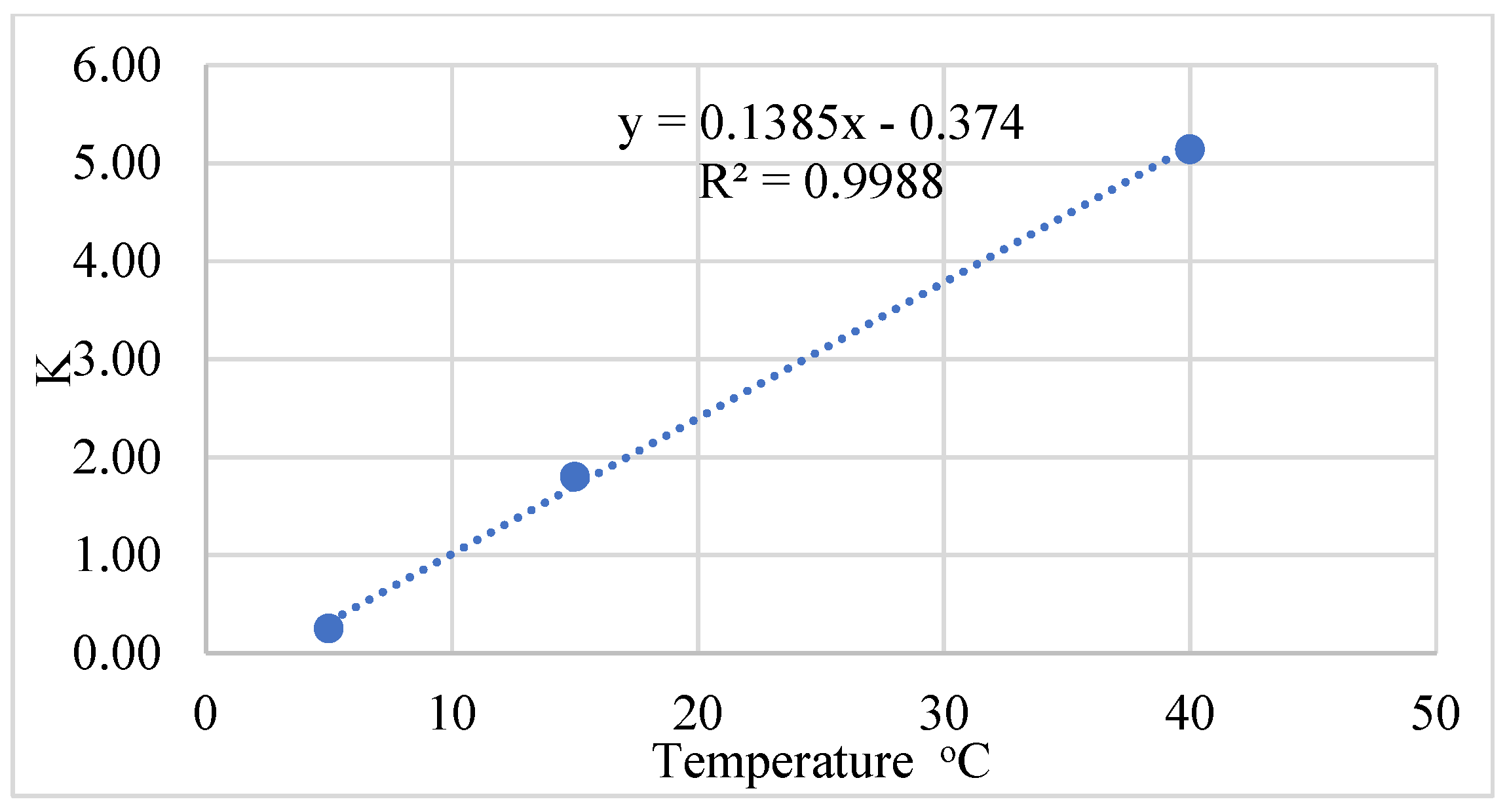
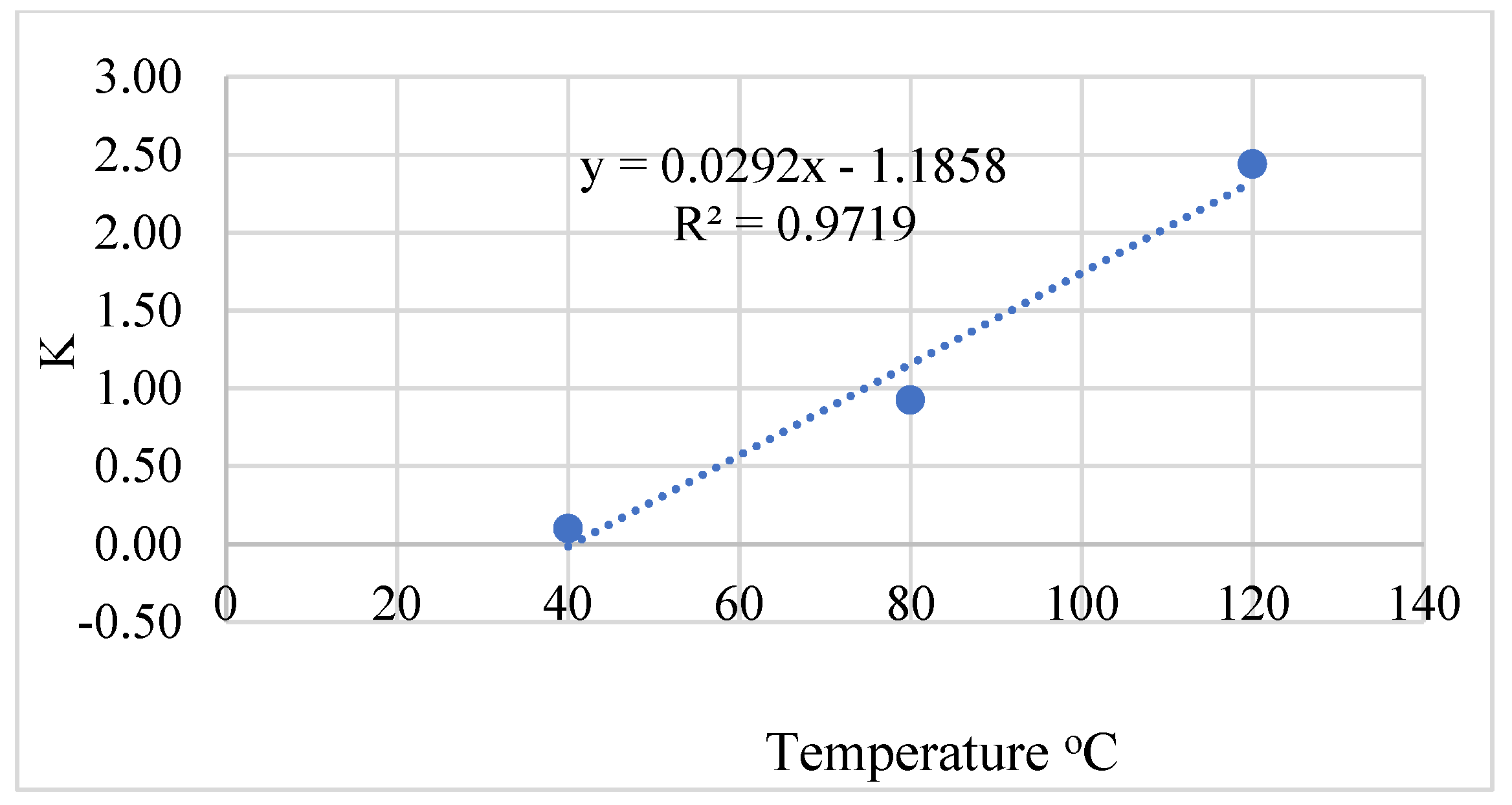
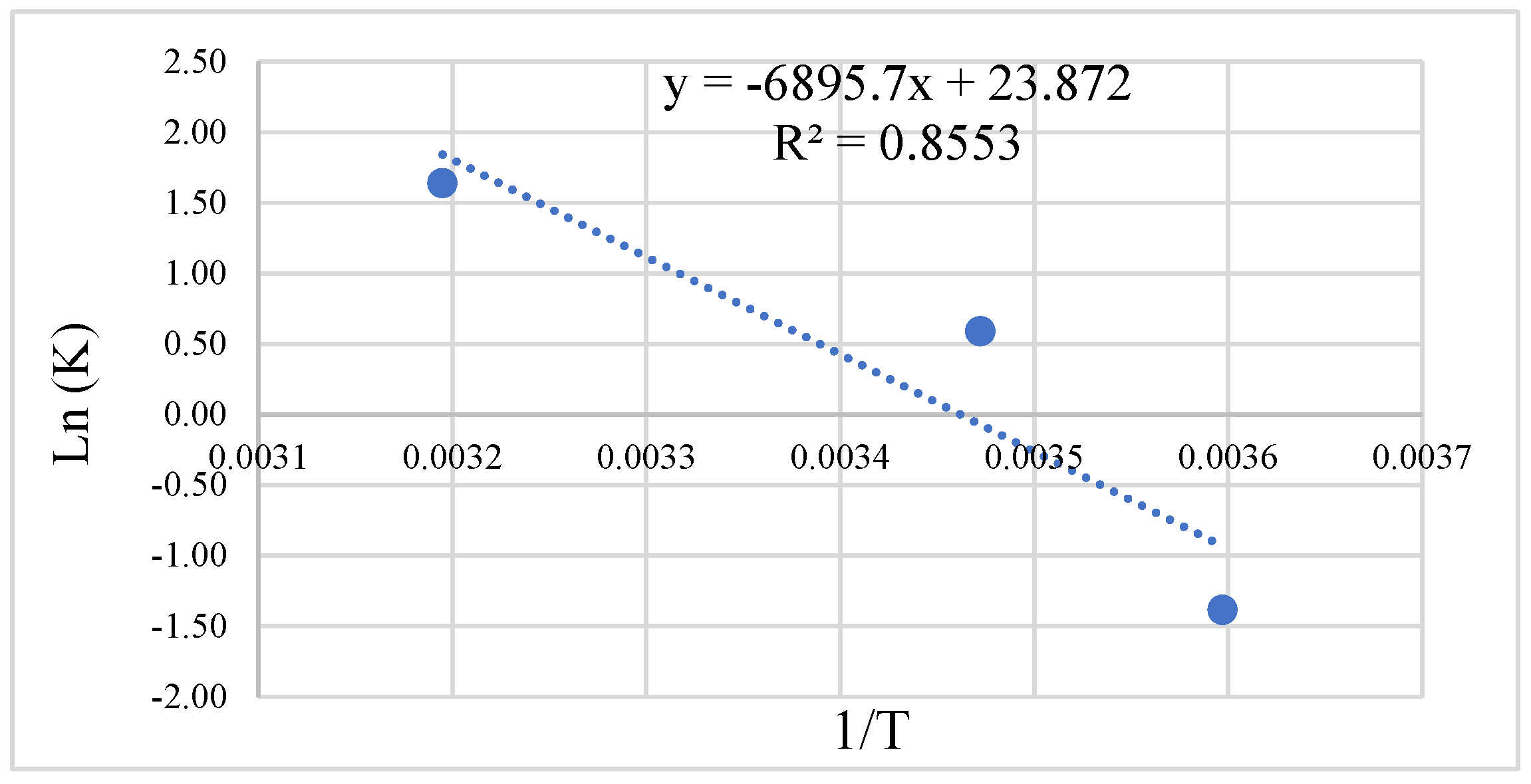
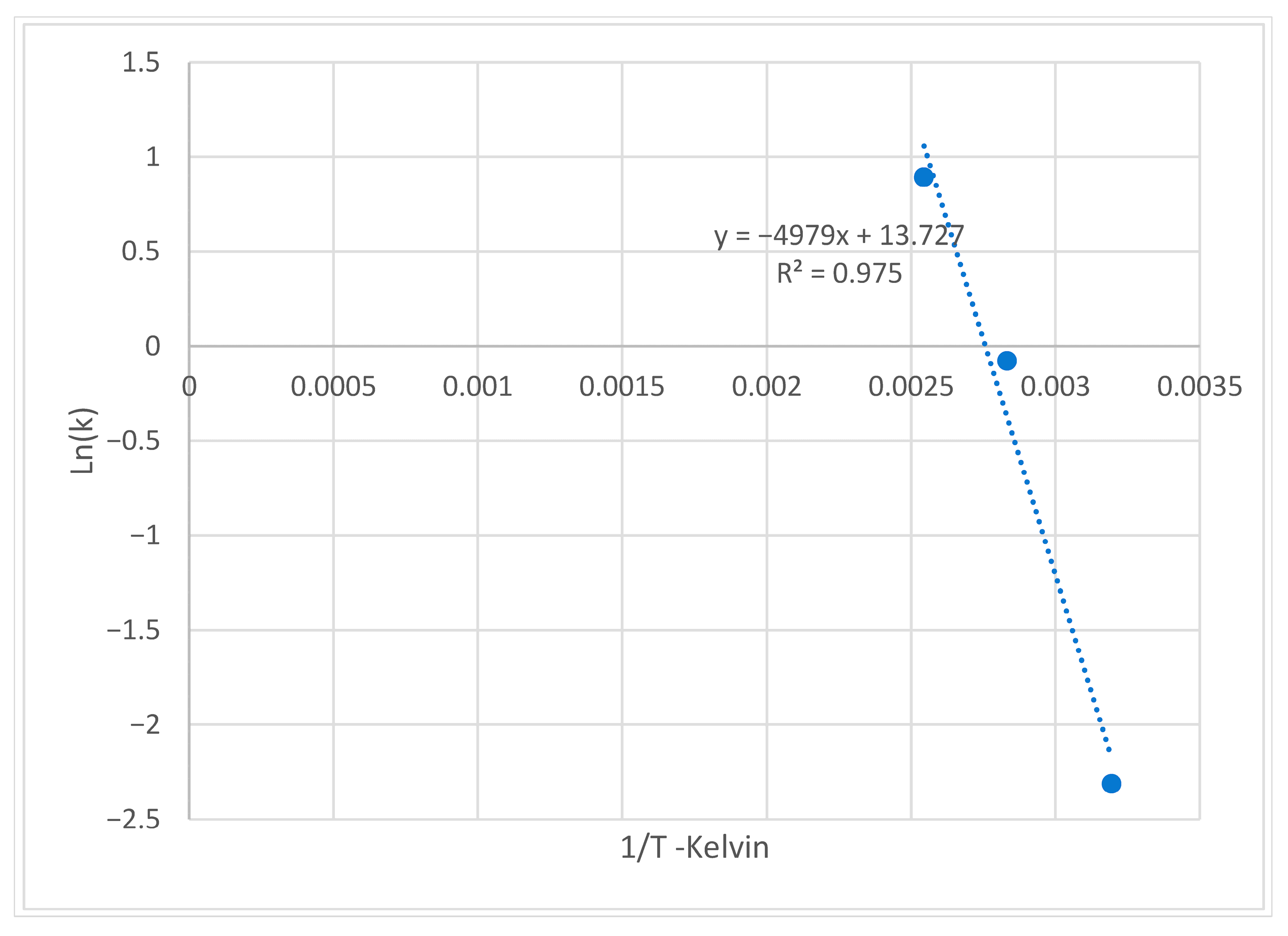
3.2. Activation Energy and Datum Temperature
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alonso, S.; Palomo, A. Alkaline activation of metakaolin and calcium hydroxide mixtures: Influence of temperature, activator concentration and solids ratio. Mater. Lett. 2001, 47, 55–62. [Google Scholar] [CrossRef]
- Thomas, B.S.; Yang, J.; Bahurudeen, A.; Chinnu, S.N.; Abdalla, J.A.; Hawileh, R.A.; Hamada, H.M. Geopolymer concrete incorporating recycled aggregates: A comprehensive review. Clean. Mater. 2022, 3, 100056. [Google Scholar] [CrossRef]
- Shehata, N.; Mohamed, O.A.; Sayed, E.T.; Abdelkareem, M.A.; Olabi, A.G. Geopolymer concrete as green building materials: Recent applications, sustainable development and circular economy potentials. Sci. Total Environ. 2022, 836, 155577. [Google Scholar] [CrossRef] [PubMed]
- Tayeh, B.A.; Hamada, H.M.; Almeshal, I.; Bakar, B.H.A. Durability and mechanical properties of cement concrete comprising pozzolanic materials with alkali-activated binder: A comprehensive review. Case Stud. Constr. Mater. 2022, 17, e01429. [Google Scholar] [CrossRef]
- Bin, F.; Hosseini, S.; Chen, J.; Samui, P.; Fattahi, H.; Jahed Armaghani, D. Proposing Optimized Random Forest Models for Predicting Compressive Strength of Geopolymer Composites. Infrastructures 2024, 9, 181. [Google Scholar] [CrossRef]
- Kampli, G.; Chickerur, S.; Chitawadagi, M. IoT system implementation for real-time concrete strength prediction: Experimental design, variance evaluation, cost analysis, and implementation ease. Innov. Infrastruct. Solut. 2024, 9, 260. [Google Scholar] [CrossRef]
- Nandhini, K.; Karthikeyan, J. The early-age prediction of concrete strength using maturity models: A review. J. Build. Pathol. Rehabil. 2021, 6, 7. [Google Scholar] [CrossRef]
- Miller, D.; Ho, N.M.; Talebian, N. Monitoring of in-place strength in concrete structures using maturity method—An overview. Structures 2022, 44, 1081–1104. [Google Scholar] [CrossRef]
- Sun, B.; Noguchi, T.; Cai, G.; Chen, Q. Prediction of early compressive strength of mortars at different curing temperature and relative humidity by a modified maturity method. Struct. Concr. 2021, 22, E732–E744. [Google Scholar] [CrossRef]
- Carino, N. The Maturity Method: Theory and Application. Cem. Concr. Aggreg. 1984, 6, 61–73. [Google Scholar] [CrossRef]
- Fib Model Code. Fib Model Code for Concrete Structures; Ernst & Sohn Publishing Company: Berlin, Germany, 2010. [Google Scholar]
- EN 197-1; Cement—Part 1: Composition, Specifications and Conformity Criteria for Common Cements. European Committee for Standardization: Brussels, Belgium, 2011.
- Soutsos, M.; Vollpracht, A.; Kanavaris, F. Applicability of fib model code’s maturity function for estimating the strength development of GGBS concretes. Constr. Build. Mater. 2020, 264, 120157. [Google Scholar] [CrossRef]
- ASTM C1074-17; Standard Practice for Estimating Concrete Strength by the Maturity Method. ASTM Internationals: West Conshohocken, PA, USA, 2017.
- Lee, C.H.; Hover, K.C. Compatible Datum Temperature and Activation Energy for Concrete Maturity. ACI Mater. J. 2016, 113, 197–206. [Google Scholar] [CrossRef]
- Vollpracht, A.; Gluth, G.J.; Rogiers, B.; Uwanuakwa, I.D.; Phung, Q.T.; Villagran Zaccardi, Y.; Thiel, C.; Vanoutrive, H.; Etcheverry, J.M.; Gruyaert, E. Kamali-Bernard S. Report of RILEM TC 281-CCC: Insights into factors affecting the carbonation rate of concrete with SCMs revealed from data mining and machine learning approaches. Mater. Struct. 2024, 57, 206. [Google Scholar] [CrossRef]
- Yang, K.H.; Mun, J.S.; Cho, M.S. Effect of Curing Temperature Histories on the Compressive Strength Development of High-Strength Concrete. Adv. Mater. Sci. Eng. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Medrano, C.T.; Peña-Rodríguez, G.; García-Páez, I.H. Determination of correlation of compressive strength with maturity of concrete mixed with accelerator. J. Phys. Conf. Ser. 2019, 1386, 012066. [Google Scholar] [CrossRef]
- Geng, D.J.; Dai, N.; Jin, X.S.; Miao, E.X. Comparison of calculating methods and applications of different concrete maturity. J. Phys. Conf. Ser. 2021, 2011, 012022. [Google Scholar] [CrossRef]
- Sun, Y.; Lee, H.S. Determination of coefficient “s” and apparent activation energy for fib model code’s maturity-based strength function when applied to fly ash concrete. Constr. Build. Mater. 2023, 409, 133643. [Google Scholar] [CrossRef]
- Soutsos, M.; Kanavaris, F.; Hatzitheodorou, A. Critical analysis of strength estimates from maturity functions. Case Stud. Constr. Mater. 2018, 9, e00183. [Google Scholar] [CrossRef]
- van Deventer, J.S.J.; White, C.E.; Myers, R.J. A Roadmap for Production of Cement and Concrete with Low-CO2 Emissions. Waste Biomass Valorization 2021, 12, 4745–4775. [Google Scholar] [CrossRef]
- Duxson, P.; Fernández-Jiménez, A.; Provis, J.L.; Lukey, G.C.; Palomo, A.; van Deventer, J.S.J. Geopolymer technology: The current state of the art. J. Mater. Sci. 2007, 42, 2917–2933. [Google Scholar] [CrossRef]
- Efe, M.; Öz, A.; Bayrak, B.; Kaplan, G.; Aydın, A.C. Effect of Na2SiO3/NaOH rate and natural zeolite content on basalt fiber reinforced eco-efficient slag-based geopolymer mortar synthesis. Arch. Civ. Mech. Eng. 2024, 24, 215. [Google Scholar] [CrossRef]
- Premkumar, R.; Ramesh, B.C.; Meyyappan, P.L.; Shanmugasundaram, M. Influence of Na2SiO3/NaOH Ratio on Calcined Magnesium Silicate Based Geopolymer—Experimental and Predictive Study. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2023, 38, 1077–1085. [Google Scholar] [CrossRef]
- Jamal, A.S.; Bzeni, D.K.H.; Shi, J. Thermal and mechanical performance of lightweight geopolymer concrete with pumice aggregate. Struct. Concr. 2024, 25, 349–364. [Google Scholar] [CrossRef]
- Arioz, O.; Bzeni, D.K.H.; Zangy, R.R.A.; Arioz, E. Properties of slag-based geopolymer pervious concrete for ambient curing condition. IOP Conf. Ser. Mater. Sci. Eng. 2020, 737, 012068. [Google Scholar] [CrossRef]
- ASTM C1437:2007; Standard Test Method for Flow of Hydraulic Cement Mortar. ASTM Internationals: West Conshohocken, PA, USA, 2007.
- Hardjasaputra, H.; Cornelia, M.; Gunawan, Y.; Surjaputra, I.V.; Lie, H.A.; Rachmansyah. Study of mechanical properties of fly ash-based geopolymer concrete. IOP Conf. Ser. Mater. Sci. Eng. 2019, 615, 012009. [Google Scholar] [CrossRef]
- ASTM C 109/C 109M-08; Compressive Strength of Hydraulic Cement Mortars (Using 2-in. or [50-mm] Cube Specimens)1. ASTM Internationals: West Conshohocken, PA, USA, 2009.
- Davidovits, J. Geopolymer Cement a Review, Published in Geopolymer Science and Technics, Technical Paper #21, Geopolymer Institute Library. 2013, p. 6. Available online: www.geopolymer.org (accessed on 21 June 2025).
- Shilar, F.A.; Ganachari, S.V.; Patil, V.B.; Khan, T.M.Y.; Javed, S.; Baig, R.U. Optimization of Alkaline Activator on the Strength Properties of Geopolymer Concrete. Polymers 2022, 14, 2434. [Google Scholar] [CrossRef]
- Mohammed, A.S.S.K.; Géber, R. Effect of liquid-solid ratio on metakaolin-based geopolymer binder properties. Pollack Period. 2025, 20, 110–116. [Google Scholar] [CrossRef]
- Mohammed, A.A.; Ahmed, H.U.; Mosavi, A. Survey of Mechanical Properties of Geopolymer Concrete: A Comprehensive Review and Data Analysis. Materials 2021, 14, 4690. [Google Scholar] [CrossRef]
- Ferreira, L.; Branco, F.G.; Júlio, E. Maturity Method for Alkali-Activated Mortar Mixtures. In Proceedings of the ICCS13 First International Conference on Concrete Sustainability, Tokyo, Japan, 27–29 May 2013; pp. 459–465. [Google Scholar]
- Adam, A.A.; Horianto, X.X.X. The Effect of Temperature and Duration of Curing on the Strength of Fly Ash Based Geopolymer Mortar. Procedia Eng. 2014, 95, 410–414. [Google Scholar] [CrossRef]
- Hassan, A.; Arif, M.; Shariq, M. Effect of curing condition on the mechanical properties of fly ash-based geopolymer concrete. SN Appl. Sci. 2019, 1, 1694. [Google Scholar] [CrossRef]
- Muhammad, N.; Baharom, S.; Amirah Mohamed Ghazali, N.; Asiah Alias, N. Effect of Heat Curing Temperatures on Fly Ash-Based Geopolymer Concrete. Int. J. Eng. Technol. 2019, 8, 15–19. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Abdalla, A.A.; Mohammed, A.S.; Mohammed, A.A.; Mosavi, A. Statistical Methods for Modeling the Compressive Strength of Geopolymer Mortar. Materials 2022, 15, 1868. [Google Scholar] [CrossRef] [PubMed]


| Oxides (%) | SiO2 | Al2O3 | Fe2O3 | CaO | MgO | MnO | SO3 | LOI |
|---|---|---|---|---|---|---|---|---|
| FA | 62.71 | 28.31 | 3.39 | 0.84 | 0.40 | -- | 0.38 | 0.46 |
| GGBFS | 38 | 12 | 0.8 | 34 | 11 | 0.7 | 1.5 | 0.7 |
| Mix Designation | Source Material | B:S:G | A/B | Na2SiO3/NaOH | Molarity of NaOH | Curing Temp. °C | Curing Time |
|---|---|---|---|---|---|---|---|
| M1 | GGBFS | 1: 2.75:0 | 0.7 | 1 | 12 | 5, 15, 40 | 0.5, 1, 2, 4, 8 and 32 days |
| M2 | FA | 1:2.75:0 | 0.7 | 1 | 12 | 40, 80, 120 | |
| C1 | GGBFS | 1:2:2.86 | 0.45 | 1 | 12 | 15, 40, 80 | 2, 4, 8 days |
| C2 | FA | 1:2:2.86 | 0.45 | 1 | 12 | 15, 40, 80 |
| Mixes | Curing Temperature | Parameters | |||||
|---|---|---|---|---|---|---|---|
| T, °C | , MPa | K | to | Q = E/R (k − 1) | To (°C) | Method of Analysis | |
| Alkali-activated GGBFS-based Mortar | 5 | 25.36 | 0.256 | 0 | 6895.7 | 2.7 | Solver function in Excell |
| 15 | 25.60 | 1.82 | 0 | ||||
| 40 | 31.74 | 5.14 | 0 | ||||
| 5, 15, 40 | 25.84 | 0.564 | 0.293 | 7751.3 | 8.89 | Computer program | |
| Alkali-activated FA-based Mortar | 40 | 33.25 | 0.099 | 0 | 4979 | 40.6 | Solver function in Excell |
| 80 | 33.84 | 0.92 | 0 | ||||
| 120 | 34.77 | 2.43 | 0 | ||||
| 40, 80, 120 | 29.24 | 1.93 | 0 | 3608 | 46.67 | Computer program | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulmajid, R.R.; Bzeni, D.K.; Abed, F.H.; Hamada, H.M. Feasibility of the Maturity Concept for Strength Prediction in Geopolymer Based Materials. J. Compos. Sci. 2025, 9, 329. https://doi.org/10.3390/jcs9070329
Abdulmajid RR, Bzeni DK, Abed FH, Hamada HM. Feasibility of the Maturity Concept for Strength Prediction in Geopolymer Based Materials. Journal of Composites Science. 2025; 9(7):329. https://doi.org/10.3390/jcs9070329
Chicago/Turabian StyleAbdulmajid, Rafah R., Dillshad K. Bzeni, Farid H. Abed, and Hussein M. Hamada. 2025. "Feasibility of the Maturity Concept for Strength Prediction in Geopolymer Based Materials" Journal of Composites Science 9, no. 7: 329. https://doi.org/10.3390/jcs9070329
APA StyleAbdulmajid, R. R., Bzeni, D. K., Abed, F. H., & Hamada, H. M. (2025). Feasibility of the Maturity Concept for Strength Prediction in Geopolymer Based Materials. Journal of Composites Science, 9(7), 329. https://doi.org/10.3390/jcs9070329







