Uniaxial Compressive Stress–Strain Model for Bauxite Residue Concrete
Abstract
1. Introduction
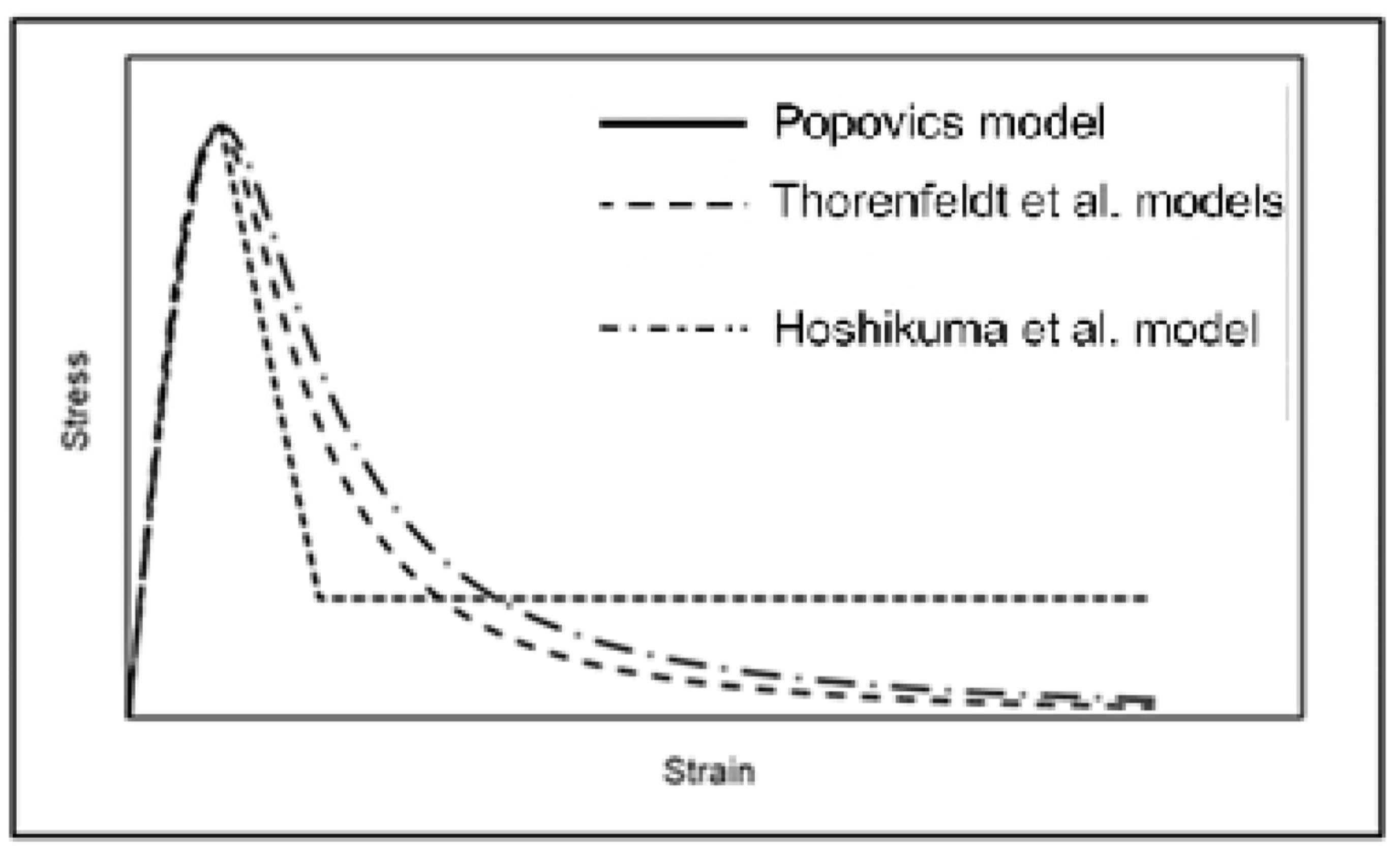
2. Review of Existing Behavior and Models of Concrete
3. Experimental Methodology
3.1. Loading System, Installation and Measuring System
3.2. Materials and Sample Preparation
4. Results
4.1. Properties of Fresh Concrete
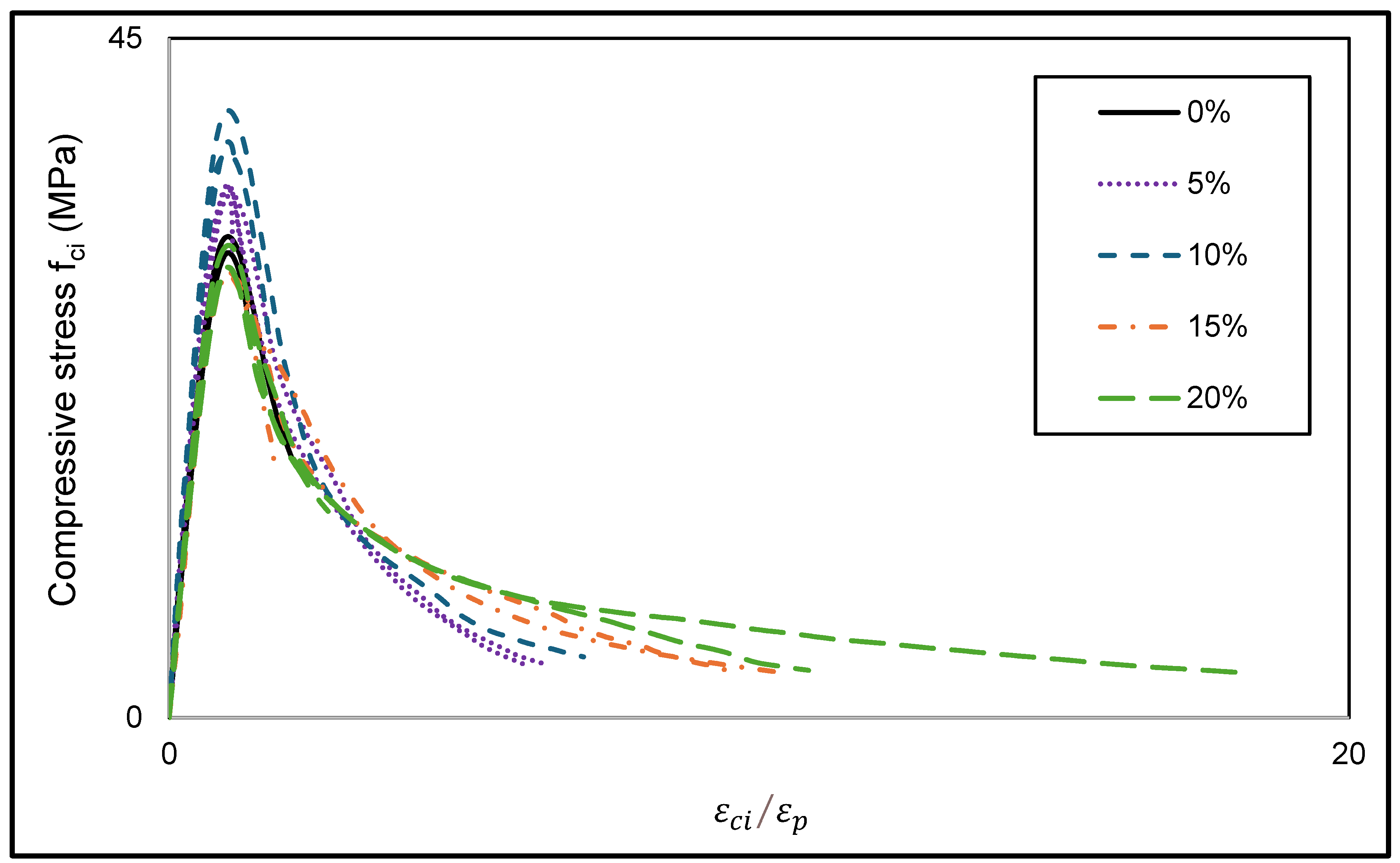
4.2. Hardened Concrete Stress–Strain Response
4.3. Observations and Failure Mode
5. Development of a Stress–Strain Model
5.1. Development of the Pre-Peak Phase
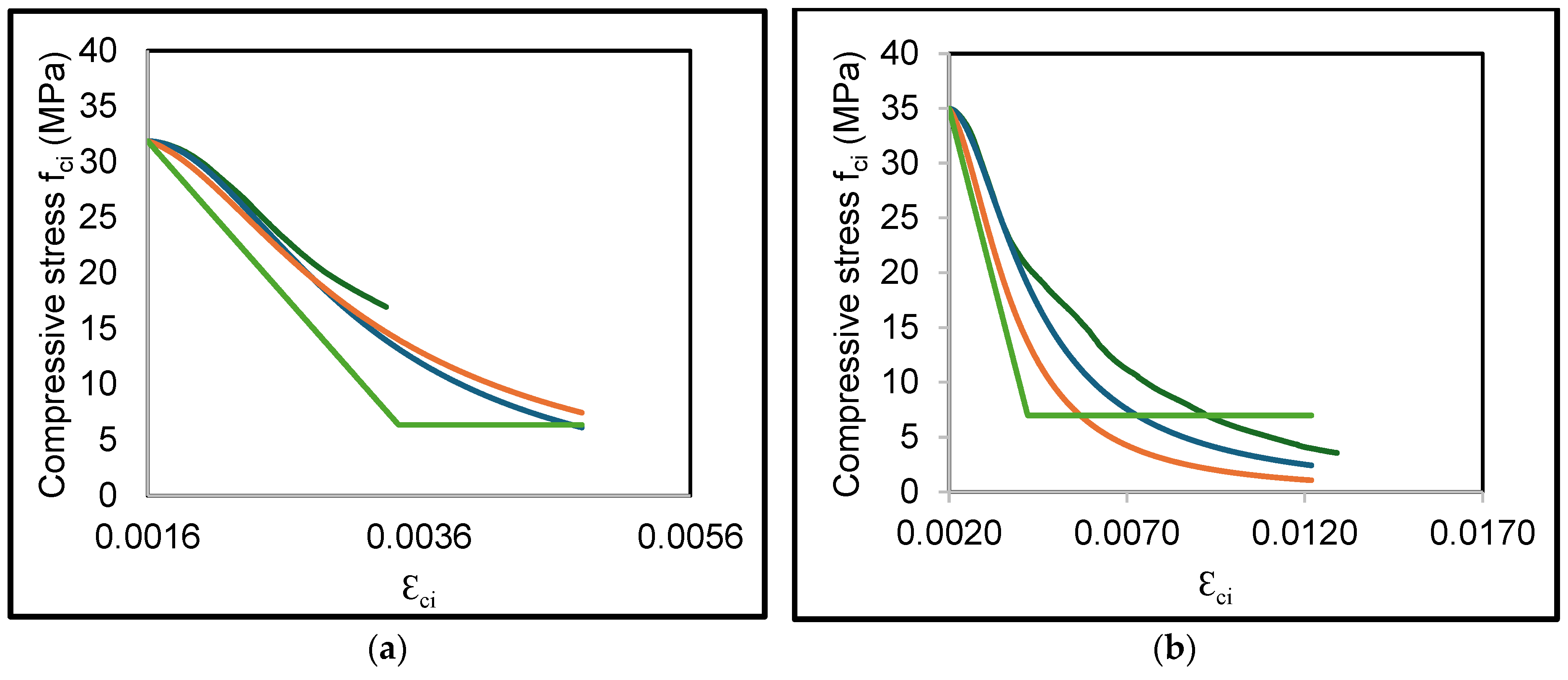
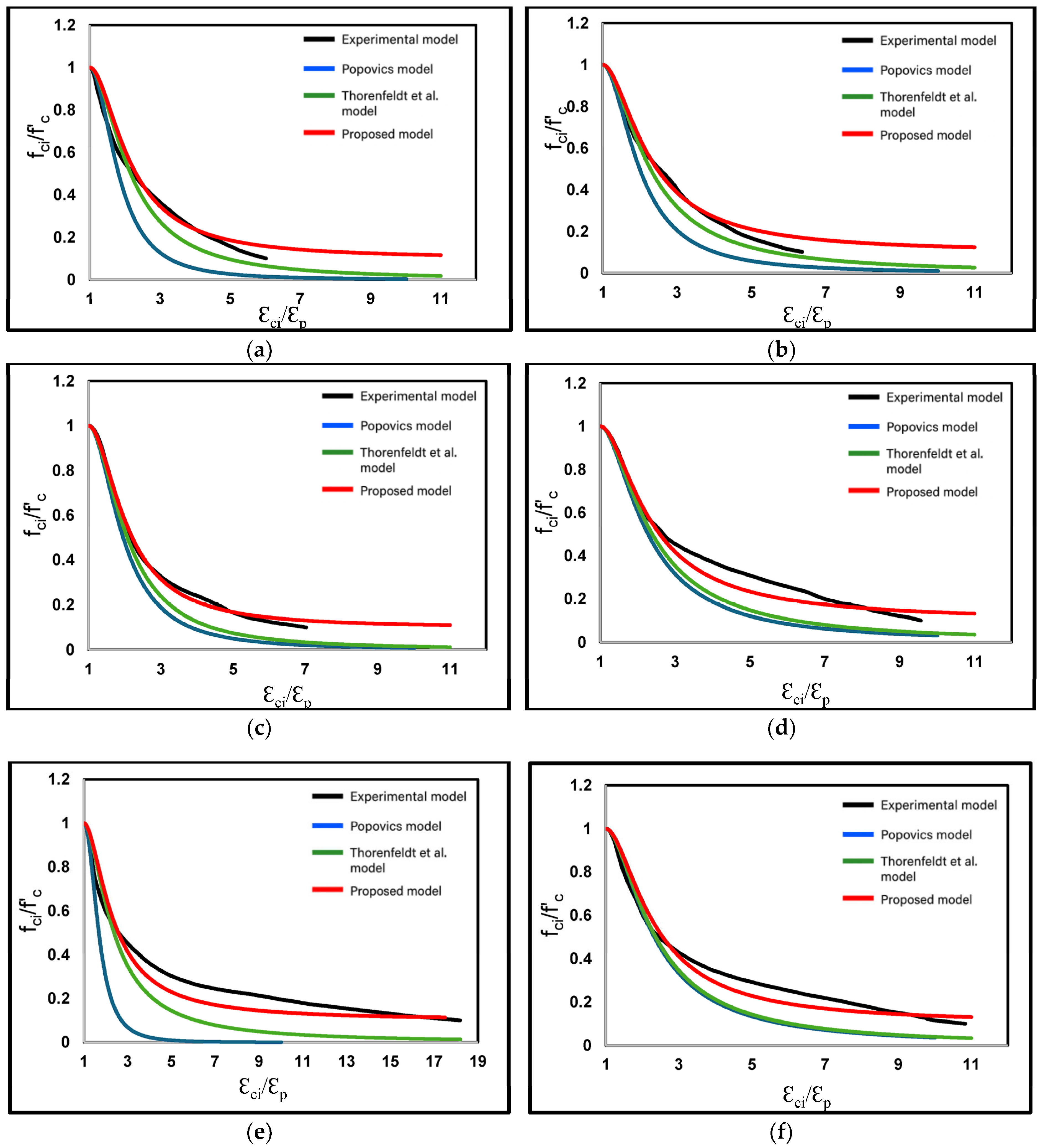
5.2. Development of the Post-Peak Phase
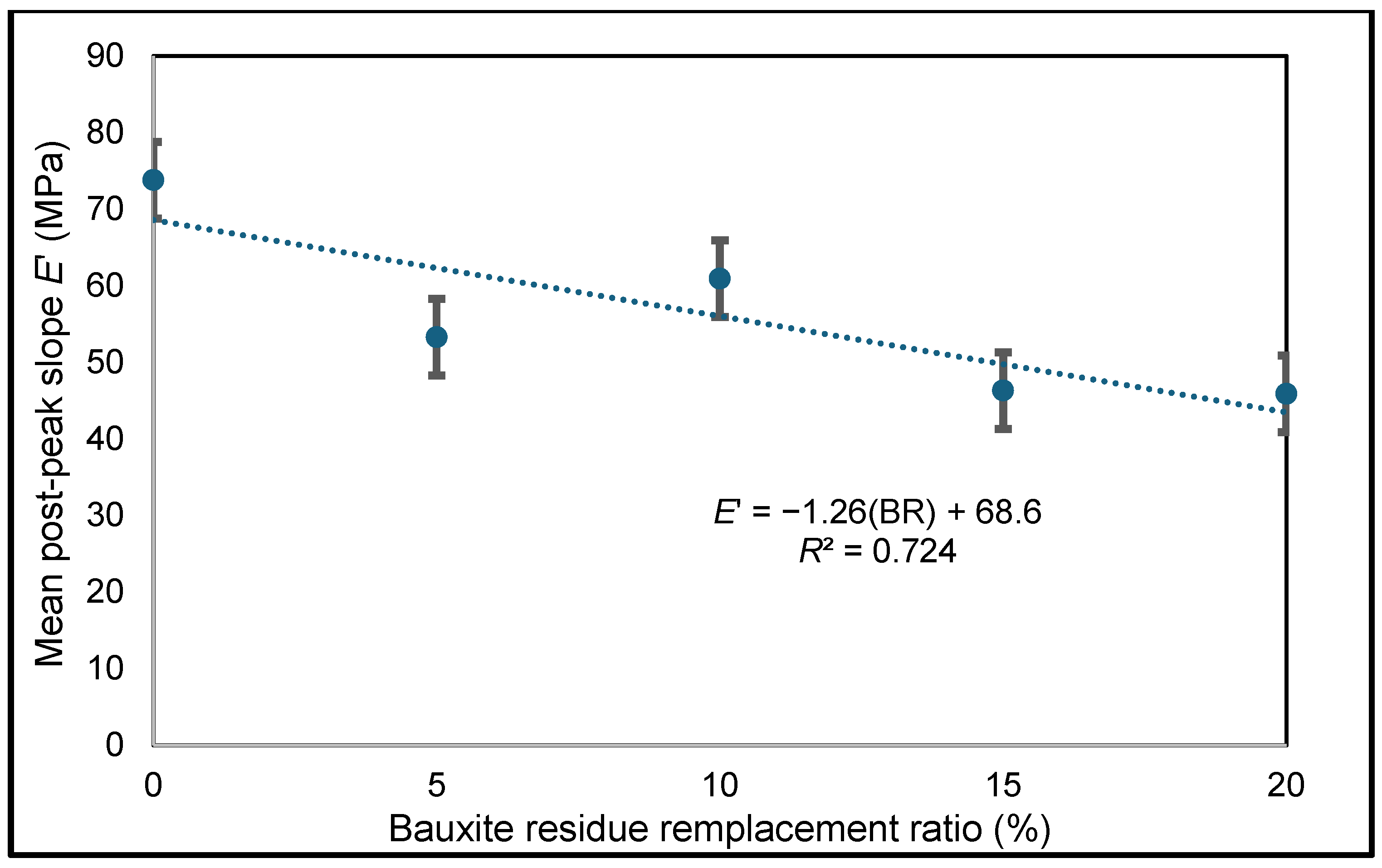
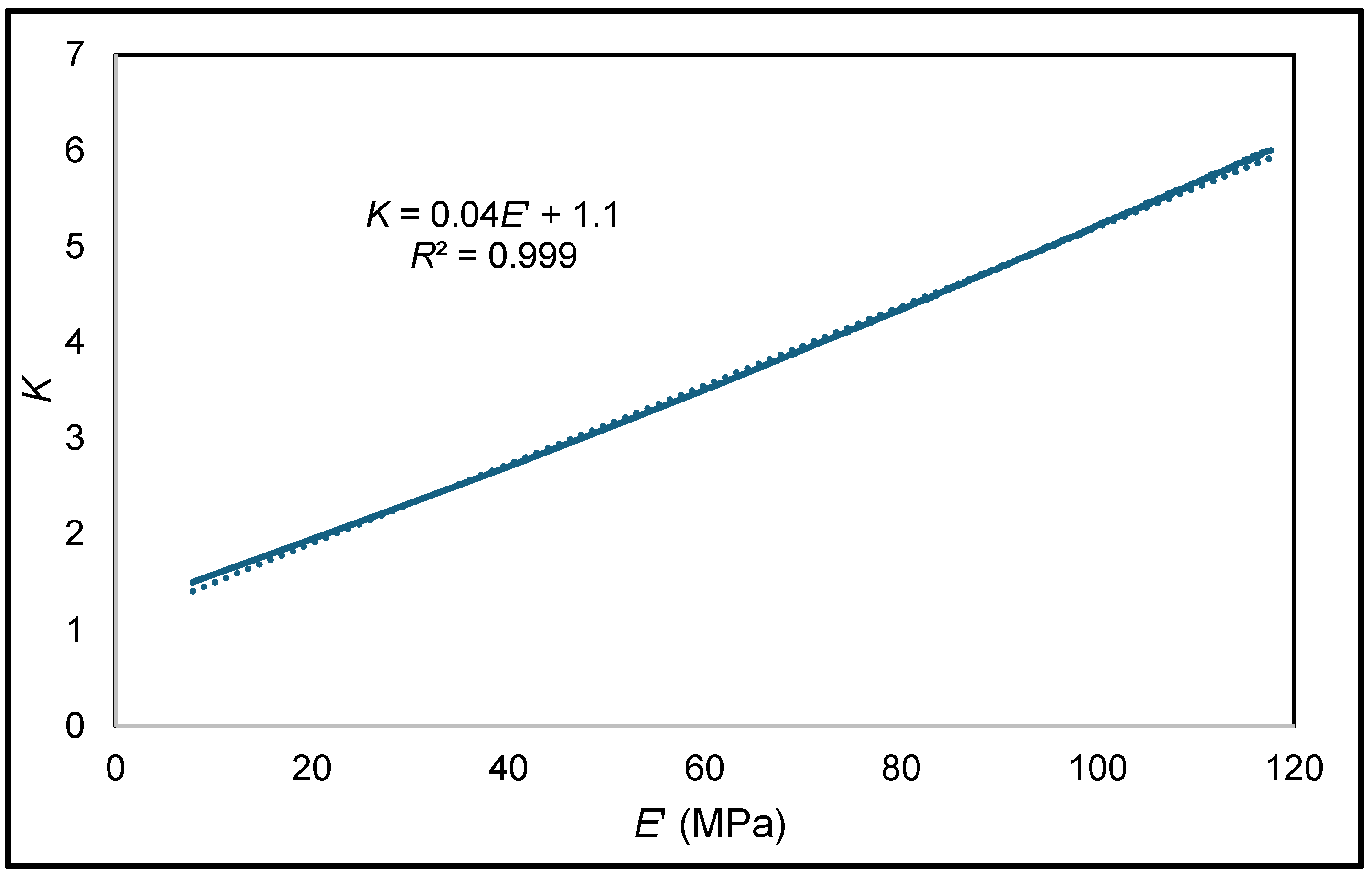
5.3. Proposal of a Post-Peak Model Adapted to Bauxite Residue Concrete
6. Conclusions
- The compressive strength and the elastic modulus significantly increased with the addition of bauxite residues relative to the control concrete lacking bauxite residue.
- The adding of bauxite residues to concrete does not significantly influence the pre-peak stress–strain response. The stress–strain response predicted by all tested models matches as well as the experimental results; however, the Popovics model provided the best fit to the experimental results and is therefore recommended for the pre-peak strain response of concrete with bauxite residue.
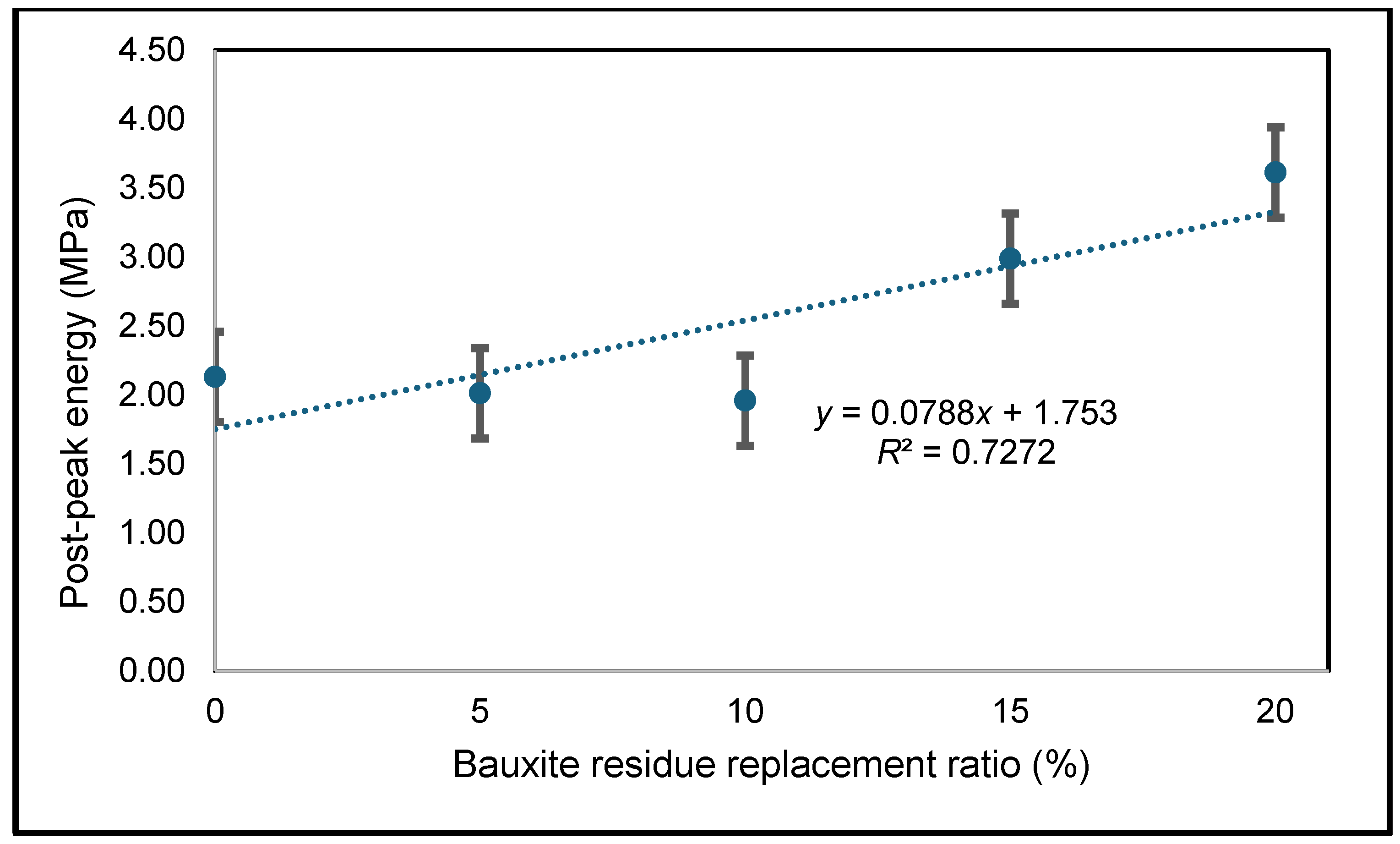
- The post-peak response of concrete resisting uniaxial compressive stress is influenced by the amount of bauxite residue used to replace cement. Increasing the amount of bauxite increases the post-peak energy.
- Existing models do not provide good predictions of the post-peak uniaxial compressive stress–strain response of concrete containing bauxite residue. This study produced a new stress–strain model to better consider the effect of the bauxite residue ratio on the post-peak rupture energy. The proposed model can adequately predict the stress–strain response of bauxite residue concrete and portland cement concrete resisting uniaxial compressive stress.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al-Amoush, H.; Abu Rajab, J. The use of electrical resistivity tomography to investigate basaltic lava tunnel based on the case study of Al-Badia cave in Jordan. Indones. J. Geosci. 2018, 5, 161–177. [Google Scholar] [CrossRef]
- Bayat, A.; Hassani, A.; Azami, O. Thermo-mechanical properties of alkali-activated slag-Red mud concrete. Road Mater. Pavement Des. 2020, 21, 411–433. [Google Scholar] [CrossRef]
- Brahami, Y.; Saeidi, A.; Fiset, M.; Ba, K. The effects of the type and quantity of recycled materials on physical and mechanical properties of concrete and mortar: A review. Sustainability 2022, 14, 14752. [Google Scholar] [CrossRef]
- Comite Euro-International du Beton. RC Elements Under Cyclic Loading: State of the Art Report; Thomas Telford Ltd.: London, UK, 1996. [Google Scholar]
- Illavarason, P.; Renjit, A.; Mohan Kumar, P. Clinical evaluation of functional vision assessment by utilizing the visual evoked potential device for cerebral palsy rehabilitation. Procedia Comput. Sci. 2018, 132, 128–140. [Google Scholar] [CrossRef]
- Collins, M.P.; Mitchell, D.; MacGregor, J.G. Structural design considerations for high-strength concrete. Concr. Int. 1993, 15, 27–34. [Google Scholar]
- Pujar, S.M.; Prakash, K.B. Effect of replacement of cement by red mud on the properties of concrete. Int. J. Sci. Eng. Res. 2014, 5, 805–814. [Google Scholar]
- Shetty, K.K.; Nayak, G.; Vijayan, V. Effect of red mud and iron ore tailings on the strength of self-compacting concrete. Eur. Sci. J. 2014, 10, 168–176. [Google Scholar]
- Ye, J.; Hu, A.; Ren, G.; Chen, M.; Tang, J.; Zhang, P.; Zhou, S.; He, Z. Enhancing sludge methanogenesis with improved redox activity of extracellular polymeric substances by hematite in red mud. Water Res. 2018, 134, 54–62. [Google Scholar] [CrossRef]
- Almusallam, T.H.; Alsayed, S.H. Stress-strain relationship of normal, high-strength and lightweight concrete. Mag. Concr. Res. 1995, 47, 39–44. [Google Scholar] [CrossRef]
- Bae, B.I.; Choi, H.K.; Lee, B.S.; Bang, C.H. Compressive behavior and mechanical characteristics and their application to stress-strain relationship of steel fiber-reinforced reactive powder concrete. Adv. Mater. Sci. Eng. 2016, 2016, 6465218. [Google Scholar] [CrossRef]
- Yang, K.H.; Mun, J.H.; Cho, M.S.; Kang, T.H.K. Stress-strain model for various unconfined concretes in compression. ACI Mater. J. 2014, 111, 819–826. [Google Scholar] [CrossRef]
- Jansen, D.C.; Shah, S.P. Effect of length on compressive strain softening of concrete. J. Eng. Mech. 1997, 123, 25–35. [Google Scholar] [CrossRef]
- Hoshikuma, J.; Kawashima, K.; Nagaya, K.; Taylor, A.W. Stress-strain model for confined reinforced concrete in bridge piers. J. Struct. Eng. 1997, 123, 624–633. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Haj, S.T.S.A.; Darvishvand, H.R.; Ebrahimi, M. Utilizing the modified Popovics model in study of effect of water to cement ratio, size and shape of aggregate in concrete behavior. Int. J. Eng. 2021, 34, 393–402. [Google Scholar] [CrossRef]
- Newman, J.; Choo, B.S. Advanced Concrete Technology: Processes; Butterworth-Heinemann: Oxford, UK, 2003. [Google Scholar]
- Ede, A.N.; Olofinnade, O.M.; Bamigboye, G.O.; Shittu, K.K.; Ugwu, E.I. Prediction of fresh and hardened properties of normal concrete via choice of aggregate sizes, concrete mix-ratios and cement. Int. J. Civ. Eng. Technol. 2017, 8, 288–301. [Google Scholar]
- Neetu, N.; Rabbani, A. Influence of size of aggregates on the compressive strength of concrete. Int. J. Eng. Dev. Res. 2017, 5, 27–30. [Google Scholar]
- Ogundipe, O.M.; Olanike, A.O.; Nnochiri, E.S.; Ale, P.O. Development of soil distribution and liquefaction potential maps for downtown area in Yangon. Civ. Eng. J. 2018, 4, 836–842. [Google Scholar] [CrossRef]
- Yu, F.; Sun, D.; Wang, J.; Hu, M. Influence of aggregate size on compressive strength of pervious concrete. Constr. Build. Mater. 2019, 209, 463–475. [Google Scholar] [CrossRef]
- Sim, J.-I.; Yang, K.-H.; Kim, H.-Y.; Choi, B.-J. Size and shape effects on compressive strength of lightweight concrete. Constr. Build. Mater. 2013, 38, 854–864. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Planas, J. Fracture and Size Effect in Concrete and Other Quasibrittle Materials; Routledge: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Markeset, G.; Hillerborg, A. Softening of concrete in compression—Localization and size effects. Cem. Concr. Res. 1995, 25, 702–708. [Google Scholar] [CrossRef]
- Miah, J.; Ali, K.; Suvash, C.P.; Miah, S.; Haque, M.M.; Islam, M.S.; Islam, M.R. Impact of partial replacement of brick coarse aggregate by waste rubber tyre on the fresh and hardened properties of concrete. Key Eng. Mater. 2021, 877, 131–137. [Google Scholar] [CrossRef]
- Kusumanjali, G.; Tejas, S.; Chatterjee, A.; Pasla, D. Utilization of bauxite residue as fine aggregate for the development of structural concrete: An approach towards sustainable construction materials. Case Stud. Constr. Mater. 2025, 22, e04348. [Google Scholar] [CrossRef]
- Salim, M.U.; Mosaberpanah, M.A.; Danish, A.; Ahmad, N.; Khalid, R.A.; Moro, C. Role of bauxite residue as a binding material and its effect on engineering properties of cementitious composites: A review. Constr. Build. Mater. 2023, 409, 133844. [Google Scholar] [CrossRef]
- Bayat, A.; Rooholamini, H.; Farahani, M.M.B. Effect of bauxite residue inclusion on the strength, shrinkage, and abrasion of alkali-activated slag concrete. Mater. Circ. Econ. 2022, 7, 331. [Google Scholar] [CrossRef]
- Choe, G.; Kang, S.; Kang, H. Mechanical properties of concrete containing liquefied red mud subjected to uniaxial compression loads. Materials 2020, 13, 854. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar] [CrossRef]
- Paultre, P. Structures en Béton Armé, 2nd ed.; Presses Internationales Polytechnique: Montreal, QC, Canada, 2017. [Google Scholar]
- ASTM C39; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2020.
- CSA A23.2; Methods of Test and Standard Practices for Concrete. Canadian Standards Association: Toronto, ON, Canada, 2019.
- CSA A23.3; Design of Concrete Structures. Canadian Standards Association: Toronto, ON, Canada, 2019.
- Thorenfeldt, M.P.; Porasz, A. Shear design for high strength concrete. CEB Bull. D’information 1989, 193, 77–83. [Google Scholar]
- CSA A23.1; Concrete Materials and Methods of Concrete Construction/Methods of Test and Standard Practices for Concrete. Canadian Standards Association: Toronto, ON, Canada, 2019.
- Tang, W.C.; Wang, Z.; Liu, Y.; Cui, H.Z. Influence of red mud on fresh and hardened properties of self-compacting concrete. Constr. Build. Mater. 2018, 178, 288–300. [Google Scholar] [CrossRef]
- Liu, Z.; Cai, C.S.; Peng, H.; Fan, F. Experimental study of the geopolymeric recycled aggregate concrete. J. Mater. Civ. Eng. 2016, 28, 04016077. [Google Scholar] [CrossRef]
- Gokceoglu, C.; Zorlu, K. A fuzzy model to predict the uniaxial compressive strength and the modulus of elasticity of a problematic rock. Eng. Appl. Artif. Intell. 2004, 17, 61–72. [Google Scholar] [CrossRef]
- Jones, N.L.; Davis, R.J.; Sabbah, W. A comparison of three-dimensional interpolation techniques for plume characterization. Groundwater 2003, 41, 411–419. [Google Scholar] [CrossRef] [PubMed]
- Wise, S. Assessing the quality for hydrological applications of digital elevation models derived from contours. Hydrol. Pro-Cesses 2000, 14, 1909–1929. [Google Scholar] [CrossRef]
- Zimmerman, D.; Pavlik, C.; Ruggles, A.; Armstrong, M.P. An experimental comparison of ordinary and universal kriging and inverse distance lightweighting. Math. Geol. 1999, 31, 375–390. [Google Scholar] [CrossRef]
- Wong, P.S.; Vecchio, F.J.; Trommels, H. VecTor2 and Formworks User’s Manual, 2nd ed.; University of Toronto: Toronto, ON, Canada, 2013. [Google Scholar]






| Percentage of Cement Replaced by BR | Cement (kg) | Fine Aggregates (kg) | Coarse Aggregates (kg) | Bauxite Residue (kg) | Water (L) | |
|---|---|---|---|---|---|---|
| Reference concrete | 0% | 370.0 | 767.5 | 1151.3 | 0 | 166.5 |
| Bauxite residue diameter <300 µm | 5% | 351.5 | 766.0 | 1149.0 | 18.5 | 169.0 |
| 10% | 333.0 | 764.5 | 1146.5 | 37.0 | 171.5 | |
| 15% | 314.5 | 762.7 | 1144.0 | 55.5 | 174.0 | |
| 20% | 296.0 | 761.1 | 1141.6 | 74.0 | 176.5 |
| Percentage of Cement Replaced by BR | Slump (mm) | Air Content (%) | Density (kg/m3) |
|---|---|---|---|
| 0% | 83 | 6.00 | 2276 |
| 5% | 57 | 5.60 | 2310 |
| 10% | 64 | 5.70 | 2355 |
| 15% | 65 | 5.60 | 2296 |
| 20% | 88 | 5.90 | 2298 |
| Percentage of Cement Replaced by BR | Test | (MPa) | (×10−3) | (GPa) | E′ (MPa) |
|---|---|---|---|---|---|
| 0% | 1 | 31.9 | 1.59 | 27.6 | 52.4 |
| 2 | 30.8 | 1.17 | 35.2 | 96.6 | |
| 3 | 30.5 | 1.19 | 35.1 | 72.3 | |
| 4 | 32.1 | 1.19 | 37.3 | – | |
| 5% | 1 | 35.3 | 1.33 | 35.0 | 50.6 |
| 2 | 35.2 | 1.31 | 35.6 | 76.0 | |
| 3 | 35.0 | 2.03 | 23.9 | 45.7 | |
| 4 | 35.6 | 1.38 | 33.7 | 59.2 | |
| 10% | 1 | 37.4 | 1.75 | 31.0 | 71.2 |
| 2 | 40.2 | 1.54 | 35.8 | 55.2 | |
| 3 | 39.6 | 1.40 | 38.8 | 100.1 | |
| 4 | 38.6 | 1.17 | 23.5 | – | |
| 15% | 1 | 29.4 | 1.25 | 32.6 | 25.0 |
| 2 | 29.5 | 1.36 | 32.1 | 42.1 | |
| 3 | 31.6 | 1.28 | 37.3 | 45.3 | |
| 4 | 31.6 | 1.27 | 27.0 | 44.6 | |
| 20% | 1 | 29.8 | 1.50 | 42.3 | 46.0 |
| 2 | 31.3 | 1.27 | 37.2 | 42.8 | |
| 3 | 29.3 | 1.18 | 34.1 | 51.9 | |
| 4 | 32.0 | 1.32 | 27.6 | 98.5 |
| Percentage of Cement Replaced by BR | Test | (MPa) | Optimal exp n | Pop-Predicted n | Pop/exp | PopM-Predicted n | PopM/exp |
|---|---|---|---|---|---|---|---|
| 0% | 1 | 31.88 | 3.47 | 3.44 | 0.99 | 2.68 | 0.77 |
| 2 | 30.81 | 3.56 | 3.39 | 0.95 | 2.61 | 0.73 | |
| 3 | 30.51 | 4.37 | 3.71 | 0.85 | 2.59 | 0.59 | |
| 4 | 32.08 | 5.59 | 4.19 | 0.75 | 2.69 | 0.48 | |
| 5% | 1 | 34.55 | 2.97 | 3.03 | 1.02 | 2.83 | 0.95 |
| 2 | 35.33 | 3.59 | 3.24 | 0.90 | 2.88 | 0.80 | |
| 3 | 35.16 | 3.65 | 3.60 | 0.99 | 2.87 | 0.79 | |
| 4 | 34.96 | 2.98 | 3.04 | 1.02 | 2.86 | 0.96 | |
| 5 | 35.57 | 4.23 | 4.31 | 1.02 | 2.89 | 0.68 | |
| 6 | 33.72 | 3.27 | 3.50 | 1.07 | 2.78 | 0.85 | |
| 10% | 1 | 37.39 | 2.91 | 2.94 | 1.01 | 3.00 | 1.03 |
| 2 | 40.22 | 3.28 | 3.29 | 1.00 | 3.17 | 0.97 | |
| 3 | 38.16 | 3.61 | 3.15 | 0.87 | 3.04 | 0.84 | |
| 4 | 39.57 | 3.67 | 3.69 | 1.01 | 3.13 | 0.85 | |
| 5 | 36.56 | 2.24 | 2.32 | 1.04 | 2.95 | 1.32 | |
| 6 | 38.56 | 6.18 | 5.68 | 0.92 | 3.07 | 0.50 | |
| 15% | 1 | 29.27 | 2.84 | 3.00 | 1.06 | 2.52 | 0.89 |
| 2 | 29.40 | 3.65 | 2.71 | 0.74 | 2.53 | 0.69 | |
| 3 | 29.54 | 3.04 | 3.35 | 1.10 | 2.54 | 0.84 | |
| 4 | 31.61 | 5.87 | 4.33 | 0.74 | 2.66 | 0.45 | |
| 5 | 31.56 | 3.84 | 3.84 | 1.00 | 2.66 | 0.69 | |
| 20% | 1 | 29.84 | 3.35 | 3.31 | 0.99 | 2.56 | 0.76 |
| 2 | 29.81 | 3.37 | 2.94 | 0.87 | 2.55 | 0.76 | |
| 3 | 31.30 | 2.96 | 3.13 | 1.06 | 2.64 | 0.89 | |
| 4 | 29.28 | 2.89 | 3.01 | 1.04 | 2.52 | 0.87 | |
| 5 | 32.01 | 3.39 | 3.46 | 1.02 | 2.68 | 0.79 | |
| Average | 0.96 | 0.80 | |||||
| Standard deviation | 0.10 | 0.18 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brahami, Y.; Fiset, M.; Saeidi, A.; Ba, K.; Vara Prasad Chavali, R. Uniaxial Compressive Stress–Strain Model for Bauxite Residue Concrete. J. Compos. Sci. 2025, 9, 318. https://doi.org/10.3390/jcs9070318
Brahami Y, Fiset M, Saeidi A, Ba K, Vara Prasad Chavali R. Uniaxial Compressive Stress–Strain Model for Bauxite Residue Concrete. Journal of Composites Science. 2025; 9(7):318. https://doi.org/10.3390/jcs9070318
Chicago/Turabian StyleBrahami, Yassine, Mathieu Fiset, Ali Saeidi, Kadiata Ba, and Rama Vara Prasad Chavali. 2025. "Uniaxial Compressive Stress–Strain Model for Bauxite Residue Concrete" Journal of Composites Science 9, no. 7: 318. https://doi.org/10.3390/jcs9070318
APA StyleBrahami, Y., Fiset, M., Saeidi, A., Ba, K., & Vara Prasad Chavali, R. (2025). Uniaxial Compressive Stress–Strain Model for Bauxite Residue Concrete. Journal of Composites Science, 9(7), 318. https://doi.org/10.3390/jcs9070318







