Analysis and Modeling of Thermogravimetric Curves of Chemically Modified Wheat Straw Filler-Based Biocomposites Using Machine Learning Techniques

Abstract

Thermogravimetric analysis (TGA) is a technique used to investigate the thermal characteristics of materials by observing fluctuations in sample mass with changes in temperature. Amid the increasing worldwide focus on sustainable materials, biocomposites have become popular for their eco-friendly characteristics. Thermal stability is a crucial factor in determining the performance of biocomposites. The present research improved thermal properties by incorporating wheat straw residual filler into an epoxy resin matrix after various chemical treatments of wheat straw fibers, such as alkali (NaOH) or a combination of silane and alkali treatments. Machine learning (ML) analysis performed in WEKA 3.0 was conducted on thermal data derived from the thermogravimetric measurements of the biocomposites. This research took into account several factors, such as filler loading, single or dual chemical treatment, and temperature, to forecast the thermal-degradation behavior during combustion. Sixteen distinct regression models were used to predict the TGA curves. The K-Nearest Neighbor (KNN) classifier outperformed the other 15 models by achieving an R-squared value of 0.9999, indicating remarkable prediction skills. The strong correlation between the experimental data and the anticipated values confirmed the accuracy of the ML computations.

1. Introduction

Natural fiber-reinforced biocomposites have become very popular alternative materials in many engineering domains because of their various advantages, like their light weight, recyclability, and better acoustic performance [1,2,3,4]. One of the most widely used techniques for manufacturing biocomposites is the use of agricultural waste as a filler in a polymer matrix [5,6,7]. Wheat, as one of the most consumed crops, is one of the largest contributors to agricultural waste in the world [8,9,10]. However, biocomposites fabricated using raw wheat straw have poor mechanical and thermal properties, as the interaction between hydrophilic raw wheat straw and hydrophobic polymer matrices is very limited [11,12,13]. Composites based on natural fibers possess enhanced mechanical and structural properties as compared with natural fibers. However, owing to the differences in biodegradability and the costs incurred during manufacturing, their applicability is limited [11,12,13]. Therefore, various chemical treatments are implemented on raw wheat fibers to decrease the hydrophilic nature of biofillers. These treatments remove various unwanted components of the fibers and improve the impregnation of polymers in the fibers, thus improving the interfacial interaction between the matrix and the fibers [14]. Due to the high ratio of length to diameter (aspect ratio), nano-fillers enhance mechanical, physical, and structural characteristics when dispersed properly in several composites [15,16,17]. Chemical treatments also significantly improve the thermal stability of biocomposites, even in high-temperature applications [18,19,20]. There have been a few instances where an ANN has been used to predict different kinetic parameters in a reaction [21]. Experimental data were used to train and test a multilayer neural network model, and a good correlation was found with the weight loss data. The attributes considered in the study were different heating rates and different polymer matrices like lignin, cellulose, and polyethylene [22]. Feedforward ANN modeling was used to predict the TGA co-combustion characteristic curves of a blend of textile dyeing sludge (TDS) and pomelo peel (PP) under O₂/N₂ and O₂/CO₂ atmospheres. It was also found that the Bayesian Regularized Network (BRN) made more reliable predictions than the radial basis function (RBF) [23]. The TGA curves of hazelnut husk–lignite coal mixtures with different proportions subjected to different heating rates were predicted using the Levenberg–Marquardt backpropagation algorithm. The performance of this model was very good, with a coefficient of determination of 0.9995 [24].

A large number of investigations have been carried out using machine learning tools for various applications in many fields, ranging from the physical sciences to the social sciences. Here, the applications of various machine-learning regression models are discussed. The linear regression model is one of the oldest and most widely used models for prediction. The authors of one study discussed the efficiency of this model, using residual plots to determine the lack of fit, performing ANOVA F-tests, t-tests, etc. [25]. A research article reported that an extreme learning machine hierarchical learning framework-based Multilayer Perceptron model converged faster and better than existing hierarchical learning methods [26]. The simple linear regression method attempts to draw the best possible line through data points. Though this method is simple, it is a very powerful and useful method [27]. The goal of one project was to estimate inflation as precisely as feasible in the United States. Researchers have employed sequential minimal organization regression (SMOreg)-based models for forecasting inflation in the United States, according to this research [28]. K-nearest-neighbor (KNN)-based classification/regression models for prediction can be used when data are very limited or when no prior information about the distribution of the sample data is available [29]. Hybrid lazy K-star-based regression learning algorithms have been successfully used to predict the future values of quality-of-service features [30]. Researchers have reported that lazy locally weighted learning-based regression models remember all previous learning experiences and that this has an interesting impact on the problem of learning to control [31,32]. Meta-additive regression methods have been successfully used to determine the efficiency of feed and water additives in reducing the prevalence of Salmonella disease [33]. Meta-bagging-based algorithms have been used to develop fraud-detection models and have successfully been applied to real-life credit-card transactions [34,35]. The Random Committee algorithm is very effective in improving the disturbance classification accuracy for power systems compared to other models [34,35]. If a large dataset contains noise, noise filtering; data reduction plays a great role, and in such cases, regression by discretization is a powerful tool for data prediction [36]. Decision Table algorithms have been used to predict driver-injury outcomes during rear-end crashes, and their performance is reasonably good [37]. M5 rule-based algorithms have been used to predict the compressive strength and ultrasonic pulse velocity of concrete mix designs, and the accuracy of these models is also very high [38]. Random-forest-based regression models are very powerful general-purpose prediction methods, and their performance has been found to be excellent in cases where several variables are much more than several observations [39]. Random-tree-based algorithms have demonstrated that they can predict data very accurately even when the size of datasets is small [40]. REPTree-based methods are very effective in recognizing static signatures from handwritten text images using different writing features like orientation, contour, centroid, etc. [41].

Machine-learning techniques, including Random Forest (RF), Multilayer Perceptron (MLP), Support Vector Machines (SVM), Decision Trees (DT), and ensemble methods, have been effectively utilized to predict the mechanical and thermal properties of composite materials. For instance, Kibrete et al. provided a comprehensive review of the application of AI in forecasting the mechanical properties of composites, highlighting the strengths and weaknesses of various machine-learning methods [42]. Additionally, ensemble models such as RF and Gradient Boosting Regressor (GBR) have been employed to predict mechanical properties, demonstrating robustness in handling complex nonlinear data [43]. Furthermore, machine-learning methods have been applied to predict the effective thermal conductivities of composite materials, showcasing their utility in modeling thermal properties [44]. These studies underscore the versatility and effectiveness of machine-learning approaches in modeling the complex relationships inherent in the mechanical and thermal properties of composite materials. The K-Nearest Neighbor (KNN) algorithm has also been successfully applied in the field of composites for predicting material properties [45]. K-Nearest Neighbor (KNN) is a lazy-learning and non-parametric supervised machine-learning algorithm. KNN algorithms do not have any bias for features. This makes this algorithm very useful as the real-world data do not follow any mathematical assumption or distribution. Because of their utility, these algorithms have been used in a variety of disciplines. In the diagnosis of heart-disease patients, KNN might obtain greater accuracy than neural network ensemble [46]. KNN-based classification methods have been used effectively for pattern recognition in some expert and intelligence systems [47]. This study highlights the effectiveness of KNN in handling complex, nonlinear data, making it a suitable choice for predicting TGA curves in biocomposites.

Thermal stability under high temperatures is an important factor when choosing a particular fiber. However, predicting thermal degradation with respect to temperature has always been a big challenge. There are several factors, like fiber loading, chemical treatments, etc., that influence the thermal-degradation behavior of the biocomposites. In this current paper, we have tried to predict the TGA behavior of the wheat straw-reinforced epoxy composites using 16 machine-learning regression models. The attributes that were taken in this study are the level of fiber loading, single chemical treatment, and double chemical treatments. The novelty of this study lies in the application of 16 machine-learning models to predict the thermal-degradation behavior of wheat straw-reinforced epoxy composites. While previous studies have primarily focused on artificial neural networks (ANNs) for TGA curve prediction, this work explores a broader range of models, including K-Nearest Neighbor (KNN), Random Forest, and Multilayer Perceptron. The use of KNN represents a significant departure from traditional approaches, as it is the first time this algorithm has been applied to TGA data in the context of biocomposites. This study also introduces a comprehensive comparison of model performance, providing valuable insights into the suitability of different machine-learning techniques for TGA data analysis.

2. Materials and Methods

2.1. Composite Sample Preparation

A standard mixer was utilized to grind wheat straw, followed by sieving the ground material through a 450-micron sieve. The sieved wheat straw underwent a one-day treatment with a 5% NaOH solution. After treatment, the fibers were meticulously rinsed with distilled water multiple times and then dried in an oven at 60 °C for 24 h.

For the silane-treated samples, Si-69 was incorporated into the DGEBA epoxy resin in accordance with the formulation provided in

Table 1. Composition of the biocomposites.

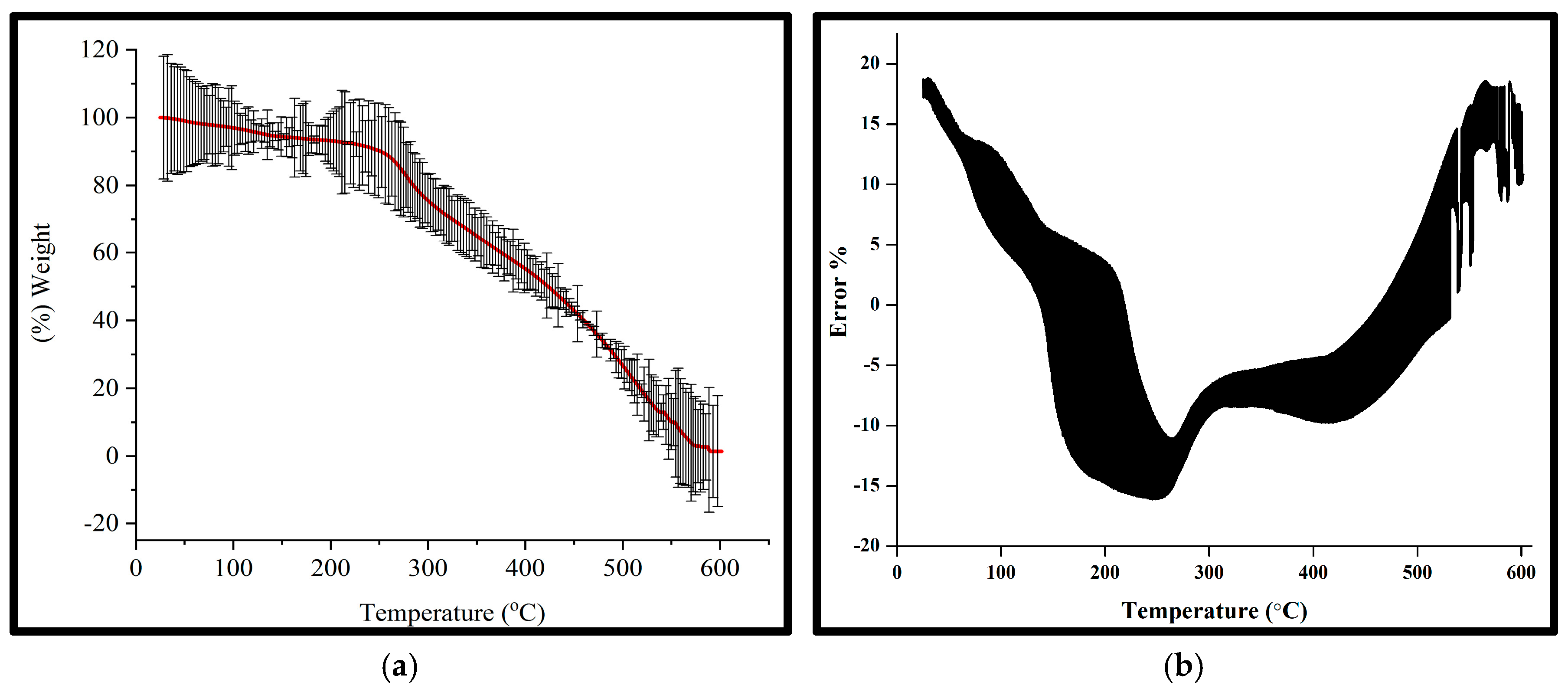
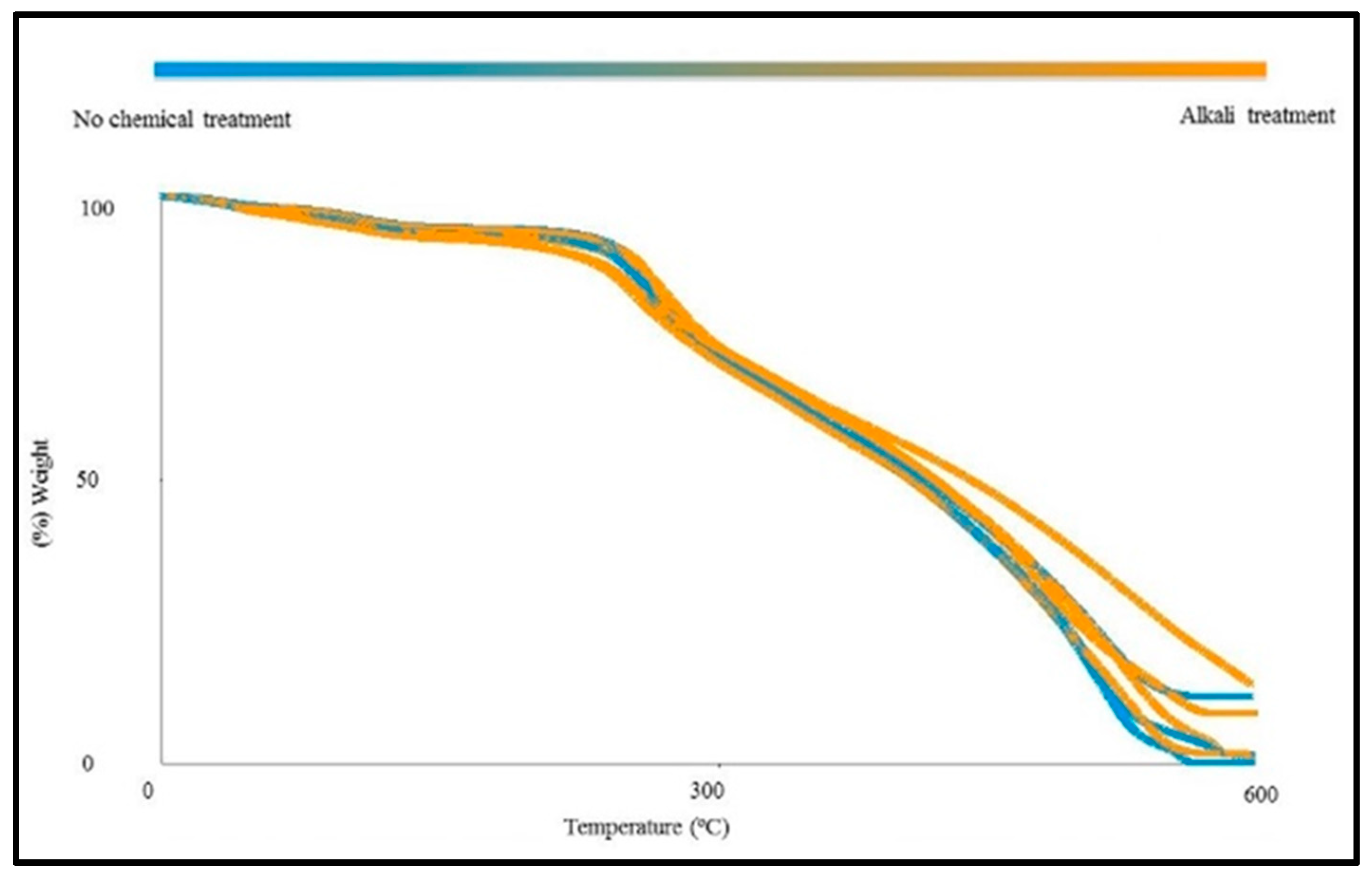
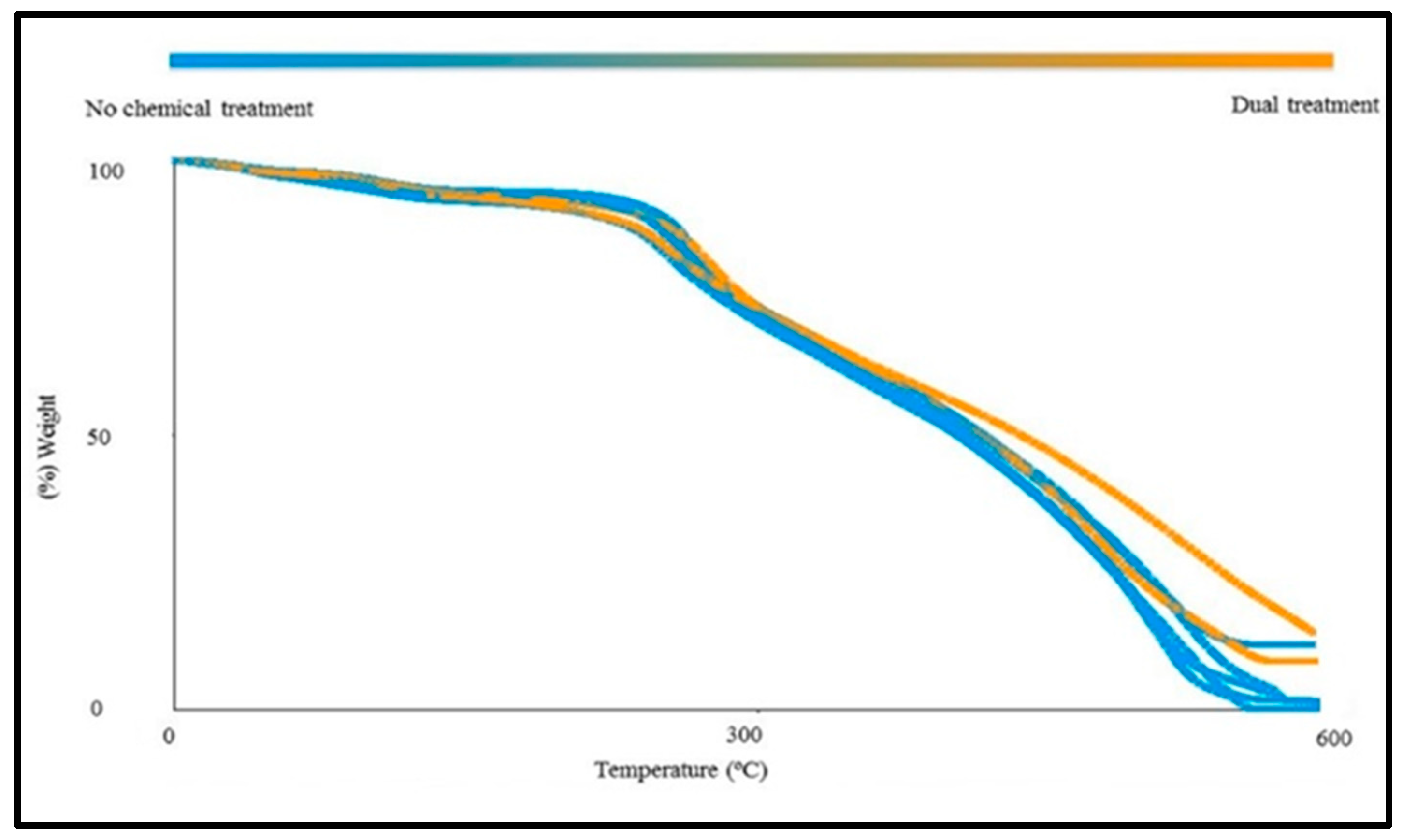
Sample	Epoxy Resin (grams)	Biofiber (grams)	Alkali Mercerization	Silicane Mercerization
Epoxy	100	0	-	-
X1	100	10	not treated	not treated
X2	100	10	treated	not treated
X3	100	10	treated	treated
Y1	100	15	not treated	not treated
Y1	100	15	treated	not treated
Y3	100	15	treated	treated

. As outlined in Table 1, two different loading levels (10 g and 15 g) of wheat straw fibers were combined with every 100 g of epoxy resin matrix. The mixing process involved mechanical stirring at 300 rpm for 30 min to ensure thorough dispersion of the biofibers within the thermoset matrix. Subsequently, the epoxy–wheat straw suspension was blended with a curing agent (DGEBA:TETA 100:15) with continuous stirring for an additional five minutes at 300 rpm.

The resulting mixture was then poured into a silicone mold measuring 100 mm × 100 mm × 6 mm. To eliminate any trapped air bubbles, the fabricated samples were subjected to a vacuum oven (ANTS, 7 kW, automatic, electric) treatment (400 torr was maintained), and curing was allowed to proceed in an ambient environment. Samples of varying dimensions were cut from the composite materials as dictated by the testing requirements [48].

2.2. Thermogravimetric (TGA) Analysis

The thermal analysis of the biocomposite samples was performed using a Shimadzu DTG-60h (error ± 0.25 °C to 1 °C) thermogravimetric analyzer (TGA). Approximately 15 mg of finely powdered samples were carefully placed into alumina ceramic crucibles (of diameter and height of 50 mm each). The TGA process involved heating the samples at a consistent rate of 10 °C per minute, starting from room temperature and reaching 800 °C under ambient conditions (in the presence of atmospheric air) so that the sample will readily oxidize due to the presence of oxygen, leading to a faster and potentially more significant weight loss compared to a nitrogen atmosphere, which is inert and primarily allows for the analysis of thermal decomposition without oxidation reactions occurring. The evaluation of these samples was carried out within alumina ceramic crucibles, and the entire process took place in ambient conditions, with the temperature rising from 25 °C to 800 °C at the specified rate of 10 °C per minute.

2.3. Scanning Electron Microscopy (SEM)

Scanning electron microscopy (SEM) is essential for polymer characterization, providing insights into microstructure and fiber/matrix interactions. Flexure-fractured composite specimens were analyzed using FE-SEM (Apreo LoVac, FEI, Hillsboro, OH, USA) after coating with gold/palladium (Au-Pd) to improve electrical conductivity via sputter coating. The analysis was conducted in a vacuum with an accelerating voltage of 20 kV.

2.4. Mechanical Properties

The flexural strength of the biocomposite samples was evaluated according to ISO 178 standard [49]. A universal testing machine (UTB-9202, Dak Systems Inc., Thane, Maharashtra, India) with a 10 kN load cell was used to assess flexural properties in a three-point bending mode on specimens measuring 80 × 10 × 4 mm.

2.5. Software and System

Weka 3.0, an open-source Java application developed by the University of Waikato in New Zealand, was used in this study. Weka comprises a comprehensive suite of data-mining and machine-learning techniques. These algorithms can be readily applied to datasets or seamlessly integrated into Java code. Weka encompasses a wide range of features, including data pre-processing, classification, regression, clustering, association rule mining, and visualization tools. These capabilities empower users to develop machine-learning strategies and address real-world data-mining tasks effectively. Notably, this experiment was conducted utilizing an Intel Core i5 CPU.

2.6. Dataset and Attributes

The dataset used in this study was obtained from thermogravimetric analysis (TGA) experiments conducted on biocomposite samples. The dataset consists of 26,789 instances, with each instance representing a specific temperature point and its corresponding weight loss percentage. The dataset was divided into training and test sets using an 80:20 split, ensuring that the training set contained a representative sample of the data for model training while the test set was used for validation. This split was chosen to balance the need for sufficient training data while retaining a robust test set for evaluating model performance. The dataset attributes include fiber loading, chemical treatment type, and temperature, as described in

Table 2. Description of dataset attributes.

Attributes	Description
Fiber loading	Two loadings (10 phr and 15 phr) of wheat straw fiber were taken in the experiment
No treatment	Raw fibers were directly used to fabricate the biocomposites
Alkali treatment	Raw fibers were subjected to NaOH treatment before being used in the epoxy matrix
Dual treatment (Alkali and silane treatment)	After NaOH treatment, silane coupling agent Si 69 was used to modify the fiber
Temperature	In an ambient setting, the temperature was changed from room temperature to 800 °C at a rate of 10 °C/min

.

2.7. Parameter Settings of the Models

A total of 16 regression models were selected for the study. A description of these models is listed in

Table 3. Parameter settings of the used machine-learning models.

Sl. No	Model/Classifier	Description
1	Linear regression [25]	Attribute selection method—M5 method; batch size—100; ridge—1.0 × 10−8; debug—false; eliminate collinear attributes—true; output additional stats—false; use QR decomposition—false
2	Multilayer perceptron [50]	GUI—false; batch size—100; debug—false; decay—false; hidden layers—a; learning rate—0.3; momentum—0.2; nominal to binary filter—true; normalize attributes—true; normalize numerical class—true; seed—0; training time—500; validation set size—0; validation threshold—20
3	Simple linear regression [51,52]	Batch size—100; debug—false; output additional stats—false
4	SVM—Sequential minimal optimization regression (SMOreg) [53]	Batch size—100; C—1.0; debug—false; filter type—normalize training data; kernel—poly kernel; reg optimizer—RegSMOImproved
5	K-nearest neighbor classifier [54,55]	KNN—1; batch size—100; cross validate—false; debug—false; distance weighting—no distance weighting; mean squared—false; nearest neighbor search algorithm—Linear NN search; window size—0
6	Lazy K star [56]	Batch size—100; debug—false; entropic auto blend—false; global blend—20; missing mode—average column entropy curves
7	Lazy locally weighted learning [57]	Batch size—100; classifier—decision stump; debug—false; nearest neighbor search algorithm—linear NN search; weighting kernel—0
8	Meta-additive regression [58]	Batch size—100; classifier—decision stamp; debug—false; minimize absolute error—false; number of iterations—10; shrinkage—1.0
9	Meta-bagging [59]	Bag size percent—100; batch size—100; calculation out of bag—0; classifier—REPTree; debug—false; number of execution slots—1; number of iterations—10; seed—1
10	Random committee [60]	Batch size—100; classifier—J48; debug—false; number of execution slots—1; number of iterations—10; seed—1
11	Regression by discretization [61]	Batch size—100; classifier—J48; debug—false; estimator—Univariate equal frequency histogram estimator; minimize absolute error—false; number of bins—10; delete empty bins—false; use equal frequency—false
12	Decision table [62]	Batch size—100; cross-validation—1; debug—false; display rules—false; evaluation measure—accuracy (discrete class); RMSE (numeric class); search—best first
13	M5 Rules [62]	Batch size—100; building regression tree—false; debug—false; minimum number of instances—4; unpruned—false; use unsmoothed—false
14	Random forest [39]	Bag size percent—100; batch size—100; break ties randomly—false; calculation out of bag—0; compute attribute importance—false; debug—false; maximum depth—0; number of execution slots—1; number of iterations—100; output out of bag complexity statistics—false
15	Random tree [63]	K value—0; allow unclassified instances—false; batch size—100; break ties randomly—false; debug—false; maximum depth—0; minimum number—1; minimum variance proportion—0.001; number of folds—0; seed—1
16	REPTree [64]	Batch size—100; debug—false; initial count—0.0; maximum depth—(−1); minimum number—2; minimum variance proportion—0.001; no pruning—false; number of folds—3; seed—1; spread initial count—false

. The parameters for each machine-learning model were carefully selected based on a combination of standard practices in the field, preliminary experiments, and cross-validation to ensure optimal performance. Below, we provide a detailed explanation of the parameter selection process for some of the key models:

• K-Nearest Neighbor (KNN)

The K value in KNN, which determines the number of nearest neighbors to consider, was selected using cross-validation. We conducted a grid search over a range of K values (from 1 to 10) and evaluated the model’s performance using the mean absolute error (MAE) as the metric. The K value that yielded the lowest MAE (K = 1) was chosen for the final model. This approach ensured that the model was neither underfitting nor overfitting the data. Additionally, we used the Euclidean distance metric, as it is well suited for continuous data like TGA curves.

• Random Forest

For the Random Forest model, the number of trees was set to 100 based on preliminary experiments that showed diminishing returns in performance beyond this number. The maximum depth of the trees was left unrestricted to allow the model to capture complex patterns in the data. The minimum number of samples required to split a node was set to 2, and the minimum number of samples required at a leaf node was set to 1, following standard practices for regression tasks.

• Multilayer Perceptron (MLP)

The MLP model was configured with a single hidden layer containing 10 neurons, as this architecture provided a good balance between model complexity and computational efficiency. The learning rate was set to 0.3, and the momentum was set to 0.2 to facilitate faster convergence during training. These parameters were selected based on preliminary experiments and were further fine-tuned using cross-validation.

• Support Vector Machine (SVM) with Sequential Minimal Optimization Regression (SMOreg)

For the SVM-SMOreg model, we used a polynomial kernel with a degree of 2, as it provided a good fit for the nonlinear relationships in the TGA data. The regularization parameter (C) was set to 1.0, which is a common default value for regression tasks. These settings were chosen based on preliminary experiments and were not extensively tuned, as the model’s performance was already satisfactory.

• Decision Trees and Ensemble Methods

For decision tree-based models (e.g., Random Tree, REPTree), the minimum number of instances per leaf was set to 2 to prevent overfitting. For ensemble methods like Random Committee and Meta-Bagging, the number of iterations was set to 10, as this provided a good balance between model performance and computational cost. These parameters were selected based on standard practices and were not extensively tuned, as the models performed well with these default settings.

• Cross-Validation and Parameter-Tuning

To ensure that the selected parameters were robust and not overfitted to the training data, we employed a 10-fold cross-validation approach. This involved dividing the dataset into 10 subsets, training the model on 9 subsets, and validating it on the remaining subset. This process was repeated 10 times, with each subset used exactly once as the validation data. The average performance across all folds was used to evaluate the model and select the optimal parameters. This approach helped mitigate the risk of overfitting and ensured that the models generalized well to unseen data.

• Justification for Parameter Choices

The parameter settings for each model were chosen to balance model complexity, computational efficiency, and predictive performance. For instance, in the case of KNN, a small K value (K = 1) was selected to capture local patterns in the data without introducing excessive noise. For Random Forest, a larger number of trees (n_estimators = 100) was chosen to ensure robust predictions, while the unrestricted tree depth allowed the model to capture complex interactions between variables. Similarly, for MLP, a relatively simple architecture (single hidden layer with 10 neurons) was used to avoid overfitting while still capturing nonlinear relationships in the data.

3. Results and Discussion

Field Emission Scanning Electron Microscopy (FE-SEM) images, detailed in our previous work [48], reveal that biofillers are well-dispersed in the cracked wheat straw–epoxy biocomposites, showing minimal agglomeration. Untreated samples exhibit weak interfacial bonding due to the hydrophobic epoxy and hydrophilic wheat straw, leading to wide gaps, cracks, and voids, which weaken mechanical properties. In contrast, alkali-treated samples displayed improved bonding as surface roughness enhances adhesion, reducing gaps and voids. Dual-treated samples showed the strongest bonding, with no visible cracks or voids, and fibers remain attached to the matrix even after flexural failure, indicating superior impregnation.

Figure 1a,b presents the flexural modulus and strength of the biocomposites. Untreated samples (X₁, Y₁) showed significant reductions due to poor interfacial bonding between wheat straw fillers and the epoxy matrix, leading to increased crack propagation and failure. Alkali treatment improved flexural strength by 11.6% and 9.4% (X₂, Y₂) and flexural modulus by 28.9% and 22.5%, respectively. Additional silane treatment in samples (X₃, Y₃) further enhanced flexural strength by 22.6% and 22.9% and flexural modulus by 41.7% and 33.3% compared to untreated samples.

The improvements are attributed to better fiber–matrix adhesion, reduced water absorption, and a stronger cross-linked network. While increased fiber loading decreased flexural strength due to more fiber ends and defects, it enhanced flexural modulus by restricting crack propagation and epoxy chain mobility. These findings align well with previous observations.

The thermal-degradation performance of the biocomposite materials was investigated through thermogravimetric analysis (TGA). Figure 2 illustrates the TGA curves of the prepared wheat straw–epoxy composites, depicting the percentage of weight loss relative to temperature. The observed weight changes are associated with moisture loss, decomposition, and oxidation of the biocomposite samples as the temperature increases. Notably, multiple thermal-degradation peaks were evident in all samples.

The initial degradation, manifesting as weight loss, was observed within the temperature range of 80 °C to 120 °C, primarily attributed to the moisture content present in the wheat straw fibers within the composites. Subsequently, a second degradation zone was observed between 210 °C and 400 °C, likely linked to the degradation of various components such as cellulose and hemicellulose present in the biocomposite fibers. The final degradation zone, occurring above 400 °C, entailed the degradation of highly cross-linked entities with greater molecular weights.

An interesting observation was that, after the initial moisture-related weight loss, the silane-treated samples exhibited enhanced thermal stability, denoted by lower weight loss at specific temperatures, in comparison to untreated and NaOH-treated samples. The dual-treated samples exhibited the highest thermal stability concerning weight loss. Additionally, the analysis in

Table 4. Char values of the biocomposites.

Code of the Sample	Char Values (% Residual Weight) at Various Temperature
	100 °C	200 °C	300 °C	400 °C	500 °C	600 °C
X1	97.55	94.25	74.87	53.79	20.30	1.25
X2	97.57	93.99	76.47	56.11	26.85	2.97
X3	97.34	93.10	77.47	58.09	37.37	12.18
Y1	96.46	93.24	74.92	53.40	21.39	0.95
Y1	95.62	91.76	73.77	53.13	21.41	2.35
Y3	96.85	92.15	75.90	56.21	24.88	10.86

revealed that in the final decomposition zone, the formation of char was most pronounced in the X₃ sample, reaching 37.37% at 500 °C, indicating improved thermal stability. This improvement could be attributed to enhanced cross-linking in the cured samples facilitated by the presence of the silane coupling agent. Conversely, untreated samples X₁ and Y₁ exhibited the lowest char values.

At higher loading (15 phr), a reduction in thermal-degradation stability was observed compared to lower loading levels (10 phr). This reduction can be attributed to the potential agglomeration of fiber particles within the biocomposite samples at higher loadings, resulting in decreased structural integrity against thermal degradation.

The comparative performances of all 16 machine-learning algorithms have been listed in

Table 5. Performance of the machine-learning models for TGA data.

Sl. No	Model/Classifier	Correlation Co-Efficient	Mean Absolute Error	Root Mean Square Error	Relative Absolute Error	Root Relative Squared Error
1	Linear regression	0.9605	7.7788	8.9331	27.8368	27.8414
2	Multilayer perceptron	0.9965	2.2441	2.7524	8.0305	8.5783
3	Simple linear regression	0.9588	7.9483	9.1132	28.4435	28.4028
4	Sequential minimal optimization regression (SMO-reg)	0.9603	7.6463	9.205	27.3625	28.6887
5	K-nearest neighbor classifier	0.9999	0.0282	0.0358	0.1008	0.1116
6	Lazy K star	0.9982	1.6495	2.497	5.9027	7.7822
7	Lazy locally weighted learning	0.9028	11.7833	12.8062	42.1672%	43.0291
8	Meta-additive regression	0.9816	4.599	6.1612	16.4577	19.2024
9	Meta-bagging	0.9998	0.4842	0.6182	1.7327	1.9267
10	Random committee	0.9999	0.3744	0.4767	1.34	1.4858
11	Regression by discretization	0.9963	2.4113	2.7736	8.6289	8.6444
12	Decision table	0.9940	2.4277	3.5203	8.6875	10.9715
13	M5 Rules	0.9995	0.7547	1.0213	2.7007	3.1831
14	Random forest	0.9999	0.2753	0.3644	0.9852	1.1358
15	Random tree	0.9997	0.6636	0.8237	2.3746	2.5673
16	REPTree	0.9997	0.676	0.8322	2.4192	2.5938

. The performances of the algorithms have been analyzed using the correlation coefficient, mean absolute error, root mean squared error, and root relative squared error of the data taken in the study. It can be seen from Table 5 that the KNN-based algorithm outperforms all other algorithms. The correlation coefficient for the KNN model is 0.9999, whereas the mean absolute error (MAE) and root mean squared error (RMSE) values are 0.0282 and 0.0358, respectively. The relative absolute error (RAE) and root relative squared error (RRSE) values are 0.1008 and 0.1116, respectively. These values are very low compared to the other algorithms used in this study, which means the KNN-based machine-learning algorithms provide better accuracy and prediction. The overall performance of Random Tree, Random Forest, and Random Committee algorithms is also very good in terms of MAE, RMSE, RAE, and RRSE. The performance of lazy locally weighted learning was the worst among all the algorithms. The correlation coefficient for the lazy locally weighted learning model is 0.9028, and MAE and RMSE values are 7.7788 and 8.9331, respectively.

Figure 3, Figure 4 and Figure 5 illustrate the percentage error deviation between predicted and actual TGA (thermogravimetric analysis) values for different machine-learning models. In these figures, the red line represents the predicted TGA values, and the black line represents the actual experimental values. Figure 3, which depicts the performance of the locally weighted learning model, shows the highest deviation, indicating poor accuracy. Figure 4 presents the simple linear regression model, which performed moderately well but still exhibited noticeable errors. In contrast, Figure 5 demonstrates the K-Nearest Neighbors (KNN) model, where the predicted values closely follow the experimental data, signifying the best accuracy among all models. The percentage error graphs (subfigures b) in each figure visually compare the accuracy of these models.

The best-performing model is KNN. The accuracy of the model is shown in Figure 5a. Figure 5b shows the percentage error of the model. It is evident from the figure that the KNN model has the least percentage error. Since it is a lazy-learning algorithm, there is no specialized training phase. This algorithm uses all the data points provided for prediction. KNN is a non-parametric algorithm. It does not assume anything regarding the underlying data. It predicts new data points based on the numerical value of the Euclidean or Manhattan distance of other data points without any bias for features. Based on the values of these distances, the algorithm then selects the K number of the nearest data points, where K is an integer. The mean of all the K outputs is calculated for the predicted output value.

The K-Nearest Neighbor (KNN) algorithm outperformed the other models due to its non-parametric nature, which makes it particularly well suited for datasets with complex and nonlinear relationships, such as TGA data. Unlike parametric models, KNN does not assume any underlying data distribution, which is advantageous given the variability in thermal-degradation behavior. Additionally, KNN’s ability to handle multi-dimensional data without requiring feature scaling contributed to its superior performance. The algorithm’s reliance on distance metrics (Euclidean distance in this case) allowed it to capture subtle patterns in the data that other models, such as linear regression, could not. Furthermore, the absence of a training phase in KNN meant that the model could adapt quickly to new data, making it highly effective for this application. While the selected parameters provided excellent performance on the TGA dataset, it is important to acknowledge that further tuning could potentially improve the model accuracy. For instance, more advanced optimization techniques, such as Bayesian optimization or genetic algorithms, could be employed to fine-tune the parameters. Additionally, the use of larger datasets could allow for more extensive parameter exploration, particularly for complex models like deep neural networks. These considerations will be addressed in future work.

The results obtained from the WEKA solver are represented in Figure 6, Figure 7 and Figure 8. It can be seen from Figure 6 that the thermal stability of the composite samples decreases with an increase in fiber loading. The thermal performance of epoxy samples with 10 phr wheat straw fiber loading is better than 15 phr fiber loading. It can be observed from Figure 7 that the thermal performance of the composite samples where alkali treatment has been given to the wheat straw fillers is better than the biocomposite samples prepared with fillers without any treatment. The heat curve in Figure 8 shows that dual chemical treatment is much more effective than single chemical treatment in improving thermal-degradation resistance. The dual treatment involving alkali (NaOH) and silane (Si-69) significantly improved the thermal stability of the biocomposites by modifying the chemical structure of the wheat straw fibers. The alkali treatment removed hemicellulose and lignin, exposing more cellulose on the fiber surface, which enhanced the interfacial bonding between the fibers and the epoxy matrix. The subsequent silane treatment further improved this bonding by forming covalent bonds between the silane molecules and the epoxy resin. This dual treatment not only increased the thermal stability of the composites but also reduced the hydrophilic nature of the fibers, leading to better compatibility with the hydrophobic epoxy matrix. The enhanced cross-linking resulting from the dual treatment was evident in the higher char residue observed in the TGA curves, particularly for the X₃ and Y₃ samples. All these results are consistent with the experimental results.

4. Conclusions and Limitations

The present study explores the utilization of wheat straw, a biobased residual filler, as a robust reinforcement material within a DGEBA-based epoxy resin. To optimize the filler properties, it underwent treatments with either alkali (NaOH) or a combination of silane and alkali.

• The thermal properties of the biocomposite samples were assessed through thermogravimetric analysis (TGA), and the results clearly demonstrated that the dual treatment involving silane and alkali for the wheat straw fibers led to a significant improvement in the thermal stability of the biocomposites when compared to both untreated and alkali-treated fibers.
• Furthermore, the study highlighted that as the loading of wheat straw fibers increased; the thermal-degradation stability exhibited a diminishing trend. To predict the thermal performance of the wheat straw biocomposite samples, 16 machine-learning algorithms were used to analyze the datasets.
• A comparative analysis of the performance of these 16 algorithms has been made. It is found that the accuracy of the KNN algorithm is the best among all in predicting the thermal performance of the biocomposites.

While the machine-learning models used in this study demonstrated strong predictive performance, it is important to acknowledge their limitations, particularly in capturing the nonlinear characteristics of TGA data. Linear models, such as simple linear regression, may not adequately capture the complex relationships between temperature, fiber loading, and chemical treatment. In contrast, non-parametric models like KNN and Random Forest are better suited for such data due to their ability to handle non-linearities and interactions between variables. However, these models can be computationally intensive, especially for large datasets. Additionally, the performance of KNN can be sensitive to the choice of distance metric and the value of K, which requires careful tuning. While the KNN model showed excellent performance, cross-validation was conducted to ensure that the model generalizes well to unseen data. The use of cross-validation helped mitigate the risk of overfitting, as the model performance was evaluated on multiple subsets of the data. Additionally, the relatively large dataset (26,789 instances) provided sufficient diversity to prevent overfitting. However, future work could explore regularization techniques and larger datasets to further reduce the risk of overfitting and improve model robustness.