Energy-Absorbing Performance of Metallic Thin-Walled Porous Tubes Filled with Liquid Crystal Elastomers Under Dynamic Crush
Abstract
1. Introduction
2. Design and Fabrications
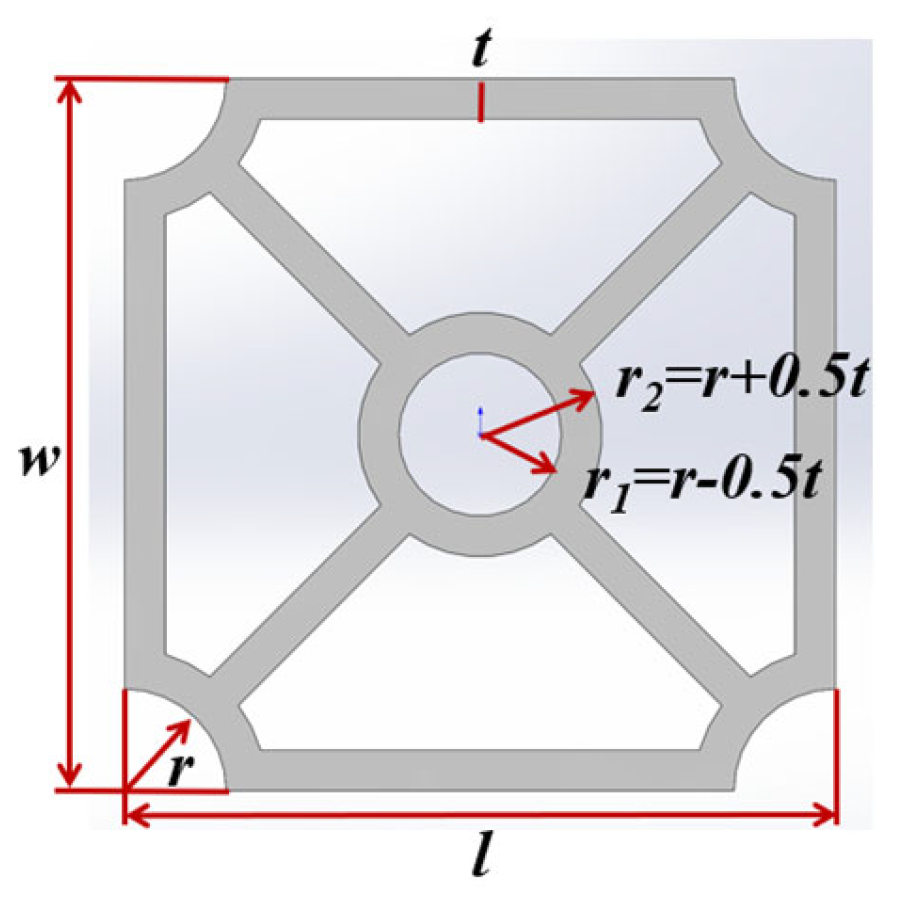
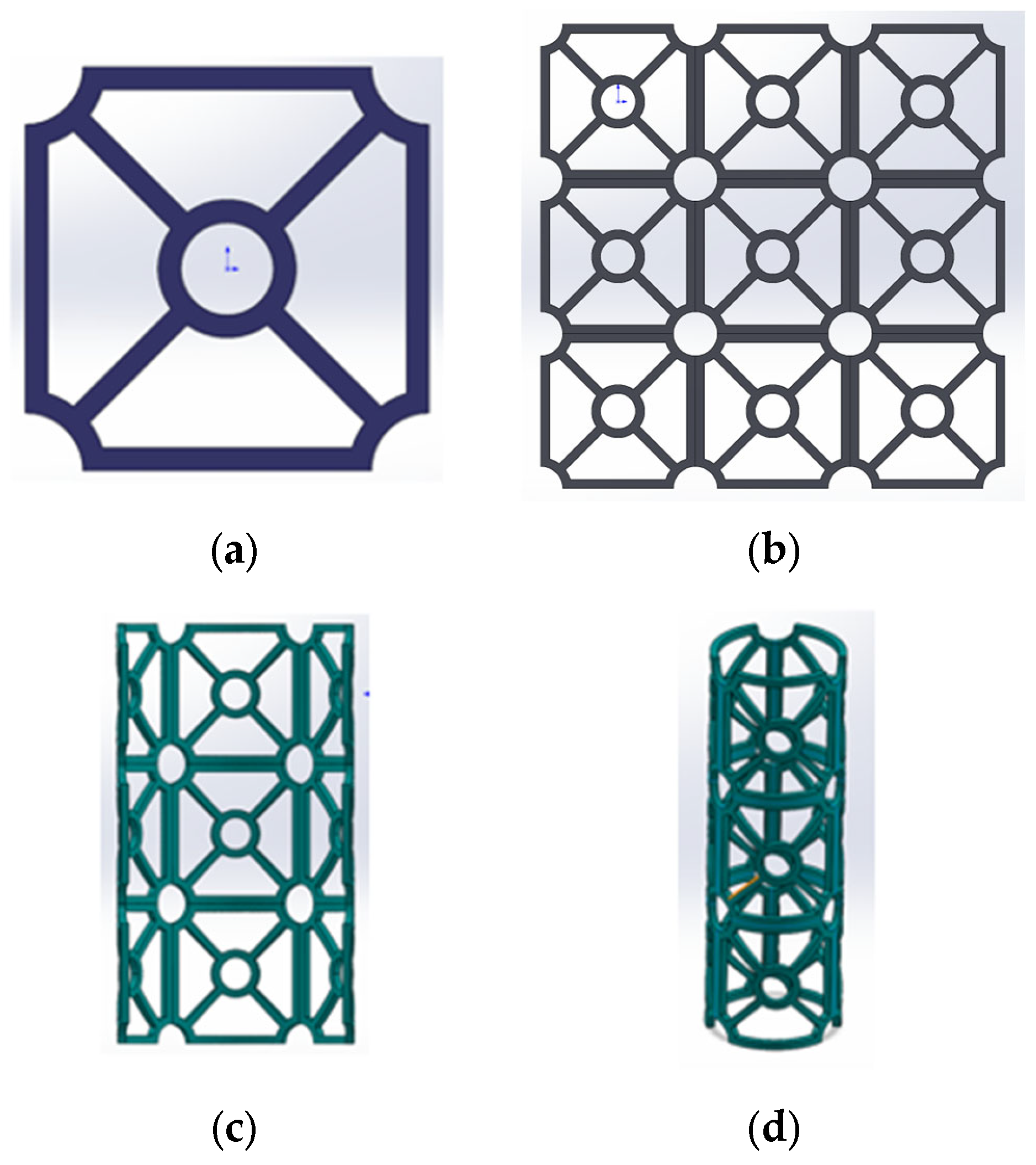
2.1. Structural Design
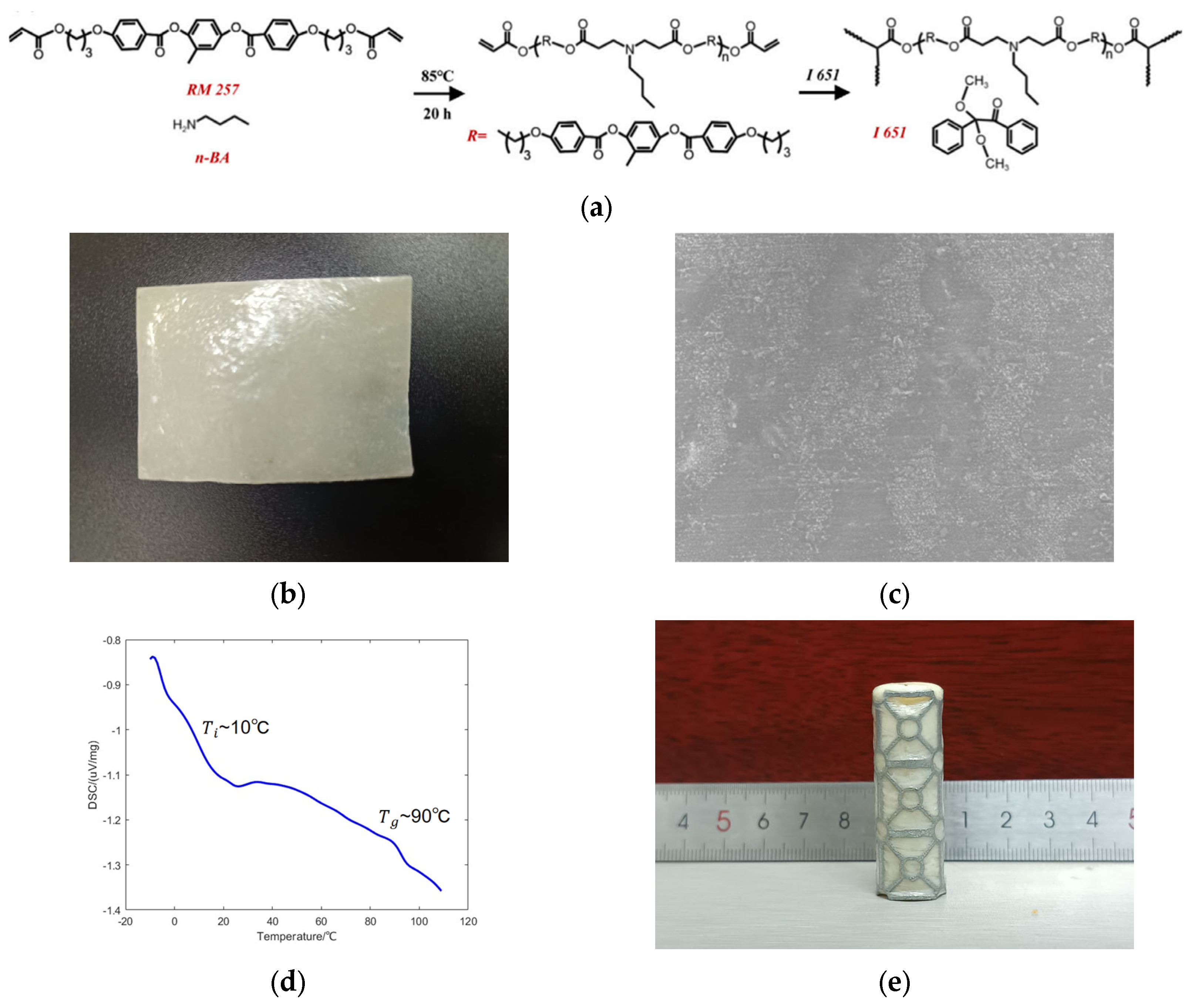
2.2. Fabrications
2.3. Mechanical Properties of AlSi10Mg
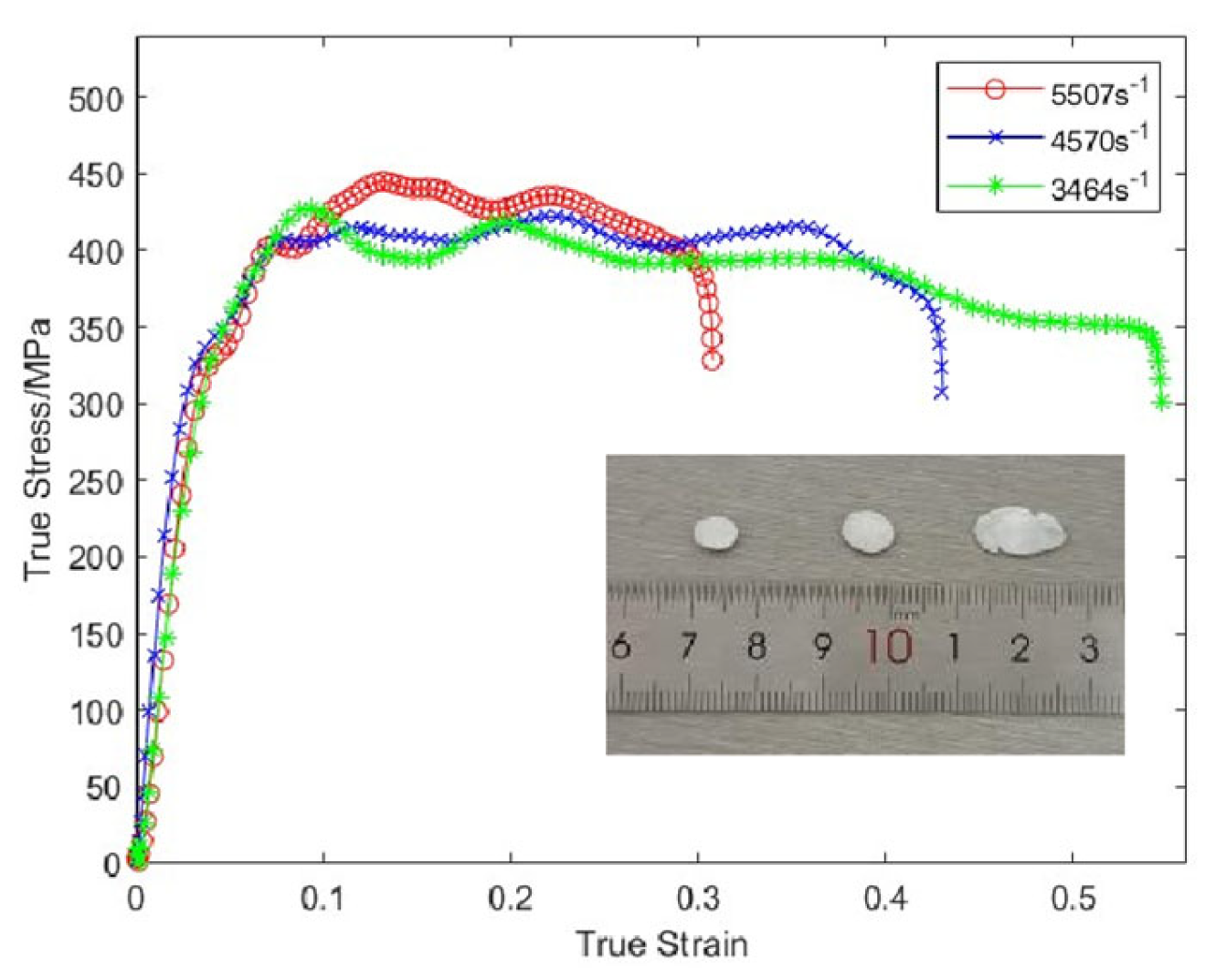
2.3.1. Quasi-Static Tensile Testing
2.3.2. Split Hopkinson Pressure Bar (SHPB) Testing
2.3.3. Evaluation Indicators of Energy-Absorbing Performance
3. Experiments, Finite Element Model, and Verification
3.1. Drop Hammer Testing
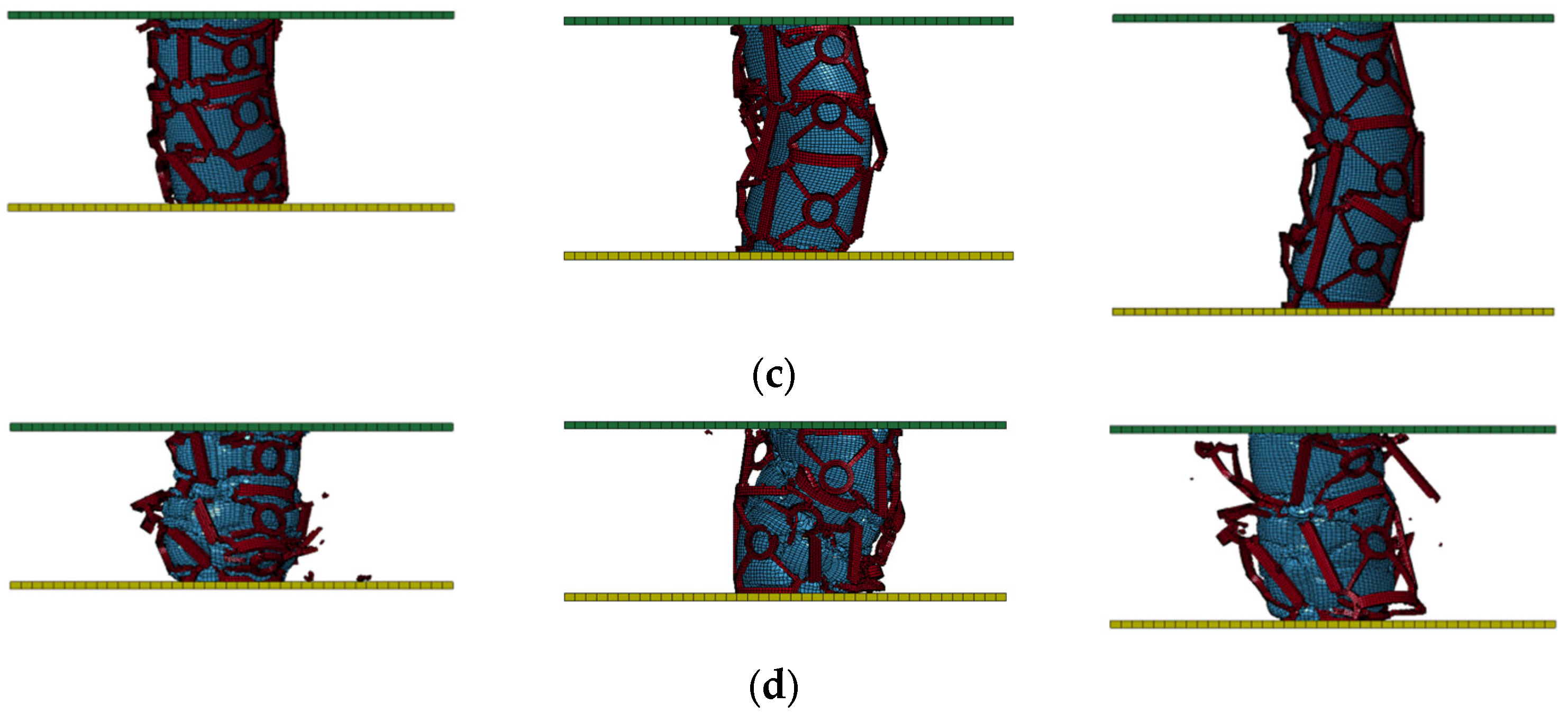
3.1.1. Deformation Modes
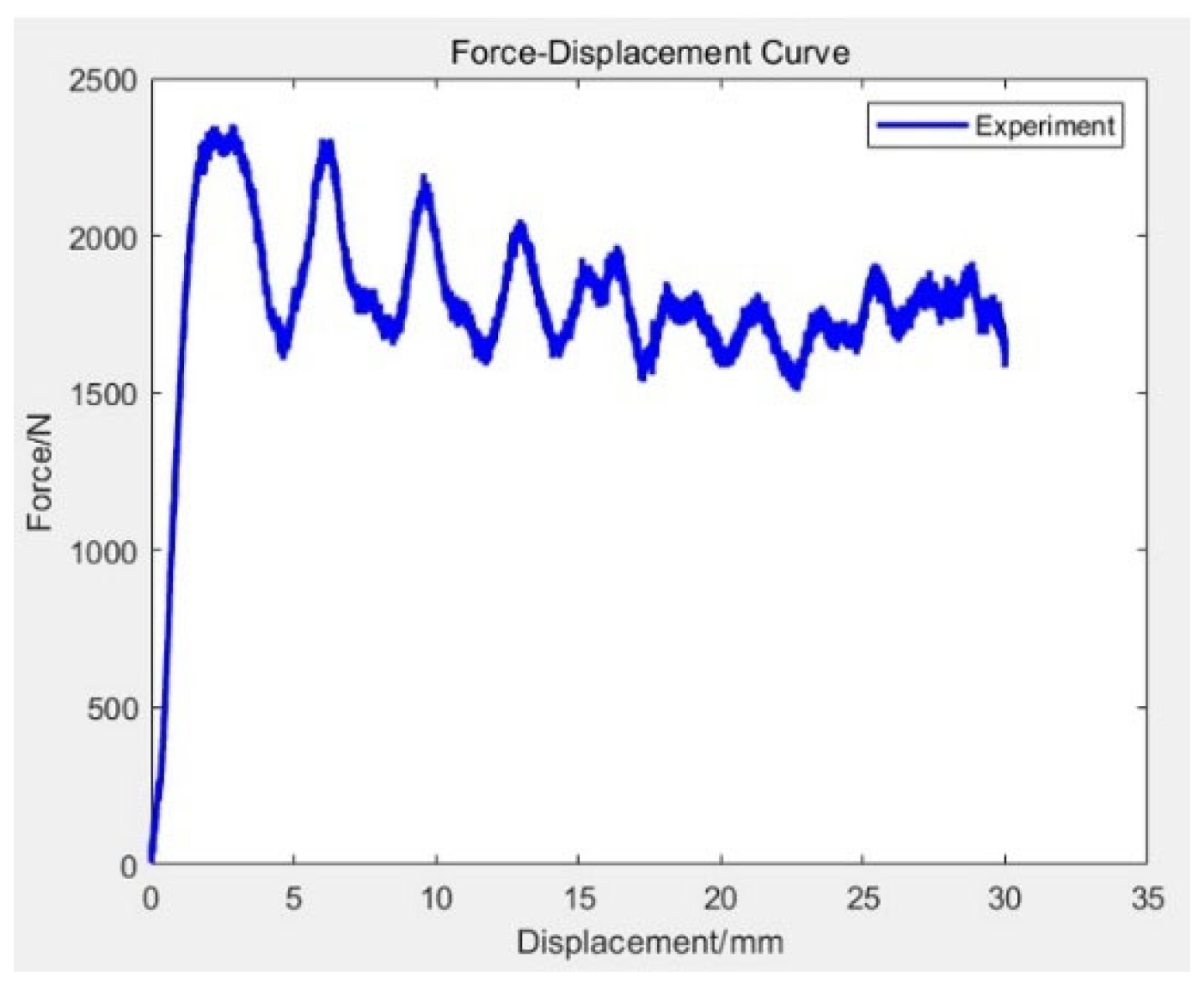
3.1.2. Energy Absorption
3.2. Establishment of Finite Element Model
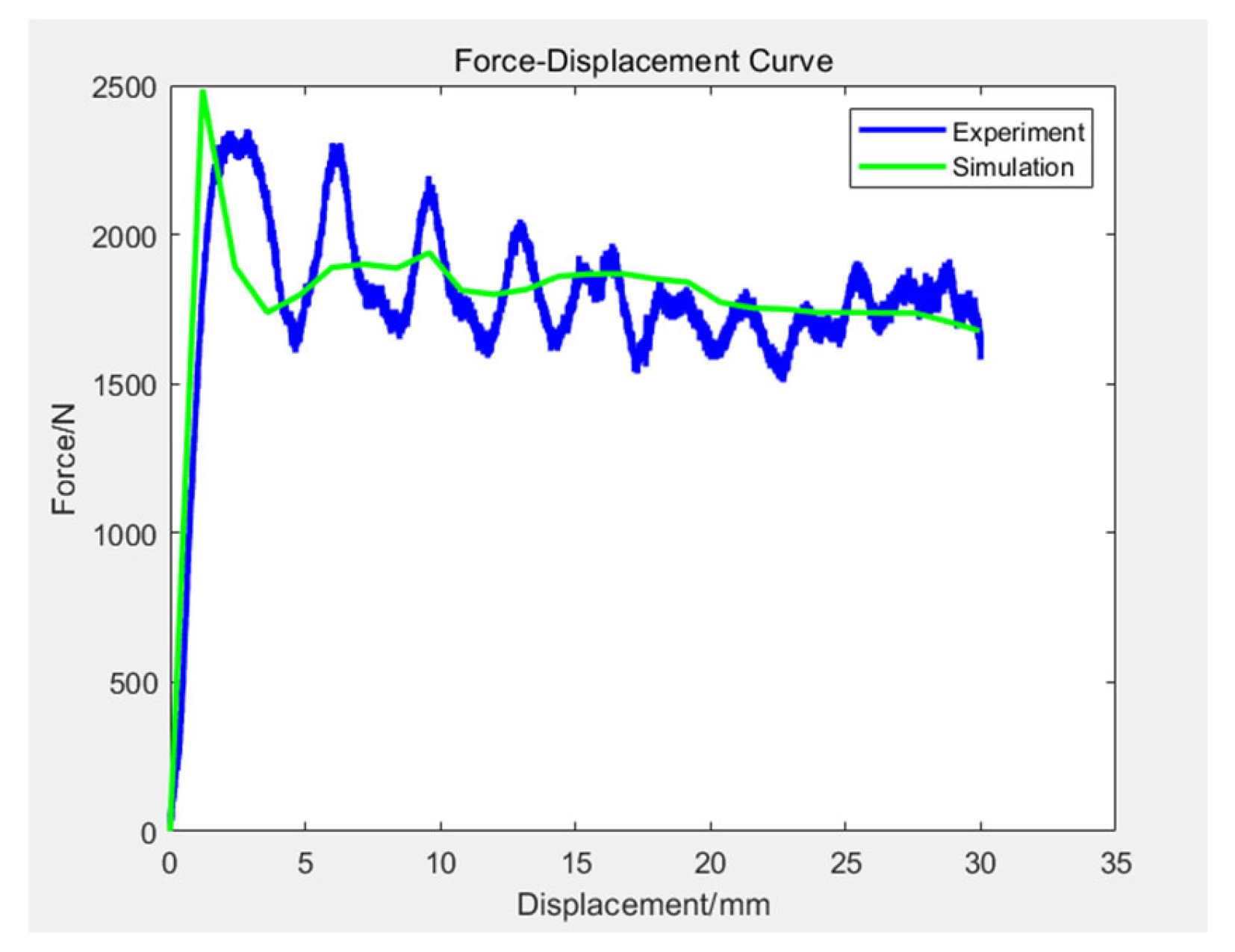
3.3. Model Verification
4. Results and Discussions
4.1. Deformation Modes
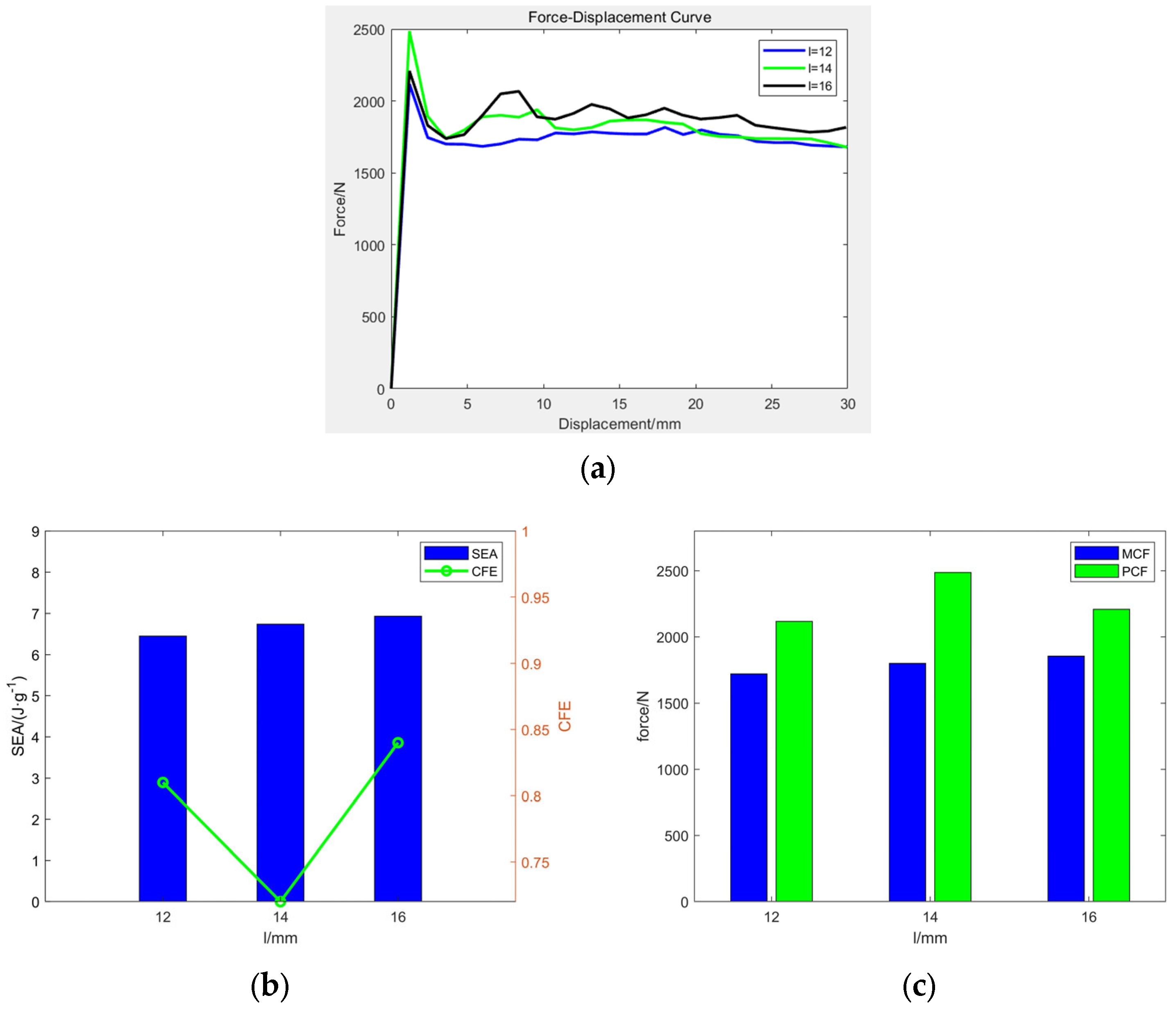
4.2. Energy Absorption Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MPTs | Metallic thin-walled porous tubes |
| LCEs | Liquid crystal elastomers |
| MPT–LCE | Metallic thin-walled porous tubes filled with liquid crystal elastomers |
| SLM | Selective laser melting |
| SHPB | Split Hopkinson Pressure Bar |
| SEA | Specific energy absorption |
| MCF | Mean crushing force |
| CFE | Crushing force efficiency |
| PCF | Peak crushing force |
References
- Moreno, C.; Winnett, J.; Williams, T. On the effect of anisotropy on the performance and simulation of shrinking tubes used as energy absorbers for railway vehicles. Thin-Walled Struct. 2021, 161, 107513. [Google Scholar] [CrossRef]
- Peng, Y.; Li, T.; Bao, C.; Zhang, J.; Xie, G.; Zhang, H. Performance analysis and multi-objective optimization of bionic dendritic furcal energy-absorbing structures for trains. Int. J. Mech. Sci. 2023, 246, 108145. [Google Scholar] [CrossRef]
- Selivanov, V.V.; Silnikov, M.V.; Markov, V.A.; Popov, Y.V.; Pusev, V.I. Using highly porous aluminum alloys and honeycomb structures in spacecraft landing gear. Acta Astronaut. 2021, 180, 105–109. [Google Scholar] [CrossRef]
- Alexander, J.M. An approximate analysis of the collapse of thin cylindrical shells under axial loading. Q. J. Mech. Appl. Math. 1960, 13, 10–15. [Google Scholar] [CrossRef]
- Andrews, K.R.F.; England, G.L.; Ghani, E. Classification of the axial collapse of cylindrical tubes under quasi-static loading. Int. J. Mech. Sci. 1983, 25, 687–696. [Google Scholar] [CrossRef]
- Tarlochan, F.; Samer, F.; Hamouda, A.M.S.; Ramesh, S.; Khalid, K. Design of thin wall structures for energy absorption applications: Enhancement of crashworthiness due to axial and oblique impact forces. Thin-Walled Struct. 2013, 71, 7–17. [Google Scholar] [CrossRef]
- Nia, A.A.; Parsapour, M. Comparative analysis of energy absorption capacity of simple and multi-cell thin-walled tubes with triangular, square, hexagonal and octagonal sections. Thin-Walled Struct. 2014, 74, 155–165. [Google Scholar]
- Baroutaji, A.; Sajjia, M.; Olabi, A.G. On the crashworthiness performance of thin-walled energy absorbers: Recent advances and future developments. Thin-Walled Struct. 2017, 118, 137–163. [Google Scholar] [CrossRef]
- Moradpour, A.; Elyasi, M.; Montazeri, S. Developing a New Thin-Walled Tube Structure and Analyzing its Crushing Performance for AA 60601 and Mild Steel Under Axial Loading. Trans. Indian Inst. Met. 2016, 69, 1107–1117. [Google Scholar] [CrossRef]
- Ylmaz, H.; Kocaba, B.; Zyurt, E. Empirical equations to estimate non-linear collapse of medium-length cylindrical shells with circular cutouts. Thin-Walled Struct. 2017, 119, 868–878. [Google Scholar] [CrossRef]
- Montazeri, S.; Elyasi, M.; Moradpour, A. Investigating the energy absorption, SEA and crushing performance of holed and grooved thin-walled tubes under axial loading with different materials. Thin-Walled Struct. 2018, 131, 646–653. [Google Scholar] [CrossRef]
- Niknejad, A.; Abedi, M.M.; Liaghat, G.H.; Nejad, M.Z. Absorbed energy by foam-filled quadrangle tubes during the crushing process by considering the interaction effects. Arch. Civ. Mech. Eng. 2015, 15, 376–391. [Google Scholar] [CrossRef]
- Hussein, R.D.; Ruan, D.; Lu, G.; Stephen, G.; Yoon, J.W. Crushing response of square aluminum tubes filled with polyurethane foam and aluminum honeycomb. Thin-Walled Struct. 2017, 110, 140–154. [Google Scholar] [CrossRef]
- Altin, M.; Güler, M.A.; Mert, S.K. The effect of percent foam fill ratio on the energy absorption capacity of axially compressed thin-walled multi-cell square and circular tubes. Int. J. Mech. Sci. 2017, 131–132, 368–379. [Google Scholar] [CrossRef]
- Yao, R.; Zhang, B.; Yin, G.; Zhao, Z. Energy absorption behaviors of foam-filled holed tube subjected to axial crushing: Experimental and theoretical investigations. Mech. Adv. Mater. Struct. 2021, 28, 2501–2514. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, J.; Zhang, Y. Recent advances in the design, fabrication, actuation mechanisms and applications of liquid crystal elastomers. Soft Sci. 2023, 3, 11. [Google Scholar] [CrossRef]
- Chen, M.; Gao, M.; Bai, L.; Zheng, H.; Qi, H.J.; Zhou, K. Recent Advances in 4D Printing of Liquid Crystal Elastomers. Adv. Mater. 2023, 35, e2209566. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Han, J.; Xu, H.; Ji, H.; Yue, Z.; Zhang, R.; Li, B.; Ji, Y.; Li, Z.; Wang, P.; et al. Nonlinear mechanical behaviour and visco-hyperelastic constitutive description of isotropic-genesis, polydomain liquid crystal elastomers at high strain rates. J. Mech. Phys. Solids 2024, 193, 105882. [Google Scholar] [CrossRef]












| Authors | Research Object | Research Methods | Main Findings | Limitations |
|---|---|---|---|---|
| Alexander [4] | thin-walled cylindrical shell | theoretical analysis and experimental comparison | Propose an approximate theory for the collapse process of thin-walled cylindrical shells under axial loads. | The ideal model is overly simplified and differs from the actual situation. |
| Andrews et al. [5] | aluminum alloy tubes | experiments | Study the axial compression mode and energy absorption characteristics, explore the influence of tube length, and provide classification charts. | Idealization of experimental conditions and limit to quasi-static loading conditions. |
| Tarlochan et al. [6] | six different cross-sectional shapes of thin-walled structures | simulations | Optimized hexagonal tube structure with excellent energy absorption capacity. | Lack of experimental verification. |
| Nia et al. [7] | simple and multi-cell thin-walled tubes with different sections | experiments and simulations | Multi-cell cross-section has stronger energy absorption capacity than simple cross-section. | Under quasi-static loading conditions, without considering dynamic loading. |
| Moradpour et al. [9] | a new thin-walled tube structure with holes | theoretical analysis and experiments | The thin-walled tube with five rows, 12 holes per row, and a diameter of 6 mm has ideal extrusion performance. | Only considers quasi-static loading conditions without considering dynamic loading situations. |
| Ylmaz et al. [10] | medium-length cylindrical shells with circular cutouts | theoretical analysis, experiments, and simulations | Circular notches significantly reduce the ultimate load of cylindrical shells. | Only considers axial compression loading conditions without involving other complex loading conditions. |
| Montazeri et al. [11] | holed and grooved thin-walled tubes | theoretical analysis, experiments, and simulations | Compared to steel perforated pipes and slotted pipes, perforated pipes absorb more energy and have a higher mass-to-energy ratio. | Only considers axial compression loading conditions without involving other complex loading conditions. |
| Niknejad et al. [12] | polyurethane foam-filled quadrilateral tubes | theoretical analysis and experimental comparison | The quadrilateral tube filled with hard foam absorbs more energy than that filled with soft foam. | The quantification method of interaction is not precise enough. |
| Hussein at al. [13] | square aluminum tubes with different filler structures | experiments | The square aluminum tube filled with polyurethane foam and aluminum honeycomb has the best crashworthiness. | Only considers quasi-static loading conditions without considering dynamic loading conditions. |
| Altin et al. [14] | thin-walled multi-cell square and circular tubes filled with foam | experiments and simulations | The square tube filled with foam performs best in crashworthiness. | Only considers quasi-static loading conditions without considering dynamic loading conditions. |
| Yao et al. [15] | foam-filled holed tube | theoretical analysis and experiments | Filling aluminum foam can significantly improve the total energy absorption and average extrusion pressure of empty perforated tubes. | Insufficient exploration of the effect of other parameter changes on energy absorption performance. |
| Xiao et al. [16] | the design, fabrication, actuation mechanisms, and applications of LCEs | literature review | This literature summarized the fabrication methods, actuation mechanisms, and diverse applications of LCEs. | Limitations in fabrication technology, insufficient actuation performance, and difficulties in 3D printing. |
| Chen et al. [17] | 4D printing of LCEs | literature review | This literature introduced the properties and fabrications of LCEs, 4D printing technology, and application fields. | Limitations in material systems, insufficient theoretical modeling, and pour printing technology. |
| Wang et al. [18] | isotropic genesis, polydomain LCEs | theoretical analysis, experiments, and simulations | I-PLCEs exhibit significant nonlinearity and strain rate correlation. A visco–hyperelastic constitutive model for the material is established. | There are certain limitations to the applicability of model parameters under different loading conditions. |
| Parameters | Symbol | Value |
|---|---|---|
| height | 42 mm | |
| the inner radius | 6.28 mm | |
| the outer radius | 7.08 mm | |
| thickness | 0.8 mm |
| Granularity Range/μm | Flowability/s | ) | ) |
|---|---|---|---|
| 15–53 | <100 | >1.2 | >1.5 |
| Parameters | Symbol | Value | Standard Deviations |
|---|---|---|---|
| density | 2.6 | 0.17 | |
| Young’s modulus | E | 9.92 GPa | 0.39 |
| Poisson’s ratio | 0.30 | 0.04 | |
| 0.2% offset yield stress | 210 MPa | 15 | |
| ultimate stress | 283 MPa | 24 | |
| fracture strain | 0.11 | 0.03 |
| Indicators | Value | Standard Deviations |
|---|---|---|
| SEA | 6.89 J/g | 0.22 |
| PCF | 2353.4 N | 94 |
| MCF | 1383.7 N | 42 |
| CFE | 0.76 | 0.06 |
| RO | E | PR | CMO | CON1 | CON2 |
|---|---|---|---|---|---|
| 7.8 | 200 GPa | 0.3 | 1 | 4 | 7 |
| Material | RO | E | PR | SIGY | ETAN |
|---|---|---|---|---|---|
| MPTs | 9.92 GPa | 0.3 | 210 MPa | 0 | |
| LCEs | 1MPa | 0.33 | 0.25 MPa | 0 |
| PCF/N | MCF/N | CFE | ||
|---|---|---|---|---|
| experiment | 2353.4 | 6.69 | 1783.7 | 0.76 |
| experimental standard deviations | 94 | 0.22 | 42 | 0.06 |
| simulation | 2485.9 | 6.74 | 1800.9 | 0.72 |
| error | 5.6% | 0.7% | 1.0% | 5.3% |
| Group | /mm | /mm | /mm | /mm | /mm | /mm |
|---|---|---|---|---|---|---|
| 12 | 14 | 2 | 42 | 5.33 | 6.13 | |
| 1 | 14 | 14 | 2 | 42 | 6.28 | 7.08 |
| 16 | 14 | 2 | 42 | 7.24 | 8.04 | |
| 14 | 12 | 2 | 36 | 6.28 | 7.08 | |
| 2 | 14 | 14 | 2 | 42 | 6.28 | 7.08 |
| 14 | 16 | 2 | 48 | 6.28 | 7.08 | |
| 14 | 14 | 1.5 | 42 | 6.28 | 7.08 | |
| 3 | 14 | 14 | 2 | 42 | 6.28 | 7.08 |
| 14 | 14 | 2.5 | 42 | 6.28 | 7.08 |
| PCF/N | MCF/N | CFE | ||
|---|---|---|---|---|
| l = 12 mm | 2117.9 | 6.45 | 1721.1 | 0.81 |
| l = 14 mm | 2485.9 | 6.74 | 1800.9 | 0.72 |
| l = 16 mm | 2208.7 | 6.93 | 1854.9 | 0.84 |
| PCF/N | MCF/N | CFE | ||
|---|---|---|---|---|
| w = 12 mm | 2079.6 | 6.91 | 1848.7 | 0.89 |
| w = 14 mm | 2485.9 | 6.74 | 1800.9 | 0.72 |
| w = 16 mm | 2261.3 | 6.60 | 1763.2 | 0.78 |
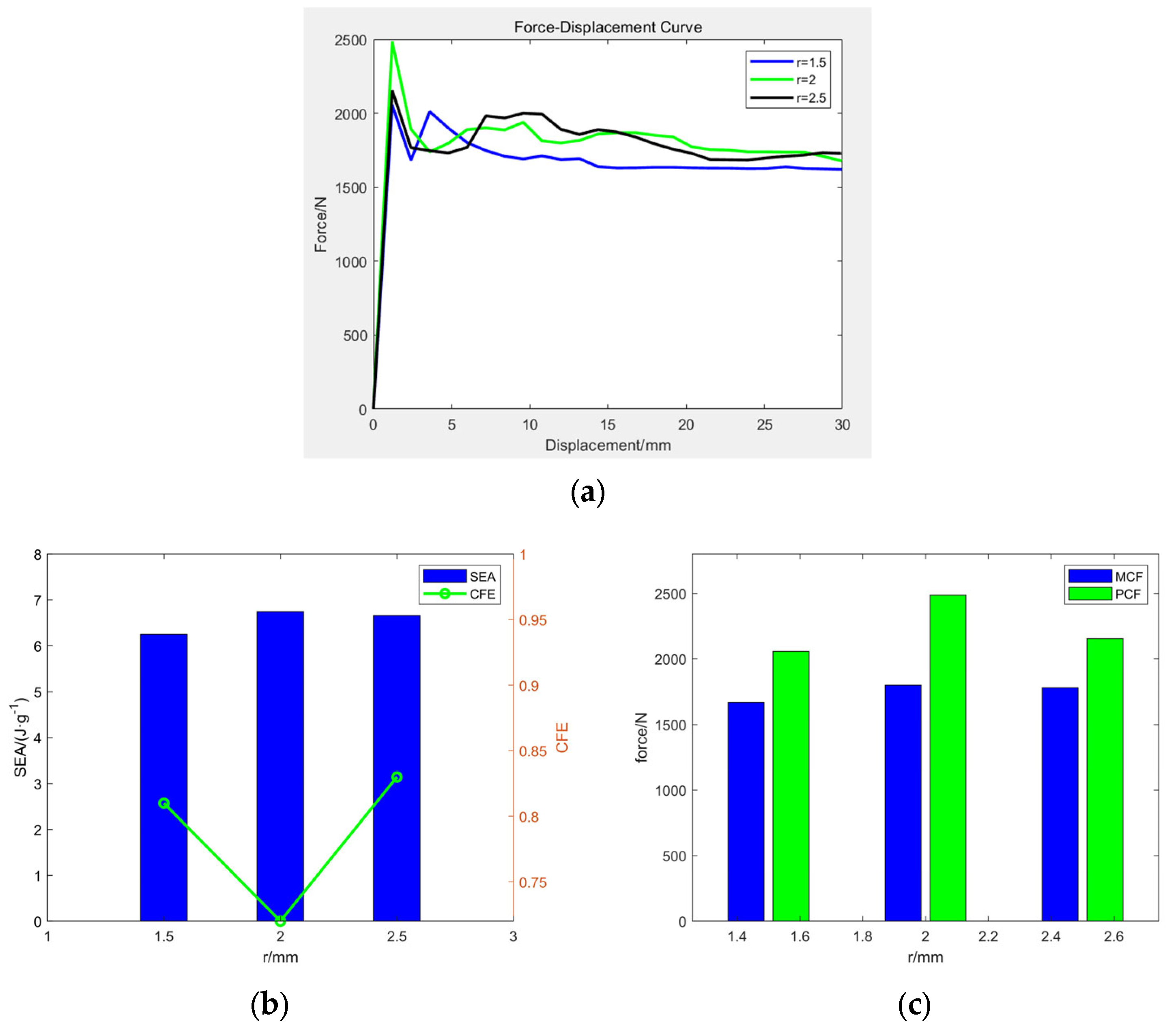
| PCF/N | MCF/N | CFE | ||
|---|---|---|---|---|
| r = 1.5 mm | 2056.9 | 6.25 | 1667.9 | 0.81 |
| r = 2 mm | 2485.9 | 6.74 | 1800.9 | 0.72 |
| r = 2.5 mm | 2155.6 | 6.66 | 1780.8 | 0.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Niu, S.; Wu, Y.; Li, B.; Li, Z.; Wang, J. Energy-Absorbing Performance of Metallic Thin-Walled Porous Tubes Filled with Liquid Crystal Elastomers Under Dynamic Crush. J. Compos. Sci. 2025, 9, 190. https://doi.org/10.3390/jcs9040190
Hu X, Niu S, Wu Y, Li B, Li Z, Wang J. Energy-Absorbing Performance of Metallic Thin-Walled Porous Tubes Filled with Liquid Crystal Elastomers Under Dynamic Crush. Journal of Composites Science. 2025; 9(4):190. https://doi.org/10.3390/jcs9040190
Chicago/Turabian StyleHu, Xu’an, Shaohua Niu, Yanxuan Wu, Bingyang Li, Zhen Li, and Jun Wang. 2025. "Energy-Absorbing Performance of Metallic Thin-Walled Porous Tubes Filled with Liquid Crystal Elastomers Under Dynamic Crush" Journal of Composites Science 9, no. 4: 190. https://doi.org/10.3390/jcs9040190
APA StyleHu, X., Niu, S., Wu, Y., Li, B., Li, Z., & Wang, J. (2025). Energy-Absorbing Performance of Metallic Thin-Walled Porous Tubes Filled with Liquid Crystal Elastomers Under Dynamic Crush. Journal of Composites Science, 9(4), 190. https://doi.org/10.3390/jcs9040190





