Dual Influence of Li Concentration and Nanoparticle Size in LiCoO2 on the Conductivity and Storage Capacity of Lithium Batteries
Abstract
:1. Introduction
2. Materials and Methods
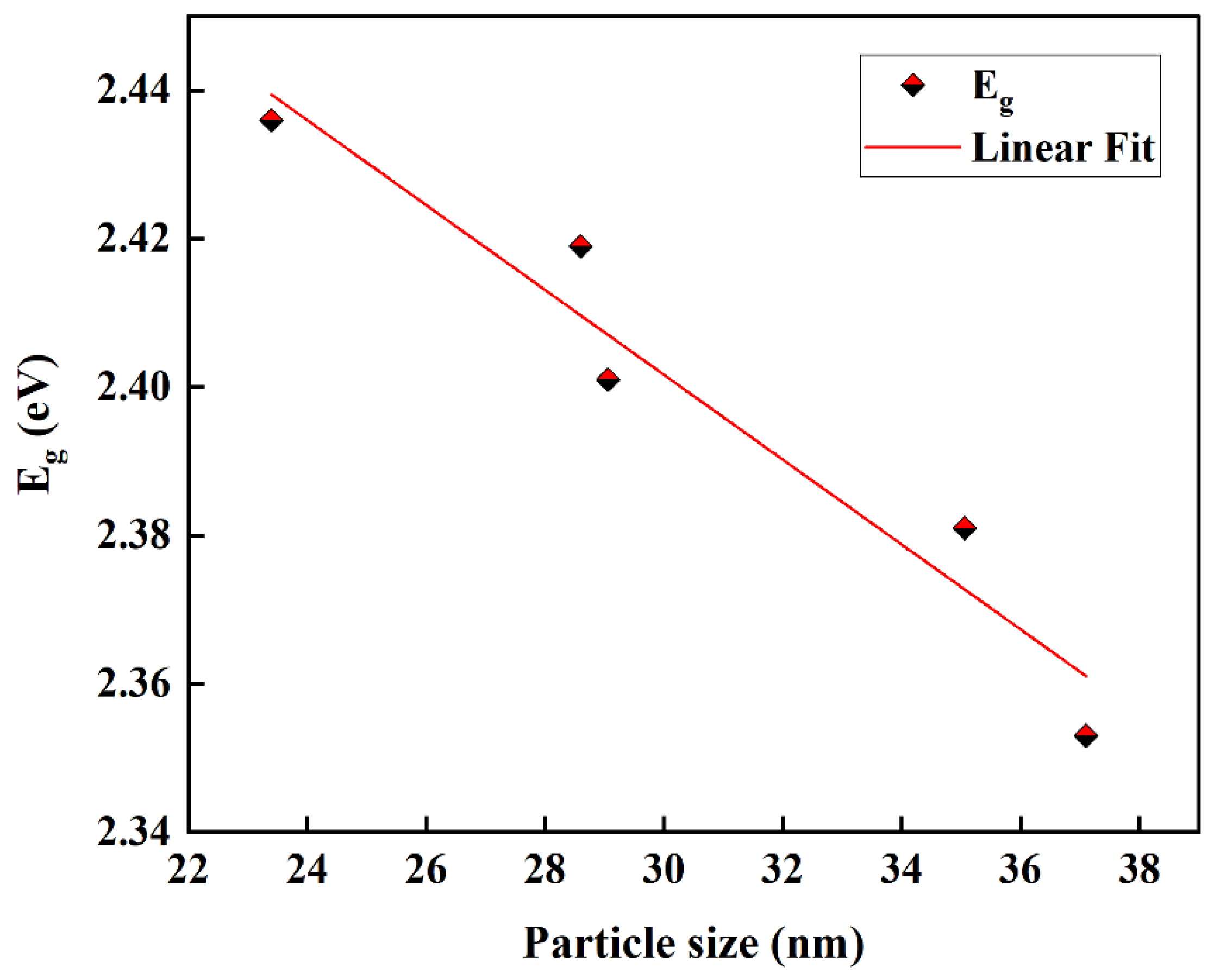
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hayat, M.B.; Ali, D.; Monyake, K.C.; Alagha, L.; Ahmed, N. Solar energy-A look into power generation, challenges, and a solar-powered future. Int. J. Energy Res. 2019, 43, 1049–1067. [Google Scholar]
- Ashok, A.; Regmi, G.; Romero-Núñez, A.; Solis-López, M.; Velumani, S.; Castaneda, H. Comparative studies of CdS thin films by chemical bath deposition techniques as a buffer layer for solar cell applications. J. Mater. Sci. Mater. Electron. 2020, 31, 7499–7518. [Google Scholar] [CrossRef]
- Bagali, D.M.U. A Review on the Solar Energy: Potential and Future Prospects. J. Emerg. Technol. Innov. Res. 2019, 6, 208–215. [Google Scholar]
- Sharkh, A.S.M.; Griffiths, G. Energy Storage Systems for Unmanned Underwater Vehicles. Underw. Technol. 2003, 25, 143–148. [Google Scholar]
- Lopes, P.P.; Stamenkovic, V.R. Past, present, and future of lead–acid batteries. Science 2020, 369, 923–924. [Google Scholar]
- Zau, A.T.P.; Chowdhury, S.D.; Olwal, T.O. Review of Battery Management Strategy in Hybrid Lead-Acid-Lithium-Ion Energy Storage System for Transport Vehicles. In Proceedings of the 2020 IEEE PES/IAS PowerAfrica, Nairobi, Kenya, 25–28 August 2020; pp. 1–5. [Google Scholar]
- Pomerantseva, E.; Bonaccorso, F.; Feng, X.; Cui, Y.; Gogotsi, Y. Energy storage: The future enabled by nanomaterials. Science 2019, 366, eaan8285. [Google Scholar]
- Kolavada, H.; Gajjar, P.N.; Gupta, S.K. Unraveling quantum capacitance in supercapacitors: Energy storage applications. J. Energy Storage 2024, 81, 110354. [Google Scholar]
- Highland, H. Nanotechnology applications in conventional lithium-ion batteries. Appl. Comput. Eng. 2024, 60, 33–41. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Lu, Y. Realizing high voltage lithium cobalt oxide in lithium-ion batteries. Ind. Eng. Chem. Res. 2019, 58, 10119–10139. [Google Scholar]
- Zhuang, Z.; Wang, J.; Jia, K.; Ji, G.; Ma, J.; Han, Z.; Piao, Z.; Gao, R.; Ji, H.; Zhong, X.; et al. Ultrahigh-Voltage LiCoO2 at 4.7 V by Interface Stabilization and Band Structure Modification. Adv. Mater. 2023, 35, 2212059. [Google Scholar]
- Wan, J.; Zhu, J.; Xiang, Y.; Zhong, G.; Liu, X.; Li, Y.; Zhang, K.H.L.; Hong, C.; Zheng, J.; Wang, K.; et al. Revealing the correlation between structure evolution and electrochemical performance of high-voltage lithium cobalt oxide. J. Energy Chem. 2021, 54, 786–794. [Google Scholar]
- Nayak, P.K.; Grinblat, J.; Levi, M.; Levi, E.; Kim, S.; Choi, J.W.; Aurbach, D. Al Doping for Mitigating the Capacity Fading and Voltage Decay of Layered Li and Mn-Rich Cathodes for Li-Ion Batteries. Adv. Energy Mater. 2016, 6, 1502398. [Google Scholar]
- Cheng, L.; Zhang, B.; Su, S.-L.; Ming, L.; Zhao, Y.; Tan, X.-X. Al-doping enables high stability of single-crystalline LiNi0.7 Co0.1 Mn0.2 O2 lithium-ion cathodes at high voltage. RSC Adv. 2021, 11, 124–128. [Google Scholar]
- Min, K.; Seo, S.-W.; Song, Y.Y.; Lee, H.S.; Cho, E. A first-principles study of the preventive effects of Al and Mg doping on the degradation in LiNi0.8 Co0.1 Mn0.1 O2 cathode materials. Phys. Chem. Chem. Phys. 2017, 19, 1762–1769. [Google Scholar]
- Dianat, A.; Seriani, N.; Bobeth, M.; Cuniberti, G. Effects of Al-doping on the properties of Li–Mn–Ni–O cathode materials for Li-ion batteries: An ab initio study. J. Mater. Chem. A 2013, 1, 9273. [Google Scholar]
- Hasan, F.; Kim, J.; Song, H.; Sung, J.H.; Kim, J.; Yoo, H.D. Effect of Particle Size and Doping on the Electrochemical Characteristics of Ca-doped LiCoO2 Cathodes. J. Electrochem. Sci. Technol. 2020, 11, 352–360. [Google Scholar] [CrossRef]
- Abualela, S.; Lv, X.; Hu, Y.; Abd-Alla, M.D. NiO nanosheets grown on carbon cloth as mesoporous cathode for High-performance lithium-sulfur battery. Mater. Lett. 2020, 268, 127622. [Google Scholar] [CrossRef]
- Roy, P.; Srivastava, S.K. Nanostructured anode materials for lithium ion batteries. J. Mater. Chem. A 2015, 3, 2454–2484. [Google Scholar]
- Chen, H.; Wang, W.; Yang, L.; Dong, L.; Wang, D.; Xu, X.; Wang, D.; Huang, J.; Lv, M.; Wang, H. A Review of Cobalt-Containing Nanomaterials, Carbon Nanomaterials and Their Composites in Preparation Methods and Application. Nanomaterials 2022, 12, 2042. [Google Scholar] [CrossRef]
- Muchuweni, E.; Mombeshora, E.T.; Muiva, C.M.; Sathiaraj, T.S. Lithium-ion batteries: Recent progress in improving the cycling and rate performances of transition metal oxide anodes by incorporating graphene-based materials. J. Energy Storage 2023, 73, 109013. [Google Scholar]
- Yu, S.; Lee, S.H.; Lee, D.J.; Sung, Y.; Hyeon, T. Conversion Reaction-Based Oxide Nanomaterials for Lithium Ion Battery Anodes. Small 2016, 12, 2146–2172. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.; Schuer, A.R.; Moon, H.; Melinte, G.; Kim, G.; Asenbauer, J.; Kazzazi, A.; Kuenzel, M.; Passerini, S. Is Cobalt in Li-Rich Layered Oxides for Li-Ion Batteries Necessary? ChemElectroChem 2024, 11, e202400391. [Google Scholar] [CrossRef]
- Zhang, J.-N.; Li, Q.; Ouyang, C.; Yu, X.; Ge, M.; Huang, X.; Hu, E.; Ma, C.; Li, S.; Xiao, R. Trace doping of multiple elements enables stable battery cycling of LiCoO2 at 46 V. Nat. Energy 2019, 4, 594–603. [Google Scholar] [CrossRef]
- Kim, J.H.; Hwang, J.; Lee, Y.-H.; Song, S.H.; Lee, J.; Lee, S.H.; Moon, W.J.; Kim, H.; Kim, D.; Yu, S.H.; et al. Improvement of Thermodynamic Phase Stability and High-Rate Capability of Li Layered Oxides. ACS Appl. Mater. Interfaces 2023, 15, 55837–55847. [Google Scholar] [CrossRef]
- Tan, X.; Zhang, Y.; Xu, S.; Yang, P.; Liu, T.; Mao, D.; Qiu, J.; Chen, Z.; Lu, Z.; Pan, F.; et al. High-Entropy Surface Complex Stabilized LiCoO2 Cathode. Adv. Energy Mater. 2023, 13, 2300147. [Google Scholar] [CrossRef]
- Lin, S.; Zhao, J. Functional electrolyte of fluorinated ether and ester for stabilizing both 4.5 V LiCoO2 cathode and lithium metal anode. ACS Appl. Mater. Interfaces 2020, 12, 8316–8323. [Google Scholar] [CrossRef]
- Chong, P.; Zhou, Z.; Wang, K.; Zhai, W.; Li, Y.; Wang, J.; Wei, M. The stabilizing of 1T-MoS2 for all-solid-state lithium-ion batteries. Batteries 2022, 9, 26. [Google Scholar] [CrossRef]
- Shang, W.; Wang, H.; Yu, W.; He, Y.; Ma, Y.; Wu, Z.; Tan, P. Transforming the Electrochemical Behaviors of Cobalt Oxide from “Supercapacitator” to “Battery” by Atomic-Level Structure Engineering for Inspiring the Advance of Co-Based Batteries. Small 2023, 19, 2300647. [Google Scholar] [CrossRef]
- Konar, R.; Maiti, S.; Shpigel, N.; Aurbach, D. Reviewing failure mechanisms modification strategies in stabilizing high-voltage LiCoO2 cathodes beyond 4.5.5.V. Energy Storage Mater. 2023, 63, 103001. [Google Scholar] [CrossRef]
- Lin, C.; Li, J.; Yin, Z.; Huang, W.; Zhao, Q.; Weng, Q.; Liu, Q.; Sun, J.; Chen, G.; Pan, F. Structural Understanding for High-Voltage Stabilization of Lithium Cobalt Oxide. Adv. Mater. 2024, 36, 2307404. [Google Scholar] [CrossRef]
- Xiong, L.; Su, N.Q.; Fang, W.-H. The Role of Self-Catalysis Induced by Co Doping in Nonaqueous Li–O2 Batteries. J. Phys. Chem. Lett. 2023, 14, 7526–7540. [Google Scholar] [CrossRef] [PubMed]
- Algethami, O.A. Investigation of structure, mechanical properties, and electrical conductivity of LixCo(1-x)O2: Validation using a nanoquantum model. Next Mater. 2025, 7, 100510. [Google Scholar] [CrossRef]
- Pinsard-Gaudart, L.; Ciomaga, V.C.; Dragos, O.; Guillot, R.; Dragoe, N. Growth and characterisation of LixCoO2 single crystals. J. Cryst. Growth 2011, 334, 165–169. [Google Scholar] [CrossRef]
- Kataoka, K.; Akimoto, J. Single-crystal growth, crystal structure analysis and physical properties of lithium overstoichiometric Li1+ xCoO2. Solid State Ion. 2014, 262, 106–109. [Google Scholar] [CrossRef]
- Han, Y.; Liu, W.; Xu, X.; Guo, M.; Zhang, X.; Wu, P.; Gao, J.; Rao, G.; Wang, S. The Abnormal Optical Property and Room-Temperature Exchange Bias Behavior in Na- and Ru-Codoped BiFeO3 Nanoparticles. J. Am. Ceram. Soc. 2016, 99, 3616–3622. [Google Scholar] [CrossRef]
- Ghosh, P.; Mahanty, S.; Raja, M.W.; Basu, R.N.; Maiti, H.S. Structure and optical absorption of combustion-synthesized nanocrystalline LiCoO2. J. Mater. Res. 2007, 22, 1162–1167. [Google Scholar] [CrossRef]
- Laubach, S.; Laubach, S.; Schmidt, P.C.; Ensling, D.; Schmid, S.; Jaegermann, W.; Thißen, A.; Nikolowski, K.; Ehrenberg, H. Changes in the crystal and electronic structure of LiCoO2 and LiNiO2 upon Li intercalation and de-intercalation. Phys. Chem. Chem. Phys. 2009, 11, 3278. [Google Scholar] [CrossRef]
- Radha, S.K.; Lambrecht, W.R.L.; Cunningham, B.; Grüning, M.; Pashov, D.; Van Schilfgaarde, M. Optical response and band structure of LiCoO2 including electron-hole interaction effects. Phys. Rev. B 2021, 104, 115120. [Google Scholar] [CrossRef]
- Song, H.; Yun, S.-W.; Chun, H.-H.; Kim, M.-G.; Chung, K.Y.; Kim, H.S.; Cho, B.-W.; Kim, Y.-T. Anomalous decrease in structural disorder due to charge redistribution in Cr-doped Li4Ti5O12 negative-electrode materials for high-rate Li-ion batteries. Energy Environ. Sci. 2012, 5, 9903. [Google Scholar] [CrossRef]
- Jang, H.; Seong, C.; Suh, Y.; Kim, H.; Lee, C. Synthesis of Lithium-Cobalt Oxide Nanoparticles by Flame Spray Pyrolysis. Aerosol Sci. Technol. 2004, 38, 1027–1032. [Google Scholar] [CrossRef]
- Zehetmaier, P.M.; Cornélis, A.; Zoller, F.; Böller, B.; Wisnet, A.; Döblinger, M.; Böhm, D.; Bein, T.; Fattakhova-Rohlfing, D. Nanosized Lithium-Rich Cobalt Oxide Particles and Their Transformation to Lithium Cobalt Oxide Cathodes with Optimized High-Rate Morphology. Chem. Mater. 2019, 31, 8685–8694. [Google Scholar]
- Sushko, M.L.; Rosso, K.M.; Liu, J. Size Effects on Li+/Electron Conductivity in TiO2 Nanoparticles. J. Phys. Chem. Lett. 2010, 1, 1967–1972. [Google Scholar]
- Greshnykh, D.; Frömsdorf, A.; Weller, H.; Klinke, C. On the Electric Conductivity of Highly Ordered Monolayers of Monodisperse Metal Nanoparticles. Nano Lett. 2009, 9, 473–478. [Google Scholar]
- Jin, Y.; Gwak, Y.; Gerhardt, R.A. Effects of nanoparticles size and interactions on dielectric properties of polymer matrix flexible dielectric nanocomposites. Adv. Compos. Mater. 2020, 29, 235–246. [Google Scholar] [CrossRef]
- Hally, D.J.T.; Paci, I. Low-frequency polarization in molecular-scale noble-metal/metal–oxide nanocomposites. Nanoscale 2018, 10, 9583–9593. [Google Scholar]
- Abualela, S.; Lv, X.; Hu, Y.; Abd-Alla, M.D.; Ewakeel, S.S.; Mohamed, A.K. Mesoporous NiCo2O4 Nanoparticles as Cathode Additive for High-Performance Lithium Sulfur Battery. In Proceedings of the Journal of Physics: Conference Series: 2020 International Conference on Physics, Mechanics and Mathematical Science, Xi’an, China, 18–19 October 2020; p. 012006. [Google Scholar]
- Zhang, Y.; Wang, N.; Bai, Z. The progress of cobalt-based anode materials for lithium ion batteries and sodium ion batteries. Appl. Sci. 2020, 10, 3098. [Google Scholar] [CrossRef]
- Kawashima, K.; Ohnishi, T.; Takada, K. High-rate capability of LiCoO2 cathodes. ACS Appl. Energy Mater. 2020, 3, 11803–11810. [Google Scholar]


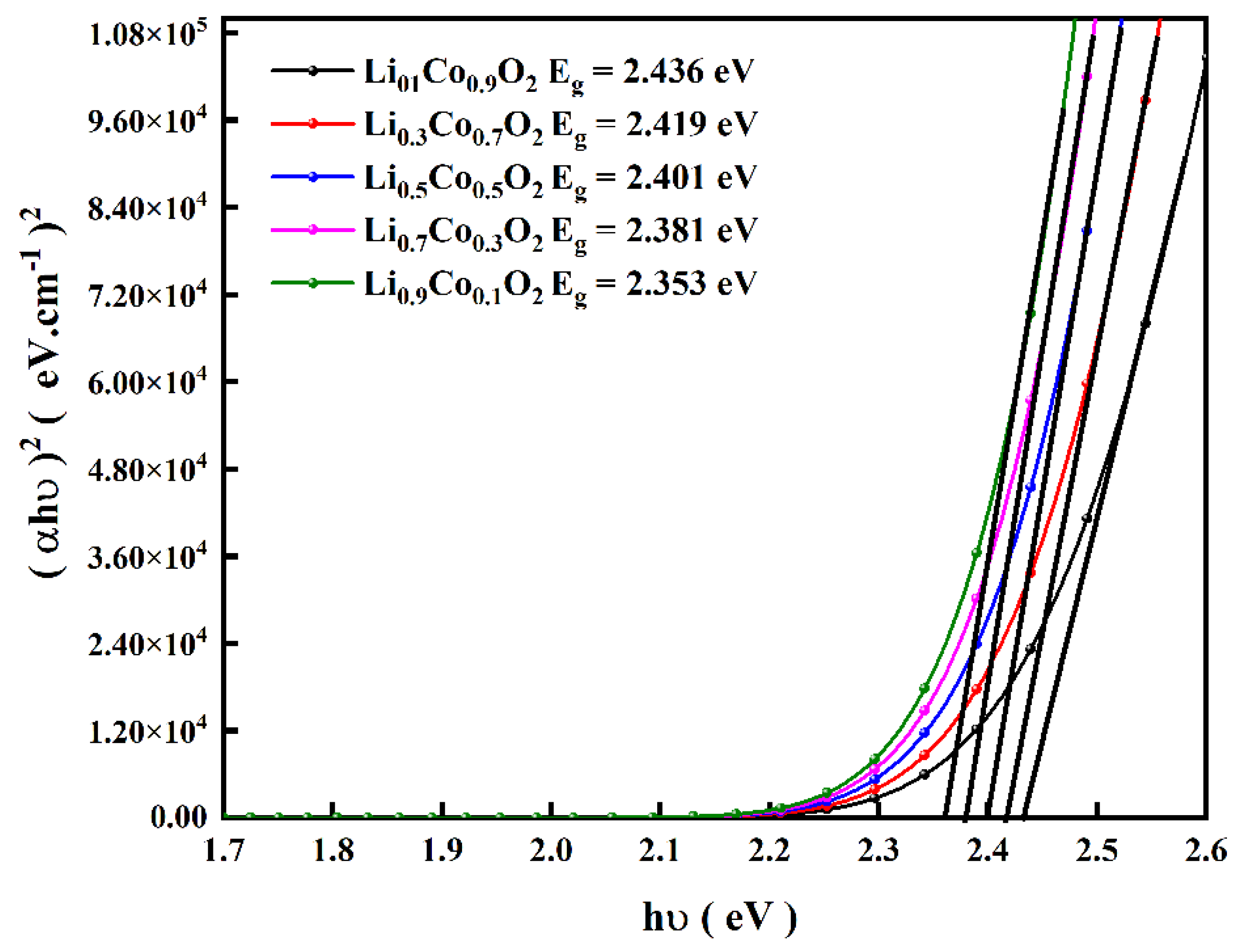


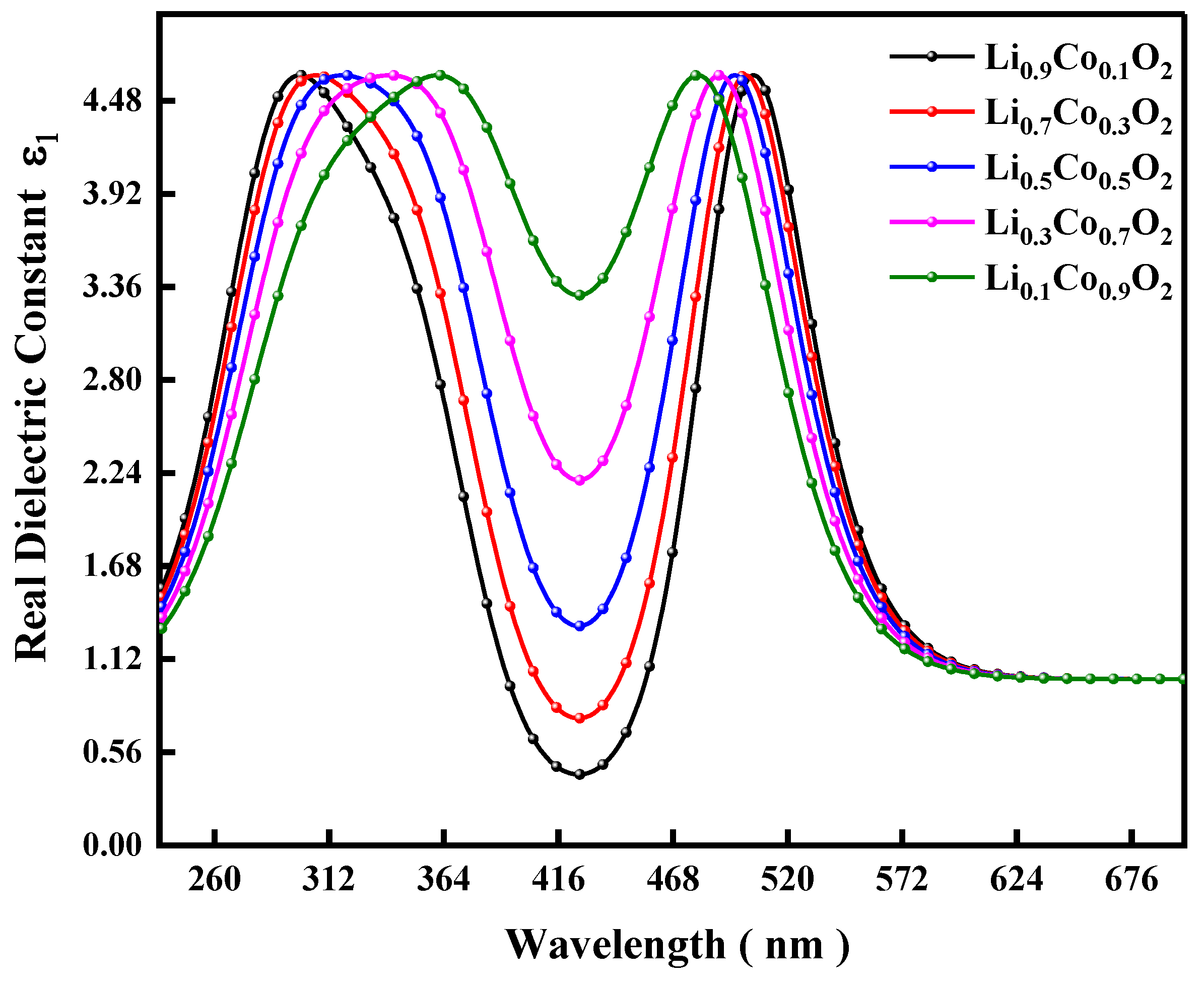
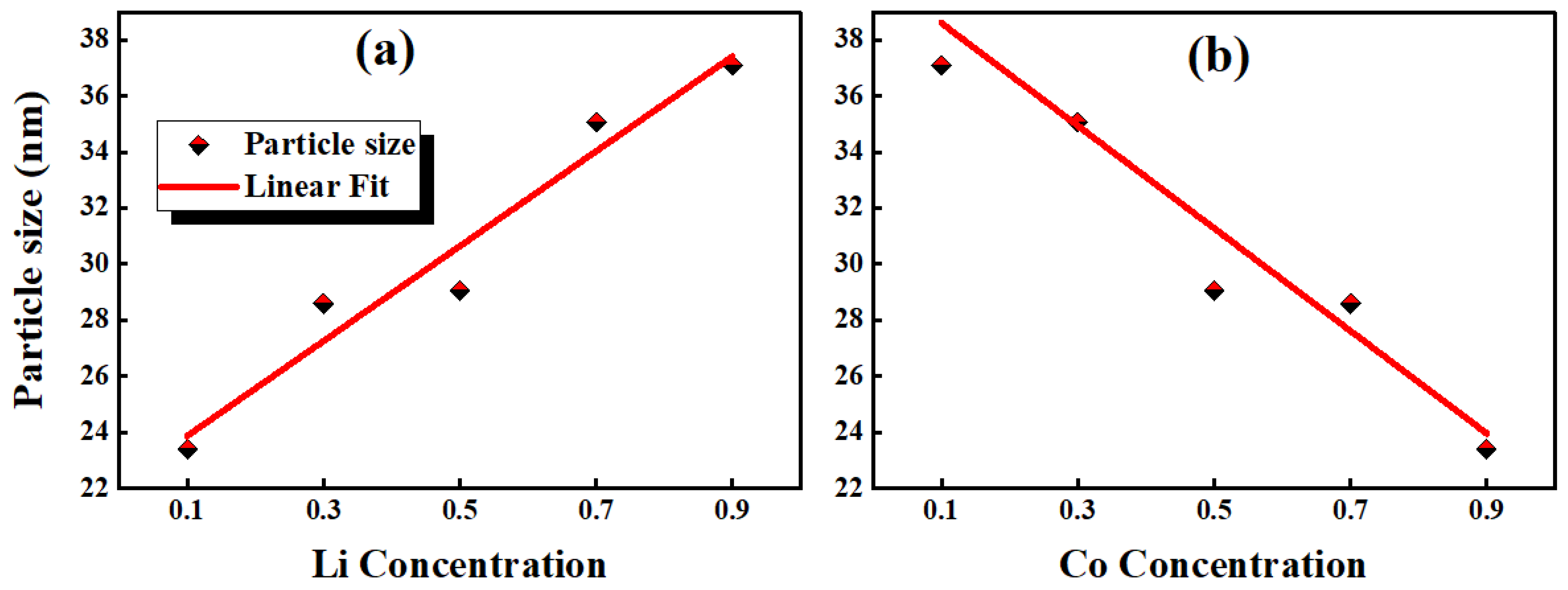
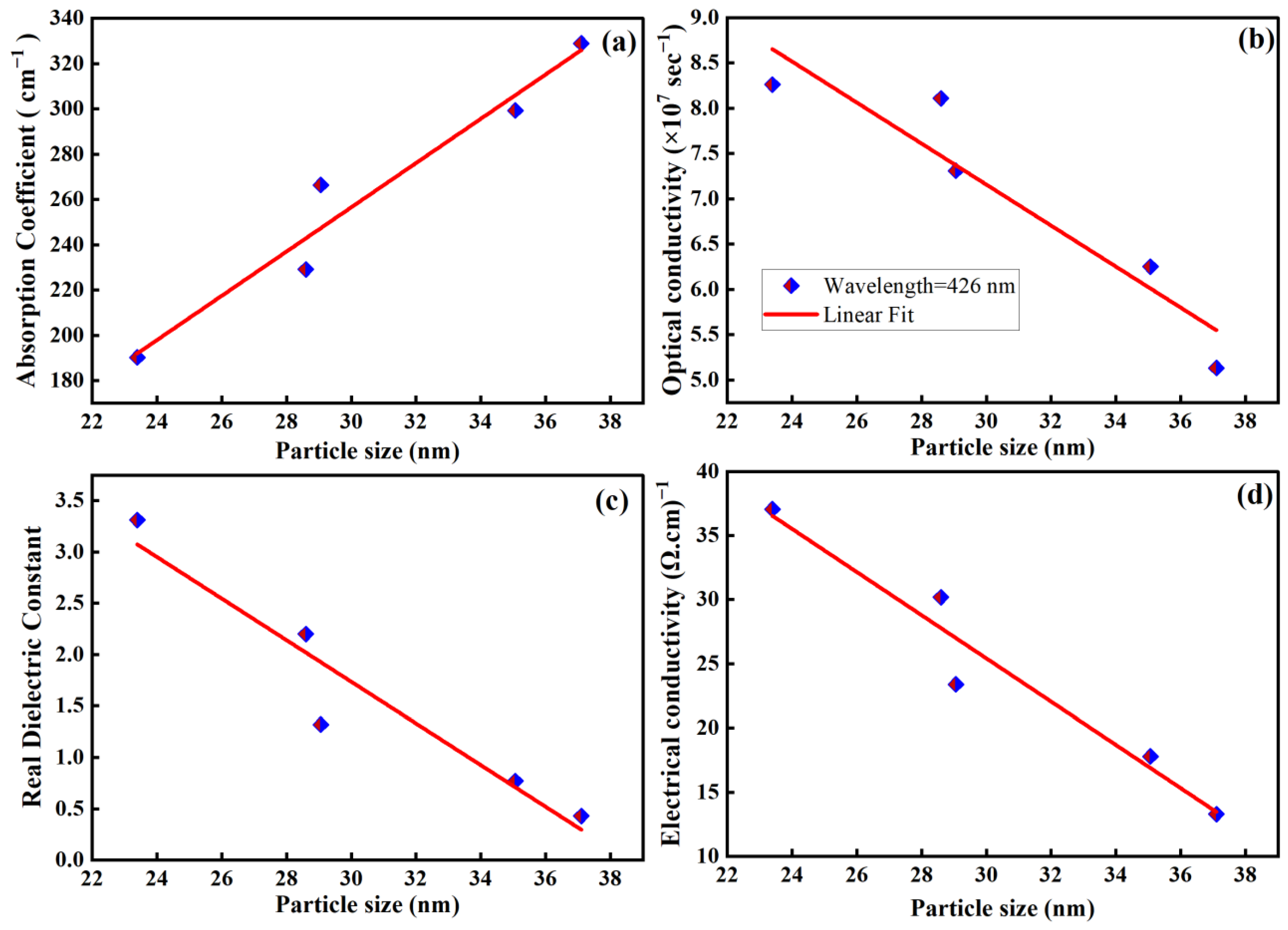

| XRD Data | Li0.9Co0.1O2 | Li0.7Co0.3O2 | Li0.5Co0.5O2 | Li0.3Co0.7 O2 | Li0.1Co0.9 O2 | |
|---|---|---|---|---|---|---|
| Space Group | R-3m | R-3m | R-3m | R-3m | R-3m | |
| Crystal System | Hexagonal | Hexagonal | Hexagonal | Hexagonal | Hexagonal | |
| Cell Parameters 10−10 m | a | 2.816 | 2.675 | 2.547 | 1.984 | 1.578 |
| b | 2.816 | 2.675 | 2.547 | 1.984 | 1.578 | |
| c | 14.052 | 13.48 | 12.84 | 9.99 | 8.854 | |
| Density (g·cm−3) | 5.05 | 5.30 | 5.57 | 7.41 | 9.04 | |
| Volume (10−10)3 | 96.5 | 92.6 | 88.2 | 68.5 | 60.7 | |
| d (10−10 m) | 2.204 | 2.114 | 2.013 | 1.564 | 1.386 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Algethami, O.A. Dual Influence of Li Concentration and Nanoparticle Size in LiCoO2 on the Conductivity and Storage Capacity of Lithium Batteries. J. Compos. Sci. 2025, 9, 170. https://doi.org/10.3390/jcs9040170
Algethami OA. Dual Influence of Li Concentration and Nanoparticle Size in LiCoO2 on the Conductivity and Storage Capacity of Lithium Batteries. Journal of Composites Science. 2025; 9(4):170. https://doi.org/10.3390/jcs9040170
Chicago/Turabian StyleAlgethami, Obaidallah A. 2025. "Dual Influence of Li Concentration and Nanoparticle Size in LiCoO2 on the Conductivity and Storage Capacity of Lithium Batteries" Journal of Composites Science 9, no. 4: 170. https://doi.org/10.3390/jcs9040170
APA StyleAlgethami, O. A. (2025). Dual Influence of Li Concentration and Nanoparticle Size in LiCoO2 on the Conductivity and Storage Capacity of Lithium Batteries. Journal of Composites Science, 9(4), 170. https://doi.org/10.3390/jcs9040170




