Auxetic Composite Sandwich for Vibration Damping Through Axisymmetric Deformation
Abstract
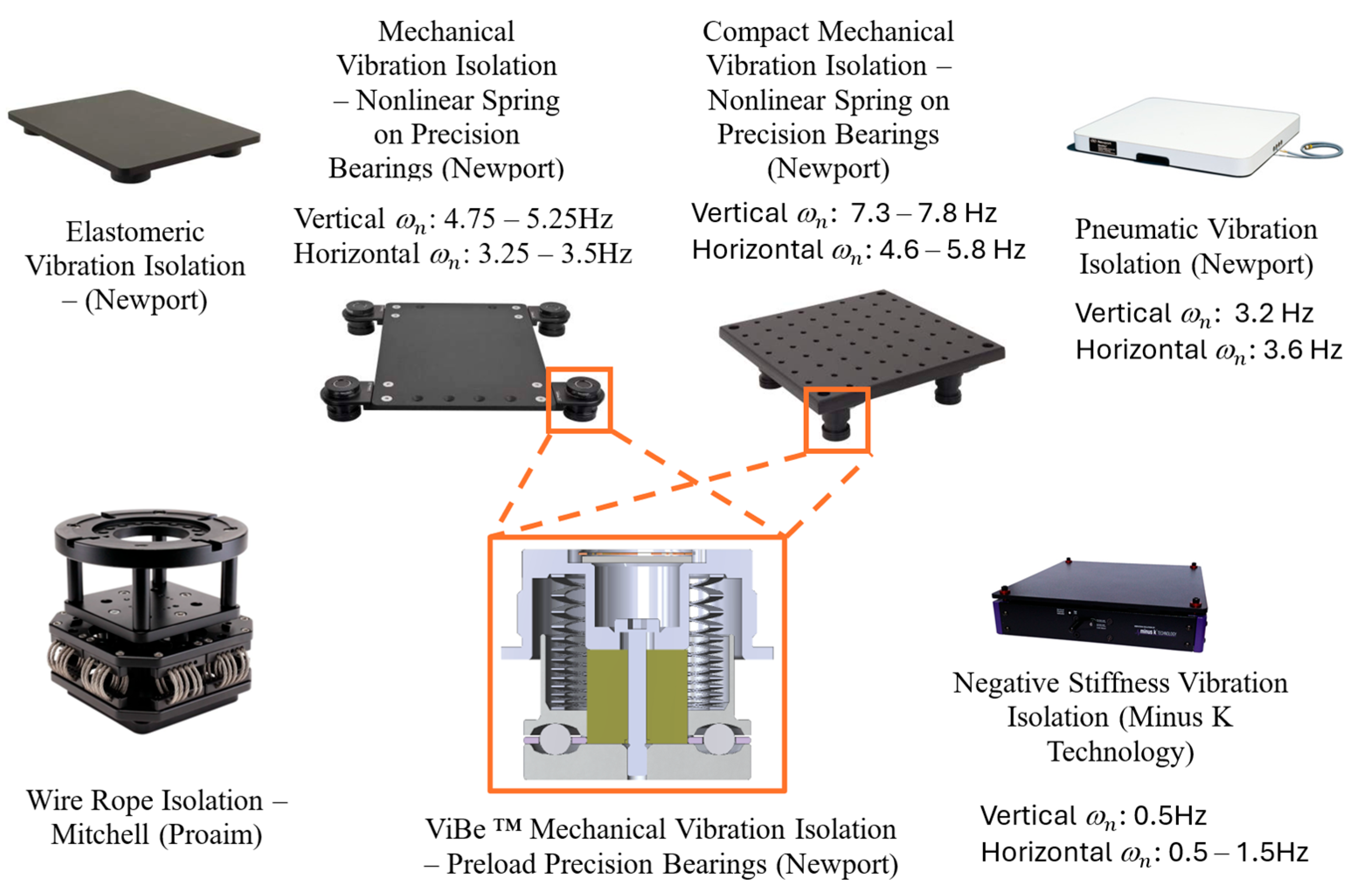
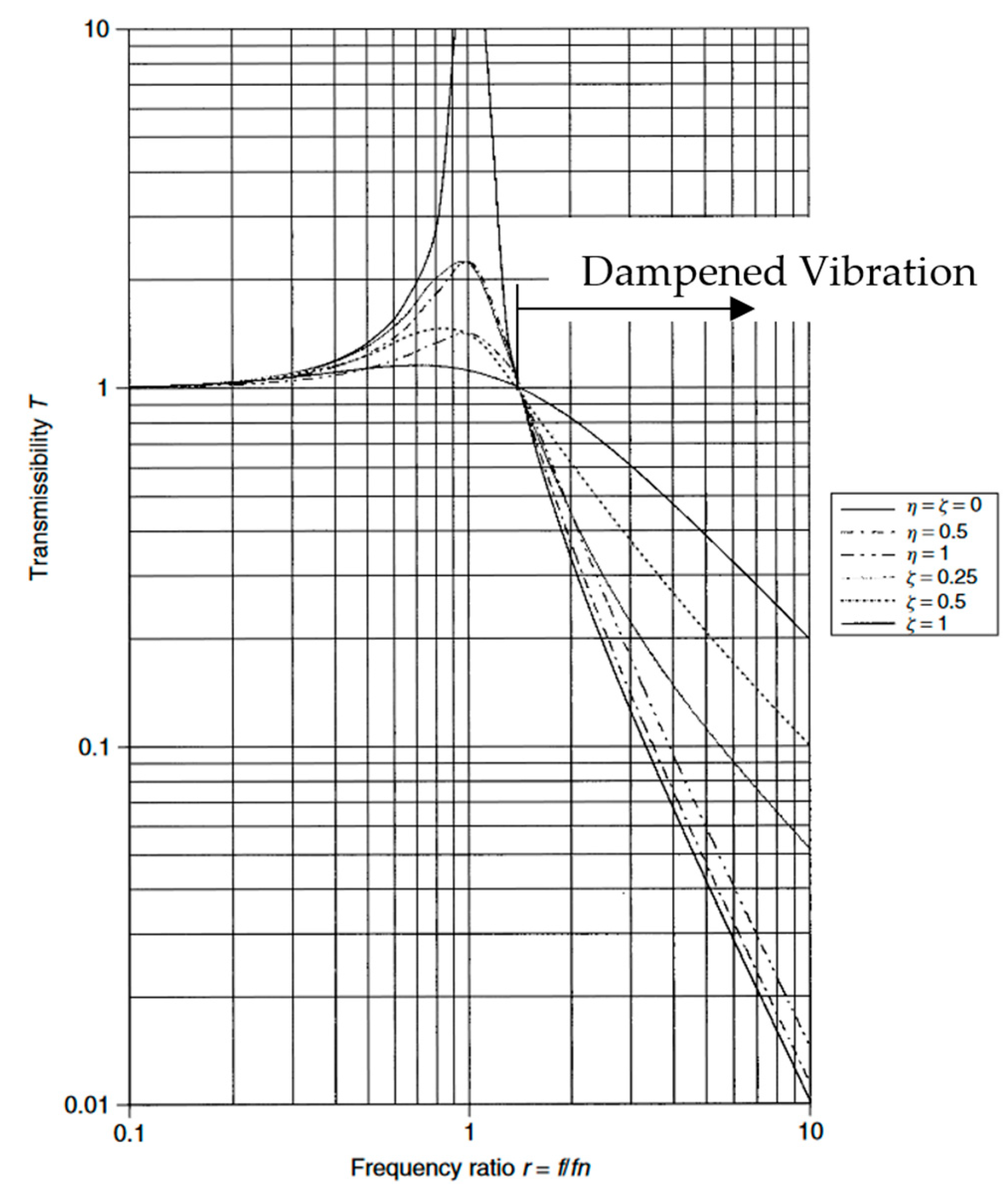
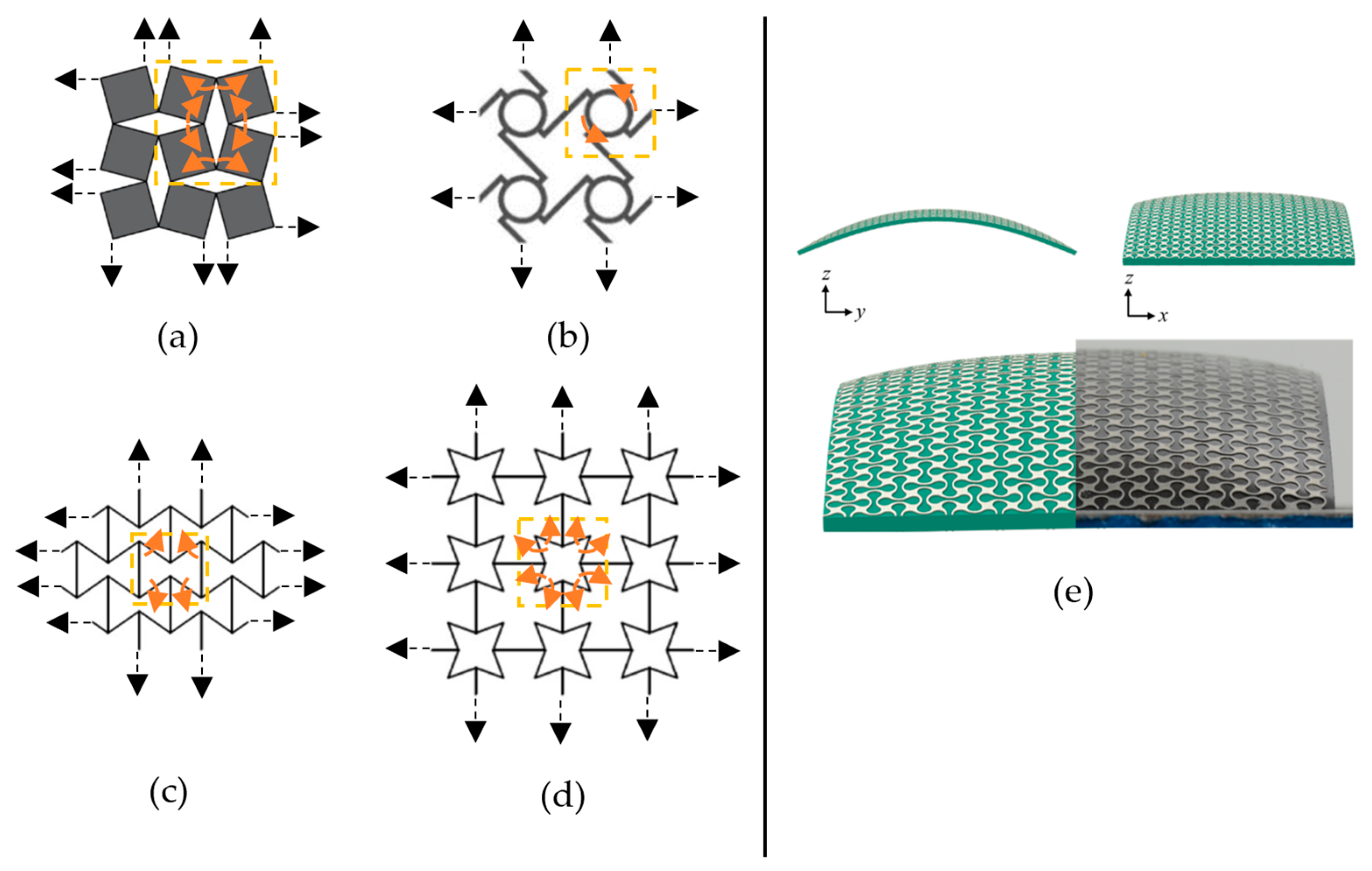
1. Introduction
2. Materials and Methods
2.1. Materials
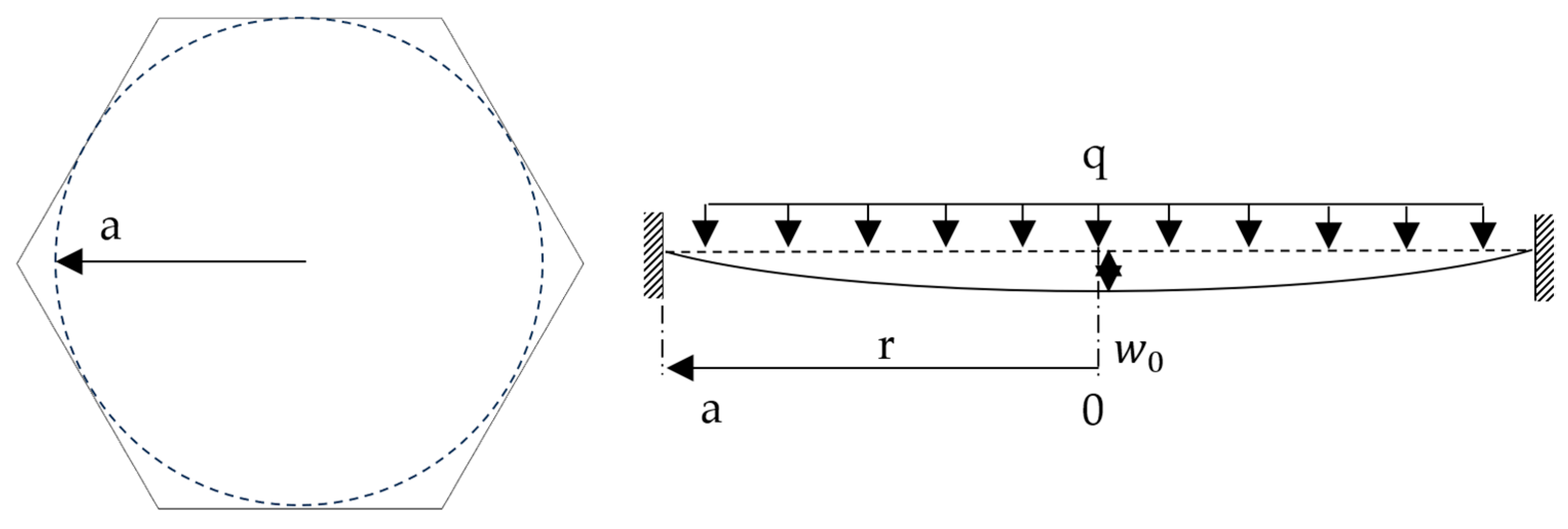
2.2. Analytical Methods
2.3. Finite Element Analysis
2.4. Experimental Study
3. Results and Discussion
3.1. Numerical Simulation
3.2. Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qian, Y.; Xie, Y.; Jia, J.; Zhang, L. Development of Active Microvibration Isolation System for Precision Space Payload. Appl. Sci. 2022, 12, 4548. [Google Scholar] [CrossRef]
- Ungar, E.E.; Zapfe, J.A. Vibration Isolation. In Noise and Vibration Control Engineering; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005; pp. 557–578. [Google Scholar] [CrossRef]
- Park, Y.-H.; Kwon, S.-C.; Koo, K.-R.; Oh, H.-U. High Damping Passive Launch Vibration Isolation System Using Superelastic SMA with Multilayered Viscous Lamina. Aerospace 2021, 8, 201. [Google Scholar] [CrossRef]
- Pan, J.; Liu, Z.; Kou, X.; Song, Q. Constrained layer damping treatment of a model support sting. Chin. J. Aeronaut. 2021, 34, 58–64. [Google Scholar] [CrossRef]
- Gong, Y.; Peng, W.; Liu, Z. Affect of Elastic Displacement Limiter on Shock Response of Double-stage Vibration Isolation System. J. Phys. Conf. Ser. 2020, 1637, 012115. [Google Scholar] [CrossRef]
- Torvik, P.J. The Analysis and Design of Constrained Layer Damping Treatments; Defense Technical Information Center: Fort Belvoir, VA, USA, 1980. [Google Scholar] [CrossRef]
- Kolpakov, A.G. Determination of the average characteristics of elastic frameworks. J. Appl. Math. Mech. 1985, 49, 739–745. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, G.; You, Z. Large deformation and energy absorption of additively manufactured auxetic materials and structures: A review. Compos. Part B Eng. 2020, 201, 108340. [Google Scholar] [CrossRef]
- Alvermann, S.; Brenn, G.; Holzapfel, G.; Schanz, M.; Sextro, W.; Steinbach, O. Effective viscoelastic behaviour of cellular auxetic materials. In Computation in Engineering and Science, 1st ed.; Verlag der Technischen Universität Graz: Graz, Austria, 2008. [Google Scholar]
- Novak, N.; Duncan, O.; Allen, T.; Alderson, A.; Vesenjak, M.; Ren, Z. Shear modulus of conventional and auxetic open-cell foam. Mech. Mater. 2021, 157, 103818. [Google Scholar] [CrossRef]
- Li, T.; Liu, F.; Wang, L. Enhancing indentation and impact resistance in auxetic composite materials. Compos. Part B Eng. 2020, 198, 108229. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, Z.; Wu, J. An overview of impact resistance of auxetic lattice structure. J. Phys. Conf. Ser. 2020, 1549, 032077. [Google Scholar] [CrossRef]
- Wang, Z.; Zulifqar, A.; Hu, H. 7—Auxetic composites in aerospace engineering. In Advanced Composite Materials for Aerospace Engineering; Rana, S., Fangueiro, R., Eds.; Woodhead Publishing: Sawston, UK, 2016; pp. 213–240. [Google Scholar] [CrossRef]
- Zhang, X.-W.; Yang, D.-Q. Numerical and Experimental Studies of a Light-Weight Auxetic Cellular Vibration Isolation Base. Shock. Vib. 2016, 2016, 4017534. [Google Scholar] [CrossRef]
- Matuszewska, A. Vibration Properties of Auxetic Beam. Vib. Phys. Syst. 2018, 29, 2018031. [Google Scholar]
- Pan, K.; Zhang, W.; Ding, J. Negative Poisson’s Ratio Re-Entrant Base Modeling and Vibration Isolation Performance Analysis. Symmetry 2022, 14, 1356. [Google Scholar] [CrossRef]
- Kim, J.; Hegde, H.; Kim, H.-Y.; Lee, C. Spindle vibration mitigation utilizing additively manufactured auxetic materials. J. Manuf. Process. 2022, 73, 633–641. [Google Scholar] [CrossRef]
- Bianchi, M.; Scarpa, F. Vibration transmissibility and damping behaviour for auxetic and conventional foams under linear and nonlinear regimes. Smart Mater. Struct. 2013, 22, 084010. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Wang, D.-W.; Ma, L. Vibration and damping performance of carbon fiber-reinforced polymer 3D double-arrow-head auxetic metamaterials. J. Mater. Sci. 2021, 56, 1443–1460. [Google Scholar] [CrossRef]
- Velásquez, M.B.; Francesconi, L.; Taylor, M. Design of low-porosity auxetic tessellations with reduced mechanical stress concentrations. Extrem. Mech. Lett. 2021, 48, 101401. [Google Scholar] [CrossRef]
- Chan, N.; Evans, K.E. Indentation Resilience of Conventional and Auxetic Foams. J. Cell. Plast. 1998, 34, 231–260. [Google Scholar] [CrossRef]
- Hu, J.S.; Wang, B.L. Crack growth behavior and thermal shock resistance of ceramic sandwich structures with an auxetic honeycomb core. Compos. Struct. 2021, 260, 113256. [Google Scholar] [CrossRef]
- Hu, J.S.; Wang, B.L.; Hirakata, H.; Wang, K.F. Thermal shock fracture analysis of auxetic honeycomb layer based on non-Fourier heat conduction. Eng. Struct. 2023, 279, 115581. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L. Auxetic materials. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2007, 221, 565–575. [Google Scholar] [CrossRef]
- Dengiz, D.; Goldbeck, H.; Curtis, S.M.; Bumke, L.; Jetter, J.; Quandt, E. Shape Memory Alloy Thin Film Auxetic Structures. Adv. Mater. Technol. 2023, 8, 2201991. [Google Scholar] [CrossRef]
- Easey, N.; Chuprynyuk, D.; Musa, W.M.S.W.; Bangs, A.; Dobah, Y.; Shterenlikht, A.; Scarpa, F. Dome-Shape Auxetic Cellular Metamaterials: Manufacturing, Modeling, and Testing. Front. Mater. 2019, 6, 86. [Google Scholar] [CrossRef]
- Peliński, K.; Smardzewski, J. Static response of synclastic sandwich panel with auxetic wood-based honeycomb cores subject to compression. Thin-Walled Struct. 2022, 179, 109559. [Google Scholar] [CrossRef]
- Wallbanks, M.; Khan, M.F.; Bodaghi, M.; Triantaphyllou, A.; Serjouei, A. On the design workflow of auxetic metamaterials for structural applications. Smart Mater. Struct. 2022, 31, 023002. [Google Scholar] [CrossRef]
- Dong, S.; Hu, H. Sensors Based on Auxetic Materials and Structures: A Review. Materials 2023, 16, 3603. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Kuang, Y.; Zhu, M. Auxetic piezoelectric energy harvesters for increased electric power output. AIP Adv. 2017, 7, 015104. [Google Scholar] [CrossRef]
- Ferguson, W.J.G.; Kuang, Y.; Evans, K.E.; Smith, C.W.; Zhu, M. Auxetic structure for increased power output of strain vibration energy harvester. Sens. Actuators A Phys. 2018, 282, 90–96. [Google Scholar] [CrossRef]
- Eghbali, P.; Younesian, D.; Moayedizadeh, A.; Ranjbar, M. Study in circular auxetic structures for efficiency enhancement in piezoelectric vibration energy harvesting. Sci. Rep. 2020, 10, 16338. [Google Scholar] [CrossRef]
- Zhou, X.; Parida, K.; Chen, J.; Xiong, J.; Zhou, Z.; Jiang, F.; Xin, Y.; Magdassi, S.; Lee, P.S. 3D Printed Auxetic Structure-Assisted Piezoelectric Energy Harvesting and Sensing. Adv. Energy Mater. 2023, 13, 2301159. [Google Scholar] [CrossRef]
- Momoh, E.O.; Jayasinghe, A.; Hajsadeghi, M.; Vinai, R.; Evans, K.E.; Kripakaran, P.; Orr, J. A state-of-the-art review on the application of auxetic materials in cementitious composites. Thin-Walled Struct. 2024, 196, 111447. [Google Scholar] [CrossRef]
- Park, E.B.; Jeong, Y.C.; Kang, K. A novel auxetic sandwich panel for use in structural applications: Fabrication and parametric study. Mater. Today Commun. 2023, 34, 105383. [Google Scholar] [CrossRef]
- Bosia, F.; Poggetto, V.F.D.; Gliozzi, A.S.; Greco, G.; Lott, M.; Miniaci, M.; Ongaro, F.; Onorato, M.; Seyyedizadeh, S.F.; Tortello, M.; et al. Optimized structures for vibration attenuation and sound control in Nature: A review. Matter 2022, 5, 3311–3340. [Google Scholar] [CrossRef]
- My Year with the Woodpeckers by Heinz Sielmann, Translated by Sodney Lightman: Good Hardback (1959) | Hall of Books. Available online: https://www.abebooks.com/Year-Woodpeckers-Heinz-Sielmann-translated-Sodney/8466038791/bd (accessed on 25 January 2024).
- Lee, N.; Horstemeyer, M.F.; Rhee, H.; Nabors, B.; Liao, J.; Williams, L.N. Hierarchical multiscale structure–property relationships of the red-bellied woodpecker (Melanerpes carolinus) beak. J. R. Soc. Interface 2014, 11, 20140274. [Google Scholar] [CrossRef] [PubMed]
- Garland, A.P.; Adstedt, K.M.; Casias, Z.J.; White, B.C.; Mook, W.M.; Kaehr, B.; Jared, B.H.; Lester, B.T.; Leathe, N.S.; Schwaller, E.; et al. Coulombic friction in metamaterials to dissipate mechanical energy. Extrem. Mech. Lett. 2020, 40, 100847. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J. Biomechanical Dynamics of Cranial Sutures during Simulated Impulsive Loading. Appl. Bionics Biomech. 2015, 2015, 596843. [Google Scholar] [CrossRef]
- Ventsel, E.; Krauthammer, T. Thin Plates and Shells: Theory, Analysis, and Applications; Marcel Dekker: New York, NY, USA, 2001. [Google Scholar]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating triangles. J. Mater. Sci. 2006, 41, 3193–3196. [Google Scholar] [CrossRef]
- Salmon, F.; Company, M.; Paul, S.; Nie, M.Q. Structural Analyst. Modeling of VHB Structural Glazing Tape for Glazing System Assembly. 2013. Available online: https://api.semanticscholar.org/CorpusID:32003661 (accessed on 22 August 2024).




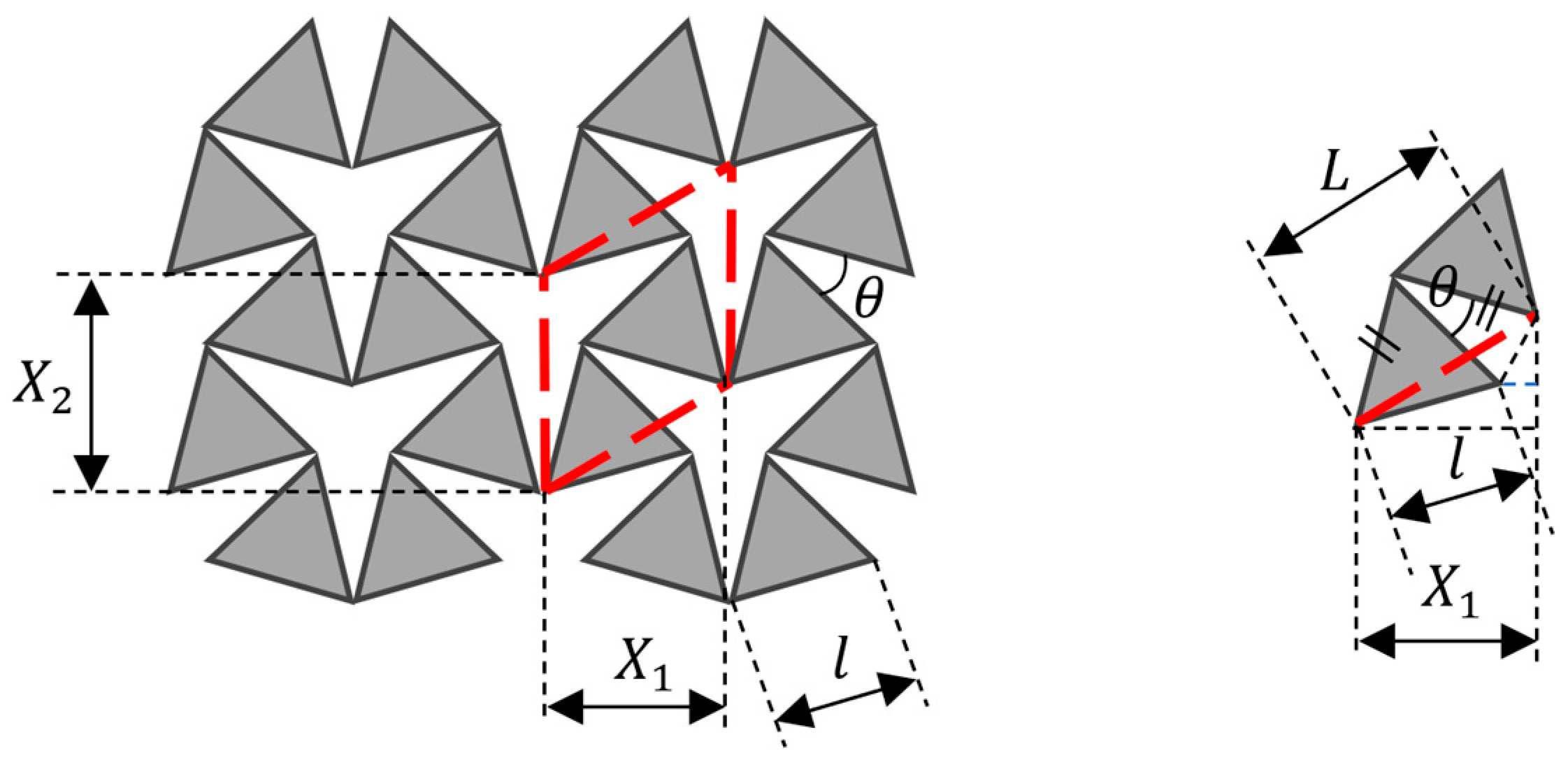













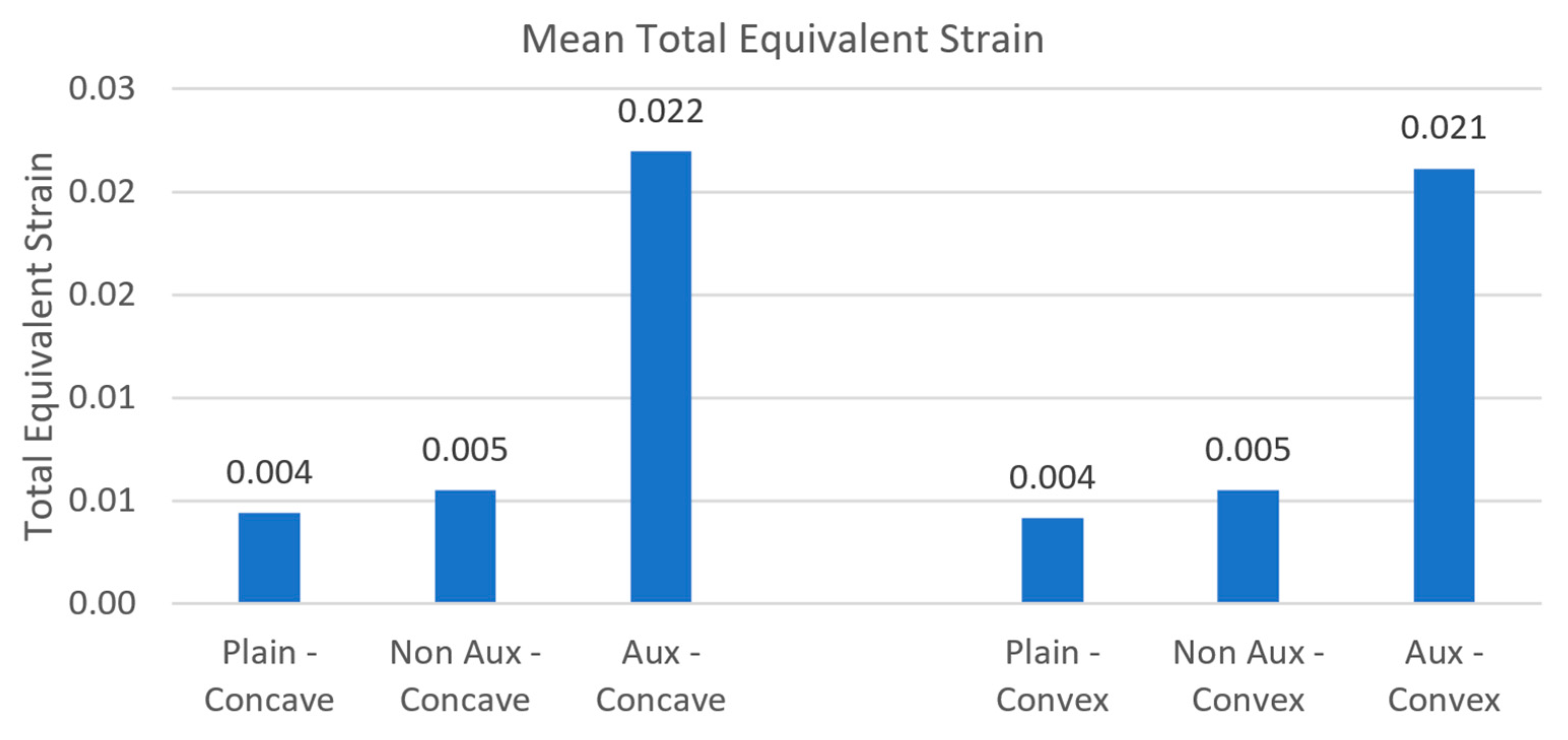



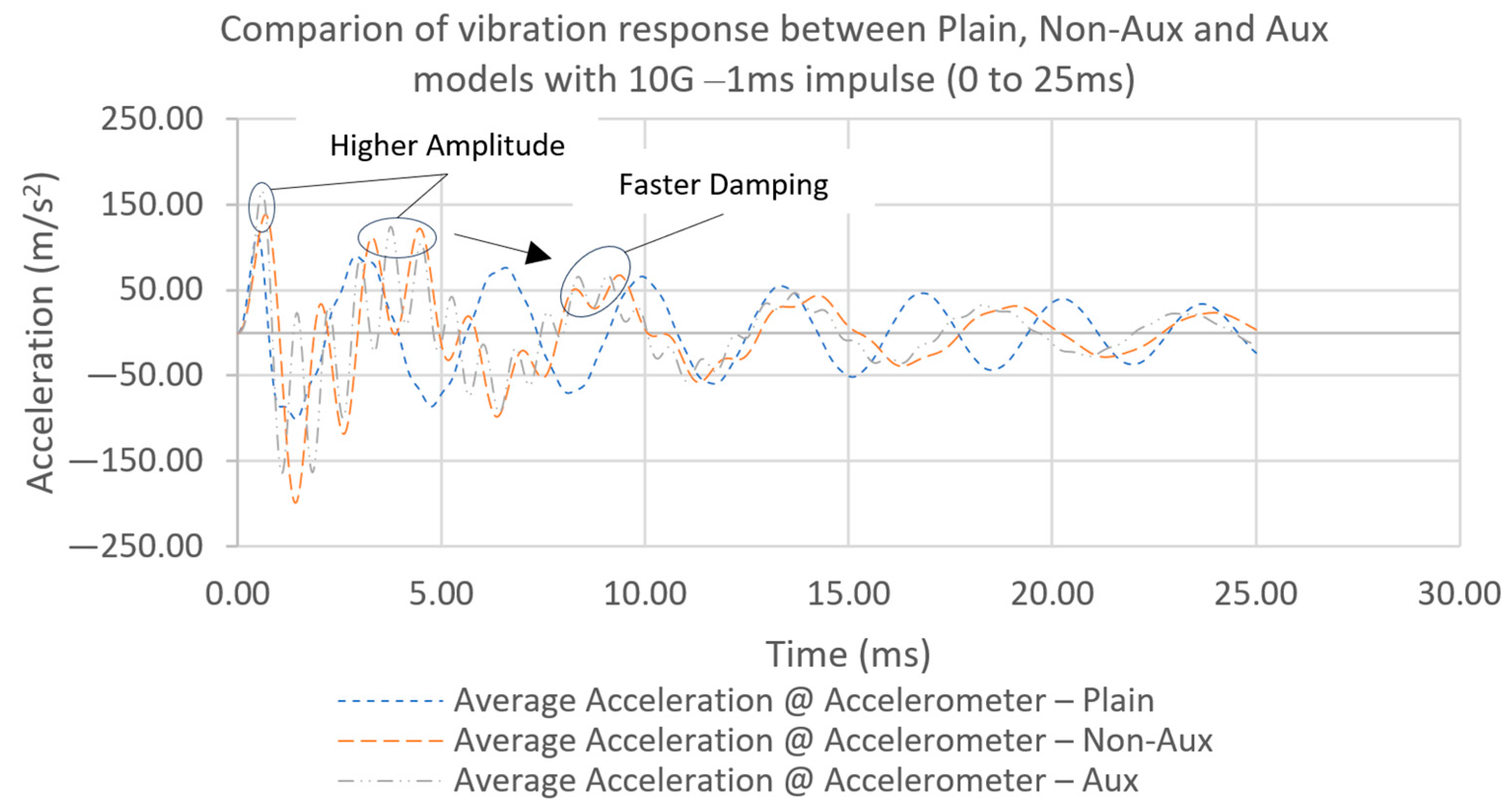








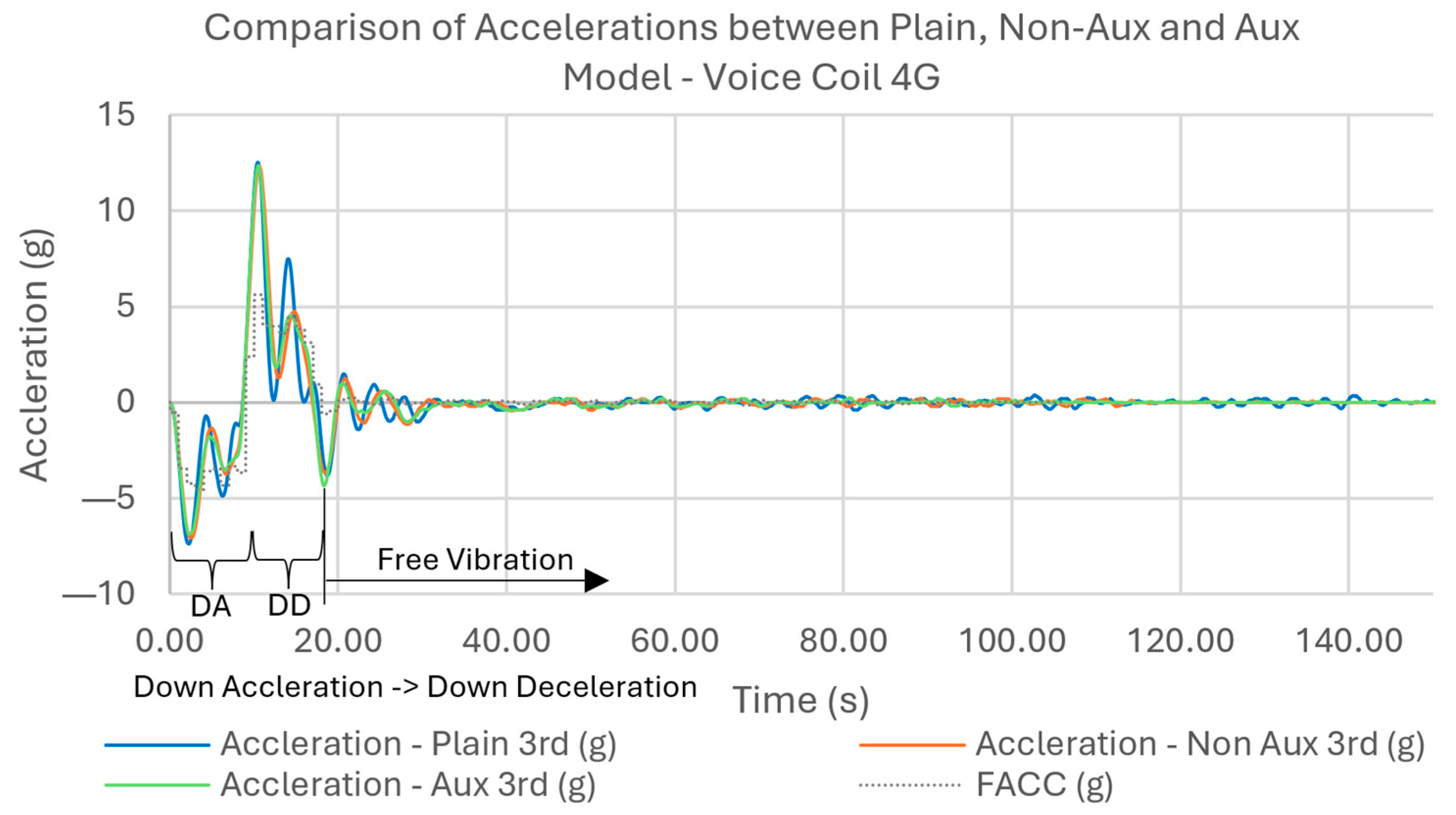



| Mesh Parameters | |
|---|---|
| Mid-Interlayer (Plain, Non-Aux, Aux) | Element Type: Tetrahedron Element Size: 1.5 mm |
| Viscoelastic Layer | Element Type: Hexahedral Element Size: 1.5 mm |
| Constraining Layer | Element Type: Hexahedral Element Size: 1.5 mm |
| Plain Model | Number of Nodes: 28,476 Number of Elements: 13,969 |
| Non-Auxetic Model | Number of Nodes: 28,520 Number of Elements: 13,767 |
| Auxetic Model | Number of Nodes: 29,219 Number of Elements: 14,128 |
| Part | Material | Properties | |
|---|---|---|---|
| Auxetic Layer | ABS (Black ABS Filament, CC3D, China) | Density: | 1030 kg/m3 |
| Young’s Modulus: | 1.63 GPa | ||
| Poisson’s Ratio: | 0.41 | ||
| Bulk Modulus: | 2.98 GPa | ||
| Shear Modulus: | 577.76 MPa | ||
| Tensile Ultimate Strength: | 36.26 MPa | ||
| Tensile Yield Strength: | 27.44 MPa | ||
| Constraining Layer | HDPE (Heavy-duty bag, Lyreco—www.lyrerco.com, Singapore) | Density: | 958.5 kg/m3 |
| Young’s Modulus: | 1.08 GPa | ||
| Poisson’s Ratio: | 0.42 | ||
| Bulk Modulus: | 2.20 GPa | ||
| Shear Modulus: | 380.74 MPa | ||
| Tensile Ultimate Strength: | 28.39 MPa | ||
| Tensile Yield Strength: | 28.39 MPa | ||
| Viscoelastic Layer | VHB5908 (Acrylic Foam Tape, 3M, USA) | Density: | 720 kg/m3 |
| Young’s Modulus: | 0.90 MPa | ||
| Poisson’s Ratio: | 0.49 | ||
| Bulk Modulus: | 149.9 MPa | ||
| Shear Modulus: | 0.3 MPa | ||
| Measuring Equipment | Model | Specifications | |
|---|---|---|---|
| Accelerometer | 8786A5—(Kistler, Switzerland) |
| ±5 g |
| 1026 mV/g | ||
| 0.8% | ||
| 27 KHz | ||
| −54 to 80 °C | ||
| 21.176 g | ||
| 21.4 mm | ||
| 14.54 mm | ||
| Stainless Steel | ||
| Accelerometer | 8640A5—(Kistler, Switzerland) |
| ±5 g |
| 1071 mV/g, 943 mV | ||
| 3% | ||
| 17 KHz | ||
| –40 to 55 °C | ||
| 3.5 g | ||
| 10.2 mm | ||
| 11.8 mm | ||
| Stainless Steel | ||
| Oscilloscope | TBS 1102B—(Tektronix, USA) |
| 100 MHz |
| 2 GS/s | ||
| 2 mV to 5 V/div. | ||
| 300 V rms | ||
| Voice Coil Test | |||
| Setup Plain | Setup non-Auxetic | Setup Aux | |
| Total Mass (g) | 24.00 | 23.90 | 23.90 |
| Granite Test | |||
| Total Mass (g) | 6.36 | 6.20 | 6.18 |
| Voice Coil Setup for Each Experiment Set | |||||
|---|---|---|---|---|---|
| Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | |
| Stroke (mm) | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 |
| Dwell (ms) | 500 | 500 | 500 | 500 | 500 |
| Velocity (mm/s) | 500 | 500 | 500 | 500 | 500 |
| Target Acceleration/Deceleration (g) | 0.5 | 1 | 2 | 3 | 4 |
| Target Acceleration/Deceleration (mm/s2) | 4905 | 9810 | 19,620 | 29,430 | 39,240 |
| Kill Deceleration | 4.905 × 105 | 4.905 × 105 | 4.905 × 105 | 4.905 × 105 | 4.905 × 105 |
| Jerk (mm/s3) | 4.91 × 108 | 4.91 × 108 | 4.91 × 108 | 4.91 × 108 | 4.91 × 108 |
| Convex Auxetic Layer—Convex | ||||
|---|---|---|---|---|
| Net Tangential Displacement @ Convex AUX Layer—Open (μm) | Net Tangential Displacement @ Convex AUX Layer—Closed (μm) | Net Radial Displacement @ Convex AUX Layer—Open (μm) | Net Radial Displacement @ Convex AUX Layer—Closed (μm) | |
| Thickness 0.125 mm | −1.15 | −1.26 | 4.08 | 1.89 |
| Thickness 0.25 mm | −1.09 | −1.57 | 5.09 | 3.00 |
| Thickness 0.5 mm | −0.17 | −1.88 | 5.48 | 4.38 |
| Thickness 1 mm | 1.09 | −2.36 | 5.04 | 4.85 |
| Thickness 2 mm | 1.44 | −2.08 | 4.06 | 4.08 |
| Thickness 4 mm | 1.00 | −1.32 | 2.59 | 2.52 |
| Bottom Auxetic Layer—Concave | ||||
|---|---|---|---|---|
| Net Tangential Displacement @ Bottom AUX Layer—Open (μm) | Net Tangential Displacement @ Bottom AUX Layer—Closed (μm) | Net Radial Displacement @ Bottom AUX Layer—Open (μm) | Net Radial Displacement @ Bottom AUX Layer—Closed (μm) | |
| Thickness 0.125 mm | −1.46 | −1.03 | −1.06 | −3.23 |
| Thickness 0.25 mm | −1.74 | −0.89 | −2.35 | −4.43 |
| Thickness 0.5 mm | −1.60 | 0.32 | −4.00 | −5.19 |
| Thickness 1 mm | −1.66 | 1.80 | −4.71 | −5.15 |
| Thickness 2 mm | −1.52 | 1.92 | −4.09 | −4.18 |
| Thickness 4 mm | −0.99 | 1.27 | −2.66 | −2.56 |
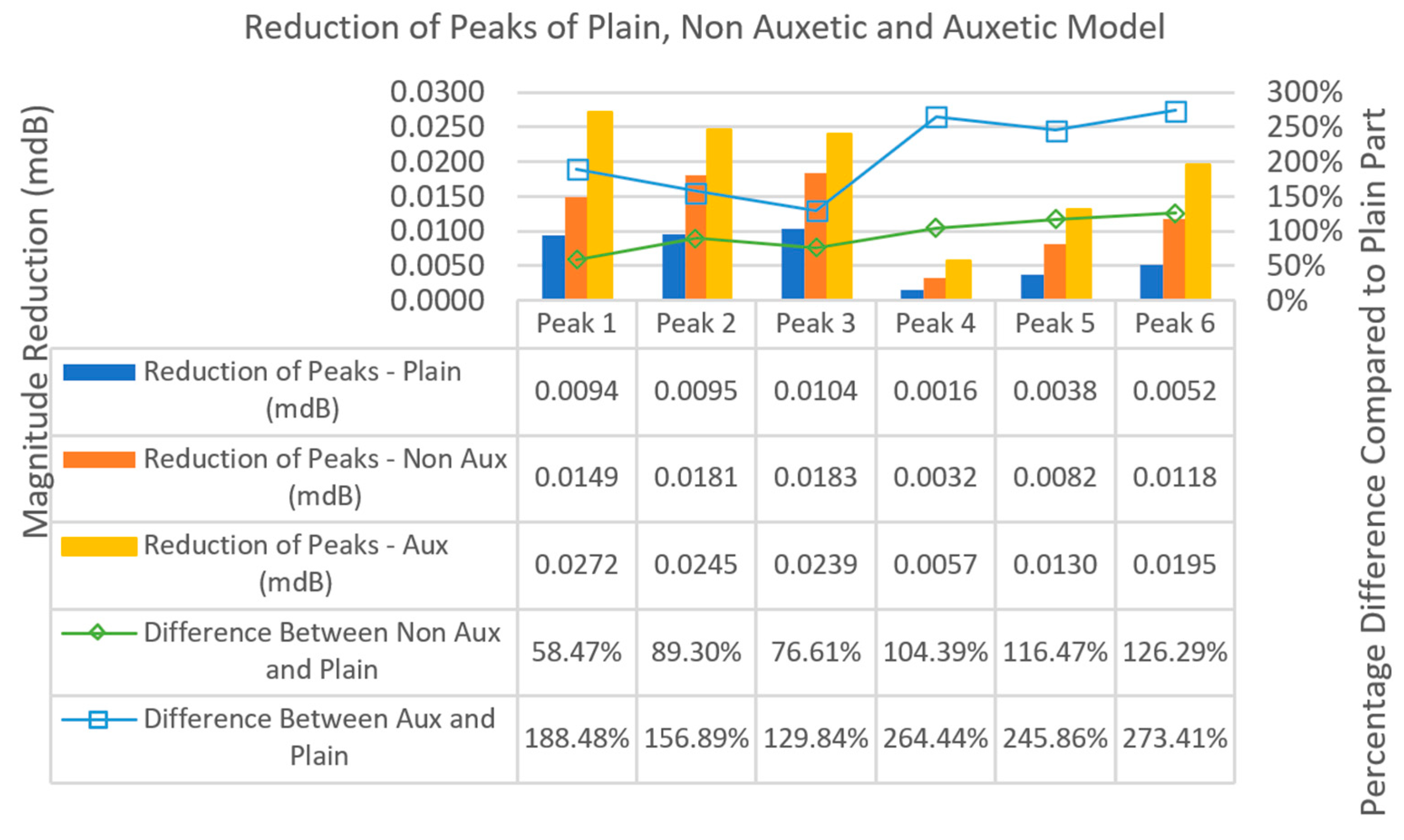
| Modal Analysis of ABS-HDPE Cell—Kistler—8640A5 (3.5063 g) | |||
| Mode (i) | Plain (fi) Hz | Non-Aux (fi) Hz | Aux (fi) Hz |
| 1 | 290.85 | 202.51 | 208.61 |
| 2 | 1054.10 | 609.30 | 731.99 |
| 3 | 1057.80 | 618.33 | 735.70 |
| 4 | 1795.00 | 812.25 | 1310.20 |
| 5 | 1795.30 | 1285.90 | 1507.80 |
| 6 | 1836.00 | 1296.30 | 1513.50 |
| Modal Analysis of ABS-HDPE Cell—Kistler—8786A5 (21.176 g) | |||
| Mode (i) | Plain (fi) Hz | Non-Aux (fi) Hz | Aux (fi) Hz |
| 1 | 133.18 | 94.86 | 97.17 |
| 2 | 480.29 | 275.44 | 326.91 |
| 3 | 482.30 | 278.92 | 328.35 |
| 4 | 807.60 | 422.06 | 678.04 |
| 5 | 807.70 | 575.31 | 680.00 |
| 6 | 1132.10 | 580.07 | 717.71 |
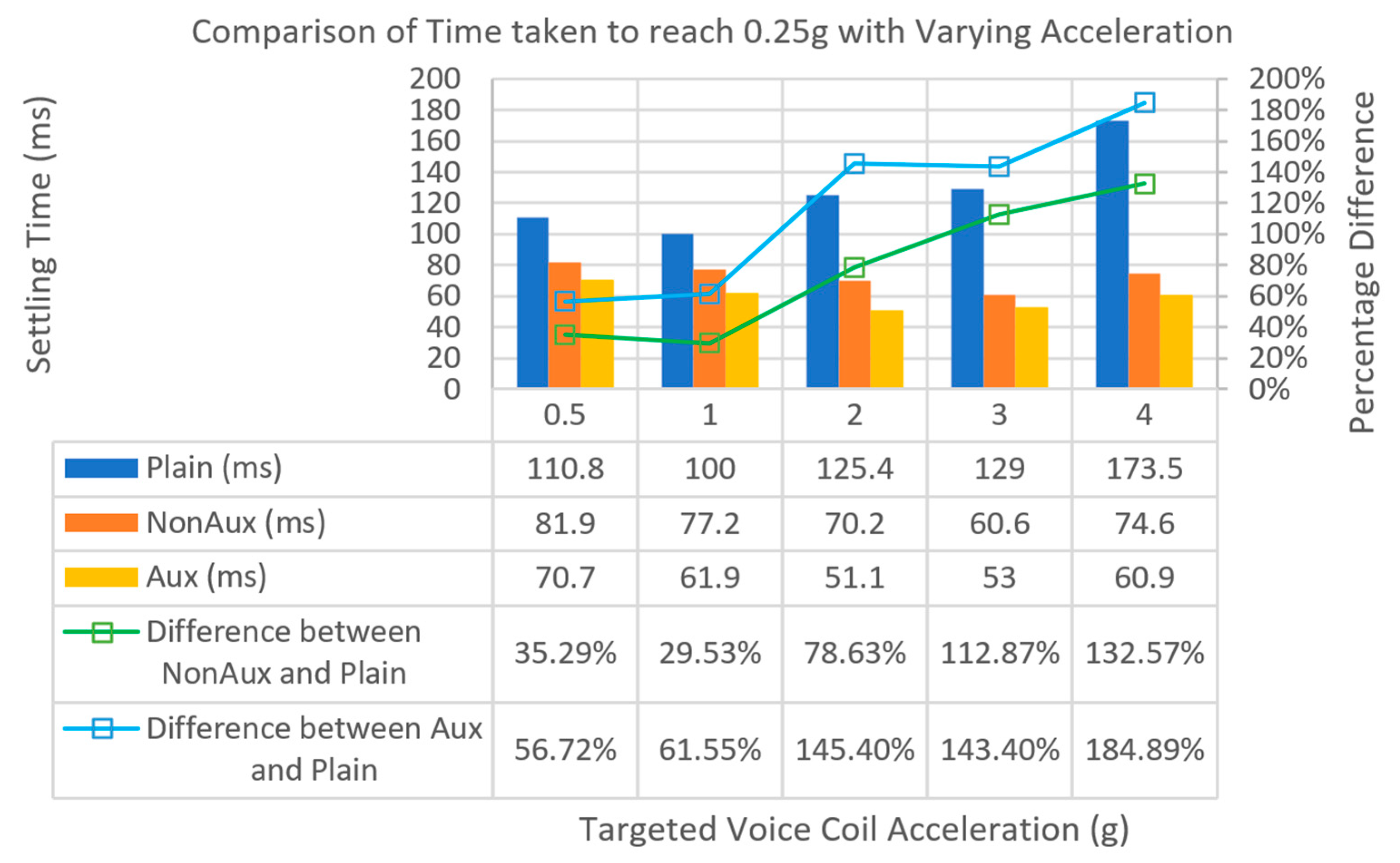
| Result Damping Ratio and Settling Time | |||||
|---|---|---|---|---|---|
| Model | Z Damping Ratio | Settling Time (1 G—9.81 m/s2) | Settling Time (0.5 G—4.905 m/s2) | Settling Time (0.2 G—1.962 m/s2) | Settling Time (0.1 G—0.981 m/s2) |
| Plain | 0.026 | 0.0512 | 0.0667 | 0.0873 | 0.1011 |
| Non-Aux | 0.047 | 0.0412 | 0.0535 | 0.0708 | 0.0832 |
| Aux | 0.046 | 0.0400 | 0.0520 | 0.0688 | 0.0808 |
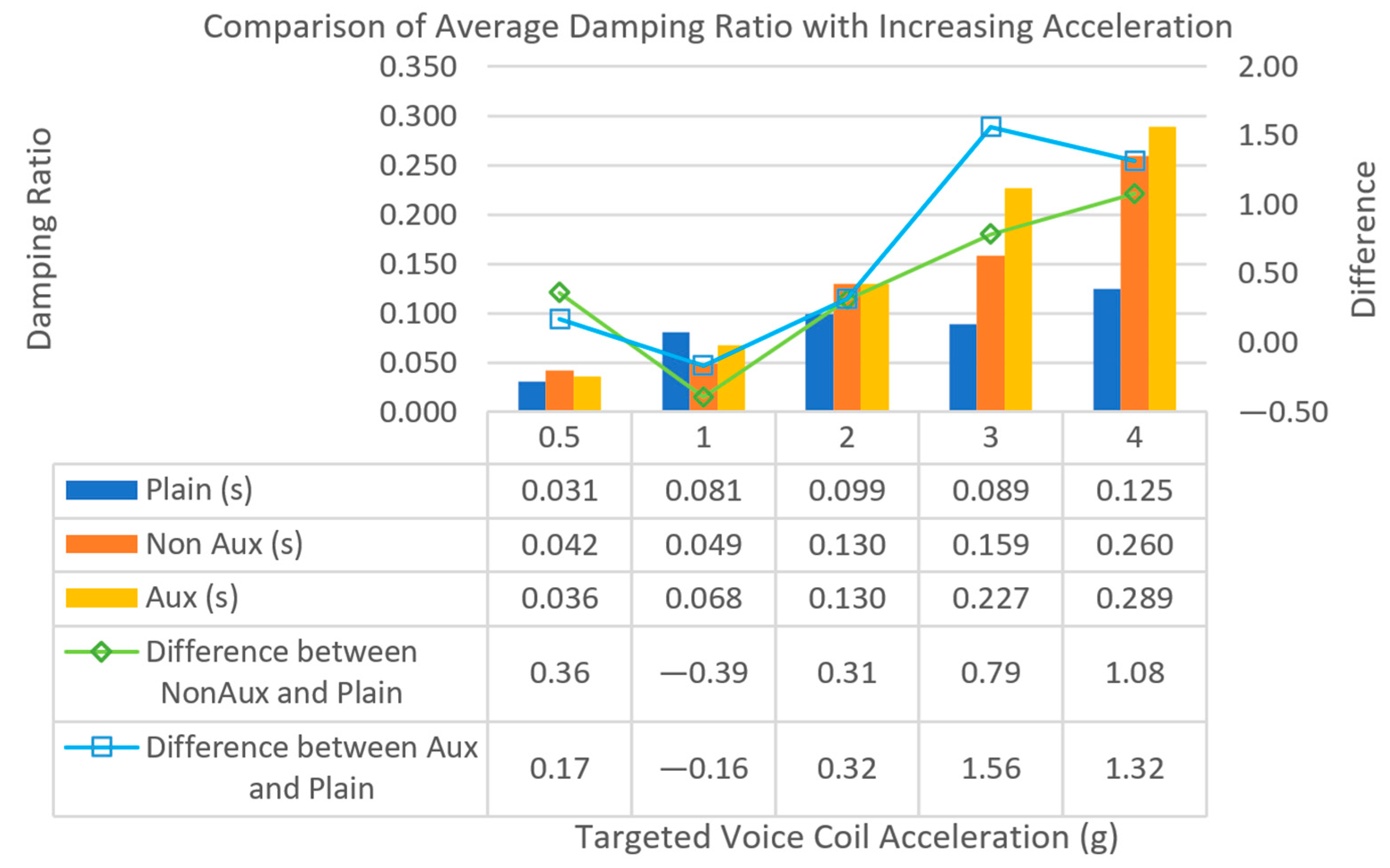
| Average Damping Ratio and Standard Deviation for Various Input Accelerations | ||
| 0.5 g | ||
| Model | Average | Standard Deviation |
| Plain | 0.031 | 0.055 |
| Non-Aux | 0.042 | 0.103 |
| Aux | 0.036 | 0.157 |
| 1 g | ||
| Model | Average | Standard Deviation |
| Plain | 0.081 | 0.055 |
| Non-Aux | 0.049 | 0.115 |
| Aux | 0.068 | 0.160 |
| 2 g | ||
| Model | Average | Standard Deviation |
| Plain | 0.099 | 0.079 |
| Non-Aux | 0.130 | 0.275 |
| Aux | 0.130 | 0.226 |
| 3 g | ||
| Model | Average | Standard Deviation |
| Plain | 0.089 | 0.128 |
| Non-Aux | 0.159 | 0.099 |
| Aux | 0.227 | 0.111 |
| 4 g | ||
| Model | Average | Standard Deviation |
| Plain | 0.125 | 0.096 |
| Non-Aux | 0.260 | 0.099 |
| Aux | 0.290 | 0.047 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yong, C.S.; Idapalapati, S.; Lim, C.W.; Goh, K.L. Auxetic Composite Sandwich for Vibration Damping Through Axisymmetric Deformation. J. Compos. Sci. 2025, 9, 162. https://doi.org/10.3390/jcs9040162
Yong CS, Idapalapati S, Lim CW, Goh KL. Auxetic Composite Sandwich for Vibration Damping Through Axisymmetric Deformation. Journal of Composites Science. 2025; 9(4):162. https://doi.org/10.3390/jcs9040162
Chicago/Turabian StyleYong, Chun Seng, Sridhar Idapalapati, Chee Wang Lim, and Kheng Lim Goh. 2025. "Auxetic Composite Sandwich for Vibration Damping Through Axisymmetric Deformation" Journal of Composites Science 9, no. 4: 162. https://doi.org/10.3390/jcs9040162
APA StyleYong, C. S., Idapalapati, S., Lim, C. W., & Goh, K. L. (2025). Auxetic Composite Sandwich for Vibration Damping Through Axisymmetric Deformation. Journal of Composites Science, 9(4), 162. https://doi.org/10.3390/jcs9040162







