Mechanical Properties and Vibrational Behavior of 3D-Printed Carbon Fiber-Reinforced Polyphenylene Sulfide and Polyamide-6 Composites with Different Infill Types
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Fabrication Parameters
2.2. Specimen Fabrication
2.3. Mechanical Testing
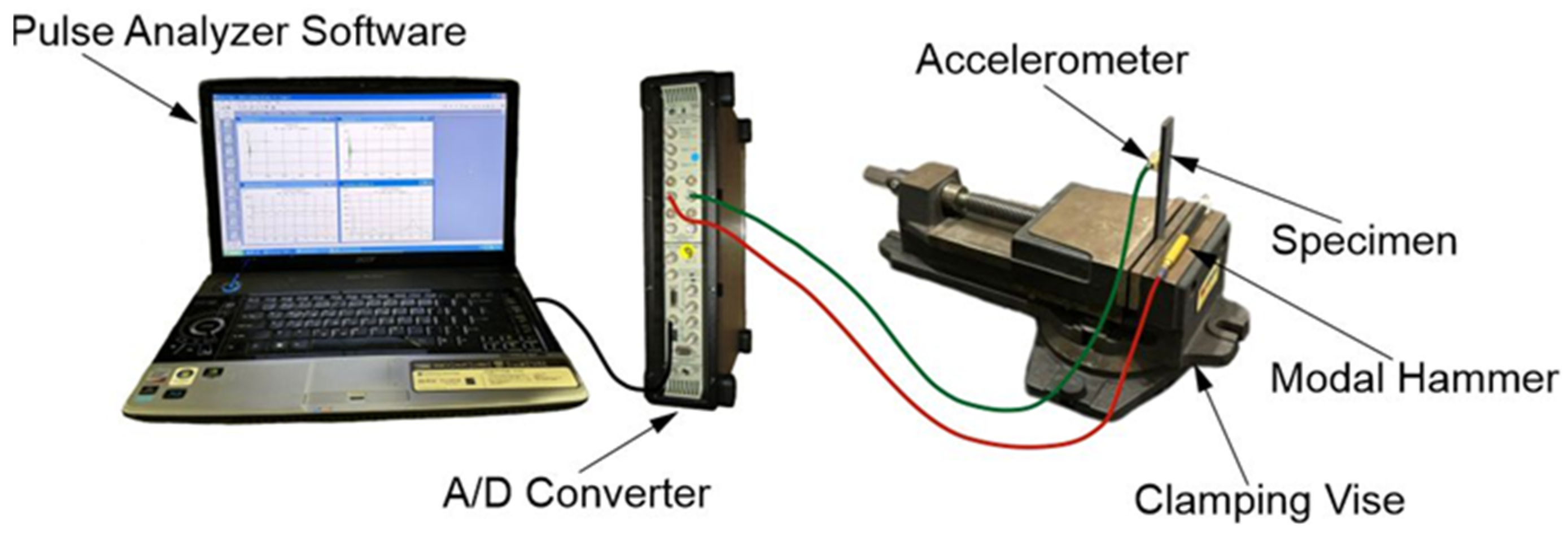
2.4. Vibration Testing
3. Results
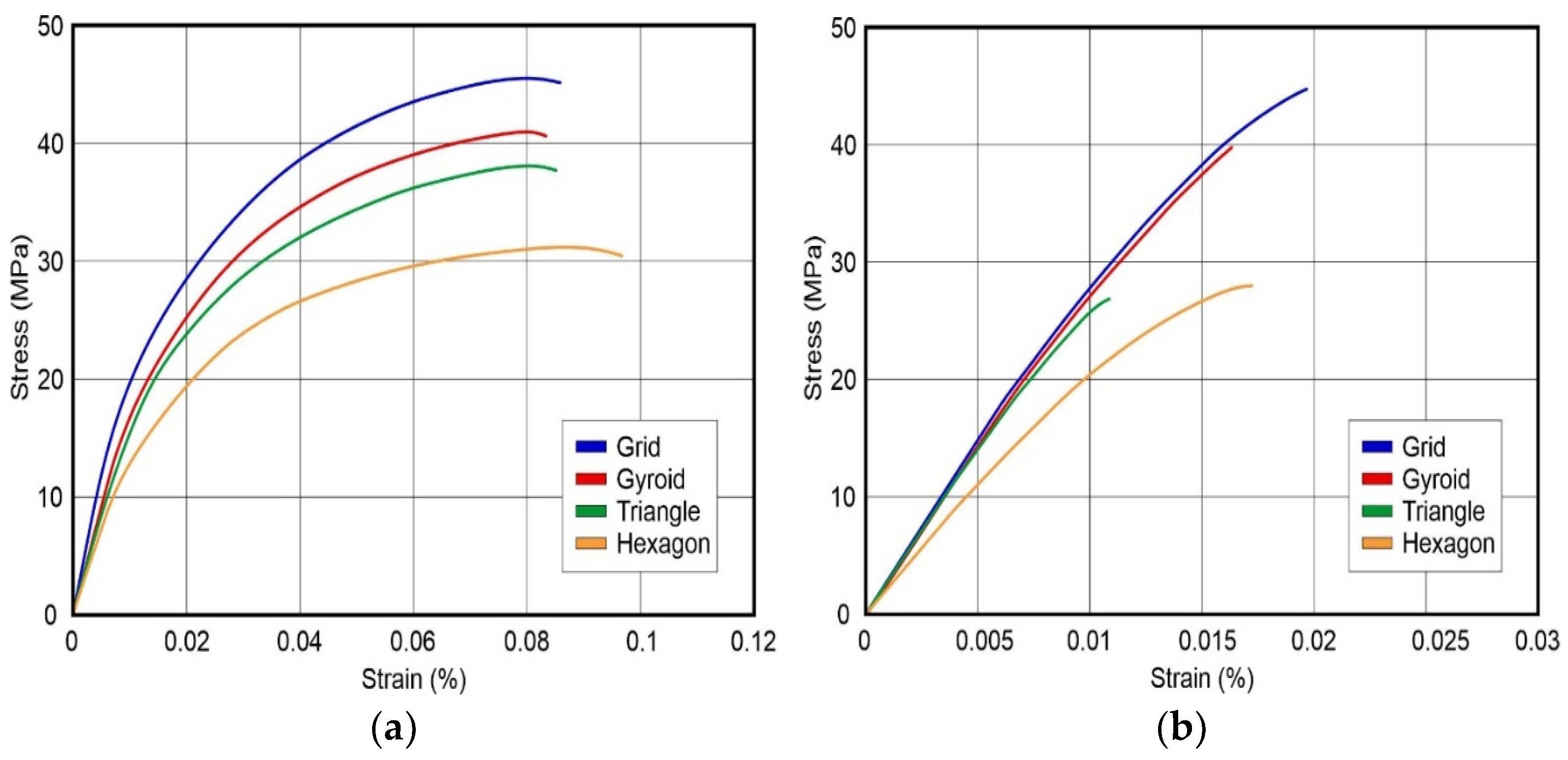
3.1. Uniaxial Tensile Strength Results
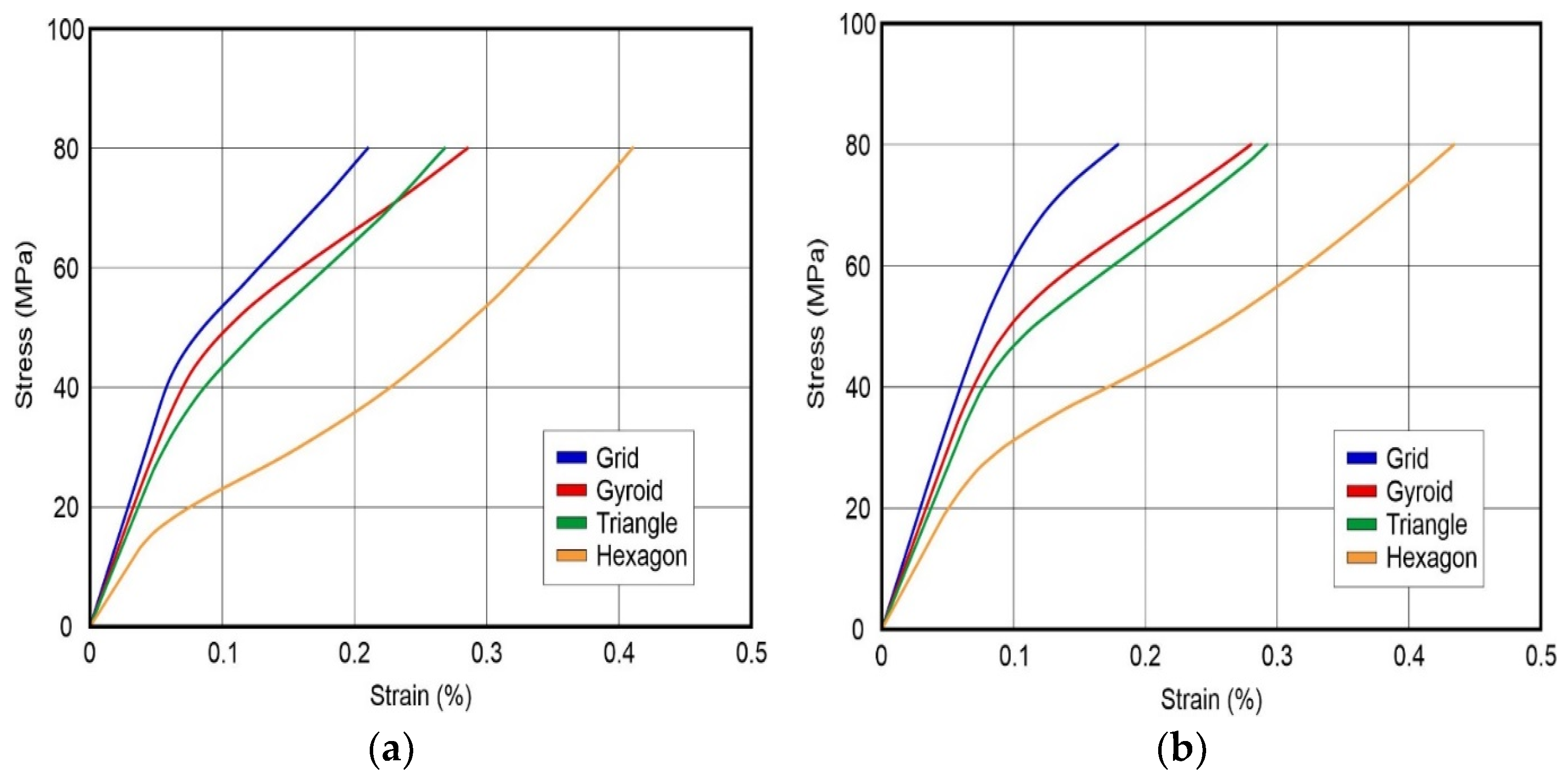
3.2. Uniaxial Compressive Strength Results
3.3. Three-Point Bending Results
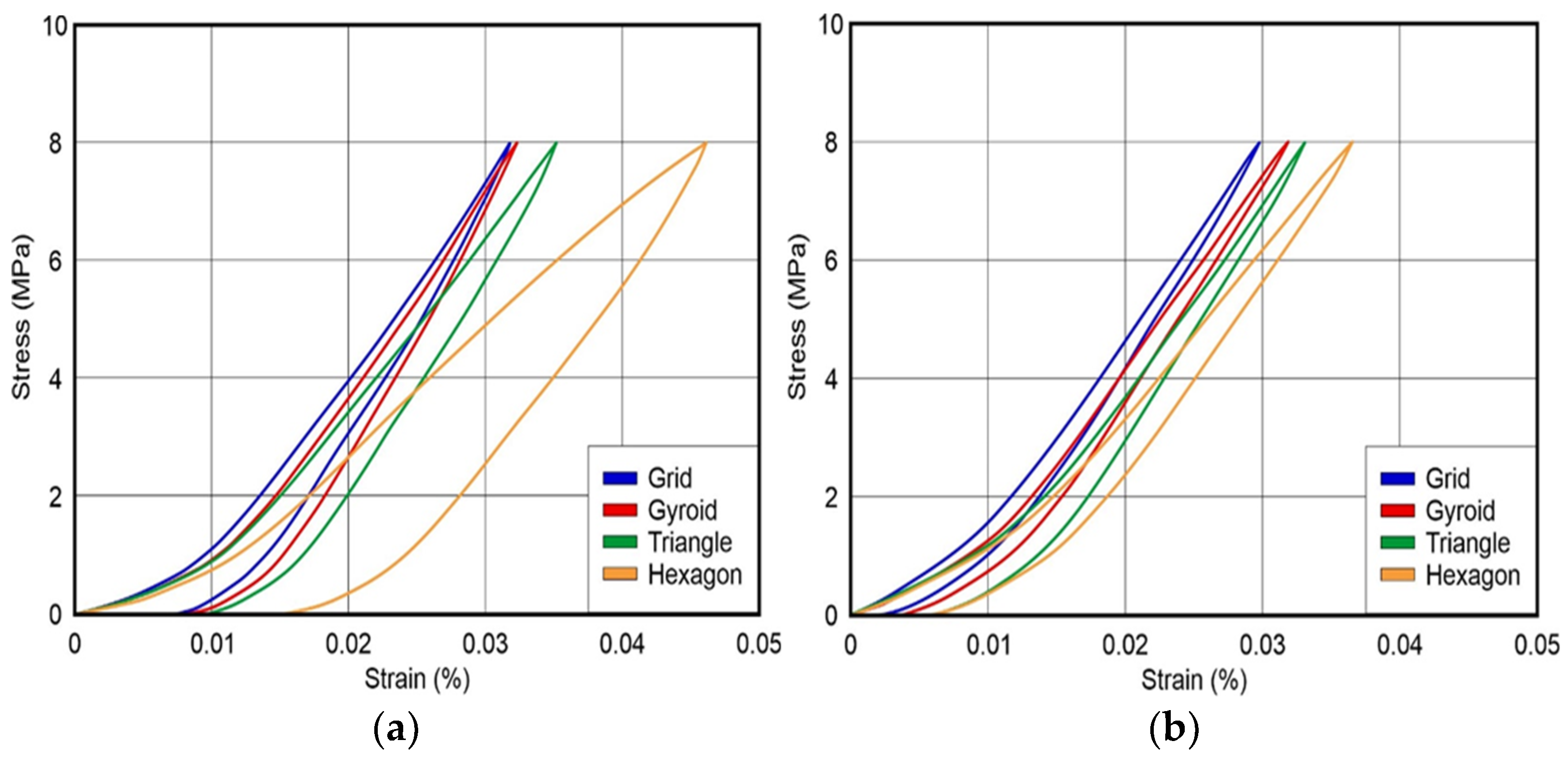
3.4. Hysteretic Behavior of Composite Specimen
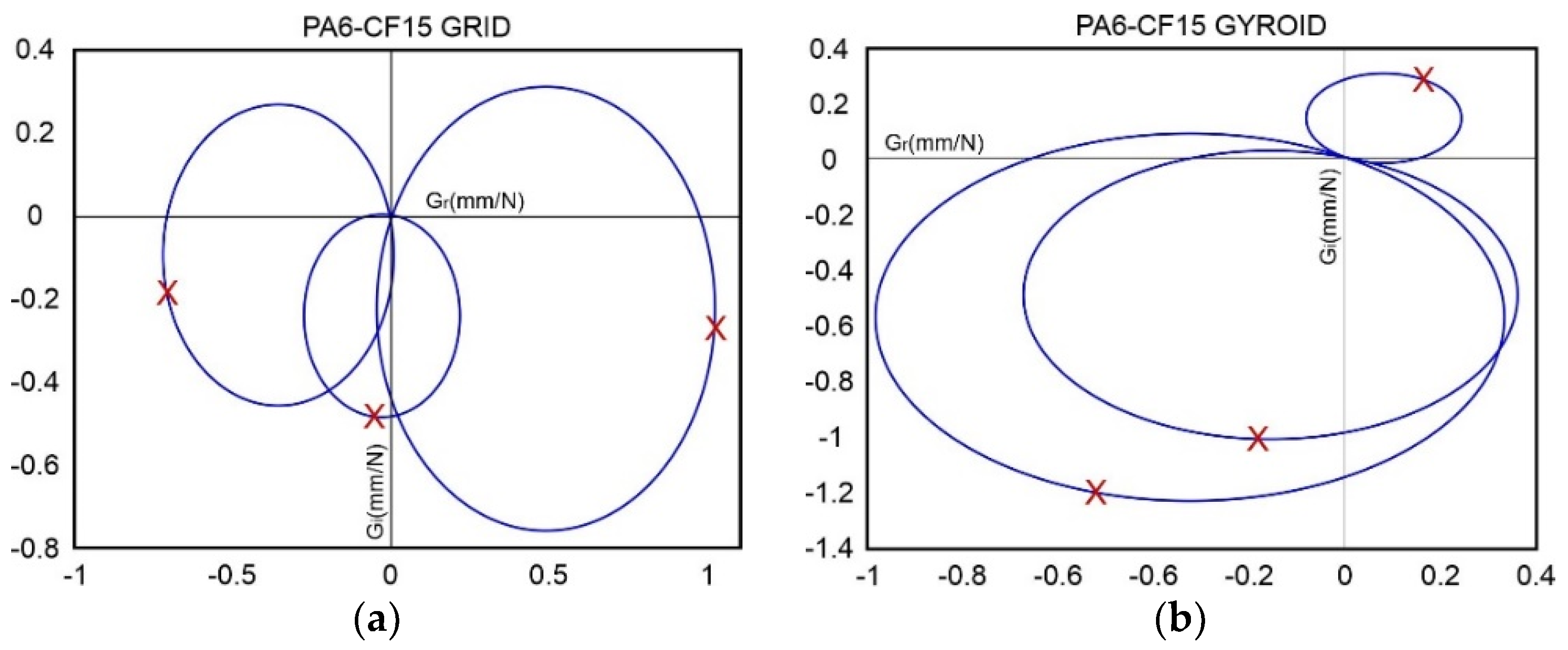
3.5. Modal Behavior of PA6 and PPS Composite Specimens
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, L.; Miller, J.; Vezza, J.; Mayster, M.; Raffay, M.; Justice, Q.; Al Tamimi, Z.; Hansotte, G.; Sunkara, L.D.; Bernat, J. Additive Manufacturing: A Comprehensive Review. Sensors 2024, 24, 2668. [Google Scholar] [CrossRef] [PubMed]
- Markets and Markets. 3D Printing Market Size, Share, Industry Report, Revenue Trends and Growth Drivers-Global Forecast to 2029. Available online: https://www.marketsandmarkets.com/Market-Reports/3d-printing-market-1276.html (accessed on 4 June 2024).
- Jemghili, R.; Taleb, A.A.; Mansouri, K. Additive Manufacturing Progress as a New Industrial Revolution. In Proceedings of the 2020 IEEE 2nd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Kenitra, Morocco, 2–3 December 2020; pp. 1–8. [Google Scholar]
- Mansour, M.; Tsongas, K.; Tzetzis, D. Measurement of the Mechanical and Dynamic Properties of 3D Printed Polylactic Acid Reinforced with Graphene. Polym.-Plast. Technol. Mater. 2019, 58, 1234–1244. [Google Scholar] [CrossRef]
- Caminero, M.; Chacón, J.; García-Moreno, I.; Rodríguez, G. Impact Damage Resistance of 3D Printed Continuous Fibre Reinforced Thermoplastic Composites Using Fused Deposition Modelling. Compos. Part B Eng. 2018, 148, 93–103. [Google Scholar] [CrossRef]
- Dizon, J.R.C.; Espera, A.H., Jr.; Chen, Q.; Advincula, R.C. Mechanical Characterization of 3D-Printed Polymers. Addit. Manuf. 2018, 20, 44–67. [Google Scholar] [CrossRef]
- Tymrak, B.M.; Kreiger, M.; Pearce, J.M. Mechanical Properties of Components Fabricated with Open-Source 3D Printers Under Realistic Environmental Conditions. Mater. Des. 2014, 58, 242–246. [Google Scholar] [CrossRef]
- Prpić, V.; Schauperl, Z.; Ćatić, A.; Dulčić, N.; Čimić, S. Comparison of Mechanical Properties of 3D-Printed, CAD/CAM, and Conventional Denture Base Materials. J. Prosthodont. 2020, 29, 524–528. [Google Scholar] [CrossRef]
- Wu, W.; Geng, P.; Li, G.; Zhao, D.; Zhang, H.; Zhao, J. Influence of Layer Thickness and Raster Angle on the Mechanical Properties of 3D-Printed PEEK and a Comparative Mechanical Study between PEEK and ABS. Materials 2015, 8, 5834–5846. [Google Scholar] [CrossRef] [PubMed]
- Patel, A.; Taufik, M. Nanocomposite Materials for Fused Filament Fabrication. Mater. Proc. 2021, 47, 5142–5150. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Qiu, J.; Wei, J.; Wang, S. Additive Manufacturing of Carbon Fiber Reinforced Thermoplastic Composites Using Fused Deposition Modeling. Compos. Part B Eng. 2015, 80, 369–378. [Google Scholar] [CrossRef]
- Dul, S.; Fambri, L.; Pegoretti, A. High-Performance Polyamide/Carbon Fiber Composites for Fused Filament Fabrication: Mechanical and Functional Performances. J. Mater. Eng. Perform. 2021, 30, 5066–5085. [Google Scholar] [CrossRef]
- Almeshari, B.; Junaedi, H.; Baig, M.; Almajid, A. Development of 3D Printing Short Carbon Fiber Reinforced Polypropylene Composite Filaments. J. Mater. Res. Technol. 2023, 24, 16–26. [Google Scholar] [CrossRef]
- Shulga, E.; Karamov, R.; Sergeichev, I.S.; Konev, S.D.; Shurygina, L.I.; Akhatov, I.S.; Shandakov, S.D.; Nasibulin, A.G. Fused Filament Fabricated Polypropylene Composite Reinforced by Aligned Glass Fibers. Materials 2020, 13, 3442. [Google Scholar] [CrossRef] [PubMed]
- Kabir, S.M.F.; Mathur, K.; Seyam, A.-F.M. Maximizing the Performance of 3D Printed Fiber-Reinforced Composites. J. Compos. Sci. 2021, 5, 136. [Google Scholar] [CrossRef]
- Abderrafai, Y.; Mahdavi, M.H.; Sosa-Rey, F.; Hérard, C.; Navas, I.O.; Piccirelli, N.; Lévesque, M.; Therriault, D. Additive Manufacturing of Short Carbon Fiber-Reinforced Polyamide Composites by Fused Filament Fabrication: Formulation, Manufacturing and Characterization. Mater. Des. 2022, 214, 110358. [Google Scholar] [CrossRef]
- Calignano, F.; Lorusso, M.; Roppolo, I.; Minetola, P. Investigation of the Mechanical Properties of a Carbon Fibre-Reinforced Nylon Filament for 3D Printing. Machines 2020, 8, 52. [Google Scholar] [CrossRef]
- Medel, F.; Abad, J.; Esteban, V. Stiffness and Damping Behavior of 3D Printed Specimens. Polym. Test. 2022, 109, 107529. [Google Scholar] [CrossRef]
- Somireddy, M.; Czekanski, A. Anisotropic Material Behavior of 3D Printed Composite Structures—Material Extrusion Additive Manufacturing. Mater. Des. 2020, 195, 108953. [Google Scholar] [CrossRef]
- Zohdi, N.; Yang, R. Material Anisotropy in Additively Manufactured Polymers and Polymer Composites: A Review. Polymers 2021, 13, 3368. [Google Scholar] [CrossRef]
- Mansour, G.; Papageorgiou, V.; Tzetzis, D. Carbon Fiber Polymer Reinforced 3D Printed Composites for Centrifugal Pump Impeller Manufacturing. Technologies 2024, 12, 48. [Google Scholar] [CrossRef]
- Spectrum Filaments. Available online: https://spectrumfilaments.com/en/filament/pa6-cf15/ (accessed on 9 November 2024).
- TreeD Filaments. Available online: https://treedfilaments.com/datasheets/tech/TDS_PPSCF.pdf (accessed on 9 November 2024).
- ISO 527-2; Plastics—Determination of Tensile Properties. International Organization for Standardization: Geneva, Switzerland, 2012. Available online: https://cdn.standards.iteh.ai/samples/56046/c5c3ec20cc0741289bf6def861e0a40b/ISO-527-2-2012.pdf (accessed on 24 January 2025).
- ISO 178; Plastics—Determination of Flexural Properties. International Organization for Standardization: Geneva, Switzerland, 2019. Available online: https://cdn.standards.iteh.ai/samples/70513/cd351551961842c590df25e23807b73c/ISO-178-2019.pdf (accessed on 24 January 2025).
- ASTM D395B; Standard Test Methods for Rubber Property-Compression Set. ASTM International: West Conshohocken, PA, USA, 2017. Available online: https://www.astm.org/d0395-01.html (accessed on 24 January 2025).
- Sperling, L.H. Introduction to Physical Polymer Science, 4th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2005; Chapter 3. [Google Scholar]
- Rao, S.S. Mechanical Vibrations, 5th ed.; Prentice Hall: Hoboken, NJ, USA, 2011. [Google Scholar]
- Tsongas, K.; Tzetzis, D.; Mansour, G. Mechanical and Vibration Isolation Behaviour of Acrylonitrile-Butadiene Rubber/Multiwalled Carbon Nanotube Composite Machine Mounts. Plast. Rubber Comp. 2017, 46, 458–468. [Google Scholar] [CrossRef]
- Mansour, G.; Tsongas, K.; Tzetzis, D.; Tzikas, K. Dynamic Mechanical Characterization of Polyurethane/Multi-Walled Carbon Nanotube Composite Thermoplastic Elastomers. Polym. Plast. Technol. Eng. 2017, 56, 1505–1515. [Google Scholar] [CrossRef]
- Mansour, G.; Tsongas, K.; Tzetzis, D. Modal Testing of Nanocomposite Materials Through an Optimization Algorithm. Measurement 2016, 91, 31–38. [Google Scholar] [CrossRef]
- Mansour, G.; Tsongas, K.; Tzetzis, D. Modal Testing of Epoxy Carbon-Aramid Fiber Hybrid Composites Reinforced with Silica Nanoparticles. J. Reinf. Plast. Comp. 2016, 35, 1401–1410. [Google Scholar] [CrossRef]
- Pandzic, A.; Hodzic, D. Mechanical Properties Comparison of PLA, Tough PLA and PC 3D Printed Materials with Infill Structure–Influence of Infill Pattern on Tensile Mechanical Properties. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1208, 12019. [Google Scholar] [CrossRef]
- Dudescu, C.; Racz, L. Effects of Raster Orientation, Infill Rate and Infill Pattern on the Mechanical Properties of 3D Printed Materials. Acta Univ. Cibiniensis 2017, 69, 23–30. [Google Scholar] [CrossRef]
- Chukov, D.; Stepashkin, A.; Tcherdyntsev, V.; Olifirov, L.; Kaloshkin, S. Structure and Properties of Composites based on Polyphenylene Sulfide Reinforced with Al-Cu-Fe Quasicrystalline Particles. J. Thermoplast. Compos. Mater. 2017, 31, 882–895. [Google Scholar] [CrossRef]
- Ünal, H.; Ermiş, K. Determination of Mechanical Performance of Glass Fiber Reinforced and Elastomer Filled Polyamide-6 Composites. Int. Adv. Res. Eng. J. 2021, 5, 405–411. [Google Scholar] [CrossRef]
- Martín, M.J.; Auñón, J.A.; Martín, F. Influence of Infill Pattern on Mechanical Behavior of Polymeric and Composites Specimens Manufactured Using Fused Filament Fabrication Technology. Polymers 2021, 13, 2934. [Google Scholar] [CrossRef]









| Material | Nozzle Temperature (°C) | Bed Temperature (°C) | Layer Height (mm) | Printing Speed (mm/s) | Infill Ratio (%) |
|---|---|---|---|---|---|
| PA6-CF15 | 280 | 90 | 0.2 | 60 | 100 |
| PPS-CF15 | 310 | 110 | 0.2 | 60 | 100 |
| Infill Pattern | PA6-CF15 Density (kg/m3) | PPS-CF15 Density (kg/m3) |
|---|---|---|
| Grid | 1042.1 | 1193.6 |
| Gyroid | 959.4 | 1002.7 |
| Triangle | 1017.9 | 1169.3 |
| Hexagon | 805.8 | 920.9 |
| Material | Infill Patterns | Tensile Yield Strength (MPa) | Strain at Yield (%) | Tensile Modulus (MPa) |
|---|---|---|---|---|
| PA6-CF15 | Grid | 21.5 | 0.012 | 1800 |
| Gyroid | 18.7 | 0.011 | 1710 | |
| Triangle Hexagon | 14.4 9 | 0.009 0.005 | 1580 1500 | |
| PPS-CF15 | Grid | 18.6 | 0.006 | 3080 |
| Gyroid Triangle Hexagon | 17.8 13.7 8.2 | 0.005 0.004 0.003 | 2960 2850 2060 |
| Material | Infill Patterns | Compressive Yield Strength (MPa) | Strain at Yield (%) | Compressive Modulus (MPa) |
|---|---|---|---|---|
| PA6-CF15 | Grid | 40.5 | 0.068 | 627 |
| Gyroid | 37.7 | 0.072 | 542 | |
| Triangle Hexagon | 30.8 16.4 | 0.062 0.046 | 532 349 | |
| PPS-CF15 | Grid | 53.2 | 0.084 | 648 |
| Gyroid Triangle Hexagon | 42.4 40.1 21.6 | 0.071 0.076 0.058 | 624 537 391 |
| Material | Infill Patterns | Flexural Yield Strength (MPa) | Strain at Yield (%) | Flexural Modulus (MPa) |
|---|---|---|---|---|
| PA6-CF15 | Grid | 2.12 | 0.033 | 64.3 |
| Gyroid | 1.63 | 0.030 | 54.5 | |
| Triangle Hexagon | 1.35 0.77 | 0.025 0.017 | 53.7 45.3 | |
| PPS-CF15 | Grid | 1.78 | 0.019 | 93.8 |
| Gyroid Triangle Hexagon | 1.55 1.26 0.68 | 0.017 0.014 0.011 | 91.2 89.8 61.9 |
| Material | Infill Patterns | Loss Factor, n | Energy Loss over a Cycle, ΔW | Maximum Energy of that Cycle, W |
|---|---|---|---|---|
| PA6-CF15 | Grid | 6.49% | 0.0215 | 0.1053 |
| Gyroid | 6.72% | 0.0211 | 0.1002 | |
| Triangle Hexagon | 7.96% 13.04% | 0.0292 0.0701 | 0.1169 0.1711 | |
| PPS-CF15 | Grid | 2.96% | 0.118 | 0.1266 |
| Gyroid Triangle Hexagon | 3.24% 4.7% 5.02% | 0.0133 0.0194 0.0242 | 0.1309 0.1315 0.1534 |
| Material | Infill Patterns | Resonance Frequency (Hz) | Viscous Damping | Stiffness (N/m) |
|---|---|---|---|---|
| PA6-CF15 | Grid | 80 | 2.21% | 303.5 |
| Gyroid | 76 | 2.77% | 269.5 | |
| Triangle Hexagon | 73 63 | 4.73% 5.87% | 251 227.1 | |
| PPS-CF15 | Grid | 53 | 2.16% | 436.1 |
| Gyroid Triangle Hexagon | 66 63 56 | 2.28% 2.56% 2.75% | 414.2 406.4 321 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papageorgiou, V.; Tsongas, K.; Mansour, M.T.; Tzetzis, D.; Mansour, G. Mechanical Properties and Vibrational Behavior of 3D-Printed Carbon Fiber-Reinforced Polyphenylene Sulfide and Polyamide-6 Composites with Different Infill Types. J. Compos. Sci. 2025, 9, 59. https://doi.org/10.3390/jcs9020059
Papageorgiou V, Tsongas K, Mansour MT, Tzetzis D, Mansour G. Mechanical Properties and Vibrational Behavior of 3D-Printed Carbon Fiber-Reinforced Polyphenylene Sulfide and Polyamide-6 Composites with Different Infill Types. Journal of Composites Science. 2025; 9(2):59. https://doi.org/10.3390/jcs9020059
Chicago/Turabian StylePapageorgiou, Vasileios, Konstantinos Tsongas, Michel Theodor Mansour, Dimitrios Tzetzis, and Gabriel Mansour. 2025. "Mechanical Properties and Vibrational Behavior of 3D-Printed Carbon Fiber-Reinforced Polyphenylene Sulfide and Polyamide-6 Composites with Different Infill Types" Journal of Composites Science 9, no. 2: 59. https://doi.org/10.3390/jcs9020059
APA StylePapageorgiou, V., Tsongas, K., Mansour, M. T., Tzetzis, D., & Mansour, G. (2025). Mechanical Properties and Vibrational Behavior of 3D-Printed Carbon Fiber-Reinforced Polyphenylene Sulfide and Polyamide-6 Composites with Different Infill Types. Journal of Composites Science, 9(2), 59. https://doi.org/10.3390/jcs9020059










