Hierarchical Free Vibration Analysis of Variable-Angle Tow Shells Using Unified Formulation
Abstract
1. Introduction
2. Carrera’s Unified Formulation
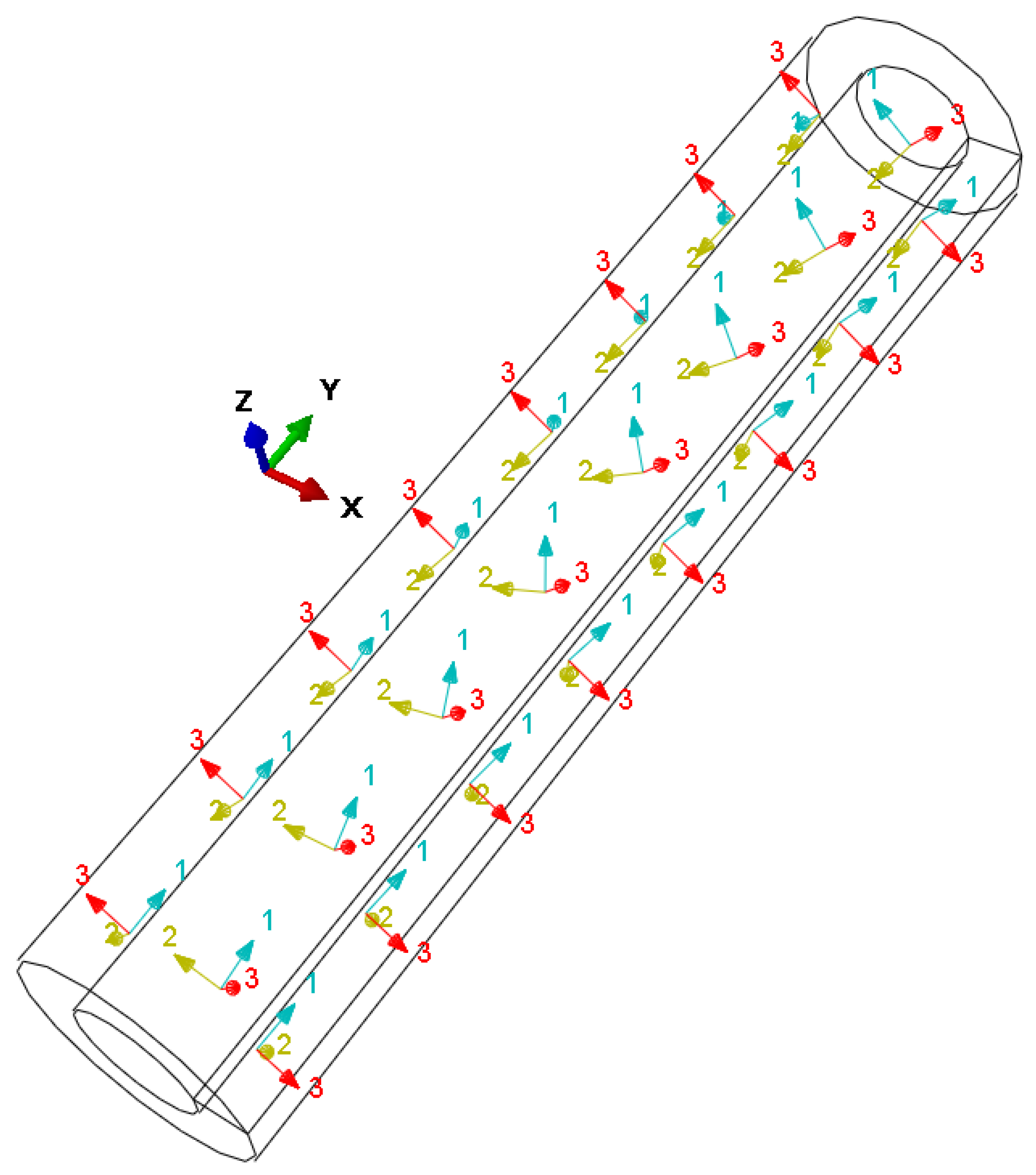
2.1. Variable Angle-Tow Composite Shells
2.2. Variational Formulation
2.3. Kinematic Assumption and Finite Element Approximation
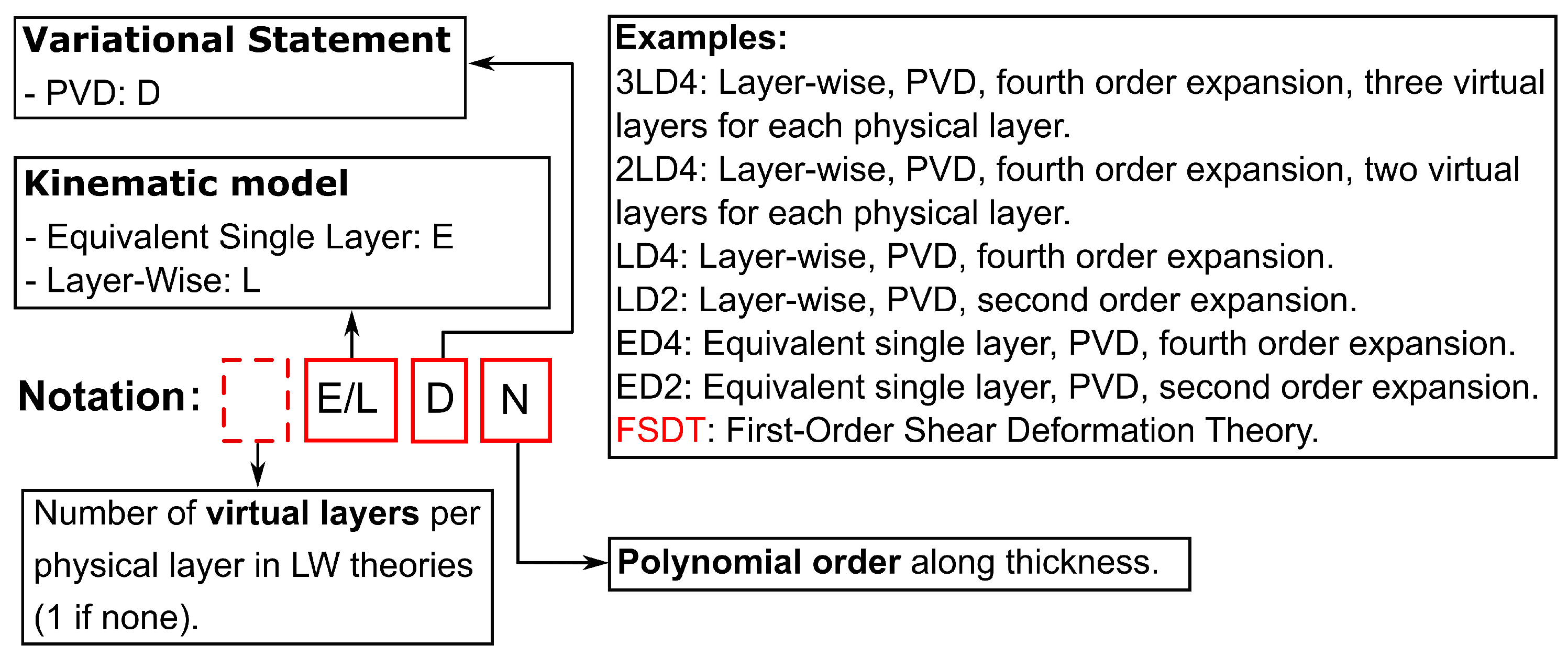
2.4. Acronym System
2.5. Locking Correction
2.6. FEM Matrices Expression
3. Numerical Results and Discussion
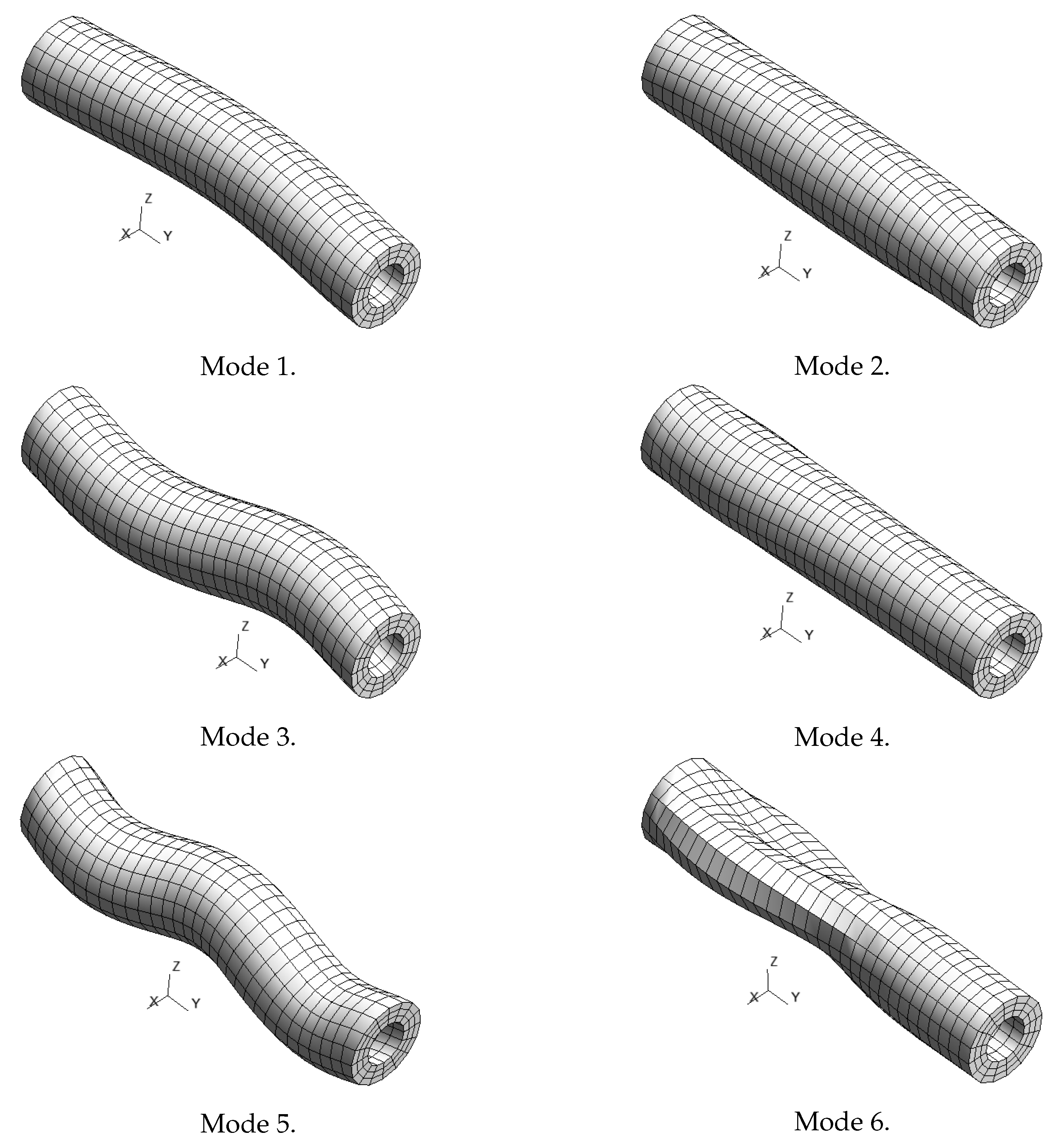
3.1. Monolayer Cylindrical Shell
3.2. Monolayer Cylinder
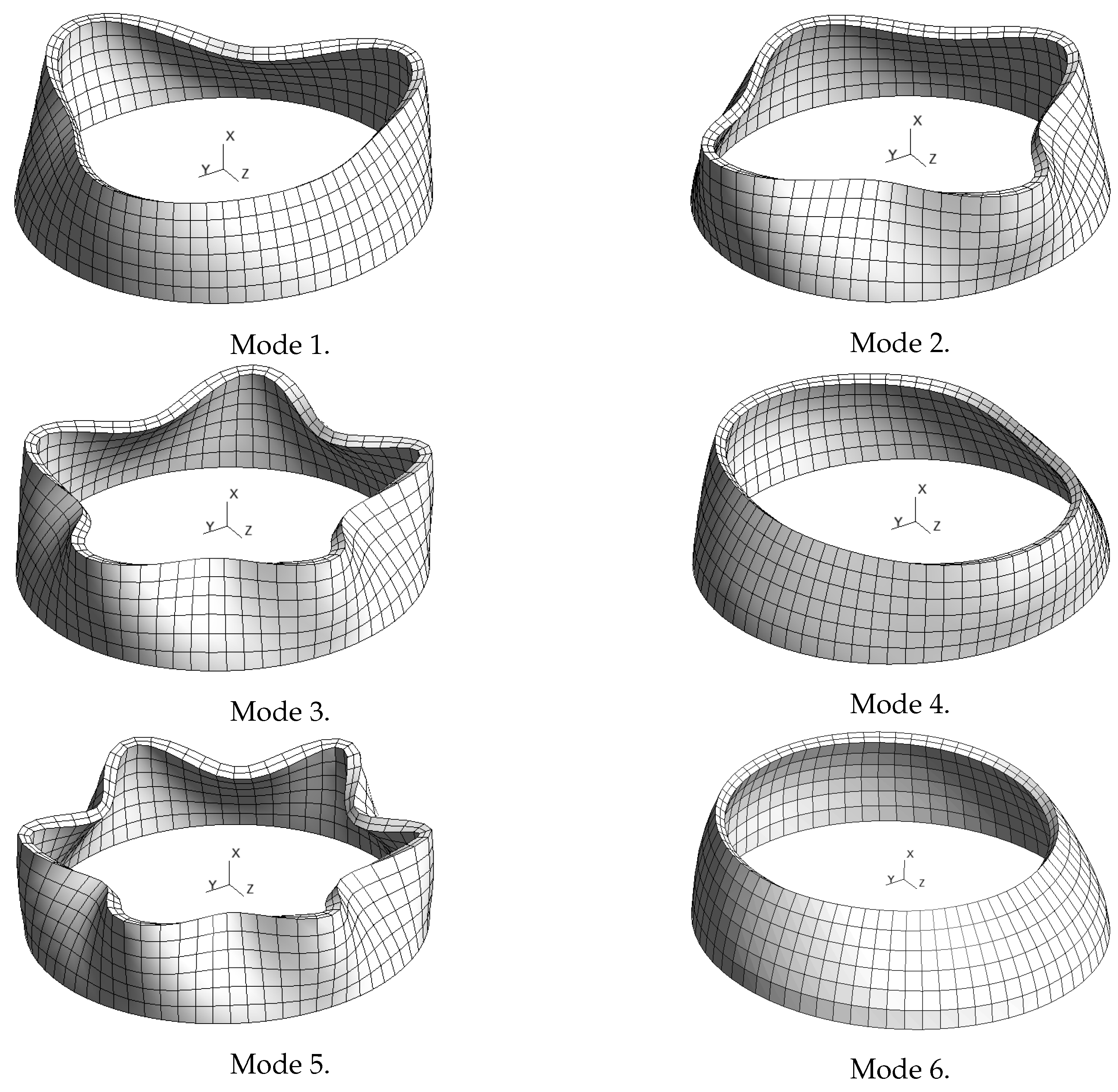
3.3. Bi-Layer Spherical Segment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Brasington, A.; Sacco, C.; Halbritter, J.; Wehbe, R.; Harik, R. Automated fiber placement: A review of history, current technologies, and future paths forward. Compos. Part C Open Access 2021, 6, 100182. [Google Scholar] [CrossRef]
- Kim, C.; Potter, K.; Weaver, M. Continuous tow shearing for manufacturing variable angle tow composites. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1347–1356. [Google Scholar] [CrossRef]
- Zhuo, P.; Li, S.; Ashcroft, A.; Jones, I. Material extrusion additive manufacturing of continuous fibre reinforced polymer matrix composites: A review and outlook. Compos. Part B Eng. 2021, 224, 109143. [Google Scholar] [CrossRef]
- Brooks, T.R.; Martins, J.R.; Kennedy, G.J. High-fidelity aerostructural optimization of tow-steered composite wings. J. Fluids Struct. 2019, 88, 122–147. [Google Scholar] [CrossRef]
- Grenoble, R.W.; Nguyen, T.; McKenney, M.J.; Przekop, A.; Juarez, P.D.; Gregory, E.D.; Jegley, D.C. Fabrication of a composite tow-steered structure for air-launch vehicle applications. In Proceedings of the AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Love, A.E.H. XVI. The small free vibrations and deformation of a thin elastic shell. Philos. Trans. R. Soc. A 1888, 179, 491–546. [Google Scholar]
- Donnell, L.H. Stability of Thin-Walled Tubes Under Torsion; NASA: Washington, DC, USA, 1933.
- Flügge, W. Stresses in Shells; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lindberg, G.M.; Olson, M.D.; Cowper, G.R. New developments in the finite element analysis of shells. Q. Bull. Div. Mech. Eng. Natl. Aeronaut. Establ. 1969, 4, 1–38. [Google Scholar]
- Clough, R.W.; Johnson, C.P. A finite element approximation for the analysis of thin shells. Int. J. Solids 1969, 4, 43–60. [Google Scholar] [CrossRef]
- Bogner, F.K.; Fox, R.L.; Schmit, L.A. A cylindrical shell discrete element. AIAA J. 1967, 5, 745–750. [Google Scholar] [CrossRef]
- Maksymyuk, V.A. Locking phenomenon in computational methods of the shell theory. Int. J. Appl. Mech. 2020, 56, 347–350. [Google Scholar] [CrossRef]
- Bathe, K.-J.; Dvorkin, E.N. A formulation of general shell elements—The use of mixed interpolation of tensorial components. Int. J. Numer. Methods Eng. 1986, 22, 697–722. [Google Scholar] [CrossRef]
- Bathe, K.-J.; Bucalem, M.L. Higher-order MITC general shell elements. Int. J. Numer. Methods Eng. 1993, 36, 3729–3754. [Google Scholar]
- Carrera, E. Theories and finite elements for multilayered plates and shells: A unified compact formulation with numerical assessment and benchmarking. Arch. Comput. Methods Eng. 2003, 10, 215–296. [Google Scholar] [CrossRef]
- Carrera, E.; Campisi, C.; Cinefra, M.; Soave, M. Evaluation of various trough the thickness and curvature approximations for free vibrational analysis of cylindrical and spherical shells. Int. J. Signal Imaging Syst. Eng. 2008, 1, 197. [Google Scholar]
- Giunta, G.; Biscani, F.; Belouettar, S.; Carrera, E. Hierarchical modelling of doubly curved laminated composite shells under distributed and localised loadings. Compos. B Eng. 2011, 42, 682–691. [Google Scholar] [CrossRef]
- Giunta, G.; Melta, N.; Belouettar, S.; Ferreira, A.J.M.; Carrera, E. A thermo-mechanical analysis of isotropic and composite beams via collocation with radial basis functions. J. Therm. Stresses 2013, 36, 1169–1199. [Google Scholar] [CrossRef]
- Brischetto, S.; Polit, O.; Carrera, E. Refined shell model for the linear analysis of isotropic and composite elastic structures. Eur. J. Mech. A-Solids 2012, 34, 102–119. [Google Scholar] [CrossRef]
- Cinefra, M.; Carrera, E. Shell finite elements with different through-the-thickness kinematics for the linear analysis of cylindrical multilayered structures. Int. J. Numer. Meth. Eng. 2013, 93, 160–182. [Google Scholar] [CrossRef]
- Cinefra, M.; Chinosi, C.; Della Croce, L. MITC9 shell elements based on refined theories for the analysis of isotropic cylindrical structures. Int. J. Numer. Meth. Eng. 2013, 20, 91–100. [Google Scholar] [CrossRef][Green Version]
- Cinefra, M.; Kumar, S.K.; Carrera, E. MITC9 Shell elements based on RMVT and CUF for the analysis of laminated composite plates and shells. Compos. Struct. 2019, 209, 383–390. [Google Scholar] [CrossRef]
- Kumar, S.K.; Harursampath, D.; Carrera, E.; Cinefra, M.; Valvano, S. Modal analysis of delaminated plates and shells using Carrera Unified Formulation–MITC9 shell element. Mech. Adv. Mater. Struct. 2018, 25, 681–697. [Google Scholar] [CrossRef]
- Carrera, E.; Zozulya, V.V. Carrera unified formulation (CUF) for shells of revolution. I. Higher-order theory. Acta Mech. 2023, 234, 109–136. [Google Scholar] [CrossRef]
- Carrera, E.; Zozulya, V.V. Carrera unified formulation (CUF) for the shells of revolution. II. Navier close form solutions. Acta Mech. 2023, 234, 137–161. [Google Scholar] [CrossRef]
- Carrera, E.; Zozulya, V.V. Carrera unified formulation (CUF) for the shells of revolution. Numerical evaluation. Mech. Adv. Mater. Struct. 2024, 31, 1597–1619. [Google Scholar] [CrossRef]
- Tornabene, F.; Liverani, A.; Caligiana, G. General anisotropic doubly-curved shell theory: A differential quadrature solution for free vibrations of shells and panels of revolution with a free-form meridian. J. Sound Vib. 2012, 331, 4848–4869. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Carrera, E. Static analysis of doubly-curved anisotropic shells and panels using CUF approach, differential geometry and differential quadrature method. Compos. Struct. 2014, 107, 675–697. [Google Scholar] [CrossRef]
- Wu, K.; Tatting, B.; Smith, B.; Stevens, R.; Occhipinti, G.; Swift, J.; Achary, D.; Thornburgh, R. Design and manufacturing of tow-steered composite shells using fiber placement. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4–7 May 2009; p. 2700. [Google Scholar]
- Hyer, M.W.; Charette, R.F. Innovative Design of Composite Structures: The Use of Curvilinear Fiber Format in Composite Structure Design; NASA: Washington, DC, USA, 1990.
- Tornabene, F.; Fantuzzi, N.; Baciocchi, M. Higher-order structural theories for the static analysis of doubly-curved laminated composite panels reinforced by curvilinear fibers. Thin-Walled Struct. 2016, 102, 222–245. [Google Scholar] [CrossRef]
- Sánchez-Majano, A.R.; Azzara, R.; Pagani, A.; Carrera, E. Accurate stress analysis of variable angle tow shells by high-order equivalent-single-layer and layer-wise finite element models. Materials 2021, 14, 6486. [Google Scholar] [CrossRef]
- Sciascia, G.; Oliveri, V.; Weaver, P.M. Eigenfrequencies of prestressed variable stiffness composite shells. Compos. Struct. 2021, 270, 114019. [Google Scholar] [CrossRef]
- He, T.; Huang, W.; Kuang, Z.; Huang, Q.; Hou, R.; Giunta, G.; Belouettar, S.; Hu, H. A seven-parameter high-order finite element model for multi-stable analysis of variable stiffness laminated shells. Thin-Walled Struct. 2023, 190, 110983. [Google Scholar] [CrossRef]
- Blom, A.W.; Setoodeh, S.; Hol, J.; Gürdal, Z. Design of variable-stiffness conical shells for maximum fundamental eigenfrequency. Comput. Struct. 2008, 86, 870–878. [Google Scholar] [CrossRef]
- Carvalho, J.; Sohouli, A.; Suleman, A. Fundamental Frequency Optimization of Variable Angle Tow Laminates with Embedded Gap Defects. J. Compos. Sci. 2022, 6, 64. [Google Scholar] [CrossRef]
- Catapano, A.; Montemurro, M.; Balcou, J.-A.; Panettieri, E. Rapid prototyping of variable angle-tow composites. Aerotec. Missili Spaz. 2019, 98, 257–271. [Google Scholar] [CrossRef]
- Montemurro, M.; Catapano, A. A general b-spline surfaces theoretical framework for optimisation of variable angle-tow laminates. Compos. Struct. 2019, 209, 561–578. [Google Scholar] [CrossRef]
- Montemurro, M.; Catapano, A. On the effective integration of manufacturability constraints within the multi-scale methodology for designing variable angle-tow laminates. Compos. Struct. 2017, 161, 145–159. [Google Scholar] [CrossRef]
- Fiordilino, G.A.; Izzi, M.I.; Montemurro, M. A general isogeometric polar approach for the optimisation of variable stiffness composites: Application to eigenvalue buckling problems. Mech. Mater. 2021, 153, 103574. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Leissa, A.W. Vibration of Shells; Scientific and Technical Information Office, National Aeronautics and Space Administration: Washington, DC, USA, 1973.
- Kraus, H. Thin Elastic Shells: An Introduction to the Theoretical Foundations and the Analysis of Their Static and Dynamic Behavior; John Wiley & Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
- Washizu, K. Variational Methods in Elasticity and Plasticity; Pergamon Press: Oxford, UK, 1974. [Google Scholar]
- Gürdal, Z.; Tatting, B.F.; Wu, C.K. Variable stiffness composite panels: Effects of stiffness variation on the in-plane and buckling response. Compos. Part A Appl. Sci. Manuf. 2008, 39, 911–922. [Google Scholar] [CrossRef]
- Carrera, E. On the use of the murakami’s zig-zag function in the modeling of layered plates and shells. Comput. Struct. 2004, 82, 541–554. [Google Scholar] [CrossRef]
- Bathe, K.-J. Finite Element Procedures; Prentice Hall: Hoboken, NJ, USA, 2006. [Google Scholar]
- ABAQUS. Abaqus Theory Manual; Dassault Systèmes: Vélizy-Villacoublay, France, 2003. [Google Scholar]
- Viglietti, A.; Zappino, E.; Carrera, E. Analysis of variable angle tow composites structures using variable kinematic models. Compos. Part B Eng. 2019, 171, 272–283. [Google Scholar] [CrossRef]







| Case | [GPa] | [GPa] | [GPa] | [GPa] | , |
|---|---|---|---|---|---|
| 1, 2, 3 | 50 | 10 | 5 | 5 |
| DOF | |
|---|---|
| Abaqus 3D | 503,355 |
| 2LD4 | 23,247 |
| 2LD2 | 12,915 |
| ED6 | 18,081 |
| ED4 | 12,915 |
| ED2 | 7749 |
| FSDT | 5166 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| Abaqus 3D | 10.843 | 13.862 | 16.123 | 18.316 | 20.670 | 21.881 |
| 2LD4 | 10.858 | 13.911 | 16.145 | 18.374 | 20.701 | 21.946 |
| 2LD2 | 10.859 | 13.912 | 16.145 | 18.375 | 20.702 | 21.947 |
| ED6 | 10.858 | 13.911 | 16.145 | 18.374 | 20.701 | 21.946 |
| ED4 | 10.858 | 13.911 | 16.145 | 18.374 | 20.701 | 21.946 |
| ED2 | 10.861 | 13.918 | 16.149 | 18.386 | 20.708 | 21.963 |
| FSDT | 10.852 | 13.893 | 16.142 | 18.366 | 20.700 | 21.944 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| Abaqus 3D | 40.262 | 52.831 | 63.309 | 65.599 | 77.539 | 81.103 |
| 2LD4 | 40.283 | 52.854 | 63.353 | 65.669 | 77.597 | 81.175 |
| 2LD2 | 40.309 | 52.900 | 63.429 | 65.787 | 77.723 | 81.371 |
| ED6 | 40.283 | 52.854 | 63.353 | 65.669 | 77.597 | 81.176 |
| ED4 | 40.286 | 52.858 | 63.362 | 65.685 | 77.613 | 81.202 |
| ED2 | 40.596 | 53.404 | 64.197 | 66.943 | 78.937 | 83.210 |
| FSDT | 40.551 | 53.374 | 64.144 | 66.830 | 78.881 | 83.132 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 4.7 | 1.0 | – * | 7.8 | 0.3 | 1.7 | |
| – * | – * | – * | – * | – * | 0.2 | |
| 34.8 | 3.9 | 11.7 | 0.3 | 0.2 | – * |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| Abaqus 3D | 55.388 | 70.438 | 86.799 | 93.100 | 103.030 | 108.270 |
| 2LD4 | 55.402 | 70.459 | 86.828 | 93.155 | 103.049 | 108.317 |
| 2LD2 | 55.545 | 70.674 | 87.128 | 93.550 | 103.195 | 108.755 |
| ED6 | 55.403 | 70.460 | 86.829 | 93.157 | 103.050 | 108.318 |
| ED4 | 55.425 | 70.494 | 86.881 | 93.239 | 103.080 | 108.401 |
| ED2 | 56.714 | 72.344 | 89.328 | 95.873 | 104.149 | 111.735 |
| FSDT | 56.610 | 72.277 | 89.261 | 95.692 | 103.999 | 111.657 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| Abaqus 3D | 21.656 | 24.166 | 32.512 | 43.473 | 46.874 | 48.037 |
| 2LD4 | 21.737 | 24.172 | 32.531 | 45.266 | 46.876 | 47.853 |
| 2LD2 | 21.738 | 24.172 | 32.532 | 45.269 | 46.876 | 47.855 |
| ED6 | 21.737 | 24.172 | 32.531 | 45.266 | 46.876 | 47.853 |
| ED4 | 21.737 | 24.172 | 32.531 | 45.266 | 46.876 | 47.853 |
| ED2 | 21.750 | 24.173 | 32.550 | 45.301 | 46.876 | 47.873 |
| FSDT | 21.760 | 24.155 | 32.590 | 45.277 | 46.874 | 47.928 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| Abaqus 3D | 26.336 | 47.354 | 57.253 | 88.047 | 94.851 | 103.540 |
| 2LD4 | 26.338 | 47.364 | 57.258 | 88.065 | 94.879 | 103.581 |
| 2LD2 | 26.346 | 47.365 | 57.284 | 88.067 | 94.934 | 103.585 |
| ED6 | 26.338 | 47.364 | 57.258 | 88.065 | 94.879 | 103.581 |
| ED4 | 26.340 | 47.364 | 57.263 | 88.066 | 94.889 | 103.581 |
| ED2 | 26.397 | 47.374 | 57.473 | 88.075 | 95.344 | 103.621 |
| FSDT | 26.405 | 47.256 | 57.537 | 87.897 | 95.515 | 103.286 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 0.6 | – * | 2.7 | – * | 1.8 | – * | |
| – * | 1.7 | – * | 59.4 | – * | 9.7 | |
| 72.1 | – * | – * | – * | 9.2 | – * |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| Abaqus 3D | 29.694 | 47.943 | 64.012 | 88.485 | 105.250 | 106.100 |
| 2LD4 | 29.697 | 47.958 | 64.017 | 88.495 | 105.278 | 106.165 |
| 2LD2 | 29.728 | 47.964 | 64.109 | 88.504 | 105.447 | 106.200 |
| ED6 | 29.697 | 47.958 | 64.017 | 88.495 | 105.278 | 106.165 |
| ED4 | 29.705 | 47.959 | 64.041 | 88.497 | 105.323 | 106.171 |
| ED2 | 29.874 | 47.994 | 64.540 | 88.528 | 106.222 | 106.339 |
| FSDT | 29.972 | 47.984 | 64.819 | 88.273 | 106.695 | 106.618 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| Abaqus 3D | 51.095 | 57.514 | 59.244 | 73.896 | 85.980 | 91.735 |
| LD4 | 51.666 | 57.842 | 60.297 | 75.704 | 86.271 | 94.557 |
| LD2 | 51.667 | 57.843 | 60.298 | 75.707 | 86.272 | 94.561 |
| ED6 | 51.666 | 57.843 | 60.297 | 75.705 | 86.272 | 94.557 |
| ED4 | 51.666 | 57.843 | 60.297 | 75.705 | 86.272 | 94.558 |
| ED2 | 51.674 | 57.849 | 60.309 | 75.722 | 86.278 | 94.582 |
| FSDT | 51.606 | 57.714 | 60.280 | 75.711 | 86.084 | 94.573 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| Abaqus 3D | 18.724 | 19.391 | 24.738 | 25.494 | 32.710 | 35.354 |
| LD4 | 18.789 | 19.489 | 24.917 | 25.555 | 32.978 | 35.473 |
| LD2 | 18.795 | 19.501 | 24.937 | 25.558 | 33.009 | 35.475 |
| ED6 | 18.789 | 19.489 | 24.918 | 25.555 | 32.979 | 35.475 |
| ED4 | 18.790 | 19.491 | 24.921 | 25.557 | 32.984 | 35.480 |
| ED2 | 18.836 | 19.562 | 25.046 | 25.595 | 33.182 | 35.541 |
| FSDT | 18.808 | 19.554 | 25.056 | 25.573 | 33.213 | 35.533 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| – * | – * | – * | – * | – * | 0.3 | |
| 0.1 | – * | – * | – * | – * | 0.2 | |
| – * | – * | – * | – * | – * | 43.4 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| Abaqus 3D | 25.989 | 28.627 | 32.082 | 36.316 | 42.619 | 51.291 |
| LD4 | 26.068 | 28.699 | 32.207 | 36.407 | 42.808 | 51.430 |
| LD2 | 26.097 | 28.721 | 32.267 | 36.417 | 42.905 | 51.440 |
| ED6 | 26.068 | 28.701 | 32.208 | 36.414 | 42.811 | 51.440 |
| ED4 | 26.074 | 28.709 | 32.217 | 36.430 | 42.824 | 51.459 |
| ED2 | 26.271 | 28.853 | 32.597 | 36.575 | 43.442 | 51.645 |
| FSDT | 26.261 | 28.862 | 32.631 | 36.572 | 43.524 | 51.620 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iannotta, D.A.; Giunta, G.; Kirkayak, L.; Montemurro, M. Hierarchical Free Vibration Analysis of Variable-Angle Tow Shells Using Unified Formulation. J. Compos. Sci. 2025, 9, 55. https://doi.org/10.3390/jcs9020055
Iannotta DA, Giunta G, Kirkayak L, Montemurro M. Hierarchical Free Vibration Analysis of Variable-Angle Tow Shells Using Unified Formulation. Journal of Composites Science. 2025; 9(2):55. https://doi.org/10.3390/jcs9020055
Chicago/Turabian StyleIannotta, Domenico Andrea, Gaetano Giunta, Levent Kirkayak, and Marco Montemurro. 2025. "Hierarchical Free Vibration Analysis of Variable-Angle Tow Shells Using Unified Formulation" Journal of Composites Science 9, no. 2: 55. https://doi.org/10.3390/jcs9020055
APA StyleIannotta, D. A., Giunta, G., Kirkayak, L., & Montemurro, M. (2025). Hierarchical Free Vibration Analysis of Variable-Angle Tow Shells Using Unified Formulation. Journal of Composites Science, 9(2), 55. https://doi.org/10.3390/jcs9020055







