Waves After Waves: The Use of Citric Acid as Salt Crystallization Inhibitor for Improving the Resistance of Concrete in Marine Environments
Abstract
1. Introduction
1.1. Concrete Durability in Marine Environnement
1.2. Salt Crystallization Damage and Chemical Inhibitors
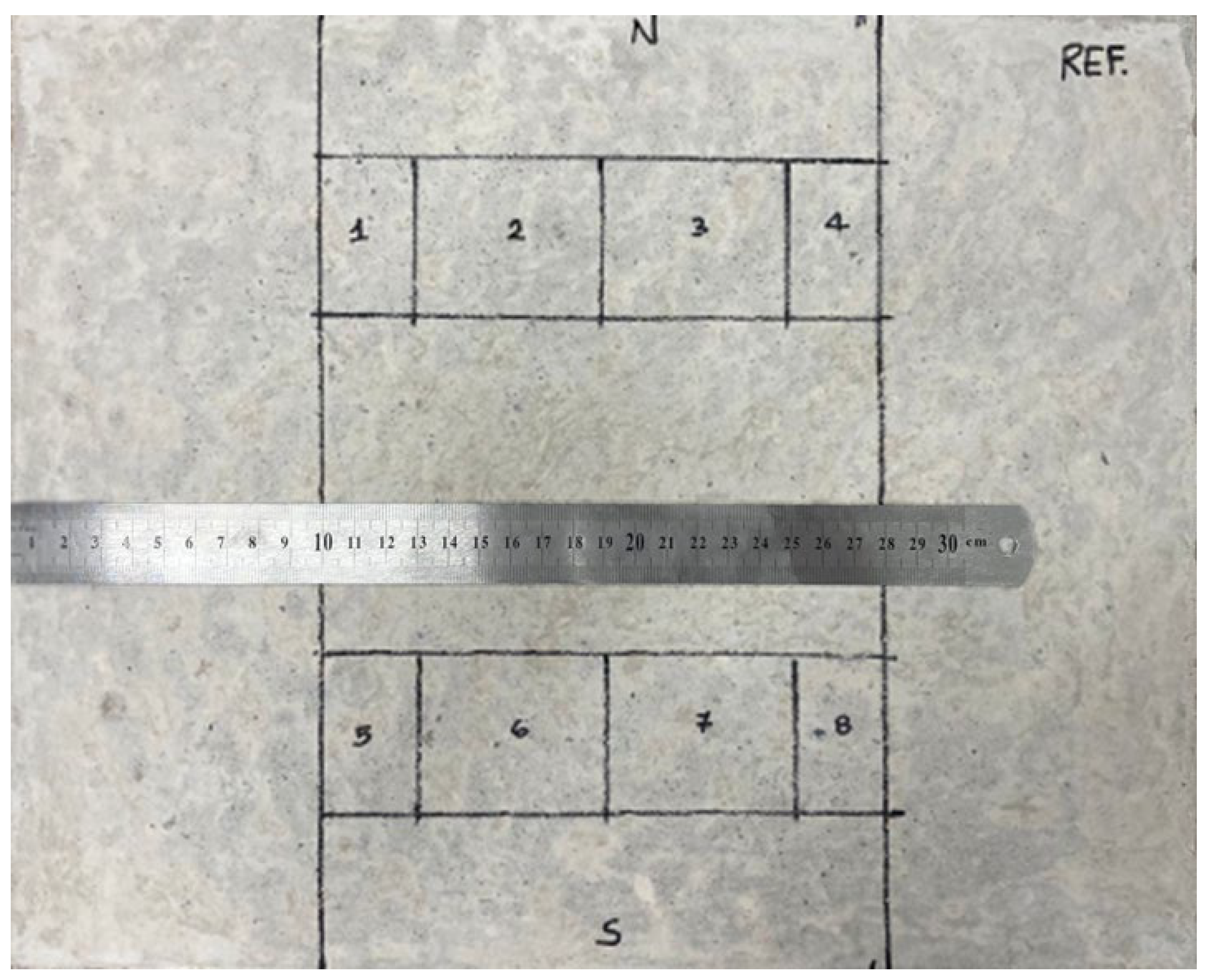
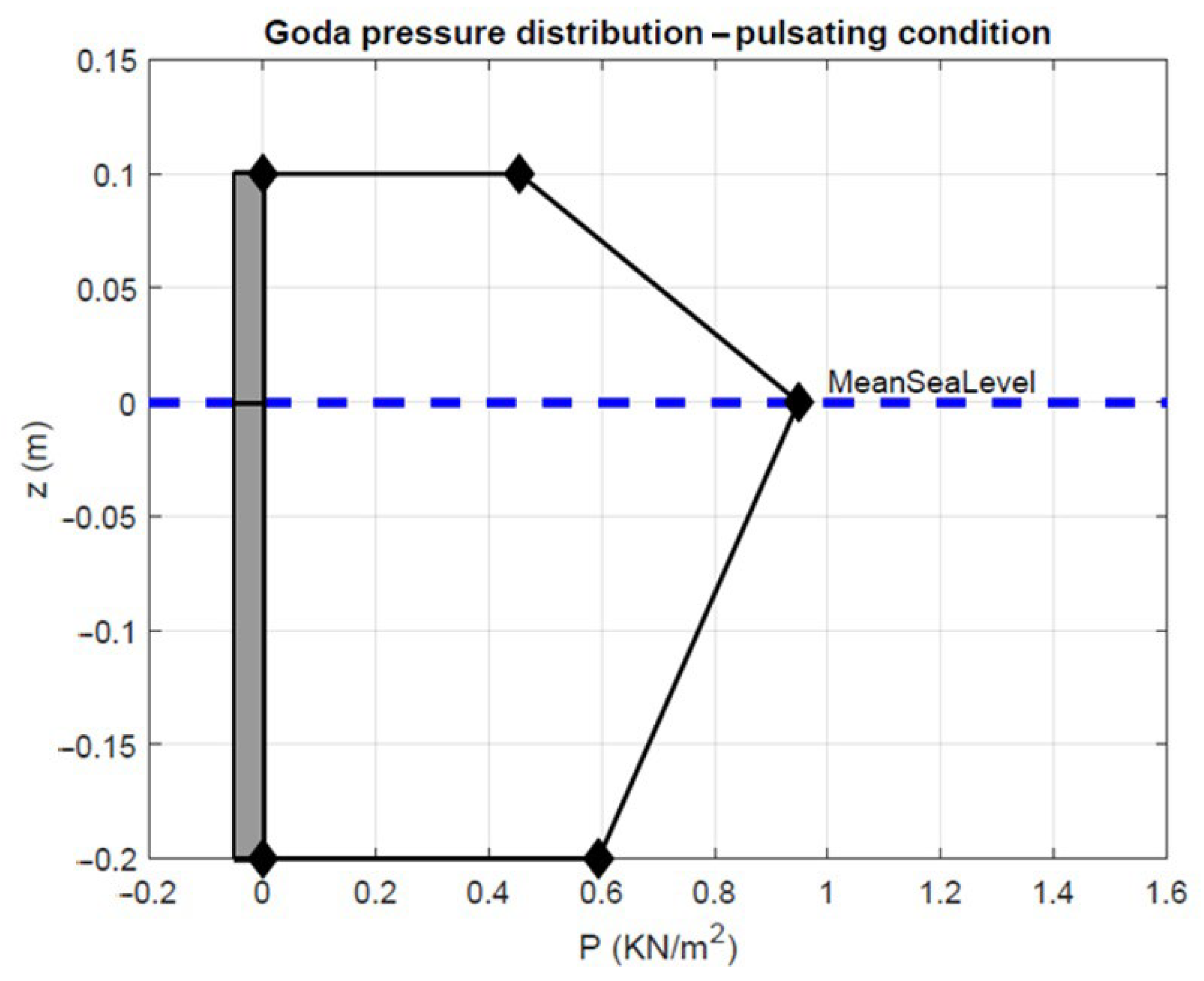
2. Materials and Methods
2.1. Pre Scenario
2.2. Post Scenario
2.3. W Scenario
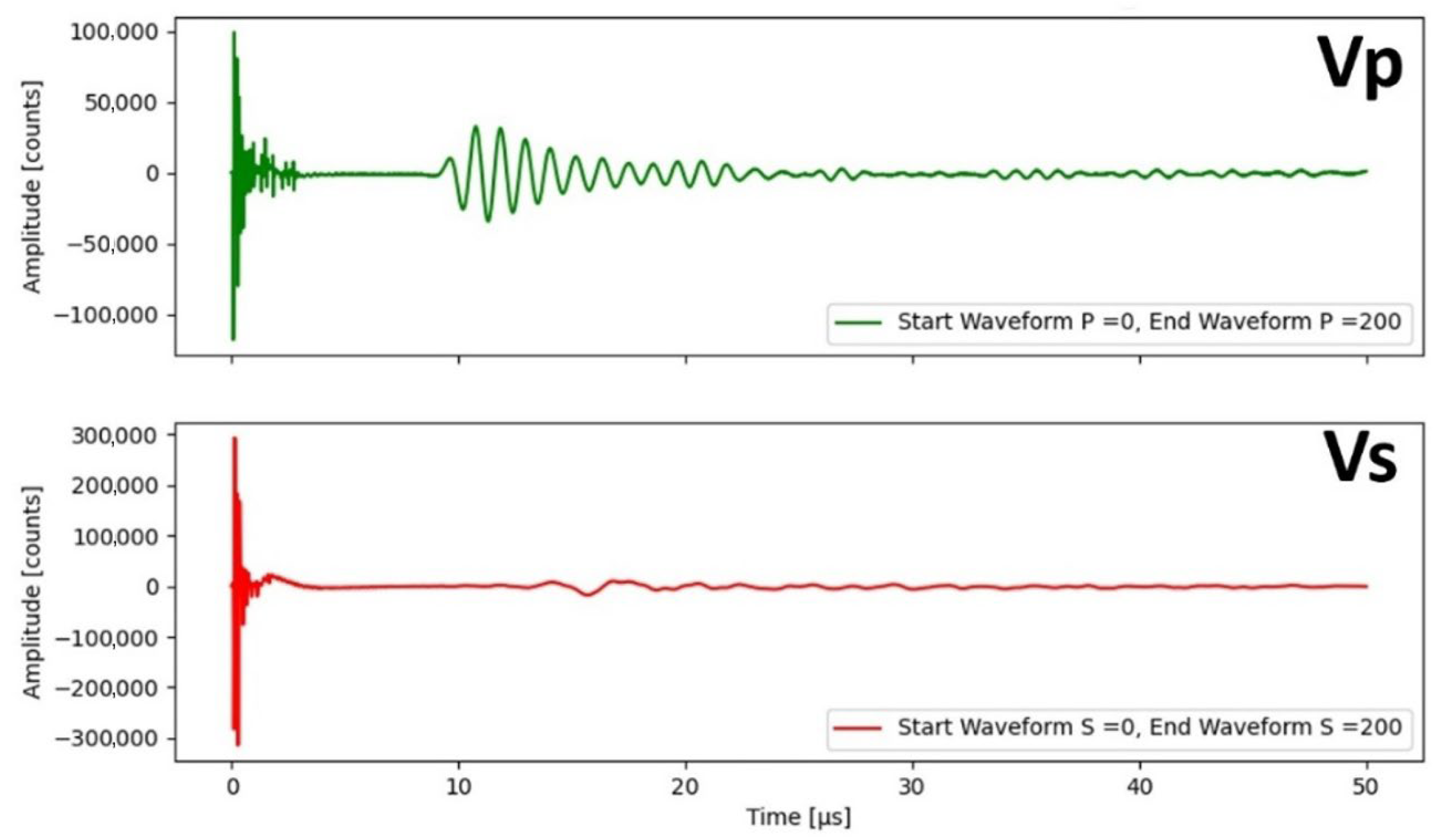
3. Results
3.1. Pre Scenario
3.2. Post Scenario
3.3. W Scenario
4. Discussion
4.1. Pre Scenario
4.2. Pre Scenario
4.3. W Scenario
5. Conclusions
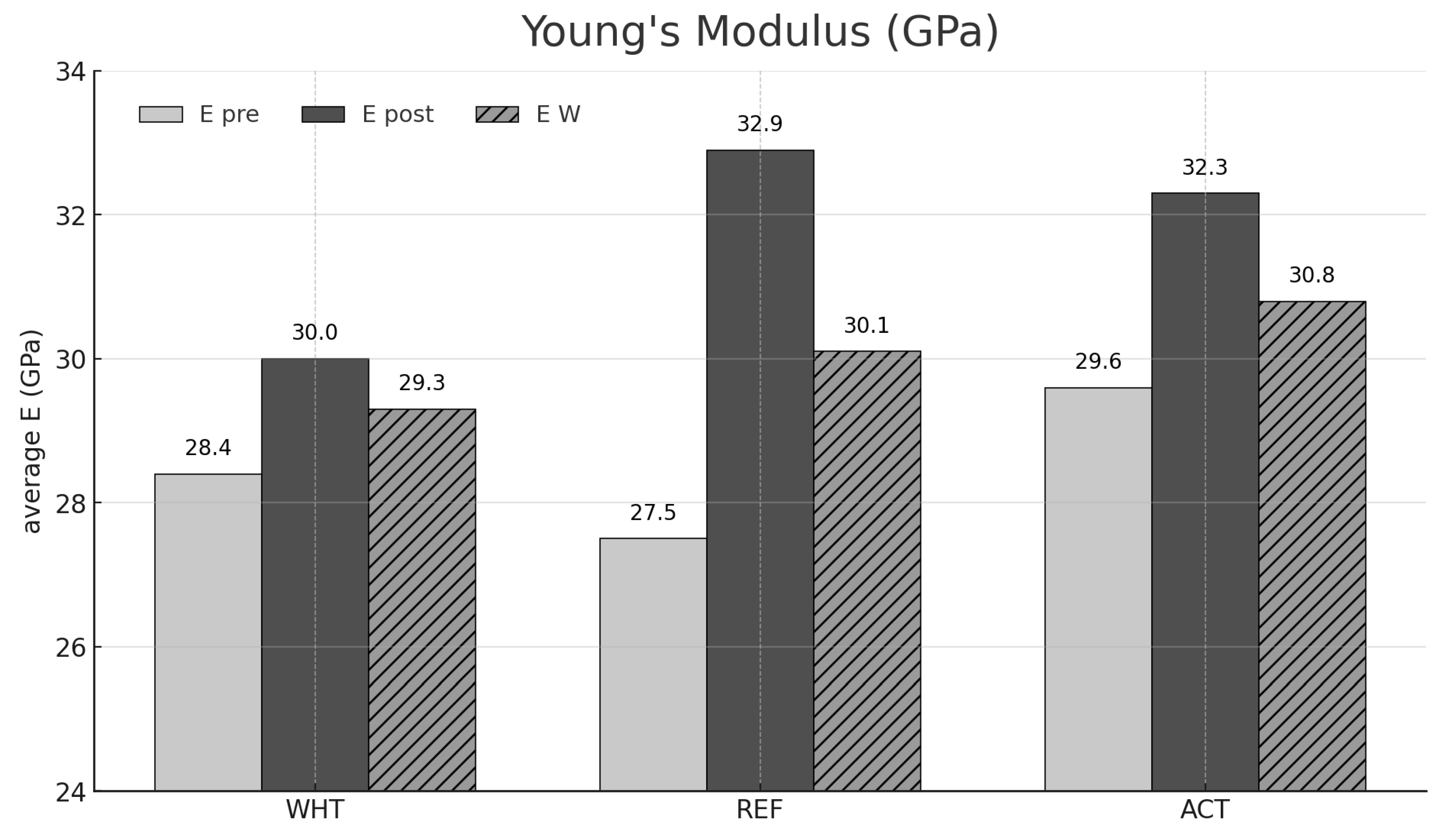
- The presence of salt crystals in concrete’s porosity led to significant changes in its elastic properties, with notable decreases in Young’s modulus and variable changes in Poisson’s ratio. This highlights the material’s vulnerability to the deteriorative effects of salt crystallization, leading to reduced stiffness and strength over time.
- The use of a salt crystallization inhibitor showcased its effectiveness in mitigating the detrimental impact of salt crystals on concrete. Samples treated with the inhibitor displayed enhanced resistance to both salt-induced damage and mechanical stress, emphasizing its potential for improving the durability of concrete structures in marine environments.
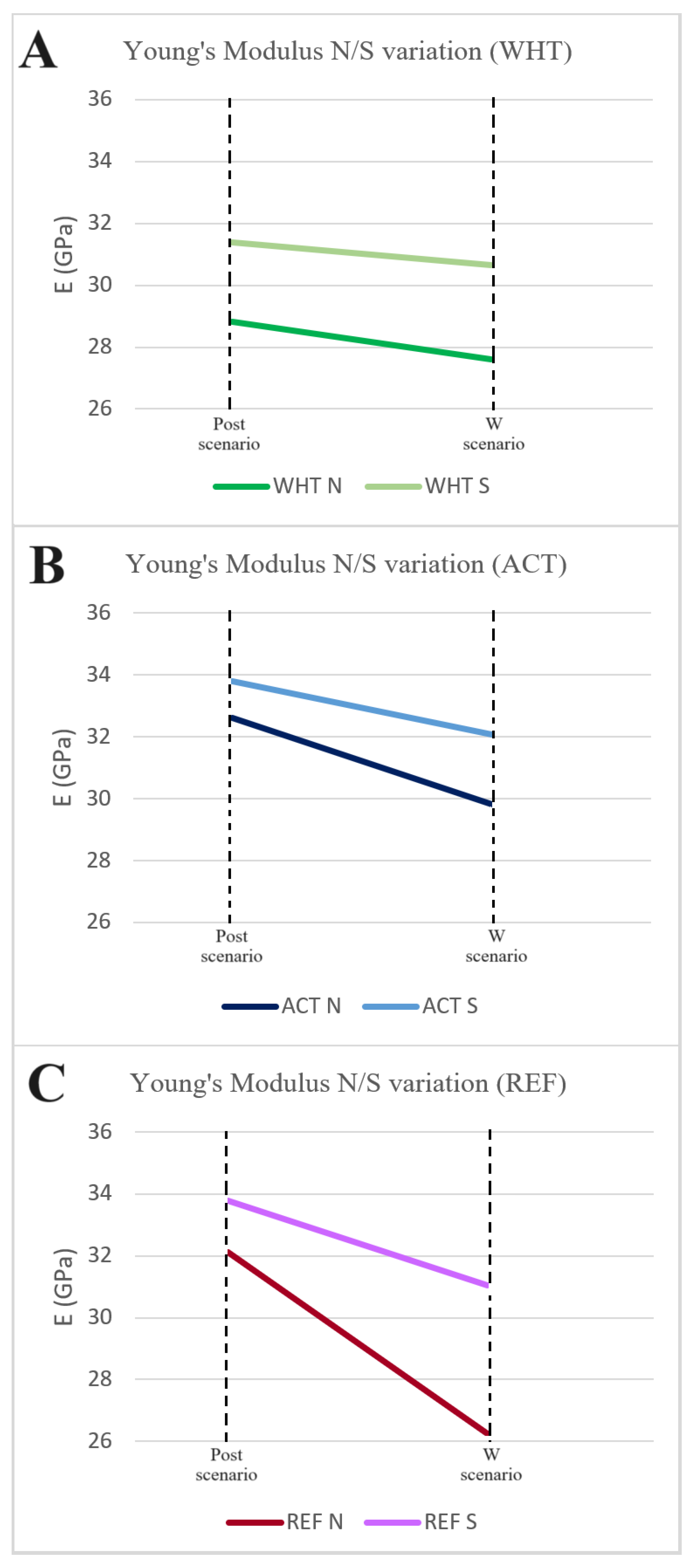
- Different regions within the concrete samples revealed varying responses to wave impacts. The upper wave impact zone experienced an overall greater damage, resulting in decreased moduli values. In contrast, the lower subaquatic stress zone showed less damage and preserved stiffness, suggesting that structural integrity can be better maintained below the waterline.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gjørv, O.E. Durability of Concrete Structures. Arab. J. Sci. Eng. 2011, 36, 151–172. [Google Scholar] [CrossRef]
- Mays, G.C. Durability of Concrete Structures: Investigation, Repair, Protection; CRC Press: Boca Raton, FL, USA, 1991; ISBN 978-0-203-47347-4. [Google Scholar]
- Tang, S.W.; Yao, Y.; Andrade, C.; Li, Z. Recent Durability Studies on Concrete Structure. Cem. Concr. Res. 2015, 78, 143–154. [Google Scholar] [CrossRef]
- Mehta, P.K. Durability of Concrete in Marine Environment–A Review. Spec. Pub. 1980, 65, 1–20. [Google Scholar] [CrossRef]
- Zhu, H.; Yu, H.; Ma, H. Electrochemical study on effect of rust inhibitors on corrosion of reinforcing bar in concrete in marine environment. Dongnan Daxue Xuebao (Ziran Kexue Ban)/J. Southeast Univ. (Nat. Sci. Ed.) 2020, 50, 109–119. [Google Scholar] [CrossRef]
- Yu, H.; Da, B.; Ma, H.; Zhu, H.; Yu, Q.; Ye, H.; Jing, X. Durability of Concrete Structures in Tropical Atoll Environment. Ocean. Eng. 2017, 135, 1–10. [Google Scholar] [CrossRef]
- Wilson, P.I. The Politics of Concrete: Institutions, Infrastructure, and Water Policy. Soc. Nat. Resour. 2015, 28, 109–115. [Google Scholar] [CrossRef]
- Meyer, C. The Greening of the Concrete Industry. Cem. Concr. Compos. 2009, 31, 601–605. [Google Scholar] [CrossRef]
- Saetta, A.; Scotta, R.; Vitaliani, R. Mechanical Behavior of Concrete under Physical-Chemical Attacks. J. Eng. Mech. 1998, 124, 1100–1109. [Google Scholar] [CrossRef]
- Shoukry, S.N.; William, G.W.; Downie, B.; Riad, M.Y. Effect of Moisture and Temperature on the Mechanical Properties of Concrete. Constr. Build. Mater. 2011, 25, 688–696. [Google Scholar] [CrossRef]
- Falegnami, A.; Tomassi, A.; Gunella, C.; Amalfitano, S.; Corbelli, G.; Armonaite, K.; Fornaro, C.; Giorgi, L.; Pollini, A.; Caforio, A.; et al. Defining Conceptual Artefacts to Manage and Design Simplicities in Complex Adaptive Systems. Heliyon 2024, 10, e41033. [Google Scholar] [CrossRef]
- Tomassi, A.; Falegnami, A.; Romano, E. Unveiling Simplexity: A New Paradigm for Understanding Complex Adaptive Systems and Driving Technological Innovation. Innovations 2025, 6, 100954. [Google Scholar] [CrossRef]
- Tomassi, A.; Falegnami, A.; Romano, E. Talking Resilience: Embedded Natural Language Cyber-Organizations by Design. Systems 2025, 13, 247. [Google Scholar] [CrossRef]
- Yin, G.-J.; Zuo, X.-B.; Tang, Y.-J.; Ayinde, O.; Wang, J.-L. Numerical Simulation on Time-Dependent Mechanical Behavior of Concrete under Coupled Axial Loading and Sulfate Attack. Ocean Eng. 2017, 142, 115–124. [Google Scholar] [CrossRef]
- Cusson, D.; Lounis, Z.; Daigle, L. Durability Monitoring for Improved Service Life Predictions of Concrete Bridge Decks in Corrosive Environments. Comput.-Aided Civ. Infrastruct. Eng. 2011, 26, 524–541. [Google Scholar] [CrossRef]
- Omar, T.; Nehdi, M.L. Condition Assessment of Reinforced Concrete Bridges: Current Practice and Research Challenges. Infrastructures 2018, 3, 36. [Google Scholar] [CrossRef]
- Kawamura, K.; Miyamoto, A. Condition State Evaluation of Existing Reinforced Concrete Bridges Using Neuro-Fuzzy Hybrid System. Comput. Struct. 2003, 81, 1931–1940. [Google Scholar] [CrossRef]
- Shah, A.A.; Ribakov, Y. Non-Destructive Evaluation of Concrete in Damaged and Undamaged States. Mater. Des. 2009, 30, 3504–3511. [Google Scholar] [CrossRef]
- Fan, W.; Zhong, Z.; Huang, X.; Sun, W.; Mao, W. Multi-Platform Simulation of Reinforced Concrete Structures under Impact Loading. Eng. Struct. 2022, 266, 114523. [Google Scholar] [CrossRef]
- Ferreira, R.M. Probability-Based Durability Analysis of Concrete Structures in Marine Environment; Escola de Engenharia-Universidade do Minho: Guimarães, Portugal, 2004. [Google Scholar]
- Ting, M.Z.Y.; Wong, K.S.; Rahman, M.E.; Meheron, S.J. Deterioration of Marine Concrete Exposed to Wetting-Drying Action. J. Clean. Prod. 2021, 278, 123383. [Google Scholar] [CrossRef]
- Sayward, J.M. Salt Action on Concrete; U.S. Army Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1984. [Google Scholar]
- Abdollahnia, H.; Alizadeh Elizei, M.H.; Reza Kashyzadeh, K. Multiaxial Fatigue Life Assessment of Integral Concrete Bridge with a Real-Scale and Complicated Geometry Due to the Simultaneous Effects of Temperature Variations and Sea Waves Clash. J. Mar. Sci. Eng. 2021, 9, 1433. [Google Scholar] [CrossRef]
- Sainflou, G. Essai Sur Les Digues Meritimes Verticales. Ann. Pnots Chaussees 1928, 98, 5–48. [Google Scholar]
- Castellino, M.; Lara, J.L.; Romano, A.; Losada, I.J.; De Girolamo, P. Wave Loading for Recurved Parapet Walls in Non-Breaking Wave Conditions. Analysis of the Induced Impulsive Forces. In Coastal Engineering 2018, Proceedings of the 36th International Conference on Coastal Engineering (ICCE 2018), Baltimore, MD, USA, 30 July–3 August 2018; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2018; Volume 36. [Google Scholar]
- Castellino, M.; Romano, A.; Lara, J.L.; Losada, I.J.; De Girolamo, P. Confined-Crest Impact: Forces Dimensional Analysis and Extension of the Goda’s Formulae to Recurved Parapets. Coast. Eng. 2021, 163, 103814. [Google Scholar] [CrossRef]
- Cuomo, G.; Allsop, W.; Bruce, T.; Pearson, J. Breaking Wave Loads at Vertical Seawalls and Breakwaters. Coast. Eng. 2010, 57, 424–439. [Google Scholar] [CrossRef]
- Johanning, L.; Smith, G.H.; Wolfram, J. Measurements of Static and Dynamic Mooring Line Damping and Their Importance for Floating WEC Devices. Ocean Eng. 2007, 34, 1918–1934. [Google Scholar] [CrossRef]
- Kirk, C.L.; Etok, E.U.; Cooper, M.T. Dynamic and Static Analysis of a Marine Riser. Appl. Ocean. Res. 1979, 1, 125–135. [Google Scholar] [CrossRef]
- Bracciale, M.P.; Sammut, S.; Cassar, J.; Santarelli, M.L.; Marrocchi, A. Molecular Crystallization Inhibitors for Salt Damage Control in Porous Materials: An Overview. Molecules 2020, 25, 1873. [Google Scholar] [CrossRef]
- Lubelli, B.; van Hees, R.P. Effectiveness of Crystallization Inhibitors in Preventing Salt Damage in Building Materials. J. Cult. Herit. 2007, 8, 223–234. [Google Scholar] [CrossRef]
- Scherer, G.W. Stress from Crystallization of Salt. Cem. Concr. Res. 2004, 34, 1613–1624. [Google Scholar] [CrossRef]
- Flatt, R.J.; Scherer, G.W. Thermodynamics of Crystallization Stresses in DEF. Cem. Concr. Res. 2008, 38, 325–336. [Google Scholar] [CrossRef]
- Vomocil, J.A. Porosity. In Methods of Soil Analysis: Part 1 Physical and Mineralogical Properties, Including Statistics of Measurement and Sampling; John Wiley & Sons: Hoboken, NJ, USA, 1965; Volume 9, pp. 299–314. [Google Scholar]
- Bretti, G.; Ceseri, M.; Natalini, R.; Ciacchella, M.C.; Santarelli, M.L.; Tiracorrendo, G. A Forecasting Model for the Porosity Variation during the Carbonation Process. GEM-Int. J. Geomath. 2022, 13, 13. [Google Scholar]
- Kowacz, M.; Putnis, C.; Putnis, A. The Effect of Cation: Anion Ratio in Solution on the Mechanism of Barite Growth at Constant Supersaturation: Role of the Desolvation Process on the Growth Kinetics. Geochim. Cosmochim. Acta 2007, 71, 5168–5179. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, X.; Ma, H.; Hou, D. Advanced Concrete Technology; John Wiley & Sons: Hoboken, NJ, USA, 2022; ISBN 1-119-80625-9. [Google Scholar]
- Morad, S. Carbonate Cementation in Sandstones: Distribution Patterns and Geochemical Evolution. Carbonate Cem. Sandstones Distrib. Patterns Geochem. Evol. 1998, 1–26. [Google Scholar]
- Tung, H.-H.; Paul, E.L.; Midler, M.; McCauley, J.A. Crystallization of Organic Compounds: An Industrial Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2023; ISBN 1-119-87946-9. [Google Scholar]
- Ciacchella, M.C. Control of Crystallization Pressure in Cementitious Materials Using a Bio-Based Inhibitor; Sapienza Università di Roma: Rome, Italy, 2025. [Google Scholar]
- Bodsworth, A.N.F. Investigation of Atmospheric Phase Transitions in Low Temperature, Mixed Aerosols; University of British Columbia: Vancouver, BC, Canada, 2010. [Google Scholar]
- Charola, A.E. Salts in the Deterioration of Porous Materials: An Overview. J. Am. Inst. Conserv. 2000, 39, 327–343. [Google Scholar] [CrossRef]
- Tovbin, Y.K. Second Law of Thermodynamics, Gibbs’ Thermodynamics, and Relaxation Times of Thermodynamic Parameters. Russ. J. Phys. Chem. A 2021, 95, 637–658. [Google Scholar] [CrossRef]
- Zerres, H.; Prausnitz, J.M. Thermodynamics of Phase Equilibria in Aqueous-organic Systems with Salt. AIChE J. 1994, 40, 676–691. [Google Scholar] [CrossRef]
- Mahmood, W.; Ayub, T. Mechanical Properties and Corrosion Resistance of Recycled Aggregate Concrete Exposed to Accelerated and Natural Marine Environment. J. Build. Eng. 2023, 66, 105867. [Google Scholar] [CrossRef]
- Qu, F.; Li, W.; Dong, W.; Tam, V.W.; Yu, T. Durability Deterioration of Concrete under Marine Environment from Material to Structure: A Critical Review. J. Build. Eng. 2021, 35, 102074. [Google Scholar] [CrossRef]
- Li, S.; Jin, Z.; Pang, B.; Li, J. Durability Performance of an RC Beam under Real Marine All Corrosion Zones Exposure for 7 Years. Case Stud. Constr. Mater. 2022, 17, e01516. [Google Scholar] [CrossRef]
- Kim, S.; Usman, M.; Park, C.; Hanif, A. Durability of Slag Waste Incorporated Steel Fiber-Reinforced Concrete in Marine Environment. J. Build. Eng. 2021, 33, 101641. [Google Scholar] [CrossRef]
- Sosa, I.; Thomas, C.; Polanco, J.A.; Setién, J.; Tamayo, P. Durability in Marine Environment of High-Performance Concrete with Electric Arc Furnace Slags and Cupola Slag Admixture. In Proceedings of the XV International Conference on Durability of Building Materials and Components, Barcelona, Catalonia, 20–23 October 2020. [Google Scholar]
- Prajeesha, M.; Packialakshmi, S. Evaluation of Bacterial Concrete Corrosion Resistance in Marine Settings: A Morphological Analysis Perspective. Int. Res. J. Educ. Technol. 2024, 6. [Google Scholar]
- Li, K.; Zeng, J.; Tang, L.; Sørensen, H.E.; Castro Borges, P.; Geiker, M.R.; Pedersen, M.T.; Zhang, P.; Surana, S.; Maddalena, R. Long-Term Field Exposure of Structural Concretes in Marine Environment: State-of-the-Art Review by RILEM TC 289-DCM. Mater. Struct. 2022, 55, 205. [Google Scholar] [CrossRef]
- Melchers, R.E. Long-Term Durability of Marine Reinforced Concrete Structures. J. Mar. Sci. Eng. 2020, 8, 290. [Google Scholar] [CrossRef]
- Ahmed, A.; Guo, S.; Zhang, Z.; Shi, C.; Zhu, D. A Review on Durability of Fiber Reinforced Polymer (FRP) Bars Reinforced Seawater Sea Sand Concrete. Constr. Build. Mater. 2020, 256, 119484. [Google Scholar] [CrossRef]
- Zeng, J.-J.; Hao, Z.-H.; Sun, H.-Q.; Zeng, W.-B.; Fan, T.-H.; Zhuge, Y. Durability Assessment of Ultra-High-Performance Concrete (UHPC) and FRP Grid-Reinforced UHPC Plates under Marine Environments. Eng. Struct. 2025, 323, 119313. [Google Scholar] [CrossRef]
- Khalil, W.I. Using Citric Acid as an Admixture and It’s Influence on Some Properties of Concrete. Eng. Tech. J. 2009, 27, 33–46. [Google Scholar] [CrossRef]
- Saleh, M.M.; Darwish, S.S.; Elzoghby, M. The Effectiveness of Some Crystallization Inhibitors in Preventing Salt Damage to Limestone. J. Cryst. Growth 2022, 585, 126606. [Google Scholar] [CrossRef]
- Ribeiro, M.; Tavares, C.; Ferreira, A. Chemical Resistance of Epoxy and Polyester Polymer Concrete to Acids and Salts. J. Polym. Eng. 2002, 22, 27–44. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Q.; Zhang, R.; Zheng, X. Corrosion Behavior of Coral Aggregate Concrete in Marine Environments and Anti-Corrosion Methods for Improvement: A Review. Eng. Rep. 2025, 7, e70229. [Google Scholar] [CrossRef]
- Falegnami, A.; Romano, E.; Tomassi, A. The Emergence of the GreenSCENT Competence Framework. In The European Green Deal in Education; Routledge: London, UK, 2024; pp. 204–216. ISBN 978-1-00-349259-7. [Google Scholar]
- Tomassi, A.; Falegnami, A.; Meleo, L.; Romano, E. The GreenSCENT Competence Frameworks. In The European Green Deal in Education; Routledge: London, UK, 2024; ISBN 978-1-00-349259-7. [Google Scholar]
- UNI EN 197-1:2011; Cement. Part 1: Composition, Specification and Conformity Criteria for Common Cements. Italian Organization for Standardization (UNI): Milan, Italy, 2012. Available online: https://store.uni.com/uni-en-197-1-2011 (accessed on 27 December 2023).
- Panzera, T.H.; Rubio, J.C.; Bowen, C.R.; Vasconcelos, W.L.; Strecker, K. Correlation between Structure and Pulse Velocity of Cementitious Composites. Adv. Cem. Res. 2008, 20, 101–108. [Google Scholar] [CrossRef]
- Bogas, J.A.; Gomes, M.G.; Gomes, A. Compressive Strength Evaluation of Structural Lightweight Concrete by Non-Destructive Ultrasonic Pulse Velocity Method. Ultrasonics 2013, 53, 962–972. [Google Scholar] [CrossRef]
- Tomassi, A.; De Franco, R.; Trippetta, F. High-Resolution Synthetic Seismic Modelling: Elucidating Facies Heterogeneity in Carbonate Ramp Systems. Pet. Geosci. 2024, 31, petgeo2024-047. [Google Scholar] [CrossRef]
- De Fazio, N.; Placidi, L.; Tomassi, A.; Fraddosio, A.; Castellano, A.; Paparella, F. Different Mechanical Models for the Study of Ultrasonic Wave Dispersion for Mechanical Characterization of Construction Materials. Int. J. Solids Struct. 2025, 315, 113352. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook; Cambridge University Press: Cambridge, UK, 2020; ISBN 978-1-108-42026-6. [Google Scholar]
- Saxena, N.; Mavko, G. Estimating Elastic Moduli of Rocks from Thin Sections: Digital Rock Study of 3D Properties from 2D Images. Comput. Geosci. 2016, 88, 9–21. [Google Scholar] [CrossRef]
- Olsen, C.; Christensen, H.F.; Fabricius, I.L. Static and Dynamic Young’s Moduli of Chalk from the North Sea. Geophysics 2008, 73, E41–E50. [Google Scholar] [CrossRef]
- Guillot, F.M.; Trivett, D.H. A Dynamic Young’s Modulus Measurement System for Highly Compliant Polymers. J. Acoust. Soc. Am. 2003, 114, 1334–1345. [Google Scholar] [CrossRef]
- Tomassi, A.; Trippetta, F.; de Franco, R.; Ruggieri, R. From Petrophysical Properties to Forward-Seismic Modeling of Facies Heterogeneity in the Carbonate Realm (Majella Massif, Central Italy). J. Pet. Sci. Eng. 2022, 211, 110242. [Google Scholar] [CrossRef]
- Tomassi, A.; Trippetta, F.; de Franco, R.; Ruggieri, R. How Petrophysical Properties Influence the Seismic Signature of Carbonate Fault Damage Zone: Insights from Forward-Seismic Modelling. J. Struct. Geol. 2023, 167, 104802. [Google Scholar] [CrossRef]
- Goda, Y. New Wave Pressure Formulae for Composite Breakwaters. In Coastal Engineering; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2015; pp. 1702–1720. [Google Scholar]
- Martinelli, L.; Ruol, P.; Volpato, M.; Favaretto, C.; Castellino, M.; De Girolamo, P.; Franco, L.; Romano, A.; Sammarco, P. Experimental Investigation on Non-Breaking Wave Forces and Overtopping at the Recurved Parapets of Vertical Breakwaters. Coast. Eng. 2018, 141, 52–67. [Google Scholar] [CrossRef]
- Goda, Y.; Suzuki, Y. Estimation of Incident and Reflected Waves in Random Wave Experiments. In Coastal Engineering 1976; American Society of Civil Engineers (ASCE): Reston, VA, USA, 1976; pp. 828–845. [Google Scholar]
- Mansard, E.P.; Funke, E.R. The Measurement of Incident and Reflected Spectra Using a Least Squares Method. In Coastal Engineering 1980; American Society of Civil Engineers (ASCE): Reston, VA, USA, 1980; pp. 154–172. [Google Scholar]
- Hashin, Z. The Elastic Moduli of Heterogeneous Materials. J. Appl. Mech. Trans. ASME 1960, 29, 143–150. [Google Scholar] [CrossRef]
- Hill, R. A Self-Consistent Mechanics of Composite Materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Mehta, P.K. Concrete. Structure, Properties and Materials; Department of Civil and Environmental Engineering, University of California at Berkeley: Berkeley, CA, USA, 1986. [Google Scholar]
- Mori, T.; Tanaka, K. Average Stress in Matrix and Average Elastic Energy of Materials with Misfitting Inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Hu, L.M.; Gao, D.Y.; Li, Y.Z.; Song, S.Q. Analysis of the Influence of Long Curing Age on the Compressive Strength of Plastic Concrete. Adv. Mater. Res. 2012, 382, 200–203. [Google Scholar] [CrossRef]
- Gard, J.A.; Taylor, H.F.W. Calcium Silicate Hydrate (II) (“C-S-H(II)”). Cem. Concr. Res. 1976, 6, 667–677. [Google Scholar] [CrossRef]
- Sui, T.; Fan, L.; Wen, Z.; Wang, J.; Zhang, Z. Study on the Properties of High Strength Concrete Using High Belite Cement. J. Adv. Concr. Technol. 2004, 2, 201–206. [Google Scholar] [CrossRef]
- Chatterji, S.; Jeffery, J.W. Studies of Early Stages of Paste Hydration of Cement Compounds, II. J. Am. Ceram. Soc. 1963, 46, 187–191. [Google Scholar] [CrossRef]
- John, E.; Lothenbach, B. Cement Hydration Mechanisms through Time–a Review. J. Mater. Sci. 2023, 58, 9805–9833. [Google Scholar] [CrossRef]
- Zhutovsky, S.; Kovler, K.; Bentur, A. Assessment of Distance of Water Migration in Internal Curing of High-Strength Concrete. In ACI SP-220 Autogenous Deformation Concrete; American Concrete Institute: Farmington Hills, MI, USA, 2004; pp. 181–197. [Google Scholar]
- Flatt, R.J. Salt Damage in Porous Materials: How High Supersaturations Are Generated. J. Cryst. Growth 2002, 242, 435–454. [Google Scholar] [CrossRef]
- Schulze, O.; Popp, T.; Kern, H. Development of Damage and Permeability in Deforming Rock Salt. Eng. Geol. 2001, 61, 163–180. [Google Scholar] [CrossRef]
- Trippetta, F.; Collettini, C.; Vinciguerra, S.; Meredith, P. Laboratory Measurements of the Physical Properties of Triassic Evaporites from Central Italy and Correlation with Geophysical Data. Tectonophysics 2010, 492, 121–132. [Google Scholar] [CrossRef]
- Moropoulou, A.; Haralampopoulos, G.; Tsiourva, T.; Auger, F.; Birginie, J.M. Artificial Weathering and Non-Destructive Tests for the Performance Evaluation of Consolidation Materials Applied on Porous Stones. Mater. Struct. 2003, 36, 210–217. [Google Scholar] [CrossRef]
- Jaffer, S.J.; Hansson, C.M. Chloride-Induced Corrosion Products of Steel in Cracked-Concrete Subjected to Different Loading Conditions. Cem. Concr. Res. 2009, 39, 116–125. [Google Scholar] [CrossRef]
- Zhang, D.; Ghouleh, Z.; Shao, Y. Review on Carbonation Curing of Cement-Based Materials. J. CO2 Util. 2017, 21, 119–131. [Google Scholar] [CrossRef]
- Sakr, M.R.; Bassuoni, M.T.; Hooton, R.D.; Drimalas, T.; Haynes, H.; Folliard, K.J. Physical Salt Attack on Concrete: Mechanisms, Influential Factors, and Protection. ACI Mater. J. 2020, 117, 253–268. [Google Scholar] [CrossRef]
- Tsui, N.; Flatt, R.J.; Scherer, G.W. Crystallization Damage by Sodium Sulfate. J. Cult. Herit. 2003, 4, 109–115. [Google Scholar] [CrossRef]
- Holly, I.; Bilčík, J. Effect of Chloride-Induced Steel Corrosion on Working Life of Concrete Structures. Solid State Phenom. 2018, 272, 226–231. [Google Scholar] [CrossRef]
- Jamshidi, A. An Investigation on Ultrasonic Wave Velocity of Laminated Sandstone under Freeze-Thaw and Salt Crystallization Cycles: Insights from Anisotropy Effects. J. Build. Eng. 2023, 71, 106461. [Google Scholar] [CrossRef]
- Sun, Z. Seismic Anisotropy in Salt from Theoretical Study, Modelling, and Field Experiments; University of Calgary: Calgary, Canada, 1995; ISBN 0-612-03226-4. [Google Scholar]
- Zong, J.; Stewart, R.; Dyaur, N. Salt Anisotropy: Ultrasonic Lab Experiments and Traveltime Ramifications. In SEG Technical Program Expanded Abstracts 2014; SEG Technical Program Expanded Abstracts, Society of Exploration Geophysicists: Houston, TX, USA, 2014; pp. 383–388. [Google Scholar]
- Kennett, B.L.N.; Engdahl, E.R.; Buland, R. Constraints on Seismic Velocities in the Earth from Traveltimes. Geophys. J. Int. 1995, 122, 108–124. [Google Scholar] [CrossRef]
- Müller, T.M.; Gurevich, B.; Lebedev, M. Seismic Wave Attenuation and Dispersion Resulting from Wave-Induced Flow in Porous Rocks—A Review. Geophysics 2010, 75, 75A147–75A164. [Google Scholar] [CrossRef]
- International Offshore Mechanics and Arctic Engineering Symposium. In Proceedings of the Sixth International Symposium & Exhibit on Offshore Mechanics and Arctic Engineering, Houston, TX, USA, 1–6 March 1987; American Society of Mechanical Engineers: New York, NY, USA, 1987.
- Uenishi, K.; Yamachi, H.; Nakamori, J. Precise Dynamic Disintegration of Concrete Structures by Controlling Wave Motion. Procedia Struct. Integr. 2022, 42, 755–761. [Google Scholar] [CrossRef]



| WHT (Pre) Avg. | σ | REF (Pre) Avg. | σ | ACT (Pre) Avg. | σ | |
|---|---|---|---|---|---|---|
| Vp (km/s) | 3.65263 | 0.16350 | 3.62351 | 0.18203 | 3.79683 | 0.16986 |
| Vs (km/s) | 2.35981 | 0.09729 | 2.27259 | 0.13966 | 2.34762 | 0.07057 |
| Vp/Vs | 1.55012 | 0.09387 | 1.59617 | 0.05759 | 1.61816 | 0.07736 |
| WHT (Post) avg. | REF (Post) avg. | ACT (Post) avg. | ||||
| Vp (km/s) | 3.78018 | 0.10621 | 4.08359 | 0.11280 | 3.97100 | 0.03887 |
| Vs (km/s) | 2.38496 | 0.09275 | 2.43249 | 0.09851 | 2.44634 | 0.02101 |
| Vp/Vs | 1.58599 | 0.04306 | 1.67289 | 0.06588 | 1.62332 | 0.01920 |
| WHT (W) avg. | REF (W) avg. | ACT (W) avg. | ||||
| Vp (km/s) | 3.80518 | 0.06426 | 3.80630 | 0.14725 | 3.83220 | 0.05082 |
| Vs (km/s) | 2.32514 | 0.04671 | 2.37994 | 0.08789 | 2.41718 | 0.02734 |
| Vp/Vs | 1.63687 | 0.03967 | 1.60046 | 0.05258 | 1.58608 | 0.02348 |
| E [GPa] | |||||
|---|---|---|---|---|---|
| WHT (Pre) Avg. | σ | REF (Pre) Avg. | σ | ACT (Pre) Avg. | σ |
| 28.46317 | 1.7366 | 27.48818 | 2.9997 | 29.59530 | 1.6528 |
| WHT (post) N+S avg. | REF (Post) N+S avg. | ACT (post) N+S avg. | |||
| 30.0930 | 1.8767 | 32.9468 | 1.7623 | 32.3576 | 0.4480 |
| WHT (post) N avg. | REF (Post) N avg. | ACT (post) N avg. | |||
| 28.8079 | 1.1449 | 32.1152 | 0.8718 | 32.6957 | 0.4561 |
| WHT (post) N avg. | REF (Post) S avg. | ACT (post) S avg. | |||
| 30.6568 | 1.5826 | 33.9612 | 2.1547 | 31.8894 | 0.3102 |
| WHT (W) avg. | REF (W) avg. | ACT (W) avg. | |||
| 28.38736 | 0.8338 | 29.16198 | 1.6379 | 29.85483 | 0.9109 |
| WHT (W) N avg. | REF (W) N avg. | ACT (W) N avg. | |||
| 27.6179 | 0.8019 | 26.2626 | 1.0177 | 28.8201 | 1.2499 |
| WHT (W) S avg. | REF (W) S avg. | ACT (W) S avg. | |||
| 29.6568 | 0.8864 | 31.0612 | 1.7514 | 30.8894 | 0.6089 |
| WHT (Pre) avg. | REF (Pre) avg. | ACT (Pre) avg. | |
|---|---|---|---|
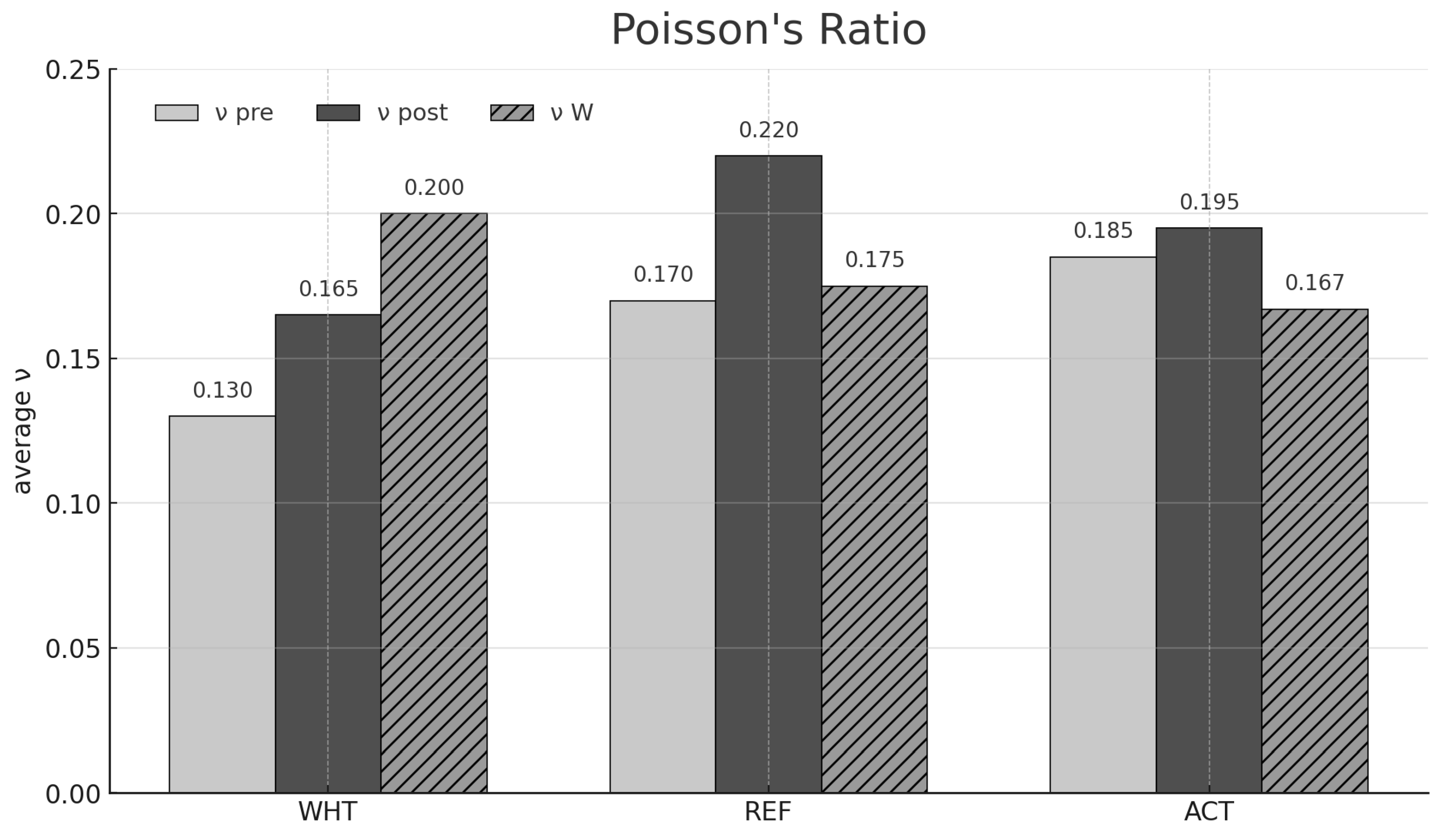
| n | 0.131039351 | 0.173609794 | 0.185821307 |
| WHT (Post) avg. | REF (Post) avg. | ACT (Post) avg. | |
| n | 0.168079907 | 0.218993204 | 0.193896367 |
| WHT (W) avg. | REF (W) avg. | ACT (W) avg. | |
| n | 0.200387612 | 0.176104918 | 0.166669406 |
| WHT (Pre → Post) | REF (Pre → Post) | ACT (Pre → Post) | |
|---|---|---|---|
| Vp Increase % | 3.49 | 12.69 | 4.58 |
| Vs Increase % | 1.06 | 7.03 | 4.20 |
| Vp/Vs Increase % | 2.31 | 4.80 | 0.31 |
| Sample | WHT (Post → W) | REF (Post → W) | ACT (Post → W) |
|---|---|---|---|
| Vp Variation % | 0.66 | −6.79 | −3.49 |
| Vs Variation % | −2.50 | −2.16 | −1.19 |
| Vp/Vs Variation % | 3.20 | −4.32 | −2.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciacchella, M.C.; Castellino, M.; Tomassi, A.; Trippetta, F.; Marrocchi, A.; Bracciale, M.P. Waves After Waves: The Use of Citric Acid as Salt Crystallization Inhibitor for Improving the Resistance of Concrete in Marine Environments. J. Compos. Sci. 2025, 9, 639. https://doi.org/10.3390/jcs9110639
Ciacchella MC, Castellino M, Tomassi A, Trippetta F, Marrocchi A, Bracciale MP. Waves After Waves: The Use of Citric Acid as Salt Crystallization Inhibitor for Improving the Resistance of Concrete in Marine Environments. Journal of Composites Science. 2025; 9(11):639. https://doi.org/10.3390/jcs9110639
Chicago/Turabian StyleCiacchella, Maria Carla, Myrta Castellino, Andrea Tomassi, Fabio Trippetta, Assunta Marrocchi, and Maria Paola Bracciale. 2025. "Waves After Waves: The Use of Citric Acid as Salt Crystallization Inhibitor for Improving the Resistance of Concrete in Marine Environments" Journal of Composites Science 9, no. 11: 639. https://doi.org/10.3390/jcs9110639
APA StyleCiacchella, M. C., Castellino, M., Tomassi, A., Trippetta, F., Marrocchi, A., & Bracciale, M. P. (2025). Waves After Waves: The Use of Citric Acid as Salt Crystallization Inhibitor for Improving the Resistance of Concrete in Marine Environments. Journal of Composites Science, 9(11), 639. https://doi.org/10.3390/jcs9110639









