Advancements in ZnFe₂O₄ Synthesis: A Comparative Study of Sol–Gel and Solid-State Methods for Next-Generation Battery Applications

Abstract

The article examines the synthesis and electrophysical properties of spinel ferrite ZnFe₂O₄, produced using the sol–gel method with a solid-state finishing process; as well as through classical ceramic technology with mechanochemical activation. The study includes a detailed analysis of the phase composition and crystalline structure using X-ray diffraction; infrared spectroscopy; mass spectrometry; and thermogravimetric and differential thermal analyses. These methods help identify thermal effects and the stages of synthesis. Impedance spectroscopy is used to investigate the electrophysical properties, revealing a significant influence of firing temperature on electrical ionic conductivity. The results show that the electrophysical properties differ based on the synthesis conditions and methods. This suggests potential applications for ZnFe₂O₄ as a cathode material in metal-ion batteries. The work highlights the importance of optimizing synthesis conditions to achieve high-performance characteristics in electrode materials.

1. Introduction

Currently, the market is extensively represented by electrochemical energy storage devices, with lithium-ion batteries (LIBs) being the most prominent [1,2,3,4]. The advantages of LIBs include a high voltage per cell of 4.2 V, a specific energy capacity of up to 270 Wh/kg, a substantial number of charge–discharge cycles before capacity degradation, low self-discharge rates, high load currents, and an operational temperature range from −20 °C to +60 °C [5,6,7,8,9,10,11]. However, a major drawback of LIBs is safety; they can be flammable and even explosive in certain conditions. Another significant disadvantage is their high production cost due to the use of expensive materials such as lithium and cobalt [12,13,14,15,16,17,18,19,20], along with their negative environmental impact [20,21]. Nevertheless, there is currently no equivalent alternative to LIBs in the field of energy storage. Therefore, one of the most pressing challenges is the development of a new type of energy storage device, which could be a metal-ion battery (MIB).

Recently, the number of research efforts in this direction has significantly increased [22,23,24,25,26]. It is expected that the active ion in MIBs will be a high-valent cation. One of the first developments in this area was the work of D. Aurbach [27], which focused on creating magnesium-ion batteries. The main advantages of MIBs are expected to be theoretically high capacity, lower cost, and enhanced safety [22,23]. This is primarily due to the fact that the cathode material is multivalent, unlike lithium-based systems, leading to increased energy storage capacity [28]. Additionally, the cost of materials used in MIBs is considerably lower. The components of MIBs include crystalline electrodes (cathode/anode) and an electrolyte. Recent trends among researchers are focused on finding and creating a fully solid-state battery with a solid electrolyte, which would allow for the development of efficient and safe power sources [29,30].

Zn-ferrites, specifically spinel ferrite ZnFe₂O₄, are among such materials. As a non-standard ceramic material, ZnFe₂O₄ possesses exceptional characteristics, including chemical and thermal stability, as well as lower toxicity compared to other metallic elements [31]. Notably, this compound is already widely used in various applications, including magnetic data storage systems, 5G mobile communication networks, supercapacitor technologies, and devices designed for water splitting to produce gaseous hydrogen [31]. Certain successes in the development of such MIBs have already been achieved [23,24,25,27,28,29]. The first results with a similar structural compound used as a cathode material, where vanadium replaces iron, are encouraging [22,32]. While ZnFe₂O₄ has been previously studied, a direct and systematic comparison of its structural and electrophysical properties synthesized by versatile wet-chemistry and classic solid-state routes, specifically tailored for battery applications, is still lacking. The novelty of this work lies in this comprehensive comparative approach. We not only juxtapose the phase formation mechanisms, microstructural characteristics, and ionic conductivity of sol–gel derived ZnFe₂O₄ with its ceramic counterpart but also establish clear correlations between the synthesis methodology, the resulting material’s properties (such as specific surface area and particle size), and its potential as a cathode for Zn-ion batteries. Furthermore, for the first time in the context of these synthesis methods, we provide a crystallochemical analysis using the topological (Voronoi-Dirichlet) approach, which reveals a 3D network of channels for Zn²⁺ migration within the ZnFe₂O₄ spinel structure, providing a fundamental rationale for the observed ionic conductivity. This study provides crucial insights into selecting the optimal synthesis pathway to engineer ZnFe₂O₄ with desired characteristics for next-generation energy storage, laying a solid foundation for future electrochemical testing. The aim of this work was to synthesize spinel ferrite ZnFe₂O₄ using a combined method, employing sol–gel technology with a solid-state finishing process and classical ceramic technology, followed by an investigation of its properties based on the synthesis method and conditions, as a prospective cathode material.

2. Materials and Methods

2.1. Materials Synthesis

The synthesis of electrode materials based on zinc ferrite (ZnFe₂O₄) was carried out using two approaches: co-precipitation and solid-state methods. In the study, the following reagents were used, sourced from NevaReaktiv LLC (St. Petersburg, Russia): for the co-precipitation method, zinc chloride (purity 96.00%), iron(III) chloride (purity 98.00%), and sodium hydroxide (purity 98.00%); and for the solid-state method, iron(III) oxide (purity 99.50%) and zinc oxide (purity 99.50%).

2.2. Synthesis of ZnFe₂O₄

During co-precipitation, the equilibrium pH values were taken as stationary values obtained using a pH meter (Anion 7000, InfraSPAK-Analyt, Novosibirsk, Russia) with an accuracy of ±0.02. In cases where pH drift occurred over time, the stationary value was determined by extrapolating the pH versus 1/t (where t is time) to 1/t = 0. A selective hydrogen ion electrode (ESL-43-07, Anion, Novosibirsk, Russia) was used as the indicator electrode, with a isopotential point of pH = 7 ± 0.3, while a silver/silver chloride electrode (Ag/AgCl) with a saturated KCl solution (EVL-1M3, Anion, Novosibirsk, Russia) served as the reference electrode, having a potential of 202 ± 2 mV at 20 °C relative to the standard hydrogen electrode.

In the solid-state approach, the sample preparation of the mixed precursor (iron(III) and zinc(II) oxides) involved preliminary homogenization in an agate mortar, followed by mechanochemical activation in a planetary ball mill “Aktivator-2 SL”at 1380 rpm, using zirconium oxide-lined drums and zirconium oxide balls (Aktivator Machine Engineering Plant, Novosibirsk, Russia) and an inverter (FVS 11-4015 PL, Toshiba, Kawasaki, Japan). The duration of the mechanochemical activation process was 30 min.

Thermal treatment of the air-dry precursors was performed in a muffle furnace (MIMP-P, MIUS, Tula, Russia) with a heating rate of 10 °C/min. The synthesis temperature was chosen based on the results from differential thermal analysis and varied over a wide range.

2.3. Combined Co-Precipitation and Solid-State Method

The combination of co-precipitation and solid-state methods involved the following steps: initially, chlorides of iron(III) and zinc(II) were mixed in the required molar ratio under intensive stirring. Subsequently, a sodium hydroxide solution was introduced at room temperature to precipitate the solid precursor phase until pH values just before the dissolution point of zinc hydroxide (pH = 10.5) were reached [32]. Schematic representation of the synthesis process is shown on Figure 1.

After hydrodynamic processing for 30–60 min, the formed suspension was filtered under vacuum using a Bunsen flask on a Büchner funnel with blue ribbon filter paper. The filtered precursor was washed with deionized water on the filter to remove residual mother solution. In the second stage, the precursor was dried at room temperature and subjected to treatment in a muffle furnace under various temperature regimes (

Table 1. Chemical composition of synthesized ZnFe₂O₄ compounds.

Calcination Conditions		Chemical Composition, at. %
Time τ, h	Temp. T, °C	Zn	Fe	O
1	400	14.2792	28.57128	57.14952
1	450	14.22281	28.49077	57.28641
1	500	14.26083	28.57845	57.16072
2	500	14.30297	28.5582	57.13883
3	500	14.25965	28.5409	57.19945
4	500	14.27144	28.50211	57.22645
5	500	14.20987	28.49205	57.29809
1	800	14.23474	28.51646	57.2488

).

2.4. Solid-State Method

To obtain the target product, iron(III) and zinc(II) oxides were mixed in the required molar ratio, followed by sample preparation in a planetary ball mill. The precursor was then subjected to thermal treatment in a muffle furnace under various temperature regimes. The process of obtaining zinc ferrite-based compounds is schematically illustrated in Figure 2.

2.5. Characterization Methods

X-ray phase analysis of the washed synthesized compounds was performed using a Shimadzu XRD 6000 diffractometer (Shimadzu Corporation, Kyoto, Japan) with Cu Kα radiation. The X-ray diffraction patterns were recorded with a step of 0.02° (2θ), and the signal accumulation time at each point was 1 s. One of the advantages of this diffractometer is its high-precision vertical goniometer, which has a maximum rotation speed of 1000° per minute and an angle reproducibility of 2Θ ±0.001°. It also features a highly stable X-ray generator, which maintains voltage and current deviations within ±0.01%.

Additionally, a multifunctional X-ray diffractometer, Rigaku MiniFlex 600 (Cu K_α radiation), equipped with SmartLab Studio II software (ver. 4.1, RIGAKU, Tokyo, Japan), was used. This versatile instrument is designed for qualitative and quantitative phase analysis of polycrystalline materials. The graphite monochromator, combined with a standard scintillation counter, enhances sensitivity by optimizing the signal-to-background ratio. The software allows for determining crystallite sizes, assessing lattice distortion levels, refining lattice parameters, and conducting structure refinement using the Rietveld method. Phase identification was carried out using databases from ICDD, PDF-4+ 2021.

To determine the elemental chemical composition of the washed materials, concentrated nitric acid (purity 99.00%, NevaReaktiv, St. Petersburg, Russia) and hydrochloric acid (purity 99.00%, NevaReaktiv, St. Petersburg, Russia) were used, along with high-purity argon gas (purity 99.9999%, Belife Gas, St. Petersburg, Russia) and deionized water (18 MΩ·cm). A multi-element standard solution, Multi-element ICP-MS Calibration STD-No. 1 (Perkin Elmer, New Haven, CT, USA), was employed for instrument calibration, along with the multi-element standard solution IV-STOK-21 (Inorganic Ventures, Christiansburg, VA, USA), which has a mass concentration of the analyzed elements of 10 mg/dm³ and an error not exceeding 0.5% at a confidence level of 0.95 for constructing calibration characteristics. A 2% HNO₃ solution was used as the background solution for diluting the samples.

Sample weighing was carried out using analytical balances of the Acculab Atilon ATL-220 d 4-I type (“Acculab”, Westfield, NJ, USA) with a precision of 0.0001 g and an accuracy of no more than ±0.01 mg.

The acid digestion of the samples was conducted using an LH-302 heating plate (LOIP, St. Petersburg, Russia) with a glass-ceramic working surface and a maximum heating temperature of 375 °C. Auxiliary equipment included a water purification system Milli-Q^® IQ 7000 (Millipore, Billerica, MA, USA), an acid purification system BSB 939-IR (Berghoff, Eningen unter Achalm, Germany), a graduated cylinder with a scale (N-1-800 mL), polypropylene test tubes (“Handy park”) with capacities of 15 and 50 cm³, and a test tube rack with 20 and 60 slots. For solution dilution, single-channel mechanical dispensers with capacities of 20, 50, 100, and 200 µL from Biohit Proline Plus (Biohit Oyj, Kajaani, Finland) were used, with an accuracy of ±0.6/±0.5/±0.5/and ±0.4%, respectively. Measurements were performed using an ELAN 9000 DRC-e mass spectrometer (Perkin Elmer, Shelton, CT, USA) with inductively coupled argon plasma in a closed cooling system, with sample introduction via a peristaltic pump and AS-93+ autosampler.

The identification of the obtained zinc ferrite samples was conducted using infrared spectroscopy. The IR absorption spectra of the zinc ferrite samples in KBr pellets (produced by Specac Ltd., Orpington, UK, medium for IR spectroscopy) were recorded on a single-beam Fourier-transform infrared spectrophotometer, IRTracer-100 (Shimadzu Corporation, Kyoto, Japan), over the wavenumber range of 4000–400 cm⁻¹ range at room temperature.

The specific surface area of the synthesized calcined washed materials (S_er) was determined using the Brunauer–Emmett–Teller (BET) method based on nitrogen adsorption/desorption isotherms on a TriStar II 3020 specific surface area analyzer (Micromeritics Instrument Corporation, Norcross, GA, USA). A weighed sample was placed in an adsorber using analytical balances with a precision of 0.0001 g (AB-210A, Sartorius, St. Petersburg, Russia) and an accuracy of ±0.05 mg. The adsorber containing the sample was then placed in a VacPrep 061 degasser (Micromeritics Instrument Corporation, Norcross, GA, USA). The degassing process was conducted at a temperature of 250 °C for 24 h under vacuum (using an RV5 Edwards pump, Edwards Vacuum, Burgess Hill, UK). Afterwards, the adsorber with the sample was purged with inert gas, having first cooled it to room temperature. High-purity nitrogen gas (99.999%, PGS-SERVICE, St. Petersburg, Russia) was used as the inert gas. Finally, the adsorber with the sample was placed in the TriStar II 3020 analyzer to measure the specific surface area.

Differential thermal (DTA) and thermogravimetric (TG) analyses were conducted using a NETZSCH STA 409 PC/PG system (NETZSCH-Gerätebau GmbH, Selb, Germany). This synchronous thermal analysis instrument allows for simultaneous measurements of mass changes and thermal effects over a temperature range from 20 to 1500 °C.

Scanning electron microscopy (SEM) on a Carl Zeiss ULTRA 55 Plus instrument (Carl Zeiss Microscopy GmbH, Oberkochen, Germany) was used to obtain images of the surface of the material under study. To determine the elemental composition of the samples, we used energy dispersive spectroscopy (EDS) using an attachment to an Oxford X Max 80 electron microscope (Oxford Instruments, Abingdon, UK).

2.6. Study on Electrophysical Characteristics

The electrophysical characteristics of the investigated material were studied using impedance spectroscopy with a high-precision impedance analyzer, Matrix MCR-9010 (MATRIX TECHNOLOGY INC., Beijing, China). This analytical method involves measuring the flow of alternating electric current through the sample and subsequently determining its complex resistance (impedance magnitude |Z|) and phase shift angle φ as a function of the measuring field frequency. From the obtained data, the real part of the impedance Z′(f) = |Z|cos(φ) and the imaginary part Z″(f) = |Z|sin(φ) are calculated.

The main objective of the analysis is to find an equivalent circuit model whose impedance closely simulates the experimental data (impedance spectra of the investigated samples). This means that individual elements of the circuit or a combination of elements can be correlated with the intrinsic conductivity and polarization of both the sample itself and its surface at the phase boundaries.

Measurements of impedance |Z| and phase shift angle φ are conducted after applying electrodes to the surfaces of the studied materials. Silver paste was used for electrode applications. A thin layer of silver was deposited on the samples, allowing them to be treated as flat capacitors. The readings of the complex impedance (Z*) were recorded over a frequency range of 10 Hz to 10⁷ Hz.

Data analysis was performed using the EIS Spectrum Analyser software (ver. 1.0 Physico-Chemical Research Institute, Belarusian State University). EIS Spectrum Analyser is a standalone program for analysis and simulation of impedance spectra. This standalone program has been adapted to solve a wide range of tasks in the common (stationary) impedance spectroscopy. In addition to data fitting to equivalent circuits with resistors, capacitors, inductors, constant phase, Warburg (3 types), user-defined and Gerischer elements, the EIS Spectrum Analyser provides various tests for data consistency and quality of fit. It has also a built-in impedance spectra simulation routine, tools for impedance data processing (subtraction of circuit elements and subcircuits, normalisation for electrode surface area) and plotting in various formats.

3. Results and Discussion

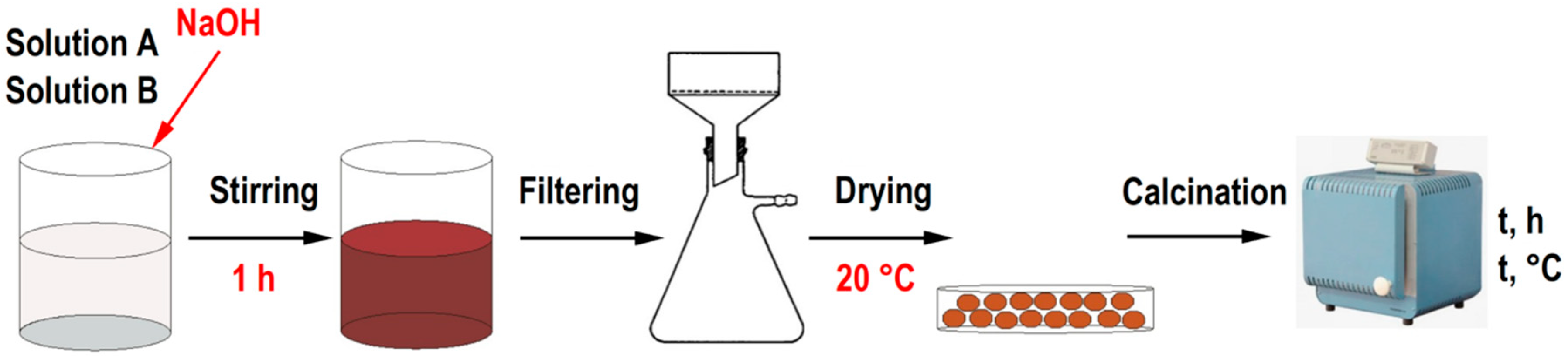
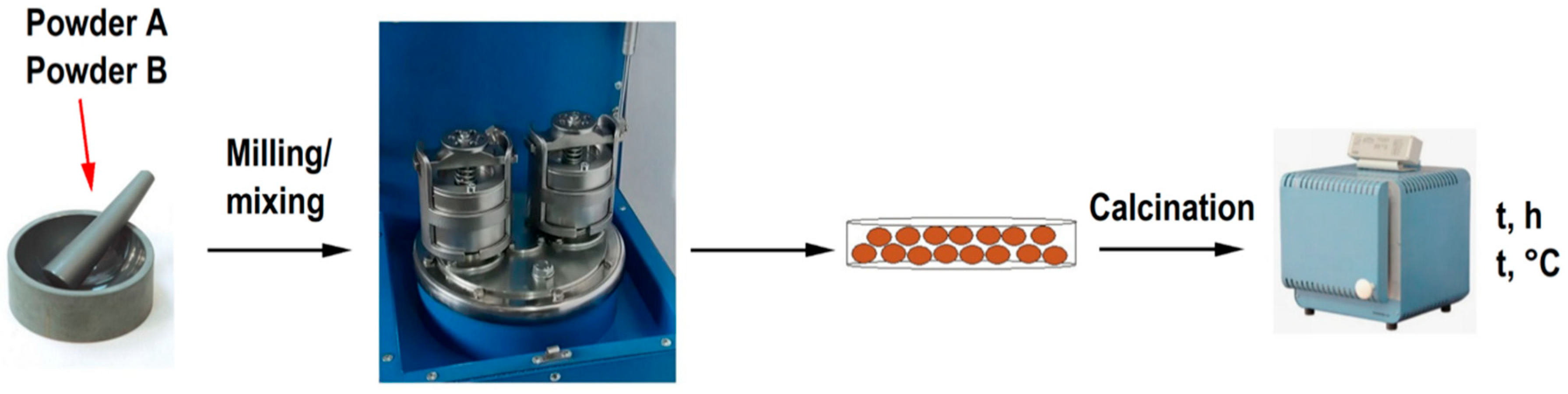
3.1. Combined Co-Precipitation and Solid-State Method

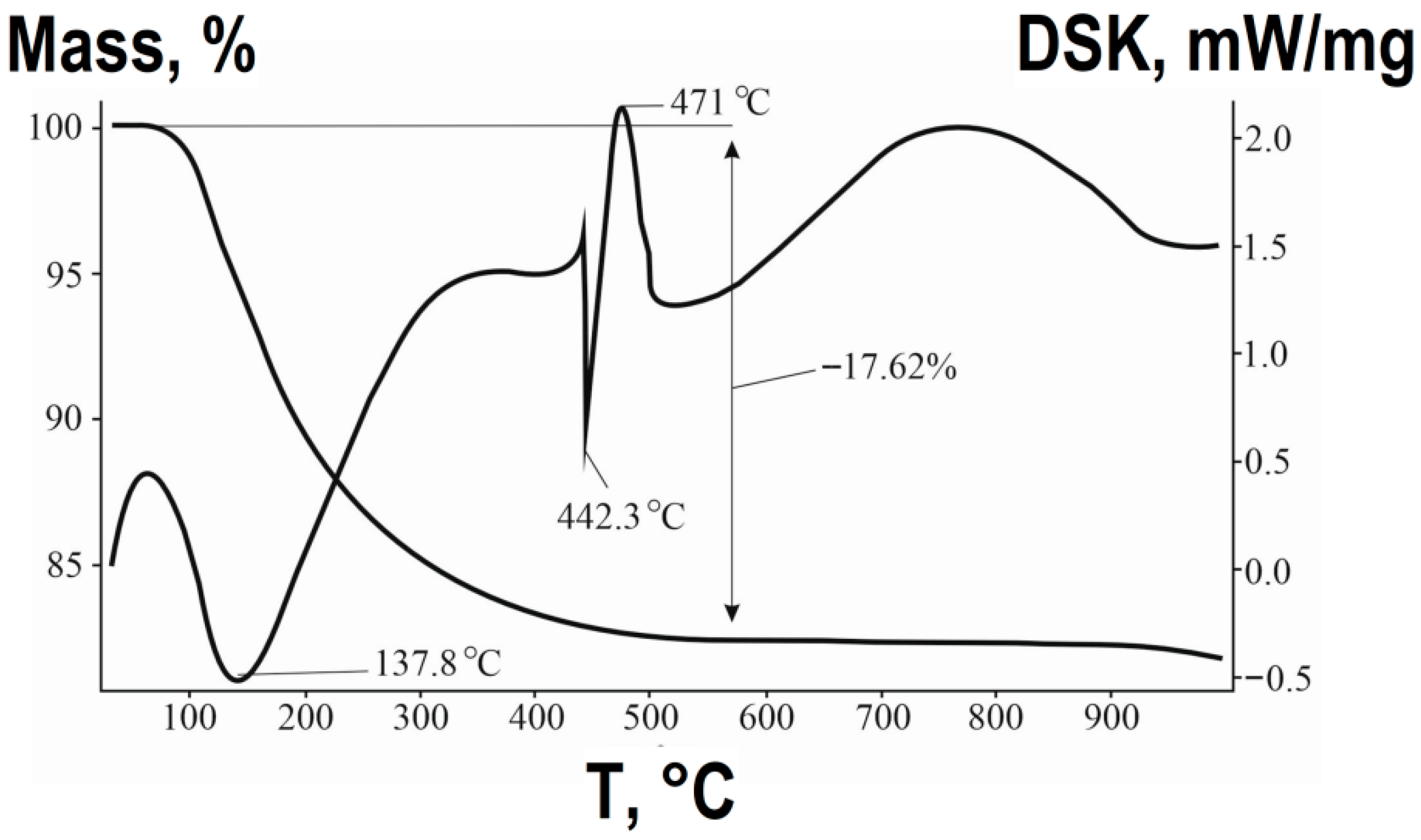
Before thermal treatment of the samples, DTA and TG studies of the synthesized air-dry precursor were conducted, and the results are presented in Figure 3.

Based on the TG-DTA results (Figure 3), the chemical transformation during the synthesis of ZnFe₂O₄ via the combined method can be described by a multi-step process. The significant mass loss (~20–25%) observed up to approximately 400 °C is primarily attributed to the removal of water molecules. This process involves two main stages:

The initial endothermic effect is associated with the evaporation of residual adsorbed water from the highly developed surface of the precursor gel and the decomposition of aqua complexes [Fe(H₂O)₆]³⁺ and [Zn(H₂O)₆]²⁺, leading to the formation of amorphous hydroxides (~30–150 °C).

The subsequent mass loss corresponds to the endothermic decomposition of the precipitated hydroxides (FeOOH and Zn(OH)₂) (~150–440 °C). This stage involves the condensation and removal of structural hydroxyl groups (dehydroxylation), resulting in the formation of amorphous iron and zinc oxides:

$$\mathbf{2}\mathit{F}\mathit{e}\mathit{O}\mathit{O}\mathit{H}\to {\mathit{F}\mathit{e}}_{\mathbf{2}}{\mathit{O}}_{\mathbf{3}}+{\mathit{H}}_{\mathbf{2}}\mathit{O} \left(\mathrm{endothermic}\right)$$

$$\mathit{Z}\mathit{n}{\left(\mathit{O}\mathit{H}\right)}_{\mathbf{2}}\to \mathit{Z}\mathit{n}\mathit{O}+{\mathit{H}}_{\mathbf{2}}\mathit{O} \left(\mathrm{endothermic}\right)$$

The formation of the target spinel phase occurs in the temperature range of 440–470 °C, as evidenced by the distinct exothermic effect on the DTA curve, which is not accompanied by a significant mass change. This effect corresponds to the solid-state reaction between the newly formed ZnO and Fe₂O₃ nanoparticles, leading to the crystallization of the zinc ferrite phase:

$$\mathit{Z}\mathit{n}\mathit{O}+{\mathit{F}\mathit{e}}_{\mathbf{2}}{\mathit{O}}_{\mathbf{3}}\to \mathit{Z}\mathit{n}{\mathit{F}\mathit{e}}_{\mathbf{2}}{\mathit{O}}_{\mathbf{4}} (\mathrm{exothermic}, \mathrm{crystallization})$$

The high reactivity of the nanoscale oxides, obtained from the molecularly mixed precursor, allows this reaction to proceed at a significantly lower temperature compared to the classical ceramic method.

The thermal treatment of samples, in investigating the conditions for the formation of the target phase obtained through the combined approach, was conducted at various temperatures. The influence of the time factor on the formation and physical parameters of zinc ferrite compounds was also studied (see Figure 4 and Table 1). To economically optimize the synthesis conditions, research was conducted on the potential reduction in the temperature required for obtaining the target phase.

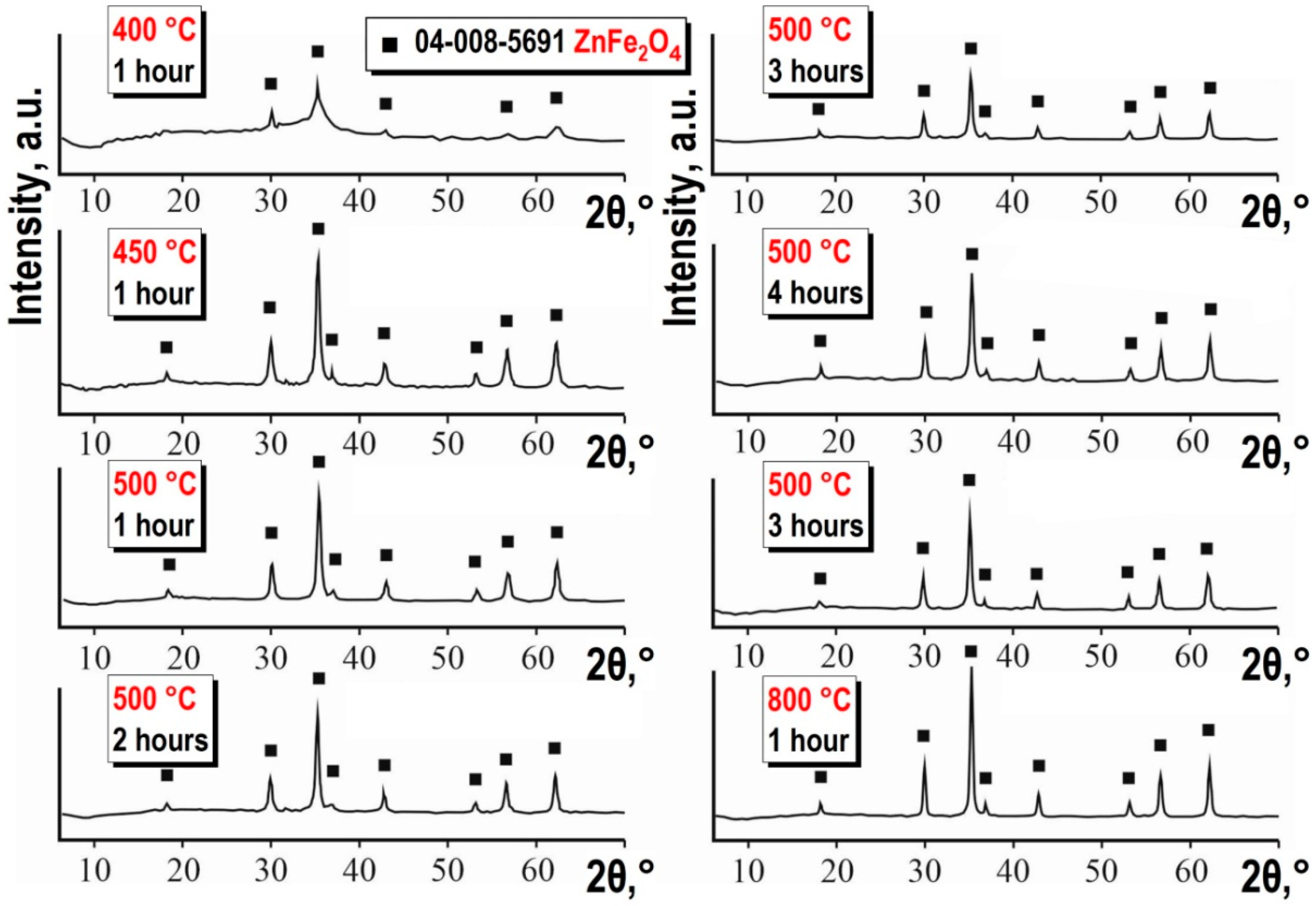
From the X-ray diffraction patterns (see Figure 4), it is evident that thermal treatment of the precursor at 400 °C for 1 h results in the formation of an amorphous phase of ZnFe₂O₄. Clearly, these synthesis conditions do not adequately facilitate the crystallization processes of zinc ferrite, as confirmed by the DTA data (see Figure 3). Increasing the temperature of the process for obtaining the target product promotes the formation of ZnFe₂O₄ phases with well-defined crystallinity (see Figure 4), starting from 450 °C. Both the increase in calcination temperature and duration do not affect the phase composition of the synthesized product (see Figure 4). Raising the temperature to 800 °C results in sharper and well-resolved reflections (see Figure 4).

Table 2. Texture characteristics of ZnFe₂O₄ samples obtained via combined method.

Calcination Conditions		Texture Properties
Temp. T, °C	Time τ, h	Surface Area ABET, m2/g	Average Particle Size D, nm
400	1	106.16	4.8 ± 1
450	1	54.41	17.9 ± 1.8
500	1	44.82	25.9 ± 0.4
800	1	19.97	45.9 ± 0.8

and Figure 5 present the specific surface area values for the indicated sample compositions, determined by the BET method based on nitrogen adsorption/desorption isotherms using the TriStar II 3020 specific surface area analyzer.

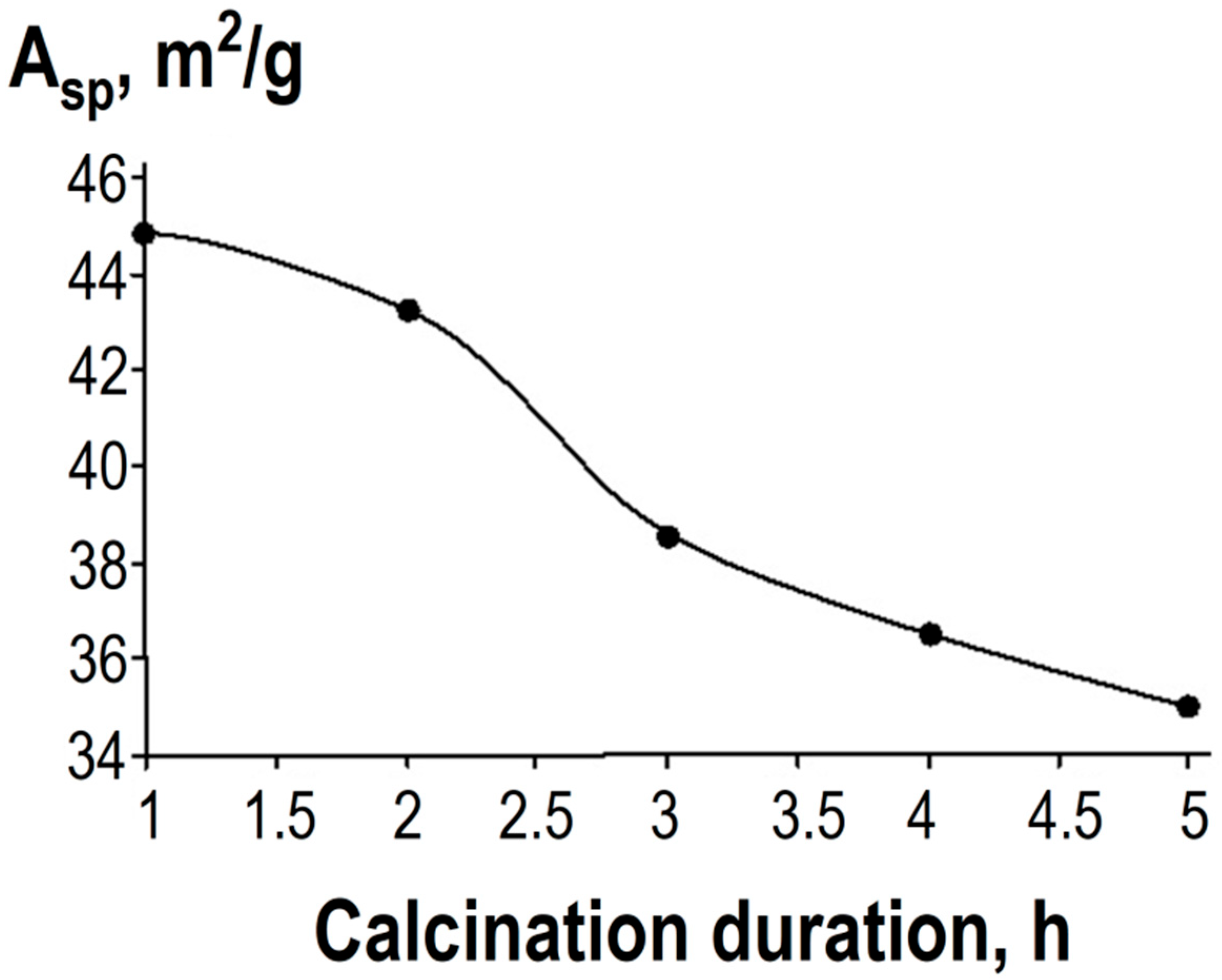
It is evident that reducing the synthesis temperature of the target product (see Table 2) facilitates the formation of nanosized compounds with a more developed specific surface area—the specific surface area increases by 2.7 times when comparing the parameters of samples calcined at 450 °C and 800 °C. Additionally, it was experimentally found that increasing the duration of thermal treatment leads to a decrease in specific surface area due to the agglomeration of product particles (see Figure 5)—the specific surface area decreases by 1.3 times when comparing the parameters of samples calcined at 500 °C for varying durations.

To validate the results of the X-ray phase analysis, a chemical analysis of the obtained zinc ferrite compounds was conducted, the results of which confirm the formation of the target phase (see

Table 3. Parameters of the elementary cell of the crystal lattice of ZnFe₂O₄ samples synthesized at various temperatures.

Tsyn, °C	a, Ǻ	α, °	V, Ǻ3	Space Group	Rwp, %
800	8.44324	90	601.904	$\mathrm{F}\mathrm{d}\overline{3}\mathrm{m}$	1.51
900	8.44332	90	601.922	$\mathrm{F}\mathrm{d}\overline{3}\mathrm{m}$	1.77
1000	8.44351	90	601.962	$\mathrm{F}\mathrm{d}\overline{3}\mathrm{m}$	1.83

).

3.2. Solid-State Method

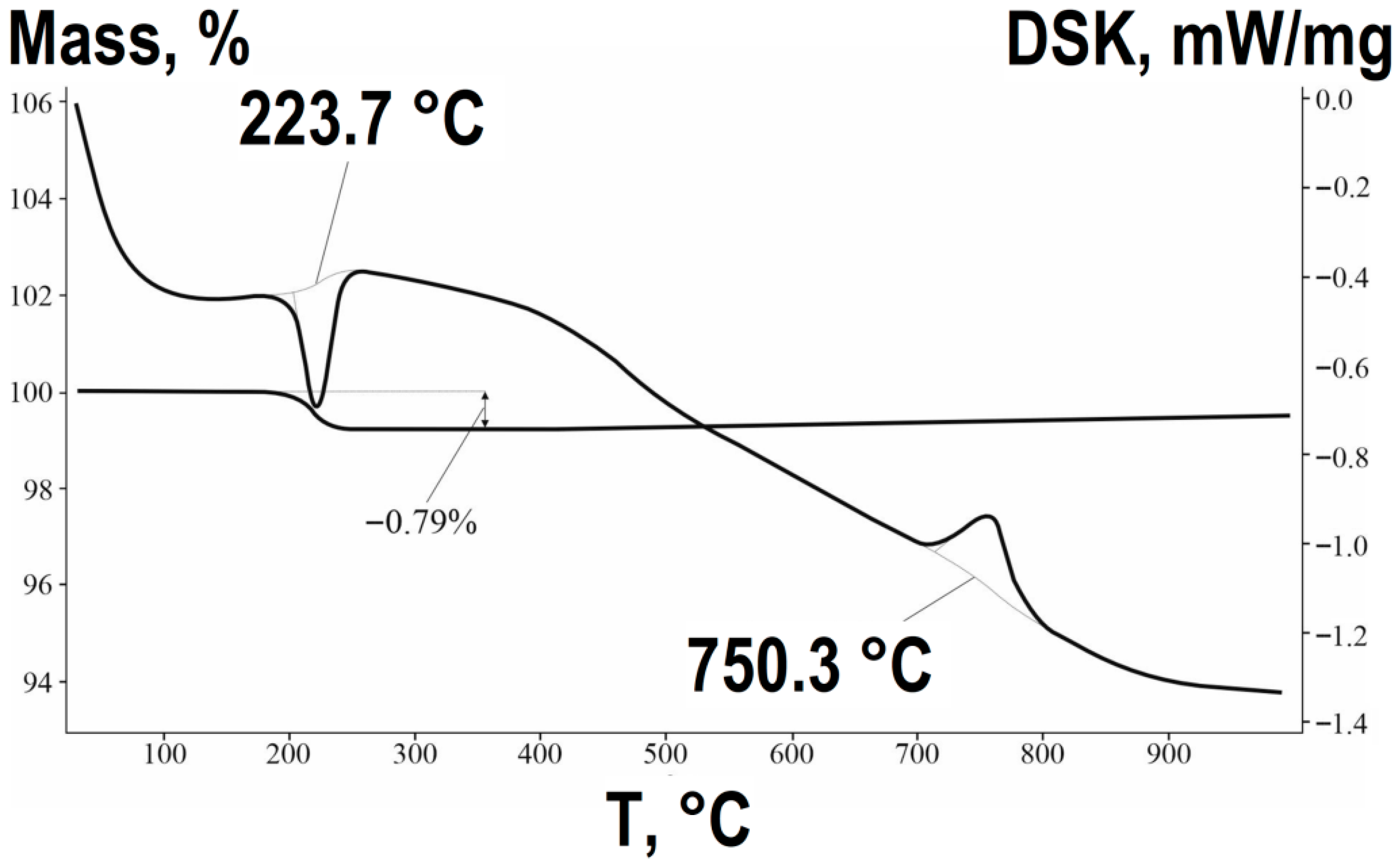
The TG-DTA analysis for the solid-state method (Figure 6) reveals a fundamentally different and much simpler process. The slight mass loss (~0.79%) and the corresponding endothermic effect in the range of 198–225 °C are associated solely with the removal of moisture adsorbed by the oxide powder mixture from the atmosphere. The key chemical transformation is the direct solid-state reaction between micron-sized ZnO and Fe₂O₃ particles, which initiates at temperatures above ~700 °C. The sharp exothermic peak at 715–750 °C, without any associated mass loss, marks the crystallization and formation of the well-defined ZnFe₂O₄ spinel structure according to the reaction:

$$\mathit{Z}\mathit{n}\mathit{O}+{\mathit{F}\mathit{e}}_{\mathbf{2}}{\mathit{O}}_{\mathbf{3}}\to \mathit{Z}\mathit{n}{\mathit{F}\mathit{e}}_{\mathbf{2}}{\mathit{O}}_{\mathbf{4}} (\mathrm{exothermic}, \mathrm{crystallization})$$

The high temperature required for this single-step reaction is characteristic of the classical ceramic method, where diffusion between solid oxide particles is the rate-limiting step.

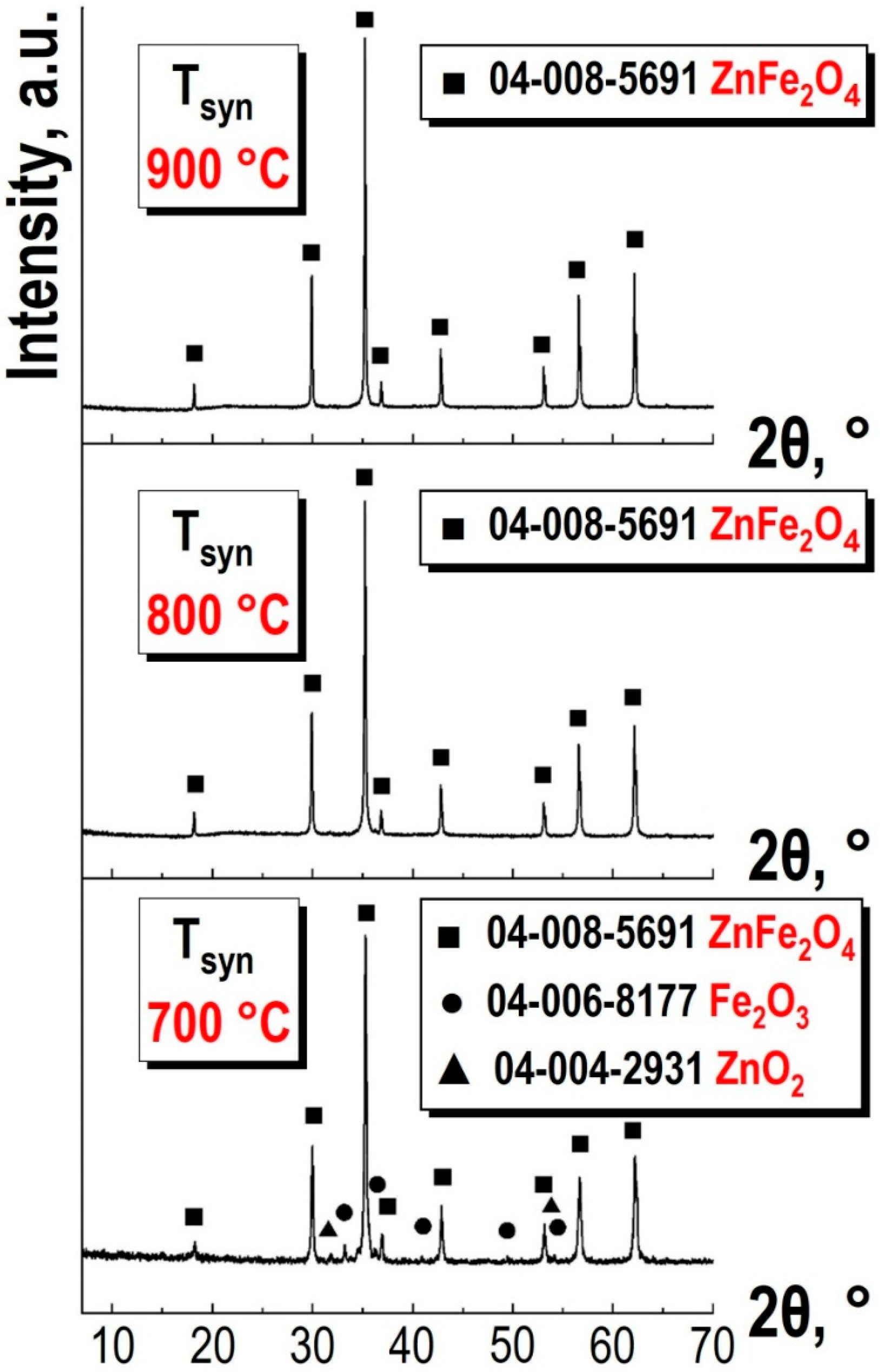
Figure 7 presents the results of X-ray phase analysis for samples of spinel ferrite ZnFe₂O₄ synthesized at various temperatures (the synthesis temperatures are indicated in the figure).

At a synthesis temperature of 700 °C, a monophasic product is not formed. The sample contains iron and zinc oxides: 6% Fe₂O₃ and 4% ZnO. Increasing the temperature to 800 °C results in the formation of the target product—spinel ferrite ZnFe₂O₄—which correlates with the DTA results (see Figure 6). Further increasing the synthesis temperature to 900 °C causes the lines in the X-ray diffraction spectrum to become sharper and better resolved compared to the sample obtained at 800 °C.

The results of the X-ray structural analysis are presented in Table 3. As can be seen from the data presented in Table 3, increasing the synthesis temperature has little effect on the parameters of the elementary cell of the crystal lattice.

A comprehensive SEM analysis of the materials synthesized via different methods (Figure 8) revealed distinctive morphological characteristics and microstructural features across varying synthesis conditions. The surface morphology examination demonstrated a systematic evolution of structural organization at the microscale level.

The conventional solid-state synthesis route yielded notable changes in particle morphology with increasing temperature. Initial stages showed loosely packed quasi-spherical agglomerates with distinct particle boundaries and minimal coalescence. As the synthesis temperature increased, progressive particle growth and agglomeration became evident, ultimately leading to the formation of virtually monolithic ceramics with well-defined grain boundaries and advanced sintering features (Figure 8a–c).

In contrast, the combined synthesis approach (Figure 8d) resulted in markedly different microstructural characteristics. This method produced ceramics with significantly finer morphology, exhibiting substantially smaller agglomerate sizes and more uniform particle distribution. The observed difference in microstructural development can be attributed to the modified synthesis pathway, which effectively controlled particle growth and agglomeration processes.

EDS mapping analysis provided additional insights into the spatial distribution of constituent elements. The color-coded elemental maps revealed homogeneous distribution of Zn, Fe, and O throughout the analyzed areas, confirming uniform phase composition across all samples. This compositional uniformity suggests successful formation of the desired phase structure, regardless of the synthesis method employed.

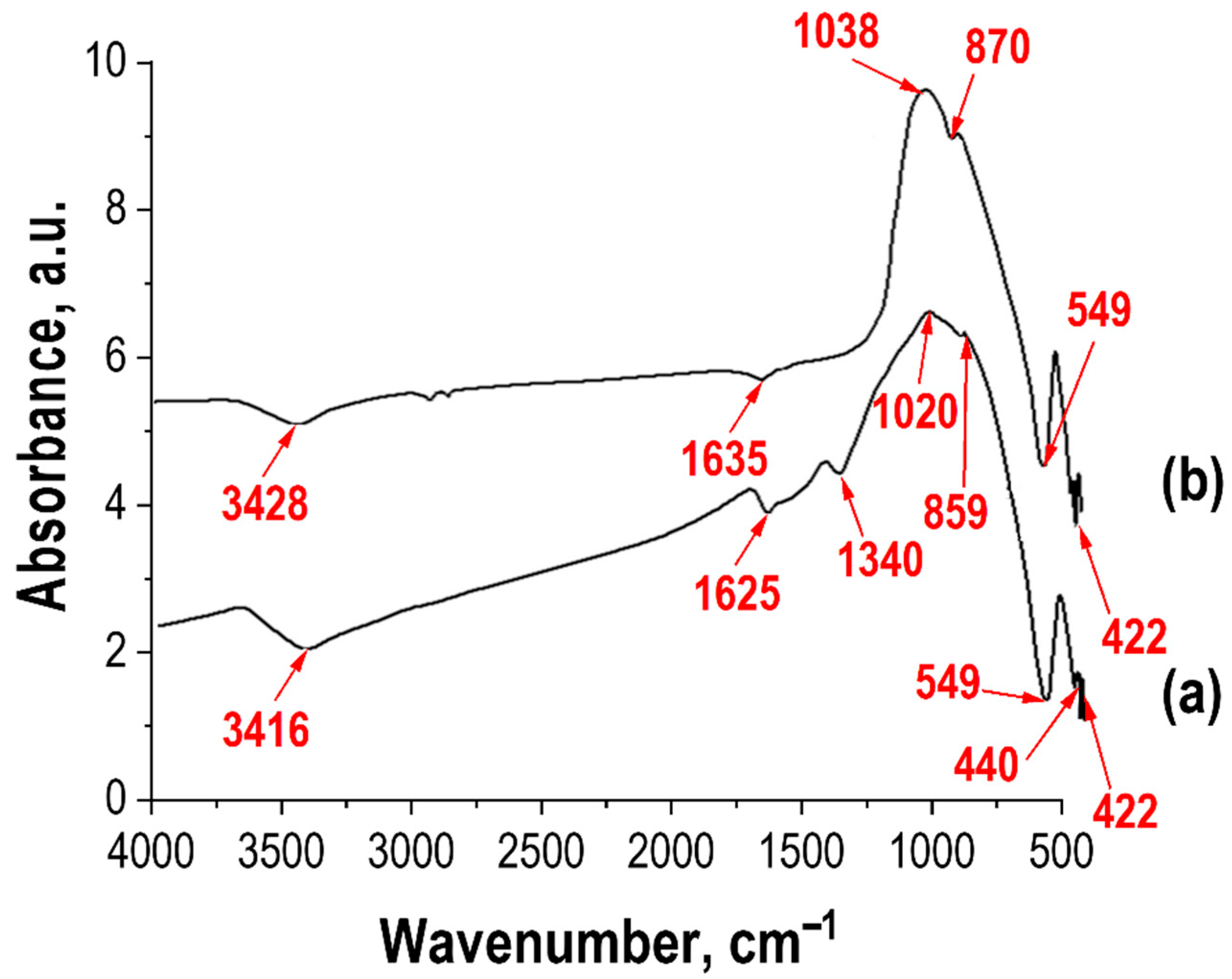
Fourier-transform infrared (FTIR) spectra can be used to determine the crystalline structure and molecular composition of the synthesized zinc ferrite compounds. FTIR studies were conducted on two synthesized samples using different approaches (see Figure 9). The analysis data (Figure 9) show that strong absorption peaks appear in the range of 500–1630 cm⁻¹. The shape of the curves is identical, which may indicate similarity in their compositions. Broad absorption band in the range of 3627–3500 cm⁻¹ (see Figure 9) corresponds to the contribution from hydroxyl ions (OH) [33,34,35,36]. The presence of this band indicates the high surface activity of the ferrite microparticles, which is associated with the presence of broken bonds and, consequently, a high probability of adsorption by hydroxyl ions (OH)⁻ and H⁺ active hydroxyl groups.

The absorption band near ~1630 cm⁻¹ corresponds to the bending vibrations δ(OH), while the absorption bands at ~859–870 cm⁻¹ and ~1020–1038 cm⁻¹ (see Figure 9) are associated with the bending vibrations of the Zn–O–H and Fe–O–H bonds, respectively. For all ferrite compositions, broad absorption bands are observed in the spectral range from 50 to 1000 cm⁻¹ (see Figure 9), which are associated with lattice vibrations of the Fe–O and Zn–O bonds [36,37,38]. The absorption peak near ~550 cm⁻¹ is characterized by the vibrations of the Fe–O–Zn bonds. Additionally, for the sample synthesized from solutions (see Figure 9), absorption bands are observed in the region of 1350 cm⁻¹, which may be attributed not only to the presence of hydroxyl groups but also to adsorbed forms of O₂ and CO₂ due to the developed surface [39].

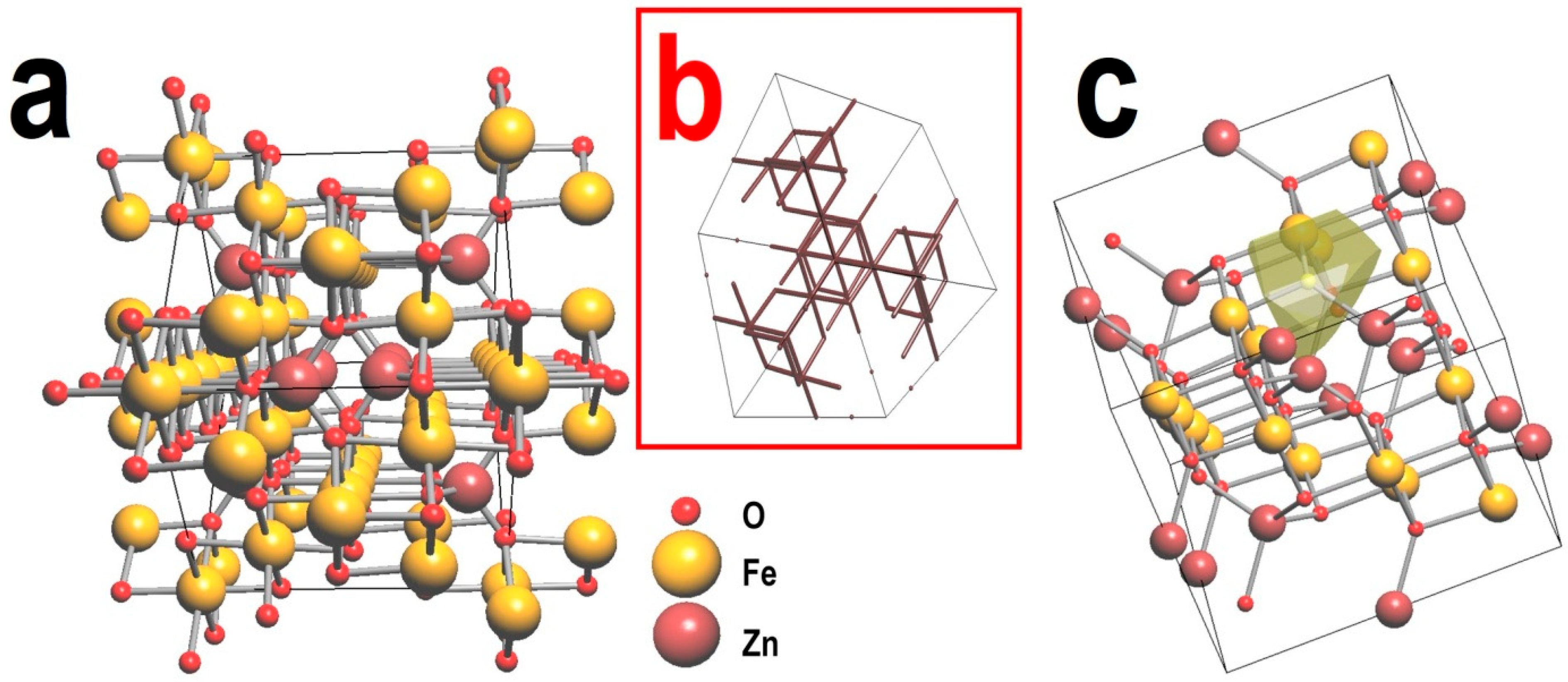
Absorption bands in the range of ~420–440 cm⁻¹ (see Figure 9) are related to the vibrations of the Fe–O bonds [40,41,42]. To investigate the potential ionic conductivity of zinc cations, a crystallochemical analysis methodology was employed using the ToposPro software package [43]. The “free space” within the crystal lattice (see Figure 10) contains a network of cavities and channels that are geometrically accessible for mobile ions, thus influencing the emergence of ionic conductivity. This study is based on a geometrical-topological (GT) approach, which involves partitioning the crystal space into convex polyhedra, specifically Voronoi polyhedra, which serve as geometric representations of the positions of atoms or cavities within the crystal structure [44]. A Voronoi polyhedron represents a region of crystal space where planes intersect at the midpoint of contact between a target ion and neighboring ions (see Figure 10). Each ion within the structure corresponds to its unique Voronoi polyhedron, while the overall structure can be comprehensively represented by the complete set of polyhedra that collectively occupy the crystal space [44].

The vertices of the Voronoi polyhedra corresponding to the positions of the atoms represent the centroids of fundamental vacancies in the structure. The edges between these vertices denote elementary pathways connecting such vacancies. These vacancies and pathways are characterized by corresponding radii, denoted as R_sd and r_chan. The calculation of R_sd involves determining the radius of a sphere whose volume is equal to the volume of the Voronoi polyhedron generated from all atomic positions within the structure. Conversely, r_chan is calculated as the radius of the circle inscribed around the edge of the Voronoi polyhedron, representing atomic positions, where all constituent atoms along the trajectory are located on the specified circle.

Fundamental vacancies and pathways are accessible for ionic migration provided that their radii meet specific criteria:

$$R_{sd}\ge R_{sd}\left(min\right)$$

(1)

$$r_{chan}\ge r_{chan}\left(min\right)$$

(2)

The minimum radial separation distances, denoted as R_sd(min), are presented in tabular form and are typically provided for various ions in reference materials [45]. Conversely, the minimum channel radius r_chan(min) is calculated by combining the ionic radii of both the working ion (r_wi) and the surrounding ion (r_env) with a deformation coefficient (γ). This calculation takes into account the potential polarizability or deformation of the working ion during its migration:

r_chan(min) = γ (r_wi + r_env)

(3)

The complete representation of voids and channels in the crystal structure is achieved when their sizes meet the conditions (9) and (10). Notably, if this migration map demonstrates infinite periodicity in any direction, whether one-dimensional, two-dimensional, or three-dimensional—it indicates that the underlying crystal structure possesses the necessary prerequisites for facilitating ionic conductivity.

Using the ToposPro software, the crystal structure of ZnFe₂O₄ was analyzed for its capability to support ionic conductivity of Zn²⁺ cations (see Figure 10). The parameters for the analysis were selected based on literature data [45]: Zn²⁺ (r_wi = 0.83 Å), R_sd(min) = 1.20, r_chan(min) = 1.60, γ = 0.80. The calculations revealed that the crystal structure of zinc ferrite contains 3D channels for facilitating ionic conductivity of Zn²⁺ cations (see Figure 10).

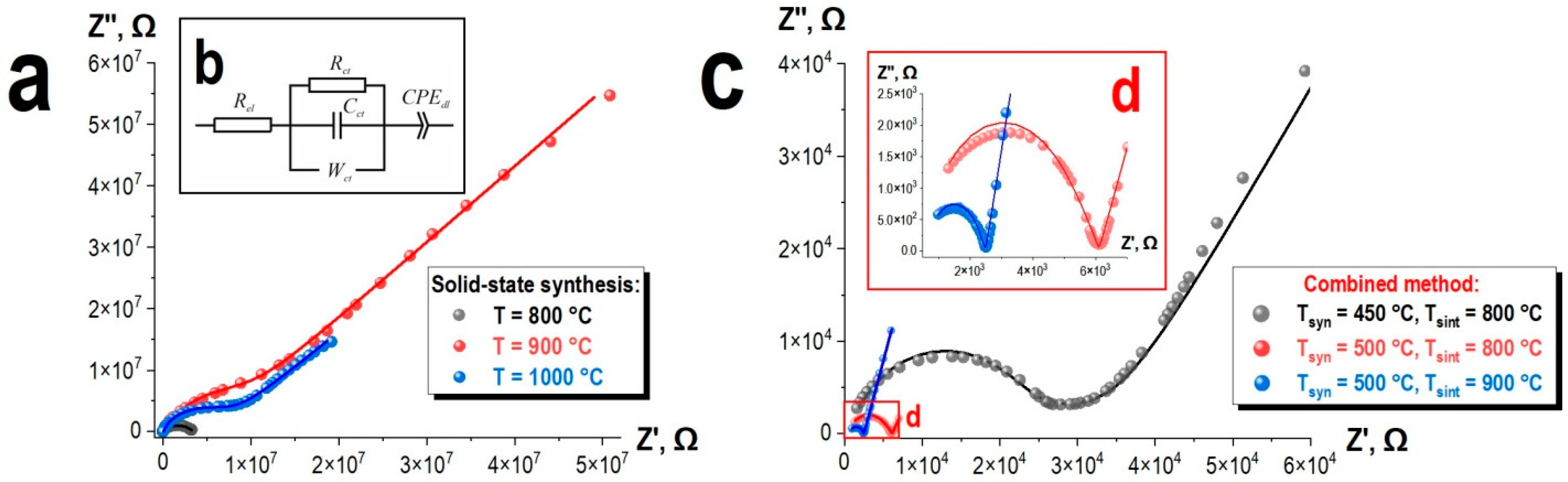
Based on the results of the TG analysis, electrophysical studies were conducted on the synthesized zinc ferrites ZnFe₂O₄ with a spinel-type structure using impedance spectroscopy. The complex impedance diagrams obtained at room temperature for the compound synthesized by the solid-state method at various temperatures are presented in Figure 11a.

The appearance of the diagrams for samples synthesized at temperatures of 900 °C and 1000 °C is similar (see Figure 11a), unlike the sample synthesized at 800 °C, which does not exhibit an inclined line in the low-frequency region (see Figure 11a). Diagram shapes for samples synthesized at temperatures of 900 °C and 1000 °C are characteristic of ionic conductors, where the low-frequency relaxation process indicates the formation of a double electric layer at the sample-electrode interface.

It is likely that for the sample synthesized at 800 °C, the absence of a low-frequency “tail” on the impedance diagram is related to its considerably higher resistance (compared to the samples obtained at 900 °C and 1000 °C), suggesting that such a low-frequency relaxation process should be observed at even lower frequencies. However, the Matrix MCR-9010 instrument has technical limitations, with a minimum accessible frequency of 10 Hz. Within the Maxwell–Wagner picture, interfacial (grain-boundary/electrode) polarization has a characteristic frequency f_c = 1/(2πR_iC_i). The larger resistance of this specimen shifts the corresponding relaxation below the experimental frequency window, while the bulk arc remains visible. This correlation rationalizes the impedance features without invoking a change in transport mechanism.

The overall equivalent circuit model for the samples synthesized by the solid-state method is depicted in Figure 11b. This model was chosen due to its alignment with the underlying physical mechanisms and its ability to accurately model the experimental Nyquist plots. The use of a Warburg element is a logical choice when considering the spectral data, as the initial part of the high-frequency range exhibits linearity within a limited interval, characteristic of diffusion-based processes. The resistance R_el characterizes electronic conductivity, while R_ct, C_ct, W_ct characterize the cathode material. The constant phase element CPE_dl is associated with the formation of a double electric layer, which appears as an inclined line on the impedance diagram (see Figure 11). For the sample synthesized at 800 °C, the CPE_dl element is absent. The impedance Nyquist plots were processed using the EIS Spectrum Analyser software to achieve the most accurate calculation of the parameters of the equivalent circuit model. The obtained impedance dependencies for the investigated samples are extrapolated to the real part of the impedance axis, i.e., in the limit as the frequency of the measuring field approaches zero. The results of such calculations are shown as a line. There is a good correlation between the calculated results and the measured data, with the results of the calculations presented in

Table 4. Parameters of the equivalent circuit model for ZnFe₂O₄ synthesized by the solid-state method.

Tsyn, °C	Cct, F	Rel, Ω	Rct, Ω	Wct, Ω∙s−0.5	CPEdl, F	ndl
800	8.14 × 10−12	350	3.48 × 107	4.62 × 108	-	-
900	2.72 × 10−11	511.11	5.23 × 106	2 × 1011	1.36 × 10−9	0.3
1000	8.71 × 10−12	4.8 × 10−1	6.55 × 105	1.62 × 109	3.19 × 10−9	0.55

.

Comparing the impedance diagrams presented in Figure 11, it is evident that increasing the synthesis temperature leads to an increase in the conductivity of the cathode material by almost two orders of magnitude. The values of the specific electronic and ionic conductivities are provided in

Table 5. Values of specific conductivity for ZnFe₂O₄ synthesized by the solid-state method.

Tsyn, °C	σel, S/cm	σct, S/cm
800	5.7 × 10−2	5.75 × 10−7
900	3.9 × 10−2	3.82 × 10−6
1000	41.6	3.05 × 10−5

.

The complex impedance diagrams obtained at room temperature for the compounds synthesized by the combined method are presented in Figure 11c. Their appearance is also characteristic of ionic conductors [46,47,48,49]. It is evident that the conductivity of the samples synthesized by the combined method (see Figure 12) has significantly increased compared to the samples obtained by the solid-state method (see Figure 11c,d). The shape of the Nyquist plots was also modeled using the equivalent circuit model shown in Figure 11b. The results of the calculations for the obtained data are presented in

Table 6. Parameters of the equivalent circuit model for ZnFe₂O₄ synthesized by the combined method.

Tsyn, °C	Tsint, °C	Cct, F	Rel, Ω	Rct, Ω	Wct, Ω∙s−0.5	CPEdl, F	ndl
450	800	9.99 × 10−11	72.73	36,242	4.07 × 107	1.54 × 10−6	0.62
500	800	9.23 × 10−11	499.8	5598	2.34 × 107	3.11 × 10−5	0.68
500	900	9.48 × 10−11	498.7	1994	6.21 × 108	3.01 × 10−6	0.8

and are shown in Figure 11c,d as lines.

For the samples obtained by the combined method, the same trend is observed as for the samples synthesized by the solid-state method. Increasing the synthesis temperature (from 450 °C to 500 °C) leads to an increase in conductivity by nearly an order of magnitude (see

Table 7. Values of the specific conductivity for the ZnFe₂O₄ samples synthesized by the combined method.

Tsyn, °C	Tsint, °C	σel, S/cm	σct, S/cm
450	800	0.27	5.52 × 10−4
500	800	0.04	3.57 × 10−3
500	900	0.04	1 × 10−2

). Additionally, raising the sintering temperature also results in an increase in conductivity (see Table 7).

Earlier, a research team conducted a study on zinc ferrite ZnFe₂O₄ with a spinel structure using density functional theory (DFT) [30]. The results of the quantum-chemical modeling of Zn²⁺ ionic conductivity in this compound indicated a theoretical ionic conductivity value of σ = 5 × 10⁻⁶ S/cm [30]. Our study has shown that the electrophysical properties of ZnFe₂O₄ vary depending on the synthesis conditions and methods. It was found that only two samples obtained by the solid-state method at T = 800 °C and 900 °C exhibited unsatisfactory conductivity (less than theoretical) and are unsuitable for use as cathode materials. However, both methods allow for the production of samples with significantly higher specific ionic conductivity.

Samples obtained by the combined method exhibit higher ionic conductivity compared to those produced by the solid-state method. This is attributed to the fact that synthesis using the sol–gel technique results in compounds with smaller particle sizes and a more developed specific surface area. Additionally, the sintering temperature of the ceramics also influences ionic conductivity—an increase in temperature leads to enhanced conductivity.

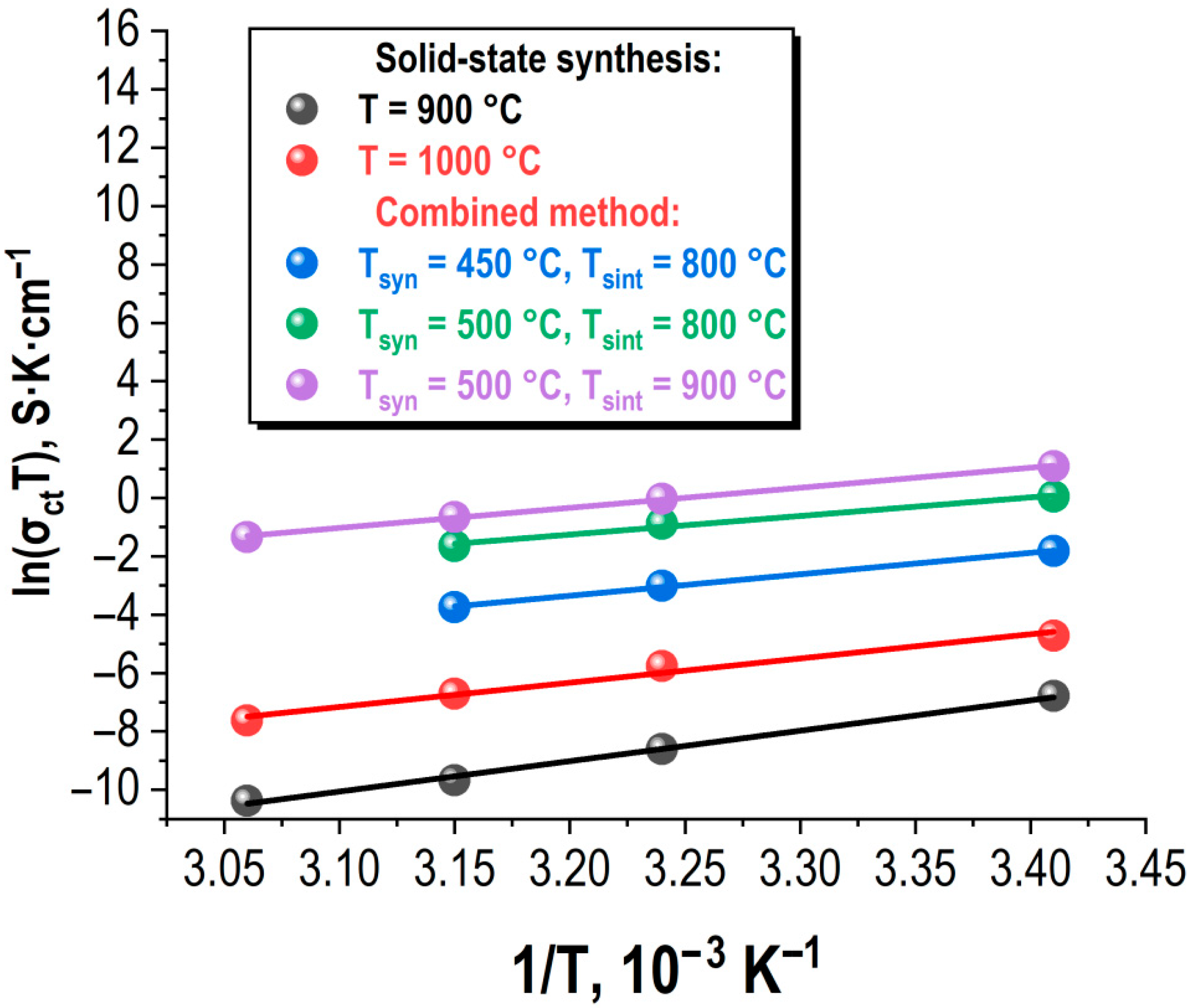
The conducted studies over a practically significant temperature range (20–55 °C) revealed that as the samples are heated, the specific ionic conductivity decreases (see Figure 12), regardless of the synthesis method and sintering conditions of the ceramics.

The studies were conducted in a stepwise heating mode, followed by stabilization and holding at a specified temperature. The obtained dependencies σ_ct(T) satisfy the Arrhenius law:

$${\sigma }_{ct}T=A_{0}exp\left({\displaystyle \frac{E_a}{kT}}\right)$$

(4)

where σ_ct is the static specific conductivity of the cathode material, A₀ is the pre-exponential factor, E_a is the activation energy, representing the effective height of the potential barrier that the cation must overcome to hop from a lattice site to a vacancy, k is the Boltzmann constant, and T is the temperature.

From the obtained dependencies, the values of the activation energy of charge carriers were determined, as indicated in Figure 12. The activation energy values for the compositions synthesized by various methods and under different conditions are similar and fall within the range of approximately 0.8 to 0.85 eV.

The temperature dependence of conductivity is attributed to ionic transport in spinel ZnFe₂O₄. The activation energies from Arrhenius fits (≈0.80–0.85 eV) fall in the typical range for vacancy-assisted ionic migration in ferrites, indicating that the governing mechanism remains unchanged across synthesis routes. Elemental analysis reveals a slight Zn deficiency (cation non-stoichiometry). In spinel oxides, such non-stoichiometry is commonly compensated by cation vacancies and/or by changes in cation distribution/valence to preserve charge neutrality; for ZnFe₂O₄ this may include vacancies on the Zn (A) sublattice and/or on octahedral (B) sites together with partial inversion.

4. Conclusions

Ceramic samples of spinel ferrite ZnFe₂O₄ were synthesized using two methods: a combined approach utilizing sol–gel technology with a solid-state finishing process and classical ceramic technology. The conditions under which the target product is formed were established based on the synthesis method: for the combined approach, the synthesis temperature (T_sint.) should be ≥450 °C for 1 h; for the classical ceramic technology, T_sint. should be ≥800 °C for 1 h.

X-ray diffraction analysis was used to determine the parameters of the elementary cell of the crystal lattice. It was found that the synthesis temperature does not significantly affect these parameters. The crystal structure of ZnFe₂O₄ was analyzed using the GT method for the potential ionic conductivity of the Zn cation, revealing a network of 3D conduction channels within the crystal structure of zinc ferrite.

Impedance spectroscopy was employed to investigate the electrophysical properties of the synthesized zinc ferrite (ZnFe₂O₄) with a spinel crystal structure. Values of specific electronic and ionic conductivity were determined. It was established that the electrophysical properties vary depending on the synthesis conditions and methods. Only two samples obtained via solid-state synthesis at temperatures of 800 °C and 900 °C exhibited unsatisfactory conductivity (below theoretical values) and are not suitable for use as cathode materials. However, both methods allow for the production of samples with significantly higher specific ionic conductivity than theoretical values, making them applicable as cathode materials for new types of batteries (MIBs). Samples produced by the combined method showed higher ionic conductivity compared to those synthesized via solid-state methods. This is attributed to the sol–gel synthesis, which results in compounds with smaller particle sizes and a more developed specific surface area. Additionally, the sintering temperature of the ceramics also affects ionic conductivity—higher temperatures lead to increased conductivity. The temperature dependence of specific ionic conductivity was investigated within a practically significant temperature range for cathode materials. It was found that as the temperature of the studied materials increases, the values of ionic conductivity decrease. The activation energy of charge carriers, specifically the zinc cation, was calculated.