Acoustic Emission During Failure of a Composite Under the von Mises Criterion with Local Structural Defects
Abstract
1. Introduction
2. Analysis
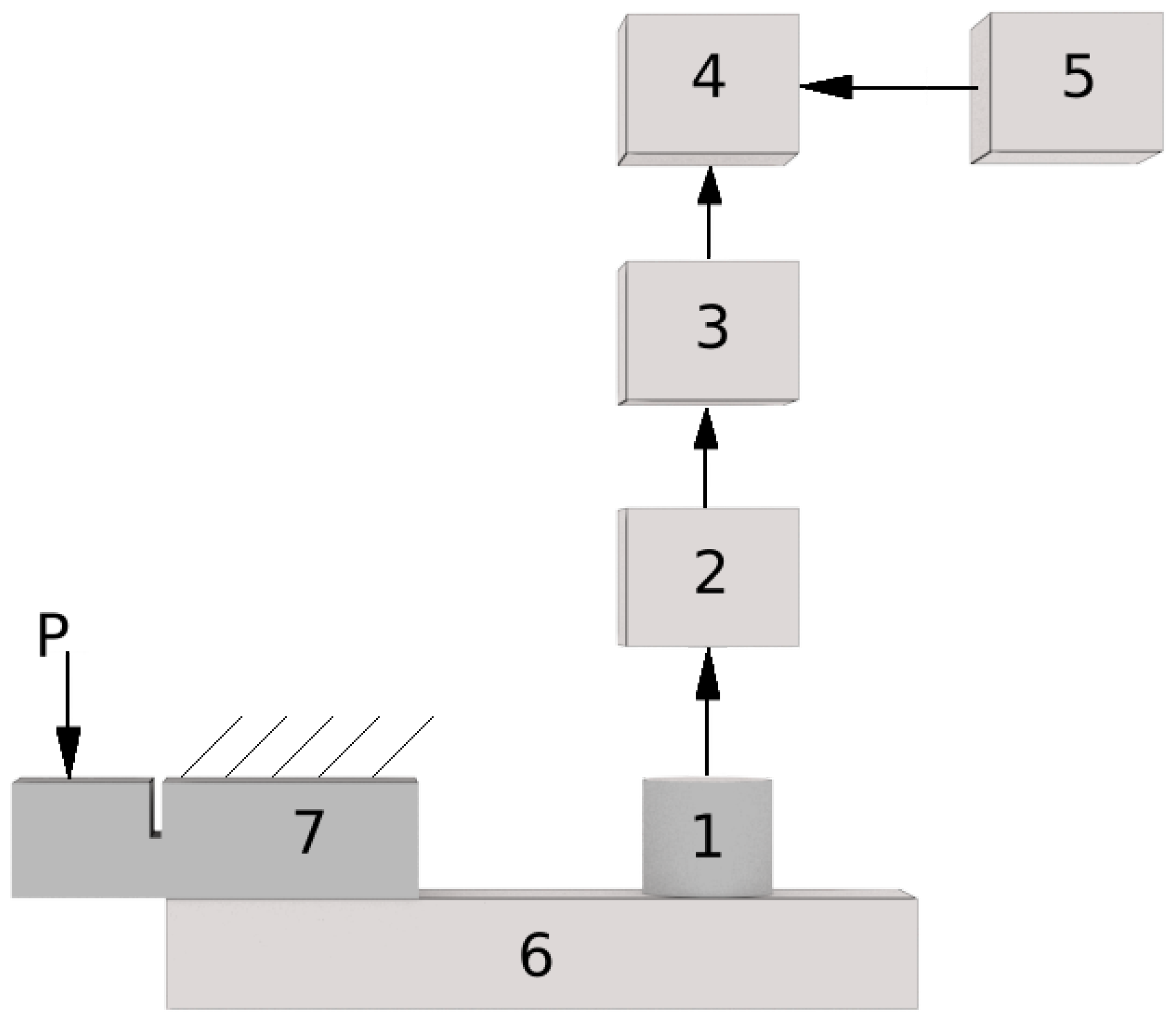
2.1. Simulation Conditions
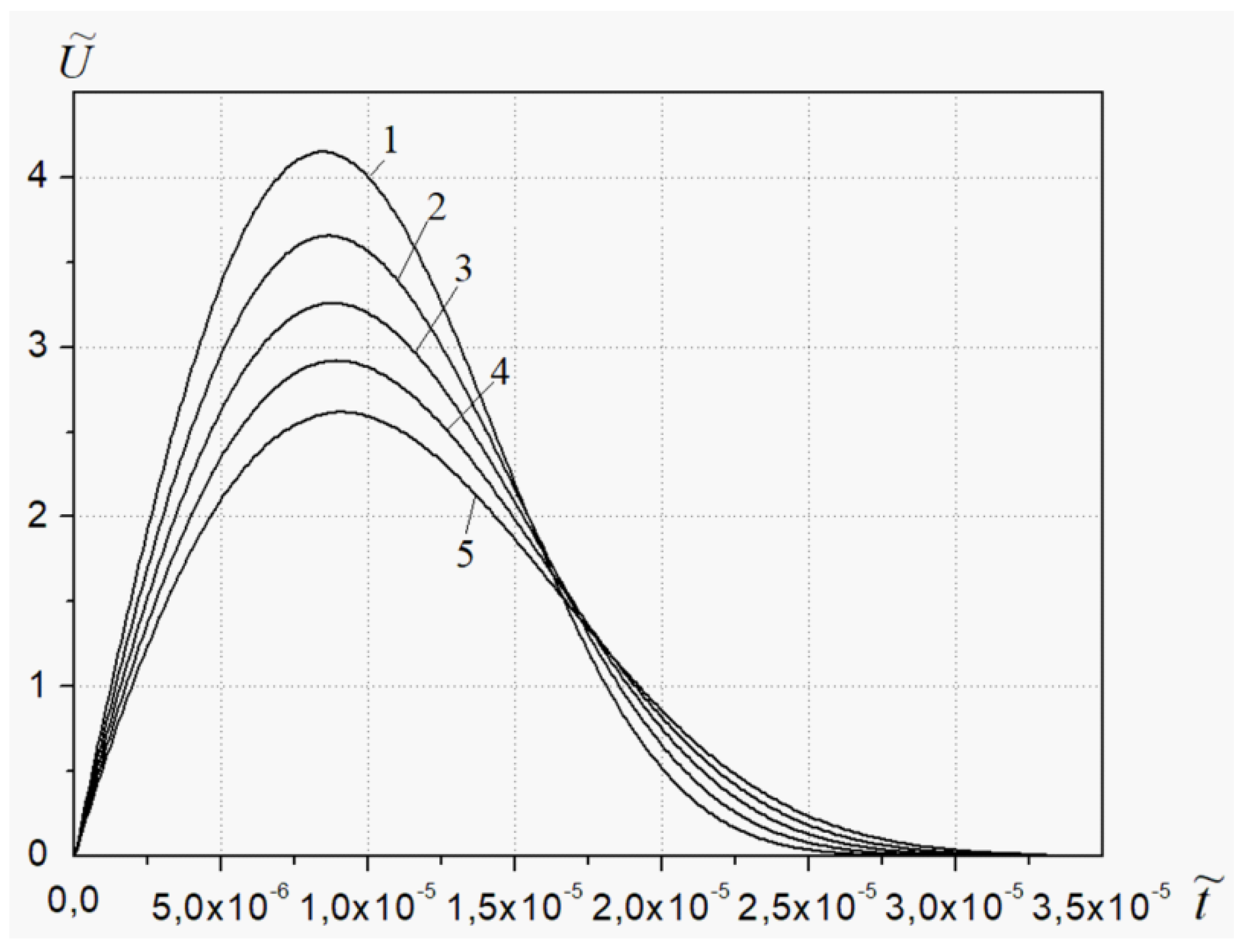
2.2. Simulation Results
3. Discussion of Research Results
- A decrease in the failure rate with increasing failure initiation time leads to a reduction in the amplitude of the generated AE signals.
- At the same time, the greater the failure initiation time (corresponding to a smaller defect size), the longer the duration of the AE signal.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmed, O.S.; Aabid, A.; Ali, J.S.M.; Hrairi, M.; Yatim, N.M. Progresses and Challenges of Composite Laminates in Thin-Walled Structures: A Systematic Review. ACS Omega 2023, 8, 30824–30837. [Google Scholar] [CrossRef]
- Chen, J.; Yu, Z.; Jin, H. Nondestructive testing and evaluation techniques of defects in fiber-reinforced polymer composites: A review. Front. Mater. 2022, 9, 986645. [Google Scholar] [CrossRef]
- Oliveira, T.L.L.; Hadded, M.; Mimouni, S.; Schaan, R.B. The Role of Non-Destructive Testing of Composite Materials for Aerospace Applications. NDT 2025, 3, 3. [Google Scholar] [CrossRef]
- Li, H.; Xu, J.S.; Chen, X.; Zhang, J.F.; Li, J. A nonlinear viscoelastic constitutive model with damage and experimental validation for composite solid propellant. Sci. Rep. 2023, 13, 2049. [Google Scholar] [CrossRef]
- Reis, L.M.M.; Ribeiro, M.L.; Madureira, F.; Morelli, A.C.; Monteiro, S.N.; Arantes, V.L. An experimental investigation of the mechanical properties and failure mode of 3D stitched composites. J. Mater. Res. Technol. 2024, 29, 90–100. [Google Scholar] [CrossRef]
- Bisoi, A.; Tüfekci, M.; Öztekin, V.; Goy, E.D.; Salles, L. Experimental Investigation of Mechanical Properties of Additively Manufactured Fibre-Reinforced Composite Structures for Robotic Applications. Appl. Compos. Mater. 2024, 3, 421–446. [Google Scholar] [CrossRef]
- Sławski, S.; Szymiczek, M.; Kaczmarczyk, J.; Domin, J.; Duda, S. Experimental and Numerical Investigation of Striker Shape Influence on the Destruction Image in Multilayered Composite after Low Velocity Impact. Appl. Sci. 2020, 10, 288. [Google Scholar] [CrossRef]
- Sencu, R.M.; Zhang, J.; Wang, Y.; Withers, P.; Soutis, C. Multiscale image-based modelling of damage and fracture in carbon fibre reinforced polymer composites. Compos. Sci. Technol. 2020, 198, 108243. [Google Scholar] [CrossRef]
- Kurumatani, M.; Kato, T.; Sasaki, H. Damage model for simulating cohesive fracture behavior of multi-phase composite materials. Adv. Model. Simul. Eng. Sci. 2023, 10, 2. [Google Scholar] [CrossRef]
- Martin-Santos, E.; Barbu, L.G.; Cruz, P. Damage and Failure Modeling of Composite Material Structures Using the Pam-Crash Code. Mathematics 2024, 12, 3847. [Google Scholar] [CrossRef]
- Saeedifar, M.; Zarouchas, D. Damage characterization of laminated composites using acoustic emission: A review. Compos. Part B Eng. 2020, 195, 108039. [Google Scholar] [CrossRef]
- Panasiuk, K.; Dudzik, K. Determining the Stages of Deformation and Destruction of Composite Materials in a Static Tensile Test by Acoustic Emission. Materials 2022, 15, 313. [Google Scholar] [CrossRef]
- Almeida, R.S.M.; Magalhães, M.D.; Karim, M.N.; Tushtev, K.; Rezwan, K. Identifying damage mechanisms of composites by acoustic emission and supervised machine learning. Mater. Des. 2023, 227, 111745. [Google Scholar] [CrossRef]
- Gee, M.; Roshanmanesh, S.; Hayati, F.; Papaelias, M. Multi-Variant Damage Assessment in Composite Materials Using Acoustic Emission. Sensors 2025, 25, 3795. [Google Scholar] [CrossRef] [PubMed]
- Godin, N.; Reynaud, P.; Fantozzi, G. Challenges and Limitations in the Identification of Acoustic Emission Signature of Damage Mechanisms in Composite Materials. Appl. Sci. 2018, 8, 1267. [Google Scholar] [CrossRef]
- Muir, C.; Swaminathan, B.; Fields, K.; Almansour, A.S.; Sevener, K.; Smith, C.; Presby, M.; Kiser, J.D.; Pollock, T.M.; Daly, S. A machine learning framework for damage mechanism identification from acoustic emissions in unidirectional SiC/SiC composites. Comput. Mater. 2021, 7, 146. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, P.F.; Shen, G.T.; Li, Q.; Liu, S.; Zhou, W. Acoustic emission study on damage mechanism of composite materials repaired with bi-adhesive and damage classification model. Adhes. Sci. Technol. 2024, 38, 1718–1737. [Google Scholar] [CrossRef]
- Tan, W.; Martínez-Pañeda, E. Phase field predictions of microscopic fracture and R-curve behaviour of fibre-reinforced composites. Compos. Sci. Technol. 2021, 202, 108539. [Google Scholar] [CrossRef]
- Macías, J.; Arteiro, A.; Otero, F.; Camanho, P.P.; Reinoso, J. Micro-mechanical analysis of composite materials using Phase-Field models of brittle fracture. Eur. J. Mech. A Solids 2023, 102, 105069. [Google Scholar] [CrossRef]
- Behbahani, A.E.; Barros, J.A.O.; Ventura-Gouveia, A. Plastic-damage smeared crack model to simulate the behaviour of structures made by cement based materials. Int. J. Solids Struct. 2015, 73–74, 20–40. [Google Scholar] [CrossRef]
- Lu, X.; Ridha, M.; Tan, V.B.C.; Tay, T.E. Adaptive discrete-smeared crack (A-DiSC) model for multi-scale progressive damage in composites. Compos. Part A Appl. Sci. Manuf. 2019, 126, 105569. [Google Scholar] [CrossRef]
- Oskay, C.; Su, Z.; Kapusuzoglu, B. Discrete eigenseparation-based reduced order homogenization method for failure modeling of composite materials. Comput. Methods Appl. Mech. Eng. 2020, 359, 12656. [Google Scholar] [CrossRef]
- Wana, L.; Sheng, Y.; McCarthy, E.D.; Yang, D. A novel approach for 3D discrete element modelling the progressive delamination in unidirectional CFRP composites. Eng. Fract. Mech. 2023, 277, 108982. [Google Scholar] [CrossRef]
- Noguchi, H.; Yukawa, S. Fracture process of composite material in a spring network model. Phys. Rev. E 2024, 110, 045001. [Google Scholar] [CrossRef]
- Senapati, S.; Roy, S.; Banerjee, A.; Rajesh, R. Record statistics of fracture in the random spring network model. Phys. Rev. E 2024, 110, 035004. [Google Scholar] [CrossRef]
- Moreno, Y.; Gomez, J.B.; Pacheco, A.F. Self-organized criticality in a fibre bundle-type model. Physica A Stat. Mech. Its Appl. 1999, 274, 400–409. [Google Scholar] [CrossRef]
- Chakrabarti, B.K.; Biswas, S.; Pradhan, S. Cooperative Dynamics in the Fiber Bundle Model. Front. Phys. 2020, 8, 613392. [Google Scholar] [CrossRef]
- Raischel, F.; Kun, F.; Herrmann, H.J. Fiber Bundle Models for Composite Materials. In Proceedings of the Conference on Damage in Composite Materials, Stuttgart, Germany, 18–19 September 2006. [Google Scholar]
- Lennartz-Sassinek, S.; Danku, Z.; Kun, F.; Main, I.G.; Zaiser, M. Damage growth in fibre bundle models with localized load sharing and environmentally-assisted ageing. J. Phys. Conf. Ser. 2013, 410, 012064. [Google Scholar] [CrossRef]
- Hader, A.; Boughaleb, Y.; Achik, I.; Sbiaai, K. Failure kinetic and scaling behavior of the composite materials: Fiber Bundle Model with the local load-sharing rule (LLS). Opt. Mater. 2014, 36, 3–7. [Google Scholar] [CrossRef]
- Tanasehte, M.; Hader, A.; Sbiaai, H.; Achik, I.; Boughaleb, Y. The effect of fibers-matrix interaction on the composite materials elongation. IOP Conf. Ser. Mater. Sci. Eng. 2020, 948, 012032. [Google Scholar] [CrossRef]
- Yamada, Y.; Yamazaki, Y. Avalanche Distribution of Fiber Bundle Model with Random Displacement. J. Phys. Soc. Jpn. 2019, 88, 023002. [Google Scholar] [CrossRef]
- Villette, F.; Baroth, J.; Dufour, F.C.; Bloch, J.F.; Du Roscoat, S.R. Influence of material heterogeneities on crack propagation statistics using a Fiber Bundle Model. Int. J. Fract. 2020, 221, 87–100. [Google Scholar] [CrossRef]
- Kádár, V.; Pál, G.; Kun, F. Record statistics of bursts signals the onset of acceleration towards failure. Sci. Rep. 2020, 10, 2508. [Google Scholar] [CrossRef]
- Hao, D.P.; Tang, G.; Xia, H.; Xun, Z.P.; Han, K. The avalanche process of the fiber bundle model with defect. Physica A Stat. Mech. Its Appl. 2017, 472, 77–85. [Google Scholar] [CrossRef]
- Raischel, F.; Kun, F.; Herrmann, H.J. Simple beam model for the shear failure of interfaces. Phys. Rev. E 2005, 72, 046126. [Google Scholar] [CrossRef]
- Reiweger, I.; Schweizer, J.; Dual, J.; Herrmann, H.J. Modelling snow failure with a fibre bundle model. J. Glaciol. 2009, 55, 997–1002. [Google Scholar] [CrossRef]
- Capelli, A.; Reiweger, I.; Schweizer, J. Studying Snow Failure With Fiber Bundle Models. Front. Phys. 2020, 8, 236. [Google Scholar] [CrossRef]
- Michlmayr, G.; Cohen, D.; Or, D. Shear-induced force fluctuations and acoustic emissions in granular material. J. Geophys. Res. Solid Earth 2013, 118, 6086–6098. [Google Scholar] [CrossRef]
- Rios-Soberanis, C.R. An Approach to Acoustic Emission Technique Applications to Evaluate Damage Mechanisms in Composite Materials. MATEC Web Conf. 2015, 5, 03009. [Google Scholar] [CrossRef]
- Pradhan, S. Can we predict the failure point of a loaded composite material. Comput. Phys. Commun. 2011, 182, 1984–1988. [Google Scholar] [CrossRef]
- Bosia, F.; Pugno, N.; Lacidogna, G.; Carpinteri, A. Mesoscopic modeling of acoustic emission through an energetic approach. Int. J. Solids Struct. 2008, 45, 5856–5866. [Google Scholar] [CrossRef]
- Pradhan, S.; Kjellstadli, J.T.; Hansen, A. Variation of Elastic Energy Shows Reliable Signal of Upcoming Catastrophic Failure. Front. Phys. 2019, 7, 106. [Google Scholar] [CrossRef]
- Vas, L.M.; Kocsis, Z.; Czigány, T.; Tamás, P.; Romhány, G. Novel evaluation method of acoustic emission data based on statistical fiber bundle cells. J. Compos. Mater. 2019, 53, 2429–2446. [Google Scholar] [CrossRef]
- Turcotte, D.L.; Newman, W.I.; Shcherbakov, R. Micro and macroscopic models of rock fracture. Geophys. J. Int. 2003, 152, 718–728. [Google Scholar] [CrossRef]
- Nanjo, K.Z. A fiber-bundle model for the continuum deformation of brittle material. Int. J. Fract. 2016, 204, 225–237. [Google Scholar] [CrossRef]
- Pradhan, S.; Hemmer, P.C. Energy bursts in fiber bundle models of composite materials. Phys. Rev. E 2008, 77, 031138. [Google Scholar] [CrossRef]
- Bodaballa, N.K.; Biswas, S.; Roy, S. Correlation Between Avalanches and Emitted Energies During Fracture With a Variable Stress Release Range. Front. Phys. 2022, 10, 768853. [Google Scholar] [CrossRef]
- Roy, S.; Biswas, S. Size Distribution of Emitted Energies in Local Load Sharing Fiber Bundles. Front. Phys. 2021, 9, 643602. [Google Scholar] [CrossRef]
- Filonenko, S.; Stadychenko, V. Influence of Loading Speed on Acoustic Emission During Destruction of a Composite by Von Mises Criterion. Am. J. Mech. Mater. Eng. 2020, 4, 54–59. [Google Scholar] [CrossRef]
- Filonenko, S.; Stakhova, A. Amplitude-Energy Parameters of Acoustic Radiation with Composite Properties Changing and Mises Destruction. J. Autom. Mob. Robot. Intell. Syst. 2022, 16, 19–24. [Google Scholar]
- Filonenko, S.; Stakhova, A. Patterns of Acoustic Emission Changes with Alterations in the Damage Area of a Composite Material According to the Mises Criterion. J. Autom. Mob. Robot. Intell. Syst. 2025, 19, 50–58. [Google Scholar] [CrossRef]
- Filonenko, S.F.; Stakhova, A.P. Acoustic emission during composites fracture according to von Mises criterion and changing of its properties dispersion. Electron. Control Syst. 2022, 1, 28–35. [Google Scholar] [CrossRef]
- Hao, D.P.; Tang, G.; Xun, Z.P.; Xia, H.; Han, K. The avalanche process of the fiber bundle model with defect in local load sharing. Physica A Stat. Mech. Its Appl. 2018, 505, 1095–1102. [Google Scholar] [CrossRef]






| 0.001 | 0.008897277688462064 |
| 0.002 | 0.016761288967306002 |
| 0.003 | 0.023884393144868957 |
| 0.004 | 0.03037385029676163 |
| 0.005 | 0.03629375023308743 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filonenko, S.; Stakhova, A.; Sokol, M. Acoustic Emission During Failure of a Composite Under the von Mises Criterion with Local Structural Defects. J. Compos. Sci. 2025, 9, 630. https://doi.org/10.3390/jcs9110630
Filonenko S, Stakhova A, Sokol M. Acoustic Emission During Failure of a Composite Under the von Mises Criterion with Local Structural Defects. Journal of Composites Science. 2025; 9(11):630. https://doi.org/10.3390/jcs9110630
Chicago/Turabian StyleFilonenko, Sergii, Anzhelika Stakhova, and Milan Sokol. 2025. "Acoustic Emission During Failure of a Composite Under the von Mises Criterion with Local Structural Defects" Journal of Composites Science 9, no. 11: 630. https://doi.org/10.3390/jcs9110630
APA StyleFilonenko, S., Stakhova, A., & Sokol, M. (2025). Acoustic Emission During Failure of a Composite Under the von Mises Criterion with Local Structural Defects. Journal of Composites Science, 9(11), 630. https://doi.org/10.3390/jcs9110630







