Natural Frequency Optimization of Stiffener Structure for Ceramic Matrix Composites Combustion Liner in Aero-Engines

Abstract

To mitigate vibration in thin-walled composite combustion liners of aero-engines, this study proposes an optimization strategy for stiffener design to maximize natural frequencies and suppress resonance. The approach enhances structural dynamics by installing transverse and longitudinal stiffeners along the tubular wall, with their dimensions and orientations systematically optimized. Design variables were chosen: combustion liner wall thickness, stiffener thickness, transverse stiffener width/angle, longitudinal stiffener width, and composite lamination layup scheme. The orthogonal experiments were completed and followed by range analysis and variance analysis. The results demonstrated that wall thickness had the most significant impact on the natural frequency, and the 45° lamination scheme showed a superior performance compared to other configurations. Finally, a predictive equation was developed using a multiple linear regression model. The optimized stiffener configuration markedly enhances natural frequencies, mitigating vibration-induced instability. This methodological framework provides a systematic basis for designing optimized stiffener layouts in composite combustion liners for aero-engines.

1. Introduction

Owing to their superior thermomechanical properties, ceramic matrix composites (CMCs) have been the focus of extensive research for high-temperature aero-engine components worldwide since the 1980s [1,2,3]. These components include combustion chamber, combustion liners, turbine outer rings, turbine guide vanes, turbine rotor blades, turbine shrouds, control/sealing vanes, mixers, and shrouds, as well as afterburner flame stabilizers. As alternatives to high-temperature alloys in critical aero-engine components, CMCs offer low density, high strength, and superior resistance to heat, wear, corrosion, and oxidation, thereby extending service life and improving emission efficiency [4,5].

As a critical component of combustion chambers and one of the engine’s most heat-intensive parts, the combustion liner has seen structural complexity increase with advancing aviation engine technology. Typically featuring annular thin-walled construction with membrane holes in the tube walls, this component endures simultaneous exposure to high-temperature gases, high-speed cooling airflow, and mechanical forces. These combined stresses make it prone to issues like cracking failures and deformation imbalance, making combustion liner failures an increasingly prominent technical concern [6].

Current research on combustion liners by scholars worldwide primarily focuses on simulating and designing gas film orifice flow fields, optimizing wall cooling systems, and predicting/fostering fatigue durability [7]. The General Electric (GE) Corporation developed the SiC/SiC combustion chamber combustion liner, which underwent 5000 h full lifecycle testing at 1200 °C operating conditions and 500 h of high-temperature exposure [8]. Results demonstrated that this design could withstand wall temperatures up to 1316 °C while reducing structural weight by 30%, significantly enhancing overall engine chamber performance. Van Roode et al. [9] investigated the impact of manufacturing processes and Environmental Barrier Coatings (EBCs) on SiC/SiC combustion liners. Tests showed that melt infiltration (MI) SiC/SiC combustion liners without EBCs outperformed chemical vapor infiltration (CVI) SiC/SiC counterparts in durability, with EBCs extending service life by 2–3 times. Li Gong’s team [10] created a CMC floating wall combustion liner using floating tile technology. The CMC design features simplified structures for easier machining and gaps around tiles to minimize thermal stress. Simulation results indicated that the chamber could withstand 1400 K temperatures while requiring 10% less cooling gas than high-temperature alloy combustion chambers. Edward et al. [11] addressed the issue of excessive or uneven radial deformation in thin-walled combustion liner structures by designing reinforcing ribs to enhance both circumferential and radial stiffness. This approach ensures stable combustion and uniform outlet flow field distribution without significant weight gain. Andrei et al. [12] developed a device for evaluating cooling efficiency of air film holes in combustion liners. The setup involves positioning the workpiece under high-temperature airflow with parallel upper airflow and perpendicular lower cooling airflow, using optical pressure-sensitive material brightness on the workpiece surface to assess cooling effectiveness. Xie Jie et al. [13] conducted numerical studies on convective heat transfer characteristics within air film holes. Their results demonstrated that the surface heat transfer coefficient increases with rising airflow Reynolds number, while increasing the hole inclination angle significantly enhances convective heat transfer coefficients across the entire hole perimeter.

In the field of stiffener optimization design for thin-walled structures, relevant optimization theories have become relatively mature and are gradually being applied in aerospace and other manufacturing industries [14,15,16]. Conventional stiffener configurations include evenly distributed linear stiffeners, orthogonal rectangular grid stiffeners, and triangular grid stiffeners. With the development of parametric methods, Mulani et al. [17] utilized spline curves to optimize stiffener designs for T-beam and I-beam structures, employing B-spline curves as geometric descriptors. Zhang et al. [18] achieved optimized stiffener layout design for three-dimensional curved thin-walled shell structures using geometric background mesh methods. Aage et al. [19] published a Nature paper on wing box stiffener topology optimization, employing nearly 1.1 billion solid element design variables to optimize stiffener topology for the Boeing 777 wing. Afonso et al. [20] adopted shell unit thickness as a design variable to optimize stiffener layouts for plate-shell structures. Inspired by the branching growth patterns of plant canopies, Ding et al. [21] proposed an adaptive biomimetic stiffener growth design method, which not only optimizes structural layout but also generates new stiffeners, thereby expanding the design space. To enhance structural dynamic performance against vibrational resonance, Liu et al. [22] proposed a multiscale topology optimization framework for maximizing the natural frequency of multi-morphology lattice structures, addressing the problems of numerical convergence, microstructural connectivity, etc. Similarly, Wang et al. [23] proposed a data-driven topology optimization approach to enable the multiscale cellular designs with multiple choices of microstructure classes with a newly proposed latent-variable Gaussian process. Also, Shah et al. [24] considered natural frequency in multi-material topology optimization and solved complex three-dimensional (3D) problems.

However, most works considering natural frequency optimization are realized on theoretical models, and thin-walled engineering structures such as combustion liners have rarely been considered. The challenges include the local heat/fluid boundary conditions and composite material manufacturing constraints.

This study conducted simulation and optimization of vibration buckling issues in thin-walled structures of ceramic matrix composite combustion liners, proposing a ribbed wall design scheme. The optimization objective is set to be maximization of the first order natural frequency, thus enhancing the dynamic performance against resonance. The design focuses on three key parameters: tube wall thickness, longitudinal rib thickness and width, and circumferential rib thickness and width, as well as lamination direction. With the fundamental frequency of structural vibrations as the design objective, orthogonal experiments were designed and optimized through analysis to evaluate the impact of each parameter.

The remainder of this paper is organized as follow: Section 2 describes in detail the design of the stiffener and simulation setups in this paper. In Section 3, a series of orthogonal experiments is designed and performed with the results illustrated. In Section 4, the analysis of range, variance and multiple linear regression is conducted. The influence of stiffener parameters is analyzed. The conclusions of this paper are drawn in Section 5.

2. Materials and Methods

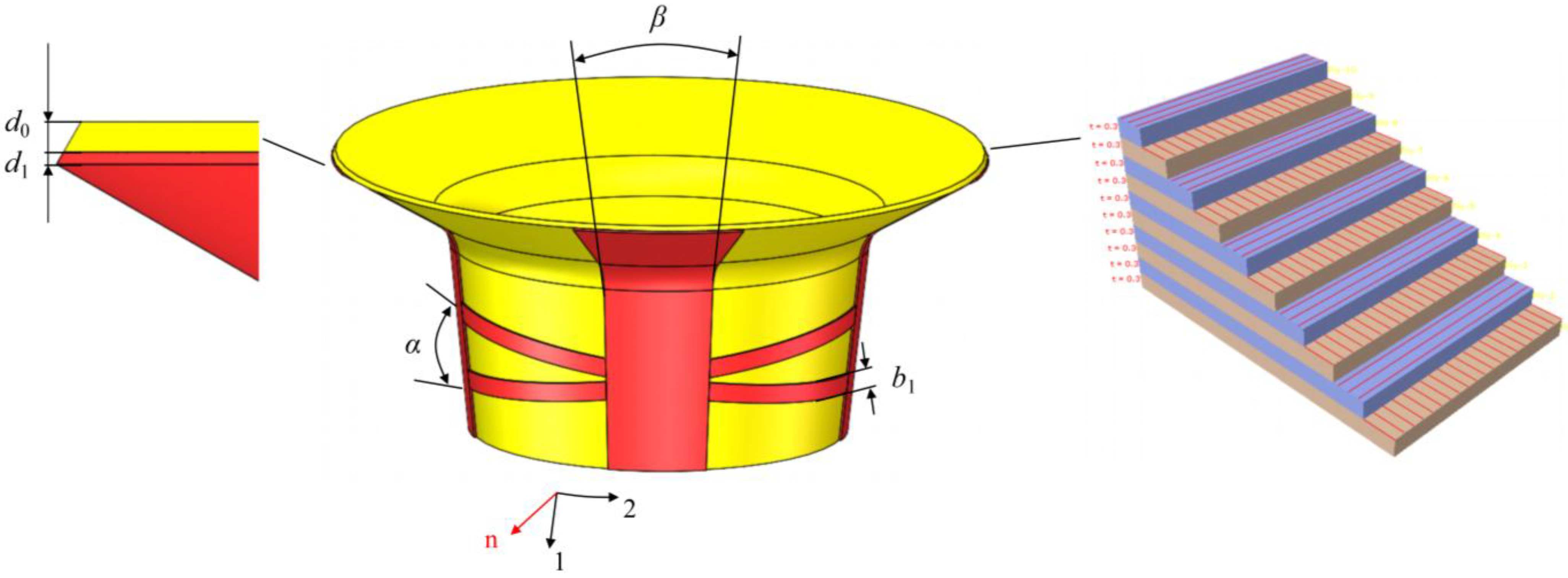
Figure 1 shows a simplified model of a combustion liner, formed by two straight segments and a transition arc. Stiffener design patterns along the tube wall are illustrated in Figure 2, featuring longitudinal and transverse stiffeners. The longitudinal stiffeners span the entire axial direction, consisting of four groups evenly distributed at 90° intervals. Transverse stiffeners are exclusively arranged in the lower smooth section, forming two symmetrically positioned groups along the circumferential direction with adjustable angles relative to the horizontal plane.

The material of the combustion liner structure is set as ceramic matrix composite. The material properties of unidirectional ply are taken according to the data in literature [25], measured from the material Prepreg HiPerComp™ (General Electric Company, Boston, MA, USA) of 8-ply laminates, with a balanced [0-90–90-0]s stacking of uniaxial plies, and nominally 22–25% by volume of Hi-Nicalon™ (Nippon Carbon Company, Tokyo, Japan) fibers. Here, the material data is used for informative purposes only, and not for engineering specifications. The fiber main direction is taken as 1, the vertical fiber direction in the lamination plane is taken as 2, and the normal direction in the lamination plane is taken as 3 (Figure 3). The specific parameters are shown in

Table 1. Parameters of ceramic matrix composites.

Material Properties	Value	Temperature/°C	Value	Temperature/°C
Density	2.80 g/cm3	25	2.76 g/cm3	1200
Tensile modulus E11	285 GPa	25	243 GPa	1200
Tensile modulus E22	285 GPa	25	243 GPa	1200
Tensile modulus E33	201 GPa	25	171 GPa	1200
Shear modulus G12	14.5 GPa	25	12.3 GPa	1200
Shear modulus G13	12.8 GPa	25	10.9 GPa	1200
Shear modulus G23	12.8 GPa	25	10.9 GPa	1200
Poisson’s ratio ν12	0.12	25	0.12	1200
Poisson’s ratio ν13	0.24	25	0.24	1200
Poisson’s ratio ν23	0.24	25	0.24	1200

.

The design parameters selected include combustion liner basic wall thickness d₀, stiffener thickness d₁, transverse stiffener width b₁, transverse stiffener angle α, longitudinal stiffener angle β, and fiber layer scheme M. All stiffener cross-sections are defined as rectangular. All stiffener structures are employed on the outer surface of the combustion liner, thus ensuring the heat/fluid boundary conditions of inner surface. A finite element model was established to conduct natural frequency simulation analysis, investigating how different stiffener configurations affect the fundamental frequency of the combustion liner. The schematic diagram of design parameters is shown in Figure 4. The computational analysis in this work is fulfilled by commercial software ABAQUS (version 6.14), and the optimization procedure is implemented by the development of Python (version 2.7) scripts embedded in ABAQUS.

3. Results

Orthogonal Experiment Design

Firstly, we conducted a qualitative analysis of how design parameters affect the fundamental frequency. The CMC single-layer thickness was set to be a uniform value of 0.3 mm, and the unreinforced 0/90° layered structure was chosen as the original baseline design (Case 1). The modal displacement cloud diagrams and corresponding 1st order natural frequency for the unreinforced structure at room temperature are shown in Figure 5. The modal cloud was rendered at double thickness to clearly demonstrate thickness effects and stiffener variations. Subsequently, three randomized stiffener designs were implemented as illustrated in Figure 6. It is evident that all designs realize a certain degree of improvement in fundamental frequency compared to the original case (control group).

Consequently, the influence of each stiffener parameter was analyzed as a single-factor variable, as shown in Figure 7. Compared with the unstiffened structure, the effects of design variables on the fundamental frequency were essentially linear, with wall thickness and lamination scheme exerting the greatest influence on the 1st-order natural frequency.

Thereafter, quantitative analysis was conducted on the orthogonal experimental designs for each parameter, with selected parameter levels as shown in

Table 2. Design parameter level selection.

Design Parameter	Wall Thickness d0 (mm)	Stiffener Thickness d1 (mm)	Longitudinal Stiffener Angle β (°)	Transverse Stiffener Width b1 (mm)	Transverse Stiffener Angle α (°)	Layer Scheme M (°)
Level 1	2.4	0.6	25	5	0	0/90
Level 2	3	1.2	30	10	15	0/90/45/−45
Level 3	3.6	1.8	35	15	30	45/−45

. The study involved six design parameters, each containing three levels (L18 (3.6) orthogonal experiment design), as detailed in

Table 3. Orthogonal test table.

Number	Factor 1	Factor 2	Factor 3	Factor 4	Factor 5	Factor 6
1	1	1	1	1	1	1
2	1	1	2	2	3	3
3	1	2	1	3	3	2
4	1	2	3	1	2	3
5	1	3	2	3	2	1
6	1	3	3	2	1	2
7	2	1	1	3	2	3
8	2	1	3	1	3	2
9	2	2	2	2	2	2
10	2	2	3	3	1	1
11	2	3	1	2	3	1
12	2	3	2	1	1	3
13	3	1	2	3	1	2
14	3	1	3	2	2	1
15	3	2	1	2	1	3
16	3	2	2	1	3	1
17	3	3	1	1	2	2
18	3	3	3	3	3	3

. Simulation experiments were performed based on the orthogonal table, with experimental data recorded under 25 °C and 1200 °C conditions presented in

Table 4. Results of orthogonal test.

No.	Wall Thickness d0 (mm)	Stiffener Thickness d1 (mm)	Longitudinal Stiffener Angle β (°)	Transverse Stiffener Width b1 (mm)	Transverse Stiffener Angle α (°)	Layer Scheme M (°)	25 °C Fundamental Frequency f (Hz)	1200 °C Fundamental Frequency f (Hz)
1	2.4	0.6	25	5	0	0/90	264.18	245.62
2	2.4	0.6	30	10	30	45/−45	322.03	299.40
3	2.4	1.2	25	15	30	90/45	307.13	285.55
4	2.4	1.2	35	5	15	45/−45	321.64	299.04
5	2.4	1.8	30	15	15	0/90	347.46	323.05
6	2.4	1.8	35	10	0	90/45	353.32	328.50
7	3	0.6	25	15	15	45/−45	401.09	372.91
8	3	0.6	35	5	30	90/45	350.86	326.21
9	3	1.2	30	10	15	90/45	385.21	358.15
10	3	1.2	35	15	0	0/90	367.85	342.00
11	3	1.8	25	10	30	0/90	379.90	353.21
12	3	1.8	30	5	0	45/−45	394.63	366.91
13	3.6	0.6	30	15	0	90/45	437.71	406.97
14	3.6	0.6	35	10	15	0/90	394.04	366.32
15	3.6	1.2	25	10	0	45/−45	476.79	443.33
16	3.6	1.2	30	5	30	0/90	402.16	373.83
17	3.6	1.8	25	5	15	90/45	456.88	424.84
18	3.6	1.8	35	15	30	45/−45	499.78	464.67

and Figure 8. The results demonstrate that combustion liner fundamental frequency under high-temperature conditions consistently exhibits lower values compared to those obtained at room temperature.

4. Discussion

4.1. Range Analysis

A range analysis was conducted based on the orthogonal experimental results. The indicator Kavg measures the influence of six experimental factors on the combustion liner fundamental frequency at different levels, while the range R reflects the impact of factor-level variations on experimental outcomes. A larger range value indicates more significant effects of the corresponding factor, whereas smaller ranges suggest relatively minor impacts. As shown in

Table 5. Range analysis results (25 °C).

Project		Wall Thickness d0 (mm)	Stiffener Thickness d1 (mm)	Longitudinal Stiffener Angle β (°)	Transverse Stiffener Width b1 (mm)	Transverse Stiffener Angle α (°)	Layer Scheme M (°)
Horizontal numbers		3	3	3	3	3	3
Number of tests per level		6	6	6	6	6	6
Kavg	Level 1	319.29	361.65	381.00	365.06	382.41	359.27
	Level 2	379.92	376.80	381.53	385.22	384.39	381.85
	Level 3	444.56	405.33	381.25	393.50	376.98	402.66
Best level		3	3	3	3	2	3
R		125.27	43.68	0.54	28.45	7.41	43.40

and

Table 6. Range analysis results (1200 °C).

Project		Wall Thickness d0 (mm)	Stiffener Thickness d1 (mm)	Longitudinal Stiffener Angle β (°)	Transverse Stiffener Width b1 (mm)	Transverse Stiffener Angle α (°)	Layer Scheme M (°)
Horizontal numbers		3	3	3	3	3	3
Number of tests per level		6	6	6	6	6	6
Kavg	Level 1	296.86	336.24	354.24	339.41	355.55	334.00
	Level 2	353.23	350.32	354.72	358.15	357.38	355.04
	Level 3	413.33	376.86	354.45	365.86	350.48	374.38
Best level		3	3	3	3	2	3
R		116.47	40.62	0.48	26.45	6.91	40.37

, the wall thickness has the most substantial effect on the combustion liner fundamental frequency, followed by stiffener thickness, layering configuration, and transverse bar width, with longitudinal bar angle and transverse bar inclination showing minimal influence. Notably, the fundamental frequency at 1200 °C was lower than that at 25 °C due to decreased material elastic modulus under high temperatures. This degradation effect caused by high temperature would also result in negative effect on the material’s long-term durability and fatigue life. However, the trend of parameter effects on fundamental frequency remained consistent across different temperature conditions.

After analyzing the influence of design parameters, the aforementioned results can be interpreted as follows: The base thickness determines the overall stiffness of the structure and plays a crucial role in determining the fundamental frequency of thin-walled structures. Increasing the basic wall thickness significantly enhances the fundamental frequency of the combustion liner, but this also leads to the gain of mass. Therefore, it is essential to optimize thickness design while maintaining performance. Stiffener thickness similarly has a substantial impact on the combustion liner’s fundamental frequency. By increasing stiffener thickness, local stiffness of the combustion liner can be enhanced, thereby improving its fundamental frequency. The selection of lamination schemes also significantly affects the combustion liner’s fundamental frequency. Since the first-order mode is dominated by lateral oblique vibrations, a 45° lamination significantly increases oblique stiffness and raises the corresponding vibration frequency. The transverse stiffener width strongly affects the combustion liner’s natural frequency, with increased width enhancing tube stiffness. In contrast, longitudinal and transverse stiffener angles have a smaller impact but should still be considered to ensure optimal overall performance.

4.2. Analysis of Variance

Although range analysis can evaluate the sensitivity of different design parameters on the objectives, it has limitations in determining the depth and significance of such impacts. This study employs analysis of variance (ANOVA) on orthogonal experiment results, with the core principle being to decompose experimental data variance into two components: differences caused by varying factors and random errors. The selection of ANOVA is justified for this analysis as the investigation involves natural frequency optimization across multiple kinds of combustion liner parameters, i.e., thickness, angle, and material layup. ANOVA is the appropriate tool because it can efficiently determine the significant differences between these parameters. The total factor variance (Sum Square, SS) represents the variance between individual factor levels’ means and the overall mean, while the mean square error (Mean Square, MS) is calculated by dividing the total variance by degrees of freedom, reflecting the degree of variation among observed values across different factor levels. Significance is ultimately determined through F-values and p-Values derived from MS calculations, where p < 0.05 indicates significant effects. As shown in

Table 7. Analysis of variance results (25 °C).

Project		Wall Thickness d0 (mm)	Stiffener Thickness d1 (mm)	Longitudinal Stiffener Angle β (°)	Transverse Stiffener Width b1 (mm)	Transverse Stiffener Angle α (°)	Layer Scheme M (°)
Factor degrees of freedom		2	2	2	2	2	2
Quadratic sum	Level 1	3839.73	384.44	0.07	262.46	1.33	483.73
	Level 2	1.78	19.91	0.08	15.65	9.78	0.35
	Level 3	4007.03	579.34	0.00	149.93	18.34	458.01
Sum square		47,091.27	5902.16	0.87	2568.21	176.72	5652.54
Mean square		23,545.63	2951.08	0.44	1284.11	88.36	2826.27
F Value		100.51	12.60	0.00	5.48	0.38	12.06
p Value		0.000	0.011	0.987	0.052	0.787	0.012
Significance		Highly significant	Significant	Not significant	Not significant	Not significant	Significant

and

Table 8. Analysis of variance results (1200 °C).

Project		Wall Thickness d0 (mm)	Stiffener Thickness d1 (mm)	Longitudinal Stiffener Angle β (°)	Transverse Stiffener Width b1 (mm)	Transverse Stiffener Angle α (°)	Layer Scheme M (°)
Factor degrees of freedom		2	2	2	2	2	2
Quadratic sum	Level 1	3319.25	332.47	0.05	226.92	1.17	418.92
	Level 2	1.54	17.27	0.06	13.53	8.48	0.32
	Level 3	3463.87	501.27	0.00	129.63	15.96	396.20
Sum square		40,707.95	5106.03	0.68	2220.48	153.63	4892.56
Mean square		20,353.98	2553.01	0.34	1110.24	76.82	2446.28
F Value		100.40	12.59	0.00	5.48	0.38	12.07
p Value		0.000	0.011	0.987	0.052	0.787	0.012
Significance		Highly significant	Significant	Not significant	Not significant	Not significant	Significant

, the significant trends in parameters at 25 °C and 1200 °C align with the findings from factor analysis in Section Orthogonal Experiment Design. The wall thickness demonstrates particularly significant effects on fundamental frequency, followed by stiffener thickness and layer design schemes, while other factors show no significant impact. These ANOVA results correspond to the conclusions drawn from factor influence analysis in Section Orthogonal Experiment Design.

4.3. Multiple Linear Regression

Furthermore, a multiple linear regression model was established based on the orthogonal experimental results for regression analysis. The model assumes that the response (fundamental frequency f) exhibits linear relationships with the following factors: wall thickness d₀, stiffener thickness d₁, longitudinal stiffener angle β, transverse stiffener width b₁, transverse stiffener angle α, and layer scheme M.

$$f=B+w_1\cdot d_0+w_2\cdot d_1+w_3\cdot \beta +w_4\cdot b_1+w_5\cdot \alpha +w_6\cdot M$$

(1)

To ensure dimensional consistency, all factors underwent normalization mapping, with their values scaled to levels 1, 2, and 3. The coefficients and analysis results of the multiple linear regression are presented in

Table 9. Results of multiple linear regression.

Project	25 °C		1200 °C
	Coefficient Values	VIF	Coefficient Values	VIF
Constant B	145.659	-	135.423	-
Wall thickness coefficient w1	62.633	1.000	58.233	1.000
Stiffener thickness coefficient w2	21.838	1.000	20.313	1.000
Longitudinal stiffener angle coefficient w3	0.127	1.000	0.107	1.000
Transverse stiffener width coefficient w4	14.222	1.000	13.225	1.000
Transverse stiffener angle coefficient w5	−2.718	1.000	−2.538	1.000
Layer scheme coefficient w6	21.698	1.000	20.186	1.000
R2	0.974	-	0.974	-
F Value	70.005	-	69.913	-
p Value	0.000	-	0.000	-
D-W	1.937	-	1.938	-

. The physical meaning of the coefficients w₁, …, w₆ represents the influence level of each design variable to natural frequency, in which the sign represents positive or negative influence, and the absolute value represents the sensitivity. The model demonstrates an R² value of 0.974, indicating that the wall thickness, stiffener thickness, longitudinal stiffener width-angle, transverse stiffener width, transverse stiffener angle, and pavement design scheme collectively account for 97.4% of the variation in the fundamental frequency. The F-test results confirm the model’s validity (p = 0.000 < 0.05), demonstrating that at least one of the six factors influences the fundamental frequency. Multicollinearity tests revealed all Variance Inflation Factors (VIF) below 5, confirming no multicollinearity issues. Additionally, D-W values near 2 suggest no autocorrelation, indicating no inherent correlations between sample data points, thus validating the model’s overall robustness.

Finally, based on the positive/negative coefficients of the linear regression model, we optimized stiffener parameters to achieve maximum fundamental frequency response. The design selected maximum values for wall thickness, stiffener thickness, longitudinal stiffener angle, transverse stiffener width, and pavement layout scheme while minimizing the transverse stiffener angle. Finite element modal analysis was conducted. As the 1200 °C and 25 °C modal cloud images showed remarkable similarity, only the 25 °C results are presented here. Figure 9 illustrates the optimized modal displacement results of the combustion liner stiffener structure. Compared to unreinforced structures, this design achieves approximately 60% improvement in fundamental frequency while swapping the sequence of modes 3, 4 with modes 5, 6.

5. Conclusions

This study optimized reinforced configurations of CMC combustion liner structures to enhance natural frequencies. Using an orthogonal experimental design with six variables—wall thickness, stiffener thickness, transverse stiffener width and angle, longitudinal stiffener width, and lamination scheme—the analysis showed that wall thickness had the greatest influence, followed by stiffener thickness, lamination scheme, and transverse stiffener width. Notably, the 45° lamination scheme showed superior performance compared to other configurations in improving structural frequency. Multivariate linear regression analysis effectively characterized the frequency response through these six variables, explaining 97.4% of variation while demonstrating no multicollinearity or self-correlation issues, validating the model’s effectiveness. Under 1200 °C conditions, although the stiffener design achieved identical results as at 25 °C, reduced material stiffness at elevated temperatures led to decreased fundamental frequency. The regression model ultimately identified optimized stiffener parameters that significantly improved frequency performance while altering low-order modal order characteristics.

This study establishes a theoretical basis for optimizing composite combustion liner structures in aero-engines and provides practical guidance for similar designs. By tailoring stiffener configurations and lamination schemes, natural frequencies can be effectively increased, enhancing vibration resistance and extending service life. Future work will explore diverse stiffener geometries and layering strategies, with the goal of implementing and validating these designs in operational aero-engine systems.