Investigations of Edge Cutting Effects on Mechanical Behaviors of 3D Braided Composites with Different Braiding Angles
Abstract
1. Introduction
2. Experimental and Numerical Details
2.1. Experimental Details
2.2. Numerical Details
3. Results and Discussions
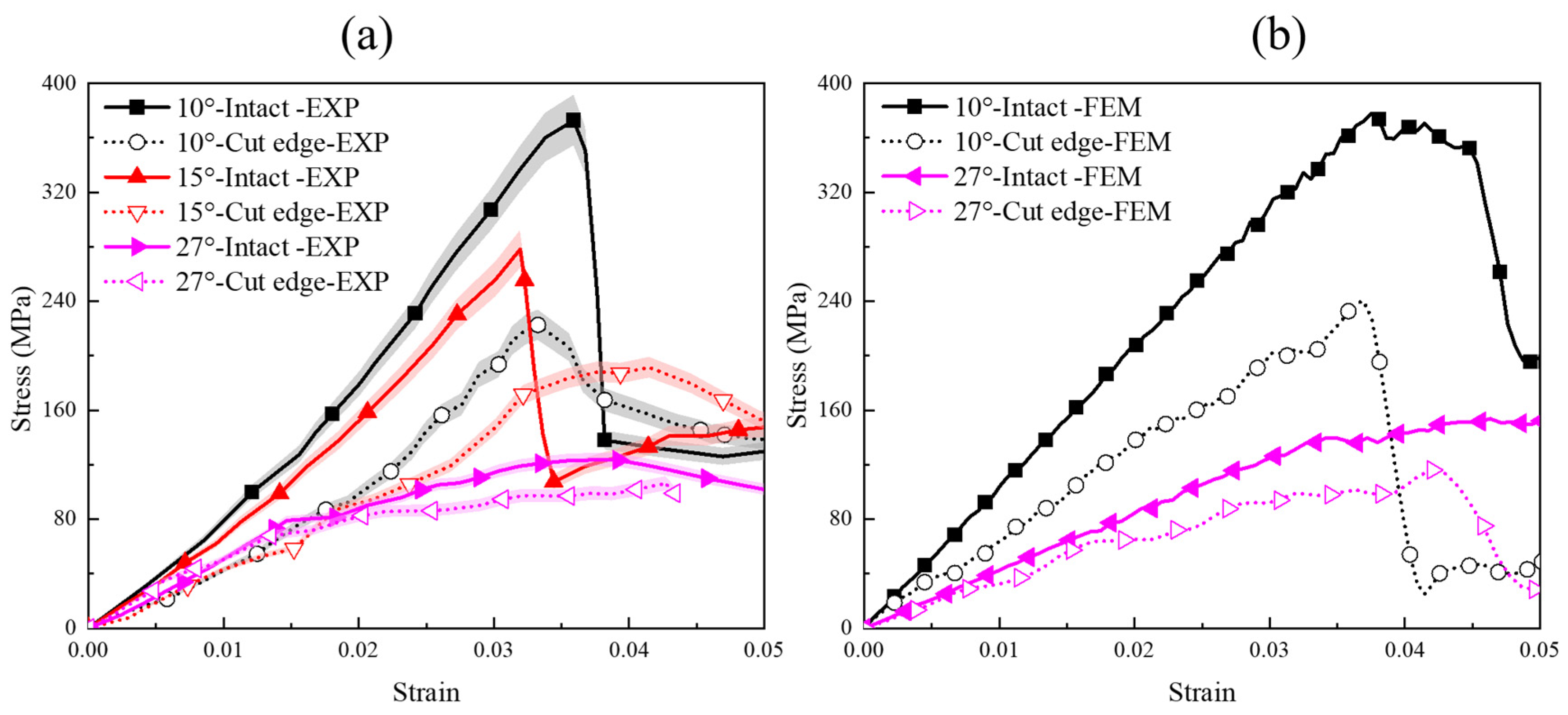
3.1. Compressive Results
3.1.1. Comparisons of Stress–Strain Curves
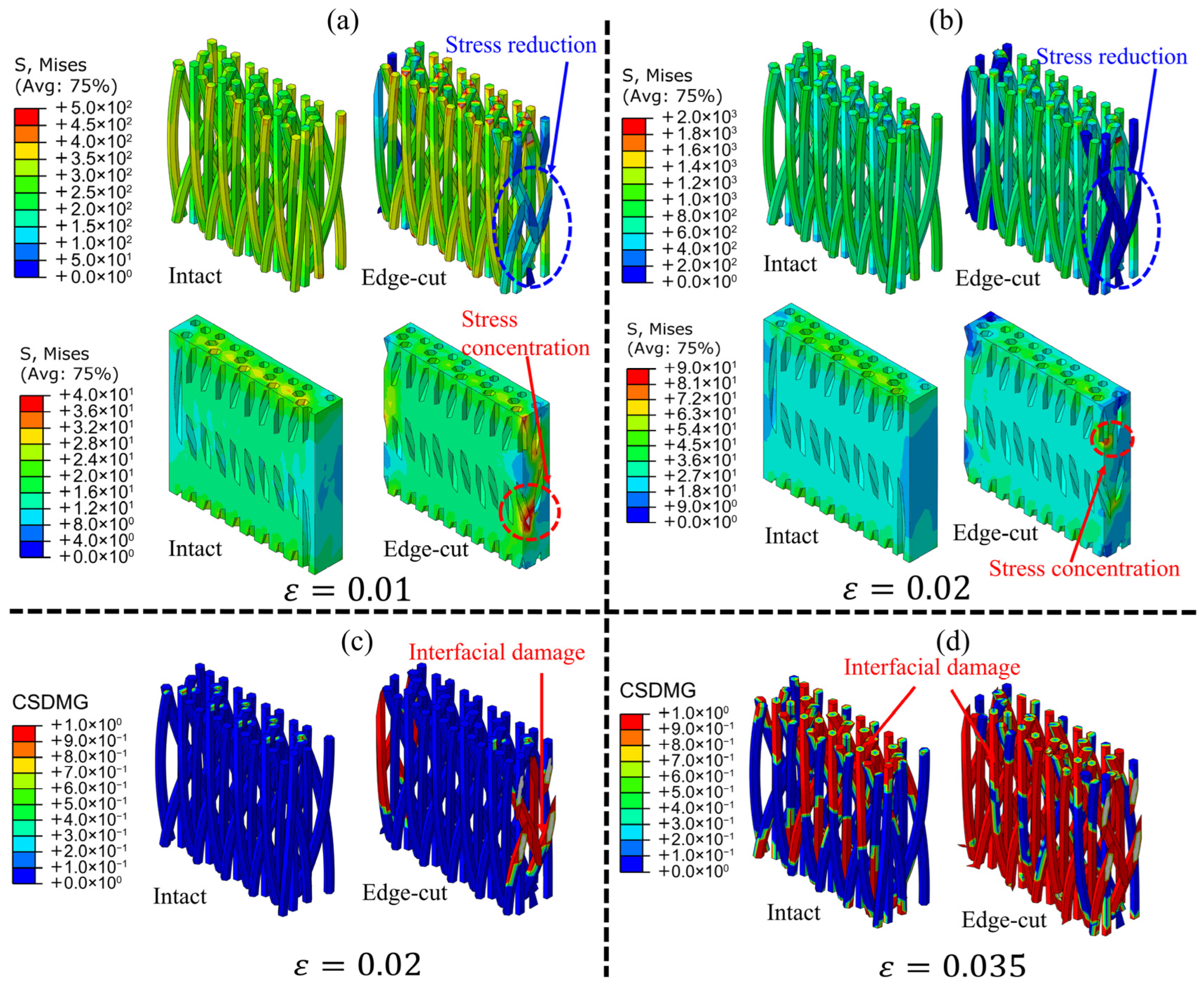
3.1.2. Comparisons of Stress Contours in the Numerical Results
3.2. Three-Point Bending Results
3.2.1. Variations of Stress–Strain Curves
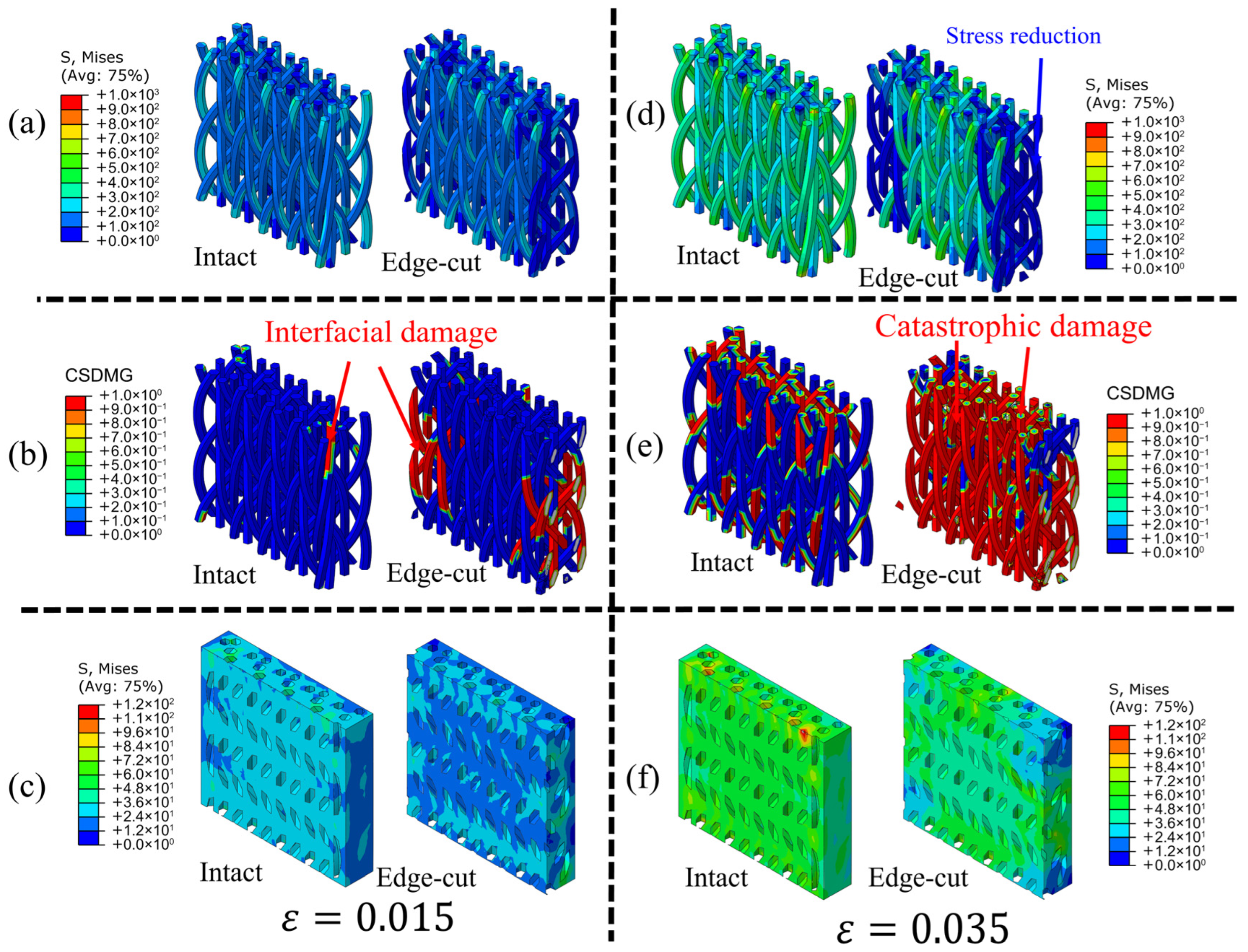
3.2.2. Variations of Stress Contours in the Numerical Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, Y.N.; Quan, Z.Z.; Ren, W.; Qin, X.H.; Yu, J.Y. Multifunctional 3D Carbon Fiber/Epoxy Braided Composites with Excellent Compression Performance and Electromagnetic Interference Shielding. Mater. Lett. 2024, 372, 137036. [Google Scholar] [CrossRef]
- Jiang, L.L.; Li, Z.G.; Wang, D.Y.; Zhai, J.J.; Kong, X.X. Theoretical Analysis of Thermophysical Properties of 3D Carbon/Epoxy Braided Composites with Varying Temperature. Polymers 2024, 16, 1166. [Google Scholar] [CrossRef]
- Yan, H.; Xu, X.Y.; Fu, B.; Fan, X.; Kan, Y.; Yao, X.F. Constitutive Model and Damage of Self-Healing 3D Braided Composites with Microcapsules. Compos. Commun. 2023, 40, 101586. [Google Scholar] [CrossRef]
- Liu, S.K.; Wang, L.Y.; Siddique, A.; Umair, M.; Shi, C.Y.; Pei, X.Y.; Liu, S.Q.; Yin, Y.; Shi, H.T.; Xu, Z.W. Irradiation Multi-Scale Damage and Interface Effects of 3D Braided Carbon Fiber/Epoxy Composites Subjected to High Dose γ-Rays. Compos. Part B Eng. 2024, 281, 111575. [Google Scholar] [CrossRef]
- Li, G.; Wu, T.W.; Xue, Y.S.; Li, Z.Y.; Sun, B.Z.; Gu, B.H. Tensile Damage Self-Monitoring of Carbon Fiber/Epoxy 3D Braided Composites with Electrical Resistance Method. Eng. Fract. Mech. 2024, 296, 109870. [Google Scholar] [CrossRef]
- Qi, Y.Y.; Huang, S.W.; Zhang, H.X.; Gu, B.H.; Sun, B.Z.; Zhang, W. Shape Memory Behaviors of Three-Dimensional Five-Directional Braided Composites with Different Axial Yarns Arrangements. Compos. Struct. 2024, 338, 118105. [Google Scholar] [CrossRef]
- Li, C.Y.; Shi, M.X.; Xing, W.J.; Song, J.J.; Shan, J.T.; Zhang, L.; Feng, C.H. Mechanical Properties of Modified Aramid Three-Dimensional Braided Composites. Polym. Adv. Technol. 2024, 35, e6197. [Google Scholar] [CrossRef]
- Cui, J.K.; Li, D.S.; Jiang, L. Comparison Study on Bending Properties and Failure of 3D5d and 3D6d Carbon/Phenolic Braided Composites at Room and Elevated Temperatures. Compos. Commun. 2023, 42, 101676. [Google Scholar] [CrossRef]
- Yang, X.; Li, D.S.; Jiang, L. Liquid Nitrogen Temperature Effects on the Mechanical Behaviors of Three-Dimensional Seven-Directional Braided Composites. Mater. Lett. 2023, 349, 134786. [Google Scholar] [CrossRef]
- Zuo, H.M.; Li, D.S.; Jiang, L. Transverse Bending Fatigue Behaviors and Failure Mechanisms of 3D Five-Directional Braided Composites at Different Temperatures. Mater. Lett. 2022, 316, 132030. [Google Scholar] [CrossRef]
- Zuo, H.M.; Li, D.S.; Jiang, L.; Fang, D.N. Longitudinal Compression Fatigue Properties of 3D Five-Directional Braided Composites at Different Temperatures. Compos. Struct. 2022, 291, 115602. [Google Scholar] [CrossRef]
- Li, A.; Qiao, K.; Curiel-Sosa, J.L.; Zhang, C. Numerical Study on Off-Axis Tensile Behavior of 3D Braided Composites at Elevated Temperature. Mech. Adv. Mater. Struct. 2024, 31, 1717–1730. [Google Scholar] [CrossRef]
- Li, Z.J.; Dai, H.L.; Liu, Z.G.; Wang, Y. Micro-CT Based Parametric Modeling and Damage Analysis of Three-Dimensional Rotary-Five-Directional Braided Composites under Tensile Load. Compos. Struct. 2023, 309, 116734. [Google Scholar] [CrossRef]
- Du, X.B.; Li, D.S.; Jiang, L.; Fang, D.N. Numerical Investigation on Tensile Behavior of Three-Dimensional Six-Directional Braided Composites. Int. J. Mech. Sci. 2023, 237, 107815. [Google Scholar] [CrossRef]
- Zhu, H.; Du, X.B.; Li, D.S.; Jiang, L. Investigation of Parameterized Braiding Parameters and Loading Directions on Compressive Behavior and Failure Mechanism of 3D Four-Directional Braided Composites. Compos. Struct. 2022, 287, 115357. [Google Scholar] [CrossRef]
- Fang, J.; Zhang, J.J.; Sun, B.Z.; Gu, B.H. Mode I Fracture Mechanisms and Crack Evolution Behavior of Three-Dimensional Braided Composites. Text. Res. J. 2023, 93, 4023–4034. [Google Scholar] [CrossRef]
- Huang, Z.H.; Ma, W.S.; Xu, W.T.; Mao, F.; Chen, C.; Zhao, J.N.; Xu, Y.H. The Formation Mechanism of Gradient Properties and the Regulation Mechanism of Elastic Properties in Three-Dimensional Tubular Braided Composites. Polym. Compos. 2024, 45, 16574–16588. [Google Scholar] [CrossRef]
- Zhang, D.; Zheng, X.T.; Zhou, J.; Song, X.Y.; Jia, P.; Liu, H.B.; Liu, X.C. Effect of Braiding Architectures on the Mechanical and Failure Behavior of 3D Braided Composites: Experimental Investigation. Polymers 2022, 14, 1916. [Google Scholar] [CrossRef]
- Gao, C.T.; Dai, W.J.; Gu, J.P.; Zeng, H.; Sun, H.Y. Mechanical Properties of 3D 4-Directional Braided Composites with a Central Circular Hole under Tension. Mech. Adv. Mater. Struct. 2024, 31, 5856–5868. [Google Scholar] [CrossRef]
- Gao, C.T.; Gu, J.P.; Zeng, H.; Khatibi, A.A.; Sun, H.Y. Prediction of the Stress Distributions and Strength Properties of 3-D Braided Composites with an Eccentric Circular Hole. Mech. Mater. 2023, 185, 104776. [Google Scholar] [CrossRef]
- Huang, H.; Guo, Z.T.; Shan, Z.D.; Sun, Z.; Liu, J.H.; Wang, D.; Wang, W.; Liu, J.L.; Tan, C.C. Prediction of Elastic Properties of 3D4D Rotary Braided Composites with Voids Using Multi-Scale Finite Element and Surrogate Models. Compos. Struct. 2024, 328, 117579. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Li, H.M.; Liu, X.; Gao, Y.H.; Guan, C.Y. Trans-Scale Elastic–Plastic Damage Analysis of 3D Tubular Braided Composites with Void Defects. Int. J. Solids Struct. 2023, 274, 112288. [Google Scholar] [CrossRef]
- Ge, L.; Li, H.M.; Gao, Y.H.; Lou, R.S.; Liu, K.; Zhong, J.H.; Fang, D.N. Parametric Analyses on Multiscale Elastic Behavior of 3D Braided Composites with Pore Defects. Compos. Struct. 2022, 287, 115332. [Google Scholar] [CrossRef]
- Ge, L.; Li, H.M.; Zhong, J.H.; Zhang, C.; Fang, D.N. Micro-CT Based Trans-Scale Damage Analysis of 3D Braided Composites with Pore Defects. Compos. Sci. Technol. 2021, 211, 108830. [Google Scholar] [CrossRef]
- Fu, Y.T.; Yao, X.F.; Gao, X.H. Micro-Mesoscopic Prediction of Void Defect in 3D Braided Composites. Compos. Part A Appl. Sci. Manuf. 2021, 147, 106450. [Google Scholar] [CrossRef]
- Guo, J.H.; Ke, Y.N.; Wu, Y.Y.; Gu, B.H.; Sun, B.Z. Effects of Defect Sizes at Different Locations on Compressive Behaviors of 3D Braided Composites. Thin-Walled Struct. 2022, 179, 109563. [Google Scholar] [CrossRef]
- Zhai, J.J.; Kong, X.X.; Wang, L.C.; Yan, S.; Jiang, L.L.; Cai, Z.W. Nonlinear Mechanical Property of 3D Braided Composites with Multi-Types Micro-Distortion: A Quantitative Evaluation. Polymers 2023, 15, 1428. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Kong, X.X.; Zhai, J.J.; Guo, Z.T.; Yan, S.; Duan, Y.K.; Zheng, Z.J. Advances in Multiscale Modeling and Mechanical Properties Characterization of 3D-Braided Composites. Adv. Eng. Mater. 2024, 26, 2401457. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, S.; Zhao, Z.; Liu, F.; Zhang, H.; Shen, M. Key Issues in Microstructure Modeling of 3D Braided Composites. Mater. Res. Express 2023, 10, 036302. [Google Scholar] [CrossRef]
- He, C.W.; Ge, J.R.; Lian, Y.P.; Geng, L.C.; Chen, Y.F.; Fang, D.N. A Concurrent Three-Scale Scheme FE-SCA2 for the Nonlinear Mechanical Behavior of Braided Composites. Comput. Methods Appl. Mech. Eng. 2022, 393, 114827. [Google Scholar] [CrossRef]
- Lomov, S.V.; Bogdanovich, A.E.; Ivanov, D.S.; Mungalov, D.; Karahan, M.; Verpoest, I. A Comparative Study of Tensile Properties of Non-Crimp 3D Orthogonal Weave and Multi-Layer Plain Weave E-Glass Composites. Part 1: Materials, Methods and Principal Results. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1134–1143. [Google Scholar] [CrossRef]
- Karahan, M.; Lomov, S.V.; Bogdanovich, A.E.; Mungalov, D.; Verpoest, I. Internal Geometry Evaluation of Non-Crimp 3D Orthogonal Woven Carbon Fabric Composite. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1301–1311. [Google Scholar] [CrossRef]
- Karahan, M.; Karahan, N. Stiffness Determination of Bi- and Triaxial Flat Braided Carbon/Vinyl Ester Composites Using Micromechanics Method. Tekstilec 2024, 67, 346–356. [Google Scholar] [CrossRef]
- Li, J.L.; Jiao, Y.N.; Sun, Y.; Wei, L.M. Experimental Investigation of Cut-Edge Effect on Mechanical Properties of Three-Dimensional Braided Composites. Mater. Des. 2007, 28, 2417–2424. [Google Scholar] [CrossRef]
- Wang, Y.B.; Liu, Z.G.; Lei, B.; Huang, X.; Li, X.K. Investigation on the Bearing Abilities of Three-Dimensional Full Five-Directional Braided Composites with Cut-Edge. Appl. Compos. Mater. 2017, 24, 893–910. [Google Scholar] [CrossRef]
- Zhang, D.T.; Yu, S.; Feng, G.Y.; Xiao, X.L.; Ma, Q.R.; Qian, K. Numerical Identification of Meso Length-Effect and Full-Field Edge-Effect of 3D Braided Composites. Appl. Compos. Mater. 2018, 25, 1133–1154. [Google Scholar] [CrossRef]
- Karahan, M.; Karahan, N. Investigation of the Tensile Properties of Natural and Natural/Synthetic Hybrid Fiber Woven Fabric Composites. J. Reinf. Plast. Compos. 2015, 34, 795–806. [Google Scholar] [CrossRef]
- ASTM D7264/D7264M-21; Standard Test Method for Flexural Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2021. [CrossRef]
- ASTM D6641/D6641M-16; Standard Test Method for Compressive Properties of Polymer Matrix Composite Materials Using a Combined Loading Compression (CLC) Test Fixture. ASTM International: West Conshohocken, PA, USA, 2016. [CrossRef]
- Liu, T.; Fan, W.; Wu, X.Y. Comparisons of influence of random defects on the impact compressive behavior of three different textile structural composites. Mater. Des. 2019, 181, 108073. [Google Scholar] [CrossRef]
- Liu, T.; Wu, X.Y.; Sun, B.Z.; Fan, W.; Han, W.L.; Yi, H.L. Investigations of defect effect on dynamic compressive failure of 3D circular braided composite tubes with numerical simulation method. Thin-Walled Struct. 2021, 160, 107381. [Google Scholar] [CrossRef]
- Liu, T.; Wen, D.Y.; Shen, Q.L.; Liang, J.H.; Chen, Y.; Fang, Z.; Zhang, M.Y.; Cheng, S.Q.; Gao, Y.X.; Gao, X.Z. A novel modeling method to study compressive behaviors of 3D braided composites considering effects of fiber breakage and waviness defects. Compos. Struct. 2024, 340, 118206. [Google Scholar] [CrossRef]





| Values | |
|---|---|
| Axial modulus of braided yarn, E11 (GPa) | 160 |
| Transversal modulus of braided yarn, E22 = E33 (GPa) | 14 |
| Poisson’s ratio of braided yarn, ν 12 = ν 13 | 0.265 |
| Shear modulus of braided yarn, G12 = G13 (GPa) | 9 |
| Shear modulus of braided yarn, G23 (GPa) | 5 |
| Young’s Modulus of resin matrix, E (GPa) | 2.3 |
| Poisson’s ratio of resin matrix, ν | 0.3 |
| Modulus of interface, K (N/mm3) | 3000 |
| Matrix strength of interface, t (MPa) | 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Zhang, Z.; Liu, T.; Wu, Z.; Zhang, H.; Zhu, R.; Chen, Y.; Ouyang, Y.; Dong, J. Investigations of Edge Cutting Effects on Mechanical Behaviors of 3D Braided Composites with Different Braiding Angles. J. Compos. Sci. 2025, 9, 573. https://doi.org/10.3390/jcs9110573
Bai Y, Zhang Z, Liu T, Wu Z, Zhang H, Zhu R, Chen Y, Ouyang Y, Dong J. Investigations of Edge Cutting Effects on Mechanical Behaviors of 3D Braided Composites with Different Braiding Angles. Journal of Composites Science. 2025; 9(11):573. https://doi.org/10.3390/jcs9110573
Chicago/Turabian StyleBai, Yafei, Zhen Zhang, Tao Liu, Ziyi Wu, Haolong Zhang, Ruixing Zhu, Yue Chen, Yiwei Ouyang, and Jingjing Dong. 2025. "Investigations of Edge Cutting Effects on Mechanical Behaviors of 3D Braided Composites with Different Braiding Angles" Journal of Composites Science 9, no. 11: 573. https://doi.org/10.3390/jcs9110573
APA StyleBai, Y., Zhang, Z., Liu, T., Wu, Z., Zhang, H., Zhu, R., Chen, Y., Ouyang, Y., & Dong, J. (2025). Investigations of Edge Cutting Effects on Mechanical Behaviors of 3D Braided Composites with Different Braiding Angles. Journal of Composites Science, 9(11), 573. https://doi.org/10.3390/jcs9110573








