Shear Capacity of Fiber-Reinforced Polymer (FRP)–Reinforced Concrete (RC) Beams Without Stirrups: Comparative Modeling with FRP Modulus, Longitudinal Ratio, and Shear Span-to-Depth
Abstract
1. Introduction
2. Methodology
- Data Collection: The study uses a database of 402 data points from experimental tests on concrete beams reinforced with FRP bars without stirrups. These data were collected from existing literature as demonstrated in Table 1.
- Variable Selection: Identifying and considering key variables that influence shear strength, including beam size (depth and width), reinforcement index, modulus of elasticity of FRP bars, concrete compressive strengths, and shear/span ratio.
- Model Development: Proposing different models for predicting shear strength by considering various combinations of the variables. The models are developed using both linear and nonlinear regression analysis methods.
- Comparison with Existing Models: The predicted results from the proposed models are compared with 15 existing models from codes, standards, and literature to evaluate their accuracy and correlation with experimental data.
- Analysis and Recommendation: The study analyses the performance of these models, identifies the best-performing model, and recommends it for predicting the shear strength of concrete beams reinforced with FRP bars.
2.1. Database Assembly, Screening, and Validation
2.2. Modeling
2.2.1. Multi-Non-Linear Regression (MNLR) Model
2.2.2. Modified ACI Equations
2.2.3. Multi-Linear Regression (MLR) Model
2.2.4. Power Function Models
3. Results and Discussion
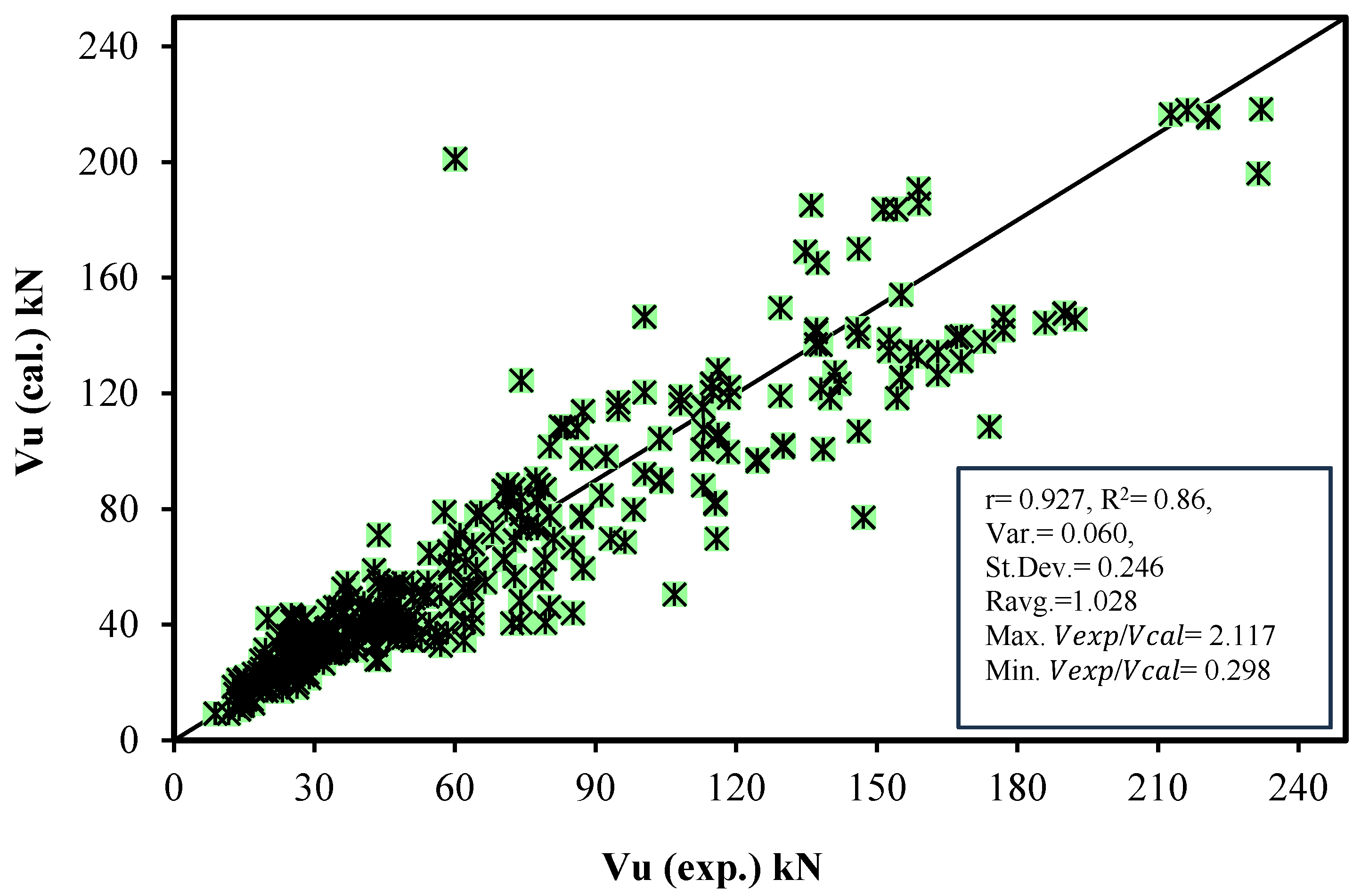
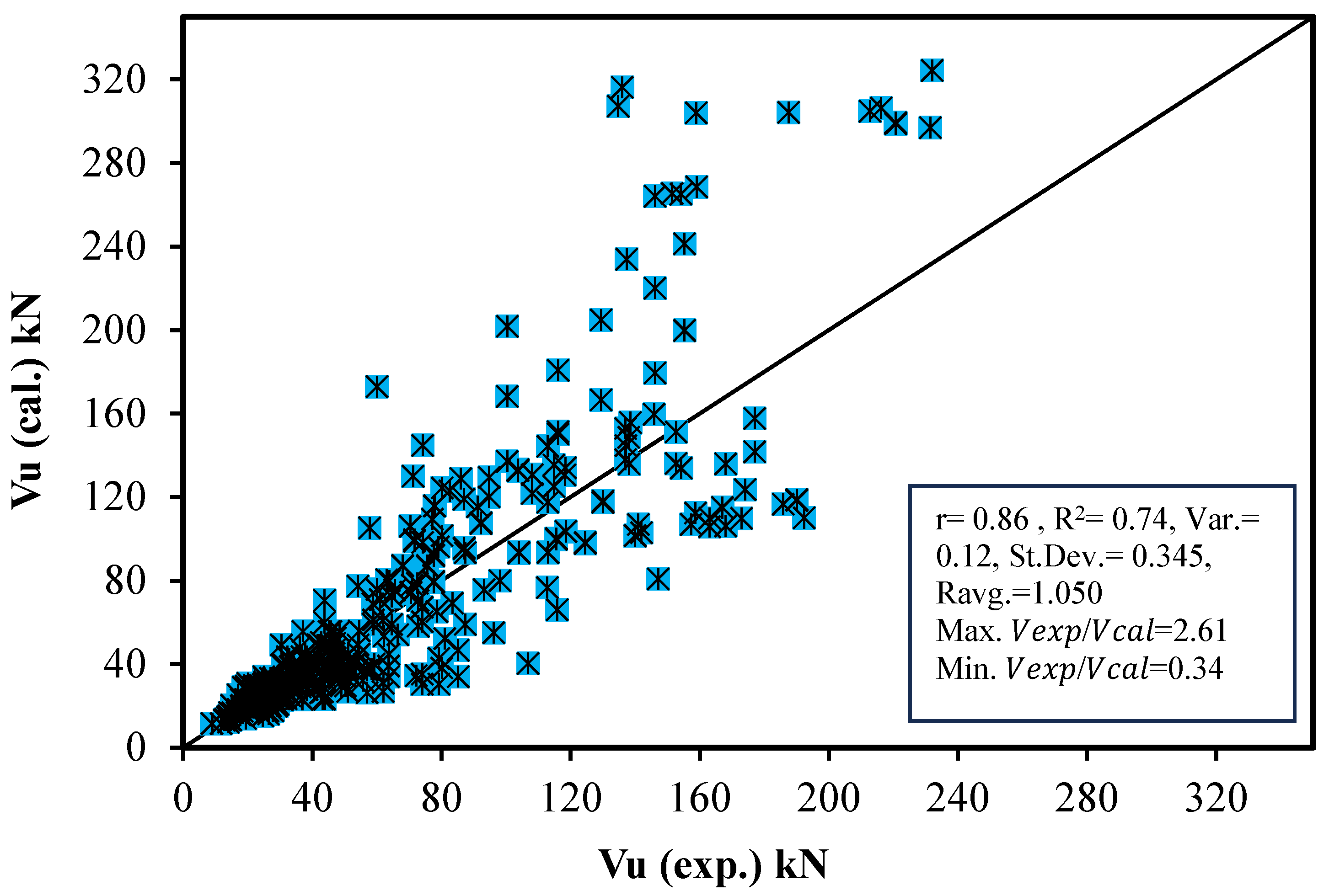
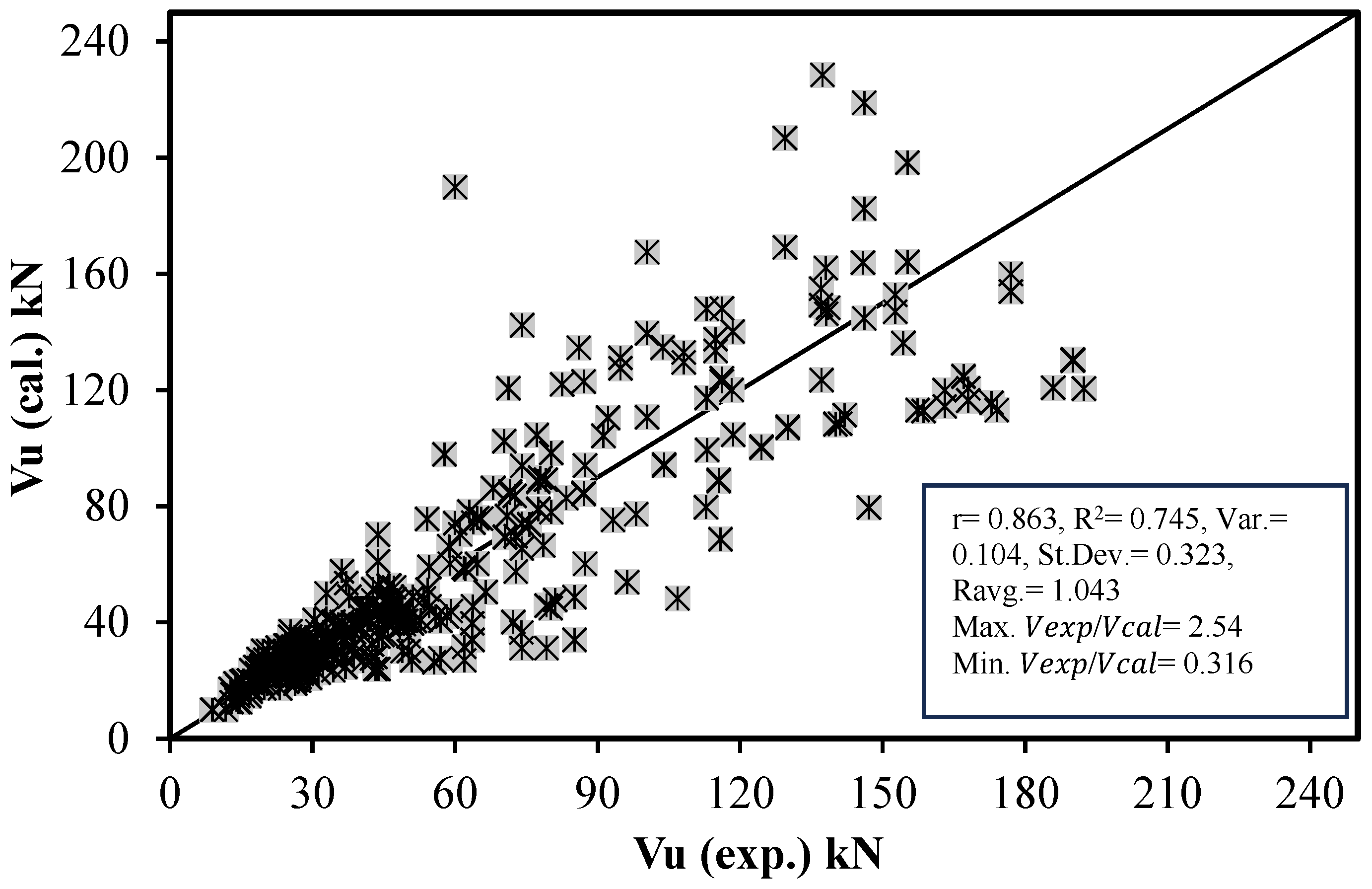
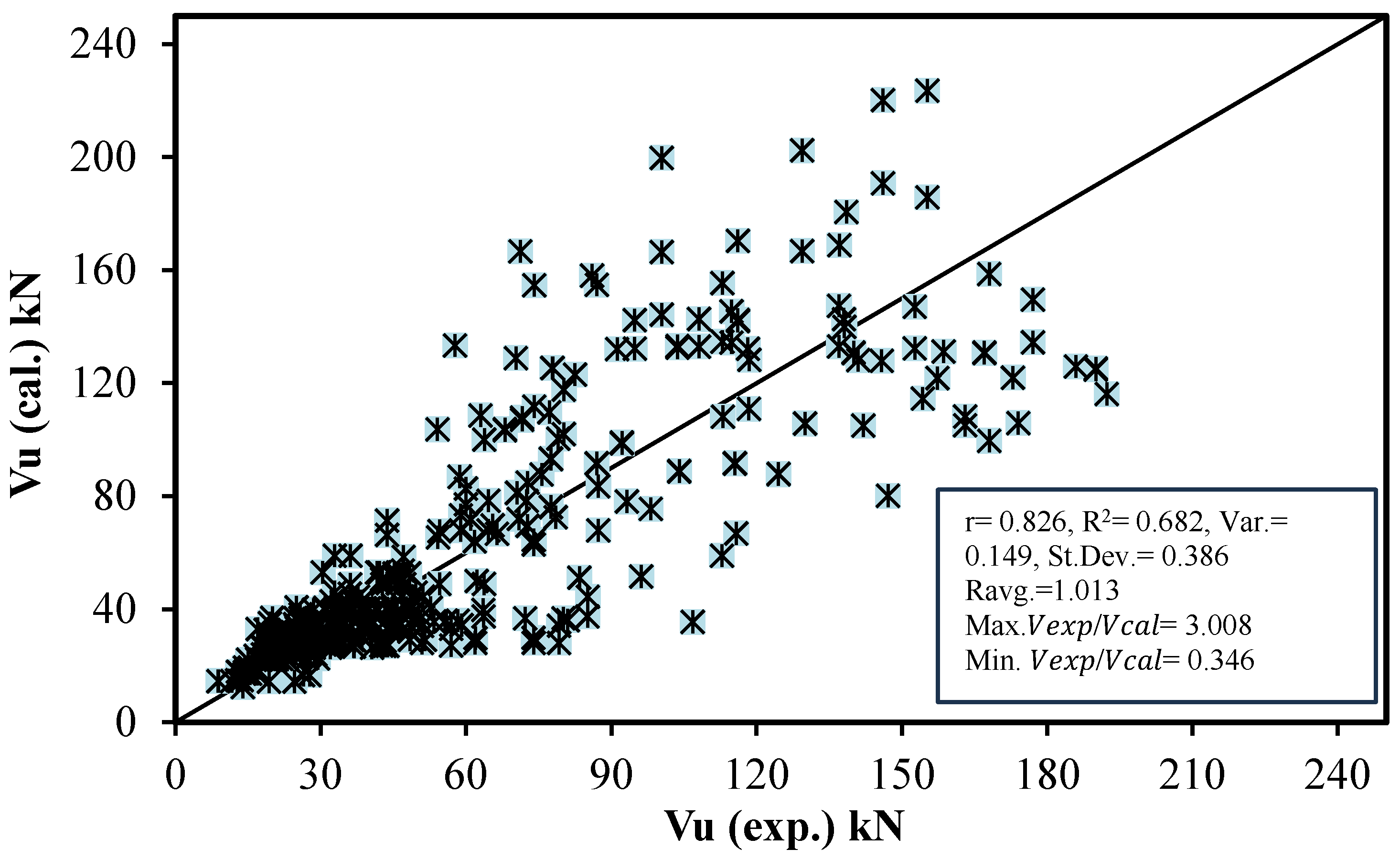
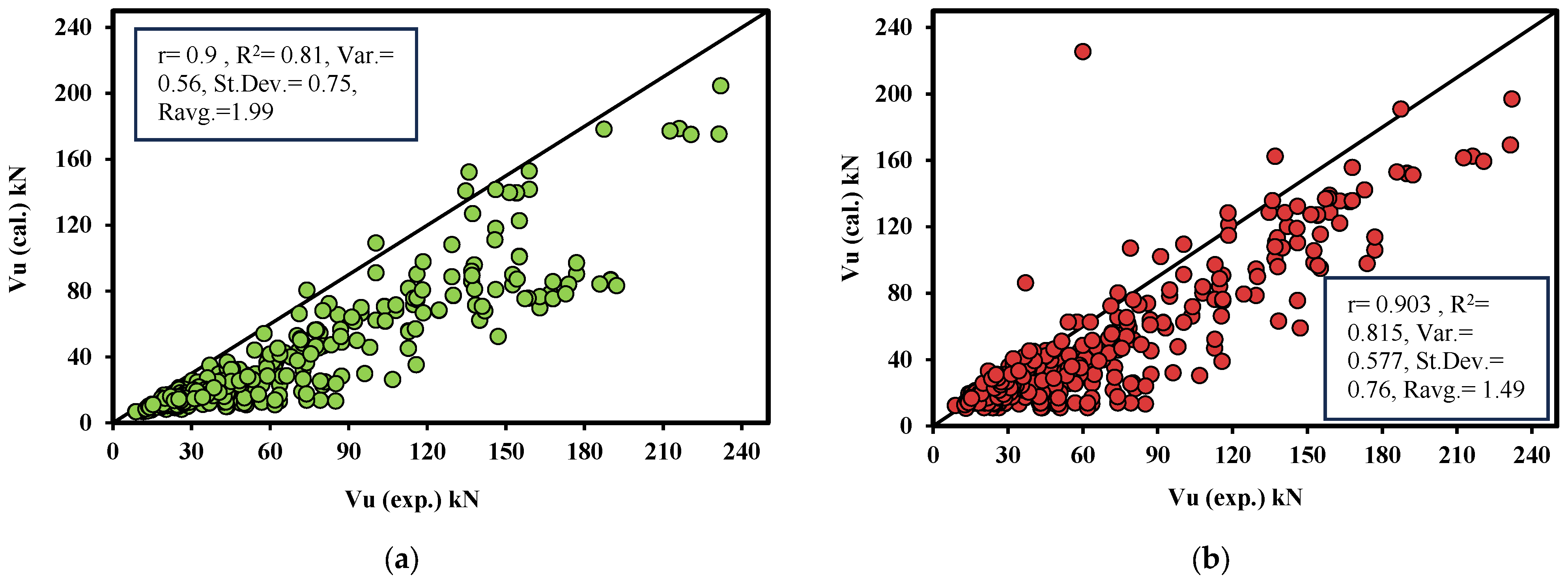
3.1. Relationship Between Predicted and Measured Shear Strength
3.1.1. Multi-Non-Linear Regression (MNLR) Model
3.1.2. Modified ACI Equations
3.1.3. Multi-Linear Regression (MLR) Model
3.2. Evaluation of Proposed Models
3.3. Effect of Parameters
3.3.1. Shear Span-to-Depth Ratio (a/d)
3.3.2. Longitudinal Reinforcement and Axial Stiffness (ρf, ρf·Ef, Ef/Es)
3.3.3. Concrete Compressive Strength (f′c)
3.3.4. Member Size Effects (bw, d)
3.3.5. Interactions and Model Hierarchy
3.3.6. Design Implications
3.4. Segmented Validation and Boundary Assessment
- Shear span-to-depth: low a/d < 2.5, medium 2.5 ≤ a/d ≤ 4.5, high a/d > 4.5.
- FRP elastic modulus Ef: low < 50 GPa (typical GFRP), medium 50–100 GPa, high > 100 GPa (CFRP/BFRP upper range).
- Longitudinal reinforcement: ρf low/med/high (tertiles), and axial stiffness ρfEf low/med/high (tertiles).
- Member depth d: shallow d < 200 mm, intermediate 200–400 mm, deep d > 400 mm; we additionally flag very deep d ≥ 800 mm.
- Concrete strength f’c: low < 30 MPa, medium 30–60 MPa, high > 60 MPa.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thimmegowda, D.Y.; Hindi, J.; Markunti, G.B.; Kakunje, M. Enhancement of Mechanical Properties of Natural Fiber Reinforced Polymer Composites Using Different Approaches—A Review. J. Compos. Sci. 2025, 9, 220. [Google Scholar] [CrossRef]
- ACI Committee 440. Guide for the Design and Construction of Concrete Reinforced with FRP Bars; ACI 440.1R-01; American Concrete Institute: Farmington Hills, MI, USA, 2001. [Google Scholar]
- CSA S806-02; Design and Construction of Building Components with Fibre-Reinforced Polymers. Canadian Standards Association (CSA): Rexdale, ON, Canada, 2002; 177p.
- JSCE. Recommendation for Design and Construction of Concrete Structures Using Continuous Fiber Reinforced Materials; Machida, A., Ed.; Research Committee on Continuous Fiber Reinforced Materials; Japan Society of Civil Engineers: Tokyo, Japan, 1997. [Google Scholar]
- Tureyen, A.K.; Frosch, R.J. Shear Strength of FRP-Reinforced Concrete Beams without Stirrups. ACI Struct. J. 2002, 99, 427–443. [Google Scholar]
- El-Sayed, A.K.; El-Salakawy, E.F.; Benmokrane, B. Shear capacity of high-strength concrete beams reinforced with FRP bars. ACI Struct. J. 2006, 103, 383–389. [Google Scholar]
- Comité Euro-International du Béton; Fédération Internationale de la Précontrainte (CEB–FIP). Model Code 1990; Thomas Telford: London, UK, 1993. [Google Scholar]
- JSCE. Standard Specifications for Design and Construction of Concrete Structures. Part 1: Design; Japan Society of Civil Engineers: Tokyo, Japan, 1998. [Google Scholar]
- BS 8110:1985; Structural Use of Concrete—Code of Practice. British Standards Institution (BSI): London, UK, 1985.
- Hassan, B.R.; Yousif, A.R. Shear performance and strength of reinforced concrete non-prismatic beams with basalt fiber-reinforced polymer rebars. Structures 2024, 65, 106571. [Google Scholar]
- Ketenci, M.S.; Doğan, G. Enhancing the shear strengthening of reinforced concrete T-shaped beams using innovative fiber blocks/panels. Structures 2024, 63, 106294. [Google Scholar] [CrossRef]
- Zhao, W.; Maruyama, K. Shear behavior of concrete beams reinforced by FRP rods as longitudinal and shear reinforcement. In Non-Metallic (FRP) Reinforcement for Concrete Structures (FRPRCS-2); Taerwe, L., Ed.; CRC Press: Ghent, Belgium, 1995; pp. 352–359. [Google Scholar]
- Kar, S.; Biswal, K.C. Shear strengthening of reinforced concrete T-beams using fiber-reinforced polymer composites: A data analysis. Arab. J. Sci. Eng. 2020, 45, 4203–4234. [Google Scholar] [CrossRef]
- Askandar, N.H.; Jumaa, G.B.; Ahmed, G.H. Modeling for torsional strength prediction of strengthened RC beams. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 2535–2553. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Ibna Zahid, Z.; Islam, M.M. Development of shear capacity prediction model for FRP-RC beam without web reinforcement. Adv. Mater. Sci. Eng. 2016, 2016, 4356967. [Google Scholar] [CrossRef]
- Alam, M.S.; Hussein, A. Relationship between the shear capacity and the flexural cracking load of FRP-reinforced concrete beams. Constr. Build. Mater. 2017, 154, 819–828. [Google Scholar] [CrossRef]
- Razaqpur, A.G.; Isgor, O.B.; Greenaway, S.; Selley, A. Concrete contribution to the shear resistance of fiber-reinforced polymer reinforced concrete members. J. Compos. Constr. 2004, 8, 452–460. [Google Scholar] [CrossRef]
- El-Sayed, A.K.; Salakawy, E.; Benmokrane, B. Shear strength of one-way concrete slabs reinforced with fiber-reinforced polymer composite bars. J. Compos. Constr. 2005, 9, 147–157. [Google Scholar] [CrossRef]
- Rosa, I.C.; Firmo, J.P.; Correia, J.R.; Bisby, L.A. Fire behavior of GFRP-reinforced concrete structural members: A state-of-the-art review. J. Compos. Constr. 2023, 27, 03123002. [Google Scholar] [CrossRef]
- Matta, M.; Nanni, A.; Galati, N.; Mosele, F. Size effect on shear strength of concrete beams reinforced with FRP bars. In Proceedings of the 6th International Conference on Fracture Mechanics of Concrete and Concrete Structures (FraMCoS’08); 2008; Volume 2, pp. 17–22. [Google Scholar]
- Yost, J.R.; Gross, S.P.; Dinehart, D.W. Shear strength of normal-strength concrete beams reinforced with deformed GFRP bars. J. Compos. Constr. 2001, 5, 268–275. [Google Scholar] [CrossRef]
- Razaqpur, A.G.; Shedid, M.; Isgor, O.B. Shear strength of fiber-reinforced polymer reinforced concrete beams subjected to unsymmetric loading. J. Compos. Constr. 2011, 15, 512. [Google Scholar] [CrossRef]
- Abdul-Salam, B.; Farghaly, A.S.; Benmokrane, B. Evaluation of shear behaviour for one-way concrete slabs reinforced with carbon FRP bars. In Proceedings of the CSCE 2013 General Conference, Montréal, QC, Canada, 29 May–1 June 2013. [Google Scholar]
- Kim, C.H.; Jang, H.S. Concrete shear strength of normal and lightweight concrete beams reinforced with FRP bars. J. Compos. Constr. 2014, 18, 04013038. [Google Scholar] [CrossRef]
- Ashour, A.F.; Kara, I.F. Size effect on shear strength of FRP-reinforced concrete beams. Compos. Part B Eng. 2014, 60, 612–620. [Google Scholar] [CrossRef]
- Ashour, A.F. Flexural and shear capacities of concrete beams reinforced with GFRP bars. Constr. Build. Mater. 2006, 20, 1005–1015. [Google Scholar] [CrossRef]
- Guadagnini, M.; Pilakoutas, K.; Waldron, P. Shear resistance of FRP-RC beams: Experimental study. J. Compos. Constr. 2006, 10, 464–473. [Google Scholar] [CrossRef]
- Olivito, R.S.; Zuccarello, F.A. On the shear behaviour of concrete beams reinforced by carbon fibre-reinforced polymer bars: An experimental investigation by means of acoustic emission technique. Strain 2010, 46, 470–481. [Google Scholar] [CrossRef]
- Michaluk, C.R.; Rizkalla, S.H.; Tadros, G.; Benmokrane, B. Flexural behavior of one-way concrete slabs reinforced by fiber-reinforced plastic reinforcements. ACI Struct. J. 1998, 95, 353–365. [Google Scholar]
- Issa, M.A.; Ovitigala, T.; Ibrahim, M. Shear behavior of basalt fiber-reinforced concrete beams with and without basalt FRP stirrups. J. Compos. Constr. 2016, 20, 04015083. [Google Scholar] [CrossRef]
- El Refai, A.; Abed, F. Concrete contribution to shear strength of beams reinforced with basalt fiber-reinforced bars. J. Compos. Constr. 2016, 20, 04015082. [Google Scholar] [CrossRef]
- Deitz, D.H.; Harik, I.E.; Gesund, H. One-way slabs reinforced with glass fiber-reinforced polymer reinforcing bars. In Proceedings of the 4th International Symposium, Bordeaux, France, 13–16 September 1999; American Concrete Institute: Detroit, MI, USA, 1999; pp. 279–286. [Google Scholar]
- El-Sayed, A.K.; El-Salakawy, E.F.; Benmokrane, B. Shear strength of FRP-reinforced concrete beams without transverse reinforcement. ACI Struct. J. 2006, 103, 235–243. [Google Scholar] [CrossRef]
- Alkhrdaji, T.; Wideman, M.; Belarbi, A.; Nanni, A. Shear strength of RC beams and slabs. In Composites in Construction; Figueiras, J., Juvandes, L., Faria, R., Eds.; A.A. Balkema: Lisse, The Netherlands, 2001; pp. 409–414. [Google Scholar]
- Tariq, M.; Newhook, J.P. Shear testing of FRP-reinforced concrete without transverse reinforcement. In Proceedings of the Annual Conference of the Canadian Society for Civil Engineering, Moncton, NB, Canada, 4–7 June 2003; pp. 1330–1339. [Google Scholar]
- Mizukawa, Y.; Sato, Y.; Ueda, T.; Kakuta, Y. A study on shear fatigue behavior of concrete beams with FRP rods. In Proceedings of the 3rd International Symposium on Non-Metallic (FRP) Reinforcement for Concrete Structures (FRPRCS-3), Sapporo, Japan, 14–16 October 1997; Japan Concrete Institute: Sapporo, Japan, 1997; pp. 309–316. [Google Scholar]
- Alam, M.S. Influence of Different Parameters on Shear Strength of FRP-Reinforced Concrete Beams without Web Reinforcement. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2010. [Google Scholar]
- Steiner, S.; El-Sayed, A.K.; Benmokrane, B.; Matta, F.; Nanni, A. Shear strength of large-size concrete beams reinforced with glass FRP bars. In Proceedings of the 5th International Conference on Advanced Composite Materials in Bridges and Structures (ACMBS-V), Winnipeg, MB, Canada, 22–24 September 2008. [Google Scholar]
- Duranovic, N.; Pilakoutas, K.; Waldron, P. Tests on concrete beams reinforced with glass fiber-reinforced plastic bars. In Proceedings of the 3rd International Symposium on Non-Metallic (FRP) Reinforcement for Concrete Structures (FRPRCS-3), Sapporo, Japan, 14–16 October 1997; Japan Concrete Institute: Sapporo, Japan, 1997; pp. 479–486. [Google Scholar]
- Bentz, E.C.; Massam, L.; Collins, M.P. Shear strength of large concrete members with FRP reinforcement. J. Compos. Constr. 2010, 14, 637–646. [Google Scholar] [CrossRef]
- Matta, F.; El-Sayed, A.K.; Nanni, A.; Benmokrane, B. Size effect on concrete shear strength in beams reinforced with fiber-reinforced polymer bars. ACI Struct. J. 2013, 110, 617–628. [Google Scholar] [CrossRef]
- Gross, S.P.; Yost, J.R.; Dinehart, D.; Suensen, E.; Liu, N. Shear strength of normal- and high-strength concrete beams reinforced with GFRP reinforcing bars. In Proceedings of the International Conference on High Performance Materials in Bridges; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2003; pp. 426–437. [Google Scholar]
- Jang, H.; Kim, M.; Cho, J.; Kim, C. Concrete shear strength of beams reinforced with FRP bars according to flexural reinforcement ratio and shear span-to-depth ratio. In Proceedings of the 9th International Symposium on Fiber-Reinforced Polymer Reinforcement for Concrete Structures (FRPRCS-9), Adelaide, Australia, 12–15 July 2009. [Google Scholar]
- Tottori, S.; Wakui, H. Shear Capacity of RC and PC Beams Using FRP Reinforcement; ACI Special Publication: Farmington Hills, MI, USA, 1993; Volume 138. [Google Scholar]
- Nagasaka, T.; Fukuyama, H.; Tanigak, M. Shear Performance of Concrete Beams Reinforced with FRP Stirrups; ACI Special Publication: Farmington Hills, MI, USA, 1993; Volume 138. [Google Scholar]
- Nakamura, H.; Higai, T. Evaluation of shear strength of concrete beams reinforced with FRP. Proc. Jpn. Soc. Civ. Eng. 1995, 26, 89–100. [Google Scholar] [CrossRef] [PubMed]
- Massam, L. The Behaviour of GFRP Reinforced Concrete Beams in Shear. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 1993. [Google Scholar]
- Alkhrdaji, T.; Nanni, A. Surface-bonded FRP reinforcement for strengthening/repair of reinforced concrete structures. In Proceedings of the ICRI–NRCC Workshop, Baltimore, MD, USA, 30 October 1999; p. 19. [Google Scholar]
- Gross, S.P.; Walkup, S.L.; Musselman, E.S.; Stefanski, D.J. Influence of gross-to-cracked section moment of inertia ratio on long-term deflections in GFRP-reinforced concrete members. J. Compos. Constr. 2018, 22, 04018059. [Google Scholar] [CrossRef]
- Swamy, R.N.; Aburawi, M. Structural implications of using GFRP bars as concrete reinforcement. In Proceedings of the 3rd International Symposium on Non-Metallic (FRP) Reinforcement for Concrete Structures (FRPRCS-3), Sapporo, Japan, 14–16 October 1997; Japan Concrete Institute: Sapporo, Japan, 1997; Volume 2, pp. 503–510. [Google Scholar]
- Maruyama, K.; Zhao, W.J. Flexural and shear behavior of concrete beams reinforced with FRP rods. In Corrosion and Corrosion Protection of Steel in Concrete; Sheffield Academic Press: London, UK, 1994; pp. 1330–1339. [Google Scholar]
- Lubell, A.; Sherwood, T.; Bentz, E.C.; Collins, M.P. Safe shear design of large wide beams. Concr. Int. 2004, 26, 66–78. [Google Scholar]
- Alam, M.S.; Hussein, A. Effect of member depth on shear strength of high-strength FRP-reinforced concrete beams. J. Compos. Constr. 2012, 16, 119–126. [Google Scholar] [CrossRef]
- Kilpatrick, A.E.; Easden, L.R. Shear Capacity of GFRP-Reinforced High Strength Concrete Slabs. In Developments in Mechanics of Structures and Materials; Deeks, A.J., Hao, H., Eds.; Taylor & Francis: Abingdon, UK, 2005; Volume 1, pp. 119–124. [Google Scholar]
- Kilpatrick, A.E.; Dawborn, R. Flexural Shear Capacity of High Strength Concrete Slabs Reinforced with Longitudinal GFRP Bars. In Proceedings of the FIB Conference, Naples, Italy, 5–8 June 2006; pp. 1–10. [Google Scholar]
- Niewels, J. Zum Tragverhalten von Betonbauteilen mit Faserverbundkunststoff-Bewehrung. Ph.D. Thesis, Aachen University, Aachen, Germany, 2008. [Google Scholar]
- El-Sayed, A.K.; Soudki, K.; Kling, E. Flexural Behaviour of Self-Consolidating Concrete Slabs Reinforced with GFRP Bars. In Proceedings of the FRPRCS-9, Sydney, Australia, 13–15 July 2009. [Google Scholar]
- Caporale, A.; Luciano, R. Indagine Sperimentale e Numerica sulla Resistenza a Taglio di Travi di Calcestruzzo Armate con Barre di GFRP. In XXXVIII Convegno Nazionale AIAS; AIAS: Washington, DC, USA, 2009; p. 10. [Google Scholar]
- Jumaa, G.B.; Yousif, A.R. Predicting shear capacity of FRP-reinforced concrete beams without stirrups by artificial neural networks, gene expression programming, and regression analysis. Adv. Civ. Eng. 2018, 2018, 5157824. 16p. [Google Scholar] [CrossRef]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary (ACI 318R-19); American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- ISIS Canada. Reinforced Concrete Structures with Fibre-Reinforced Polymers: Design Manual No. 3; ISIS-M03-01; Intelligent Sensing for Innovative Structures, The Canadian Network of Centres of Excellence, University of Manitoba: Winnipeg, MB, Canada, 2001; 81p. [Google Scholar]
- CAN/CSA-S806-02; Design and Construction of Building Components with Fibre-Reinforced Polymers. Canadian Standards Association (CSA): Mississauga, ON, Canada, 2004.
- ISE, Institution of Structural Engineers (IStructE). Interim Guidance on the Design of Reinforced Concrete Structures Using Fibre Composite Reinforcement; Institution of Structural Engineers: London, UK, 1999. [Google Scholar]
- CAN3-A23.3-M94; Design of Concrete Structures for Buildings. Canadian Standards Association (CSA): Rexdale, ON, Canada, 1994.










| No. | Reference | No. of Samples | d (mm) | a/d | b (mm) | ρf (%) | f′c (MPa) | Ef (GPa) | Vu (kN) | Failure Mode |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Tureyen and Frosch [5] | 6 | 360 | 3.4 | 457 | 0.96–1.92 | 34.5 | 37.6–47 | 94.8–177 | Diagonal Tension |
| 2 | El-Sayed et al. [6] | 17 | 154–326 | 3.1–6.5 | 250–1000 | 0.39–2.63 | 40–63 | 39–134 | 60–190 | Shear Failure |
| 3 | Razaqpur et al. [17] | 7 | 225 | 1.82–4.5 | 200 | 0.25–0.88 | 40.5–49 | 145 | 36.11–96.18 | Shear Failure |
| 4 | Alam and Hussein [16] | 29 | 305–744 | 2.5 | 250 | 0.18–1.47 | 34.5–88.3 | 46.3 | 58.6–155.2 | Shear Failure |
| 5 | Matta et al. [20] | 13 | 146–883 | 3.11–3.13 | 114–457 | 0.59–1.17 | 29.5–59.7 | 41–48.2 | 17.9–212.7 | Shear Failure |
| 6 | El-Sayed et al. [18] | 8 | 154.1–165.3 | 6–6.5 | 1000 | 0.39–2.63 | 40 | 40–114 | 113–190 | Diagonal Tension |
| 7 | Yost et al. [21] | 20 | 225 | 4.06–4.08 | 121–254 | 1.1–2.27 | 36.3 | 40.3 | 13.9–51.1 | Diagonal Tension |
| 8 | Razaqpur et al. [22] | 6 | 200–500 | 3.5–6.5 | 300 | 0.28–0.35 | 52.3 | 114 | 54.1–71.2 | Shear Tension |
| 9 | Abdul-Salam et al. [23] | 9 | 140 | 6.2 | 1000 | 0.52–1.25 | 41.3–86.2 | 140–144 | 118.5–192.3 | Diagonal Tension |
| 10 | Kim and Jang [24] | 34 | 214–216 | 2.5–4.5 | 150–200 | 0.33–0.79 | 30 | 48.2–147.9 | 16.9–35.4 | Shear Failure |
| 11 | Ashour and Kara [25] | 6 | 170–370 | 2.7–5.9 | 200 | 0.12–0.52 | 22.14–28.7 | 141.4 | 17.58–36.12 | Shear Failure |
| 12 | Ashour [26] | 6 | 168–263 | 2.53–4.09 | 150 | 0.45–1.3 | 28.9–50.2 | 32–38 | 13.1–3.9 | Shear Tension |
| 13 | Guadagnini et al. [27] | 3 | 150–223 | 1.1–3.35 | 150–224 | 1.28–2.28 | 42.8–43 | 45–46 | 27.9–81 | Diagonal Tension |
| 14 | Olivito and Zuccarello [28] | 4 | 170 | 5.88 | 150 | 1.33–2.22 | 20–26.6 | 113 | 19.3–27.7 | Shear Tension |
| 15 | Michaluk et al. [29] | 2 | 104–154 | 8.44–12.5 | 1000 | 0.76–0.96 | 66 | 41.3 | 37.03–79.05 | Shear compression |
| 16 | Issa et al. [30] | 6 | 165–170 | 5.65–7 | 300 | 0.803–4.121 | 35.9 | 48–53 | 29.3–51.5 | Diagonal Tension |
| 17 | El Refai and Abed [31] | 8 | 206–220 | 2.5–3.3 | 152 | 0.31–1.52 | 49 | 50 | 17–31.6 | Diagonal Tension |
| 18 | Deitz et al. [32] | 5 | 157.5 | 4.5–5.8 | 305 | 0.73 | 27–30.8 | 40 | 28–30.8 | Shear Failure |
| 19 | El-Sayed et al. [33] | 10 | 326 | 3.07 | 250 | 0.87–1.72 | 43.6–50 | 39–134 | 60–124.5 | Shear Failure |
| 20 | Zhao and Maruyama [12] | 3 | 250 | 3 | 150 | 1.51–3.02 | 34.3 | 105 | 40.5–46 | Shear Failure |
| 21 | Alkhrdaji et al. [34] | 3 | 279–287 | 2.61–2.69 | 178 | 0.77–2.3 | 24.1 | 40 | 72.2–106.8 | Shear Tension |
| 22 | Tariq and Newhook [35] | 12 | 310–346 | 2.8–3.7 | 130–160 | 0.72–1.54 | 34.1–43.2 | 42–120 | 42.7–63.7 | Diagonal Tension |
| 23 | Mizukawa et al. [36] | 1 | 260 | 3 | 200 | 1.3 | 34.7 | 130 | 62.2 | Shear Failure |
| 24 | Alam [37] | 28 | 296–744 | 1.5–3.5 | 250–300 | 0.22–1.43 | 34.5–88.3 | 46.3–144 | 43.7–155.2 | Shear Failure |
| 25 | Steiner et al. [38] | 2 | 457–889 | 3.09–3.1 | 457–889 | 0.6–1.19 | 29.6 | 41 | 159–187.5 | Shear Failure |
| 26 | Duranovic et al. [39] | 2 | 210 | 3.7 | 150 | 1.31 | 32.9–38.1 | 45 | 22.8–27.3 | Shear Failure |
| 27 | Bentz et al. [40] | 5 | 188–857 | 3.5–4.1 | 450 | 0.55–2.54 | 35 | 37 | 74–232 | Shear Failure |
| 28 | Matta et al. [41] | 7 | 294–883 | 3.1 | 114–457 | 0.59 | 29.5–38.8 | 40.7–40.8 | 18.1–158.9 | Shear Failure |
| 29 | Gross et al. [42] | 12 | 141–143 | 6.4–6.5 | 89–159 | 0.33–0.76 | 60.3–81.4 | 139 | 11.7–23.1 | Shear Tension |
| 30 | Jang et al. [43] | 54 | 220–225 | 1.5–4.5 | 150–200 | 0.3–0.8 | 30 | 25.1–147.9 | 18–85.12 | Shear Failure |
| 31 | Tottori and Wakui [44] | 6 | 325 | 2.2–4.3 | 200 | 0.7–0.9 | 44.6–46.9 | 58–192 | 47.1–147.1 | Diagonal Tension |
| 32 | Nagasaka et al. [45] | 2 | 253 | 1.8 | 250 | 1.9 | 22.9–34.1 | 56–96 | 83.4–112.8 | Shear Failure |
| 33 | Nakamura and Higai [46] | 2 | 150 | 4 | 300 | 1.3–1.8 | 22.7–27.8 | 29 | 33.1–36.3 | Shear Failure |
| 34 | Massam [47] | 7 | 187–938 | 3.3–4.1 | 450 | 0.5 | 35–46 | 26.5–29.4 | 39–231.4 | Shear compression |
| 35 | Alkhrdaji et al. [48] | 3 | 279–287 | 2.61–2.69 | 178 | 0.77–2.3 | 24.1 | 40 | 36.1–53.4 | Shear Tension |
| 36 | Gross et al. [49] | 12 | 224–225 | 4.06–4.08 | 150–203 | 1.25–2.56 | 79.6 | 40.3 | 30.4–48.3 | Shear Failure |
| 37 | Swamy and Aburawi [50] | 1 | 222 | 3.15 | 154 | 1.55 | 39 | 34 | 19.5 | Shear Failure |
| 38 | Maruyama and Zhao [51] | 4 | 250 | 3 | 150 | 0.55–2.2 | 27.5–34.9 | 94 | 38.3–59.1 | Shear Failure |
| 49 | Lubell et al. [52] | 1 | 970 | 3.14 | 450 | 0.46 | 40 | 40 | 136 | Shear Failure |
| 40 | Alam and Hussain [53] | 6 | 291–594 | 2.5 | 250–300 | 0.42–1.37 | 65.3–74.2 | 46.3–144 | 71.6–155.2 | Shear Failure |
| 41 | Kilpatrick and Easden [54] | 12 | 78–83 | 3.61–6.41 | 420 | 0.61–2.61 | 61–93 | 40–42 | 20–55.6 | Shear compression |
| 42 | Kilpatrick and Dawborn [55] | 9 | 73–75 | 6–6.16 | 420 | 0.68–1.16 | 48–92 | 42 | 23.5–34.3 | Shear Failure |
| 43 | Niewels [56] | 3 | 404–441 | 3.02–3.71 | 300 | 3.25–3.98 | 43 | 44–63 | 118.4–154.3 | Shear Failure |
| 44 | Elsayed et al. [57] | 2 | 262 | 6.68 | 600 | 0.77–1.53 | 68 | 48 | 91.2–118.2 | Shear compression |
| 45 | Caporale and Luciano [58] | 4 | 170 | 4.12 | 150 | 0.92–1.54 | 20–26.6 | 46 | 12.7–15.4 | Shear Failure |
| Remarks | Total = 402 | Ranged from 73 to 970 mm | Ranged from 1.1 to 12.5 | Ranged from 89 to 1000 mm | Ranged from 0.12 to 122% | Ranged from 20 to 93 MPa | Ranged from 25.1 to 192 GPa | Ranged from 8.8 to 232 kN | Shear Failure | |
| No. | References | Models Form Literature | |
|---|---|---|---|
| 1 | CSA-S806 [2] | d | (19) |
| where d ≤ 300 mm = 0.75. | |||
| d | (20) | ||
| where d > 300 = 0.75. | |||
| 2 | JSCE [4] | (21) | |
| βd = ≤ 0.72 = member safety factor = 1.3 = design axial compressive force = decompression moment = design bending moment | |||
| 3 | Chewdhury and Islam [15] | (22) | |
| 4 | Michaluk et al. [29] | d | (23) |
| 5 | Jumma and Yousif [59] | (24) | |
| 6 | ACI 318-19 [60] | d | (25) |
| 7 | Deitz et al. [32] | d | (26) |
| 8 | ISIS—M03-01 [61] | d | (27) |
| d | (28) | ||
| 9 | CSA 2004 [62] | (29) | |
| (30) | |||
| 10 | ISE 1999 [63] | (31) | |
| 11 | CSA/CAN3-A23.3-M94 [43] | d | (32) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasheed, M.H.F.; Taha, B.O.; Agha, A.Z.S.; Arbili, M.M.; Abdulrahman, P.I. Shear Capacity of Fiber-Reinforced Polymer (FRP)–Reinforced Concrete (RC) Beams Without Stirrups: Comparative Modeling with FRP Modulus, Longitudinal Ratio, and Shear Span-to-Depth. J. Compos. Sci. 2025, 9, 554. https://doi.org/10.3390/jcs9100554
Rasheed MHF, Taha BO, Agha AZS, Arbili MM, Abdulrahman PI. Shear Capacity of Fiber-Reinforced Polymer (FRP)–Reinforced Concrete (RC) Beams Without Stirrups: Comparative Modeling with FRP Modulus, Longitudinal Ratio, and Shear Span-to-Depth. Journal of Composites Science. 2025; 9(10):554. https://doi.org/10.3390/jcs9100554
Chicago/Turabian StyleRasheed, Mereen Hassan Fahmi, Bahman Omar Taha, Ayad Zaki Saber Agha, Mohamed M. Arbili, and Payam Ismael Abdulrahman. 2025. "Shear Capacity of Fiber-Reinforced Polymer (FRP)–Reinforced Concrete (RC) Beams Without Stirrups: Comparative Modeling with FRP Modulus, Longitudinal Ratio, and Shear Span-to-Depth" Journal of Composites Science 9, no. 10: 554. https://doi.org/10.3390/jcs9100554
APA StyleRasheed, M. H. F., Taha, B. O., Agha, A. Z. S., Arbili, M. M., & Abdulrahman, P. I. (2025). Shear Capacity of Fiber-Reinforced Polymer (FRP)–Reinforced Concrete (RC) Beams Without Stirrups: Comparative Modeling with FRP Modulus, Longitudinal Ratio, and Shear Span-to-Depth. Journal of Composites Science, 9(10), 554. https://doi.org/10.3390/jcs9100554








