Behavior of Composite Concrete-Filled Double-Web Steel Beams: A Numerical and Experimental Investigation
Abstract
1. Introduction
2. Literature Review
2.1. Innovation of Concrete Filled Steel Sections
2.1.1. High-Performance Technology
2.1.2. Time- and Cost-Effective Technology
2.1.3. Sustainable Technology
2.1.4. Applicable Technology in Analysis Software
3. Materials and Methods
3.1. Specimens Description
- NMF: Normal concrete beam middle-filled (filled between loads)
- NEF: Normal concrete beam edges-filled (hollow between loads)
- NFF: Normal concrete beam fully filled
- RMF: Recycle concrete beam middle-filled (filled between loads)
- REF: Recycle concrete beam edges-filled (hollow between loads)
- RFF: Recycle concrete beam fully filled.
3.2. Material Properties
3.2.1. Cement
3.2.2. Fine Aggregate
3.2.3. Coarse Aggregate
3.2.4. Recycle Coarse Aggregate
3.2.5. Water
3.2.6. Concrete Mixes and Compressive Strength
Normal Concrete
Recycled Aggregate Concrete
Compressive Strength
3.2.7. Steel Plates
3.2.8. Procedure of Beam Assembling
3.3. Experimental Testing Procedures and Numerical Analysis Model
3.3.1. Experimental Testing Procedure
3.3.2. Numerical Analysis Model
4. Discussion of Experimental and Numerical Results
4.1. Control Beam CB
4.2. Beams Filled with Normal Concrete
4.2.1. Beam NMF (Group One)
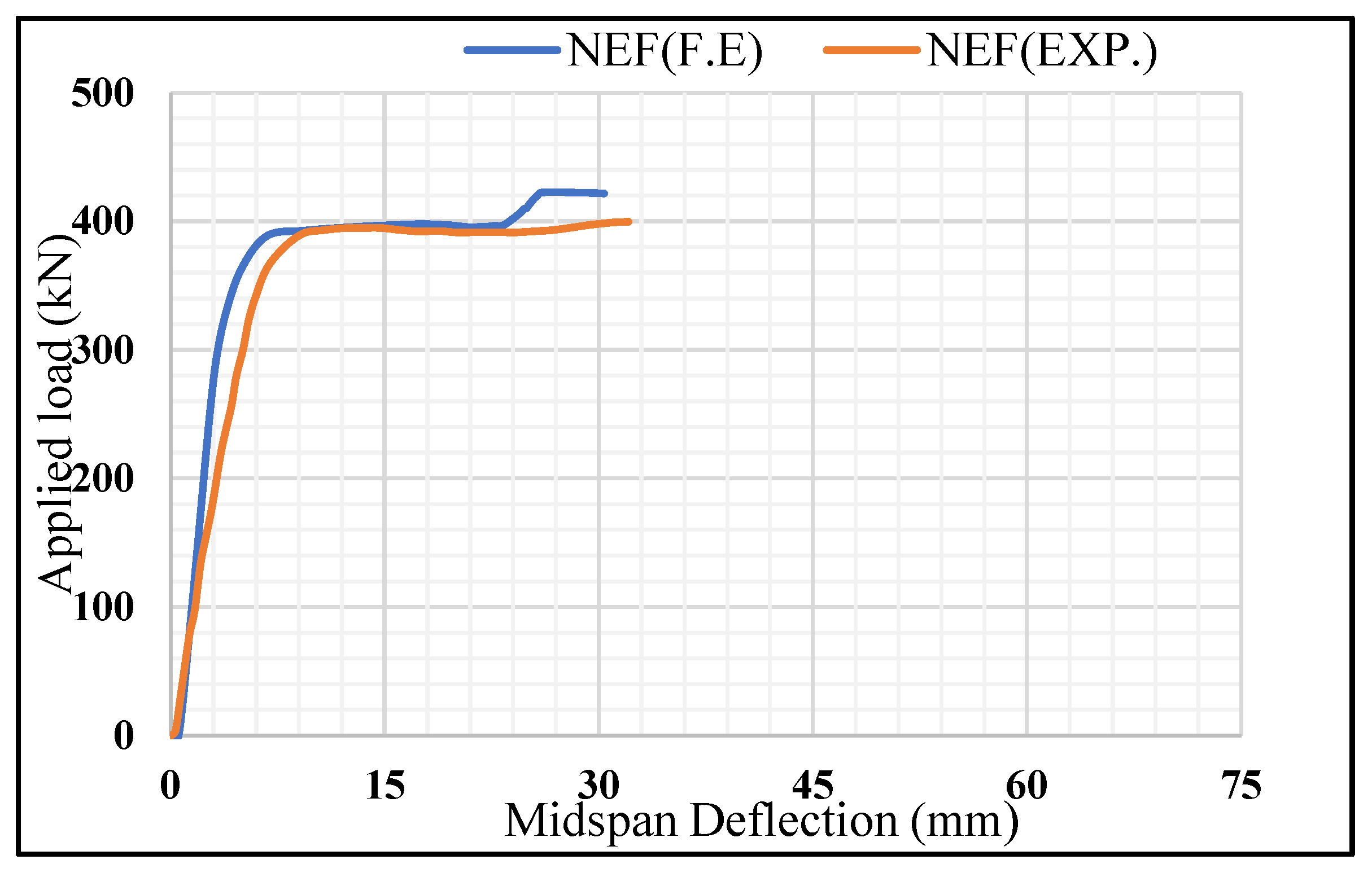
4.2.2. Beam NEF (Group One)
4.2.3. Beam NFF (Group One)
4.2.4. Comparative Analysis of Beams in Group One
4.2.5. Comparison with Other Researche Results
4.3. Beams Filled with Recycled Concrete
4.3.1. Beam RMF (Group Two)
4.3.2. Beam REF (Group Two)
4.3.3. Beam RFF (Group Two)
4.3.4. Comparative Analysis of Beams in Group Two
4.4. Stress Distribution
5. Conclusions
- The main innovation of this study is the modeling of a novel composite section (double web filled with concrete) in ABAQUS, followed by validation through experimental results. Previous studies on this section type focused mainly on experimental investigations, while this work demonstrates the feasibility of reliable numerical modeling. The approach presented here can serve as a reference for the analysis and design of structures where high performance girders are required, such as bridges, long-span decks, and mega-structures.
- The performance of composite beams was consistently superior to that of the control specimens due to the inclusion of various concrete types within the webs. Although the incorporation of conventional concrete in the central, peripheral, or full cross-sectional zones increases self-weight, it significantly enhances structural behavior and modifies failure patterns, thereby providing substantially higher load-carrying capacity compared to hollow specimens.
- Filling the beam’s web at mid-span prevents buckling, while filling the web near the supports enhances shear resistance and delays flexure–shear interaction failure. Thus, variations in concrete placement strongly affect the bearing capacity and bending performance of composite double-web beams.
- Incorporating recycled waste materials in the concrete mix consistently enhanced the structural performance and ductility of composite double-web beams compared to the control specimen.
- Recycled aggregate concrete is both sustainable and environmentally friendly, as it enhances flexural strength and stiffness by increasing sectional inertia and delaying local buckling of the double web while also providing an effective alternative to conventional concrete.
- The finite element models developed in ABAQUS demonstrated reliable accuracy in predicting the actual behavior of the double-web beams, including maximum load, load–displacement curves, and failure modes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sara Simon, S.; Kafle, B.; Al-Ameri, R. A critical review of cold-formed steel built-up composite columns with Geopolymer concrete infill. J. Compos. Sci. 2024, 8, 238. [Google Scholar]
- Taufiq, H. Composite Action Between Light Steel Sections and Concrete for Beams and Columns; University of Surrey: Guildford, UK, 2020. [Google Scholar]
- Fadhel, M.; AlSaraj, W. Steel Tubes Filled by Concrete Under Flexural and Compression: A Review. Al-Rafidain J. Eng. Sci. 2025, 3, 530–555. [Google Scholar]
- Abdalla, S.H. Behavior of Concrete Filled Steel Tube (CFST) Under Different Loading Conditions. Ph.D. Thesis, American University of Sharjah, Sharjah, United Arab Emirates, 2012. [Google Scholar]
- Al Zand, A.W.; Ali, M.M.; Al-Ameri, R.; Badaruzzaman, W.H.W.; Tawfeeq, W.M.; Hosseinpour, E.; Yaseen, Z.M. Flexural strength of internally stiffened tubular steel beam filled with recycled concrete materials. Materials 2021, 14, 6334. [Google Scholar] [CrossRef] [PubMed]
- Behera, M.; Bhattacharyya, S.; Minocha, A.; Deoliya, R.; Maiti, S. Recycled aggregate from C&D waste & its use in concrete–A breakthrough towards sustainability in construction sector: A review. Constr. Build. Mater. 2014, 68, 501–516. [Google Scholar]
- Sabih, S.M.; Hilo, S.J.; Hamood, M.J.; Salih, S.S.; Faris, M.M.; Yousif, M.A. Numerical investigation into the strengthening of concrete-filled steel tube composite columns using carbon fiber-reinforced polymers. Buildings 2024, 14, 441. [Google Scholar] [CrossRef]
- Abed, F.H.; Nazzal, M.D.; Attom, M.F.; El-Emam, M.E.; ElMessalami, N. Use of treated wastewater in the construction of base course layers for sustainable pavement structures. J. Mater. Civ. Eng. 2018, 30, 04018140. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, K.; Feng, R.; He, K.; Wang, L. Flexural behaviour of concrete-filled stainless steel CHS subjected to static loading. J. Constr. Steel Res. 2017, 139, 30–43. [Google Scholar] [CrossRef]
- Kaishesh, A.J.; Hemzah, S.A.; Mohammed, B.H. Experimental Investigation of Double Web Steel Beam Filled with Recycled Aggregate Concrete (RAC). In Proceedings of the 2022 International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 20–22 October 2022; pp. 128–133. [Google Scholar]
- Dassault Systemes Simulia Corp. ABAQUS/CAE User’s Manual, Version 6.14; Dassault Systemes Simulia Corp: Providence, RI, USA, 2014. [Google Scholar]
- Ellobody, E. Finite Element Analysis and Design of Steel and Steel–Concrete Composite Bridges; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Wang, W.-D.; Xian, W.; Hou, C.; Shi, Y.-L. Experimental investigation and FE modelling of the flexural performance of square and rectangular SRCFST members. In Structures; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Zhang, Z.; Chen, W.; Wang, K.; Guo, X. Concrete-filled double steel tubular beams under lateral impact. Case Stud. Constr. Mater. 2022, 17, e01252. [Google Scholar] [CrossRef]
- Kaishesh, A.J.; Hemzah, S.A.; Mohammed, B.H. Experimental investigation of double web filled steel beam. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2024; p. 030123. [Google Scholar]
- Al-Zand, A.W.; Hosseinpour, E.; Tawfeeq, W.M. The effects of filling the rectangular hollow steel tube beam with concrete: An experimental case study. J. Civ. Eng. Res. 2017, 1, 23–30. [Google Scholar]
- Chang, Q.; Zhao, C.; Xing, L.; Ahmad, W.; Javed, M.F.; Fahid, A.; Musarat, M.A.; Vatin, N.I. Concrete Filled Double Steel Tube Columns Incorporating UPVC Pipes Under Uniaxial Compressive Load at Ambient and Elevated Temperature; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Pereira, P.; Evangelista, L.; De Brito, J. The effect of superplasticizers on the mechanical performance of concrete made with fine recycled concrete aggregates. Cem. Concr. Compos. 2012, 34, 1044–1052. [Google Scholar] [CrossRef]
- Abed, F.H.; Nazzal, M.D.; Attom, M.F.; El-Emam, M.E.; ElMessalami, N.; Al-Dabagh, S. The use of wastewater in construction of base course layers in pavement structures. In International Congress and Exhibition Sustainable Civil Infrastructures: Innovative Infrastructure Geotechnology; Springer: Berlin/Heidelberg, Germany, 2017; pp. 31–37. [Google Scholar]
- Attom, M.; Abed, F.; Elemam, M.; Nazal, M.; ElMessalami, N. The effect of treated waste-water on compaction and compression of fine soil. Int. J. Civ. Environ. Eng. 2016, 10, 1122–1126. [Google Scholar]
- Hansen, T.C. Recycling of Demolished Concrete and Masonry; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Ghannam, S. Flexural strength of concrete-filled Steel tubular beam with partial replacement of coarse aggregate by granite. Int. J. Civ. Eng. Technol. 2016, 7, 161–168. [Google Scholar]
- Al-Obaidi, S.; Salim, T.; Hemzah, S.A. Flexural behavior of concrete filled steel tube composite with different concrete compressive strength. Int. J. Civ. Eng. Technol. 2018, 9, 824–832. [Google Scholar]
- No. 5/2019; “Portland Cement”, The Central Organization for Standardization and Quality Control. IQS: Baghdad, Iraq, 2019.
- No. 45/1984; Aggregate from Natural Sources for Concrete and Construction. IQS: Baghdad, Iraq, 1984.
- ASTM C33-03; Standard Specification for Concrete Aggregates. ASTM: West Hoboken, NJ, USA, 2010.
- No. 1703/1992; Iraqi Standard (Materials Specification & Construction Works). IQS: Baghdad, Irac, 1992.
- ACI 211.1-91; Standard Practice for Selecting Proportions for Normal, Heavyweight, and Mass Concrete. American Concrete Institute: Farmington Hills, MI, USA, 2001.
- ASTM A370; Standard Test Methods and Definitions for Mechanical Testing of Steel Products. ASTM: West Hoboken, NJ, USA, 2017.
- Ahmed, M.; Emara, M.; Patel, V.I.; Chen, W.; Zhang, X.; Hamoda, A. Experimental and numerical analysis of the flexural performance of concrete-filled steel tubular members with partial replacement of fine aggregates with sawdust. Eng. Struct. 2025, 343, 121050. [Google Scholar] [CrossRef]
- Zhang, C.-C.; Ding, F.-X.; Sadat, S.I.; Lyu, F.; Huang, X.-Y.; Gao, R.; Yu, T.; Liu, Y.-L. Flexural Behavior of Desert Sand Concrete-Filled Steel Tube: Experimental Validation, FEM Analysis, and Design Formulas. Materials 2025, 18, 2371. [Google Scholar] [CrossRef] [PubMed]
- Han, L.-H.; Li, W.; Bjorhovde, R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Al Mustawfi, S.; Safiee, N.A.; Bakar, N.A.; Karim, I.A.; Mohd Nasir, N.A. Experiment and Analysis of a Hybrid Composite Post-tension Plate Girder. Pertanika J. Sci. Technol. 2024, 32, 1501–15026. [Google Scholar] [CrossRef]
- Abdulridha, A.M.; Al Zaidee, S.R. Experimental and Numerical Investigation of Concrete-Filled Tube Beams: A Review Paper. J. Eng. 2025, 31, 18–41. [Google Scholar] [CrossRef]
- Huang, S.; Xi, Y.; Li, X.; Men, P.; Wu, G. Flexural behaviour of damaged concrete T-beams reinforced with ultra-high performance concrete filling. Front. Mater. 2024, 11, 1410016. [Google Scholar] [CrossRef]
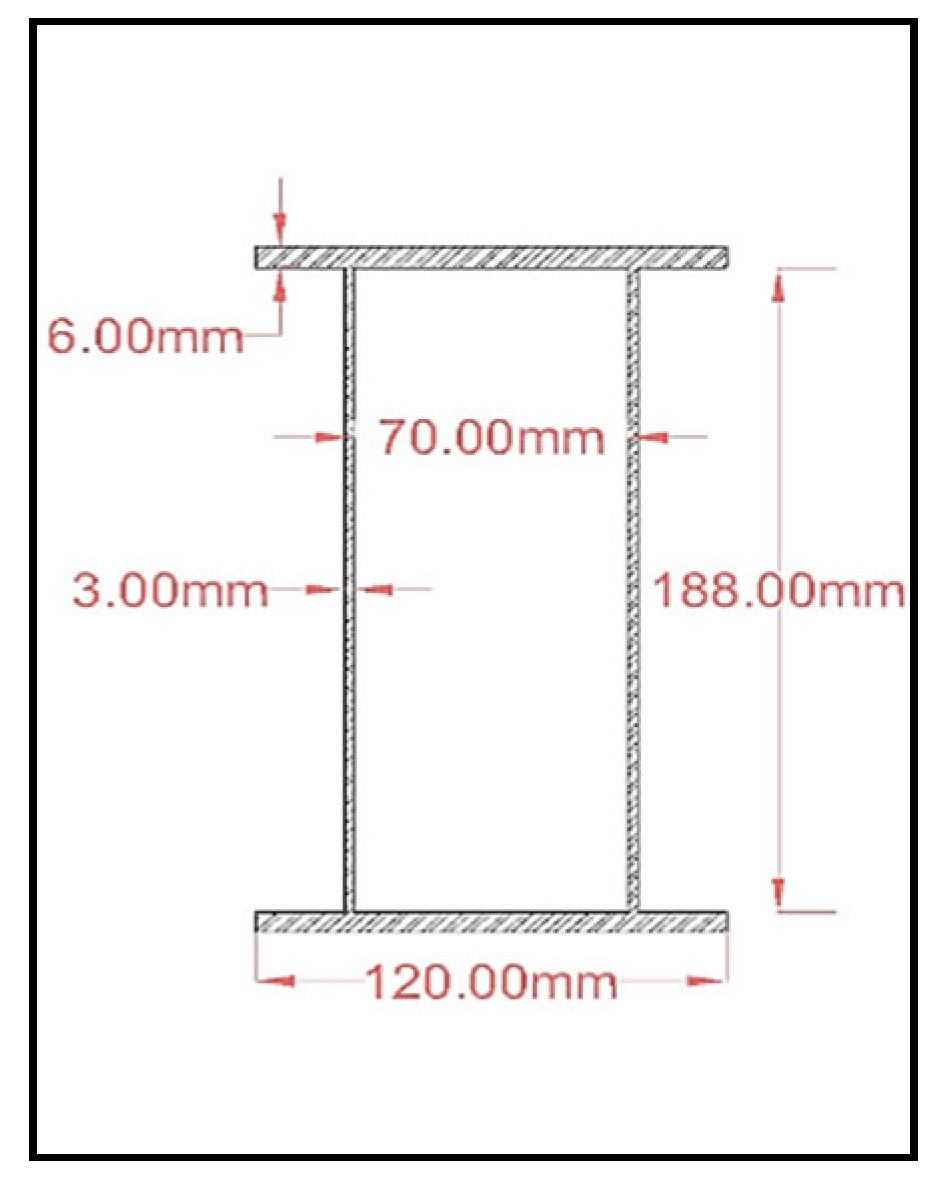






































| Group | Reference Beam | Group One | Group Two | ||||
|---|---|---|---|---|---|---|---|
| Sample | Control | NMF | NEF | NFF | RMF | REF | RFF |
| Concrete location | ---- | Middle of the beam | Both sides of the beam (partial) | Middle and sides of the beam (full) | Middle of the beam | Both sides of the beam (partial) | Middle and sides of the beam (full) |
| Oxide Composition | % by Weight | Limit According to IQS. No. 5/2019 |
|---|---|---|
| Sulfate (SO3) | 2.2 | ≤2.8% |
| Magnesium (MgO) | 3.6 | ≤5% |
| Loss on ignition (L.O.I.) | 3.2 | ≤4% |
| Lime saturation factor (L.S.F.) | 0.86 | 0.66–1.02 |
| Insoluble residue (I.R.) | 0.68 | ≤1.5 |
| Principal substances (Bouge’s equation) | % by weight | Limit according to IQS. No. 5/2019 |
| Tricalcium silicate (C3S) | 48.04 | - |
| Dicalcium silicate (C2S) | 22.5 | - |
| Aluminate tricalcium (C3A) | 1.55 | ≤3.5% |
| Physical Property | Test Result | Limit According to IQS. No. 5/2019 |
|---|---|---|
| Setting time (Vicat’s method): | ||
| Initial setting time (min) | 120 | ≥45 |
| Final setting time (hr:min) | 3:38 | ≤10 |
| Compressive strength (MPa): | ||
| Two days | 13.5 | ≥10 |
| Twenty-eight days | 33 | ≥32.5 |
| Limit According to IQS. No. 45/1984 (zone 2) | |||
|---|---|---|---|
| Sieve Size (mm) | % Passing of Fine Aggregate | Max. Limit | Min. Limit |
| 9.5 | 100 | 100 | 100 |
| 4.75 | 99 | 100 | 90 |
| 2.36 | 83 | 100 | 75 |
| 1.18 | 70 | 90 | 55 |
| 0.6 | 58 | 59 | 35 |
| 0.3 | 26 | 30 | 8 |
| 0.15 | 5 | 10 | 0 |
| Characteristics | Test Result | Limit According to IQS. No. 45/1984 |
|---|---|---|
| Sulfate content (SO3), % | 0.1 | 0.5% (max.) |
| Material finer than 75 μm | 2.1 | 5% (max.) |
| Sieve Size (mm) | % Passing of Coarse Aggregate | Limit According to ASTM C33/2003 | Limit According to IQS. No. 45/1984 |
|---|---|---|---|
| 12.5 | 100 | 100 | 100 |
| 9.5 | 100 | 100–85 | 100–85 |
| 4.75 | 14 | 30–10 | 30–10 |
| 2.36 | 3 | 10–0 | 10–0 |
| 1.8 | 0 | 5–0 | 5–0 |
| Characteristics | Test Result | Limit According to IQS. No. 45/1984 |
|---|---|---|
| Sulfate content (SO3), % | 0.062 | 0.1% (max.) |
| Material finer than 75 μm | 0.3 | 3% (max.) |
| Limit According to ASTM C33/2003 | |||
|---|---|---|---|
| Sieve Size (mm) | % Passing of Recycled Coarse Aggregate | Max. Limit | Min. Limit |
| 12.5 | 100 | 100 | 100 |
| 9.5 | 100 | 100 | 85 |
| 4.75 | 13 | 30 | 10 |
| 2.36 | 2 | 10 | 0 |
| 1.8 | 0 | 5 | 0 |
| Cement | Fine Aggregate | Coarse Aggregate | Water |
|---|---|---|---|
| 400 | 720 | 1073 | 160 |
| Cement | Fine Aggregate | Recycled Aggregate | Water |
|---|---|---|---|
| 400 | 720 | 1073 | 160 |
| No. of Cylinder | Normal Concrete | Recycled Aggregate Concrete |
|---|---|---|
| C1 | 37.2 | 30.7 |
| C2 | 38.5 | 28.1 |
| C3 | 38.5 | 31.4 |
| Average | 38 | 30 |
| No. of Coupon | Part | Yield Stress (N/mm2) | Ultimate Stress (N/mm2) | Modulus of Elasticity (GPa) |
|---|---|---|---|---|
| 1 | Flange (6 mm) | 267 | 392 | 190 |
| 2 | 287 | 408 | 190 | |
| 3 | 289 | 404 | 190 | |
| 4 | 273 | 404 | 190 | |
| Mean | 279.0 | 402.0 | 190 | |
| 5 | Web (3 mm) | - | 352 | 190 |
| 6 | 286 | 350 | 190 | |
| 7 | 287 | 358 | 190 | |
| 8 | 308 | 358 | 190 | |
| Mean | 293.7 | 354.5 | 190 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaishesh, A.J.; Kashesh, G.J.; Hemzah, S.A.; Mohammed, B.H.; Dulaimi, A.; Bernardo, L.F.A. Behavior of Composite Concrete-Filled Double-Web Steel Beams: A Numerical and Experimental Investigation. J. Compos. Sci. 2025, 9, 541. https://doi.org/10.3390/jcs9100541
Kaishesh AJ, Kashesh GJ, Hemzah SA, Mohammed BH, Dulaimi A, Bernardo LFA. Behavior of Composite Concrete-Filled Double-Web Steel Beams: A Numerical and Experimental Investigation. Journal of Composites Science. 2025; 9(10):541. https://doi.org/10.3390/jcs9100541
Chicago/Turabian StyleKaishesh, Abbas Jalal, Ghazi Jalal Kashesh, Sadjad Amir Hemzah, Bahaa Hussain Mohammed, Anmar Dulaimi, and Luís Filipe Almeida Bernardo. 2025. "Behavior of Composite Concrete-Filled Double-Web Steel Beams: A Numerical and Experimental Investigation" Journal of Composites Science 9, no. 10: 541. https://doi.org/10.3390/jcs9100541
APA StyleKaishesh, A. J., Kashesh, G. J., Hemzah, S. A., Mohammed, B. H., Dulaimi, A., & Bernardo, L. F. A. (2025). Behavior of Composite Concrete-Filled Double-Web Steel Beams: A Numerical and Experimental Investigation. Journal of Composites Science, 9(10), 541. https://doi.org/10.3390/jcs9100541








