Nonlinear Aero-Thermo-Elastic Analysis of Laminated Composite Beams with Surface-Bonded FGMs Layers Subjected to a Concentrated Harmonic Load
Abstract
1. Introduction
2. Governing Equations
3. Numerical Modeling
3.1. The Galerkin Method
3.2. The Method of Multiple Scale (MTS)
- The terms capture the linear response.
- The terms represent the first nonlinear corrections.
- Higher-order terms refine the solution to account for stronger nonlinear effects.
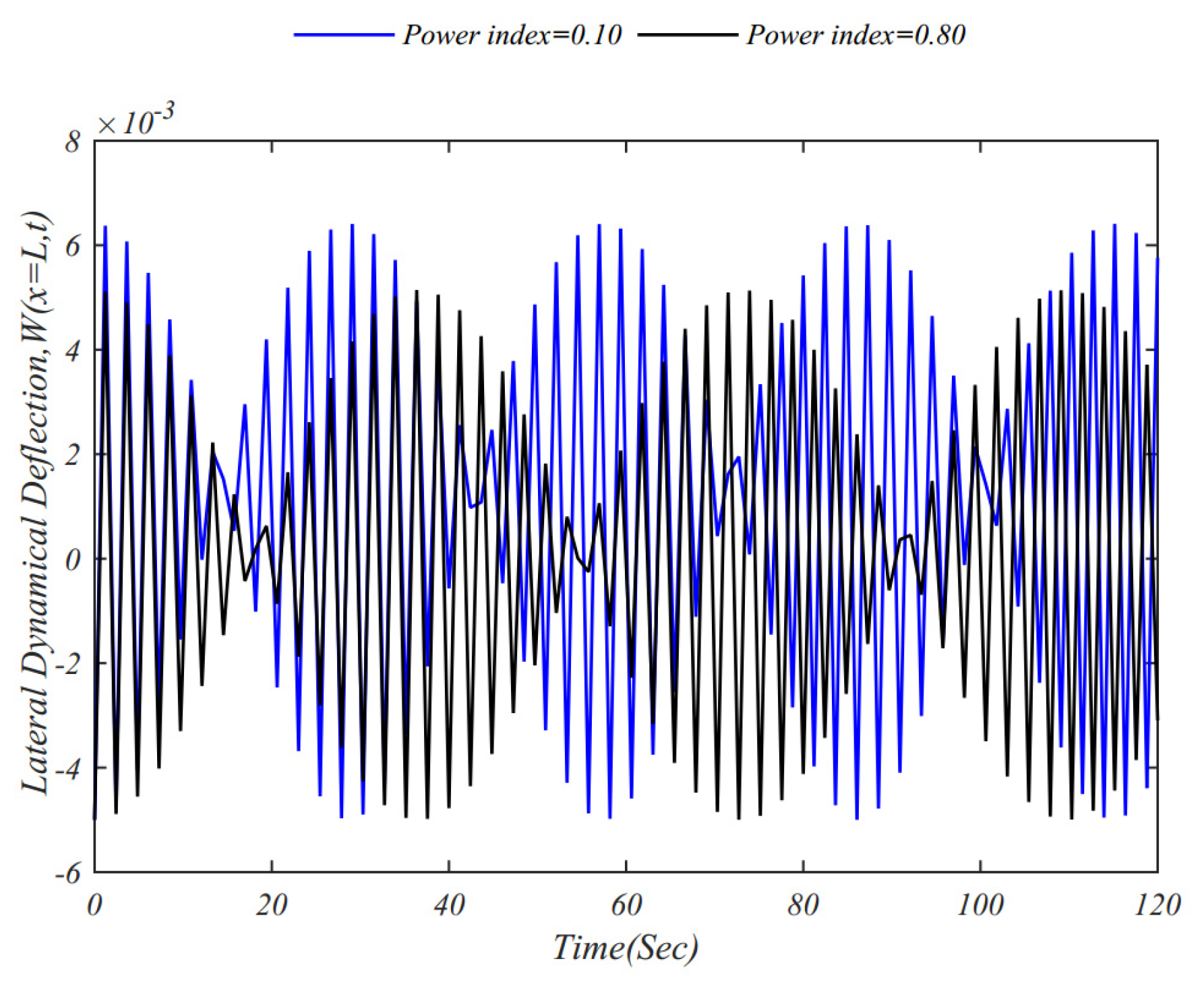
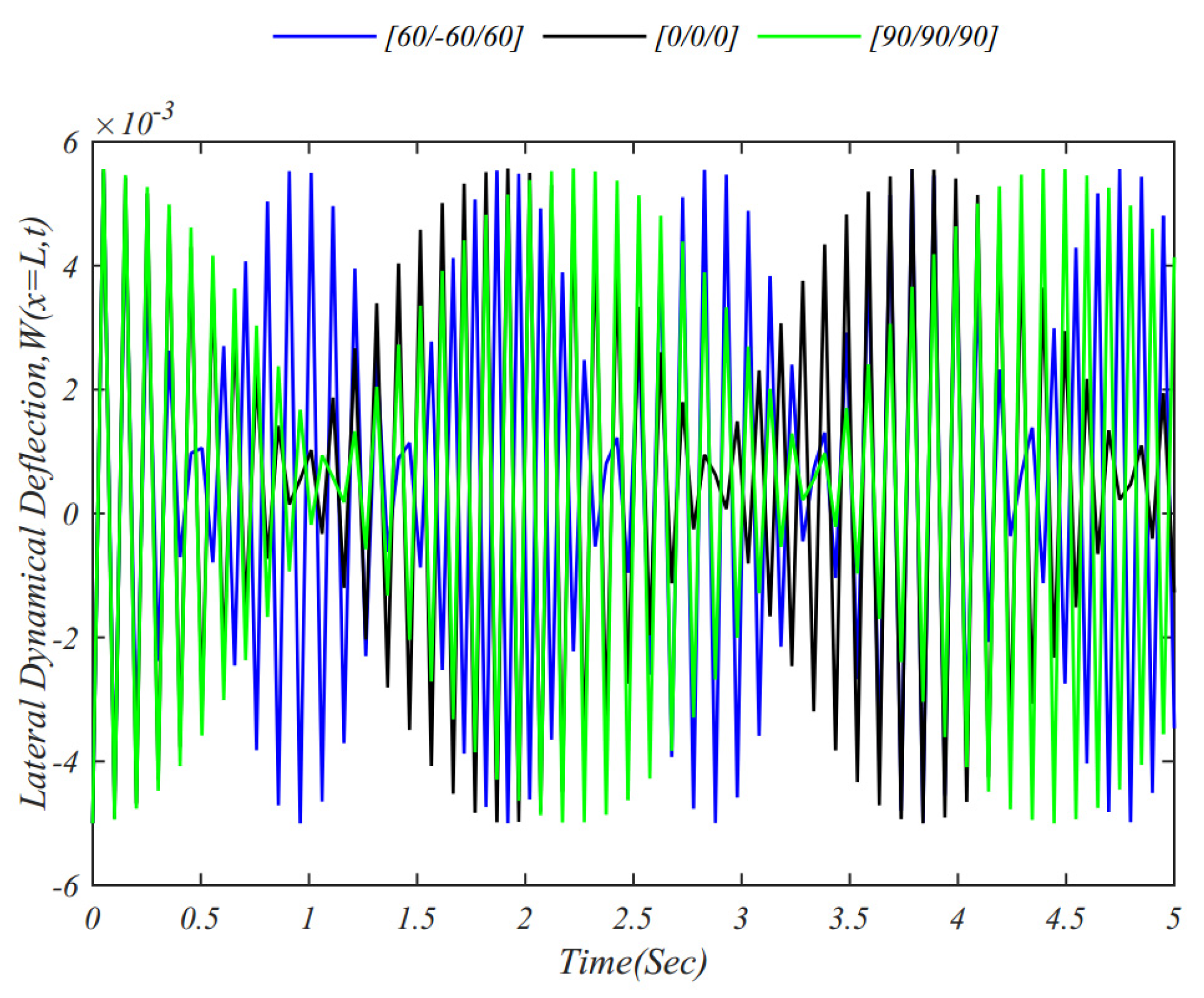
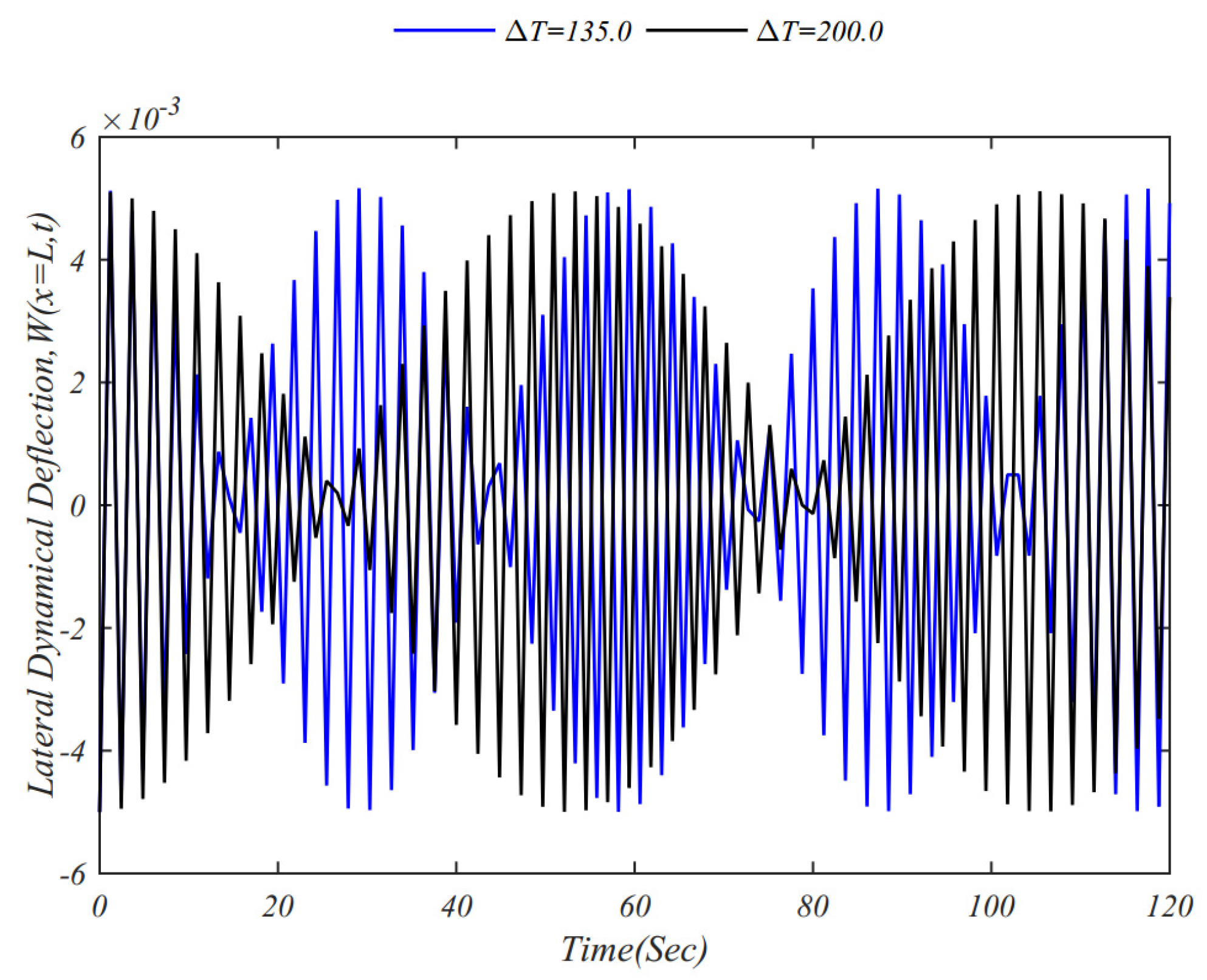
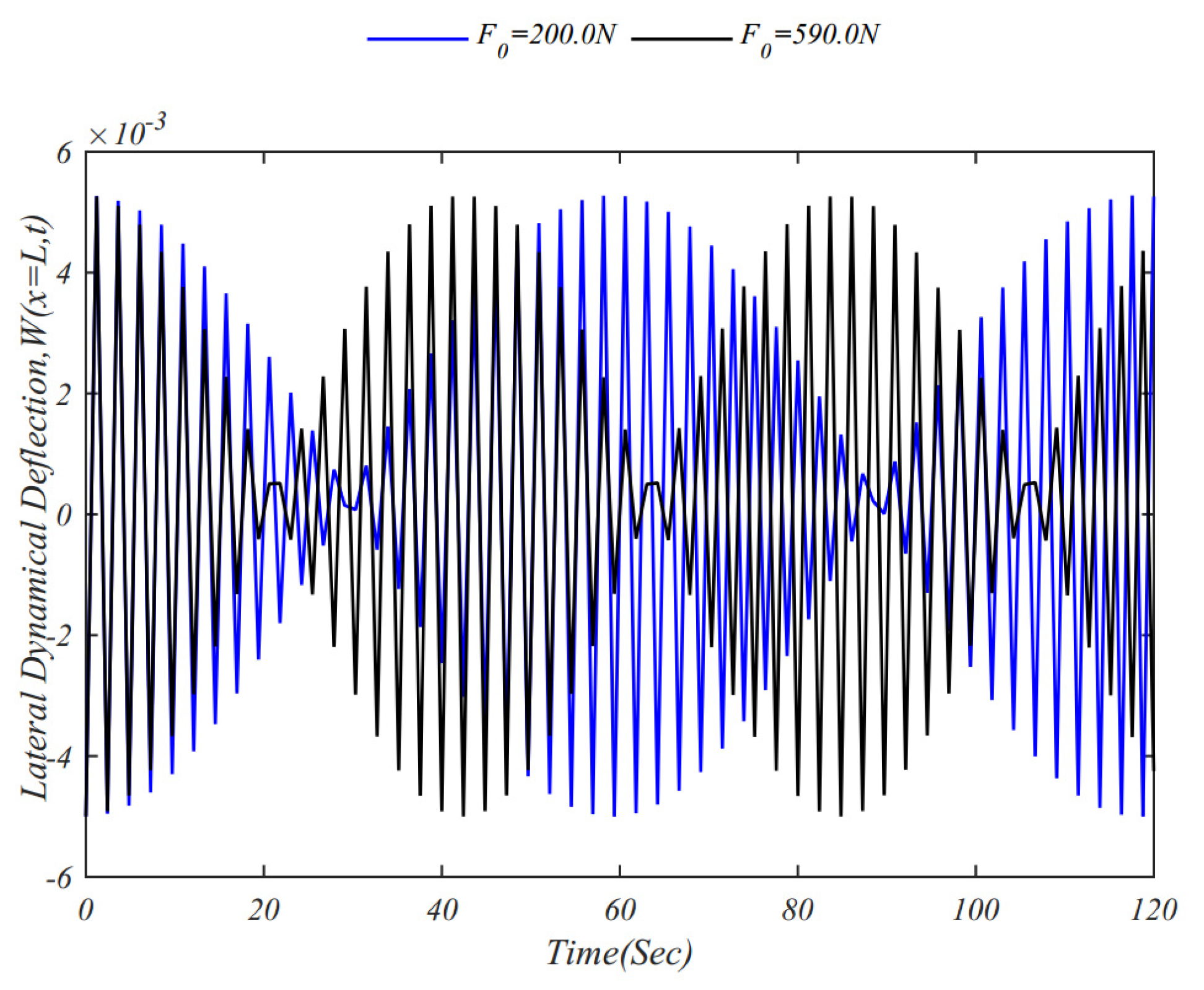
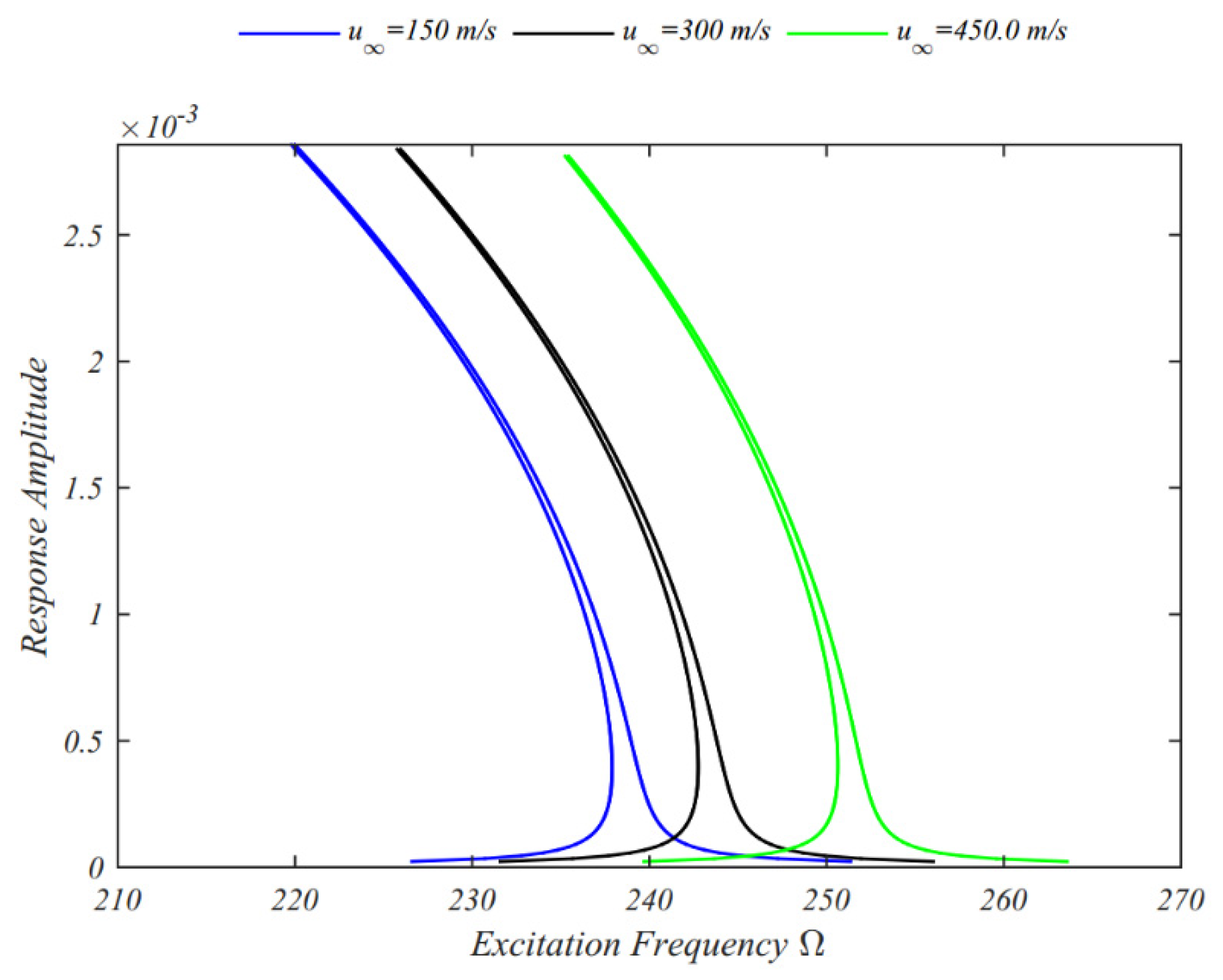
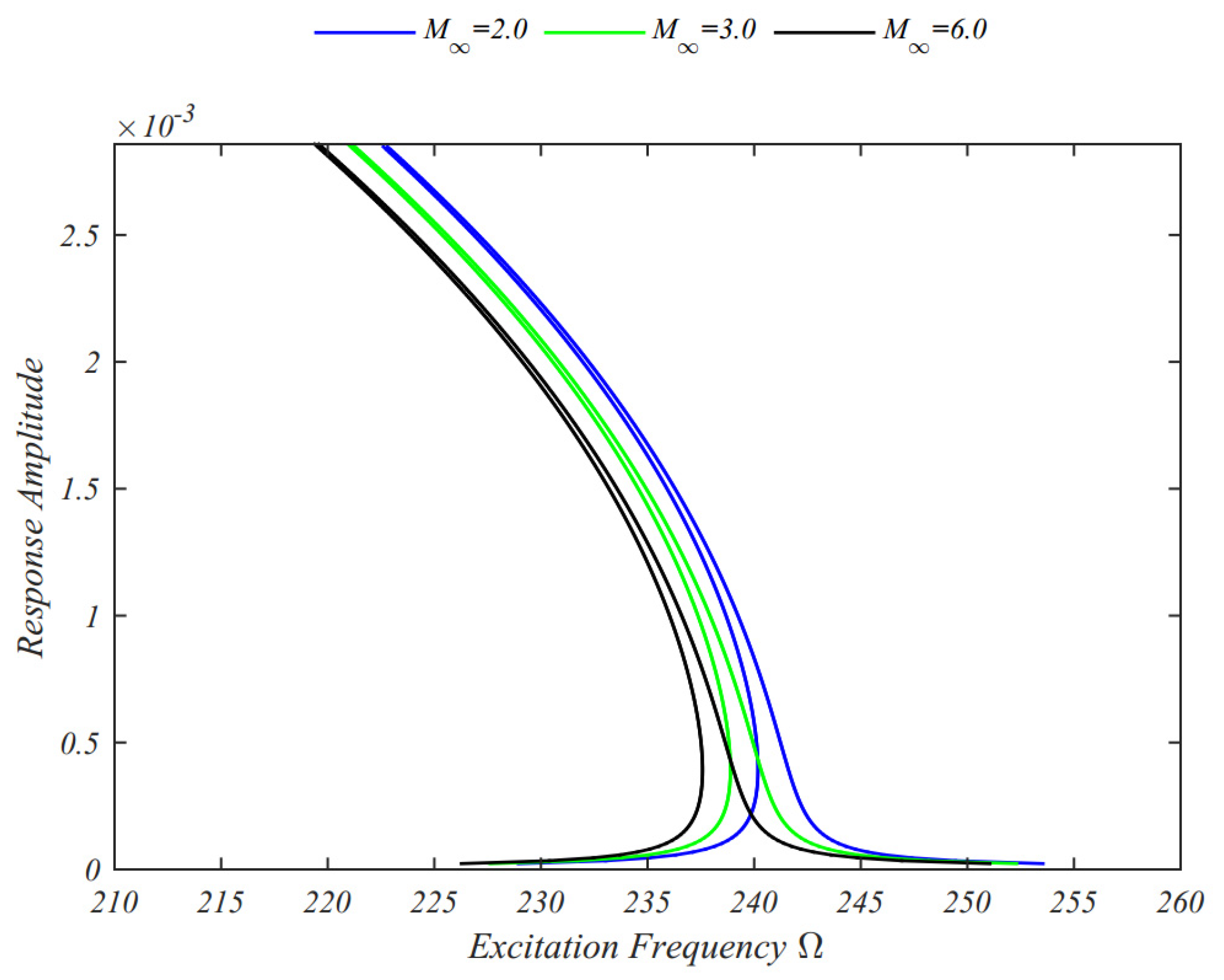
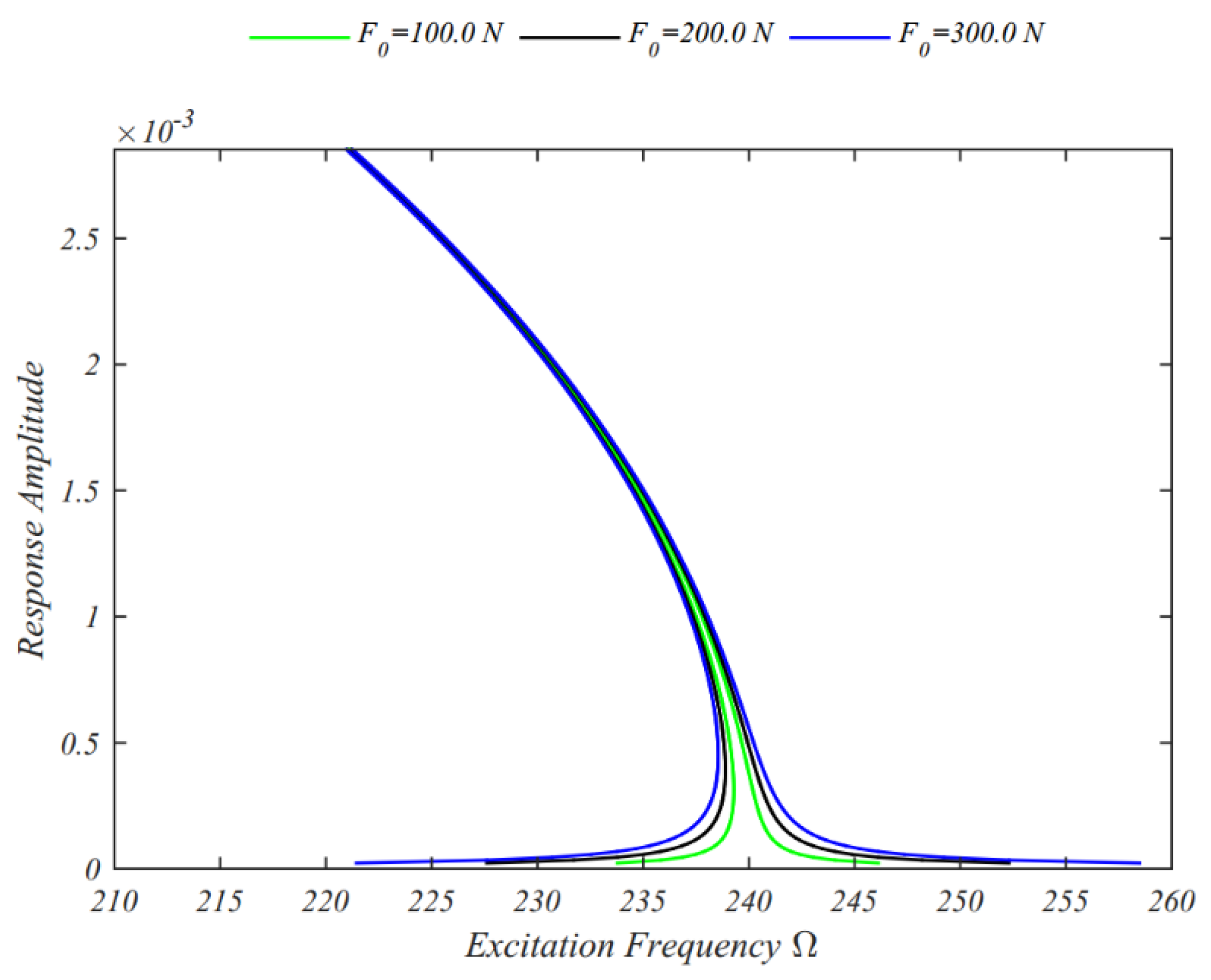
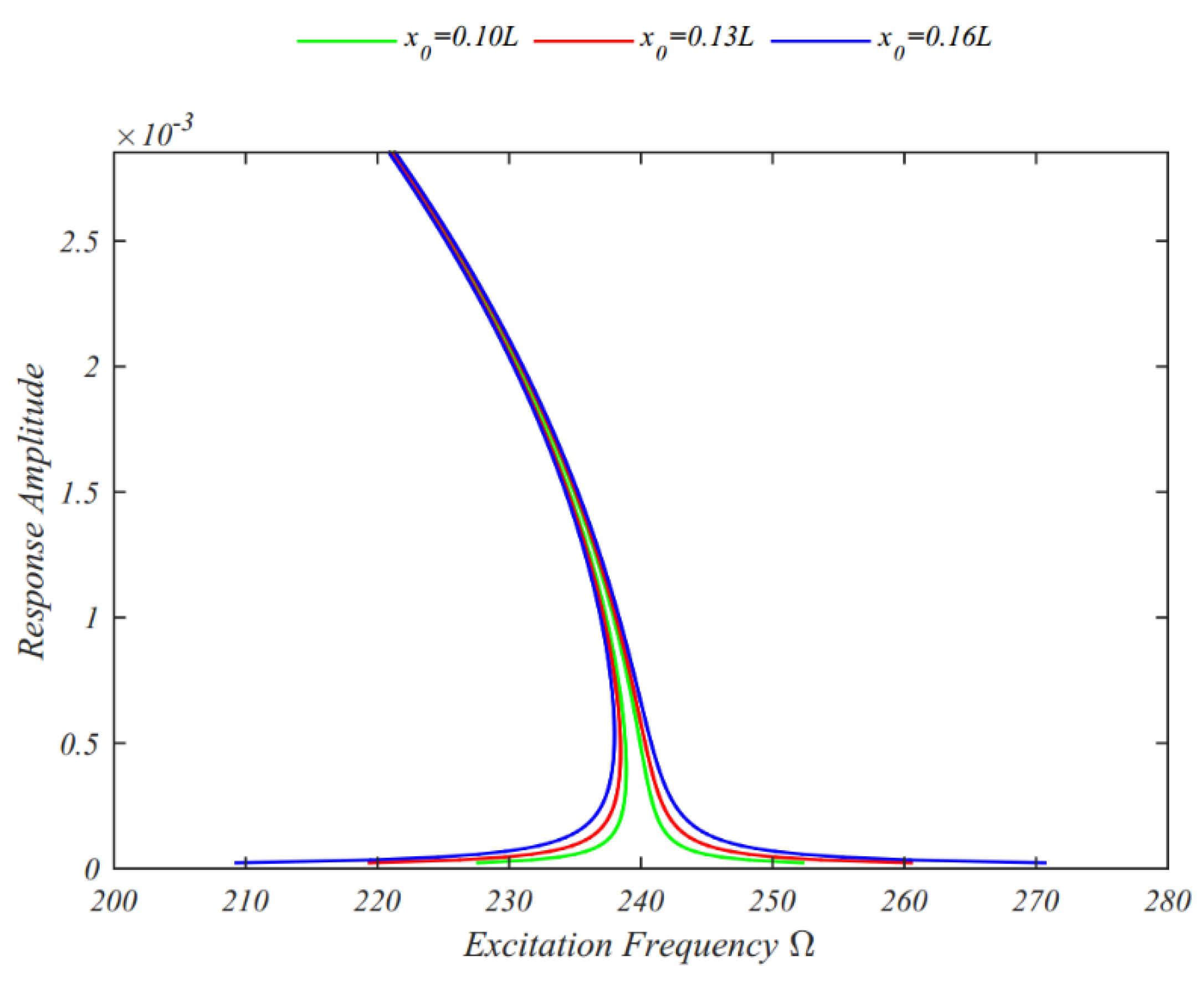
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Asadi, H.; Beheshti, A.R. On the nonlinear dynamic responses of FG-CNTRC beams exposed to aerothermal loads using third-order piston theory. Acta Mech. 2018, 229, 2413–2430. [Google Scholar] [CrossRef]
- Yao, G.; Zhang, Y.M.; Li, C.Y.; Yang, Z. Stability analysis and vibration characteristics of an axially moving plate in aero-thermal environment. Acta Mech. 2016, 227, 3517–3527. [Google Scholar] [CrossRef]
- Yao, G.; Xie, Z.; Zhu, L.; Zhang, Y. Nonlinear vibrations of an axially moving plate in aero-thermal environment. Nonlinear Dynam. 2021, 105, 2921–2933. [Google Scholar] [CrossRef]
- Li, P.; Yang, Z.; Tian, W. Nonlinear aeroelastic analysis and active flutter control of functionally graded piezoelectric material plate. Thin Walled Struct. 2023, 183, 110323. [Google Scholar] [CrossRef]
- Alimoradzadeh, M.; Tornabene, F.; Dimitri, R. Aeroelastic Oscillations of Cantilever Beams Reinforced by Carbon Nanotubes Based on a Modified Third-Order Piston Theory. Appl. Sci. 2025, 15, 8700. [Google Scholar] [CrossRef]
- El-Borgi, S.; Erdogan, F.; Hatira, F. Ben Stress Intensity Factors for an Interface Crack between a Functionally Graded Coating and a Homogeneous Substrate. Int. J. Fract. 2003, 123, 139–162. [Google Scholar] [CrossRef]
- Guo, L.C.; Wang, Z.H.; Zhang, L. A Fracture Mechanics Problem of a Functionally Graded Layered Structure with an Arbitrarily Oriented Crack Crossing the Interface. Mech. Mater. 2012, 46, 69–82. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Free Vibrations of Free-Form Doubly-Curved Shells Made of Functionally Graded Materials Using Higher-Order Equivalent Single Layer Theories. Compos. Part B Eng. 2014, 67, 490–509. [Google Scholar] [CrossRef]
- Liew, K.M.; Lei, Z.X.; Zhang, L.W. Mechanical analysis of functionally graded carbon nanotube reinforced composites: A Review. Compos Struct. 2015, 120, 90–97. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, W. Elastoplastic buckling of FGM beams in thermal environment. Contin. Mech. Thermodyn. 2021, 33, 151–161. [Google Scholar] [CrossRef]
- Malikan, M.; Wiczenbach, T.; Eremeyev, V.A. Thermal buckling of functionally graded piezomagnetic micro- and nanobeams presenting the flexomagnetic effect. Contin. Mech. Thermodyn. 2022, 34, 1051–1066. [Google Scholar] [CrossRef]
- Dowell, E.H. Nonlinear oscillations of a fluttering plate. AIAA J. 1966, 4, 1267–1275. [Google Scholar] [CrossRef]
- Dowell, E.H. Nonlinear oscillations of a fluttering plate. II. AIAA J. 1967, 5, 1856–1862. [Google Scholar] [CrossRef]
- Ye, W.L.; Dowell, E.H. Limit cycle oscillation of a fluttering cantilever plate. AIAA J. 1991, 29, 1929–1936. [Google Scholar] [CrossRef]
- Shiau, L.C.; Lu, L.T. Nonlinear flutter of two-dimensional simply supported symmetric composite laminated plates. J. Aircraft. 1992, 29, 140–145. [Google Scholar] [CrossRef]
- Song, Z.G.; Li, F.M. Investigations on the flutter properties of supersonic panels with different boundary conditions. Int. J. Dynam. Control 2014, 3, 346–353. [Google Scholar] [CrossRef]
- Sohn, K.J.; Kim, J.H. Nonlinear thermal flutter of functionally graded panels under a supersonic flow. Compos. Struct. 2009, 88, 380–387. [Google Scholar] [CrossRef]
- Koo, K.N.; Hwang, W.S. Effects of hysteretic and aerodynamic damping on supersonic panel flutter of composite plates. J. Sound Vib. 2004, 273, 569–583. [Google Scholar] [CrossRef]
- Shin, W.H.; Oh, I.K.; Lee, I. Nonlinear flutter of aerothermally buckled composite shells with damping treatments. J. Sound Vib. 2009, 324, 556–569. [Google Scholar] [CrossRef]
- Song, Z.G.; Li, F.M. Aeroelastic analysis and active flutter control of nonlinear lattice sandwich beams. Nonlinear Dyn. 2014, 76, 7–68. [Google Scholar] [CrossRef]
- Natarajan, S.; Kaleeswaran, K.; Manickam, G. Functionally graded material panel flutter by cell-based smoothed finite elements. J. Coupled Syst. Multiscale Dynam. 2013, 1, 205–215. [Google Scholar] [CrossRef]
- Natarajan, S.; Manickam, G.; Bordas, S. Supersonic flutter analysis of functionally graded material plates with cracks. Front Aerosp. Eng. 2013, 2, 91–97. [Google Scholar]
- Abbas, J.F.; Ibrahim, R.A.; Gibson, R.F. Nonlinear flutter of orthotropic composite panel under aerodynamic heating. AIAA J. 1993, 31, 1478–1488. [Google Scholar] [CrossRef]
- Xue, D.Y.; Mei, C. Finite element nonlinear panel flutter with arbitrary temperatures in supersonic flow. AIAA J. 1993, 31, 154–162. [Google Scholar] [CrossRef]
- Zhao, H.; Cao, D. A study on the aero-elastic flutter of stiffened laminated composite panel in the supersonic flow. J. Sound Vib. 2013, 332, 4668–4679. [Google Scholar] [CrossRef]
- Dixon, L.R.; Mei, C. Finite element analysis of large-amplitude panel flutter of thin laminates. AIAA J. 1993, 31, 701–707. [Google Scholar] [CrossRef]
- Kouchakzadeh, M.A.; Rasekh, M.; Haddadpour, H. Panel flutter analysis of general laminated composite plates. Compos Struct. 2010, 92, 2906–2915. [Google Scholar] [CrossRef]
- Camacho, P.; Akhavan, H.; Ribeiro, P. Linear aeroelastic analysis of cantilever hybrid composite laminated plates with curvilinear fibres and carbon nanotubes. Compos Struct. 2021, 266, 113765. [Google Scholar] [CrossRef]
- Alimoradzadeh, M.; Akbas, S.D. Superharmonic and subharmonic resonances of a carbon nanotube-reinforced composite beam. Adv. Nano Res. 2022, 12, 353–363. [Google Scholar]
- Alimoradzadeh, M.; Tornabene, F.; Esfarjani, S.M.; Dimitri, R. Finite strain-based theory for the superharmonic and subharmonic resonance of beams resting on a nonlinear viscoelastic foundation in thermal conditions, and subjected to a moving mass loading. Int J. Non-Linear Mech. 2023, 148, 104271. [Google Scholar] [CrossRef]
- Alimoradzadeh, M.; Akbaş, Ş.D. Thermal nonlinear dynamic and stability of carbon nanotube reinforced composite beams. Steel Compos. Struct. 2023, 46, 637–647. [Google Scholar]
- Alimoradzadeh, M.; Heidari, H.; Tornabene, F.; Dimitri, R. Thermo-Mechanical Buckling and Non-Linear Free Oscillation of Functionally Graded Fiber-Reinforced Composite Laminated (FG-FRCL) Beams. Appl. Sci. 2023, 13, 4904. [Google Scholar] [CrossRef]
- Alimoradzadeh, M.; Akbaş, Ş.D. Nonlinear free vibration analysis of a composite beam reinforced by carbon nanotubes. Steel Compos. Struct. 2023, 46, 335–344. [Google Scholar]
- Alimoradzadeh, M.; Akbas, S.D. Nonlinear vibration analysis of carbon nanotube-reinforced composite beams resting on nonlinear viscoelastic foundation. Geomech. Eng. 2023, 32, 125–135. [Google Scholar]
- Samadpour, M.; Asadi, H.; Wang, Q. Nonlinear aero-thermal flutter postponement of supersonic laminated composite beams with shape memory alloys. Eur. J. Mech. Solid 2016, 57, 18–28. [Google Scholar] [CrossRef]
- Alimoradzadeh, M.; Tornabene, F.; Dimitri, R. Nonlinear axial-lateral coupled vibration of functionally graded-fiber reinforced composite laminated (FG-FRCL) beams subjected to aero-thermal loads. Int. J. Non Linear Mech. 2024, 159, 104612. [Google Scholar] [CrossRef]
- Kong, S.; Zhou, S.; Nie, Z.; Wang, K. The size-dependent natural frequency of Bernoulli–Euler micro-beams. Int. J. Eng. Sci. 2008, 46, 427–437. [Google Scholar] [CrossRef]
- Fernandes, R.; Mousavi, S.M.; El-Borgi, S. Free and forced vibration nonlinear analysis of a microbeam using finite strain and velocity gradients theory. Acta Mech. 2016, 227, 2657–2670. [Google Scholar] [CrossRef]
- Ramezani, S. A micro scale geometrically non-linear Timoshenko beam model based on strain gradient elasticity theory. Int. J. Non Linear Mech. 2012, 47, 863–873. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Jafari, A. A higher-order thermomechanical vibration analysis of temperature-dependent FGM beams with porosities. J. Eng. 2016, 2016, 9561504. [Google Scholar] [CrossRef]
- Chen, Y.; Fu, Y.; Zhong, J.; Tao, C. Nonlinear dynamic responses of fiber-metal laminated beam subjected to moving harmonic loads resting on tensionless elastic foundation. Compos. Part B Eng. 2017, 131, 253–259. [Google Scholar] [CrossRef]
- Daniel, I.M.; Ishai, O.; Daniel, I.M.; Daniel, I. Engineering Mechanics of Composite Materials; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Xiang, H.J.; Yang, J. Free and forced vibration of a laminated FGM Timoshenko beam of variable thickness under heat conduction. Compos. Part B Eng. 2008, 39, 292–303. [Google Scholar] [CrossRef]
- Chen, W.J.; Li, X.P. Size-dependent free vibration analysis of composite laminated Timoshenko beam based on new modified couple stress theory. Arch. Appl. Mech. 2013, 83, 431–444. [Google Scholar] [CrossRef]
- McHugh, K.A.; Beran, P.; Freydin, M.; Dowell, E.H. Flutter and limit cycle oscillations of a cantilevered plate in supersonic/hypersonic flow. Proc. IFASD 2019, 1, 2–3. [Google Scholar]
- Mohammad-Abadi, M.; Daneshmehr, A.R. Modified couple stress theory applied to dynamic analysis of composite laminated beams by considering different beam theories. Int. J. Eng. Sci. 2015, 87, 83–102. [Google Scholar] [CrossRef]
- Inman, D.J. Vibration with Control; John Wiley & Sons, University of Michigan: Hoboken, NJ, USA, 2017. [Google Scholar]
- Norouzi, H.; Younesian, D. Chaotic vibrations of beams on nonlinear elastic foundations subjected to reciprocating loads. Mech. Res. Commun. 2015, 69, 121–128. [Google Scholar] [CrossRef]
- Laura, P.A.; Pombo, J.L.; Susemihl, E.A. A note on the vibrations of a clamped-free beam with a mass at the free end. J. Sound Vib. 1974, 37, 161–168. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T.; Holmes, P. Nonlinear oscillations. ASME J. Appl. Mech. 1980, 47, 692. [Google Scholar] [CrossRef]
- Tao, C.; Fu, Y.M.; Dai, H.L. Nonlinear dynamic analysis of fiber metal laminated beams subjected to moving loads in thermal environment. Compos. Struct. 2016, 140, 410–416. [Google Scholar] [CrossRef]
- Rao, S.S. Vibration of Continuous Systems; Wiley: New York, NY, USA, 2007; p. 317. [Google Scholar]

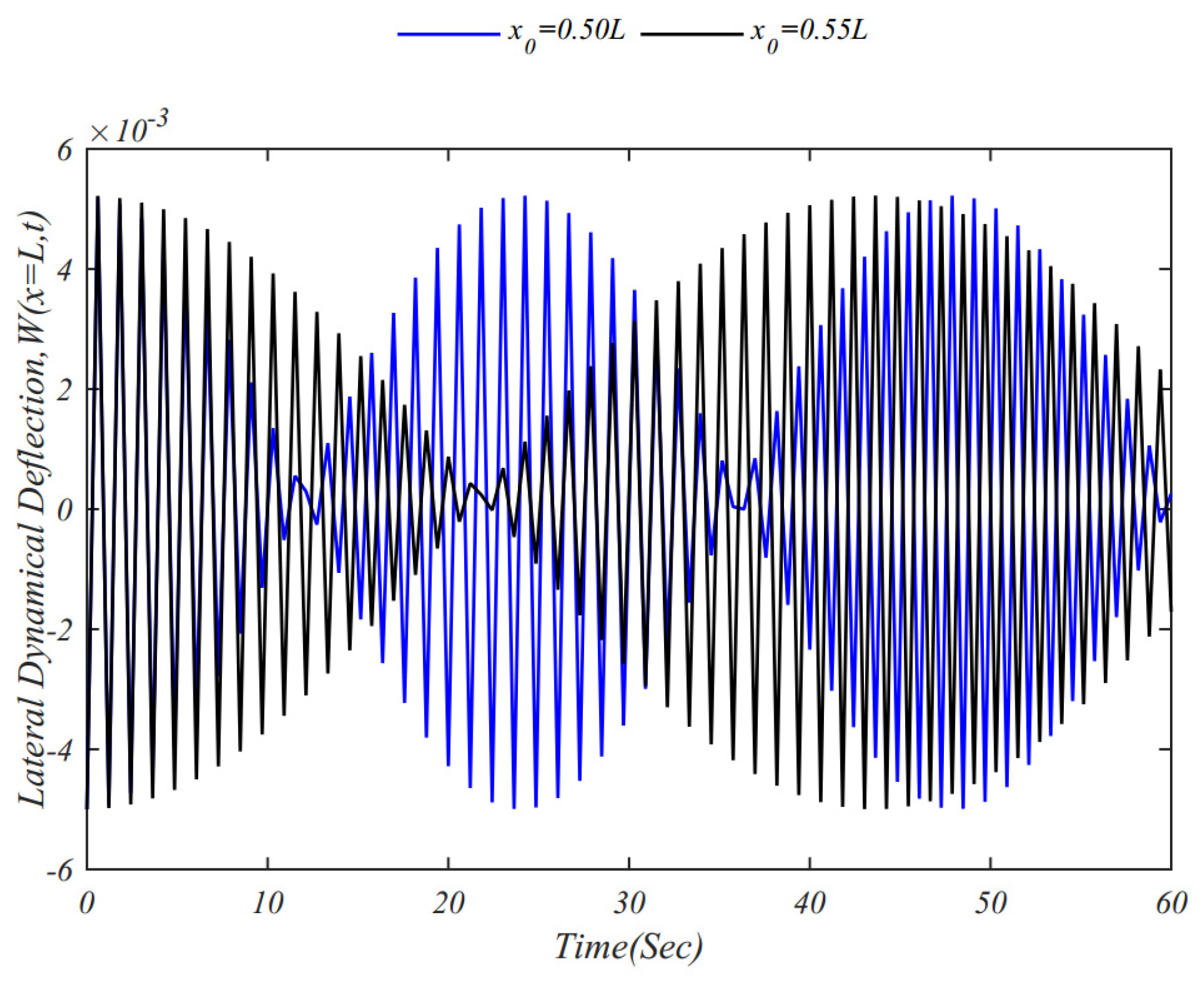
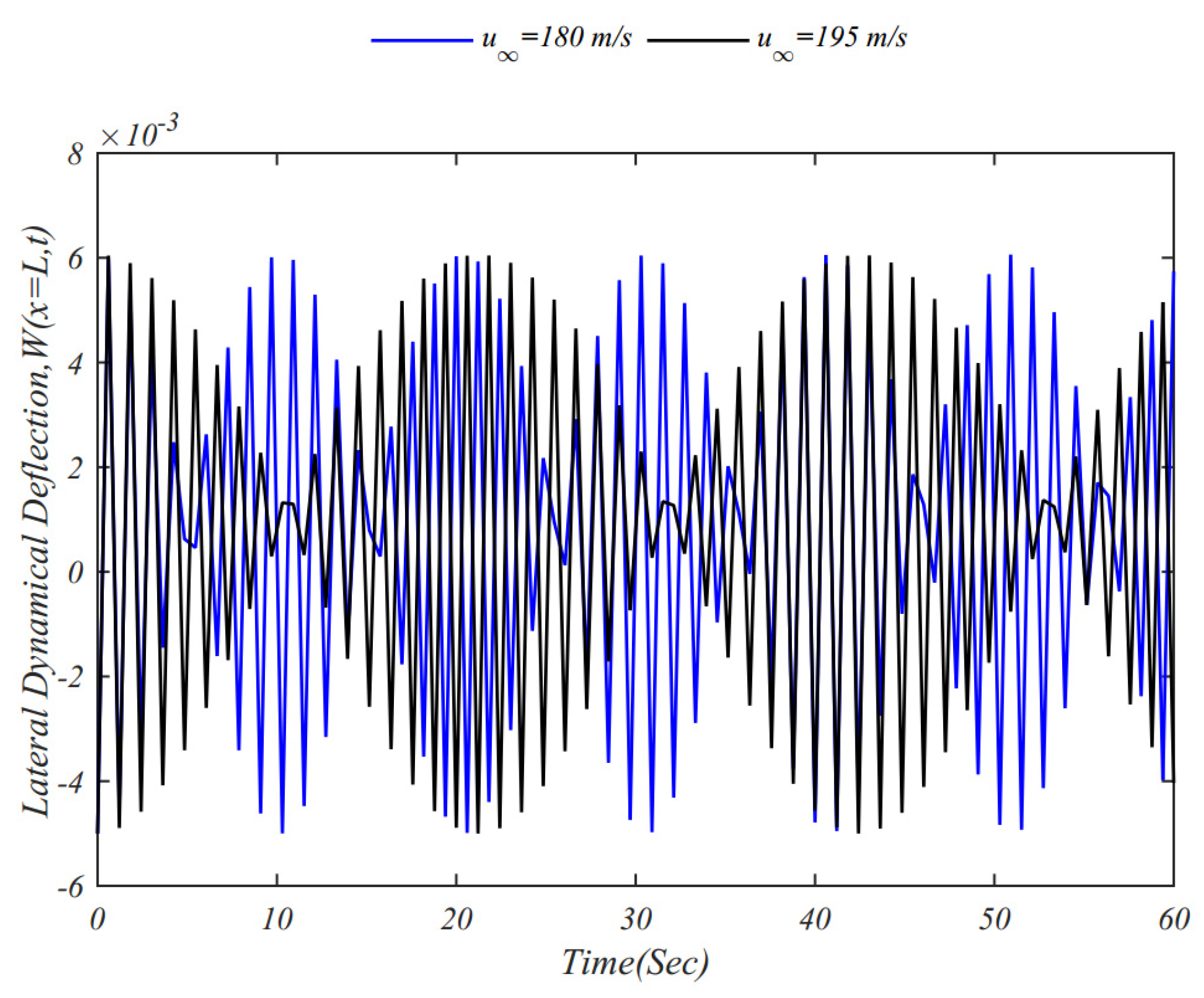

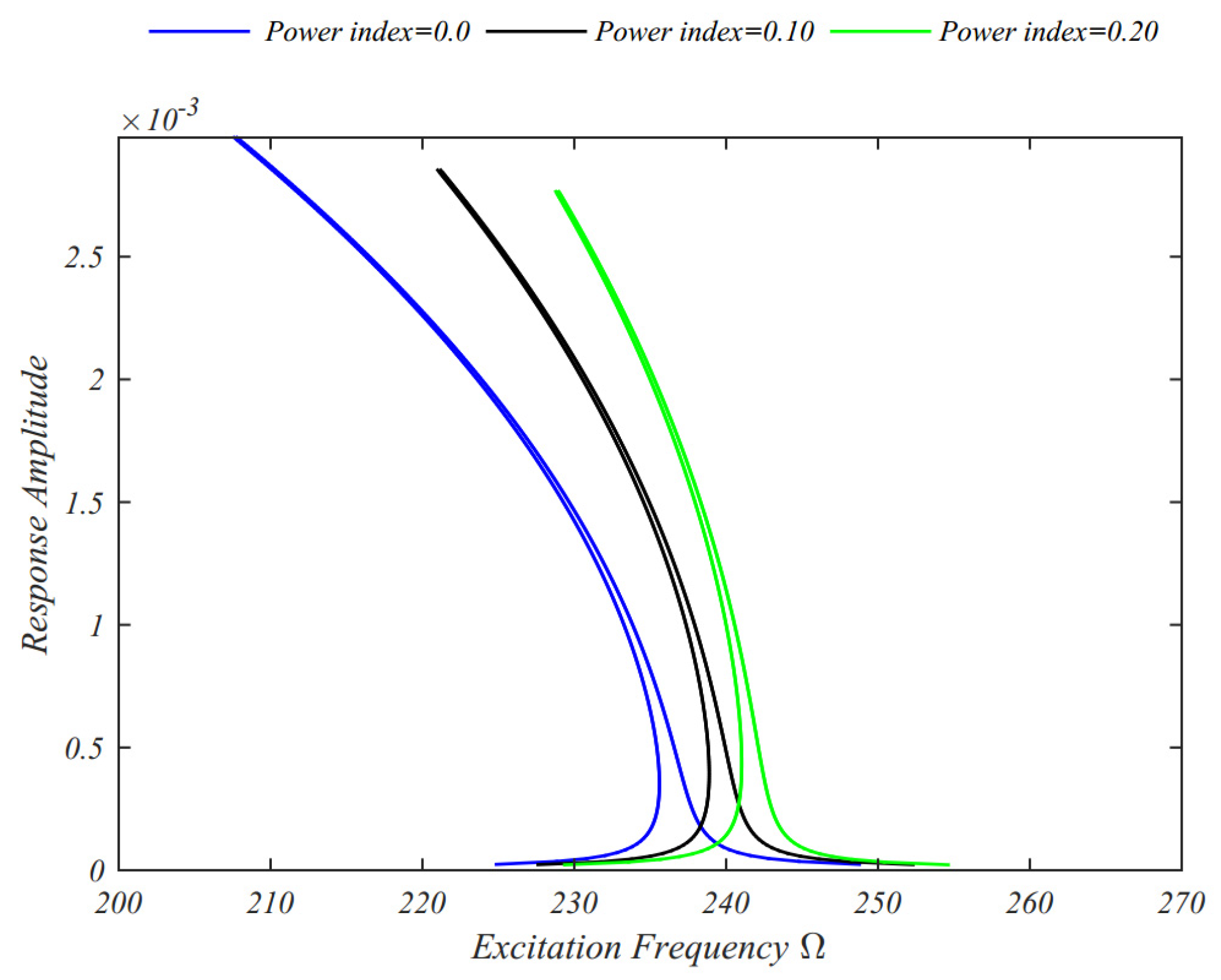
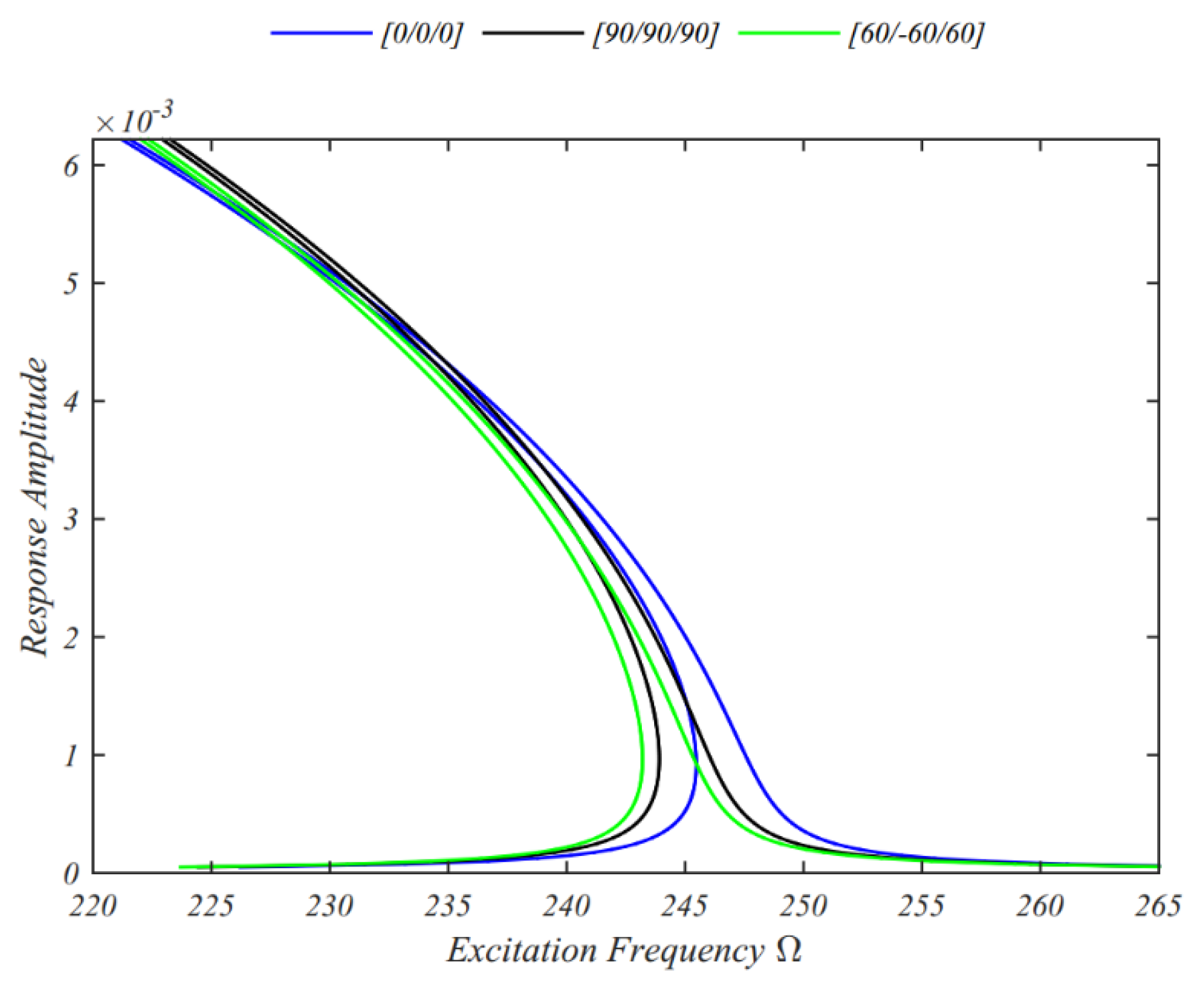

| Material | Properties | |||
|---|---|---|---|---|
| E (GPa) | () | |||
| 348.43 | 2370 | 0.24 | 5.8723 × 10−6 | |
| SUS304 | 201.04 | 8166 | 0.3262 | 12.330 × 10−6 |
| Material Properties (Glass-Polymer Composite) | |||||
|---|---|---|---|---|---|
| (GPa) | () | ||||
| 50, 15.2 | 4.7 | 2000.0 | 0.254 | 6.34 × 10−6 | 23.3 × 10−6 |
| Fundamental Frequency | |||
|---|---|---|---|
| Present Work | Rao [52] | ||
| 50.0 | 507.0912 | 492.2704 | 492.2683 |
| 60.0 | 352.1467 | 341.8544 | 341.8530 |
| 70.0 | 258.7200 | 251.1584 | 251.1573 |
| 80.0 | 198.0825 | 192.2931 | 192.2923 |
| 90.0 | 156.5096 | 151.9353 | 151.9346 |
| 100.0 | 126.7728 | 123.0676 | 123.0671 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alimoradzadeh, M.; Tornabene, F.; Dimitri, R. Nonlinear Aero-Thermo-Elastic Analysis of Laminated Composite Beams with Surface-Bonded FGMs Layers Subjected to a Concentrated Harmonic Load. J. Compos. Sci. 2025, 9, 539. https://doi.org/10.3390/jcs9100539
Alimoradzadeh M, Tornabene F, Dimitri R. Nonlinear Aero-Thermo-Elastic Analysis of Laminated Composite Beams with Surface-Bonded FGMs Layers Subjected to a Concentrated Harmonic Load. Journal of Composites Science. 2025; 9(10):539. https://doi.org/10.3390/jcs9100539
Chicago/Turabian StyleAlimoradzadeh, Mehdi, Francesco Tornabene, and Rossana Dimitri. 2025. "Nonlinear Aero-Thermo-Elastic Analysis of Laminated Composite Beams with Surface-Bonded FGMs Layers Subjected to a Concentrated Harmonic Load" Journal of Composites Science 9, no. 10: 539. https://doi.org/10.3390/jcs9100539
APA StyleAlimoradzadeh, M., Tornabene, F., & Dimitri, R. (2025). Nonlinear Aero-Thermo-Elastic Analysis of Laminated Composite Beams with Surface-Bonded FGMs Layers Subjected to a Concentrated Harmonic Load. Journal of Composites Science, 9(10), 539. https://doi.org/10.3390/jcs9100539









